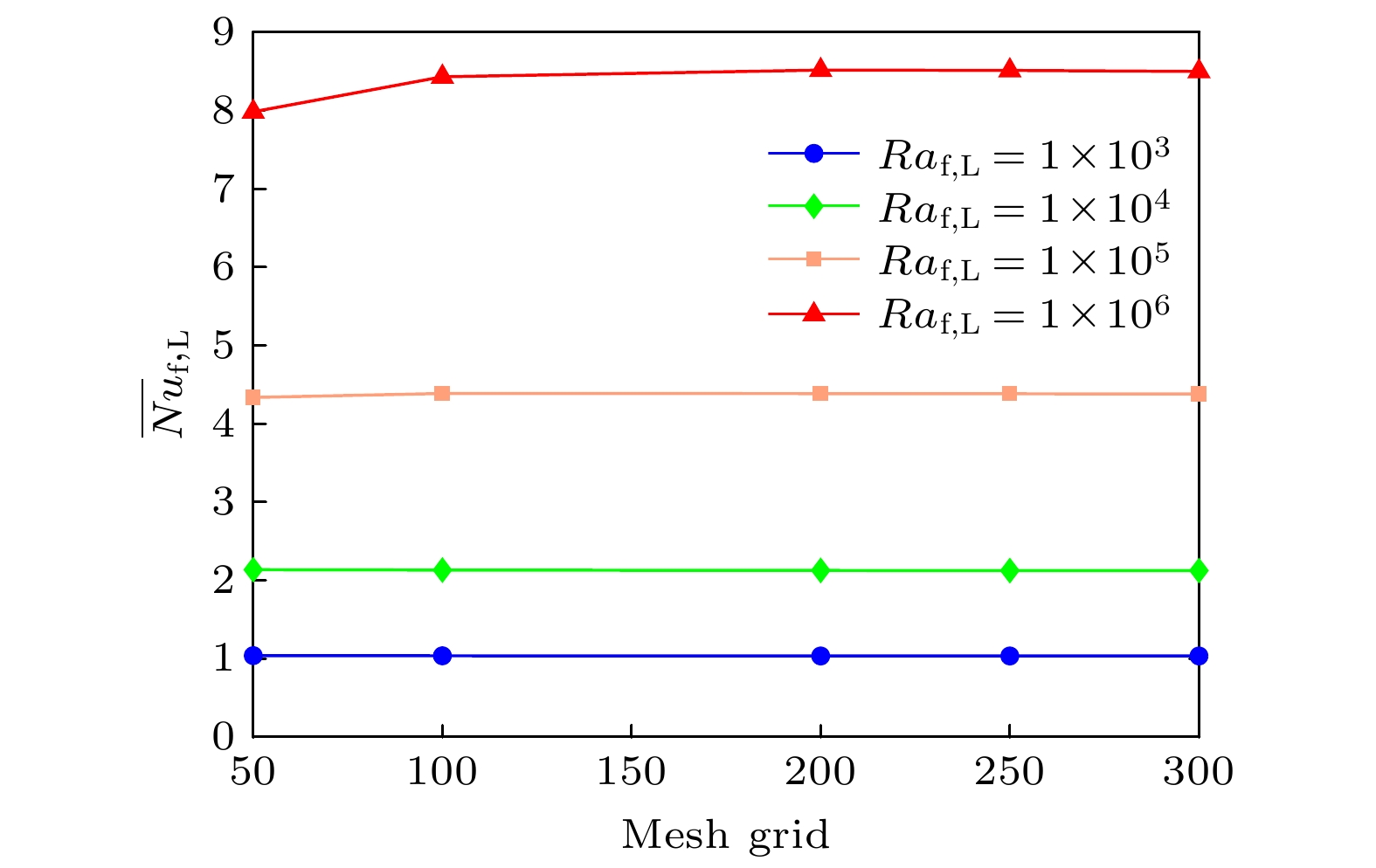
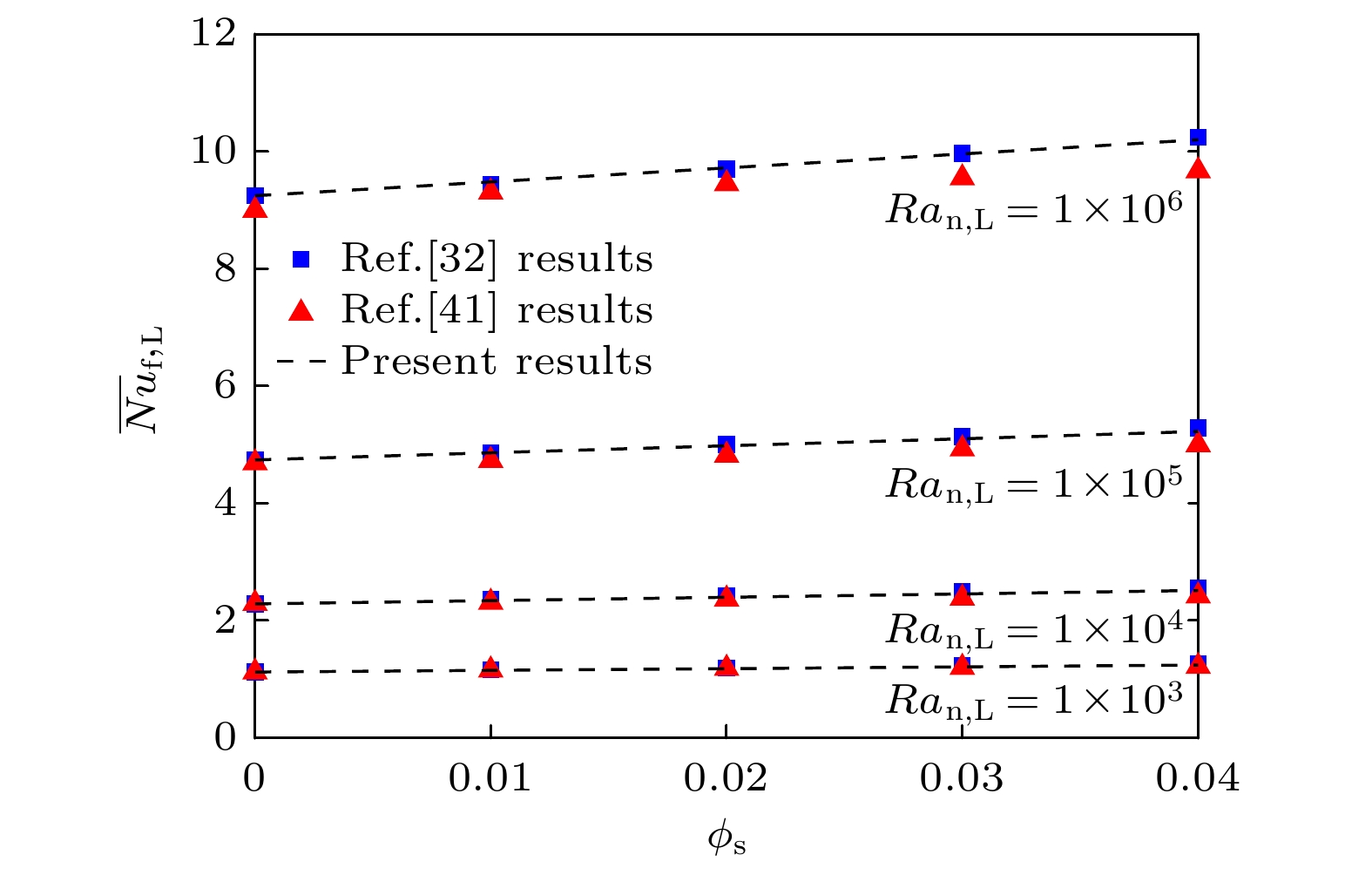
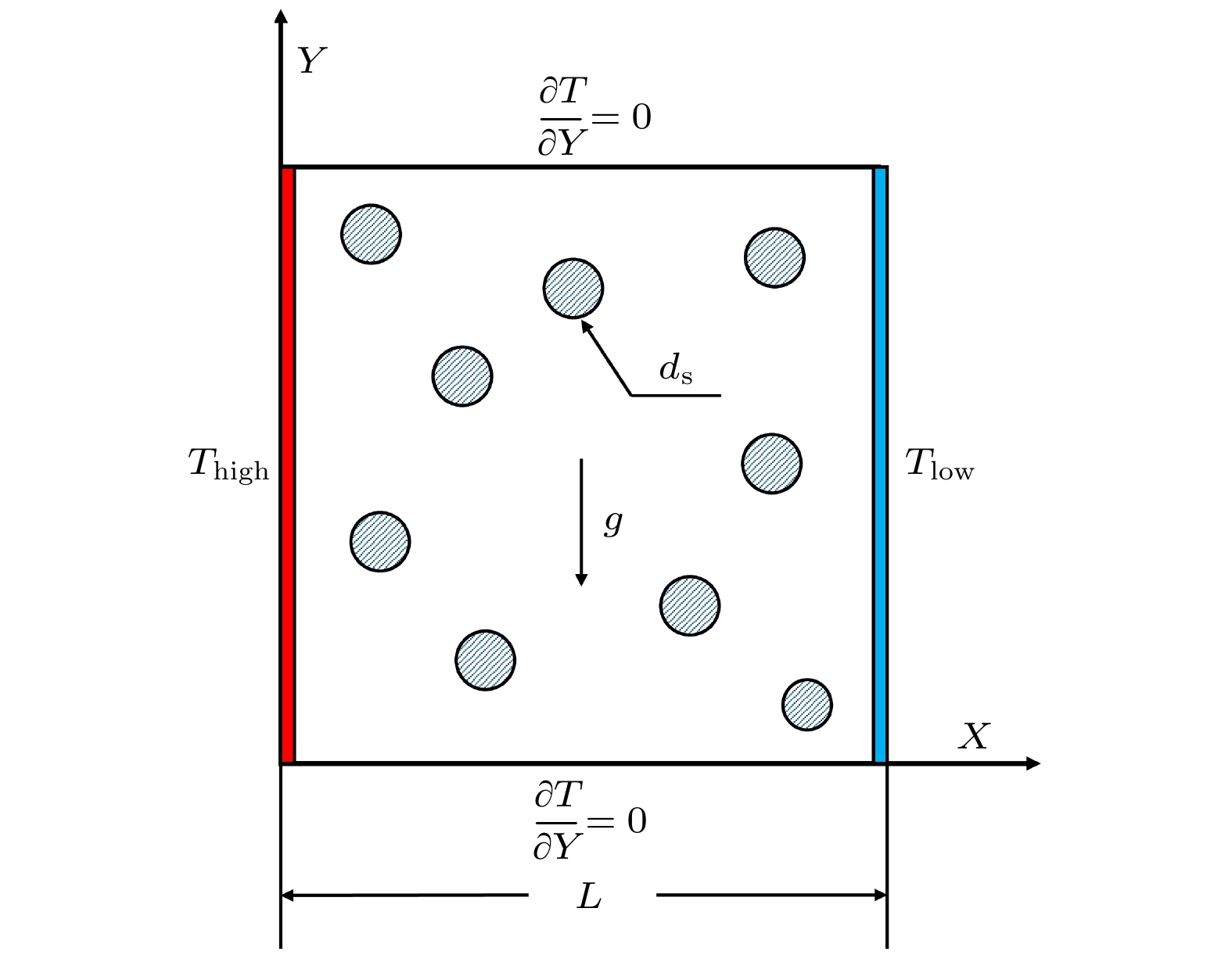
-
In this work, numerical simulation of natural convection of nanofluids within a square enclosure were investigated by using the non-dimensional lattice Boltzmann method (NDLBM). The effects of key governing parameters Knudsen number ($10^{-6} \leqslant Kn_{{\rm{f}},{\rm{s}}} \leqslant 10^4$), Rayleigh number ($10^3 \leqslant Ra_{{\rm{f}},{\rm{L}}} \leqslant 10^6$), and nanoparticle volume fraction ($10^{-2} \leqslant \phi_{\rm{s}} \leqslant 10^{-1}$) on the heat and mass transfer of nanofluids were discussed. The results show that in the low $Ra_{{\rm{f}},{\rm{L}}}$ conductive dominated regime, the nanoparticle size has little effect on heat transfer, whereas in the high $Ra_{{\rm{f}},{\rm{L}}}$ convective dominated regime, larger nanoparticle sizes significantly enhance flow intensity and heat transfer efficiency. As fixed $Ra_{{\rm{f}},{\rm{L}}}$ and $\phi_{\rm{s}}$, the heat transfer patterns change from conduction to convection dominated regimes with increasing $Kn_{{\rm{f}},{\rm{s}}}$. The influence of nanoparticle volume fraction was also investigated, and in convection dominated regime, the maximum heat transfer efficiency was achieved when $\phi_{\rm{s}} = 8 {\text{%}}$, balancing both thermal conduction and drag fore of nanofluids. Additionally, by analyzing the full maps of mean Nusselt number ($\overline {Nu}_{{\rm{f}},{\rm{L}}}$) and the enhancement ratio related to the base fluid ($Re_{{\rm{n}},{\rm{f}}}$), the maximum values of $\overline {Nu}_{{\rm{f}},{\rm{L}}}$ and $Re_{{\rm{n}},{\rm{f}}}$ occur when the nanoparticle size is $Kn_{{\rm{f}},{\rm{s}}} = 10^{-1}$ for both conductive and convective dominated regimes. To capture the effects of all key governing parameters on $\overline {Nu}_{{\rm{f}},{\rm{L}}}$, a new empirical correlation has been derived from the numerical results, providing deeper insights into how these parameters influence heat transfer performance.
-
Keywords:
- Knudsen number /
- Nanofluid /
- Natural convection /
- lattice Boltzmann method
-
图 1 物理模型和边界条件示意图
Figure 1. Sketch of the problem and boundary conditions.
图 2 不同网格数对平均努塞尔数$ \overline{Nu}_{{{\rm{f}}, {\rm{L}}}} $的影响
Figure 2. The influence of different mesh grid on the mean Nusselt number $ \overline{Nu}_{{{\rm{f}}, {\rm{L}}}} $.
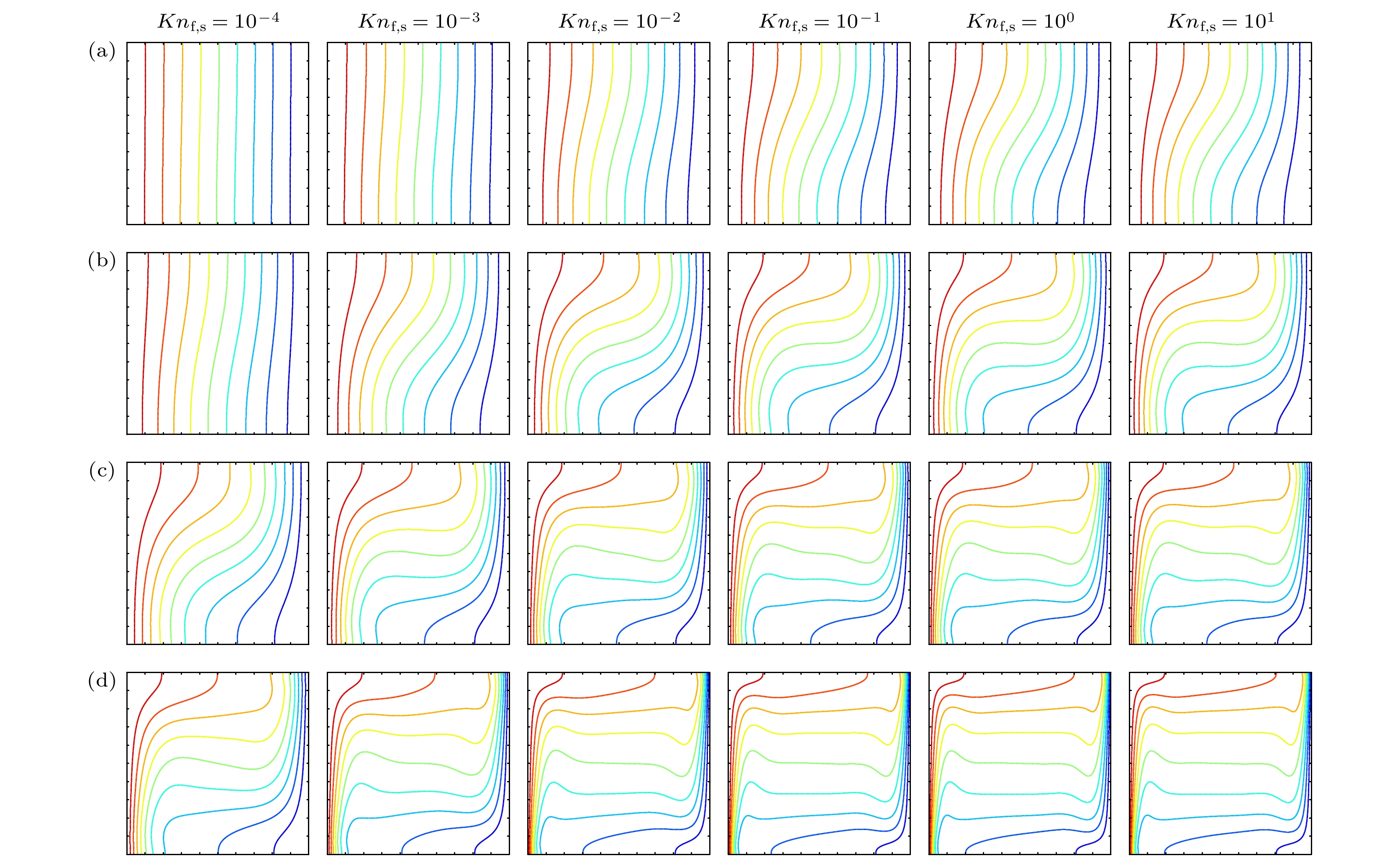
图 4 在固定颗粒体积分数$ \phi_{\rm{s}} = 8 {\text{%}} $, 不同颗粒粒径$ 1 \times 10^{-4} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^2 $和瑞利数$ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $下的无量纲速度场流线分布图像 (a) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{3} $; (b) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{4} $; (c) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{5} $; (d) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{6} $
Figure 4. Dimensionless streamlines for different nanoparticle size $ 1 \times 10^{-4} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^2 $ and Rayleigh number $ 1 \times $$ 10^{3} Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $ with fixed $ \phi_s = 8 {\text{%}} $: (a) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{3} $; (b) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{4} $; (c) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{5} $; (d) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{6} $
图 5 在固定颗粒体积分数$ \phi_{\rm{s}} = 8 {\text{%}} $, 不同颗粒粒径$ 1 \times 10^{-4} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^2 $和瑞利数$ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $下的无量纲温度场等温线分布图像 (a) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{3} $; (b) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{4} $; (c) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{5} $; (d) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{6} $
Figure 5. Dimensionless isotherms for different nanoparticle size $ 1 \times 10^{-4} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^2 $ and Rayleigh number $ 1 \times $$ 10^{3} Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $ with fixed $ \phi_s = 8 {\text{%}} $: (a) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{3} $; (b) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{4} $; (c) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{5} $; (d) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^{6} $
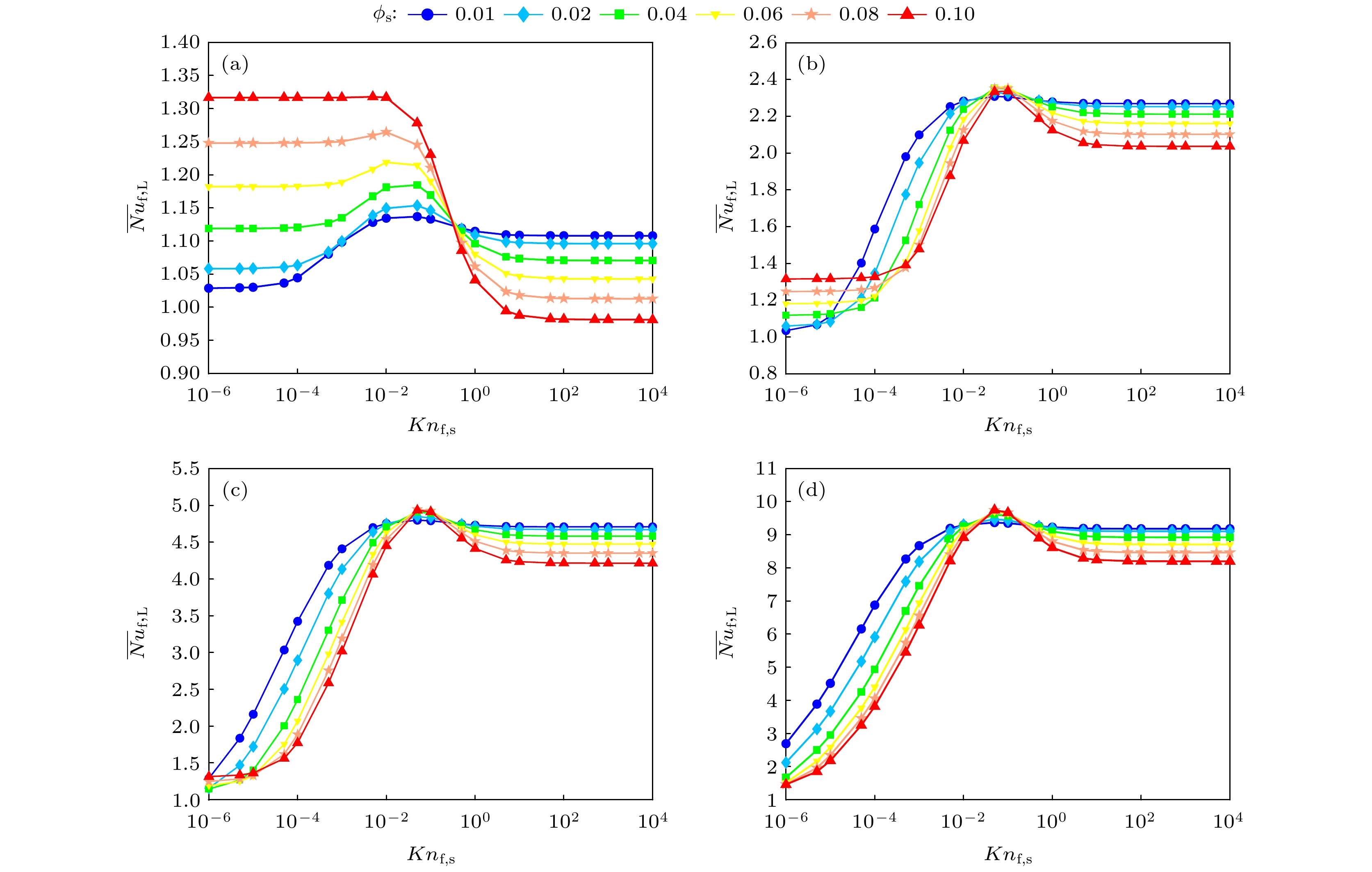
图 6 不同颗粒体积分数和瑞利数下, 平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $与克努森数$ 1 \times 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^4 $关系 (a) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^3 $; (b) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^4 $; (c) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^5 $; (d) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^6 $
Figure 6. The mean Nusselt number $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $ versus Knudsen number $ 1 \times 10^{-6} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^4 $ with different volume fraction and Rayleigh number: (a) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^3 $; (b) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^4 $; (c) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^5 $; (d) $ Ra_{{{\rm{f}}, {\rm{L}}}} = 1 \times 10^6 $.
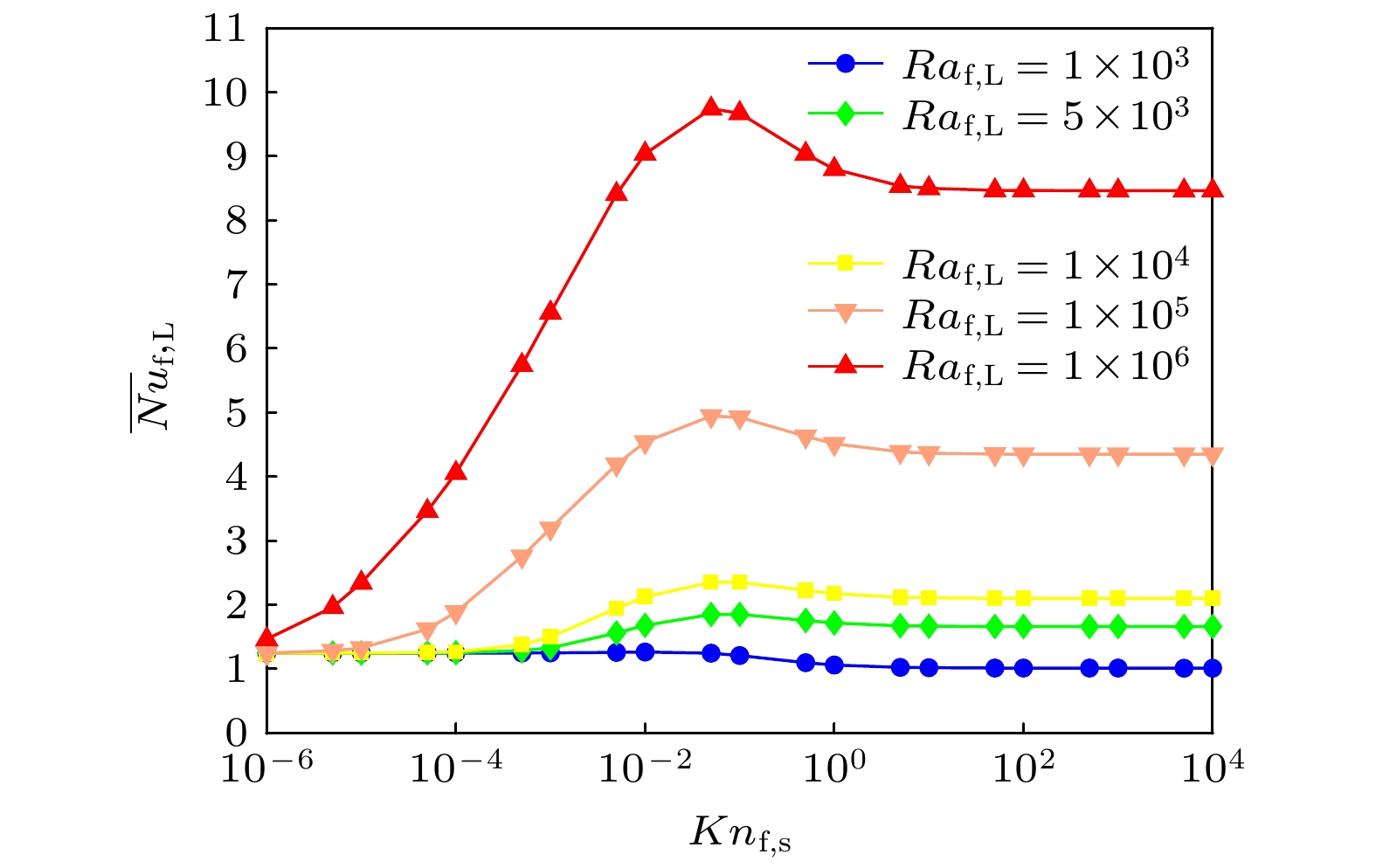
图 7 不同瑞利数$ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $和固定颗粒体积分数$ \phi_{\rm{s}} = 8{\text{%}} $下, 平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $与克努森数关系
Figure 7. The mean Nusselt number $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $ versus Knudsen number with different Rayleigh number $ 1 \times 10^{3} \leqslant $$ Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $ and fixed nanoparticle volume fraction $ \phi_{\rm{s}} = 8{\text{%}} $.
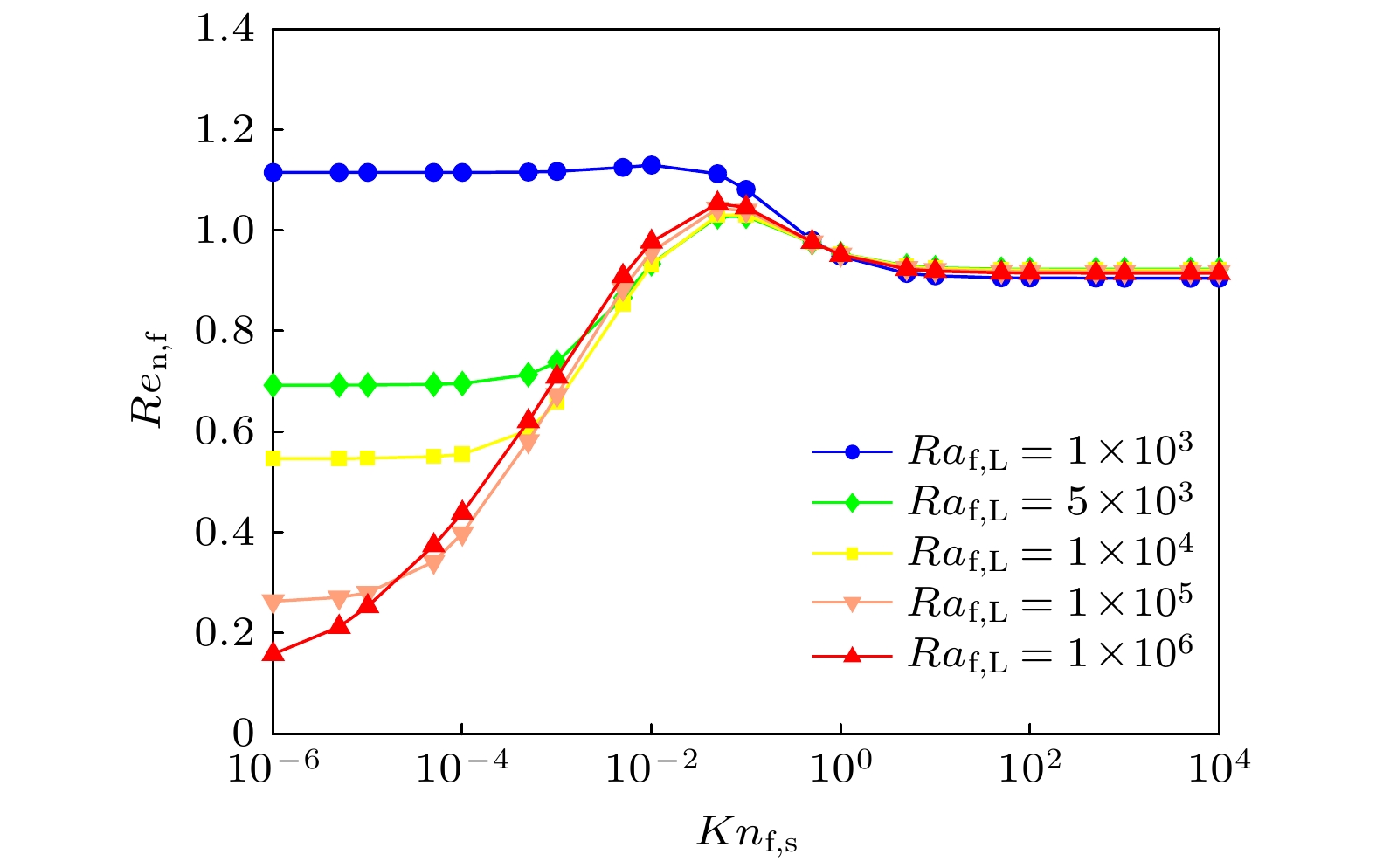
图 8 不同瑞利数$ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $和固定颗粒体积分数$ \phi_{\rm{s}} = 8{\text{%}} $下, 纳米流体相较于基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $与克努森数关系
Figure 8. The enhancement ratio $ Re_{{\rm{n}}, {\rm{f}}} $ versus Knudsen number with different Rayleigh number $ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant $$ 1 \times 10^6 $ and fixed nanoparticle volume fraction $ \phi_{\rm{s}} = 8{\text{%}} $.
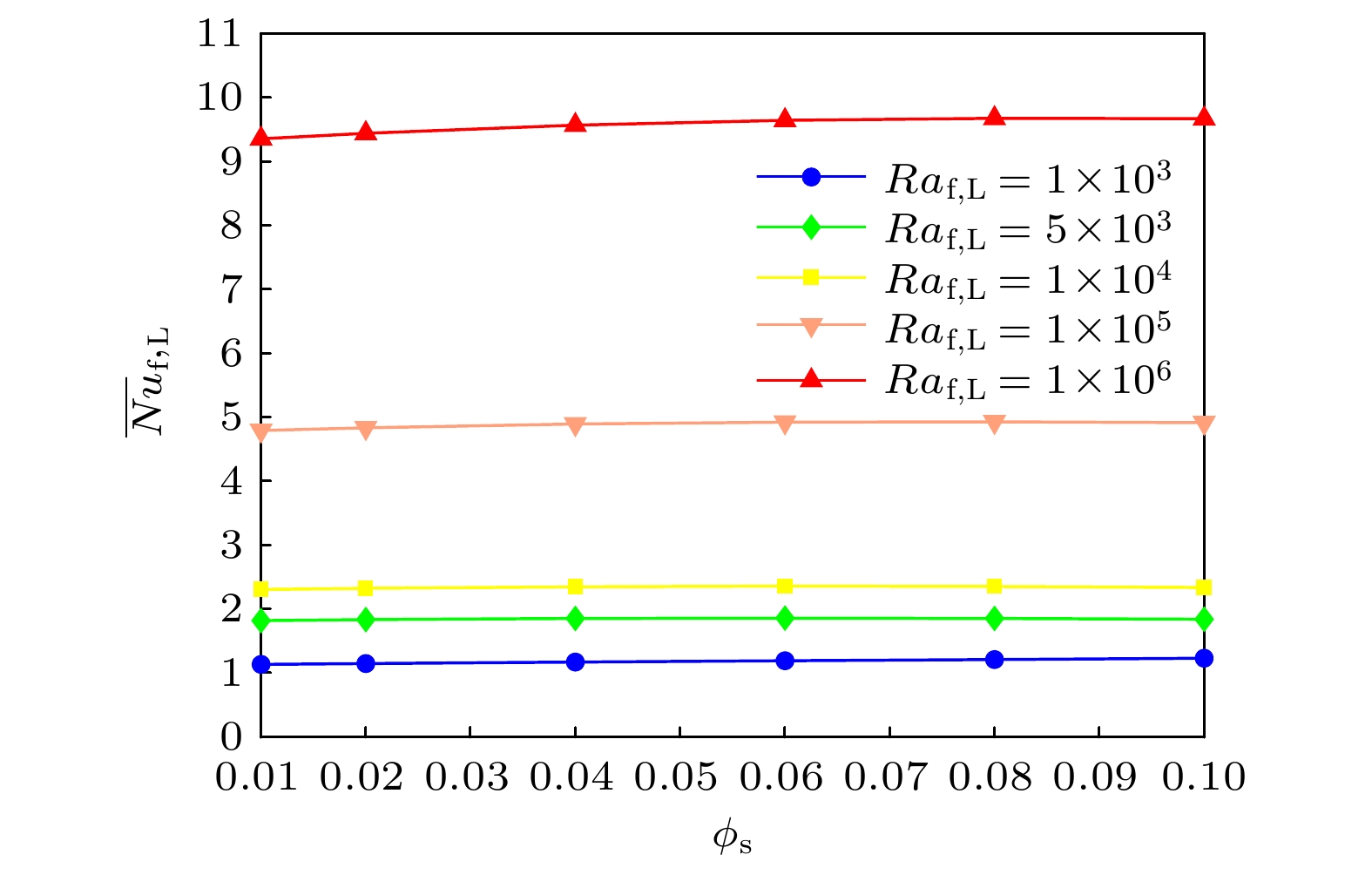
图 9 不同瑞利数$ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $和固定颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $下, 平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $与颗粒体积分数关系
Figure 9. The mean Nusselt number $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $ versus nanoparticle volume fraction with different Rayleigh number $ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $ and fixed nanoparticle size $ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $.
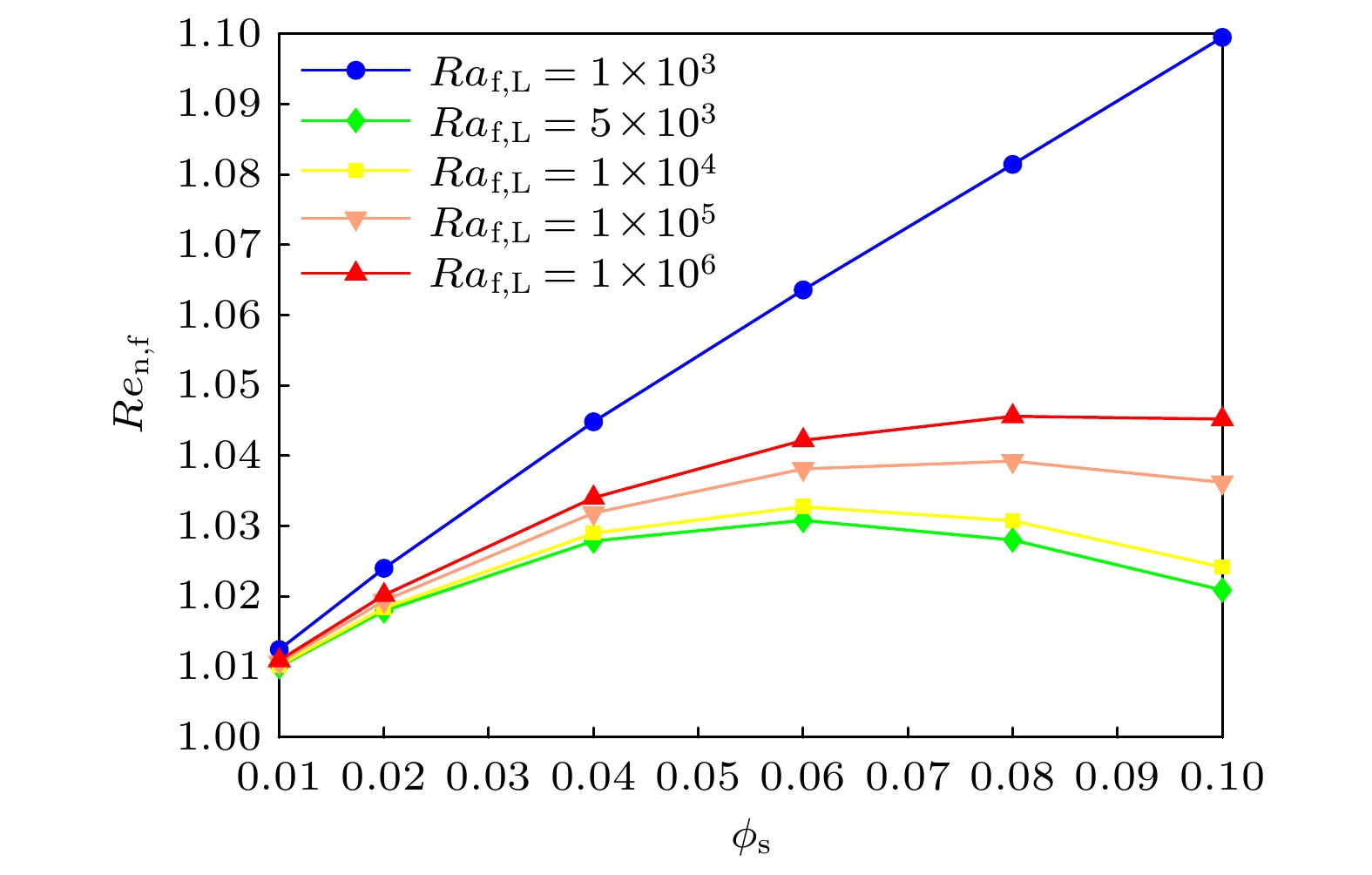
图 10 不同瑞利数$ 1 \times 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $和固定颗粒粒径$ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $下, 纳米流体相较于基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $与颗粒体积分数关系
Figure 10. The enhancement ratio $ Re_{{\rm{n}}, {\rm{f}}} $ versus nanoparticle volume fraction with different Rayleigh number $ 1 \times $$ 10^{3} \leqslant Ra_{{{\rm{f}}, {\rm{L}}}} \leqslant 1 \times 10^6 $ and fixed nanoparticle size $ Kn_{{\rm{f}}, {\rm{s}}} = 10^{-1} $.
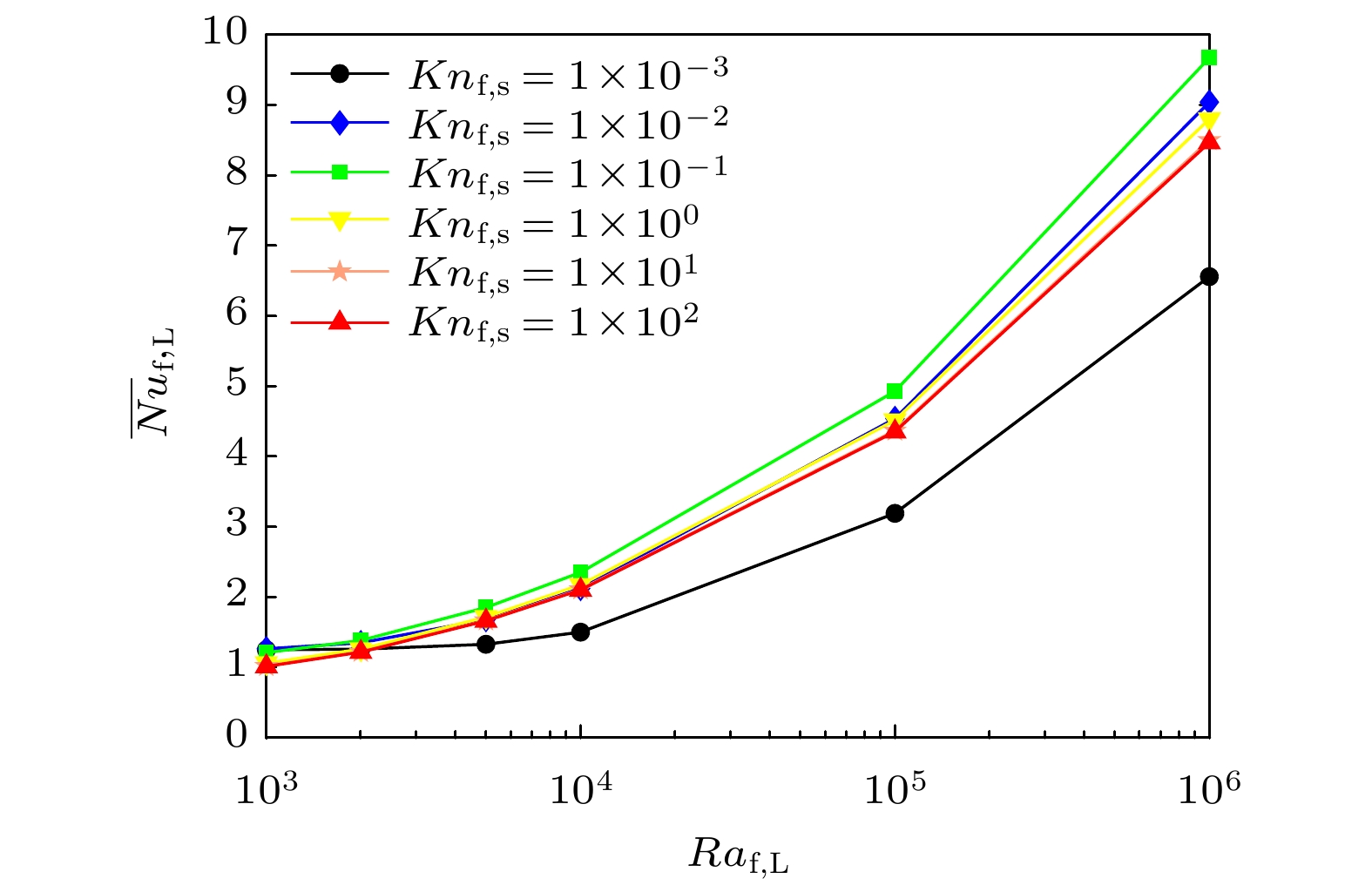
图 11 不同克努森数$ 1 \times 10^{-3} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^2 $和固定颗粒体积分数$ \phi_{\rm{s}} = 8 {\text{%}} $下, 平均努塞尔数$ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $与瑞利数关系
Figure 11. The mean Nusselt number $ \overline {Nu}_{{{\rm{f}}, {\rm{L}}}} $ versus Rayleigh number with different Knudsen number $ 1 \times 10^{-3} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant $$ 1 \times 10^2 $ and fixed nanoparticle volume fraction $ \phi_{\rm{s}} = 8 {\text{%}} $.
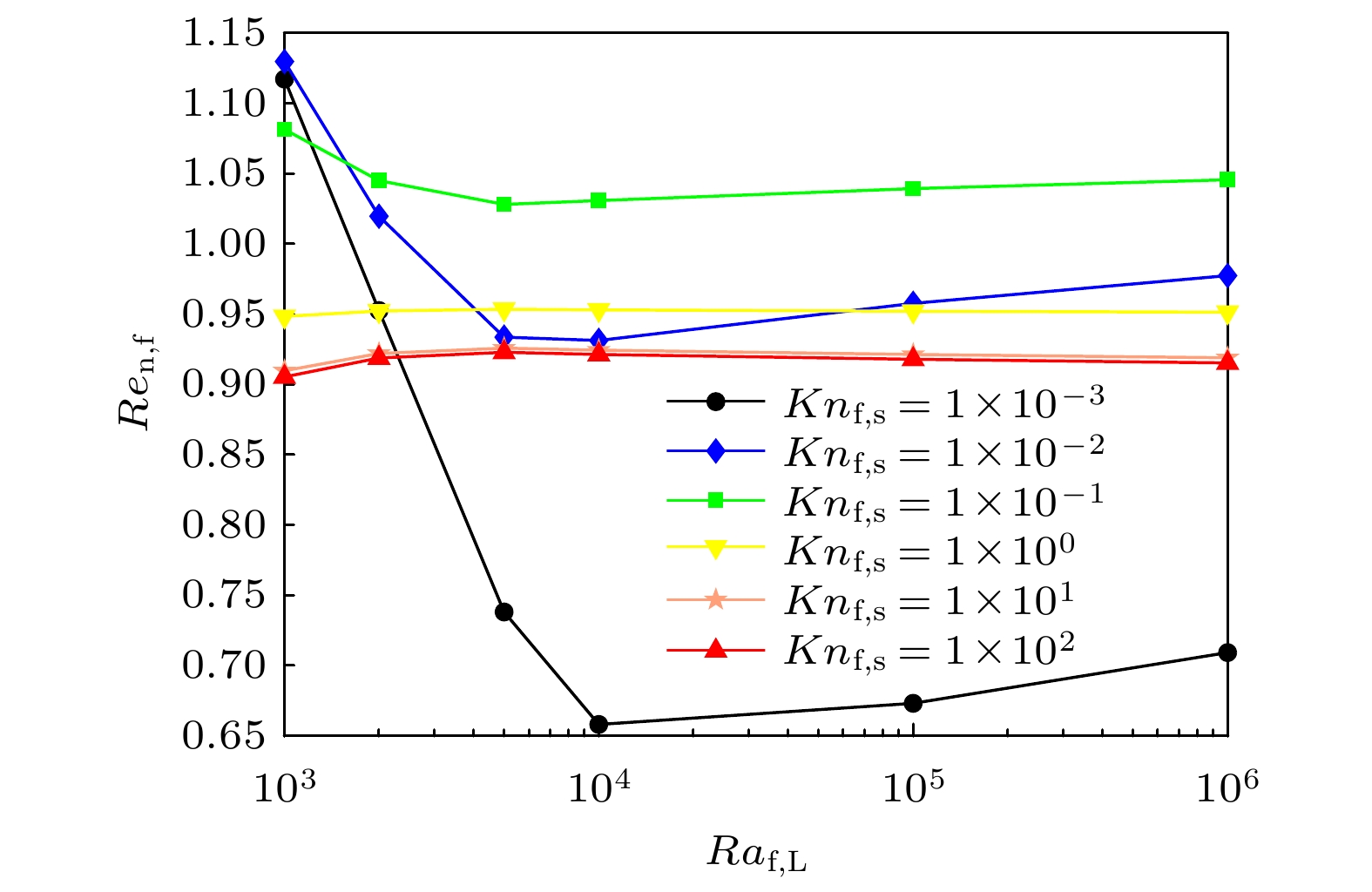
图 12 不同克努森数$ 1 \times 10^{-3} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant 1 \times 10^2 $和固定颗粒体积分数$ \phi_{\rm{s}} = 8 {\text{%}} $下, 纳米流体相较于基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $与瑞利数关系
Figure 12. The enhancement ratio $ Re_{{\rm{n}}, {\rm{f}}} $ versus Rayleigh number with different Knudsen number $ 1 \times 10^{-3} \leqslant Kn_{{\rm{f}}, {\rm{s}}} \leqslant $$ 1 \times 10^2 $ and fixed nanoparticle volume fraction $ \phi_{\rm{s}} = 8 {\text{%}} $.
图 13 全参数范围下平均努塞尔数的对数函数$ \lg (\overline {Nu}_{{{\rm{f}}, {\rm{L}}}}) = $$ l \lg (\dfrac{{{k_{\rm{n}}}}}{{{k_{\rm{f}}}}}\overline {Nu}_{{{\rm{n}}, {\rm{L}}}}) $ (a) 和纳米流体相较基液传热增加率$ Re_{{\rm{n}}, {\rm{f}}} $ (b) 随不同克努森数$ Kn_{{\rm{f}}, {\rm{s}}} $、瑞利数$ Ra_{{{\rm{f}}, {\rm{L}}}} $、颗粒体积分数$ \phi_{\rm{s}} $变化的三维等值面图
Figure 13. The three dimensional isosurfaces of logarithmic function of mean Nusselt number $ \lg (\overline {Nu}_{{{\rm{f}}, {\rm{L}}}}) = \lg (\dfrac{{{k_{\rm{n}}}}}{{{k_{\rm{f}}}}}\overline {Nu}_{{{\rm{n}}, {\rm{L}}}}) $ (a) and enhancement ratio $ Re_{{\rm{n}}, {\rm{f}}} $ (b) over the full parameter range as a function of Knudsen number $ Kn_{{\rm{f}}, {\rm{s}}} $, Rayleigh number $ Ra_{{{\rm{f}}, {\rm{L}}}} $, and nanoparticle volume fraction $ \phi_{\rm{s}} $.
-
[1] Wang X, Song Y, Li C, Zhang Y, Ali HM, Sharma S, Li R, Yang M, Gao T, Liu M, Cui X, Said Z, Zhou Z 2024 Int. J. Adv. Manuf. Technol. 131 3113
Google Scholar
[2] Sandhya M, Ramasamy D, Sudhakar K, Kadirgama K, Samykano M, Harun WSW, Najafi G, Mofijur M, Mazlan M 2021 Sustain. Energy Technol. Assess. 44 101058
[3] Said Z, Sundar LS, Tiwari AK, Ali HM, Sheikholeslami M, Bellos E, Babar H 2022 Phys. Rep. 946 1
Google Scholar
[4] Smaisim GF, Mohammed DB, Abdulhadi AM, Uktamov KF, Alsultany FH, Izzat SE, Ansari MJ, Kzar HH, Al-Gazally ME, Kianfar E 2022 J. Sol-Gel Sci. Technol. 104 1
Google Scholar
[5] 肖波齐, 范金土, 蒋国平, 陈玲霞 2012 61 317
Google Scholar
Xiao B, Fan J, Jiang G, Chen L 2012 Acta Phys. Sin. 61 317
Google Scholar
[6] Azmi WH, Sharma KV, Mamat R, Najafi G, Mohamad MS 2016 Renewable Sustainable Energy Rev. 53 1046
Google Scholar
[7] Wang X, Xu X, Choi SUS 1999 J. Thermophys. Heat Transfer 13 474
Google Scholar
[8] Das SK, Putra N, Thiesen P, Roetzel W 2003 J. Heat Transfer 125 567
Google Scholar
[9] Nguyen CT, Desgranges F, Galanis N, Roy G, Mare T, Boucher S, Minsta HA 2008 Int. J. Therm. Sci. 47 103
Google Scholar
[10] Maxwell JC 1982 A Treatise on Electricity and Magnetism (Vol. 2) (London Oxford University Press) pp 173-215
[11] Nan CW, Shi Z, Lin Y 2003 Chem. Phys. Lett. 375 666
Google Scholar
[12] Mintsa HA, Roy G, Nguyen CT, Doucet D 2009 Int. J. Therm. Sci. 48 363
Google Scholar
[13] Brinkman HC 1952 J. Chem. Phys. 20 571
Google Scholar
[14] Batchelor GK 1977 J. Fluid Mech. 83 97
Google Scholar
[15] Nguyen CT, Desgranges F, Roy G, Galanis N, Mare T, Boucher S, Minsta HA 2007 Int. J. Heat Fluid Flow 28 1492
Google Scholar
[16] Majumdar A 1993 J. Heat Transfer 115 7
Google Scholar
[17] Mazumder S, Majumdar A 2001 J. Heat Transfer 123 749
Google Scholar
[18] Su Y, Davidson JH 2018 Int. J. Heat Mass Transfer 127 303
Google Scholar
[19] Chambre PA, Schaaf SA 1961 Flow of Rarefied Gases (Princeton University Press) pp 78-146.
[20] Sui P, Su Y, Sin V, Davidson JH 2022 Int. J. Heat Mass Transfer 187 122541
Google Scholar
[21] Zarki A, Ghalambaz M, Chamkha AJ, Ghalambaz M, Rossi DD 2015 Adv. Powder Technol. 26 935
Google Scholar
[22] Sabour M, Ghalambaz M, Chamkha A 2017 Int. J. Numer. Methods Heat Fluid Flow 27 1504
Google Scholar
[23] Paul TC, Morshed A, Fox EB, Khan JA 2017 Int. J. Heat Mass Transfer 28 753
[24] Liu F, Wang L 2009 Int. J. Heat Mass Transfer 52 5849
Google Scholar
[25] Zahmatkesh I, Sheremet M, Yang L, Heris SZ, Sharifpur M, Meyer JP, Ghalambaz M, Wongwises S, Jing D, Mahian O 2021 J. Mol. Liq. 321 114430
Google Scholar
[26] Trodi A, Benhamza MEH 2017 Chem. Eng. Commun. 204 158
Google Scholar
[27] Sheikhzadeh GA, Aghaei A, Soleimani S 2018 Challenges Nano Micro Scale Sci. Technol. 6 27
[28] Dogonchi AS, Hashemi-Tilehnoee M, Waqas M, Seyyedi SM, Animasaun IL, Ganji DD 2020 Phys. A (Amsterdam, Neth.) 540 123034
Google Scholar
[29] Tarokh A, Mohamad A, Jiang L 2013 Numer. Heat Transfer, Part A 63 159
Google Scholar
[30] 张贝豪, 郑林 2020 69 164401
Google Scholar
Zhang B, Zheng L 2020 Acta Phys. Sin. 69 164401
Google Scholar
[31] Su Y, Sui P, Davidson JH 2022 Renew. Energy 184 712
Google Scholar
[32] Lai F, Yang Y 2011 Int. J. Therm. Sci. 50 1930
Google Scholar
[33] Sheikholeslami M, Gorji-Bandpy M, Domairry G 2013 Appl. Math. Mech. 34 833
Google Scholar
[34] 齐聪, 何光艳, 李意民, 何玉荣 2015 64 328
Google Scholar
Qi C, He G, Li Y, He Y 2015 Acta Phys. Sin. 64 328
Google Scholar
[35] Taher MA, Kim HD, Lee YW 2017 Heat Transfer Res. 48 1025
Google Scholar
[36] 袁俊杰, 叶欣, 单彦广 2021 计算物理 38 57
Yuan J, Ye X, Shan Y 2021 Chinese Journal of Computational Physics 38 57
[37] Ganji DD, Malvandi A 2014 Powder Technol. 263 50
Google Scholar
[38] Hwang KS, Lee JH, Jang SP 2009 Int. J. Heat Mass Transfer 50 4003
[39] Wang D, Cheng P, Quan X 2019 Int. J. Heat Mass Transfer 130 1358
Google Scholar
[40] Hua YC, Cao BY 2016 Int. J. Heat Mass Transfer 92 995
Google Scholar
[41] Ho CJ, Chen MW, Li ZW 2008 Int. J. Heat Mass Transfer 51 4506
Google Scholar
[42] Li CH, Peterson GP 2007 J. Appl. Phys. 101 044312
Google Scholar
[43] Chon CH, Kihm KD, Lee SP 2005 Appl. Phys. Lett. 87 153107
Google Scholar
DownLoad:
Metrics
- Abstract views: 240
- PDF Downloads: 8
- Cited By: 0
