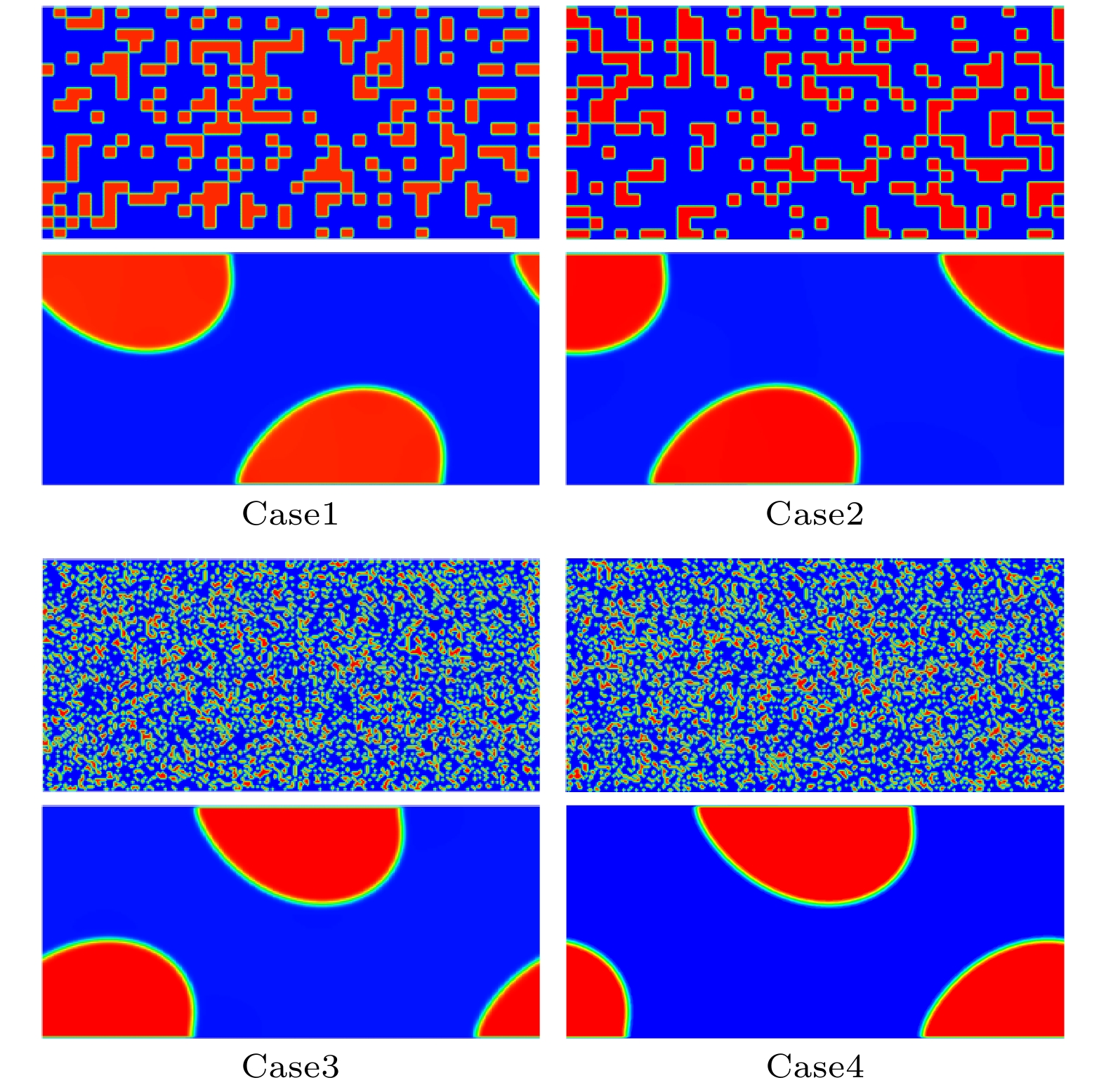
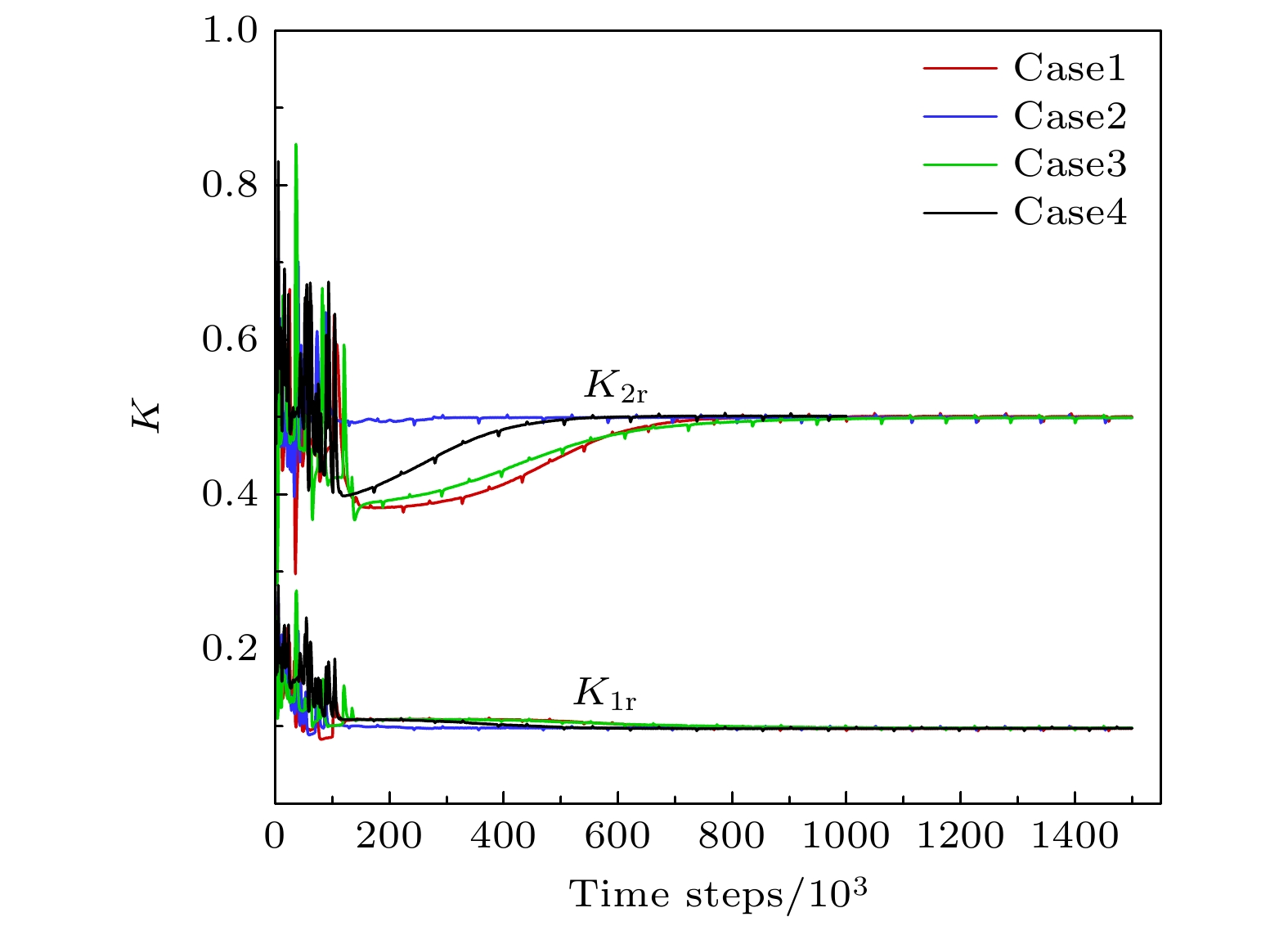
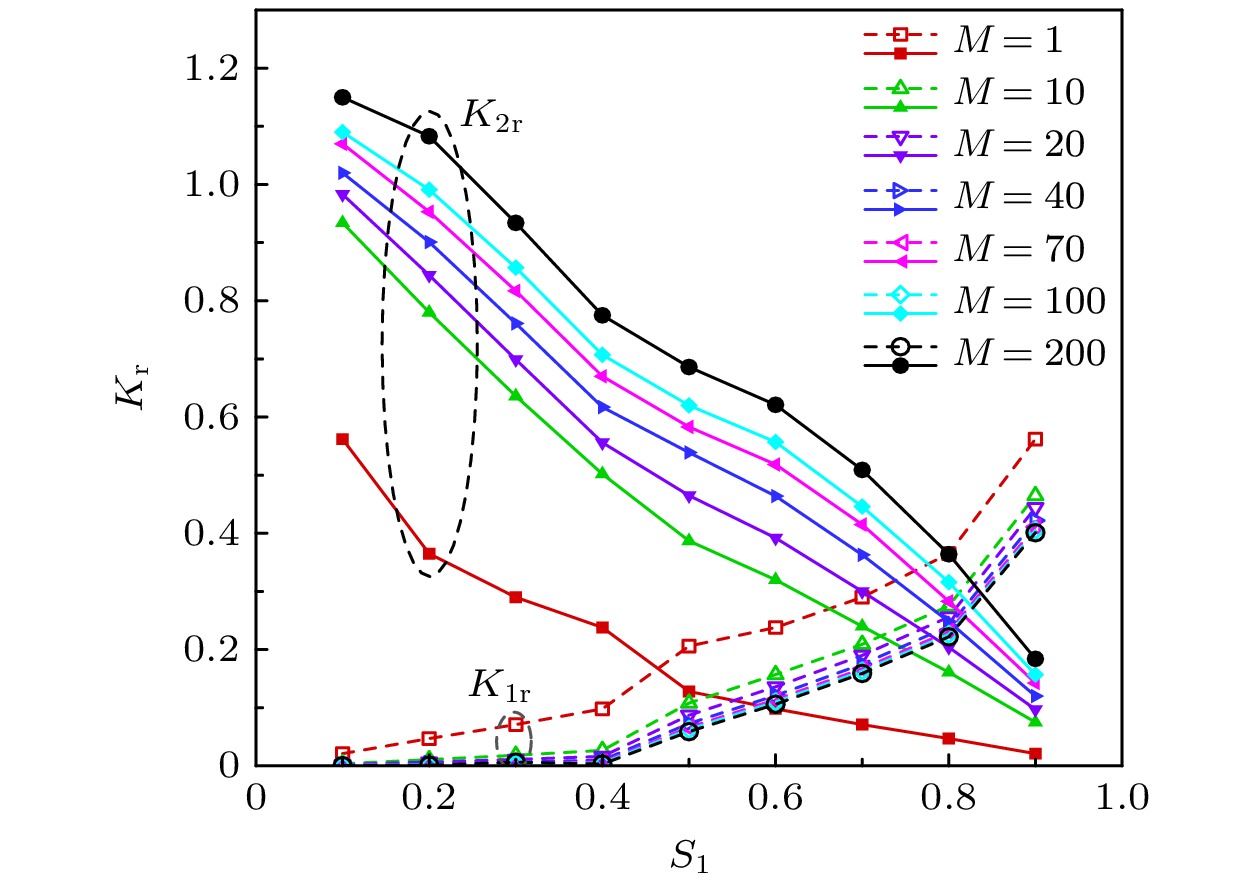
-
Immiscible two-phase flow exists in many fields such as the chemical engineering, energy engineering, and geography. It is of great significance in enhancing the oil recovery and geological carbon dioxide storage. Relative permeability is a comprehensive reflection of the effects of various factors including the saturation, contact angle, viscosity ratio, and capillary number of immiscible two-phase flow, and it is a key parameter describing such a flow and thus can directly reflect the flow capacity of each phase. As a new fluid numerical calculation method, the lattice Boltzmann method (LBM) has its own unique advantage in simulating various flows because it does not need to capture the phase interface, and thus has been widely used in recent years. In this research, the multi-relaxation time multi-component pseudopotential lattice Boltzmann method is improved to make it possible to solve the two-phase relative permeability under high viscosity ratios. It is known that the LBM is a particle-based hydrodynamic method, with the spontaneous diffusion of components in multi-component system inevitably causing a mixing between components, leading to distortion of the velocity of two-phase flow with a high viscosity ratio. The color gradient model is introduced into the pseudopotential model for the treatment of mixing, the multiple relaxation time is employed to improve the numerical stability and viscosity ratio range, and the numerical distortion caused by mixing is therefore resolved. The resulting model is validated by the use of the two-phase layered flow in a 2D infinite channel, and accurate numerical results are obtained even if the viscosity ratio reaches 1000. Based on the improved model, the two-phase flow in a two-dimensional horizontal channel is analyzed and the effects of saturation, viscosity ratio, wettability and capillary number on relative permeability and phase permeation curves are investigated. The results show that the relative permeability of the high-viscosity phase increases with the increase of the viscosity ratio, and the saturation range for maintaining high flow capacity broadens with the increase of the low-viscosity phase. There is a limit for the influence of viscous coupling effect on the relative permeability of two phases: at a certain saturation, the relative permeability of the small viscosity phase has a minimum value while that of the large viscosity phase has a maximum value, the viscous coupling effect will never make the relative permeability of the small viscosity phase to be lower than the minimum value and that of the large viscosity phase to be higher than the maximum value. Non-wetting condition plays a role in increasing the flow capacity and relative permeability of the high-viscosity phase, while the wetting condition can weaken the flow capability, relative permeability of the high-viscosity phase. When the high-viscosity phase is a non-wetting phase, the decrease of the contact area with the solid wall increases its proportion in the middle flow passage, which enables it to maintain a strong flow capability in a wide saturation range. Wall wetting tends to inhibit fluid flow and consequently reduce the relative permeability. The increase of the capillary number may cause a more obvious contact angle hysteresis effect, which reduces the relative permeability of two phases.
-
Keywords:
- two-phase flow /
- relative permeability /
- viscosity ratio /
- lattice Boltzmann method
[1] Zhao H, Ning Z, Kang Q, Chen L, Zhao T 2017 Int. Commun. Heat Mass 85 53
Google Scholar
[2] Zhang D, Papadikis K, Gu S 2016 Adv. Water Resour. 95 61
Google Scholar
[3] Dullien F A L, Dong M 1996 Transport Porous Med. 25 97
Google Scholar
[4] Bentsen R G, Manai A A 1993 Transport Porous Med. 11 243
Google Scholar
[5] Akbarabadi M, Piri M 2013 Adv. Water Resour. 52 190
Google Scholar
[6] Hao L, Cheng P 2010 Int. J. Heat Mass Tran. 53 1908
Google Scholar
[7] Li Z, Chen T, Ning Y, Zhang K, Guan Q 2019 Qin SPE Middle East Oil and Gas Show and Conference, Bahrain, March 18–21, 2019 SPE-194770-MS
[8] Wang J, Dong M, Asghari K 2006 SPE/DOE Symposium on Improved Oil Recovery, USA, April 22–26, 2006 SPE-99763-MS
[9] Inamuro T, Ogata T, Tajima S, Konishi N 2004 J. Comput. Phys. 198 628
Google Scholar
[10] Rothman D H, Keller J M 1988 J. Stat. Phys. 52 1119
Google Scholar
[11] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[12] Swift M R, Orlandini E, Osborn W R, Yeomans J M 1996 Phys. Rev. E 54 5041
Google Scholar
[13] He X, Shan X, Doolen G D 1998 Phys. Rev. E 57 R13
[14] Ramstad T, Øren P E, Bakke S 2010 SPE J. 15 917
Google Scholar
[15] Liu T, Wang M 2022 Transport Porous Med. 144 111
Google Scholar
[16] Li H, Pan C, Miller C T 2005 Phys. Rev. E 72 026705
Google Scholar
[17] Yiotis A G, Psihogios J, Kainourgiakis M E, Papaioannou A, Stubos A K 2007 Colloid. Surface. A 300 35
Google Scholar
[18] Huang H, Li Z, Liu S, Lu X Y 2009 Int. J. Numer. Meth. Fl. 61 341
Google Scholar
[19] Ghassemi A, Pak A 2011 J. Petrol Sci. Eng. 77 135
Google Scholar
[20] Gao C, Xu R N, Jiang P X 2015 Int. J. Numer. Meth Fl. 25 1957
[21] Dou Z, Zhou Z F 2013 Int. J. Heat Fluid Fl. 42 23
Google Scholar
[22] Zhang D, Li S, Jiao S, Shang Y, Dong M 2019 Int. J. Heat Mass Tran. 134 311
Google Scholar
[23] Li S, Jiang F, Wei B, Hou J, Liu H 2021 Phys. Fluids 33 063302
Google Scholar
[24] Huang H, Sukop M, Lu X 2015 Multiphase Lattice Boltzmann Methods: Theory and Application (Oxford: Wiley Blackwell) pp96–99
[25] Guo Z, Zheng C, Shi B 2008 Phys. Rev. E 77 036707
Google Scholar
[26] Zheng J, Chen Z, Xie C, Wang Z, Lei Z, Ju Y, Wang M 2018 Comput. Fluids 168 21
Google Scholar
-
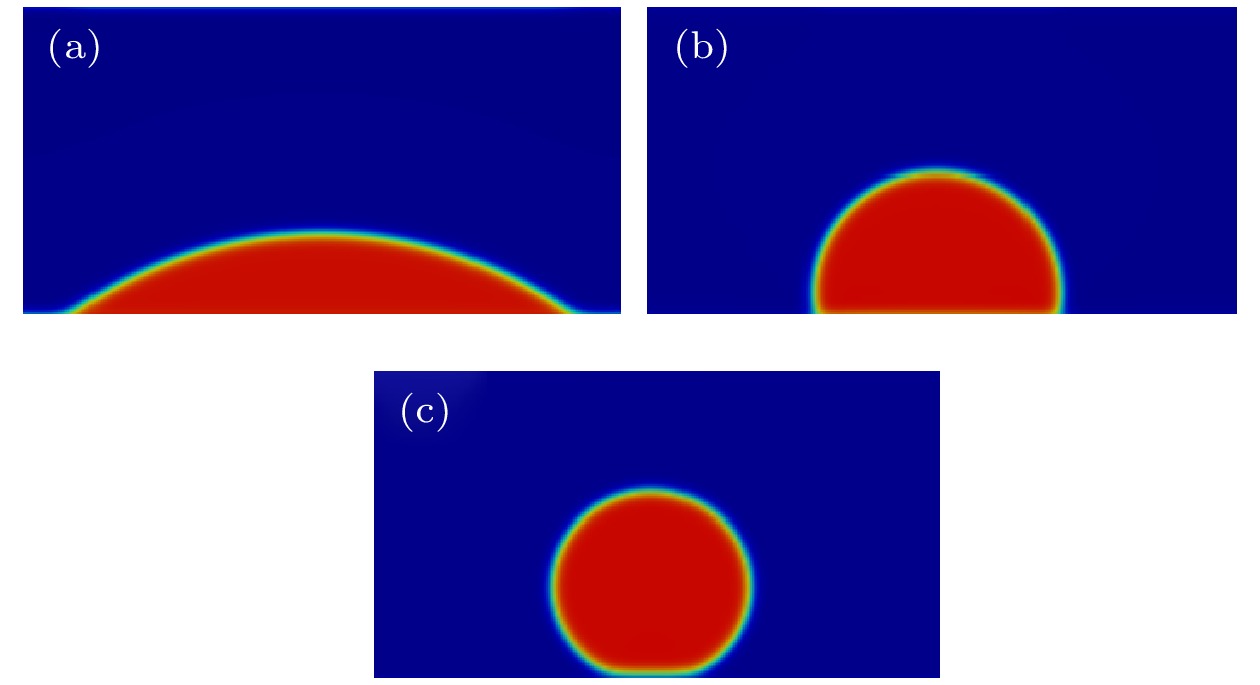
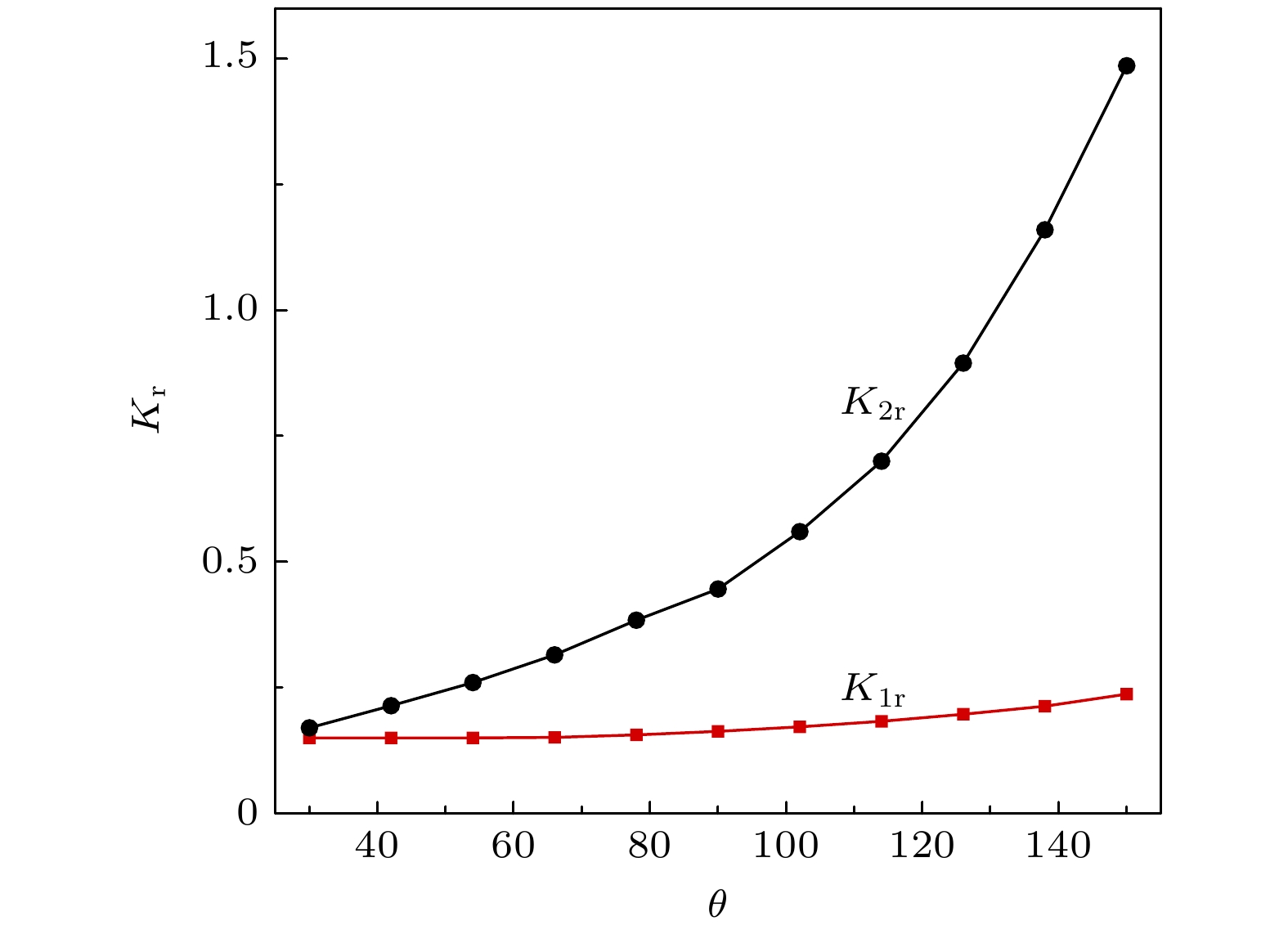
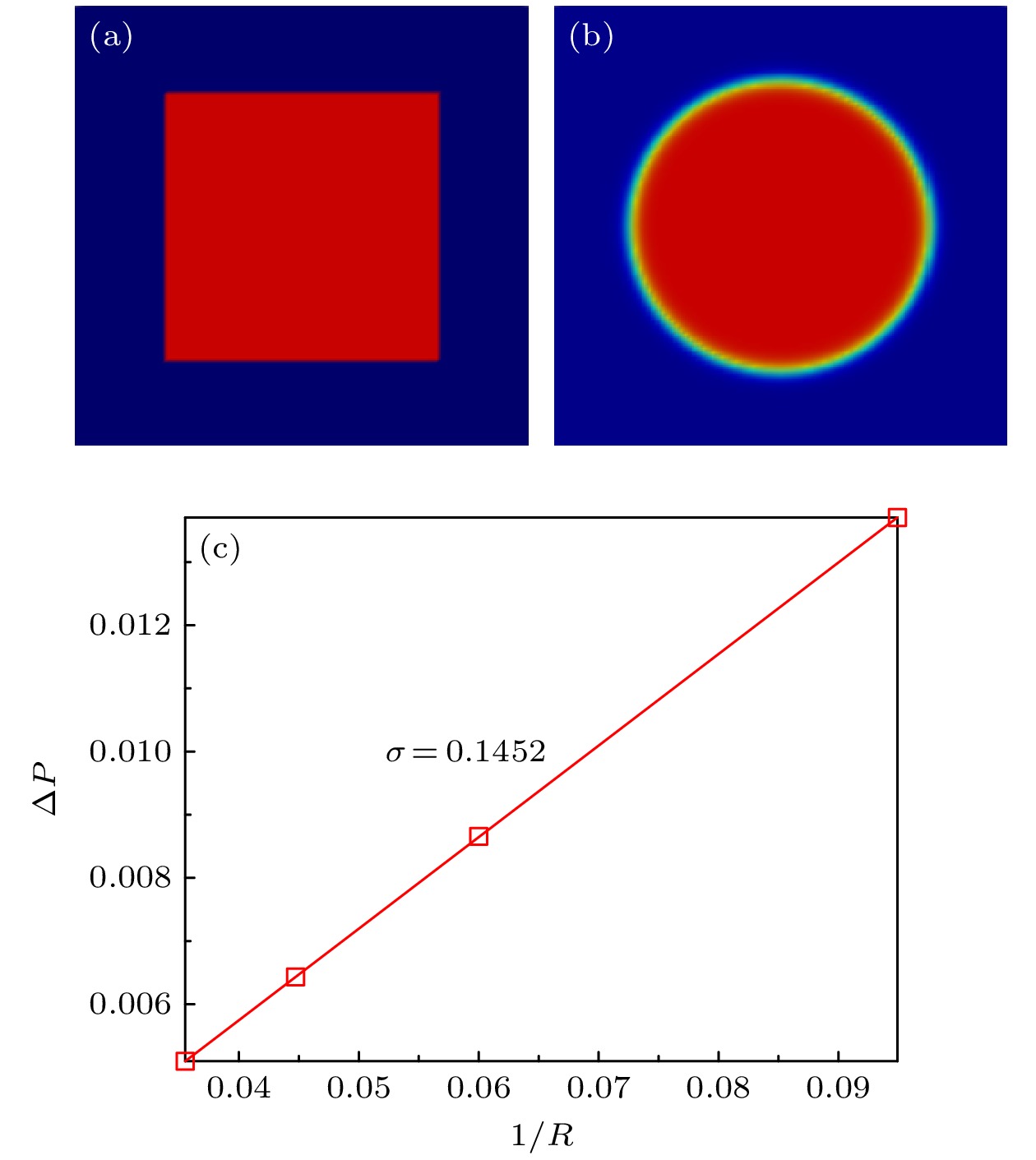
图 1 两组分表面张力验证结果 (a), (b) 方形液滴在表面张力的作用下逐渐变为圆形液滴; (c) 液滴内外的压力差与曲率半径的线性关系
Figure 1. The verification of two-component surface tension: (a), (b) The square drops gradually become round drops under the action of surface tension; (c) linear relationship between the pressure difference inside and outside the droplet and the radius of curvature.
图 2 不同接触角的模拟结果 (a) θ = 30°; (b) θ = 90°; (c) θ = 150°
Figure 2. Simulation results of the different contact angles: (a) θ = 30°; (b) θ = 90°; (c) θ = 150°.
图 3 二维直通道示意图
Figure 3. 2D horizontal channel diagram.
图 4 二维无限长直通道相对渗透率曲线 (a) M = 10; (b) M = 100; (c) M = 1000
Figure 4. Relative permeability curves of 2D infinite horizontal channel: (a) M = 10; (b) M = 100; (c) M = 1000.
图 5 不同随机初始化和最终相分布的演化结果
Figure 5. Evolution results of different random initializations and final phase distributions.
图 6 不同随机初始化情况下相对渗透率随计算时间的变化
Figure 6. Variation of relative permeability with time under different random initialization conditions.
图 7
$ {S}_{1}=0.7 $ 时, 不同黏度比下的流动形态(a1)—(a5)和速度分布(b1)—(b5) (a1), (b1) M = 1; (a2), (b2) M = 20; (a3), (b3) M = 40; (a4), (b4) M = 100; (a5), (b5) M = 200Figure 7. Flow pattern (a1)–(a5) and velocity distribution (b1)–(b5) for the different viscosity ratios at
$ {S}_{1}=0.7 $ : (a1), (b1) M = 1; (a2), (b2) M = 20; (a3), (b3) M = 40; (a4), (b4) M = 100; (a5), (b5) M = 200.
图 8 θ = 90°时, 中性润湿条件下不同黏度比时的相对渗透率曲线
Figure 8. Relative permeability curves with different viscosity ratios under neutral wetting condition at θ = 90°.
图 9 θ = 90°时, 相同饱和度下相对渗透率随黏度比变化曲线 (a)相1相对渗透率变化; (b) 相2相对渗透率变化
Figure 9. Relative permeability versus viscosity ratio at the same saturation at θ = 90°: (a) Relative permeability changes of phase 1; (b) relative permeability changes of phase 2.
图 10 M = 100时, 不同润湿条件下的相对渗透率曲线 (a)相1相对渗透率变化; (b)相2相对渗透率变化
Figure 10. Relative permeability curves under different wetting conditions at M = 100: (a) Relative permeability changes of phase 1; (b) relative permeability changes of phase 2.
图 11
$ {S}_{1}=0.7 $ 时, 不同润湿条件下的稳态相分布 (a) θ = 30°; (b) θ = 90°; (c) θ = 150°Figure 11. Stable phase distributions under the different wetting conditions for
$ {S}_{1}=0.7 $ : (a) θ = 30°; (b) θ = 90°; (c) θ = 150°.
图 12 M = 100,
${S}_{1}=0.7 \;({S}_{2}=0.3)$ 时, 相对渗透率随接触角变化曲线Figure 12. Relative permeability curve with contact angle for M = 100 and
${S}_{1}=0.7 \;({S}_{2}=0.3)$ .
图 13 M = 1, θ = 90°时, 不同毛细管数下的相渗曲线
Figure 13. Relative permeability curves for different capillary numbers at M = 1 and θ = 90°.
图 14
$ {S}_{1}=0.7 $ 时, 不同毛细管数下的相分布 (a)$ Ca= $ $ 0.021 $ ; (b)$ Ca=0.041 $ ; (c)$ Ca=0.082 $ Figure 14. Phase distributions for different capillary numbers for
$ {S}_{1}=0.7 $ : (a)$ Ca=0.021 $ ; (b)$ Ca=0.041 $ ; (c)$Ca= $ $ 0.082$ .表 1 不同黏度比下的两组分表面张力
Table 1. Surface tensions of two-component under different viscosity ratios.
黏度比M 表面张力σ 1 0.1452 20 0.1379 50 0.1330 100 0.1371 200 0.1325 
DownLoad: CSV
-
[1] Zhao H, Ning Z, Kang Q, Chen L, Zhao T 2017 Int. Commun. Heat Mass 85 53
Google Scholar
[2] Zhang D, Papadikis K, Gu S 2016 Adv. Water Resour. 95 61
Google Scholar
[3] Dullien F A L, Dong M 1996 Transport Porous Med. 25 97
Google Scholar
[4] Bentsen R G, Manai A A 1993 Transport Porous Med. 11 243
Google Scholar
[5] Akbarabadi M, Piri M 2013 Adv. Water Resour. 52 190
Google Scholar
[6] Hao L, Cheng P 2010 Int. J. Heat Mass Tran. 53 1908
Google Scholar
[7] Li Z, Chen T, Ning Y, Zhang K, Guan Q 2019 Qin SPE Middle East Oil and Gas Show and Conference, Bahrain, March 18–21, 2019 SPE-194770-MS
[8] Wang J, Dong M, Asghari K 2006 SPE/DOE Symposium on Improved Oil Recovery, USA, April 22–26, 2006 SPE-99763-MS
[9] Inamuro T, Ogata T, Tajima S, Konishi N 2004 J. Comput. Phys. 198 628
Google Scholar
[10] Rothman D H, Keller J M 1988 J. Stat. Phys. 52 1119
Google Scholar
[11] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[12] Swift M R, Orlandini E, Osborn W R, Yeomans J M 1996 Phys. Rev. E 54 5041
Google Scholar
[13] He X, Shan X, Doolen G D 1998 Phys. Rev. E 57 R13
[14] Ramstad T, Øren P E, Bakke S 2010 SPE J. 15 917
Google Scholar
[15] Liu T, Wang M 2022 Transport Porous Med. 144 111
Google Scholar
[16] Li H, Pan C, Miller C T 2005 Phys. Rev. E 72 026705
Google Scholar
[17] Yiotis A G, Psihogios J, Kainourgiakis M E, Papaioannou A, Stubos A K 2007 Colloid. Surface. A 300 35
Google Scholar
[18] Huang H, Li Z, Liu S, Lu X Y 2009 Int. J. Numer. Meth. Fl. 61 341
Google Scholar
[19] Ghassemi A, Pak A 2011 J. Petrol Sci. Eng. 77 135
Google Scholar
[20] Gao C, Xu R N, Jiang P X 2015 Int. J. Numer. Meth Fl. 25 1957
[21] Dou Z, Zhou Z F 2013 Int. J. Heat Fluid Fl. 42 23
Google Scholar
[22] Zhang D, Li S, Jiao S, Shang Y, Dong M 2019 Int. J. Heat Mass Tran. 134 311
Google Scholar
[23] Li S, Jiang F, Wei B, Hou J, Liu H 2021 Phys. Fluids 33 063302
Google Scholar
[24] Huang H, Sukop M, Lu X 2015 Multiphase Lattice Boltzmann Methods: Theory and Application (Oxford: Wiley Blackwell) pp96–99
[25] Guo Z, Zheng C, Shi B 2008 Phys. Rev. E 77 036707
Google Scholar
[26] Zheng J, Chen Z, Xie C, Wang Z, Lei Z, Ju Y, Wang M 2018 Comput. Fluids 168 21
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3722
- PDF Downloads: 103
- Cited By: 0
