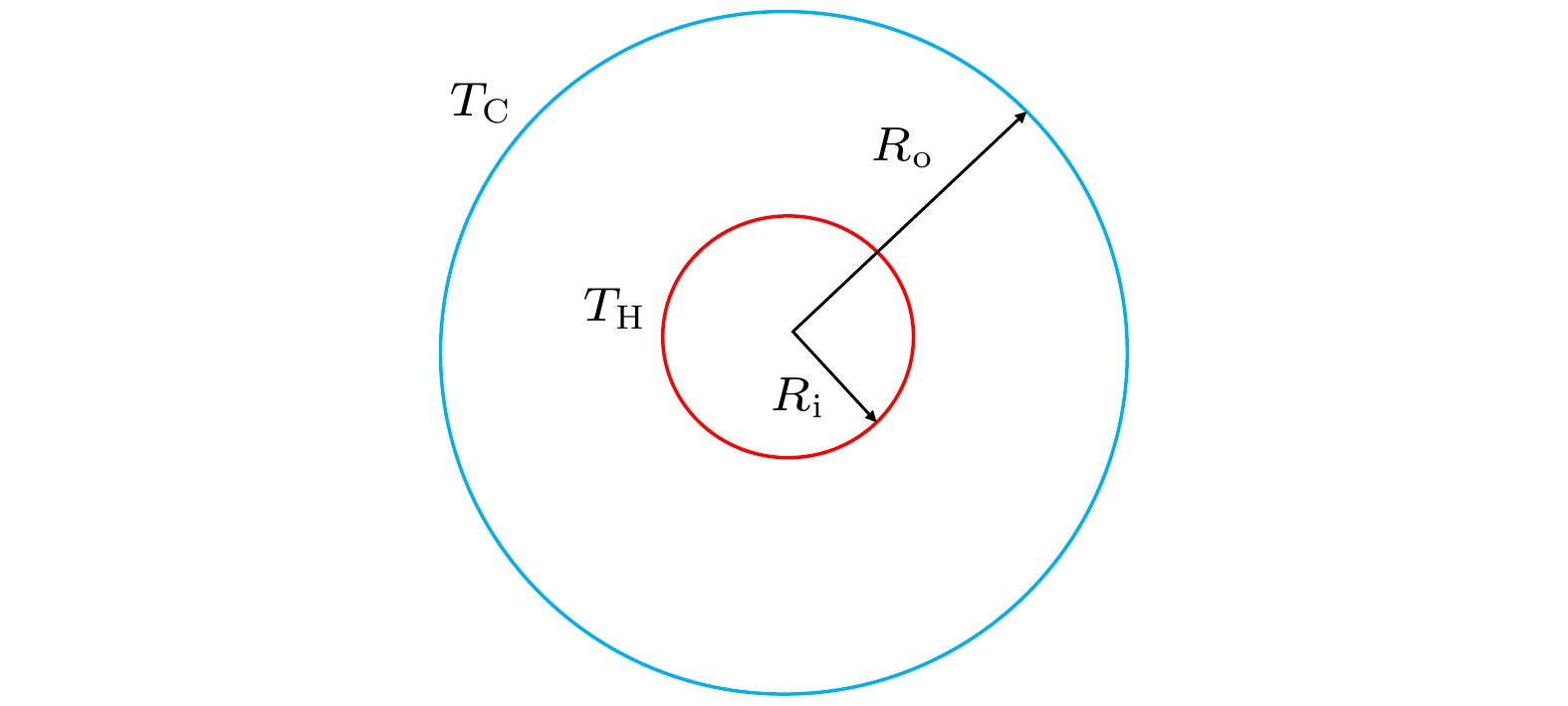
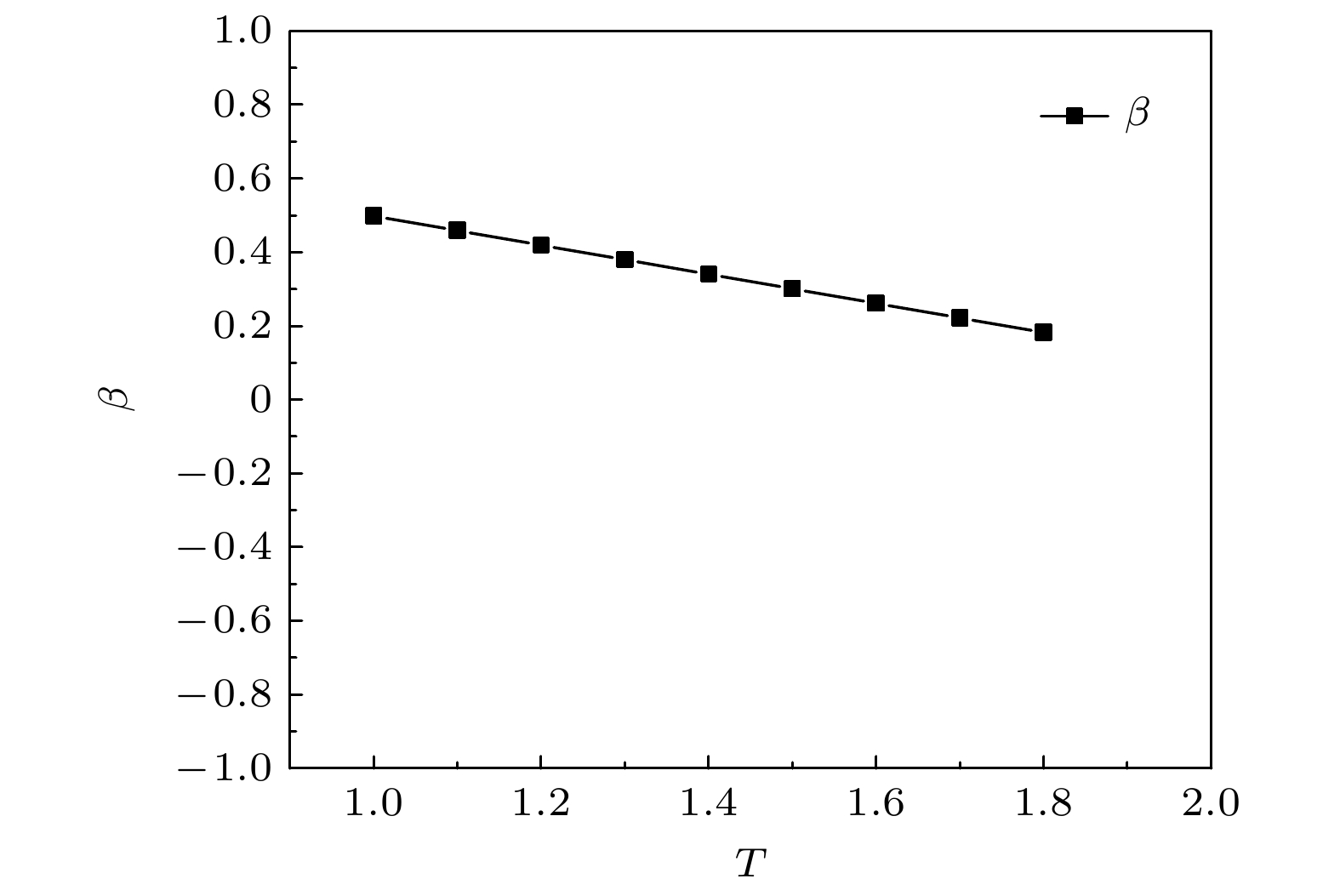
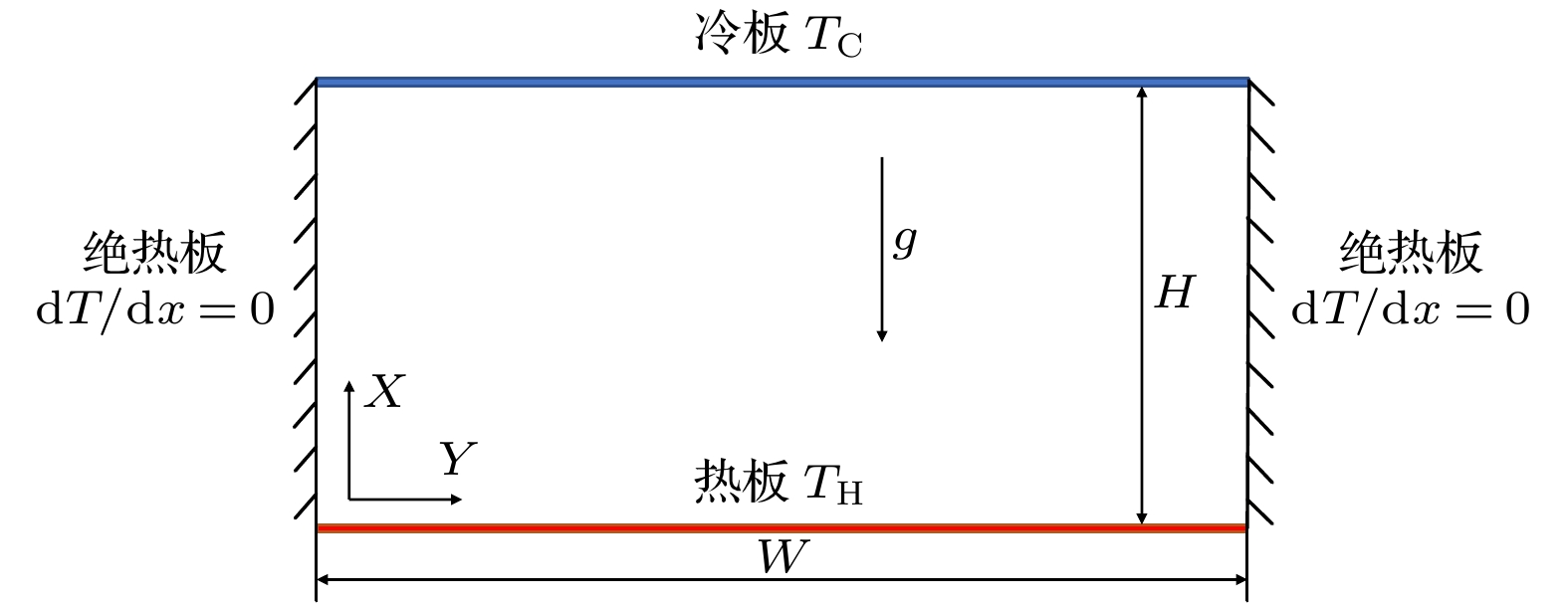
-
能量守恒耗散粒子动力学(eDPD)是一种研究热输运过程的介观尺度数值模拟方法, 然而在eDPD系统内引入Boussinesq假设以研究自然对流问题时, eDPD系统自身的热膨胀性对模拟结果的影响常常被忽略. 首先研究了eDPD系统的热膨胀性, 通过模拟获得eDPD系统的热膨胀系数β; 并由此模拟了不同瑞利数Ra、不同几何结构下的自然对流; 利用eDPD系统自身的热膨胀性, 在不引入Boussinesq假设的前提下获得了合理的温度场和速度场, 与相同Ra数下有限体积法模拟结果相比, 误差明显小于以往研究中相同条件下的对比误差. 研究表明在eDPD系统中引入Boussinesq假设时, 需要考虑eDPD系统自身热膨胀性的影响, 并且进一步对Ra数的计算进行了修正.
-
关键词:
- 能量守恒耗散粒子动力学 /
- Boussinesq假设 /
- 自然对流 /
- 热膨胀性
Energy conservation dissipative particle dynamics (eDPD) is a mesoscale numerical simulation method of studying the heat transport process. In previous studies, when the Boussinesq assumption was introduced into the eDPD system to study the natural convection, the system was generally considered to be incompressible, and the effect of the thermal expansion of the eDPD system itself on the simulation results was often neglected, which would cause errors in the simulation. In the present study, the thermal expansion characteristic of the eDPD system is first investigated, and the thermal expansion coefficient β of the eDPD system is obtained by eDPD simulation. Then, based on the thermal expansion characteristic of the eDPD system itself, the natural convection is simulated with different values of Rayleigh number Ra and different geometries, specifically, square cavity, concentric rings, and eccentric rings, and reasonable temperature and velocity fields are obtained, and they are in agreement with the simulated results by the finite volume method (FVM). The error between the eDPD simulation, in which the natural convection is driven by thermal expansion of the eDPD system itself, and FVM simulated result is considerably smaller than the errors observed in previous studies where Boussinesq assumption was directly adopted to simulate natural convection phenomena while neglecting the thermal expansion effect of eDPD system. It is shown that the effect of the eDPD system’s own thermal expansion characteristic needs to be considered when introducing the Boussinesq assumption in the eDPD system, and further, the calculation of the Ra number is modified in this paper.-
Keywords:
- energy conservation dissipative particle dynamics /
- Boussinesq hypothesis /
- natural convection /
- thermal expansion
[1] Hoogerbrugge P J, Koelman J 1992 Europhys. Lett. 19 155
Google Scholar
[2] Español P, Warren P 1995 Europhys. Lett. 30 191
Google Scholar
[3] Groot R D, Warren P 1997 J. Chem. Phys. 107 4423
Google Scholar
[4] Avalos J B, Mackie A D 1997 Europhys. Lett. 40 141
Google Scholar
[5] Español P 1997 Europhys. Lett. 40 631
Google Scholar
[6] Ripoll M, Español P, Ernst M H 1998 Int. J. Mod. Phys. C 9 1329
Google Scholar
[7] Ripoll M, Español P 2001 Int. J. Mod. Phys. C 15 7271
Google Scholar
[8] Mackie A D, Avalos J B, Navas V 1999 Phys. Chem. Chem. Phys. 1 2039
Google Scholar
[9] Avalos J B, Mackie A D 1999 J. Chem. Phys. 111 5267
Google Scholar
[10] Lukes A C J R 2009 J. Heat Trans. 131 033108
Google Scholar
[11] Homman A, Maillet J, Roussel J 2016 J. Chem. Phys. 144 024112
Google Scholar
[12] Stoltz G 2017 J. Comput. Phys. 340 451
Google Scholar
[13] Qiao R, He P 2007 Mol. Simulat. 33 677
Google Scholar
[14] Abu-Nada E 2010 Mol. Simulat. 36 382
Google Scholar
[15] Abu-Nada E 2010 Phys. Rev. E 81 056704
Google Scholar
[16] Abu-Nada E 2011 J. Heat Trans. 133 112502
Google Scholar
[17] Abu-Nada E 2015 Numer. Heat Tr. A Appl. 67 808
Google Scholar
[18] Abu-Nada E 2015 Int. J. Therm. Sci. 92 72
Google Scholar
[19] Mai-Duy N, Phan-Thien N 2013 J. Comput. Phys. 245 150
Google Scholar
[20] Pan D Y, Phan-Thien N, Mai-Duy N 2013 J. Comput. Phys. 242 196
Google Scholar
[21] 张凯 2017 硕士学位论文 (太原: 中北大学)
Zhang K 2017 M. S. Thesis (Taiyuan: North University of China
[22] Ripoll M 2002 Ph. D. Dissertation (Spain: UNED
[23] Fan X J, Phan-Thien N, Yong N T, Wu X H, Xu D 2003 Phys. Fluids 15 11
Google Scholar
[24] Koschmieder E, Pallas S 1974 Heat Mass Transfer 17 991
Google Scholar
[25] Zhang J , Önskog T 2017 Phys. Rev. E 96 043104
Google Scholar
[26] 曹知红, 罗康, 易红亮 2014工程热 35 1840
Cao Z H, Luo K, Yi H L 2014 J. Eng. Thermophys. 35 1840
[27] Cao Z H, Luo K, Yi H L 2014 Int. J. Heat Mass Tran. 74 60
Google Scholar
-
图 1 不同压强下eDPD密度随温度的变化
Fig. 1. Density variation of eDPD with temperature at different pressure level.
图 2 eDPD系统热膨胀系数随温度的变化
Fig. 2. Variation of thermal expansion coefficient of eDPD system with temperature.
图 4 eDPD模拟不同瑞利数下自然对流的温度云图 (a) Ra = 1600; (b) Ra = 1800; (c) Ra = 2000; (d) Ra = 4000
Fig. 4. Temperature clouds of natural convection under different Rayleigh numbers simulated by eDPD: (a) Ra = 1600; (b) Ra = 1800; (c) Ra = 2000; (d) Ra = 4000.
图 5 eDPD模拟不同瑞利数下自然对流的速度矢量图 (a) Ra = 1600; (b) Ra = 1800; (c) Ra = 2000; (d) Ra = 4000
Fig. 5. Natural convection velocity vectors at different Rayleigh numbers by eDPD simulations: (a) Ra = 1600; (b) Ra = 1800; (c) Ra = 2000; (d) Ra = 4000.
图 6 eDPD模拟Ra为3100时方腔内自然对流的温度云图
Fig. 6. eDPD simulation of the temperature cloud of natural convection in the square cavity when Ra is 3100.
图 7 Ra为3100时eDPD和FVM模拟的方腔内自然对流温度等温线对比图
Fig. 7. Comparison of natural convection temperature isotherms in the square cavity simulated by eDPD and FVM at 3100 of Ra.
图 8 Ra为7300时eDPD和FVM模拟的方腔内自然对流温度等温线对比图
Fig. 8. Comparison of natural convection temperature isotherms in the square cavity simulated by eDPD and FVM at 7300 of Ra.
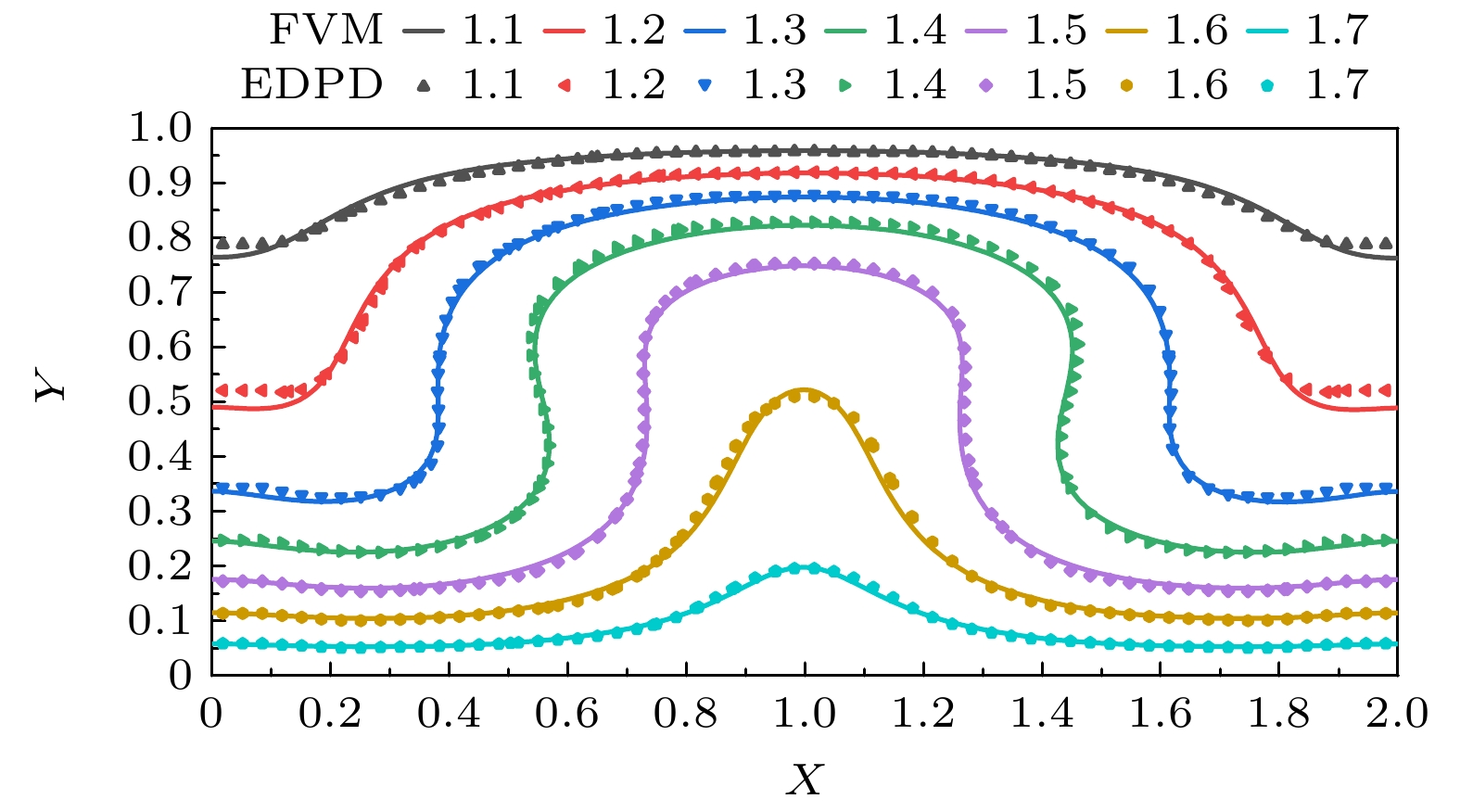
图 9 Ra为7300时eDPD和FVM模拟的方腔内自然对流速度线对比图 (a) X = 0.5时VX沿Y方向变化曲线; (b) X = 1.5时VX沿Y方向变化曲线; (c) X = 0.3时VY沿Y方向变化曲线; (d) X = 1.0时VY沿Y方向变化曲线
Fig. 9. Comparison of natural convection velocity profile in the square cavity simulated by eDPD and FVM when Ra is 7300: (a) Variation curve of VX along Y-direction at X = 0.5; (b) variation curve of VX along Y-direction at X = 1.5; (c) variation curve of VY along the Y-direction at X = 0.3; (d) variation curve of VY along the Y-direction at X = 1.0.
图 11 不同Ra的 eDPD和FVM同心圆环自然对流等温线对比图 (a) Ra = 1000; (b) Ra = 4100; (c) Ra = 7200; (d) Ra = 10400
Fig. 11. Comparison of natural convection isotherms of eDPD and FVM simulation for concentric rings at different Ra: (a) Ra = 1000; (b) Ra = 4100; (c) Ra = 7200; (d) Ra = 10400.
图 12 eDPD和FVM偏心圆环自然对流等温线对比图 (a) Ra = 4100; (b) Ra = 10400
Fig. 12. Comparison of eDPD and FVM eccentric circular natural convection isotherms: (a) Ra = 4100; (b) Ra = 10400.
图 13 不考虑eDPD自身热膨胀性时同心圆环自然对流等温线对比图
Fig. 13. Comparison of natural convection isotherms in concentric rings without considering the thermal expansion of the eDPD system.
图 14 考虑eDPD自身热膨胀性的同时引入Boussinesq假设情况下, 同心圆环自然对流等温线对比图
Fig. 14. Concentric circular natural convection isotherm comparison when considering the combined effect of thermal expansion of eDPD system and Boussinesq assuming.
-
[1] Hoogerbrugge P J, Koelman J 1992 Europhys. Lett. 19 155
Google Scholar
[2] Español P, Warren P 1995 Europhys. Lett. 30 191
Google Scholar
[3] Groot R D, Warren P 1997 J. Chem. Phys. 107 4423
Google Scholar
[4] Avalos J B, Mackie A D 1997 Europhys. Lett. 40 141
Google Scholar
[5] Español P 1997 Europhys. Lett. 40 631
Google Scholar
[6] Ripoll M, Español P, Ernst M H 1998 Int. J. Mod. Phys. C 9 1329
Google Scholar
[7] Ripoll M, Español P 2001 Int. J. Mod. Phys. C 15 7271
Google Scholar
[8] Mackie A D, Avalos J B, Navas V 1999 Phys. Chem. Chem. Phys. 1 2039
Google Scholar
[9] Avalos J B, Mackie A D 1999 J. Chem. Phys. 111 5267
Google Scholar
[10] Lukes A C J R 2009 J. Heat Trans. 131 033108
Google Scholar
[11] Homman A, Maillet J, Roussel J 2016 J. Chem. Phys. 144 024112
Google Scholar
[12] Stoltz G 2017 J. Comput. Phys. 340 451
Google Scholar
[13] Qiao R, He P 2007 Mol. Simulat. 33 677
Google Scholar
[14] Abu-Nada E 2010 Mol. Simulat. 36 382
Google Scholar
[15] Abu-Nada E 2010 Phys. Rev. E 81 056704
Google Scholar
[16] Abu-Nada E 2011 J. Heat Trans. 133 112502
Google Scholar
[17] Abu-Nada E 2015 Numer. Heat Tr. A Appl. 67 808
Google Scholar
[18] Abu-Nada E 2015 Int. J. Therm. Sci. 92 72
Google Scholar
[19] Mai-Duy N, Phan-Thien N 2013 J. Comput. Phys. 245 150
Google Scholar
[20] Pan D Y, Phan-Thien N, Mai-Duy N 2013 J. Comput. Phys. 242 196
Google Scholar
[21] 张凯 2017 硕士学位论文 (太原: 中北大学)
Zhang K 2017 M. S. Thesis (Taiyuan: North University of China
[22] Ripoll M 2002 Ph. D. Dissertation (Spain: UNED
[23] Fan X J, Phan-Thien N, Yong N T, Wu X H, Xu D 2003 Phys. Fluids 15 11
Google Scholar
[24] Koschmieder E, Pallas S 1974 Heat Mass Transfer 17 991
Google Scholar
[25] Zhang J , Önskog T 2017 Phys. Rev. E 96 043104
Google Scholar
[26] 曹知红, 罗康, 易红亮 2014工程热 35 1840
Cao Z H, Luo K, Yi H L 2014 J. Eng. Thermophys. 35 1840
[27] Cao Z H, Luo K, Yi H L 2014 Int. J. Heat Mass Tran. 74 60
Google Scholar
下载:
计量
- 文章访问数: 3561
- PDF下载量: 78
- 被引次数: 0
