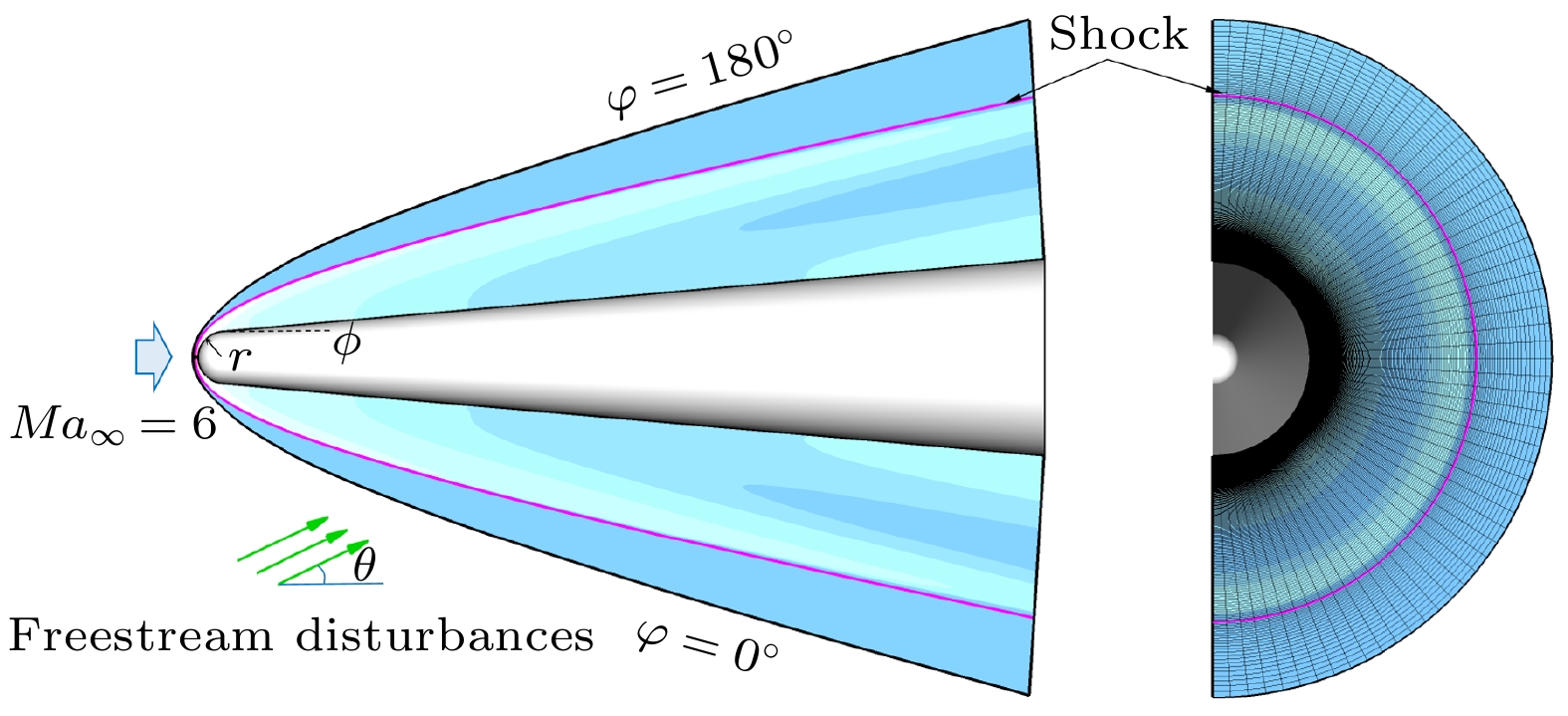
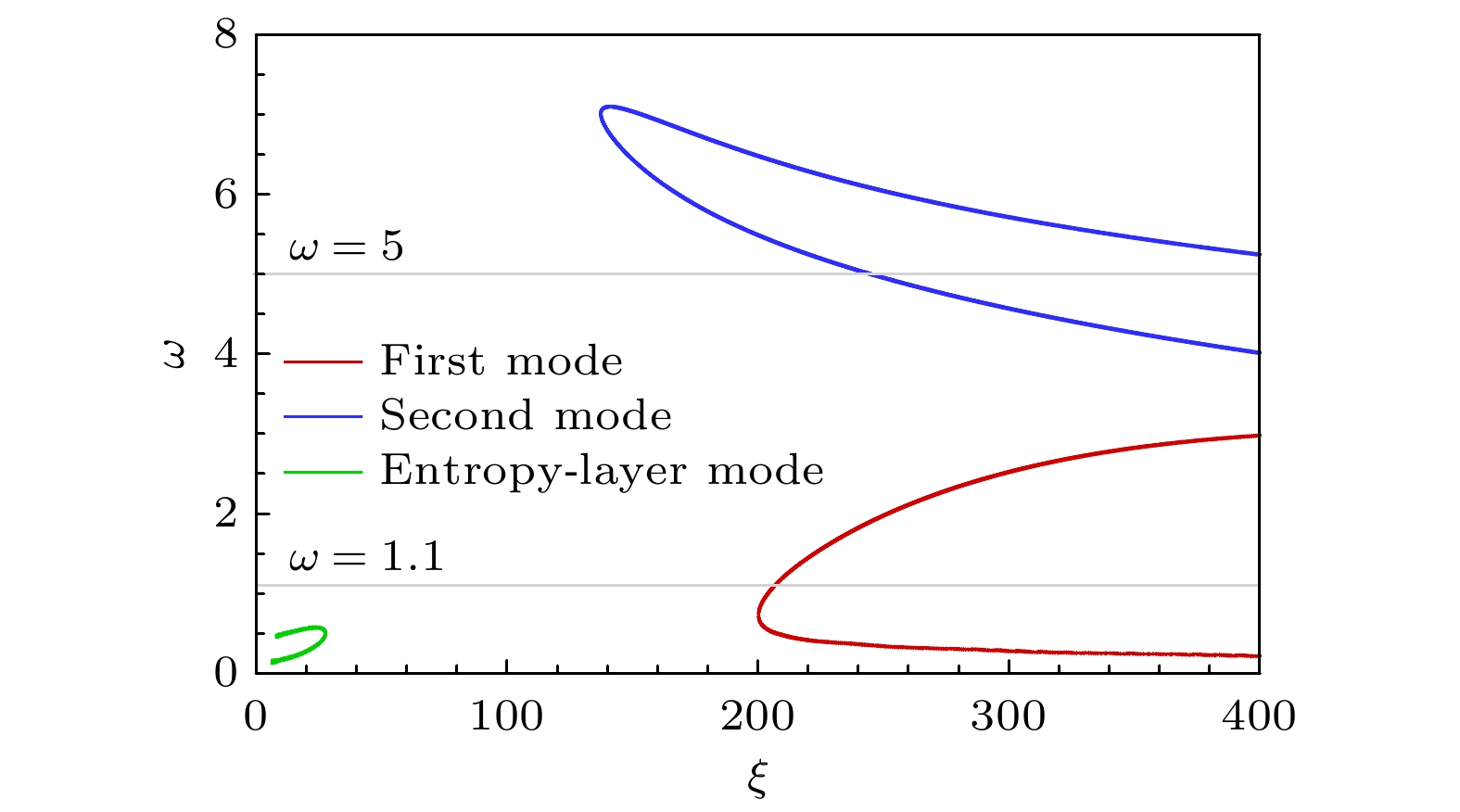
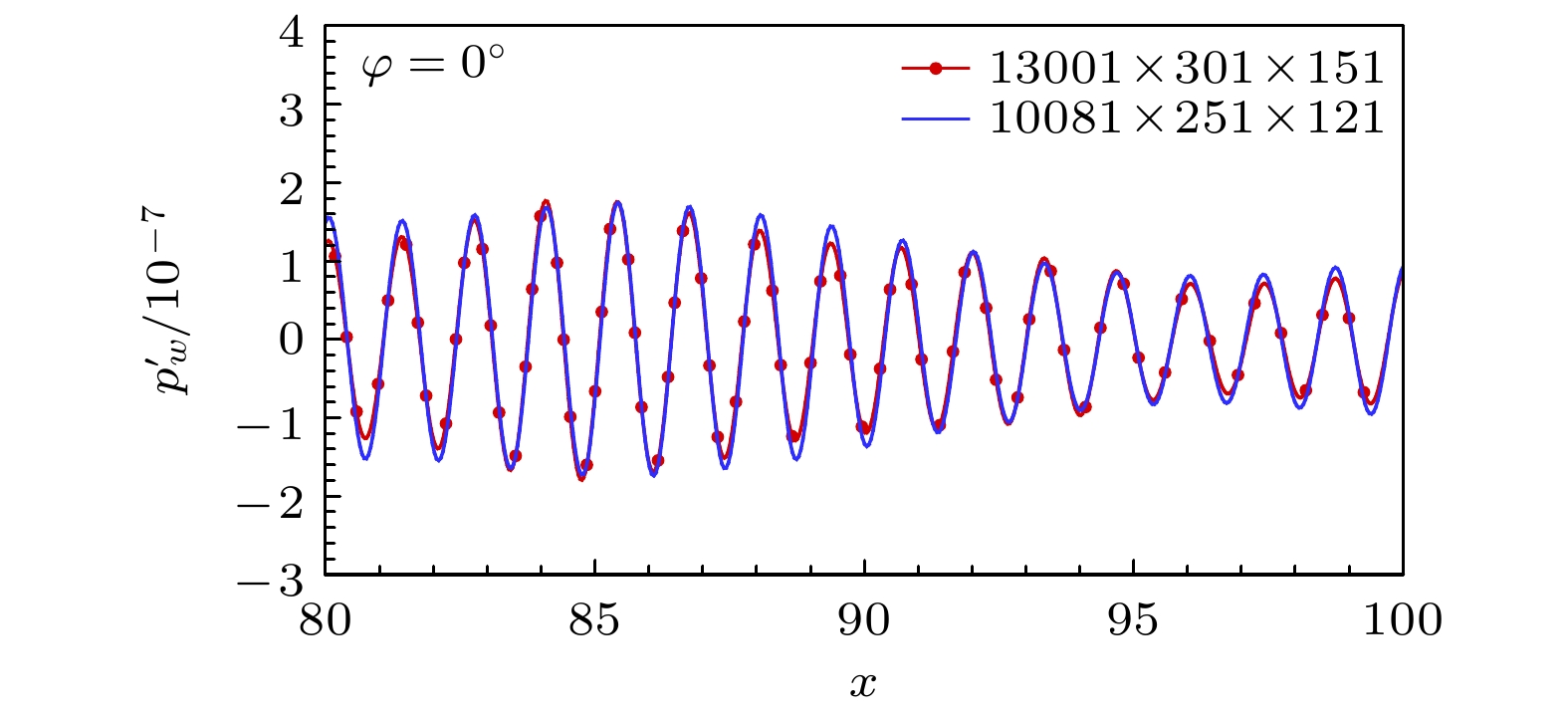
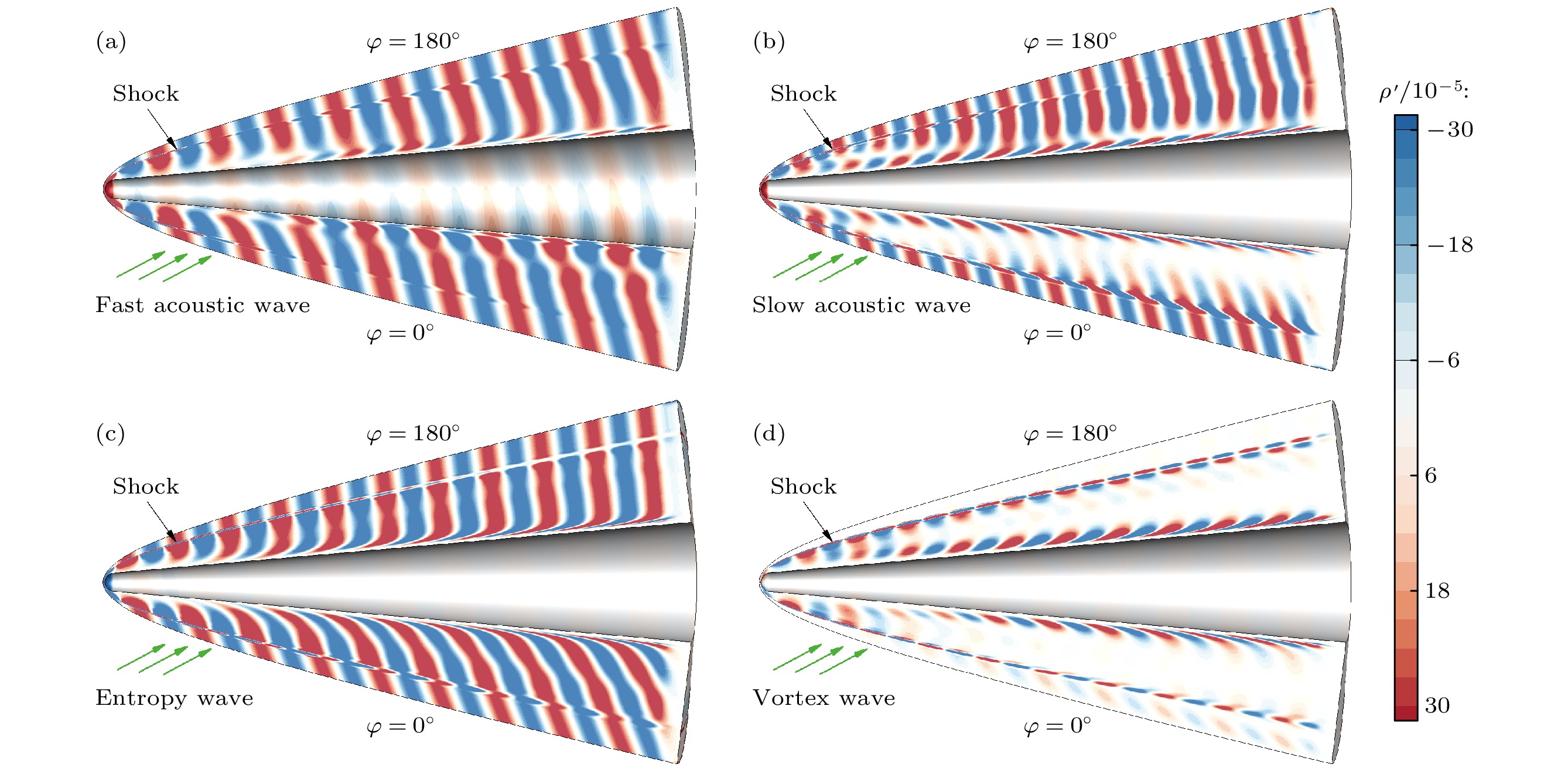
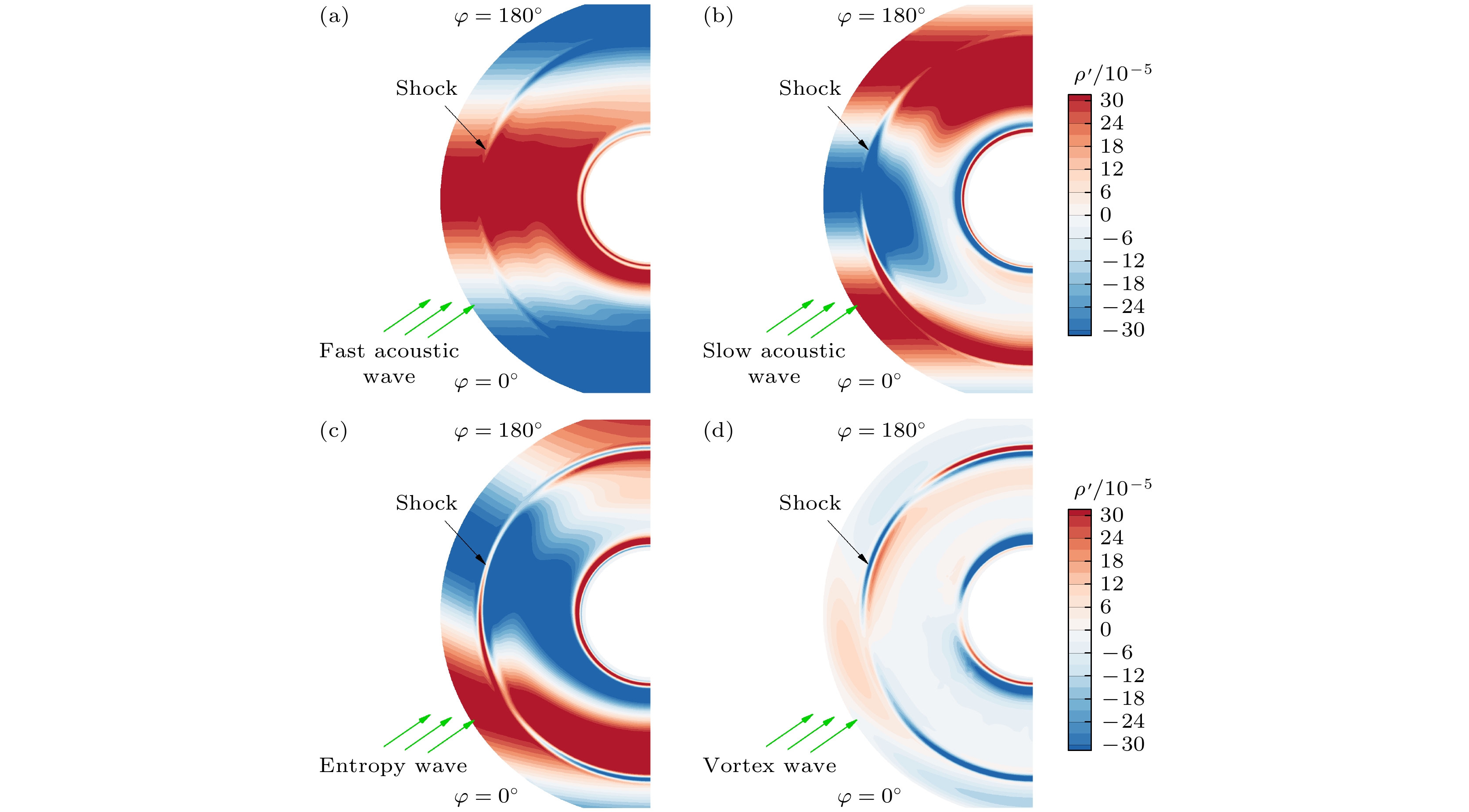
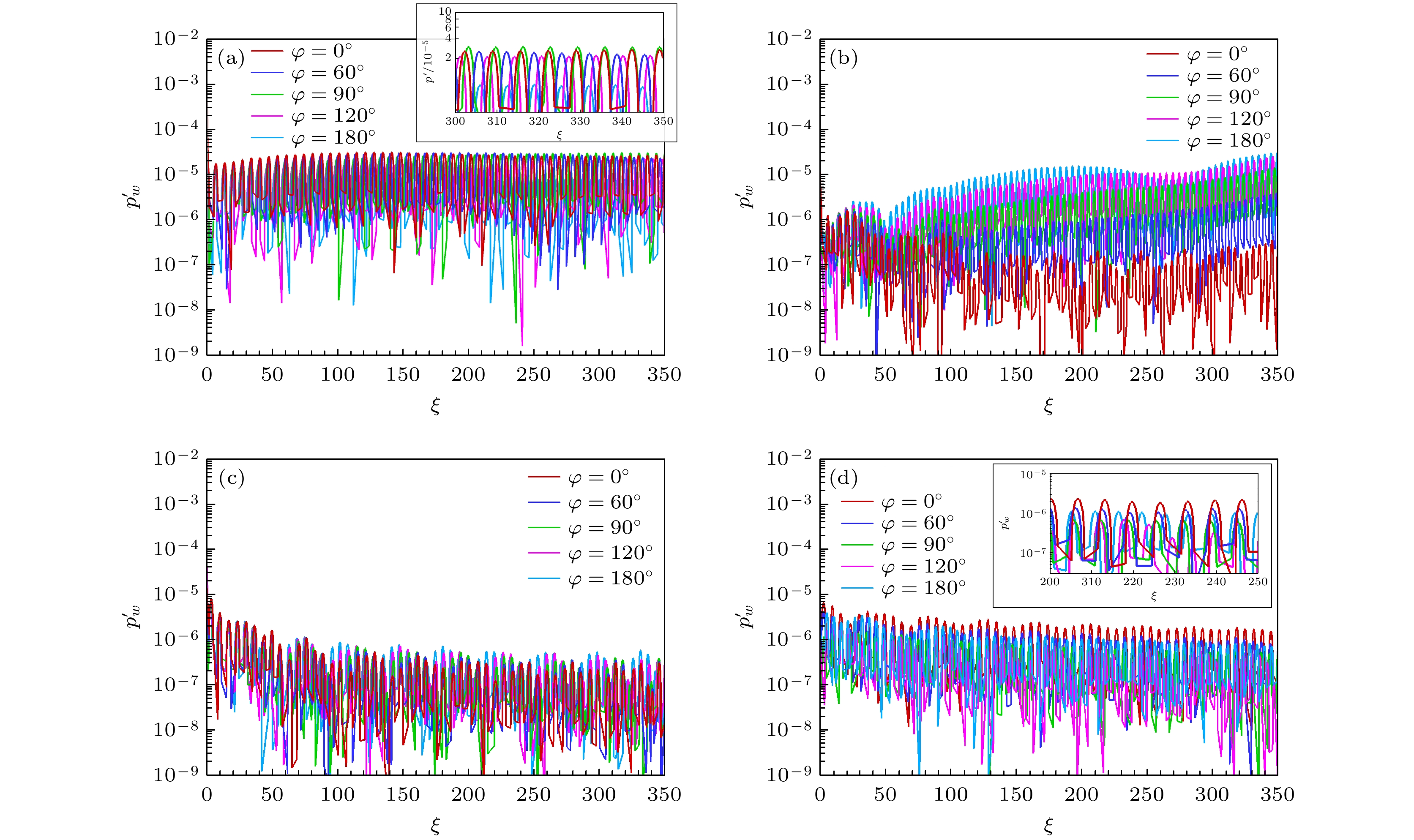
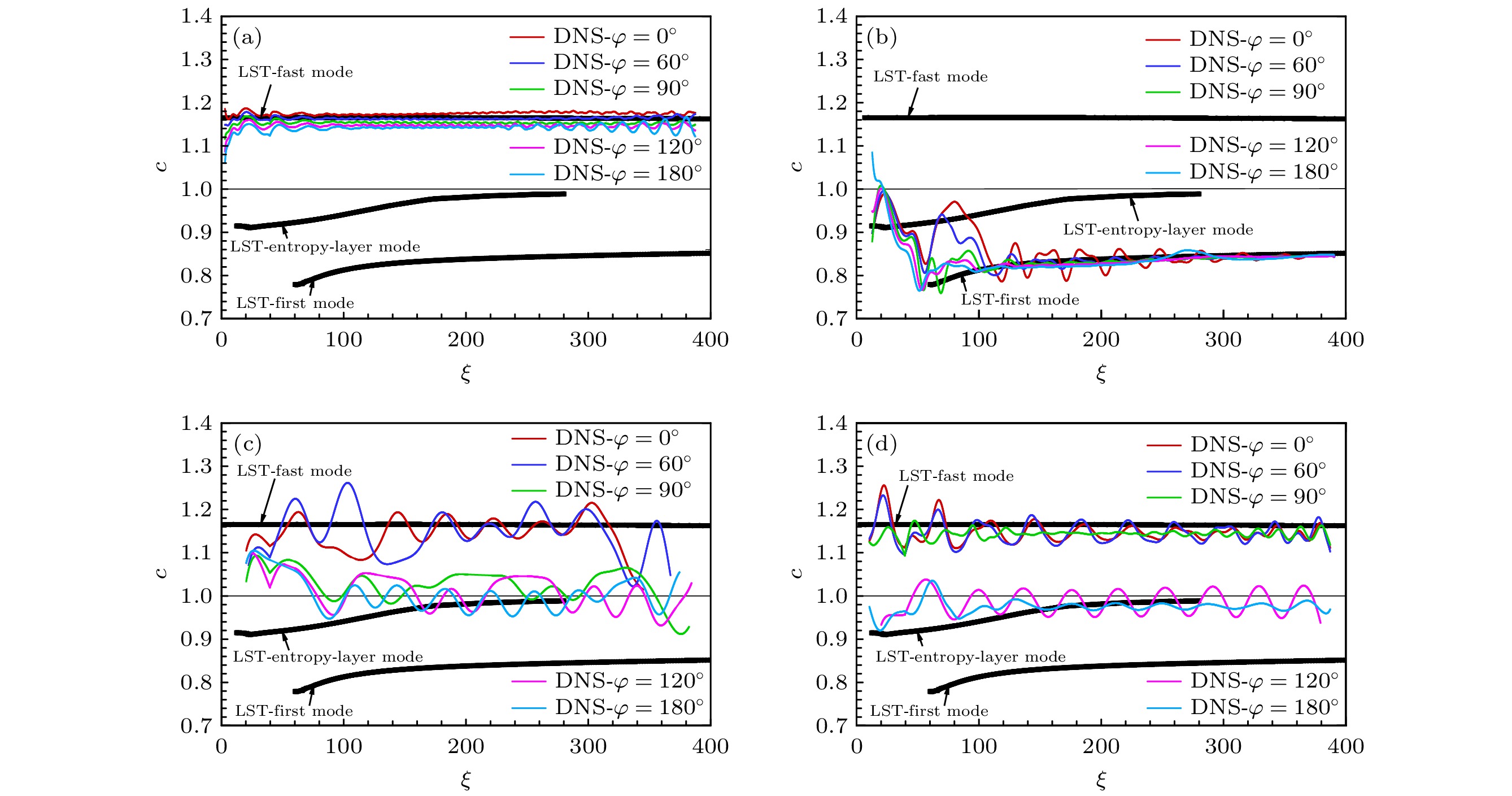
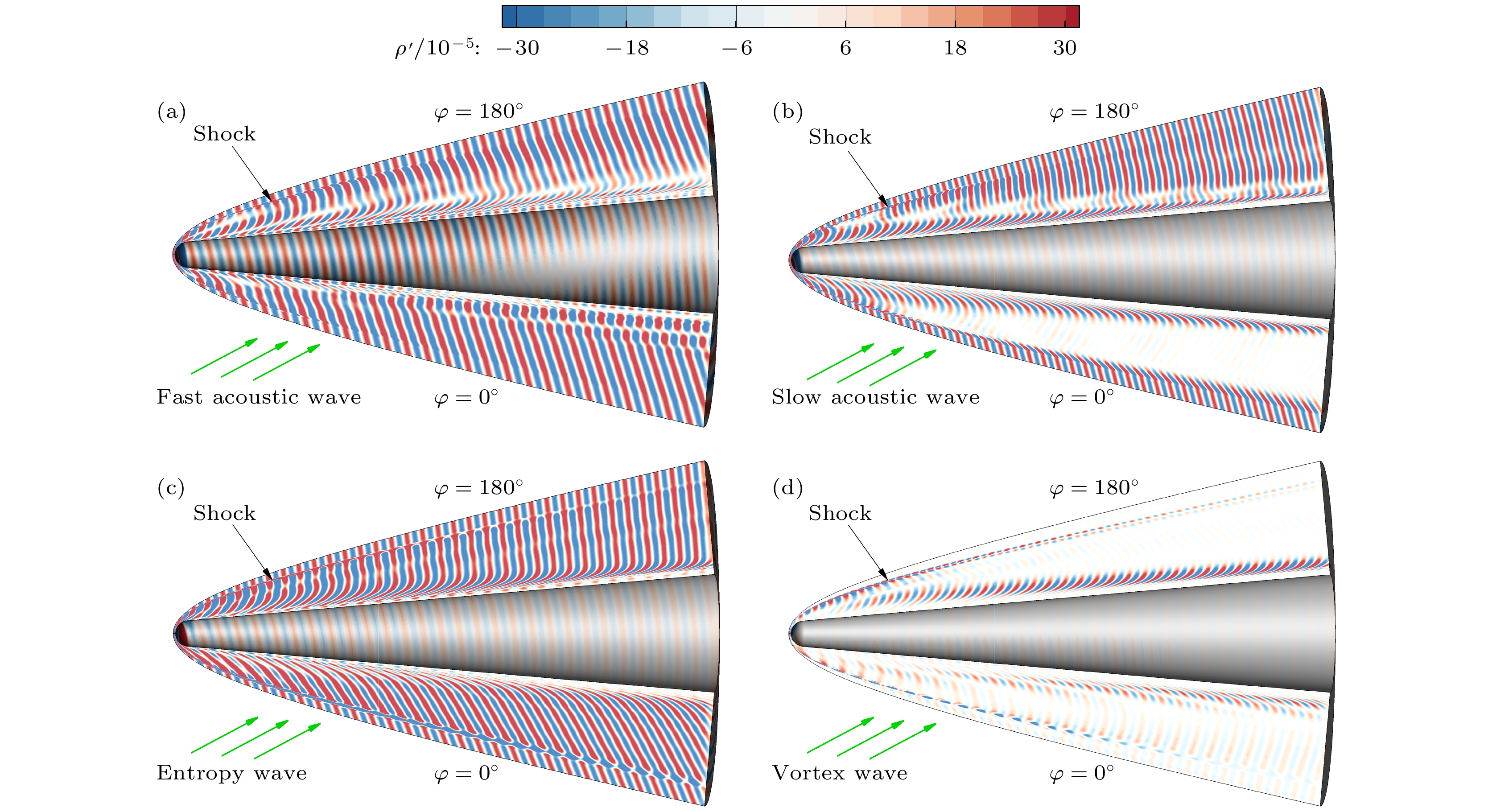
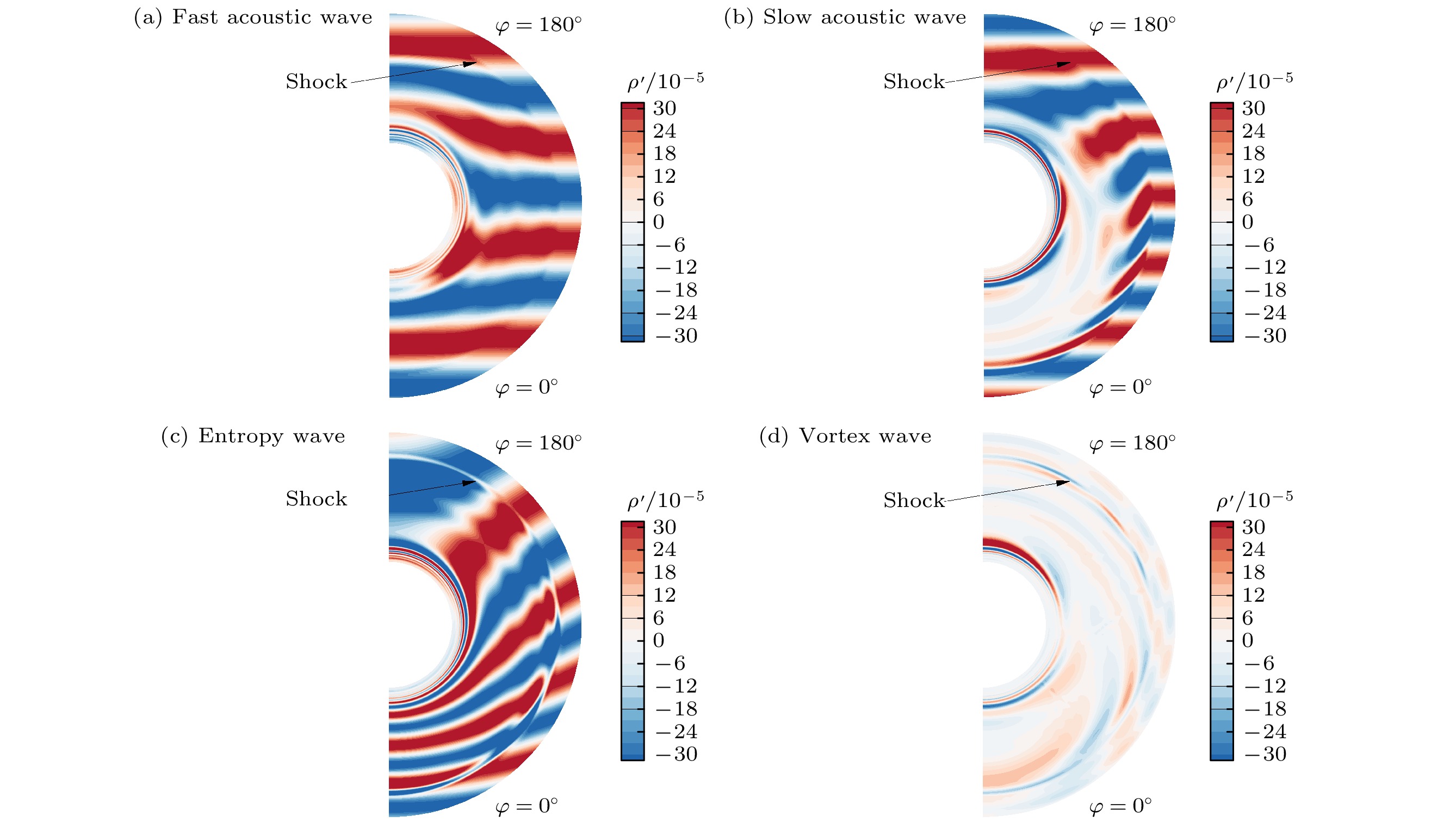
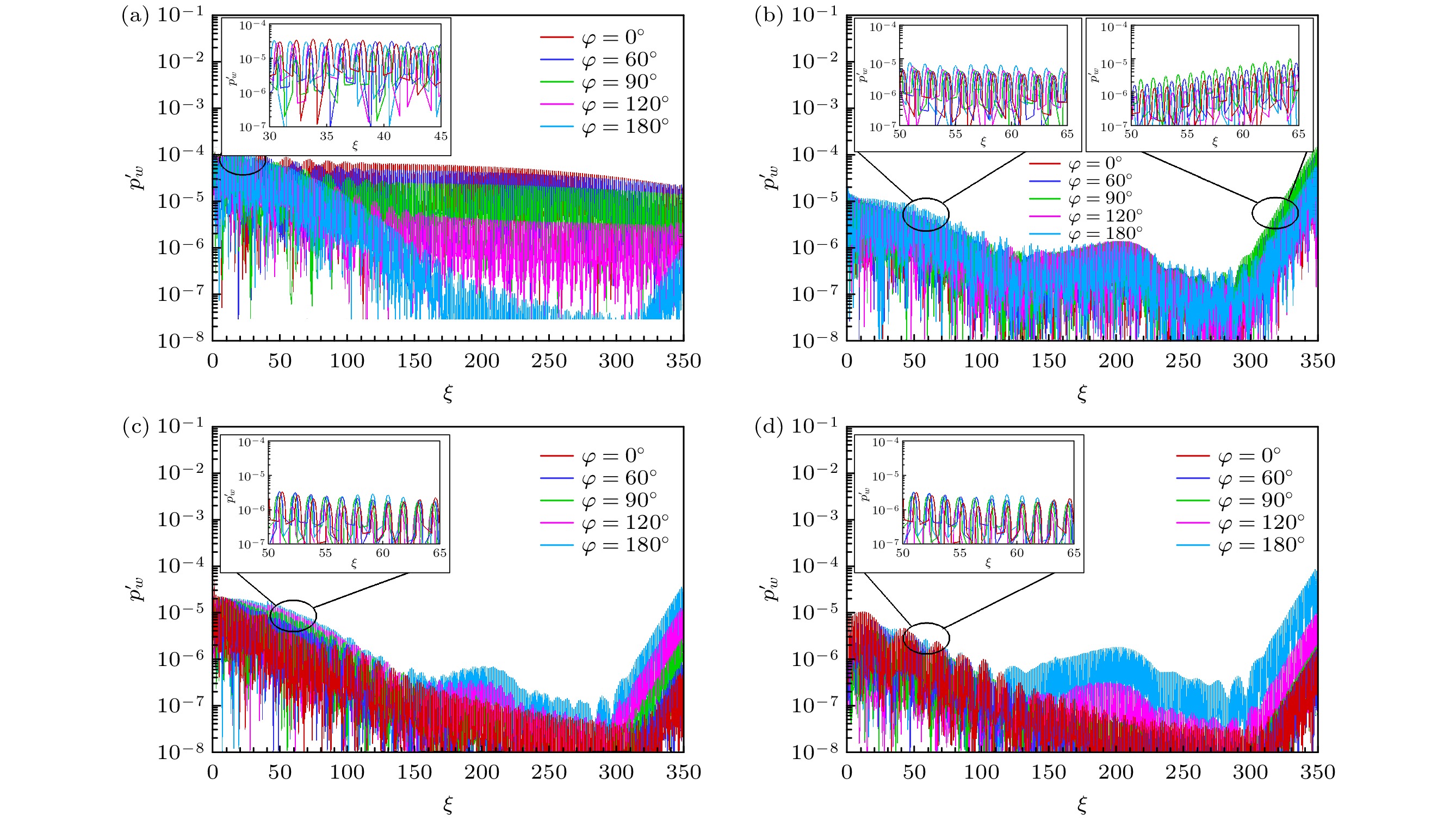
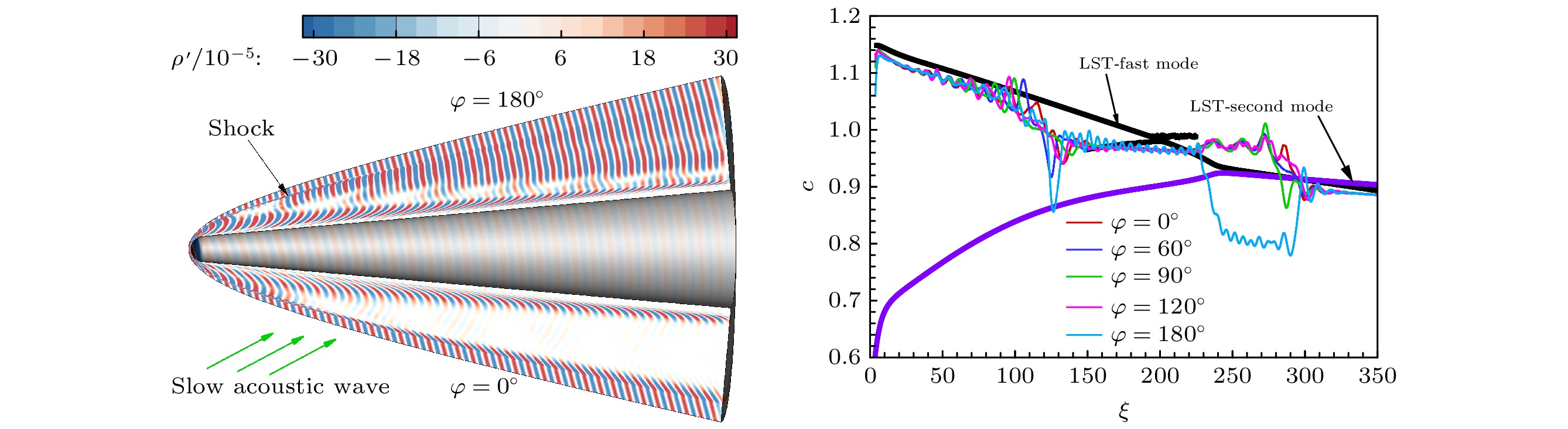
-
Receptivity to freestream disturbances is the initial stage of the boundary-layer transition process, which can determine the final path of boundary-layer disturbance triggered transition. At present, there is relatively sufficient research on the receptivity of two-dimensional boundary layers to zero incident angle disturbances. In fact, the freestream disturbances often propagate into the boundary layer in the form of non-zero incident angle, resulting in a component of spatial disturbance in the circumferential direction of rotating body (such as a cone). It is a receptivity problem with distinct three-dimensional features. However, there is relatively little research on this three-dimensional receptivity issue. The preliminary work only studied the three-dimensional receptivity to low-frequency incident slow acoustic waves. There has not been a systematic study on the three-dimensional receptivity to different types of freestream disturbances. The three-dimensional receptivity of a blunt cone to different freestream disturbances is studied in this work. Firstly, a high-resolution numerical simulation method is used to investigate the three-dimensional receptivity process by introducing freestream disturbances with an incident angle of 15°. The freestream disturbances include fast acoustic wave, slow acoustic wave, entropy wave, and vortex wave. Their frequencies are chosen as dimensionless 1.1 and 5, corresponding to the first mode frequency and the second mode frequency, respectively. Then, the phase velocity and shape function of the boundary-layer disturbances at each position of circumference for the numerical results are obtained by Fourier transform. To explain the receptivity mechanisms, the corresponding results by linear stability analysis are obtained for comparisons. The results are shown below. The first mode and the second mode of the boundary layer can be effectively excited by the incident slow acoustic waves; it is difficult for the incident fast acoustic waves to excite unstable modes in the boundary layer; the incident entropy wave and vortex wave are difficult to excite the first mode at low frequency, but can excite the second mode at high frequency. Furthermore, the incident angle of the freestream disturbances can lead to the differences in the receptivity at different circumferential positions of the cone, which can be reflected in two ways. One is the difference in the dominant disturbance form at different circumferential positions, and the other is the difference in the amplitude of boundary-layer disturbances. Under different disturbance types and frequencies, these differences between different circumferential positions exhibit different results. The strongest receptivity may occur on the incident front, the incident back, and the incident side. These phenomena may result from the combined action of the upstream head disturbance and the disturbance on the incident front.
-
Keywords:
- receptivity /
- freestream disturbances /
- numerical simulation /
- stability analysis
-
图 1 钝锥子午面示意图
Figure 1. Schematic diagram of blunt-cone meridian plane.
图 2 钝锥计算域示意图
Figure 2. Schematic diagram of blunt-cone computation domain.
图 4 频率ω = 5条件下感受性数值模拟的网格无关性验证
Figure 4. Grid independent verification of receptivity numerical simulation for ω = 5.
图 5 不同来流低频扰动波的三维感受性数值模拟
Figure 5. Three dimensional receptivity numerical simulations for different freestream disturbances with low frequency.
图 6 不同来流低频扰动波条件下x = 30处的横截面显示
Figure 6. Cross section displays at x = 30 for different freestream disturbances with low frequency.
图 7 不同来流低频扰动波条件下壁面压力脉动扰动演化 (a) 快声波; (b)慢声波; (c)熵波; (d)涡波
Figure 7. Evolution of the wall pressure fluctuations for different freestream disturbances with low frequency: (a) Fast acoustic wave; (b) slow acoustic wave; (c) entropy wave; (d) vortex wave.
图 8 不同来流低频扰动波条件下壁面扰动相速度与稳定性理论比较 (a) 快声波; (b)慢声波; (c)熵波; (d)涡波
Figure 8. Phase speeds of the wall disturbances compared with the stability theory for different freestream disturbances with low frequency: (a) Fast acoustic wave; (b) slow acoustic wave; (c) entropy wave; (d) vortex wave.
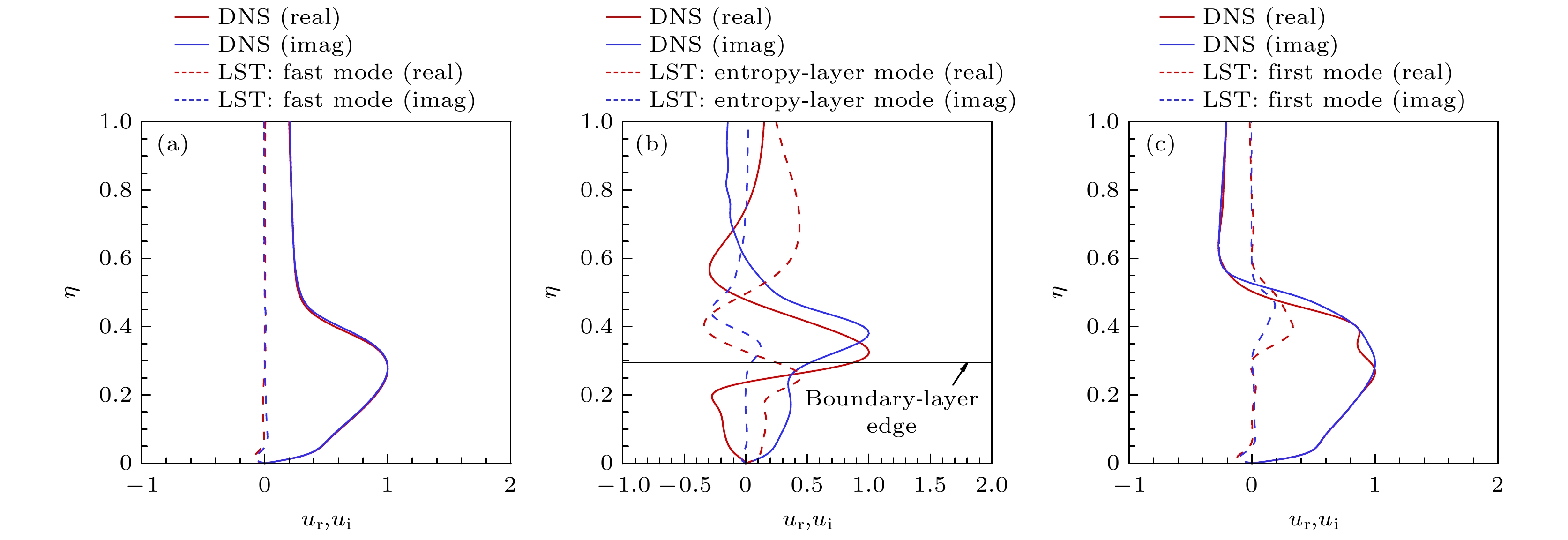
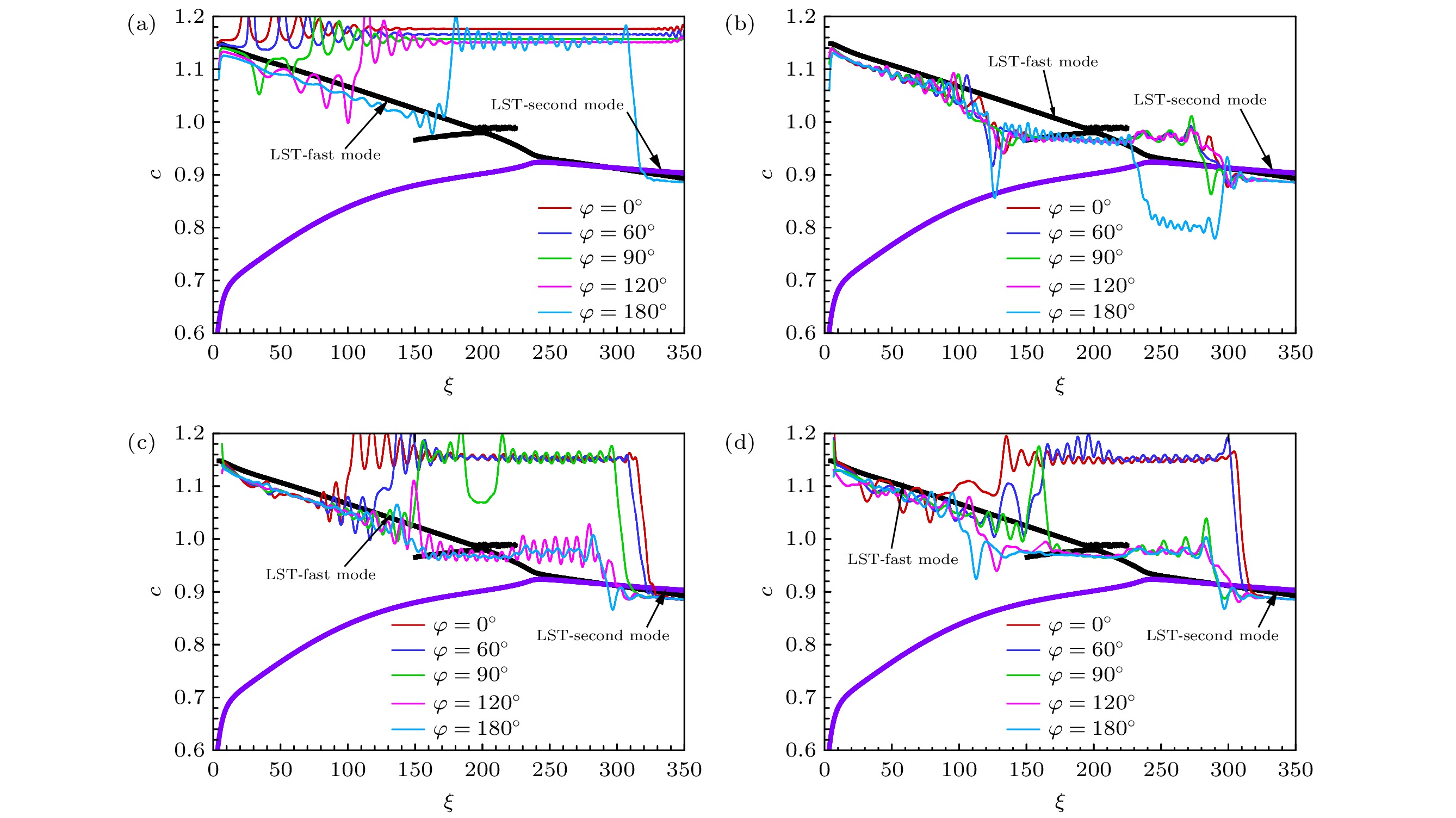
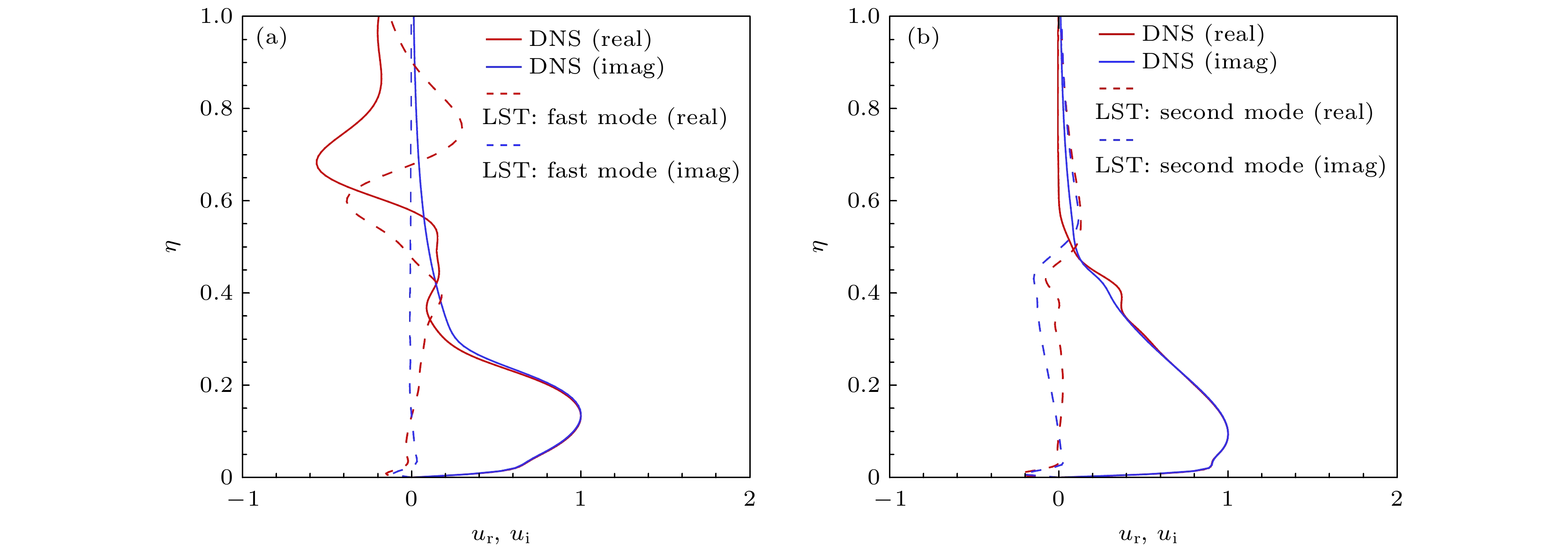
图 9 不同扰动形状函数与稳定性理论(快模态、熵层模态和第一模态)比较 (a) 快声波, ξ = 200, φ = 90; (b)慢声波, ξ = 60, φ = 90; (c)慢声波, ξ = 350, φ = 90
Figure 9. Disturbance shape functions (fast mode, entropy-layer mode, and first mode) compared with the stability theory: (a) Fast acoustic wave, ξ = 200, φ = 90; (b) slow acoustic wave, ξ = 60, φ = 90; (c) slow acoustic wave, ξ = 350, φ = 90.
图 10 不同来流高频扰动波的三维感受性数值模拟
Figure 10. Three dimensional receptivity numerical simulations for different freestream disturbances with high frequency.
图 11 不同来流高频扰动波条件下x = 30的横截面显示
Figure 11. Cross section displays at x = 30 for different freestream disturbances with high frequency.
图 12 不同来流高频扰动波条件下壁面压力脉动扰动演化 (a) 快声波; (b)慢声波; (c)熵波; (d)涡波
Figure 12. Evolution of the wall pressure fluctuations for different freestream disturbances with high frequency: (a) Fast acoustic wave; (b) slow acoustic wave; (c) entropy wave; (d) vortex wave.
图 13 不同来流高频扰动波条件下壁面扰动相速度与稳定性理论比较 (a) 快声波; (b)慢声波; (c) 熵波; (d)涡波
Figure 13. Phase speeds of the wall disturbances compared with the stability theory for different freestream disturbances with high frequency: (a) Fast acoustic wave; (b) slow acoustic wave; (c) entropy wave; (d) vortex wave.
图 14 不同扰动形状函数与稳定性理论(快模态和第二模态)比较 (a) 慢声波, ξ = 60, φ = 90; (b) 慢声波, ξ = 350, φ = 90
Figure 14. Disturbance shape functions (fast mode and second mode) compared with the stability theory: (a) Slow acoustic wave, ξ = 60, φ = 90; (b) slow acoustic wave, ξ = 350, φ = 90.
-
[1] 陈坚强, 涂国华, 张毅锋, 徐国亮, 袁先旭, 陈诚 2017 空气动力学学报 35 311
Chen J Q, Tu G H, Zhang Y F, Xu G L, Yuan X X, Chen C 2017 Acta Aero. Sin. 35 311
[2] Saric W S, Reed H L, Kerschen E J 2002 Annu. Rev. Fluid Mech. 34 291
Google Scholar
[3] 周恒, 张涵信 2017 空气动力学学报 35 151
Zhou H, Zhang H X 2017 Acta Aero. Sin. 35 151
[4] Goldstein M E 1983 J. Fluid Mech. 127 59
Google Scholar
[5] Goldstein M E 1985 J. Fluid Mech. 154 509
Google Scholar
[6] Ruban A I 1985 Fluid Dyn. 19 709
Google Scholar
[7] Choudhari M, Streett C 1992 Phys. Fluids 4 2495
[8] Choudhari M 1993 Theor. Comp. Fluid Dyn. 4 101
Google Scholar
[9] Duck P W, Ruban A I, Zhikharev C N 1996 J. Fluid Mech. 312 341
Google Scholar
[10] Hammerton P W, Kerschen E J 1996 J. Fluid Mech. 310 243
Google Scholar
[11] Wanderley J B V, Corke T C 2001 J. Fluid Mech. 429 1
Google Scholar
[12] Wu X S 2001 J. Fluid Mech. 397 285
[13] Wu X S 2001 J. Fluid Mech. 431 91
Google Scholar
[14] Dong M, Liu Y H, Wu X S 2020 J. Fluid Mech. 896 A23
Google Scholar
[15] 陆昌根, 朱晓清, 沈露予 2017 66 204702
Google Scholar
Lu C G, Zhu X Q, Shen L Y 2017 Acta Phys. Sin. 66 204702
Google Scholar
[16] Fedorov A 2011 Annu. Rev. Fluid Mech. 43 79
Google Scholar
[17] Zhong X, Wang X 2012 Annu. Rev. Fluid Mech. 44 527
Google Scholar
[18] 江贤洋, 李存标 2017 实验流体力学 31 1
Google Scholar
Jiang X Y, Lee C B 2017 J. Exp. Fluid Mech. 31 1
Google Scholar
[19] 苏彩虹 2020 空气动力学学报 38 355
Google Scholar
Su C H 2020 Acta Aero. Sin. 38 355
Google Scholar
[20] Fedorov A V, Khokhlov A P 1991 Fluid Dyn. 26 531
[21] Fedorov A V, Khokhlov A P 2001 Theor. Comp. Fluid Dyn. 14 359
Google Scholar
[22] Fedorov A V 2003 J. Fluid Mech. 491 101
Google Scholar
[23] Ma Y B, Zhong X L 2003 J. Fluid Mech. 488 31
Google Scholar
[24] Ma Y B, Zhong X L 2003 J. Fluid Mech. 488 79
Google Scholar
[25] Ma Y B, Zhong X L 2005 J. Fluid Mech. 532 63
Google Scholar
[26] Zhong X L, Ma Y B 2006 J. Fluid Mech. 556 55
Google Scholar
[27] He S M, Zhong X L 2021 AIAA J. 59 3546
Google Scholar
[28] He S M, Zhong X L 2022 Phys. Fluids 34 054104
Google Scholar
[29] Balakumar P 2006 36th AIAA Fluid Dynamics Conference and Exhibit. San Francisco, California, June 5-8, p3053
[30] Balakumar P 2015 45th AIAA Fluid Dynamics Conference Dallas, Texas, p247
[31] Balakumar P, King R A, Chou A, Owens L R, Kegerise M A 2018 AIAA J. 56 510
Google Scholar
[32] 张玉东, 傅德薰, 马延文, 李新亮 2008 中国科学. G辑, 物理学, 力学, 天文学 38 1246
Zhang Y D, Fu D X, Ma Y W, Li X L 2008 Sci. Sin. Phys. Mech. Astron. 38 1246
[33] Qin F F, Wu X S 2016 J. Fluid Mech. 797 874
Google Scholar
[34] Ba W T, Niu M H, Su C H 2022 AIAA J. 61 518
[35] Niu M H, Su C H 2023 Phy. Fluids 35 034109
Google Scholar
[36] Wan B B, Luo J S, Su C H 2018 Appl. Math. Mech. (English Edition) 39 1643
Google Scholar
[37] Wan B B, Su C H, Chen J Q AIAA J. 58 4047
[38] Chen Y F, Tu G H, Wan B B, Su C H, Yuan X X, Chen J Q Phys. Fluids 33 084114
[39] Stetson K F, Thompson E R, Donaldson J C, Siler L G 1984 AIAA 22nd Aerospace Sciences Meeting Reno, Nevada, January 9-12, 1984 p0006
[40] Fedorov A V 1990 J. Appl. Mech. Tech. Phy. 31 722
[41] 万兵兵, 罗纪生 2018 空气动力学学报 36 247
Wan B B, Luo J S 2018 Acta Aero. Sin. 36 247
[42] 欧吉辉, 万兵兵, 刘建新, 曹伟 2018 空气动力学报 36 238
Ou J H, Wan B B, Liu J X, Cao W 2018 Acta Aero. Sin. 36 238
[43] Han Y F, Zhou J T, Cao W 2022 Phys. Fluids 34 026101
Google Scholar
[44] McKenzie J F, Westphal K O 1968 Phys. Fluids 11 2350
Google Scholar
[45] Su C H, Geng J L 2017 Appl. Math. Mech. (English Edition) 38 1601
Google Scholar
[46] Huang Z F, Wang H L 2019 J. Fluid Mech. 873 1179
Google Scholar
[47] Malik M R, Balakumar P 2007 Theor. Comp. Fluid Dyn. 21 323
Google Scholar
[48] Balakumar P 2007 37th AIAA Fluid Dynamics Conference and Exhibit Miami, FL, June 25-28, 2007 p4491
[49] Wan B B, Chen J Q, Yuan X X, Hu W B, Tu G H 2022 AIAA J. 60 4523
Google Scholar
[50] Zhang S H, Zhu J, Shu C 2019 Adv. Aerod. 1
[51] Ma Y K, Mao M L, Yan Z G, Bai J W, Zhu H J 2024 J. Comp. Phy. 510 113064
Google Scholar
DownLoad:
Metrics
- Abstract views: 174
- PDF Downloads: 11
- Cited By: 0
