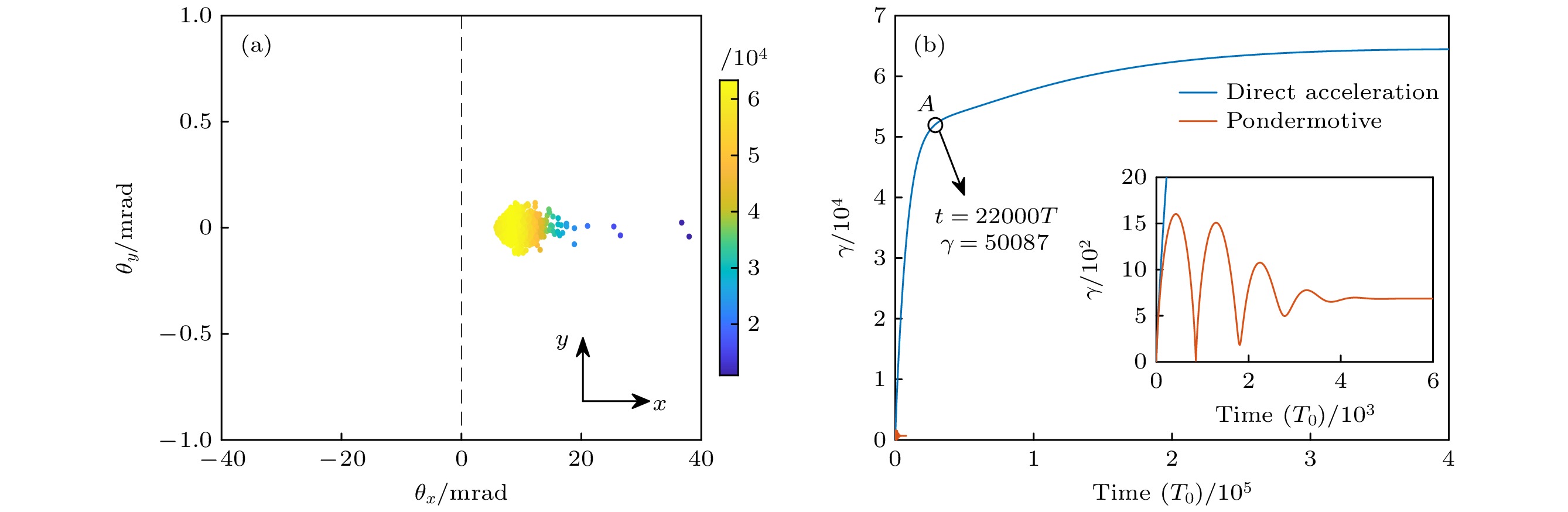
-
When an intense laser obliquely irradiates a solid, a pre-pulse will first ionize the solid surface, followed by the main pulse interacting with the plasma and ultimately being reflected by the plasma. Simultaneously, certain electrons within the plasma will be trapped in the accelerating phase of the laser field, subsequently gaining effective acceleration within the field, this phenomenon is known as phase-locked electron acceleration. Given the current intense lasers' electric field intensity nearing the TV/m range, electrons could potentially acquire energy levels on the order of hundreds of GeV or even TeV, provided they stay in the accelerating phase of the laser field long enough. Here, we initially use PIC (Particle-in-Cell) simulations to simulate the interaction process between laser pulses and plasma, thereby obtaining the properties of phase-locked electrons. In order to reduce computational demands, we turn to use a three-dimensional (3D) test particle model to calculate the subsequent interactions of these electrons with the reflected laser field. By this model, we obtain the data of the locked-phase electrons after having interacted with the reflected laser (Fig. (a)). Furthermore, we use this model to calculate the dynamical behavior of electrons under different initial conditions (Fig. (b)). Under the laser intensity of $ {a}_{0}=350 $($ {a}_{0} $ is the normalized laser vector potential), the energy of the electrons directly accelerated by the laser is enhanced to 32 GeV. In contrast, under the same laser intensity, the energy of the electrons accelerated by ponderomotive force is only 0.35 GeV. The research findings indicate that the strong laser with peak power around 10 PW can directly accelerate electrons to approximately 30 GeV. Additionally, this study outlines the optimal initial conditions for injecting electrons into the laser field and the final electron energy within the phase-locked acceleration mechanism, thereby establishing a calibration relationship with the laser field intensity. Given the continual enhancement of laser intensity and the potential application of the laser phase-locked electron acceleration mechanism to positron acceleration, this research holds promise for its implementation in fields such as miniaturized positron-electron colliders and high-energy gamma-ray sources.
-
Keywords:
- ultra-high energy electron accelerator /
- direct laser acceleration /
- phase-locked electron acceleration /
- electron-positron collider
[1] Dutta B, Ghosh S, Gurrola A, Julson D, Kamon T, Kumar J 2023 J. High Energ. Phys. 2023 164
[2] Bostedt C, Boutet S, Fritz D M, Huang Z R, Lee H J, Lemke H T, Robert A, Schlotter W F, Turner J J, Williams G J 2016 Rev. Mod. Phys. 88 015007
Google Scholar
[3] Tajima T, Dawson J M 1979 Phys. Rev. Lett. 43 267
Google Scholar
[4] Strickland D, Mourou G 1985 Opt. Commun. 56 219
Google Scholar
[5] Gonsalves A J, Nakamura K, Daniels J, Benedetti C, Pieronek C, de Raadt T C H, Steinke S, Bin J H, Bulanov S S, van Tilborg J, Geddes C G R, Schroeder C B, Tóth C, Esarey E, Swanson K, Fan-Chiang L, Bagdasarov G, Bobrova N, Gasilov V, Korn G, Sasorov P, Leemans W P 2019 Phys. Rev. Lett. 122 084801
Google Scholar
[6] Zeng Y S, Yu X Q, Tian Y 2023 Chin. J. Lasers 50 1714008 [曾雨珊, 余谢秋, 田野 2023 中国激光 50 1714008]
Google Scholar
Zeng Y S, Yu X Q, Tian Y 2023 Chin. J. Lasers 50 1714008
Google Scholar
[7] Yu X Q, Zeng Y S, Song L W, Kong D Y, Hao S B, Gui J Y, Yang X J, Xu Y, Wu X J, Leng Y X, Tian Y, Li R X 2023 Nat. Photonics 17 957
Google Scholar
[8] Lawson J D 1979 IEEE Trans. Nucl. Sci. 26 4217
Google Scholar
[9] Hartemann F V, Fochs S N, Le Sage G P, Luhmann N C Jr, Woodworth J G, Perry M D, Chen Y J, Kerman A K 1995 Phys. Rev. E 51 4833
Google Scholar
[10] Esarey E, Sprangle P, Krall J 1995 Phys. Rev. E 52 5443
Google Scholar
[11] He F, Yu W, Lu P X, Xu H, Qian L J, Shen B F, Yuan X, Li R X, Xu Z Z 2003 Phys. Rev. E 68 046407
Google Scholar
[12] Stupakov G V, Zolotorev M S 2001 Phys. Rev. Lett. 86 5274
Google Scholar
[13] Dodin I Y, Fisch N J 2003 Phys. Rev. E 68 056402
Google Scholar
[14] Salamin Y I, Keitel C H 2002 Phys. Rev. Lett. 88 095005
Google Scholar
[15] Pang J, Ho Y K, Yuan X Q, Cao N, Kong Q, Wang P X, Shao L, Esarey E H, Sessler A M 2002 Phys. Rev. E 66 066501
[16] Maltsev A, Ditmire T 2003 Phys. Rev. Lett. 90 053002
Google Scholar
[17] Tian Y, Liu J S, Wang W T, Wang C, Deng A H, Xia C Q, Li W T, Cao L H, Lu H Y, Zhang H, Xu Y, Leng Y X, Li R X, Xu Z Z 2012 Phys. Rev. Lett. 109 115002
Google Scholar
[18] Thévenet M, Leblanc A, Kahaly S, Vincenti H, Vernier A, Quéré F, Faure J 2016 Nat. Phys. 12 355
Google Scholar
[19] Zhou C L, Bai Y F, Song L W, Zeng Y S, Xu Y, Zhang D D, Lu X M, Leng Y X, Liu J S, Tian Y, Li R X, Xu Z Z 2021 Nat. Photonics 15 216
Google Scholar
[20] Thaury C, Quéré F, Geindre J, Lévy A, Ceccotti T, Monot P, Bougeard M, Réau F, d’Oliveira P, Audebert P, Marjoribanks R S, Martin P A 2007 Nat. Phys. 3 424
Google Scholar
[21] Doumy G, Quéré F, Gobert O, Perdrix M, Martin P, Audebert P, Gauthier J C, Geindre J P, Wittmann T 2004 Phys. Rev. E 69 026402
Google Scholar
[22] Quesnel B, Mora P 1998 Phys. Rev. E 58 3719
Google Scholar
[23] Ritus V I 1985 J. Russ. Laser Res. 6 497
Google Scholar
[24] Landau L D, Lifshitz E M 1971 The Classical Theory of Fields (Oxford: Pergamon Press
[25] Stupakov G, Huang Z 2008 Phys. Rev. ST Accel. Beams 11 014401
Google Scholar
[26] Piazza A D, Müller C, Hatsagortsyan K Z, Keitel C H 2012 Rev. Mod. Phys. 84 1177
Google Scholar
-
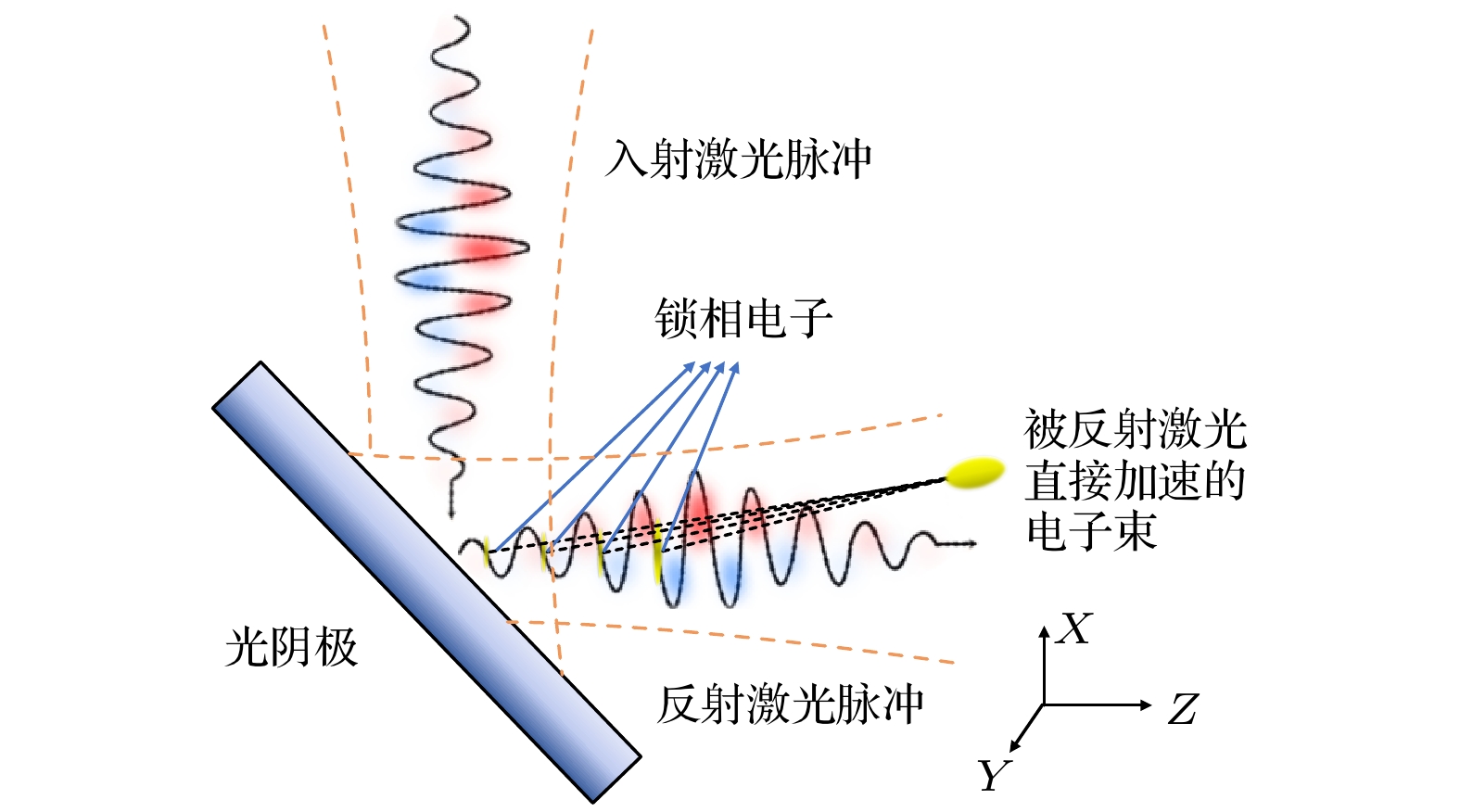
图 1 激光锁相加速电子示意图, 高斯激光脉冲以45°的入射角照射固体表面, 预脉冲会在固体表面产生等离子体, 随后主脉冲会被等离子体反射, 与此同时, 位于激光场特定相位的电子(黄色散点)会向外发射, 并被反射激光场持续加速
Figure 1. Schematic diagram of laser-driven phase-locked acceleration of electrons, the Gaussian laser main pulse is incident on the photocathode at an angle of 45° and is then reflected by the plasma mirror generated by the pre-pulse. Meanwhile, electrons (yellow scattered points) at a specific phase in the laser field are emitted outward and then directly accelerated by the reflected laser field.
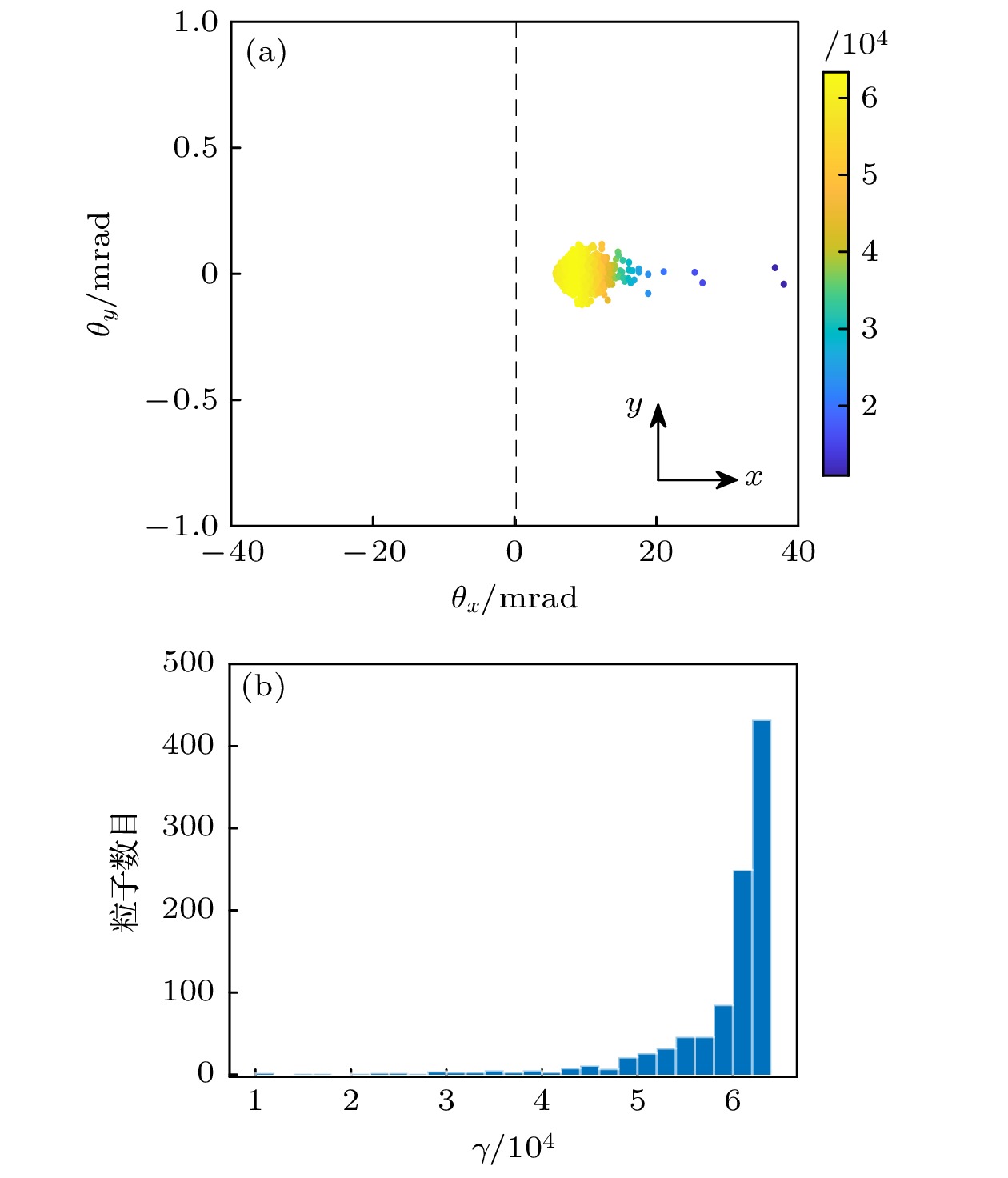
图 3 锁相电子与反射激光相互作用后电子数据 (a)电子的能量角分布, 其中$ {\theta }_{x} $=$ {\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}({p}_{x}/{p}_{z}) $, $ {\theta }_{y} $=$ {{\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}(p}_{y}/{p}_{z}) $, 颜色图为电子的γ值; (b)与反射激光相互作用后的电子能谱
Figure 3. Energy-angular distribution of the locked-phase electrons after having interacted with the reflected laser: (a) Energy-angular distribution of the electrons, where $ {\theta }_{x} $=$ {\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}({p}_{x}/{p}_{z}) $, $ {\theta }_{y} $=$ {{\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}(p}_{y}/{p}_{z}) $, the color bar represents the γ values of the electrons; (b) electron energy spectrum after the interaction with the reflected laser.
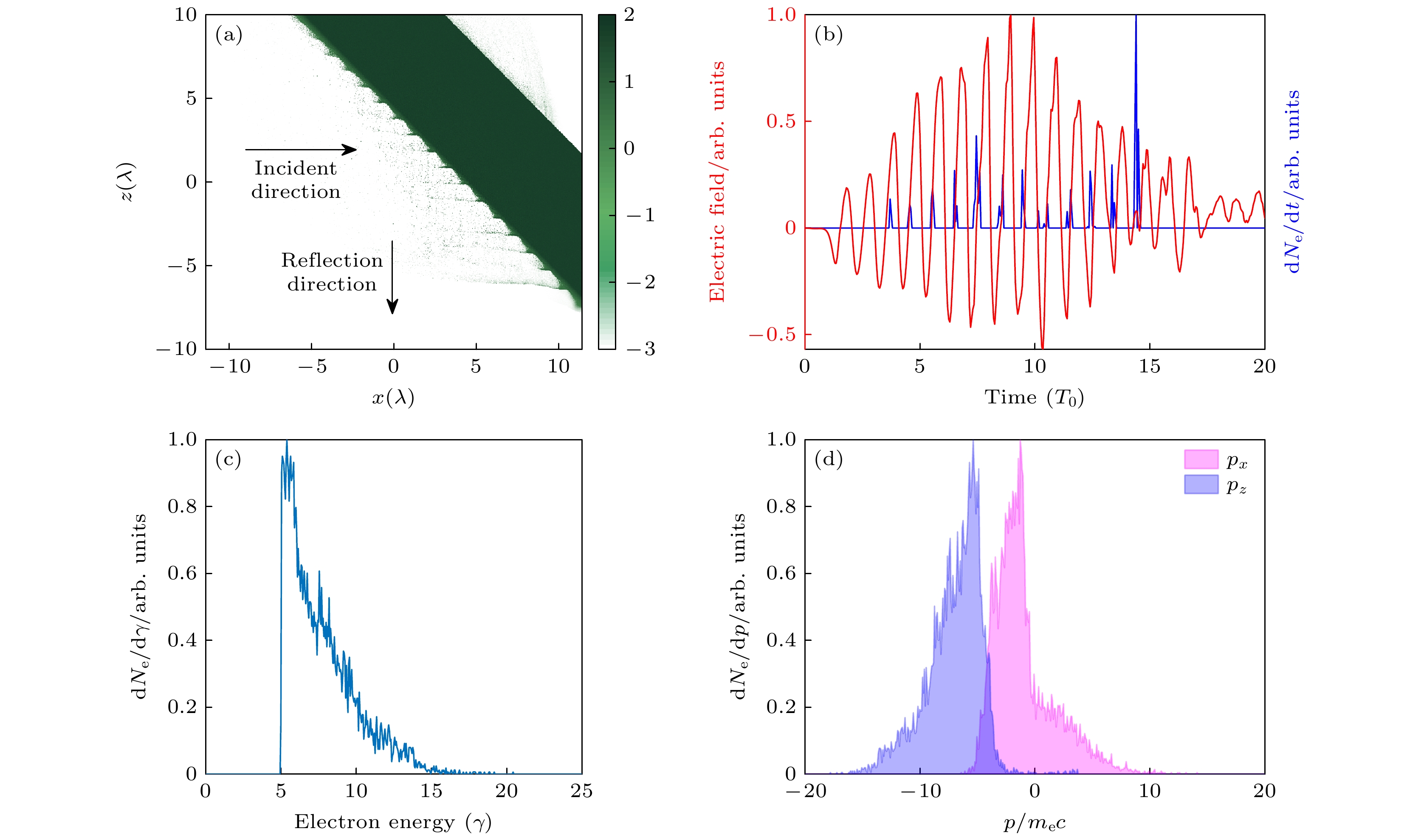
图 2 锁相电子的初始状态 (a)相互作用过程中电子密度的空间分布图, 其中x方向是入射激光的传播方向, z方向是反射激光的传播方向; (b)出射电子与反射激光场的相位关系, 红色曲线为反射激光强度, 蓝色曲线为出射电子密度, 电子在反射激光场过零点对应的相位发射; (c) γ值大于5的出射电子的能谱; (d)出射电子的动量分布, $ {p}_{x} $为电子沿激光偏振方向的动量, $ {p}_{z} $为电子沿激光传播方向的动量
Figure 2. (a) Spatial distribution map of electron density during the interaction process, where the x-direction represents the propagation direction of the incident laser and the z-direction represents the propagation direction of the reflected laser; (b) phase relationship between the emitted electrons and the reflected laser field is illustrated, with the red curve representing the intensity of the reflected laser and the blue curve indicating the electron density, electrons are emitted at the zero-crossing points of the reflected laser; (c) energy spectrum of emitted electrons with γ > 5; (d) momentum distribution of these electrons, $ {p}_{x} $ is the momentum along the polarization direction of the reflected laser and $ {p}_{z} $ is the momentum along the specular direction of the reflected laser.
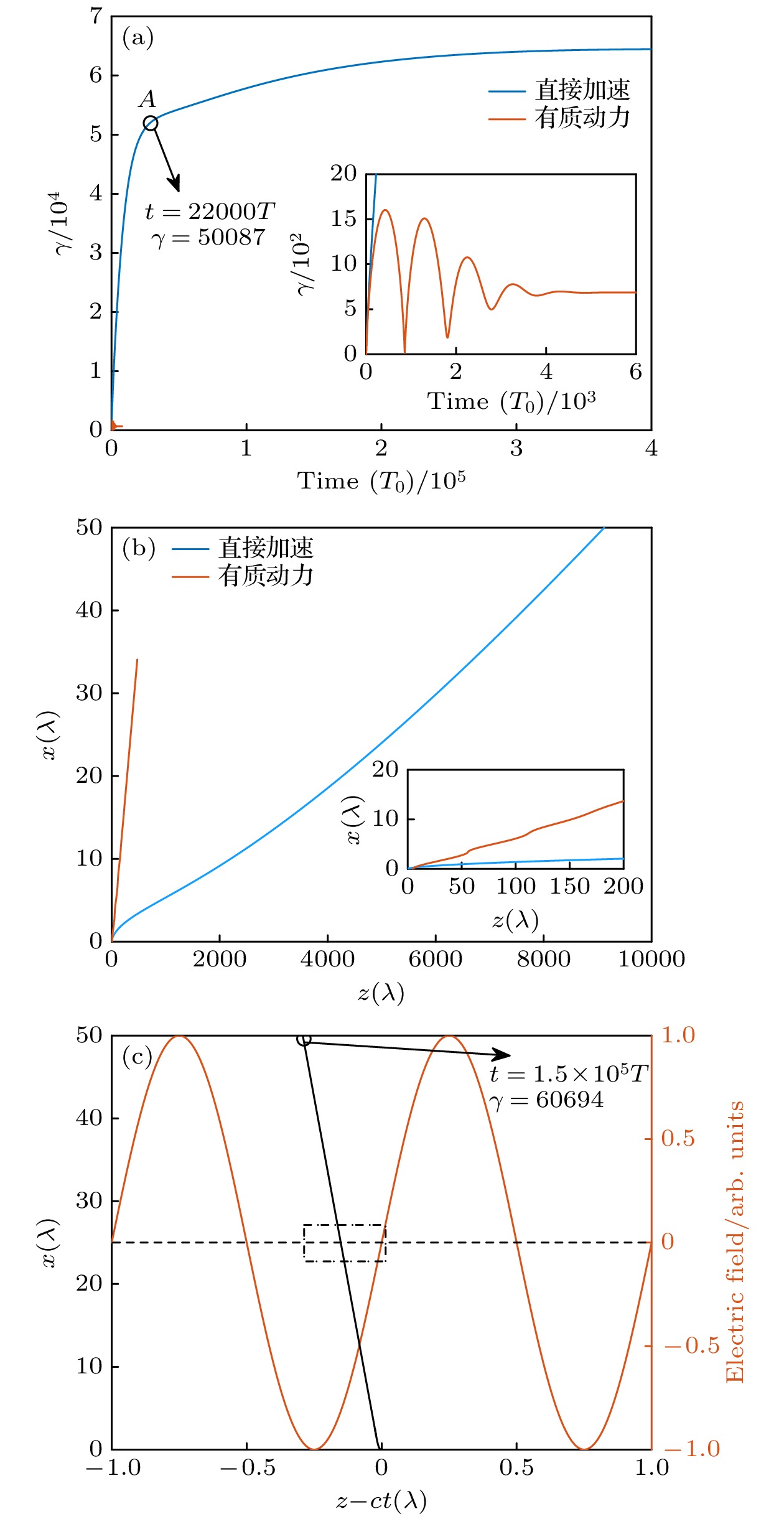
图 4 不同初始动量的电子与激光场相互作用过程 (a) 电子能量值随时间的变化, 一类电子(蓝色实线)代表激光锁相加速, 二类电子(黄色实线)代表有质动力加速机制; (b) 两种电子对应的运动轨迹; (c)随激光运动参考系下一类电子的运动轨迹, 其中红色曲线为激光场的空间分布, 虚线框标明了一类电子相对激光移动的相位范围
Figure 4. Interaction process of phase-locked electrons with the reflected laser field with different initial momenta: (a) Temporal evolution of relativistic factor γ about two typical electros, Type I (blue curve) was accelerated based on the locking-phase mechanism and the acceleration of Type II (orange curve) could be treated as the effect of pondermotive force; (b) the corresponding trajectories about the two electrons; (c) Type I’s trajectory in a frame moving with the laser beam, red curve sketches the laser field in this frame, the dashed box indicates the phase range of the movement of Type I.
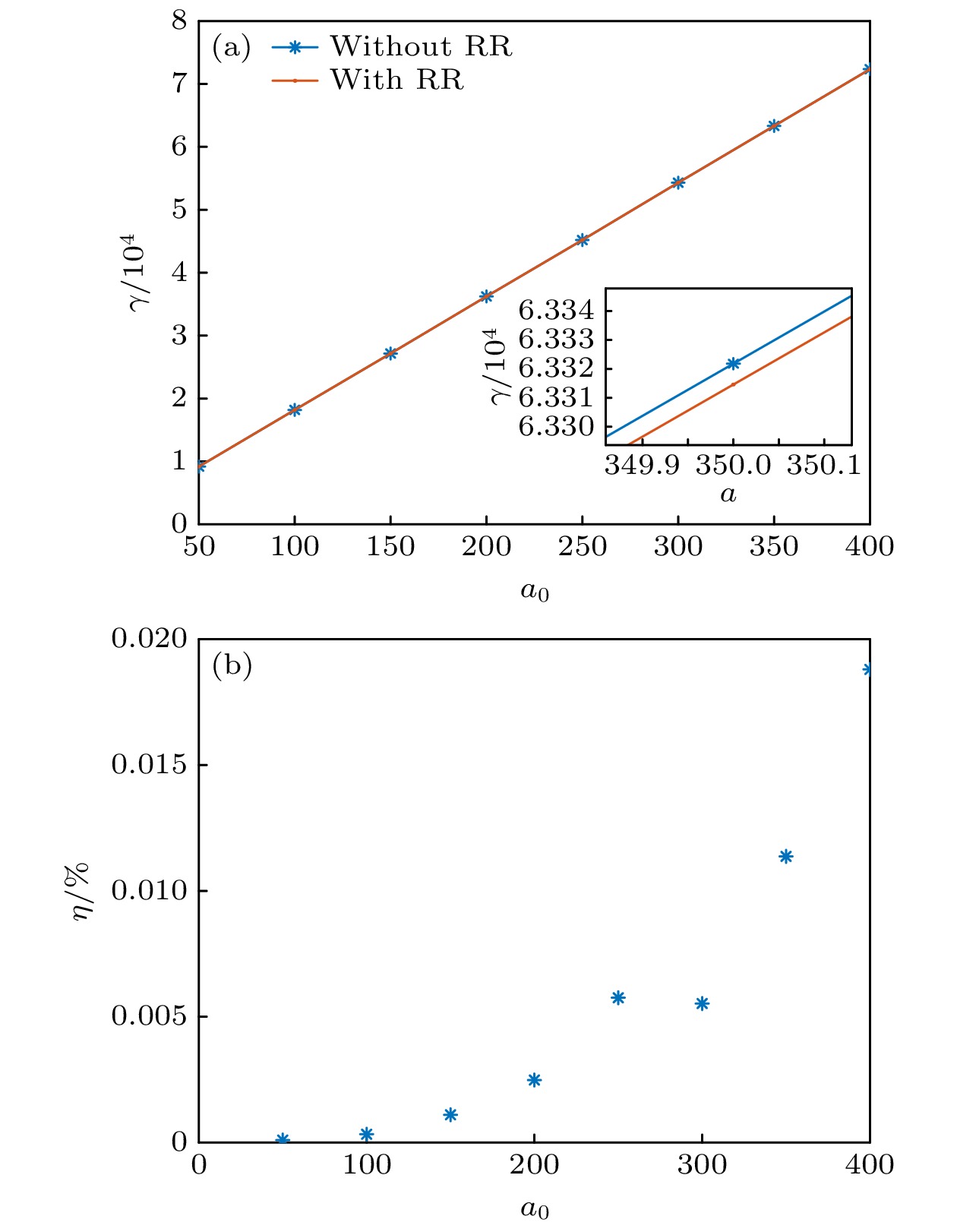
图 5 电子加速能量与激光强度的定标关系 (a)最终时刻, 电子相对论因子$ \gamma $的值与激光强度a0之间的关系, 其中蓝线为不考虑RR的结果, 红线为考虑RR的结果; (b) RR效应对电子能量的影响随a0的变化关系
Figure 5. Scaling relationship between electron acceleration energy and laser intensity: (a) Relationship between the relativistic factor γ of electrons at the final moment and the laser intensity a0, the blue line represents the results without considering radiation reaction (RR), while the red line represents the results considering RR; (b) variation of the impact of RR on electron energy with respect to the change in a0.
-
[1] Dutta B, Ghosh S, Gurrola A, Julson D, Kamon T, Kumar J 2023 J. High Energ. Phys. 2023 164
[2] Bostedt C, Boutet S, Fritz D M, Huang Z R, Lee H J, Lemke H T, Robert A, Schlotter W F, Turner J J, Williams G J 2016 Rev. Mod. Phys. 88 015007
Google Scholar
[3] Tajima T, Dawson J M 1979 Phys. Rev. Lett. 43 267
Google Scholar
[4] Strickland D, Mourou G 1985 Opt. Commun. 56 219
Google Scholar
[5] Gonsalves A J, Nakamura K, Daniels J, Benedetti C, Pieronek C, de Raadt T C H, Steinke S, Bin J H, Bulanov S S, van Tilborg J, Geddes C G R, Schroeder C B, Tóth C, Esarey E, Swanson K, Fan-Chiang L, Bagdasarov G, Bobrova N, Gasilov V, Korn G, Sasorov P, Leemans W P 2019 Phys. Rev. Lett. 122 084801
Google Scholar
[6] Zeng Y S, Yu X Q, Tian Y 2023 Chin. J. Lasers 50 1714008 [曾雨珊, 余谢秋, 田野 2023 中国激光 50 1714008]
Google Scholar
Zeng Y S, Yu X Q, Tian Y 2023 Chin. J. Lasers 50 1714008
Google Scholar
[7] Yu X Q, Zeng Y S, Song L W, Kong D Y, Hao S B, Gui J Y, Yang X J, Xu Y, Wu X J, Leng Y X, Tian Y, Li R X 2023 Nat. Photonics 17 957
Google Scholar
[8] Lawson J D 1979 IEEE Trans. Nucl. Sci. 26 4217
Google Scholar
[9] Hartemann F V, Fochs S N, Le Sage G P, Luhmann N C Jr, Woodworth J G, Perry M D, Chen Y J, Kerman A K 1995 Phys. Rev. E 51 4833
Google Scholar
[10] Esarey E, Sprangle P, Krall J 1995 Phys. Rev. E 52 5443
Google Scholar
[11] He F, Yu W, Lu P X, Xu H, Qian L J, Shen B F, Yuan X, Li R X, Xu Z Z 2003 Phys. Rev. E 68 046407
Google Scholar
[12] Stupakov G V, Zolotorev M S 2001 Phys. Rev. Lett. 86 5274
Google Scholar
[13] Dodin I Y, Fisch N J 2003 Phys. Rev. E 68 056402
Google Scholar
[14] Salamin Y I, Keitel C H 2002 Phys. Rev. Lett. 88 095005
Google Scholar
[15] Pang J, Ho Y K, Yuan X Q, Cao N, Kong Q, Wang P X, Shao L, Esarey E H, Sessler A M 2002 Phys. Rev. E 66 066501
[16] Maltsev A, Ditmire T 2003 Phys. Rev. Lett. 90 053002
Google Scholar
[17] Tian Y, Liu J S, Wang W T, Wang C, Deng A H, Xia C Q, Li W T, Cao L H, Lu H Y, Zhang H, Xu Y, Leng Y X, Li R X, Xu Z Z 2012 Phys. Rev. Lett. 109 115002
Google Scholar
[18] Thévenet M, Leblanc A, Kahaly S, Vincenti H, Vernier A, Quéré F, Faure J 2016 Nat. Phys. 12 355
Google Scholar
[19] Zhou C L, Bai Y F, Song L W, Zeng Y S, Xu Y, Zhang D D, Lu X M, Leng Y X, Liu J S, Tian Y, Li R X, Xu Z Z 2021 Nat. Photonics 15 216
Google Scholar
[20] Thaury C, Quéré F, Geindre J, Lévy A, Ceccotti T, Monot P, Bougeard M, Réau F, d’Oliveira P, Audebert P, Marjoribanks R S, Martin P A 2007 Nat. Phys. 3 424
Google Scholar
[21] Doumy G, Quéré F, Gobert O, Perdrix M, Martin P, Audebert P, Gauthier J C, Geindre J P, Wittmann T 2004 Phys. Rev. E 69 026402
Google Scholar
[22] Quesnel B, Mora P 1998 Phys. Rev. E 58 3719
Google Scholar
[23] Ritus V I 1985 J. Russ. Laser Res. 6 497
Google Scholar
[24] Landau L D, Lifshitz E M 1971 The Classical Theory of Fields (Oxford: Pergamon Press
[25] Stupakov G, Huang Z 2008 Phys. Rev. ST Accel. Beams 11 014401
Google Scholar
[26] Piazza A D, Müller C, Hatsagortsyan K Z, Keitel C H 2012 Rev. Mod. Phys. 84 1177
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 958
- PDF Downloads: 62
- Cited By: 0
