-
We study the creation of electron-positron pairs in vacuum induced by multi-photon transition process with combined oscillating fields. According to the computational quantum field theory and the split operator technique, we numerically solve the spatiotemporally dependent Dirac equation. The effects of field frequencies on the yields and energy distributions of electron-positron pairs are investigated.First, we show that even for subcritical fields, the goal of generating electron-positron pairs continuously can be achieved by combining two oscillating fields. We also find that when the sum of the field frequencies is close to
$ 2.3c ^ 2 $ (a.u.), the yield of the created pairs reaches a maximum value. In the case that only one oscillating filed is involved and single photon transition is dominant, the pair creation is also optimal at this frequency. In this way, the sum of the frequencies of the combined fields is fixed at$ 2.3c^2 $ in the later simulations. For example, oscillating fields with$\omega_1=1.1c^{2},\; \omega_2= 1.2c^{2}$ ;$\omega_1=1.0c^{2},\; \omega_2= 1.3c^{2}$ ;$ \omega_1=0.8c^{2}, $ $ \omega_2= 1.5c^{2} $ ;$\omega_1=0.5c^{2},\; \omega_2= 1.8c^{2}$ ; and$\omega_1=0.4c^{2},\; \omega_2= 1.9c^{2}$ are applied to the following study.The time evolutions of the yield of the electron-positron pairs under different frequency combinations are investigated. It is found that when the frequencies of the two fields are close to each other, the growth rate${\rm{d}}N/{\rm{d}}t$ presents an obvious periodic variation, showing a “beat” - like structure. The “beat” - like structure is found to be synchronized with the synthesized electric field. Meanwhile, the long-term growth rate${\rm{d}}N/{\rm{d}}t$ of the pairs increases significantly when the field frequency difference becomes larger.The energy distributions of the electron-positron pairs created at different frequency combinations are studied. It is found that when the frequency difference is small (eg,$\omega_1=1.0c^{2},\; \omega_2= 1.3c^{2}$ ), the energy distribution of the particles shows a quasi-monoenergetic feature, with most of the particles distributed around$ 1.1c^{2}-1.2c^{2} $ . For a large frequency difference (eg,$\omega_1=0.5c^{2},\; \omega_2= 1.8c^{2}$ ), the total yield of the pairs greatly increases. Meanwhile, the energy range of the particles is broadened significantly with the generation of more energetic particles.By analyzing and comparing the probability distributions of transitions between the negative energy and the positive energy, we find that the main reason for the spectrum-broadening and the yield-increasing is the enhancement of the multi-photon transition process. Beside the two-photon transition ($ \omega_{1}+\omega_{2} $ ), which is of high probability in all the cases, the higher-order photon transitions ($2\omega_{1}+\omega_{2},\;3\omega_{1}+\omega_{2},\;4\omega_{1}+\omega_{2}$ ) will arise with probability in the same order as the two-photon transition. These multi-photon transitions enhance the creation of the electron-positron pairs, especially the high-energy pairs. The second reason is that for a narrow field width ($ W=2/c $ ), the conservation of the momentum breaks down, the generation of electron-positron pairs corresponding to the asymmetric transitions becomes important, which further enhances the pair production and broadens the energy distribution.For a wide field width ($ W=5/c $ ), the probability of high-order photon transitions and the asymmetric transitions are suppressed compared with the case of narrow field width ($ W=2/c $ ). However, the frequencies of the combined fields still have important influence on the pair productions and energy distributions.[1] Schwinger J 1951 Phys. Rev. 82 664
Google Scholar
[2] Cowan T, Backe H, Bethge K, Bokemeyer H, Folger H, Greenberg J S, Sakaguchi K, Schwalm D, Schweppe J, Stiebing K E, Vincent P 1986 Phys. Rev. Lett. 56 444
Google Scholar
[3] Ahmad I, Austin S M, Back B B, et al. 1997 Phys. Rev. Lett. 78 618
Google Scholar
[4] Burke D L, Field R C, Horton-Smith G, Spencer J E, Walz D, Berridge S C, Bugg W M, Shmakov K, Weidemann A W, Bula C, McDonald K T, Prebys E J 1997 Phys. Rev. Lett. 79 1626
Google Scholar
[5] Bamber C, Boege S J, Koffas T, et al. 1999 Phys. Rev. D 60 092004
Google Scholar
[6] Chen H, Wilks S C, Meyerhofer D D, Bonlie J, Chen C D, Chen S N, Courtois C, Elberson L, Gregori G, Kruer W, Landoas O, Mithen J, Myatt J, Murphy C D, Nilson P, Price D, Schneider M, Shepherd R, Stoeckl C, Tabak M, Tommasini R, Beiersdorfer P 2010 Phys. Rev. Lett. 105 015003
Google Scholar
[7] Gies H, Klingmüller K 2005 Phys. Rev. D 72 065001
Google Scholar
[8] Ilderton A, Torgrimsson G, Wårdh J 2015 Phys. Rev. D 92 065001
Google Scholar
[9] Blinne A, Strobel E 2016 Phys. Rev. D 93 025014
Google Scholar
[10] Kohlfürst C, Alkofer R 2018 Phys. Rev. D 97 036026
Google Scholar
[11] Olugh O, Li Z L, Xie B S, Alkofer R 2019 Phys. Rev. D 99 036003
Google Scholar
[12] Kluger Y, Eisenberg J M, Svetitsky B, Cooper F, Mottola E 1991 Phys. Rev. Lett. 67 2427
Google Scholar
[13] Alkofer R, Hecht M B, Roberts C D, Schmidt S M, Vinnik D V 2001 Phys. Rev. Lett. 87 193902
Google Scholar
[14] Sitiwaldi I, Xie B S 2017 Phys. Lett. B 768 174
Google Scholar
[15] Krekora P, Cooley K, Su Q, Grobe R 2005 Phys. Rev. Lett. 95 070403
Google Scholar
[16] Lv Q Z, Liu Y, Li Y J, Grobe R, Su Q 2013 Phys. Rev. Lett. 111 183204
Google Scholar
[17] Tang S, Xie B S, Lu D, Wang H Y, Fu L B, Liu J 2013 Phys. Rev. A 88 012106
Google Scholar
[18] Li Z L, Xie B S, Li Y J 2019 Phys. Rev. D 100 076018
Google Scholar
[19] Wang Q, Liu J, Fu L B 2016 Sci. Rep. 6 25292
Google Scholar
[20] Wang Q, Xia Q Z, Liu J, Fu L B 2018 Chin. Phys. B 27 080302
Google Scholar
[21] Su D D, Li Y T, Lv Q Z, Zhang J 2020 Phy. Rev. D 101 054501
[22] Liu Y, Lv Q Z, Li Y T, Grobe R, Su Q 2015 Phys. Rev. A 91 052123
Google Scholar
[23] Krekora P, Su Q, Grobe R 2004 Phys. Rev. Lett. 92 040406
Google Scholar
[24] Wöllert A, Klaiber M, Bauke H, Keitel C H 2015 Phys. Rev. D 91 065022
Google Scholar
[25] Schützhold R, Gies H, Dunne G 2008 Phys. Rev. Lett. 101 130404
Google Scholar
[26] Jiang M, Su W, Lu X, Sheng Z M, Li Y T, Li Y J, Zhang J, Grobe R, Su Q 2011 Phys. Rev. A 83 053402
Google Scholar
[27] Jiang M, Su W, Lv Z Q, Lu X, Li Y J, Grobe R, Su Q 2012 Phys. Rev. A 85 033408
Google Scholar
[28] Braun J W, Su Q, Grobe R 1999 Phys. Rev. A 59 604
Google Scholar
[29] Wagner R E, Ware M R, Shields B T, Su Q, Grobe R 2011 Phys. Rev. Lett. 106 023601
Google Scholar
[30] Bandrauk A D, Shen H 1994 J. Phys. A: Math. Gen. 27 7147
Google Scholar
[31] Mocken G R, Keitel C H 2008 Comput. Phys. Commun. 178 868
Google Scholar
[32] 江淼, 郑晓冉, 林南省, 李英骏 2021 70 231202
Google Scholar
Jiang M, Zheng X R, Lin N S, Li Y J 2021 Acta Phys. Sin. 70 231202
Google Scholar
-
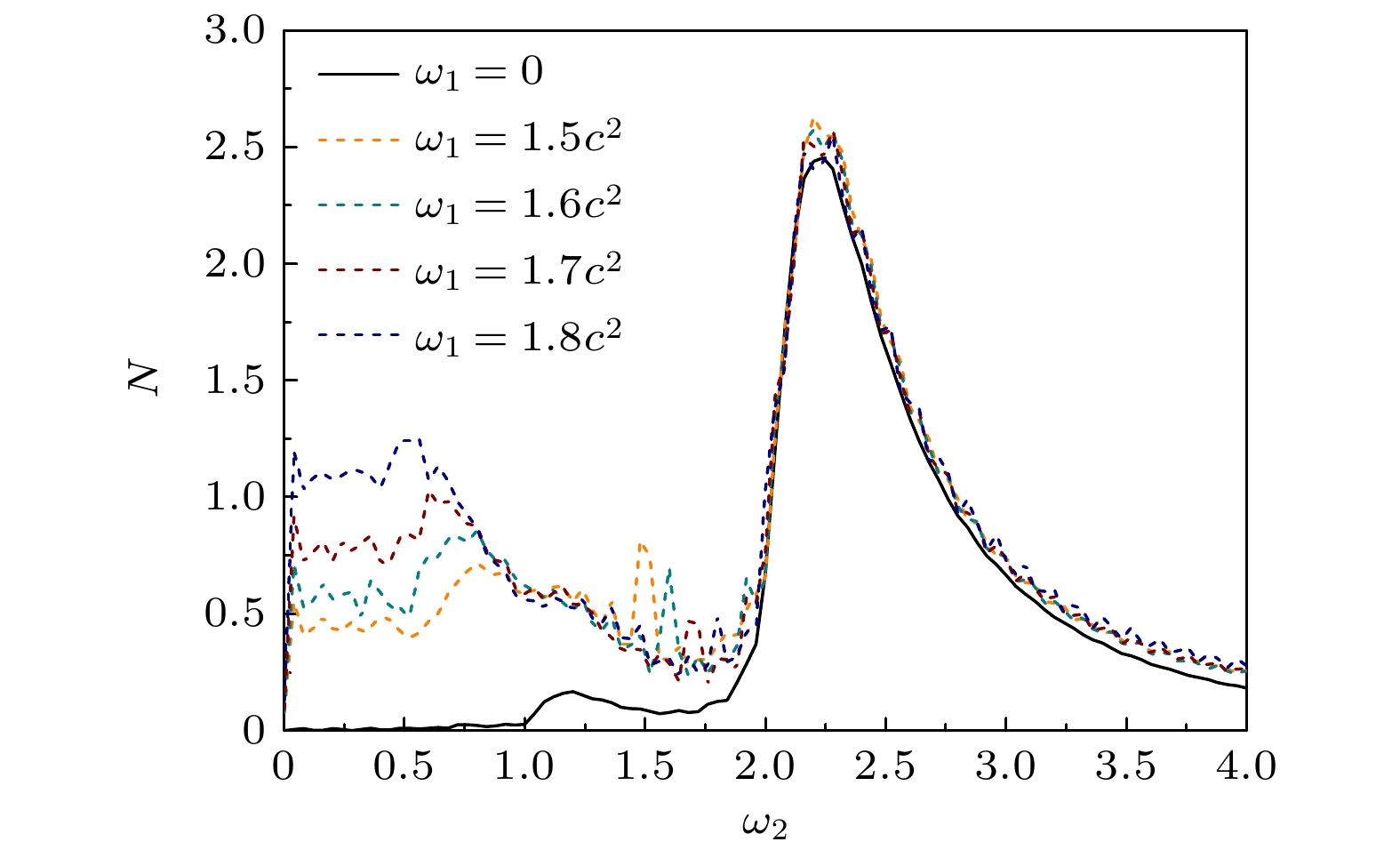
图 1 双振荡场情况下粒子对数量随外场频率
$ \omega_2 $ 的变化关系图($ t=0.003 $ 时刻), 势场高度$ V_1=V_2=2.0 c^2 $ , 宽度$ W=2/c $ . 黑色实线为单个振荡场下的粒子对数量与频率的关系Figure 1. The dashed lines give the total number of created pairs for different combined frequencies at
$ t=0.003 $ ,$ V_1= $ $ V_2=2.0 c^2 $ , and width is$ W=2/c $ . The black solid line illustrates the number of created pairs when only one oscillating field is presented
图 2 (a)保持双振荡场频率和均为
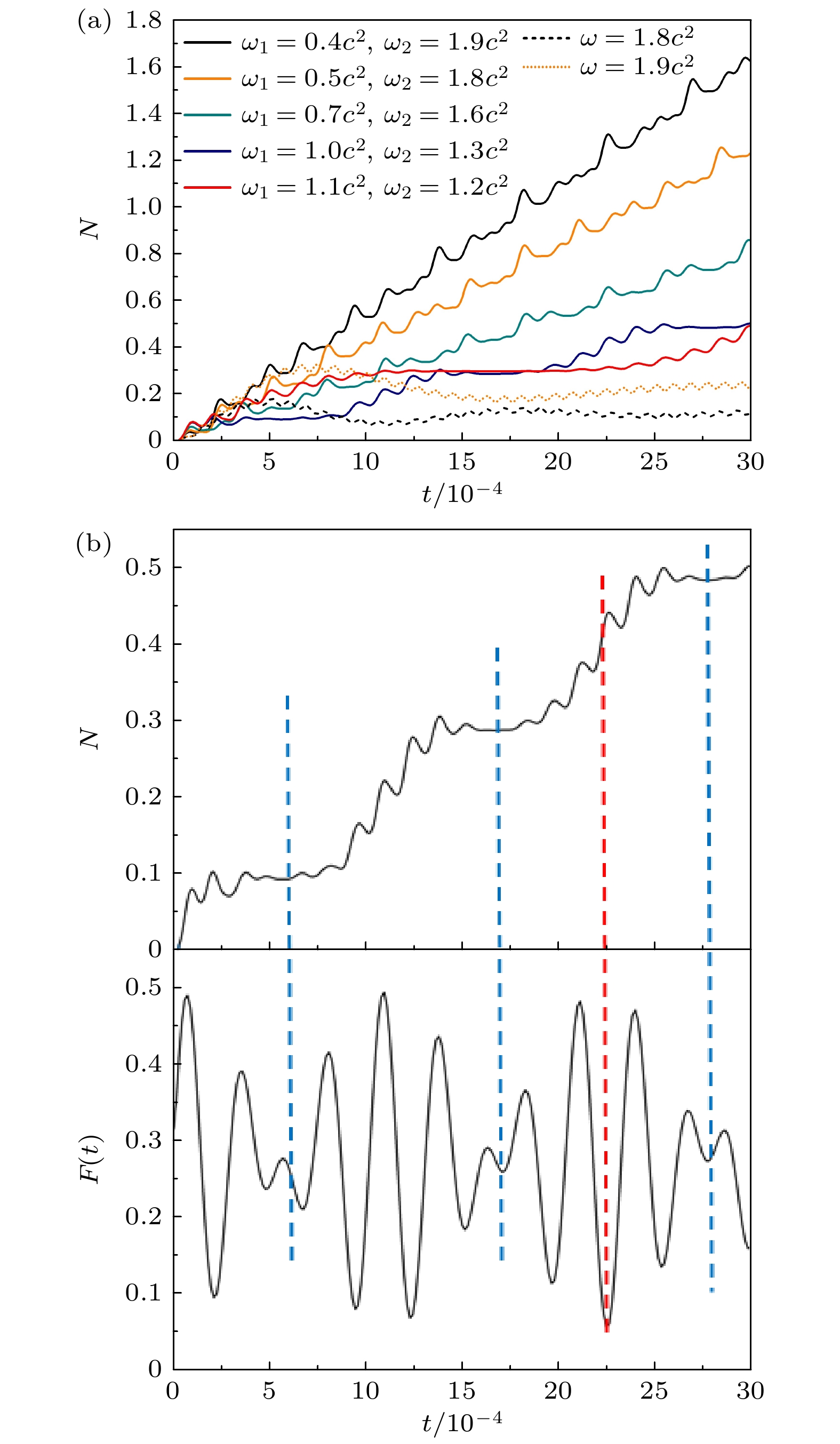
$ 2.3 c^2 $ 时不同组合场频率下电子对产量$ N $ 随时间的演化图; (b)$ N(t) $ 与$ F(t) $ 的对比图, 上半部分为$ \omega_1 = 1.0 c^2 $ ,$ \omega_2=1.3 c^2 $ 时的$ N(t) $ 曲线, 下半部分是相同条件下$ F(t) $ 的示意图. 势高$ V_1= V_2= $ $ 2.0 c^2 $ , 场宽$ W=2/c $ Figure 2. (a) Time evolution of the total number
$ N $ of created electron-positron pairs under different combined frequencies. The sum of the frequencies of the two oscillating fields are kept as$ 2.3 c^2 $ . (b) Comparison of the time evolution of pair production$ N(t) $ and$ f(t) $ . The upper part is the$ N(t) $ figure for$ \omega_1 = 1.0 c^2 $ ,$ \omega_2=1.3 c^2 $ and the below part is the sketch of$ F(t) $ under the same conditions.$V_1= V_2= $ $ 2.0 c^2 $ ,$W=2/c $ 
图 3 保持双振荡场频率之和为
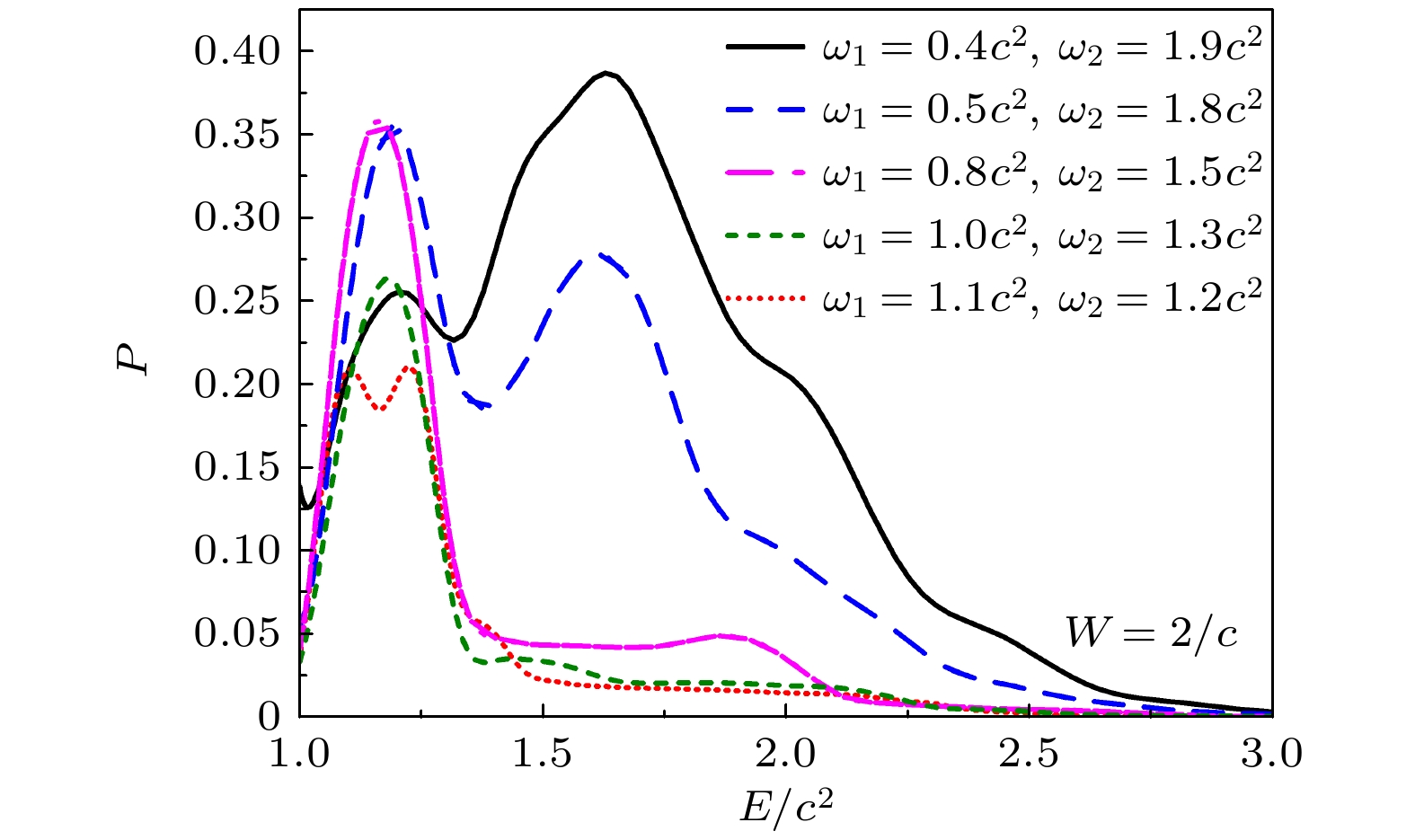
$ 2.3 c^{2} $ 时五组不同组合频率下产生粒子的能量分布概率. 演化时间$ t=0.003\; {\rm{a.u.}} $ . 势高$ V_1=V_2=2.0 c^2 $ , 场宽$ W=2/c $ Figure 3. The energy distribution of the particles created with two oscillating fields with different combined frequencies at
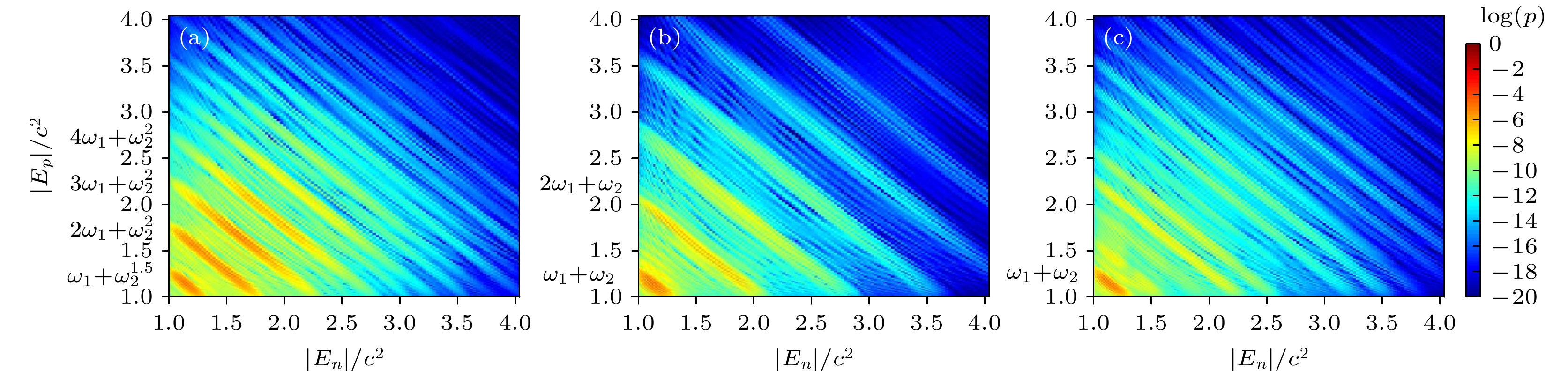
$ t=0.003 \;{\rm{a.u.}} $ .$ V_1=V_2=2.0 c^2 $ ,$ W=2/c $ 
图 4 双振荡场下粒子跃迁能量概率分布图 (a)
$\omega_1=0.5 c^{2},\; \omega_2=1.8 c^{2}$ ; (b)$\omega_1=0.8 c^{2},\; \omega_2=1.5 c^{2}$ ; (c)$ \omega_1=1.0 c^{2}, $ $ \omega_2=1.3 c^{2} $ . 势高$ V_1=V_2=2.0 c^2 $ , 场宽$ W=2/c $ Figure 4. The probability distribution of transitions with different frequency combinations: (a)
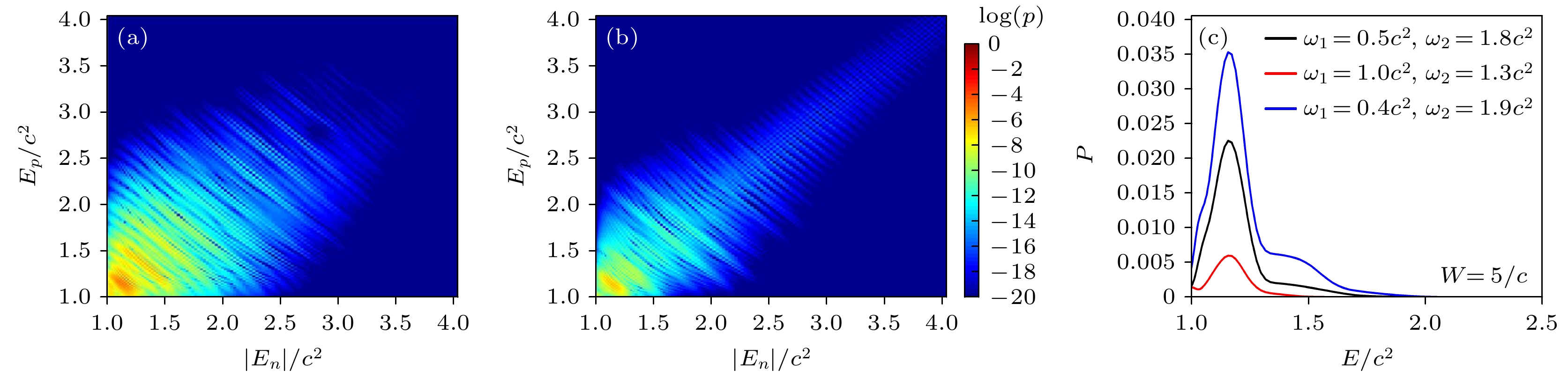
$\omega_1=0.5 c^{2},\; \omega_2=1.8 c^{2}$ ; (b)$ \omega_1=0.8 c^{2}, $ $ \omega_2=1.5 c ^{2} $ ; (c)$\omega_1=1.0 c^{2},\; \omega_2=1.3 c ^{2}$ .$ V_1=V_2=2.0 c^2 $ .$ W=2/c $ .
图 5 场宽为
$ W=5/c $ 时(a)$\omega_1=0.4 c^{2},\; \omega_2=1.9 c^{2}$ 和(b)$\omega_1=1.0 c^{2},\; \omega_2=1.3 c^{2}$ 的概率分布图. (c)不同组合频率下粒子的能量概率分布. 势高$ V_1=V_2=2.0 c^2 $ Figure 5. The probability distribution of transitions with W=5/c: (a)
$\omega_1=0.4 c^{2},\; \omega_2=1.9 c^{2}$ ; (b)$\omega_1=1.0 c^{2},\; \omega_2=1.3 c ^{2}$ . (c) The energy distributions of the particles at$ t=0.003 \;{\rm{a.u.}} $ .$ V_1=V_2=2.0 c^2 $ -
[1] Schwinger J 1951 Phys. Rev. 82 664
Google Scholar
[2] Cowan T, Backe H, Bethge K, Bokemeyer H, Folger H, Greenberg J S, Sakaguchi K, Schwalm D, Schweppe J, Stiebing K E, Vincent P 1986 Phys. Rev. Lett. 56 444
Google Scholar
[3] Ahmad I, Austin S M, Back B B, et al. 1997 Phys. Rev. Lett. 78 618
Google Scholar
[4] Burke D L, Field R C, Horton-Smith G, Spencer J E, Walz D, Berridge S C, Bugg W M, Shmakov K, Weidemann A W, Bula C, McDonald K T, Prebys E J 1997 Phys. Rev. Lett. 79 1626
Google Scholar
[5] Bamber C, Boege S J, Koffas T, et al. 1999 Phys. Rev. D 60 092004
Google Scholar
[6] Chen H, Wilks S C, Meyerhofer D D, Bonlie J, Chen C D, Chen S N, Courtois C, Elberson L, Gregori G, Kruer W, Landoas O, Mithen J, Myatt J, Murphy C D, Nilson P, Price D, Schneider M, Shepherd R, Stoeckl C, Tabak M, Tommasini R, Beiersdorfer P 2010 Phys. Rev. Lett. 105 015003
Google Scholar
[7] Gies H, Klingmüller K 2005 Phys. Rev. D 72 065001
Google Scholar
[8] Ilderton A, Torgrimsson G, Wårdh J 2015 Phys. Rev. D 92 065001
Google Scholar
[9] Blinne A, Strobel E 2016 Phys. Rev. D 93 025014
Google Scholar
[10] Kohlfürst C, Alkofer R 2018 Phys. Rev. D 97 036026
Google Scholar
[11] Olugh O, Li Z L, Xie B S, Alkofer R 2019 Phys. Rev. D 99 036003
Google Scholar
[12] Kluger Y, Eisenberg J M, Svetitsky B, Cooper F, Mottola E 1991 Phys. Rev. Lett. 67 2427
Google Scholar
[13] Alkofer R, Hecht M B, Roberts C D, Schmidt S M, Vinnik D V 2001 Phys. Rev. Lett. 87 193902
Google Scholar
[14] Sitiwaldi I, Xie B S 2017 Phys. Lett. B 768 174
Google Scholar
[15] Krekora P, Cooley K, Su Q, Grobe R 2005 Phys. Rev. Lett. 95 070403
Google Scholar
[16] Lv Q Z, Liu Y, Li Y J, Grobe R, Su Q 2013 Phys. Rev. Lett. 111 183204
Google Scholar
[17] Tang S, Xie B S, Lu D, Wang H Y, Fu L B, Liu J 2013 Phys. Rev. A 88 012106
Google Scholar
[18] Li Z L, Xie B S, Li Y J 2019 Phys. Rev. D 100 076018
Google Scholar
[19] Wang Q, Liu J, Fu L B 2016 Sci. Rep. 6 25292
Google Scholar
[20] Wang Q, Xia Q Z, Liu J, Fu L B 2018 Chin. Phys. B 27 080302
Google Scholar
[21] Su D D, Li Y T, Lv Q Z, Zhang J 2020 Phy. Rev. D 101 054501
[22] Liu Y, Lv Q Z, Li Y T, Grobe R, Su Q 2015 Phys. Rev. A 91 052123
Google Scholar
[23] Krekora P, Su Q, Grobe R 2004 Phys. Rev. Lett. 92 040406
Google Scholar
[24] Wöllert A, Klaiber M, Bauke H, Keitel C H 2015 Phys. Rev. D 91 065022
Google Scholar
[25] Schützhold R, Gies H, Dunne G 2008 Phys. Rev. Lett. 101 130404
Google Scholar
[26] Jiang M, Su W, Lu X, Sheng Z M, Li Y T, Li Y J, Zhang J, Grobe R, Su Q 2011 Phys. Rev. A 83 053402
Google Scholar
[27] Jiang M, Su W, Lv Z Q, Lu X, Li Y J, Grobe R, Su Q 2012 Phys. Rev. A 85 033408
Google Scholar
[28] Braun J W, Su Q, Grobe R 1999 Phys. Rev. A 59 604
Google Scholar
[29] Wagner R E, Ware M R, Shields B T, Su Q, Grobe R 2011 Phys. Rev. Lett. 106 023601
Google Scholar
[30] Bandrauk A D, Shen H 1994 J. Phys. A: Math. Gen. 27 7147
Google Scholar
[31] Mocken G R, Keitel C H 2008 Comput. Phys. Commun. 178 868
Google Scholar
[32] 江淼, 郑晓冉, 林南省, 李英骏 2021 70 231202
Google Scholar
Jiang M, Zheng X R, Lin N S, Li Y J 2021 Acta Phys. Sin. 70 231202
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3434
- PDF Downloads: 66
- Cited By: 0
