-
环形正负电子对撞机(CEPC)束流能量的精确标定是希格斯粒子质量宽度、W/Z玻色子质量的精确测量, 从而精确检验标准模型的基本实验依据. 基于此, 束流能量的误差控制要求在10–5水平. 康普顿背散射方法是适用于百GeV高能电子对撞机束流能量高精度标定的测量方法. 本文拟采用微波电子康普顿背散射后对散射光子能量的精确测量, 来反推CEPC束流能量, 理论预计精度可达到3 MeV左右. 首先根据设计需求选定圆波导传输TM01模微波, 并求解该条件下的电磁场分布情况及坡印廷矢量. 根据波导内光子分布传输情况提出设计思路简化计算的复杂程度, 结合高纯锗探测器灵敏度、同步辐射本底等限制条件联立方程求解符合设计要求的参数. 使用最优的一组波导内径、微波波长、电子入射角数据求得微波功率为100 W时的微分散射截面对能量的导数及对撞亮度, 进一步求得15 MeV能量的散射光子数密度, 根据该能量下同步辐射光子数密度的大小分析了信噪比. 理论上论证了该方案的可行性并讨论了该方案有待进一步研究的技术难点与问题.The accurate calibration of the beam energy of the circular electron-positron collider (CEPC) is performed to accurately measure the mass width of Higgs particle and the mass of W/Z boson, thus providing the basic experimental basis for the accurate test of the standard model. Based on this, the error control of beam energy is required to be at a level of 10–5. Compton backscattering method is suitable for high precision calibration of beam energy in the Hundred GeV high energy electron collider. In this work, the CEPC beam energy is predicted to reach a theoretical accuracy of about 3 MeV by using the accurate measurement of the scattered photon energy after microwave electron Compton backscattering. Firstly, TM01 mode microwave transmission in circular waveguide is selected according to the design requirements, and the electromagnetic field distribution and Poynting vector under this condition are solved. According to the photon distribution and transmission in the waveguide, the design idea is proposed to simplify the complexity of calculation, and the parameters conforming to the design requirements are solved by combining the simultaneous equations of the high purity germanium detector sensitivity and the background of synchrotron radiation. Using the optimal set of waveguide inner diameter, microwave wavelength and electron incident angle data, the derivative of the differential scattering cross section with respect to energy and the collision brightness are obtained when the microwave power is 100 W. The scattered photon density of 15 MeV energy is further obtained, and the signal-to-noise ratio is analyzed according to the photon density of synchrotron radiation under this energy. The feasibility of the scheme is demonstrated theoretically and the technical difficulties and problems to be further studied are discussed.
-
Keywords:
- Compton backscattering /
- circular electron-positron collider /
- beam energy calibration /
- microwave
[1] Tanabashi M, Hagiwara K, Hikasa K, et al. 2018 Phys. Rev. D 98 030001
[2] Ahmad ML A, DanieleA, et al. 2015 CEPC-SppC Preliminary Conceptual Design Report (Vol. Volume I: Physics and Detector) I 17
[3] Achasov M N, Zhang JY, Muchnoi N Y 2017 Nucl. Part. Phys. Proc. 287 19
[4] Compton A H 1923 Phys. Rev. 21 483
Google Scholar
[5] Verlinde E 1996 European School Of High-Energy Physics, Proceedings 96 1
[6] Milburn R H 1963 Phys. Rev. Lett. 10 75
Google Scholar
[7] Arutyunian F R, Tumanian V A 1963 Phys. Lett. 4 176
Google Scholar
[8] Sandorfi A M, LeVine M J, Thorn C E, Giordano G, Matone G 1983 IEEE Trans. Nucl. Sci. 30 3083
Google Scholar
[9] Schoenlein R W, Leemans W P 1996 Science 274 236
Google Scholar
[10] Pogorelsky I V 1998 Nucl. Instrum. Methods Phys. Res., Sect. A 411 172
Google Scholar
[11] Zhang J Y, Cai X, Mo X H, Fu C D, Tang G Y, Achasov M N, Muchnoi N Y, Nikolaev I B, Harris F A 2019 Nucl. Phys. B 939 391
Google Scholar
[12] Xiao-Hu M O 2014 Chin. Phys. C 38 106203
Google Scholar
[13] Zhang J Y, Fu C D, Mo X H, Zhang Z L, Li D W, Wang B Y 2011 Chin. Phys. C 35 660
Google Scholar
[14] Tang G Y, Chen S H, Chen Y, Duan Z, Ruan M Q, An G P, Huang Y S, Lou X C, Zhang J Y, Lan X F, Zhang C L 2020 Rev. Sci. Instrum. 91 033109
Google Scholar
[15] 郭硕鸿 2008 电动力学 (北京: 高等教育出版社)第1−286页
Guo S H 2008 Electrodynamics (Beijing: Higher Education Press) pp1−286(in Chinese)
[16] 赵凯华 1984 大学物理 1 1
Zhao K H 1984 College Physics 1 1
[17] Zhang J Y, Cai X, Mo X H, Guo D Z, Wang J L, Liu B Q, Achasov M N, Krasnov A A, Muchnoi N Y, Pyata E E, Mamoshkina E V, Harris F A 2016 Chin. Phys. C 40 076001
Google Scholar
[18] Shuiting X 2018 Research On Compton Scattering between Photon and High Energy Electron (Vol. I) (Wuhan: Wuhan University) pp1−13
[19] Mobilio S, Boscherini F, Meneghini C 2015 Synchrotron Radiation Basics, Methods and Applications (Berlin Heidelberg: Springer-Verlag) pp1−799
[20] White S M, Burkhardt H, Puzo P 2010 Université Paris-Sud: CERN CERN-THESIS-2010-139 154
[21] Nickolai Muchnoi N S U a N, IYF 2018 arXiv: 1803.09595 v1 [hep-ph
[22] Suzuki T https://inspirehep.net/literature/111239[2021-7-5]
[23] Si M Y, Huang Y S 2021 Rev. Sci. Instrum.
-
图 2 波导中坡印廷矢量变化情况 (a)各分量沿ρ方向变化情况; (b) 各分量沿z方向变化情况; (c)坡印廷矢量z分量在空间中的变化情况; (d) 坡印廷矢量ρ分量在空间中的变化情况
Fig. 2. Poynting vector variation in the waveguide: (a) The variations of each Poynting vector’s components along the ρ axis; (b) the variations of each Poynting vector’s components along the z axis; (c)variations of the z component of Poynting vector in space; (d) variations of the ρ component of Poynting vector in space.
图 4 单模传输波长-内径解
Fig. 4. Solution of wavelength and inner diameter for single mode transmission.
图 5 散射光子不同能量对应的dσ/dω
Fig. 5. Different energies of scattered photons corresponding to the dσ/dω.
图 6 电子束团、微波统一坐标系
Fig. 6. Unified coordinate system for electron beam cluster and microwave.
表 1 CEPC同步辐射参数值
Table 1. Parameters of CEPC synchrotron radiation.
参数 符号 值 单位 束流能量 E 120 GeV 束流电流 I 17.4 mA 转弯半径 ρ 10900 m 单位长度功率 P 435 W/m 临界能量 Ec 351.6 keV 弯转角 θ 2.844 mrad 张角 φ 4.258 Μ.25 
下载: 导出CSV
表 2 单模传输时微波-电子系统各参数值
Table 2. Parameters of microwave-electronic system in single mode transmission.
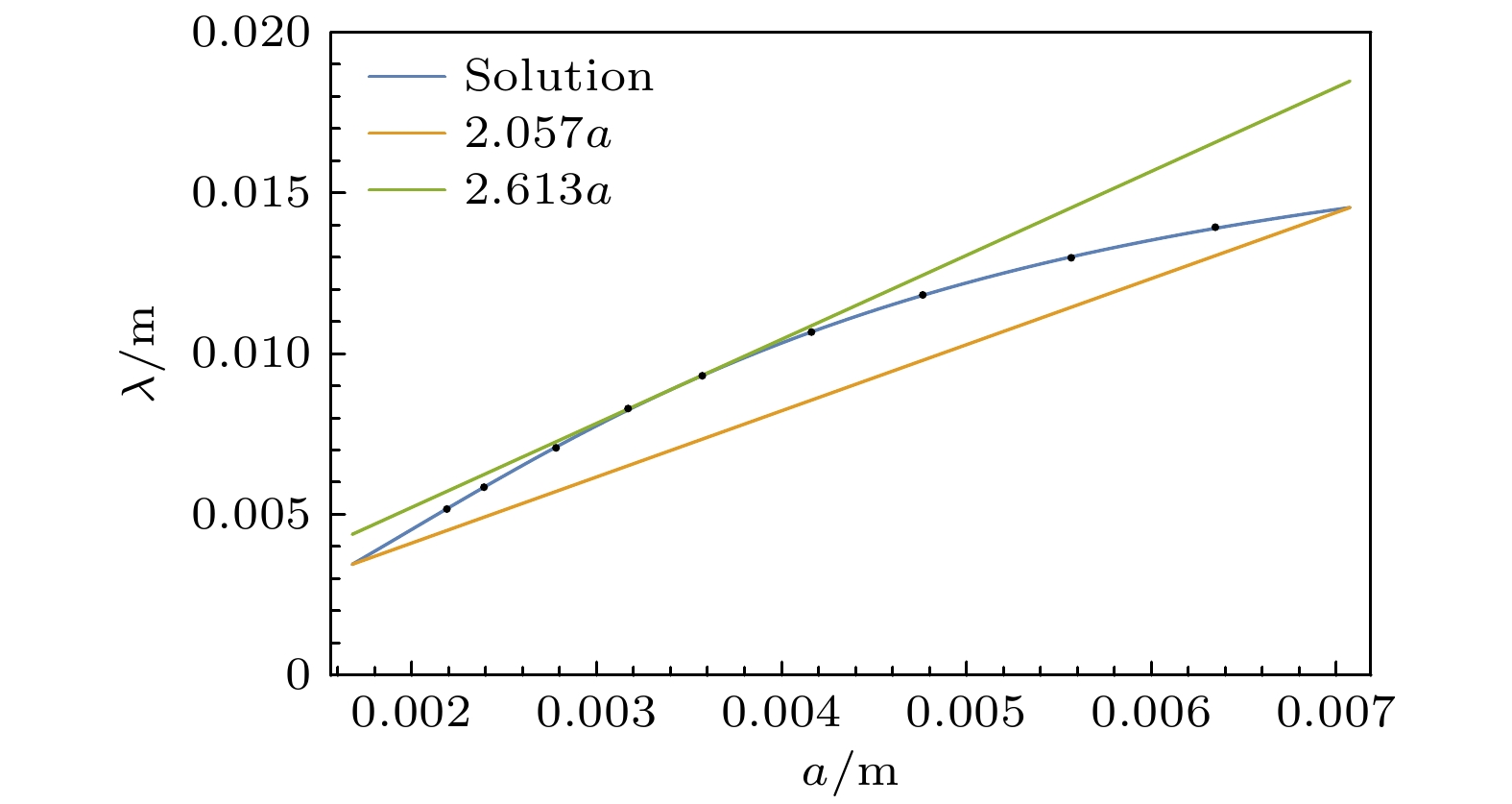
a/m λ/m vg cosψ/cosθ Tz/m Tt/S 6.35 × 10–3 1.39 × 10–2 5.45 × 10–1c 5.45 × 10–1 1.28 × 10–2 7.80 × 10–11 5.5 × 10–3 1.30 × 10–2 4.46 × 10–1c 4.46 × 10–1 1.46 × 10–2 1.09 × 10–10 4.76 × 10–3 1.18 × 10–2 3.13 × 10–1c 3.13 × 10–1 1.89 × 10–2 2.01 × 10–10 4.17 × 10–3 1.07 × 10–2 1.88 × 10–1c 1.88 × 10–1 2.85 × 10–2 5.05 × 10–10 3.57 × 10–3 9.32 × 10–2 3.54 × 10–1c 3.54 × 10–1 1.32 × 10–2 1.24 × 10–8 3.18 × 10–3 8.27 × 10–2 8.12 × 10–1c 8.12 × 10–1 5.09 × 10–2 2.09 × 10–9 2.78 × 10–3 7.11 × 10–2 2.11 × 10–1c 2.11 × 10–1 1.69 × 10–2 2.67 × 10–10 2.39 × 10–3 5.84 × 10–2 3.51 × 10–1c 3.51 × 10–1 8.32 × 10–3 7.91 × 10–11 2.18 × 10–3 5.16 × 10–3 4.26 × 10–1c 4.26 × 10–1 6.06 × 10–3 4.74 × 10–11
下载: 导出CSV
-
[1] Tanabashi M, Hagiwara K, Hikasa K, et al. 2018 Phys. Rev. D 98 030001
[2] Ahmad ML A, DanieleA, et al. 2015 CEPC-SppC Preliminary Conceptual Design Report (Vol. Volume I: Physics and Detector) I 17
[3] Achasov M N, Zhang JY, Muchnoi N Y 2017 Nucl. Part. Phys. Proc. 287 19
[4] Compton A H 1923 Phys. Rev. 21 483
Google Scholar
[5] Verlinde E 1996 European School Of High-Energy Physics, Proceedings 96 1
[6] Milburn R H 1963 Phys. Rev. Lett. 10 75
Google Scholar
[7] Arutyunian F R, Tumanian V A 1963 Phys. Lett. 4 176
Google Scholar
[8] Sandorfi A M, LeVine M J, Thorn C E, Giordano G, Matone G 1983 IEEE Trans. Nucl. Sci. 30 3083
Google Scholar
[9] Schoenlein R W, Leemans W P 1996 Science 274 236
Google Scholar
[10] Pogorelsky I V 1998 Nucl. Instrum. Methods Phys. Res., Sect. A 411 172
Google Scholar
[11] Zhang J Y, Cai X, Mo X H, Fu C D, Tang G Y, Achasov M N, Muchnoi N Y, Nikolaev I B, Harris F A 2019 Nucl. Phys. B 939 391
Google Scholar
[12] Xiao-Hu M O 2014 Chin. Phys. C 38 106203
Google Scholar
[13] Zhang J Y, Fu C D, Mo X H, Zhang Z L, Li D W, Wang B Y 2011 Chin. Phys. C 35 660
Google Scholar
[14] Tang G Y, Chen S H, Chen Y, Duan Z, Ruan M Q, An G P, Huang Y S, Lou X C, Zhang J Y, Lan X F, Zhang C L 2020 Rev. Sci. Instrum. 91 033109
Google Scholar
[15] 郭硕鸿 2008 电动力学 (北京: 高等教育出版社)第1−286页
Guo S H 2008 Electrodynamics (Beijing: Higher Education Press) pp1−286(in Chinese)
[16] 赵凯华 1984 大学物理 1 1
Zhao K H 1984 College Physics 1 1
[17] Zhang J Y, Cai X, Mo X H, Guo D Z, Wang J L, Liu B Q, Achasov M N, Krasnov A A, Muchnoi N Y, Pyata E E, Mamoshkina E V, Harris F A 2016 Chin. Phys. C 40 076001
Google Scholar
[18] Shuiting X 2018 Research On Compton Scattering between Photon and High Energy Electron (Vol. I) (Wuhan: Wuhan University) pp1−13
[19] Mobilio S, Boscherini F, Meneghini C 2015 Synchrotron Radiation Basics, Methods and Applications (Berlin Heidelberg: Springer-Verlag) pp1−799
[20] White S M, Burkhardt H, Puzo P 2010 Université Paris-Sud: CERN CERN-THESIS-2010-139 154
[21] Nickolai Muchnoi N S U a N, IYF 2018 arXiv: 1803.09595 v1 [hep-ph
[22] Suzuki T https://inspirehep.net/literature/111239[2021-7-5]
[23] Si M Y, Huang Y S 2021 Rev. Sci. Instrum.
下载:
计量
- 文章访问数: 5137
- PDF下载量: 97
- 被引次数: 0
