Theoretical study of double oscillating fields induced electron-positron pairs creation process

Li Chuan-Ke; Lin Nan-Sheng; Zhou Xian-Xian; Jiang Miao; Li Ying-Jun

doi:10.7498/aps.73.20230432

Abstract

We investigate an important aspect of electron-positron pair creation from vacuum in the presence of a strong background field, where the combined field plays a key role in the pair creation process. By utilizing computational quantum field theory, we explore electron-positron pair creation induced by double-located oscillating electric fields by numerically solving the Dirac equation in full spacetime dimensions. We demonstrate theoretically that computational quantum field theory is equivalent to the first-order time-dependent perturbation theory for single-photon transition pair creation in a spatially inhomogeneous and time-dependent electric field, and verify their equivalence through numerical simulations of pair creation in double-located oscillating fields. We show some interesting results about the periodic oscillation of the momentum spectrum structure of the created particle and the asymmetric multi-photon pair creation process due to the interference between two fields. By using first-order time-dependent perturbation theory, we find that the periodic oscillation in the momentum distribution of the created particle is affected by the field width, the field frequency and the distance between two fields. The period of the oscillation of momentum spectrum structure is changed by the distance between two fields, while the field width has an influence on both the difference between the peak and valley of the momentum spectra and the width of the momentum space available to the created particle. Increasing the frequency of the electric field results in larger momentum for the created particle pairs, while correspondingly reducing the coupling matrix element $ \langle p|V|n \rangle $ and diminishing the probability of electron-positron pair creation.The interference between two fields significantly enhances the yield of pair numbers for small distances between two fields. When the distance is too large, the number of pairs created by double oscillating fields is twice that created by a single field, and the enhancement is vanished. When the distance between two fields increases, the period of oscillation decreases. In turn, the creation of electron-positron pairs can become more monochromatic in momentum (energy), while the number of pairs created remains almost constant. As the electric field broadens, the yield of the created pairs decreases for constant potential height. Increasing the field width will reduce the number of particles for each momentum and narrow the momentum space of the created particle. Increasing the field frequency leads to the reduction of the coupling matrix element $ \langle p|V|n \rangle $ and subsequently reduces the total number of electron-positron pairs created. The field profile parameters such as frequency, width, and distance between two fields can be utilized to select a specific momentum (energy) of particles in future electron-positron pair creation experiments.

Keywords:

Authors and contacts

1.
State Key Laboratory for Tunnel Engineering, China University of Mining and Technology, Beijing 100083, China
2.
School of Science, China University of Mining and Technology, Beijing 100083, China
3.
School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu 233030, China

Corresponding author: Lin Nan-Sheng, phy.nslin@gmail.com ; Li Ying-Jun, lyj@aphy.iphy.ac.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11974419, 11605286, 12204001) and the National Key R&D Program of China (Grants No. 2018YFA0404802).

FullText HTML : translate this paragraph

References

[1]	Xie B S, Li Z L, Tang S 2017 Matter Radiat. Extremes 2 225 Google Scholar
[2]	Fedotov A, Ilderton A, Karbstein F, King B, Seipt D, Taya H, Torgrimsson G 2023 Phys. Rep. 1010 1 Google Scholar
[3]	Sauter F 1931 Z. Physik 69 742 Google Scholar
[4]	Heisenberg W, Euler H 1936 Z. Physik 98 714 Google Scholar
[5]	Schwinger J 1951 Phys. Rev. 82 664 Google Scholar
[6]	Brezin E, Itzykson C 1970 Phys. Rev. D 2 1191 Google Scholar
[7]	Kim S P, Page D N 2002 Phys. Rev. D 65 105002 Google Scholar
[8]	Schützhold R, Gies H, Dunne G V 2008 Phys. Rev. Lett. 101 130404 Google Scholar
[9]	Schneider C, Torgrimsson G, Schützhold R 2018 Phys. Rev. D 98 085009 Google Scholar
[10]	Abdukerim N, Li Z L, Xie B S 2013 Phys. Lett. B 726 820 Google Scholar
[11]	Li Z L, Lu D, Xie B S, Fu L B, Liu J, Shen B F 2014 Phys. Rev. D 89 093011 Google Scholar
[12]	Kohlfürst C, Gies H, Alkofer R 2014 Phys. Rev. Lett. 112 050402 Google Scholar
[13]	Gong C, Li Z L, Xie B S, Li Y J 2020 Phys. Rev. D 101 016008 Google Scholar
[14]	Hebenstreit F, Alkofer R, Gies H 2010 Phys. Rev. D 82 105026 Google Scholar
[15]	Hebenstreit F, Alkofer R, Gies H 2011 Phys. Rev. Lett. 107 180403 Google Scholar
[16]	Li Z L, Lu D, Xie B S 2015 Phys. Rev. D 92 085001 Google Scholar
[17]	Li Z L, Li Y J, Xie B S 2017 Phys. Rev. D 96 076010 Google Scholar
[18]	Kohlfürst C, Alkofer R 2018 Phys. Rev. D 97 036026 Google Scholar
[19]	Kohlfürst C 2019 Phys. Rev. D 99 096017 Google Scholar
[20]	Cheng T, Su Q C, Grobe R 2010 Contemp. Phys. 51 315 Google Scholar
[21]	Jiang M, Su W, Lu X, Sheng Z M, Li Y T, Li Y J, Zhang J, Grobe R, Su Q C 2011 Phys. Rev. A 83 053402 Google Scholar
[22]	Su Q C, Su W, Lü Q Z, Jiang M, Lu X, Sheng Z M, Grobe R 2012 Phys. Rev. Lett. 109 253202 Google Scholar
[23]	Jiang M, Lü Q Z, Sheng Z M, Grobe R, Su Q C 2013 Phys. Rev. A 87 042503 Google Scholar
[24]	Lü Q Z, Li Y J, Grobe R, Su Q C 2013 Phys. Rev. A 88 033403 Google Scholar
[25]	林南省, 韩禄雪, 江淼, 李英骏 2018 67 133401 Google Scholar Lin N S, Han L X, Jiang M, Li Y J 2018 Acta Phys. Sin. 67 133401 Google Scholar
[26]	Lü Q Z, Su Q C, Grobe R 2018 Phys. Rev. Lett. 121 183606 Google Scholar
[27]	Su Q C, Grobe R 2019 Phys. Rev. Lett. 122 023603 Google Scholar
[28]	Zhou X X, Li C K, Jiang M, Lin N S, Li Y J 2019 EPL 128 10001 Google Scholar
[29]	Su D D, Li Y T, Lü Q Z, Zhang J 2020 Phys. Rev. D 101 054501 Google Scholar
[30]	Gong C, Li Z L, Li Y J, Xie B S 2020 Phys. Rev. A 101 063405 Google Scholar
[31]	Zhou X X, Li C K, Lin N S, Li Y J 2021 Phys. Rev. A 103 012229 Google Scholar
[32]	Su D D, Li Y T, Su Q C, Grobe R 2021 Phys. Rev. D 103 074513 Google Scholar
[33]	Li C K, Su D D, Li Y J, Su Q C, Grobe R 2023 EPL 141 55001 Google Scholar
[34]	Dumlu C K 2009 Phys. Rev. D 79 065027 Google Scholar
[35]	Li Z L, Xie B S, Li Y J 2019 Phys. Rev. D 100 076018 Google Scholar
[36]	Li Z L, Gong C, Li Y J 2021 Phys. Rev. D 103 116018 Google Scholar
[37]	Yoon J W, Kim Y G, Choi I W, Sung J H, Lee H W, Lee S K, Nam C H 2021 Optica 8 630 Google Scholar
[38]	ELI BEAMLINES FACILITY, http://www.extreme-light-infrastructure.eu/
[39]	Burke D L, Field R C, Smith G H, Spencer J E, Walz D, Berridge S C, Bugg W M, Shmakov K, Weidemann A W, Bula C, McDonald K T, Prebys E J, Bamber C, Boege S J, Koffas T, Kotseroglou T, Melissinos A C, Meyerhofer D D, Reis D A, Ragg W 1997 Phys. Rev. Lett. 79 1626 Google Scholar
[40]	Pike O, Mackenroth F, Hill E, Rose S J 2014 Nat. Photon. 8 434 Google Scholar
[41]	Blackburn T G, Marklund M 2018 Plasma Phys. Contr. F. 60 054009 Google Scholar
[42]	Yu J Q, Lu H Y, Takahashi T, Hu R H, Gong Z, Ma W J, Huang Y S, Chen C E, Yan X Q 2019 Phys. Rev. Lett. 122 014802 Google Scholar
[43]	Golub A, Chávez S V, Ruhl H, Müller C 2021 Phys. Rev. D 103 016009 Google Scholar
[44]	MacLeod A J, Hadjisolomou P, Jeong T M, Bulanov S V 2023 Phys. Rev. A 107 012215 Google Scholar
[45]	Narozhny N B, Bulanov S S, Mur V D, Popov V S 2004 Phys. Lett. A 330 1
[46]	Dunne G V, Gies H, Schüzhold R 2009 Phys. Rev. D 80 111301 Google Scholar
[47]	Bulanov S S, Mur V D, Narozhny N B, Nees J, Popov V S 2010 Phys. Rev. Lett. 104 220404 Google Scholar
[48]	Aleksandrov I A, Plunien G, Shabaev V M 2017 Phys. Rev. D 96 076006 Google Scholar
[49]	Jiang M, Grobe R, Su Q C 2023 Phys. Rev. A 108 022813 Google Scholar

Cited By

图 1 正负电子对数量随时间的变化, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果, 蓝色线表示双振荡场产生的粒子对数量, 黑色线表示单振荡场产生的粒子对数量, 红色点线表示单振荡场产生的粒子对数量的2倍, 其中V₁ = V₂ = 0.75c², W₁= W₂ = 3/c, d = 8/c, ω = 2.5c², T = 2π/ω

Figure 1. Time evolution of the electron-positron pairs, the results calculated by the computational quantum field theory and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. The electron-positron pairs created by double oscillating filed is represented by blue line, the electron-positron pairs created by single oscillating field is represented by black line, and the twice of the pairs created by single oscillating field is represented by the red dotted line. Here, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, ω = 2.5c², T = 2π/ω.

DownLoad: Full-Size Img PowerPoint

图 2 正负电子对的动量分布, 实线和虚线分别表示计算量子场论的数值结果和一阶含时微扰理论的结果. 其中V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, ω = 2.5c², t = 20T = 40π/ω

Figure 2. Momentum spectra of the created electron-positron pairs, the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, ω = 2.5c², t = 20T = 40π/ω.

DownLoad: Full-Size Img PowerPoint

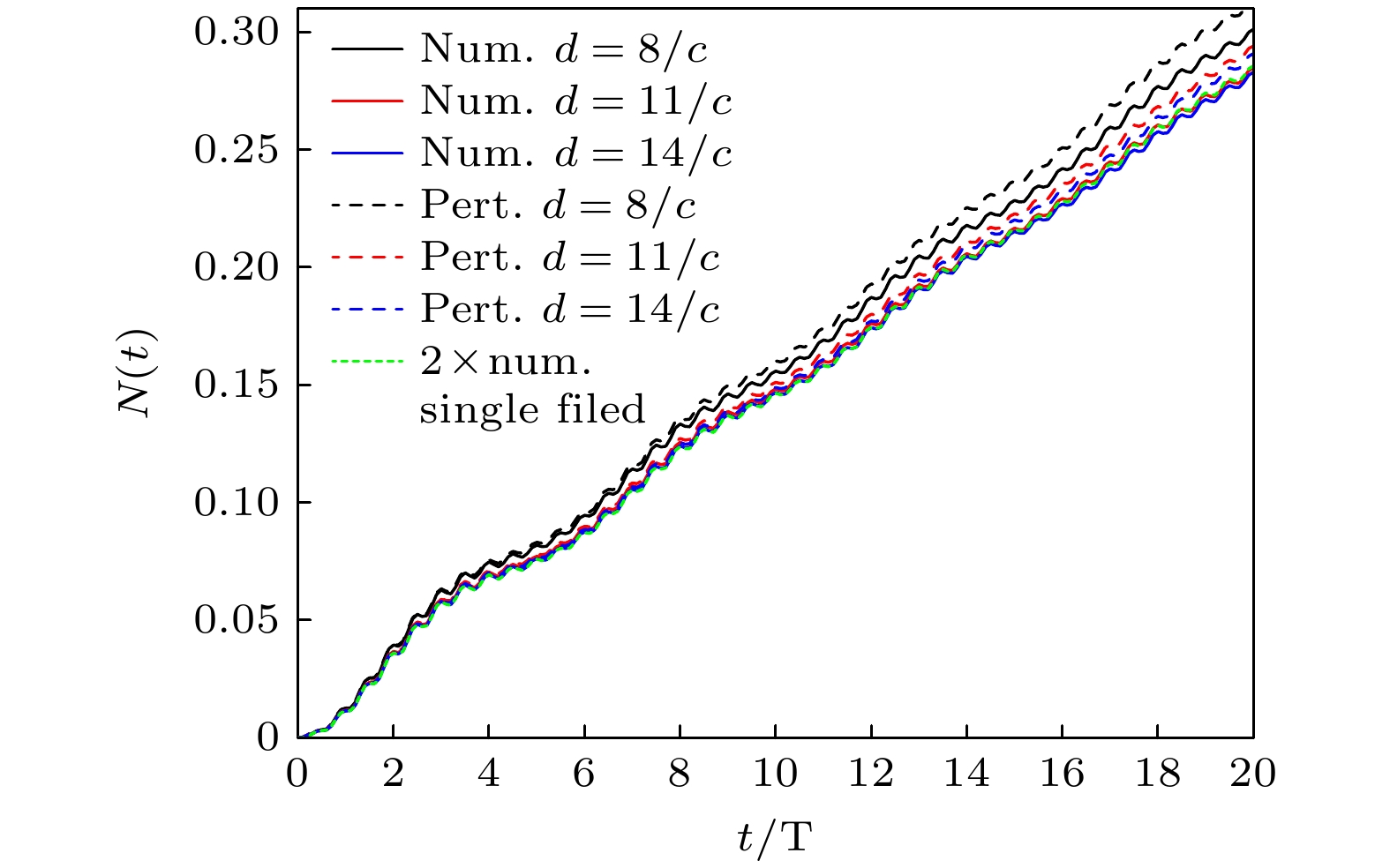
图 3 不同场间距d下正负电子对数量随时间的变化, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果. 其中V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, ω = 2.5c², T = 2π/ω

Figure 3. Time evolution of the created electron-positron pairs for different distances between the two fields (d), the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, ω = 2.5c², T = 2π/ω.

DownLoad: Full-Size Img PowerPoint

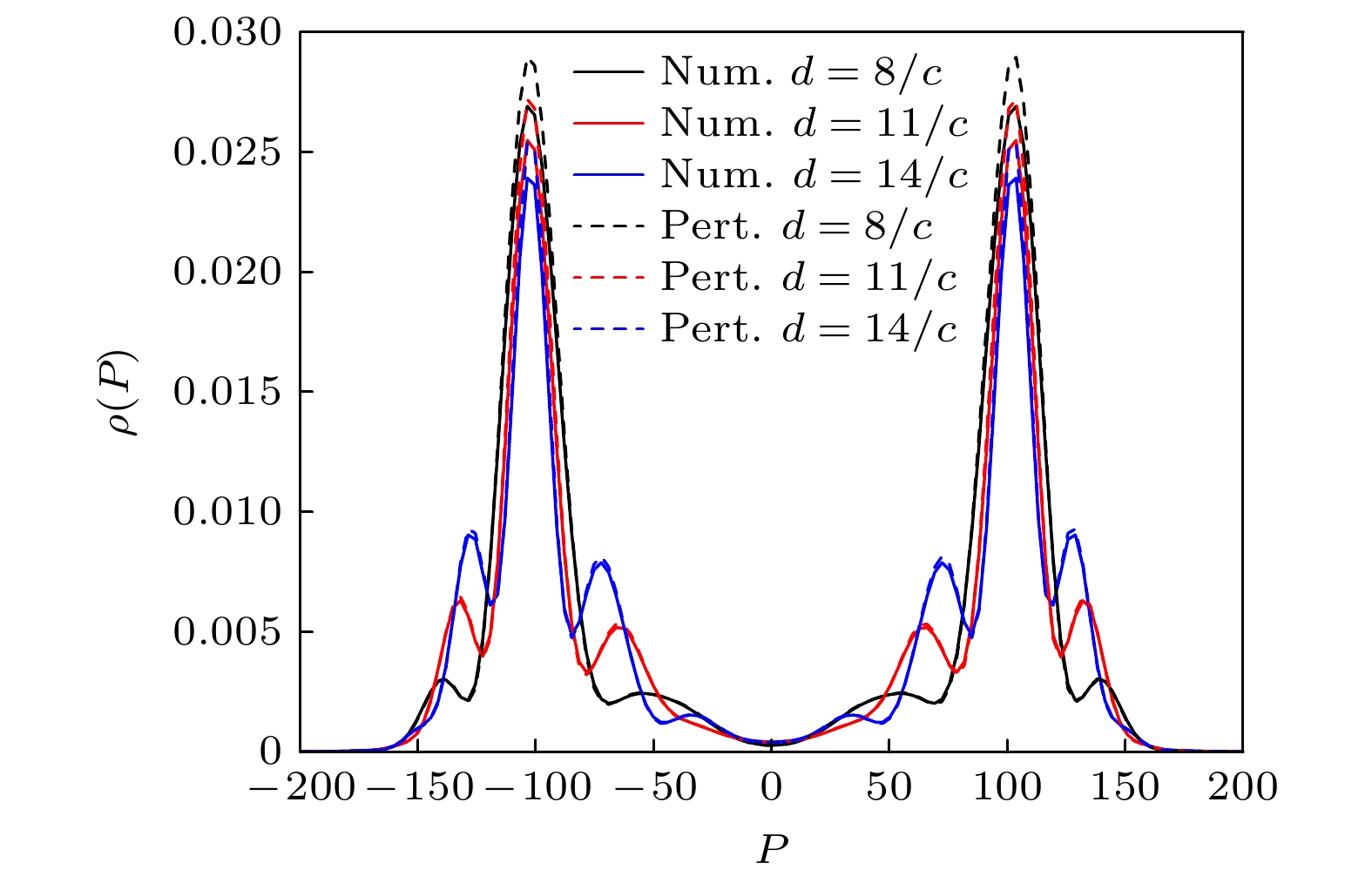
图 4 不同场间距d下正负电子对产生的动量分布, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果. 其中V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, ω = 2.5c², t = 20T = 40π/ω

Figure 4. Momentum spectra of the electron-positron pairs for different distances between the two fields (d), the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, ω = 2.5c², t = 20T = 40π/ω.

DownLoad: Full-Size Img PowerPoint

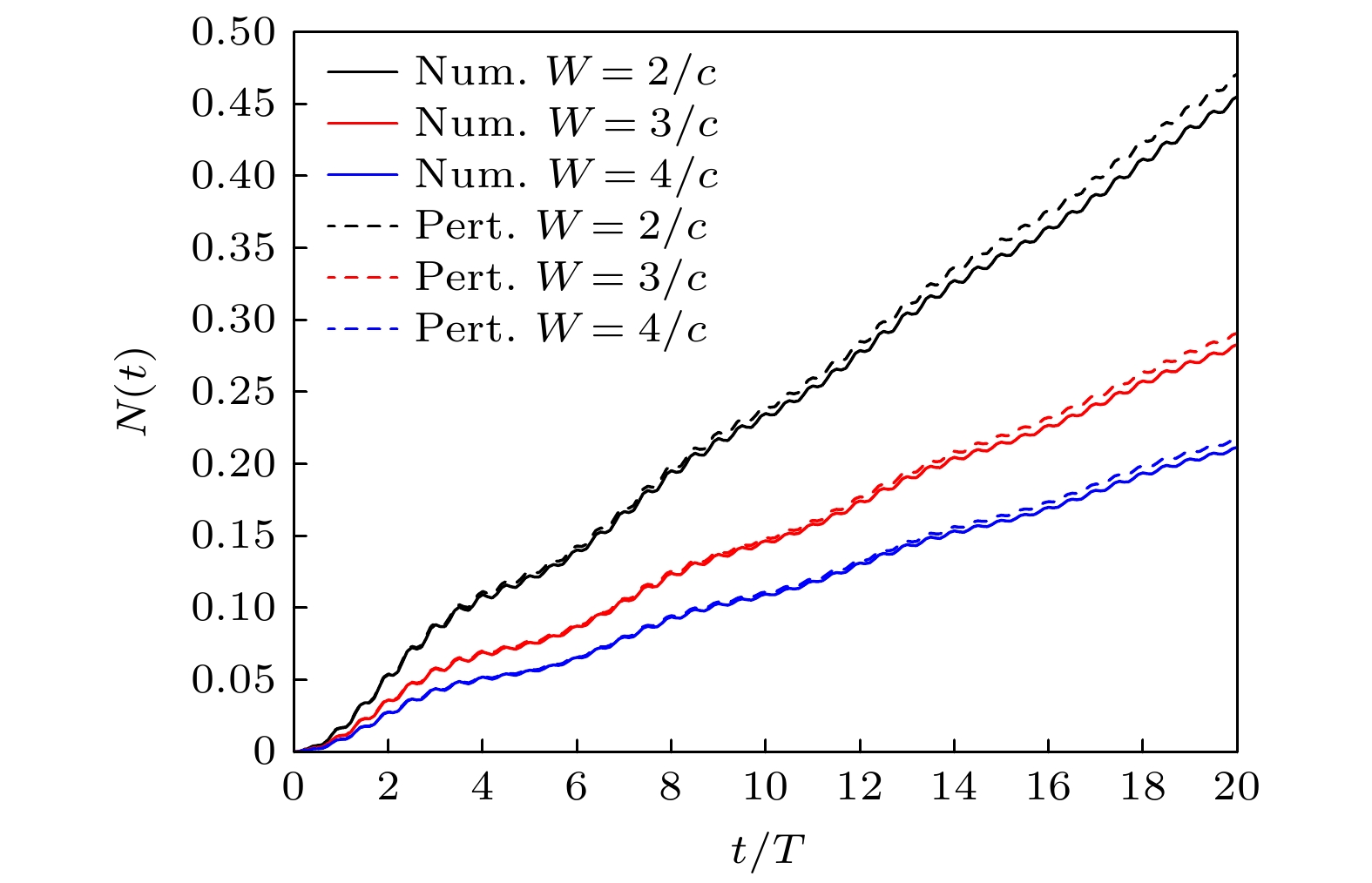
图 5 不同电场宽度W下正负电子对数量随时间的变化, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果. 其中V₁ = V₂ = 0.75c², d = 14/c, ω = 2.5c², T = 2π/ω

Figure 5. Time evolution of the created electron-positron pairs for different widths of electric field (W), the electron-positron pairs calculated by CQFT and first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², d = 14/c, ω = 2.5c², T = 2π/ω.

DownLoad: Full-Size Img PowerPoint

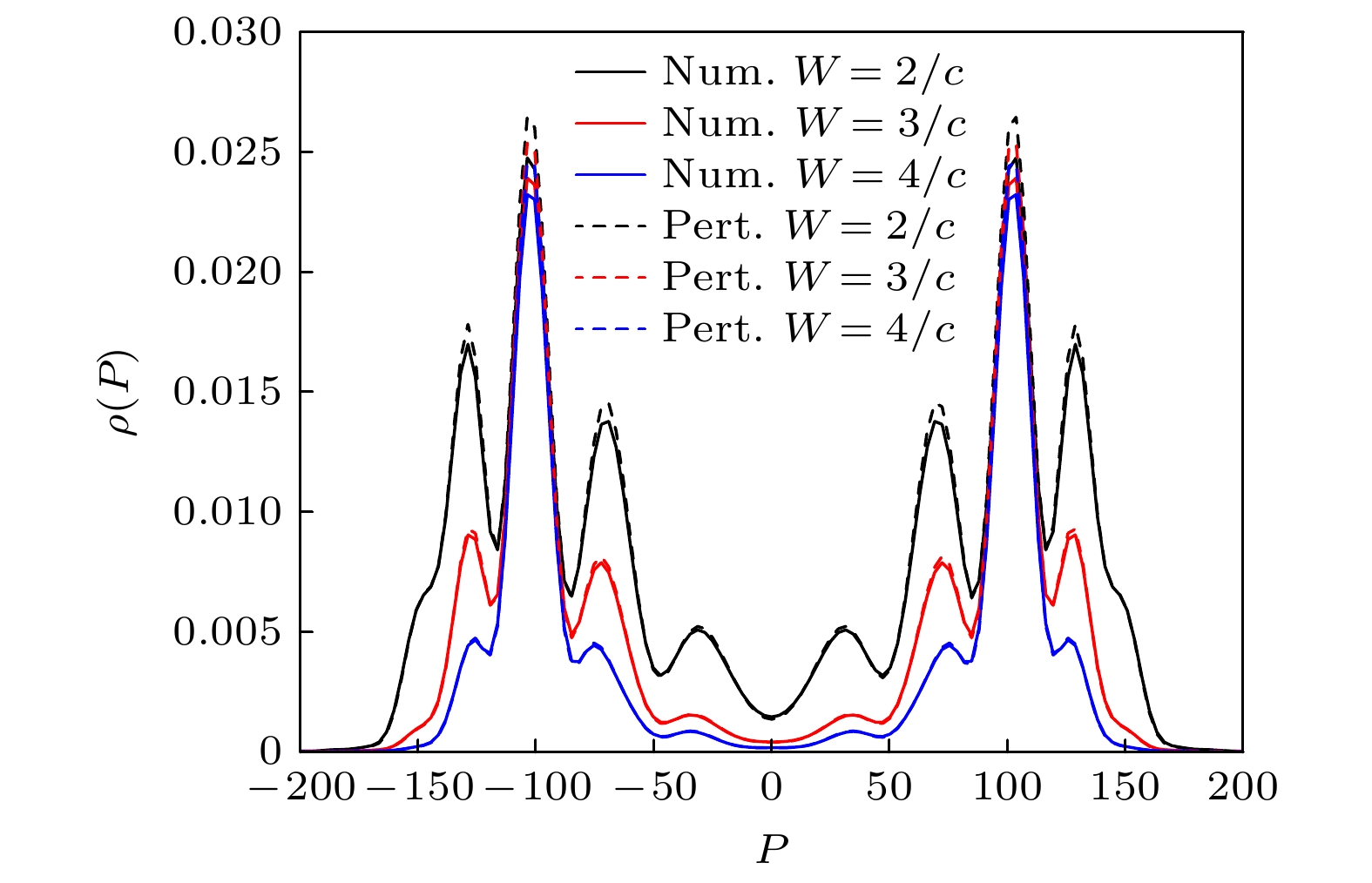
图 6 不同电场宽度(W)下正负电子对的动量分布, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果. 其中V₁ = V₂ = 0.75c², d = 14/c, ω = 2.5c², t = 20T = 40π/ω

Figure 6. Momentum spectra of the created electron-positron pairs for different widths of electric field (W), the results calculated by CQFT and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², d = 14/c, ω = 2.5c², t = 20T = 40π/ω.

DownLoad: Full-Size Img PowerPoint

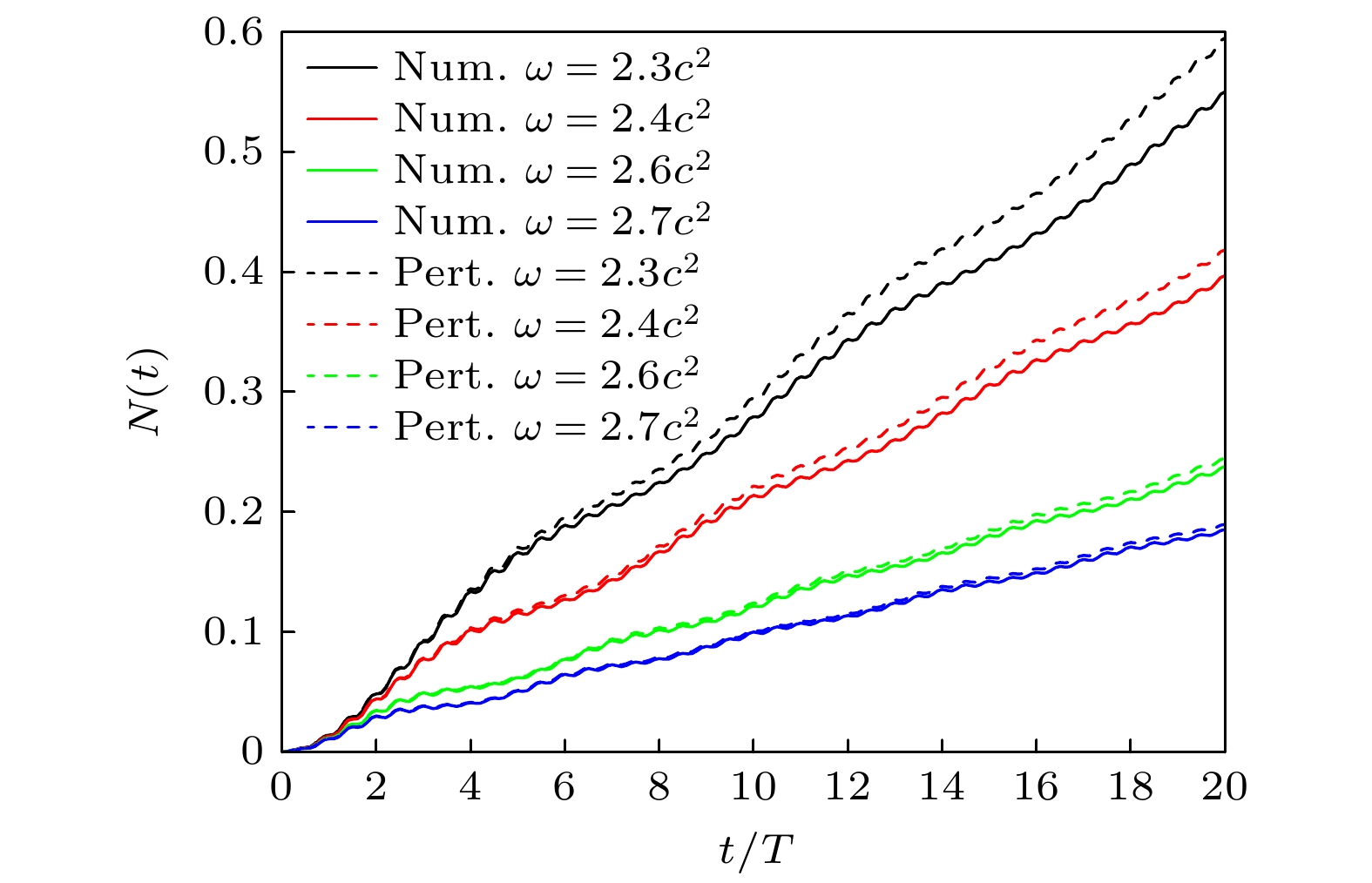
图 7 正负电子对数量随时间的变化, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果. 这里, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, T = 2π/ω

Figure 7. Time evolution of the electron-positron pairs, the results calculated by the computational quantum field theory and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, T = 2π/ω.

DownLoad: Full-Size Img PowerPoint

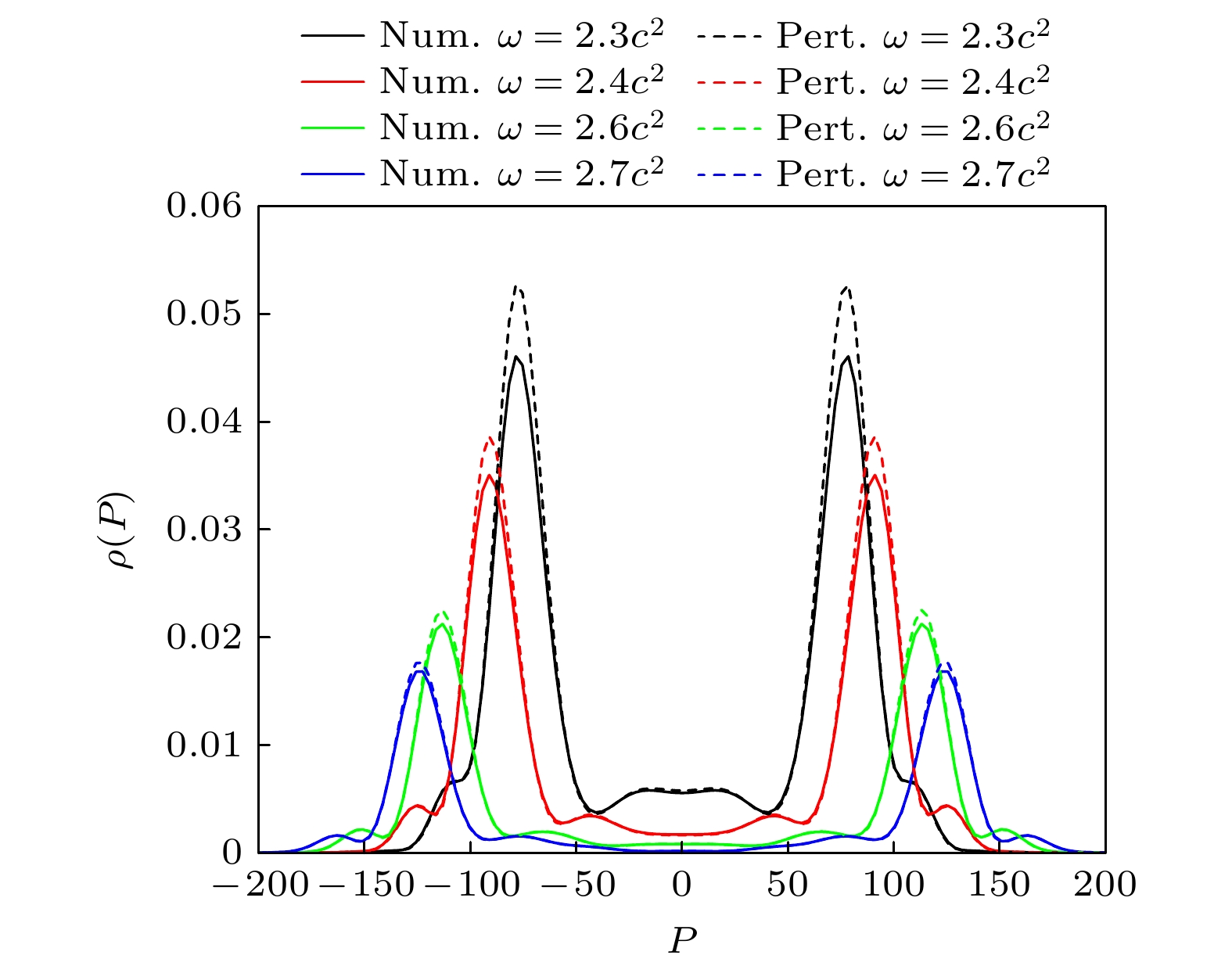
图 8 不同电场频率下正负电子对的动量分布, 实线和虚线分别表示计算量子场论的结果和一阶含时微扰理论的结果. 其中V₁= V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, T = 2π/ω

Figure 8. Momentum spectra of the created electron-positron pairs for different frequencies of electric field. The results calculated by the computational quantum field theory and the first-order time-dependent perturbation theory are represented by the solid line and the dashed line, respectively. Here, V₁ = V₂ = 0.75c², W₁ = W₂ = 3/c, d = 8/c, T = 2π/ω.

DownLoad: Full-Size Img PowerPoint

表 1 计算量子场论与一阶含时微扰理论的动量峰值强度误差

Table 1. Error of momentum peaks probability with the CQFT and the first-order time-dependent perturbation theory.

峰值强度	峰值位置/arb.units
峰值强度	53.4(–53.4)	103.7(–103.7)	138.2(–138.2)
计算量子场论	0.0024	0.0270	0.0030
含时微扰理论	0.0025	0.0290	0.0031
相对误差/%	4.17	7.41	3.33

DownLoad: CSV

表 A1 计算量子场论与一阶含时微扰理论的产生粒子对数量的平均相对误差

Table A1. Mean relative error of the particle number created by the CQFT and the first-order time-dependent perturbation theory.

电场频率 (c²)	平均相对误差/%	电场宽度 (c^–1)	平均相对误差/%	电场势高 (c²)	平均相对误差/%
1.6	6.04	0.5	12.54	0.5	5.32
1.7	674	0.6	11.52	0.6	5.79
1.8	8.76	0.7	10.56	0.7	6.33
1.9	18.11	0.8	9.71	0.8	6.96
2.0	27.41	0.9	8.95	0.9	7.68
2.1	19.24	1.0	8.30	1.0	8.48
2.2	11.29	1.1	7.76	1.1	9.36
2.3	8.07	1.2	7.31	1.2	10.33
2.4	6.97	1.3	6.94	1.3	11.38
2.5	6.64	1.4	6.66	1.4	12.51

DownLoad: CSV

map

[1]	Xie B S, Li Z L, Tang S 2017 Matter Radiat. Extremes 2 225 Google Scholar
[2]	Fedotov A, Ilderton A, Karbstein F, King B, Seipt D, Taya H, Torgrimsson G 2023 Phys. Rep. 1010 1 Google Scholar
[3]	Sauter F 1931 Z. Physik 69 742 Google Scholar
[4]	Heisenberg W, Euler H 1936 Z. Physik 98 714 Google Scholar
[5]	Schwinger J 1951 Phys. Rev. 82 664 Google Scholar
[6]	Brezin E, Itzykson C 1970 Phys. Rev. D 2 1191 Google Scholar
[7]	Kim S P, Page D N 2002 Phys. Rev. D 65 105002 Google Scholar
[8]	Schützhold R, Gies H, Dunne G V 2008 Phys. Rev. Lett. 101 130404 Google Scholar
[9]	Schneider C, Torgrimsson G, Schützhold R 2018 Phys. Rev. D 98 085009 Google Scholar
[10]	Abdukerim N, Li Z L, Xie B S 2013 Phys. Lett. B 726 820 Google Scholar
[11]	Li Z L, Lu D, Xie B S, Fu L B, Liu J, Shen B F 2014 Phys. Rev. D 89 093011 Google Scholar
[12]	Kohlfürst C, Gies H, Alkofer R 2014 Phys. Rev. Lett. 112 050402 Google Scholar
[13]	Gong C, Li Z L, Xie B S, Li Y J 2020 Phys. Rev. D 101 016008 Google Scholar
[14]	Hebenstreit F, Alkofer R, Gies H 2010 Phys. Rev. D 82 105026 Google Scholar
[15]	Hebenstreit F, Alkofer R, Gies H 2011 Phys. Rev. Lett. 107 180403 Google Scholar
[16]	Li Z L, Lu D, Xie B S 2015 Phys. Rev. D 92 085001 Google Scholar
[17]	Li Z L, Li Y J, Xie B S 2017 Phys. Rev. D 96 076010 Google Scholar
[18]	Kohlfürst C, Alkofer R 2018 Phys. Rev. D 97 036026 Google Scholar
[19]	Kohlfürst C 2019 Phys. Rev. D 99 096017 Google Scholar
[20]	Cheng T, Su Q C, Grobe R 2010 Contemp. Phys. 51 315 Google Scholar
[21]	Jiang M, Su W, Lu X, Sheng Z M, Li Y T, Li Y J, Zhang J, Grobe R, Su Q C 2011 Phys. Rev. A 83 053402 Google Scholar
[22]	Su Q C, Su W, Lü Q Z, Jiang M, Lu X, Sheng Z M, Grobe R 2012 Phys. Rev. Lett. 109 253202 Google Scholar
[23]	Jiang M, Lü Q Z, Sheng Z M, Grobe R, Su Q C 2013 Phys. Rev. A 87 042503 Google Scholar
[24]	Lü Q Z, Li Y J, Grobe R, Su Q C 2013 Phys. Rev. A 88 033403 Google Scholar
[25]	林南省, 韩禄雪, 江淼, 李英骏 2018 67 133401 Google Scholar Lin N S, Han L X, Jiang M, Li Y J 2018 Acta Phys. Sin. 67 133401 Google Scholar
[26]	Lü Q Z, Su Q C, Grobe R 2018 Phys. Rev. Lett. 121 183606 Google Scholar
[27]	Su Q C, Grobe R 2019 Phys. Rev. Lett. 122 023603 Google Scholar
[28]	Zhou X X, Li C K, Jiang M, Lin N S, Li Y J 2019 EPL 128 10001 Google Scholar
[29]	Su D D, Li Y T, Lü Q Z, Zhang J 2020 Phys. Rev. D 101 054501 Google Scholar
[30]	Gong C, Li Z L, Li Y J, Xie B S 2020 Phys. Rev. A 101 063405 Google Scholar
[31]	Zhou X X, Li C K, Lin N S, Li Y J 2021 Phys. Rev. A 103 012229 Google Scholar
[32]	Su D D, Li Y T, Su Q C, Grobe R 2021 Phys. Rev. D 103 074513 Google Scholar
[33]	Li C K, Su D D, Li Y J, Su Q C, Grobe R 2023 EPL 141 55001 Google Scholar
[34]	Dumlu C K 2009 Phys. Rev. D 79 065027 Google Scholar
[35]	Li Z L, Xie B S, Li Y J 2019 Phys. Rev. D 100 076018 Google Scholar
[36]	Li Z L, Gong C, Li Y J 2021 Phys. Rev. D 103 116018 Google Scholar
[37]	Yoon J W, Kim Y G, Choi I W, Sung J H, Lee H W, Lee S K, Nam C H 2021 Optica 8 630 Google Scholar
[38]	ELI BEAMLINES FACILITY, http://www.extreme-light-infrastructure.eu/
[39]	Burke D L, Field R C, Smith G H, Spencer J E, Walz D, Berridge S C, Bugg W M, Shmakov K, Weidemann A W, Bula C, McDonald K T, Prebys E J, Bamber C, Boege S J, Koffas T, Kotseroglou T, Melissinos A C, Meyerhofer D D, Reis D A, Ragg W 1997 Phys. Rev. Lett. 79 1626 Google Scholar
[40]	Pike O, Mackenroth F, Hill E, Rose S J 2014 Nat. Photon. 8 434 Google Scholar
[41]	Blackburn T G, Marklund M 2018 Plasma Phys. Contr. F. 60 054009 Google Scholar
[42]	Yu J Q, Lu H Y, Takahashi T, Hu R H, Gong Z, Ma W J, Huang Y S, Chen C E, Yan X Q 2019 Phys. Rev. Lett. 122 014802 Google Scholar
[43]	Golub A, Chávez S V, Ruhl H, Müller C 2021 Phys. Rev. D 103 016009 Google Scholar
[44]	MacLeod A J, Hadjisolomou P, Jeong T M, Bulanov S V 2023 Phys. Rev. A 107 012215 Google Scholar
[45]	Narozhny N B, Bulanov S S, Mur V D, Popov V S 2004 Phys. Lett. A 330 1
[46]	Dunne G V, Gies H, Schüzhold R 2009 Phys. Rev. D 80 111301 Google Scholar
[47]	Bulanov S S, Mur V D, Narozhny N B, Nees J, Popov V S 2010 Phys. Rev. Lett. 104 220404 Google Scholar
[48]	Aleksandrov I A, Plunien G, Shabaev V M 2017 Phys. Rev. D 96 076006 Google Scholar
[49]	Jiang M, Grobe R, Su Q C 2023 Phys. Rev. A 108 022813 Google Scholar

[1]	Mou Jia-Lian, Lü Jun-Guang, Sun Xi-Lei, Lan Xiao-Fei, Huang Yong-Sheng. Time of flight detector for charged particle identification based on circular electron-positron collider. Acta Physica Sinica, 2023, 72(12): 122901. doi: 10.7498/aps.72.20222271
[2]	Ye Quan-Xing, He Guang-Zhao, Wang Qian. Bottominium-like states in e⁺e^– annihilation. Acta Physica Sinica, 2023, 72(20): 201401. doi: 10.7498/aps.72.20230908
[3]	Luo Hui-Yi, Jiang Miao, Xu Miao-Hua, Li Ying-Jun. Electron-position pair creation under combined oscillation fields with different frequencies. Acta Physica Sinica, 2023, 72(2): 021201. doi: 10.7498/aps.72.20221660
[4]	Haisu Zhang, Lingling Qiao, Ya Cheng. Air-Lasing: High-Resolution Spectroscopy for Atmospheric Remote Sensing. Acta Physica Sinica, 2022, 0(0): 0-0. doi: 10.7498/aps.71.20221923
[5]	Zhang Hai-Su, Qiao Ling-Ling, Cheng Ya. Air-lasing high-resolution spectroscopy for atmospheric remote sensing. Acta Physica Sinica, 2022, 71(23): 233401. doi: 10.7498/aps.71.20221913
[6]	Wang Yang, Liu Yu, Wu Cheng-Yin. Generation, manipulation, and application of high-order harmonics in solids. Acta Physica Sinica, 2022, 71(23): 234205. doi: 10.7498/aps.71.20221319
[7]	Xie Bai-Song, Li Lie-Juan, Melike Mohamedsedik, Wang Li. Enhancement effect of frequency chirp on vacuum electron-positron pair production in strong field. Acta Physica Sinica, 2022, 71(13): 131201. doi: 10.7498/aps.71.20220148
[8]	Shen Bai-Fei, Ji Liang-Liang, Zhang Xiao-Mei, Bu Zhi-Gang, Xu Jian-Cai. High field X-ray laser physics. Acta Physica Sinica, 2021, 70(8): 084101. doi: 10.7498/aps.70.20210096
[9]	Dong Xu, Huang Yong-Sheng, Tang Guang-Yi, Chen Shan-Hong, Si Mei-Yu, Zhang Jian-Yong. Circular electron-positron collider beam energy measurement scheme based on microwave-electronic Compton backscattering. Acta Physica Sinica, 2021, 70(13): 131301. doi: 10.7498/aps.70.20202081
[10]	Sun Ting, Wang Yu, Guo Ren-Tong, Lu Zhi-Wei, Li Jian-Xing. Review on laser-driven high-energy polarized electron and positron beams and γ-rays. Acta Physica Sinica, 2021, 70(8): 087901. doi: 10.7498/aps.70.20210009
[11]	Jiang Miao, Zheng Xiao-Ran, Lin Nan-Sheng, Li Ying-Jun. Multi-photon transition effects under different external field widths in electron-positron-pair creation process. Acta Physica Sinica, 2021, 70(23): 231202. doi: 10.7498/aps.70.20202101
[12]	Zhu Xing-Long, Wang Wei-Min, Yu Tong-Pu, He Feng, Chen Min, Weng Su-Ming, Chen Li-Ming, Li Yu-Tong, Sheng Zheng-Ming, Zhang Jie. Research progress of ultrabright γ-ray radiation and electron-positron pair production driven by extremely intense laser fields. Acta Physica Sinica, 2021, 70(8): 085202. doi: 10.7498/aps.70.20202224
[13]	Li Ang, Yu Jin-Qing, Chen Yu-Qing, Yan Xue-Qing. Numerical method of electron-positron pairs generation in photon-photon collider. Acta Physica Sinica, 2020, 69(1): 019501. doi: 10.7498/aps.69.20190729
[14]	Wu Guang-Zhi, Wang Qiang, Zhou Cang-Tao, Fu Li-Bin. Positron wave interference and Klein tunnel during the production of pairs in the double-well potential. Acta Physica Sinica, 2017, 66(7): 070301. doi: 10.7498/aps.66.070301
[15]	Qiao Jian-Liang, Chang Ben-Kang, Du Xiao-Qing, Niu Jun, Zou Ji-Jun. Quantum efficiency decay mechanism for reflection-mode negative electron affinity GaN photocathode. Acta Physica Sinica, 2010, 59(4): 2855-2859. doi: 10.7498/aps.59.2855
[16]	Du Xiao-Qing, Chang Ben-Kang. Revision of quantum efficiency formula for negative electron affinity photocathodes. Acta Physica Sinica, 2009, 58(12): 8643-8650. doi: 10.7498/aps.58.8643
[17]	LI FU-BIN. IMPROVEMENTS ON THE PERTURBED HARMONIC OSCILLATOR LADDER OPERATORS METHOD IN THE NON LINEAR QUANTUM FIELD THEORY AND THE LASER THEORY. Acta Physica Sinica, 1989, 38(6): 879-890. doi: 10.7498/aps.38.879
[18]	HE ZUO-XIU, ZHANG ZHAO-XI. ON THE RENORMALIZATION THEORY OF THE ULTRAVIOLET AND INFRARED DIVERGENCES IN THE QUANTIZED THEORY OF COMPOSITE PARTICLES. Acta Physica Sinica, 1977, 26(6): 540-543. doi: 10.7498/aps.26.540
[19]	. . Acta Physica Sinica, 1975, 24(2): 145-150. doi: 10.7498/aps.24.145
[20]	HE ZUO-XIU, HUANG TAO. A NEW POSSIBLE COMPOSITE QUANTIZED FIELD THEORY. Acta Physica Sinica, 1974, 23(2): 33-72. doi: 10.7498/aps.23.33

Catalog

Vol. 73, Issue 4 - 2024-02-20

Metrics

Abstract views: 1992
PDF Downloads: 61
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板