-
Within an oscillating field with high frequency, electron-positron pairs can be generated from vacuum as the result of multi-photon transition process. In this paper, through the computational quantum field theory and the split operator technique, we use a numerical method to solve the spatiotemporally dependent Dirac equation, the result of which enables us to discuss the process of creating electron-positron pair under a time-dependent and spatially localized external field. By monitoring the total number and the energy distribution of created pairs, the effect of the field width on the creating electron-positron pair is discussed. For a wide width, the symmetric transition of single photon transition is dominant, because the momentum of the transition particle is approximately conserved due to a gradually varying space. For an oscillating field with frequency that exceeds the threshold $ 2mc^2$ , the energy of a single-photon is sufficient to cross the energy gap between the positive energy continuum and the negative energy continuum. As a result, the electron-positron pairs will be generated continuously, where a transition with symmetric energy has the maximum probability. Meanwhile, higher-order photon transition also arises, especially for three-photon transition with one photon transition completely inside the negative energy continuum. To observe the effect of this photon, we artificially cut the negative energy at a specific value. Accordingly, in the energy distribution of the created pairs, the peak corresponding to three-photon transition disappears, which indicates that the photon inside the negative energy continuum is indispensable in a three-photon transition process. For a narrow field width where the conservation of the momentum breaks down, the production corresponding to the asymmetric transition becomes obvious. In the energy distribution, the peaks representing two-photon transition and three-photon transition become wide and are split into two small peaks. For the three-photon transition, if we cut the negative energy at a specific value, it affects only the peak with lower energy, which indicates a different transition mode of the case corresponding to a wide field. Furthermore, in a narrow field the transition probability of double-photon transition greatly increases, even to a similar order of magnitude of the single photon transition. Apart from transitions with energy equal to integer multiple of the frequency of the photon appearing with asymmetric patterns, there also exists transitions with other energy. The multi-photon transition process of the particles for a narrow field width is more complicated than for a wide field width.[1] Schwinger J 1951 Phys. Rev. 82 664
Google Scholar
[2] Cowan T, Backe H, Bethge K, et al. 1986 Phys. Rev. Lett. 56 444
Google Scholar
[3] Ahmad I, Austin S M, Back B B, et al. 1997 Phys. Rev. Lett. 78 618
Google Scholar
[4] Burke D L, Field R C, Horton-Smith G, et al. 1997 Phys. Rev. Lett. 79 1626
Google Scholar
[5] Bamber C, Boege S J, Koffas T, et al. 1999 Phys. Rev. D 60 092004
Google Scholar
[6] Narozhny N B, Bulanov S S, Mur V D, Popov V S 2004 JETP Lett. 80 382
Google Scholar
[7] Di Piazza A 2004 Phys. Rev. D 70 053013
Google Scholar
[8] Müller C, Hatsagortsyan K Z, Keitel C H 2008 Phys. Rev. A 78 033408
Google Scholar
[9] Ruf M, Mocken G R, Müller C, Hatsagortsyan K Z, Keitel C H 2009 Phys. Rev. Lett. 102 080402
Google Scholar
[10] Kirk J G, Bell A R, Arka I 2009 Plasma Phys. Control. Fusion 51 085008
Google Scholar
[11] Tang S, Xie B S, Lu D, Wang H Y, Fu L B, Liu J 2013 Phys. Rev. A 88 012106
Google Scholar
[12] Liu Y, Lv Q Z, Li Y T, Grobe R, Su Q 2015 Phys. Rev. A 91 052123
Google Scholar
[13] Piccinelli G, Sánchez 2017 Phys. Rev. D 96 076014
Google Scholar
[14] Li Z L, Xie B S, Li Y J 2019 Phys. Rev. D 100 076018
Google Scholar
[15] Krekora P, Su Q, Grobe R 2004 Phys. Rev. Lett. 92 040406
Google Scholar
[16] Jiang M, Su W, Lu X, Sheng Z M, Li Y T, Li Y J, Zhang J, Grobe R, Su Q 2011 Phys. Rev. A 83 053402
Google Scholar
[17] Wöllert A, Klaiber M, Bauke H, Keitel C H 2015 Phys. Rev. D 91 065022
Google Scholar
[18] Schützhold R, Gies H, Dunne G 2008 Phys. Rev. Lett. 101 130404
Google Scholar
[19] Monin A, Voloshin M B 2010 Phys. Rev. D 81 085014
Google Scholar
[20] Jiang M, Su W, Lv Z Q, et al. 2012 Phys. Rev. A 85 033408
Google Scholar
[21] Dong S, Unger J, Bryan J, Su Q, Grobe R 2020 Phys. Rev. E 101 013310
Google Scholar
[22] Krekora P, Cooley K, Su Q, Grobe R 2005 Phys. Rev. Lett. 95 070403
Google Scholar
[23] Jiang M, Lv Q Z, Sheng Z M, Grobe R, Su Q 2013 Phys. Rev. A 87 042503
Google Scholar
[24] Lv Q Z, Liu Y, Li Y J, Grobe R, Su Q 2014 Phys. Rev. A 90 013405
Google Scholar
[25] Wang Q, Liu J, Fu L B 2016 Sci. Rep. 6 25292
Google Scholar
[26] Su D D, Li Y T, Lv Q Z, Zhang J 2020 Phys. Rev. D 101 054501
Google Scholar
[27] Braun J W, Su Q, Grobe R 1999 Phys. Rev. A 59 604
Google Scholar
[28] Wagner R E, Ware M R, Shields B T, Su Q, Grobe R 2011 Phys. Rev. Lett. 106 023601
Google Scholar
[29] Bandrauk A D, Shen H 1994 J. Phys. A: Math. Gen. 27 7147
Google Scholar
[30] Mocken G R, Keitel C H 2008 Comput. Phys. Commun. 178 868
Google Scholar
[31] Sauter F 1932 Zeitschrift für Physik 73 547
Google Scholar
-
图 1 粒子产生数随外场频率变化关系图. 其中
$t=0.002$ , 外场强度$V_1=5.5 c^2$ , 宽度$W=5/c$ Fig. 1. Total number of created pairs for different frequencies of the external field. Here
$t=0.002$ , the field intensity is$V_1=5.5 c^2$ and width is$W=5/c$ .
图 2 多光子跃迁过程示意图, 外场频率为
$\omega=2.5 c^2$ Fig. 2. Schematic diagram of the multiphoton transition, where the frequency of the field is
$\omega=2.5 c^2$ .
图 3 外场宽度
$W=5/c$ 时粒子产生量在能量上的概率分布图, 外场频率和强度分别为$\omega=2.5 c^2$ ,$V_1=8.5 c^2$ Fig. 3. Energy distribution of the created particles for a wide field width
$W=5/c$ , where the frequency and intensity of the field are$\omega=2.5 c^2$ and$V_1=8.5 c^2$ , respectively.
图 4 外场宽度
$W=1/c$ 时粒子产生量在能量上的概率分布图, 外场频率和强度分别为$\omega=2.5 c^2$ ,$V_1=8.5 c^2$ Fig. 4. Energy distribution of the created particles for a narrow field width
$W=1/c$ , here the frequency and intensity of the field are$\omega=2.5 c^2$ and$V_1=8.5 c^2$ , respectively.
图 5 场宽较小时多光子跃迁过程示意图
Fig. 5. Multi-photon transition in a narrow field, where the frequency is
$\omega=2.5 c^2$ .
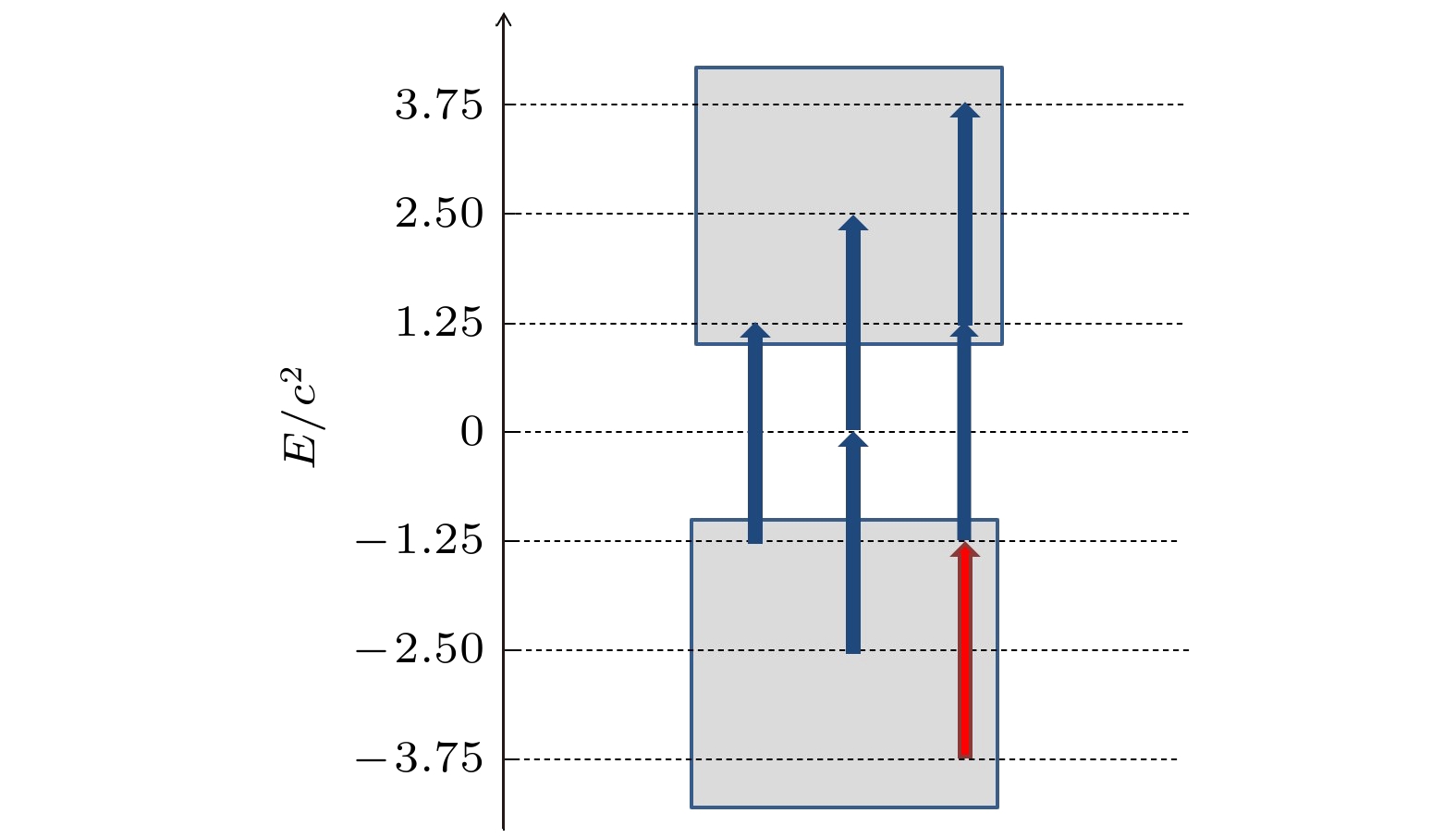
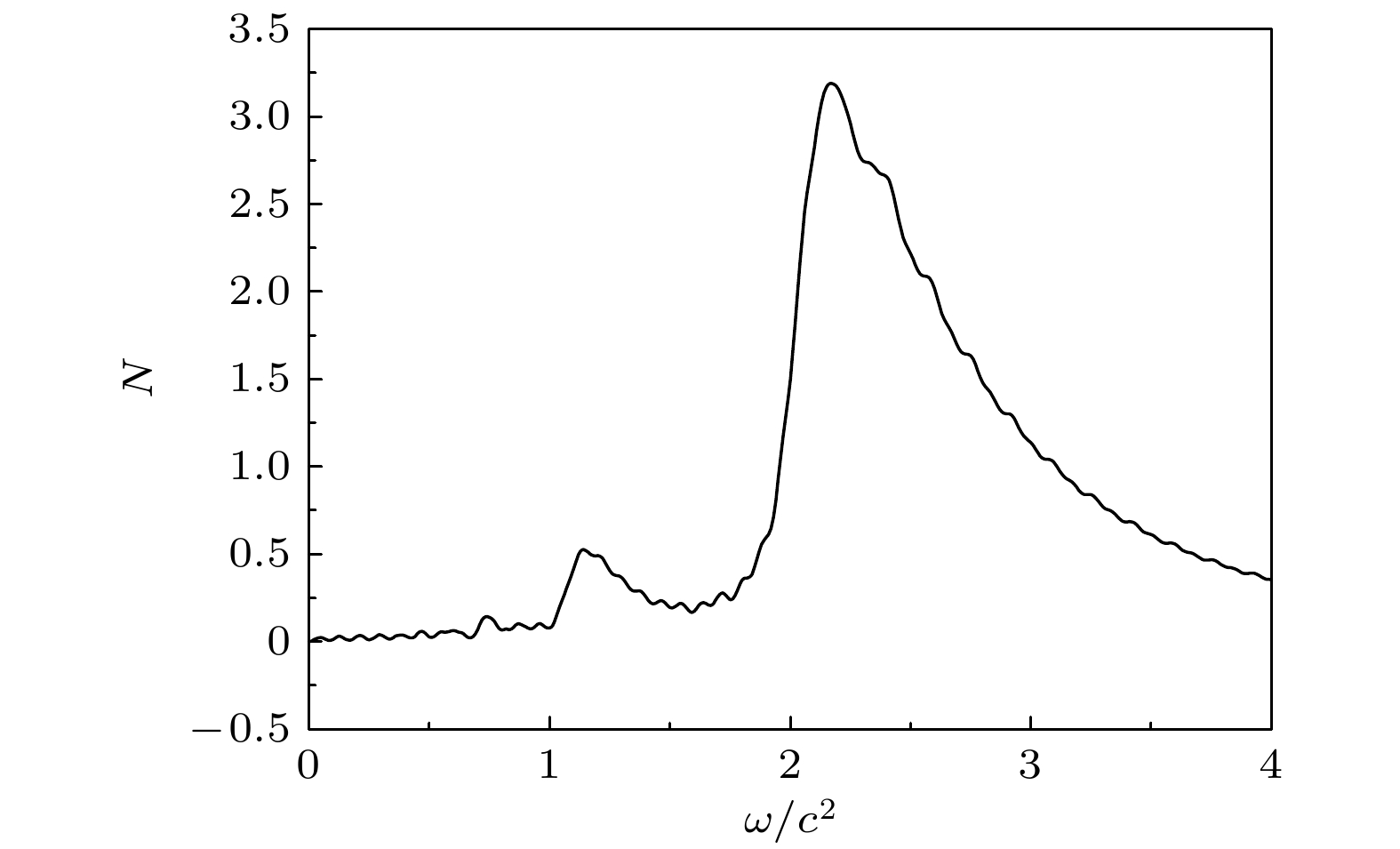
图 6 多光子跃迁过程概率在正负能量上的分布图 (a)场宽
$W= $ $ 5/c$ ; (b)场宽$W=1/c$ . 其中外场频率为$\omega=2.5 c^2 $ , 强度为$V_1=8.5 c^2$ Fig. 6. Probability of transition between the positive and negative energy: (a) Field width
$W=5/c$ ; (b) field width$W=1/c$ . The frequency and intensity of the field are$\omega=2.5 c^2$ and$V_1=8.5 c^2$ . -
[1] Schwinger J 1951 Phys. Rev. 82 664
Google Scholar
[2] Cowan T, Backe H, Bethge K, et al. 1986 Phys. Rev. Lett. 56 444
Google Scholar
[3] Ahmad I, Austin S M, Back B B, et al. 1997 Phys. Rev. Lett. 78 618
Google Scholar
[4] Burke D L, Field R C, Horton-Smith G, et al. 1997 Phys. Rev. Lett. 79 1626
Google Scholar
[5] Bamber C, Boege S J, Koffas T, et al. 1999 Phys. Rev. D 60 092004
Google Scholar
[6] Narozhny N B, Bulanov S S, Mur V D, Popov V S 2004 JETP Lett. 80 382
Google Scholar
[7] Di Piazza A 2004 Phys. Rev. D 70 053013
Google Scholar
[8] Müller C, Hatsagortsyan K Z, Keitel C H 2008 Phys. Rev. A 78 033408
Google Scholar
[9] Ruf M, Mocken G R, Müller C, Hatsagortsyan K Z, Keitel C H 2009 Phys. Rev. Lett. 102 080402
Google Scholar
[10] Kirk J G, Bell A R, Arka I 2009 Plasma Phys. Control. Fusion 51 085008
Google Scholar
[11] Tang S, Xie B S, Lu D, Wang H Y, Fu L B, Liu J 2013 Phys. Rev. A 88 012106
Google Scholar
[12] Liu Y, Lv Q Z, Li Y T, Grobe R, Su Q 2015 Phys. Rev. A 91 052123
Google Scholar
[13] Piccinelli G, Sánchez 2017 Phys. Rev. D 96 076014
Google Scholar
[14] Li Z L, Xie B S, Li Y J 2019 Phys. Rev. D 100 076018
Google Scholar
[15] Krekora P, Su Q, Grobe R 2004 Phys. Rev. Lett. 92 040406
Google Scholar
[16] Jiang M, Su W, Lu X, Sheng Z M, Li Y T, Li Y J, Zhang J, Grobe R, Su Q 2011 Phys. Rev. A 83 053402
Google Scholar
[17] Wöllert A, Klaiber M, Bauke H, Keitel C H 2015 Phys. Rev. D 91 065022
Google Scholar
[18] Schützhold R, Gies H, Dunne G 2008 Phys. Rev. Lett. 101 130404
Google Scholar
[19] Monin A, Voloshin M B 2010 Phys. Rev. D 81 085014
Google Scholar
[20] Jiang M, Su W, Lv Z Q, et al. 2012 Phys. Rev. A 85 033408
Google Scholar
[21] Dong S, Unger J, Bryan J, Su Q, Grobe R 2020 Phys. Rev. E 101 013310
Google Scholar
[22] Krekora P, Cooley K, Su Q, Grobe R 2005 Phys. Rev. Lett. 95 070403
Google Scholar
[23] Jiang M, Lv Q Z, Sheng Z M, Grobe R, Su Q 2013 Phys. Rev. A 87 042503
Google Scholar
[24] Lv Q Z, Liu Y, Li Y J, Grobe R, Su Q 2014 Phys. Rev. A 90 013405
Google Scholar
[25] Wang Q, Liu J, Fu L B 2016 Sci. Rep. 6 25292
Google Scholar
[26] Su D D, Li Y T, Lv Q Z, Zhang J 2020 Phys. Rev. D 101 054501
Google Scholar
[27] Braun J W, Su Q, Grobe R 1999 Phys. Rev. A 59 604
Google Scholar
[28] Wagner R E, Ware M R, Shields B T, Su Q, Grobe R 2011 Phys. Rev. Lett. 106 023601
Google Scholar
[29] Bandrauk A D, Shen H 1994 J. Phys. A: Math. Gen. 27 7147
Google Scholar
[30] Mocken G R, Keitel C H 2008 Comput. Phys. Commun. 178 868
Google Scholar
[31] Sauter F 1932 Zeitschrift für Physik 73 547
Google Scholar
下载:
计量
- 文章访问数: 4255
- PDF下载量: 60
- 被引次数: 0
