光子对撞机产生正负电子对的数值方法

李昂; 余金清; 陈玉清; 颜学庆

doi:10.7498/aps.69.20190729

摘要

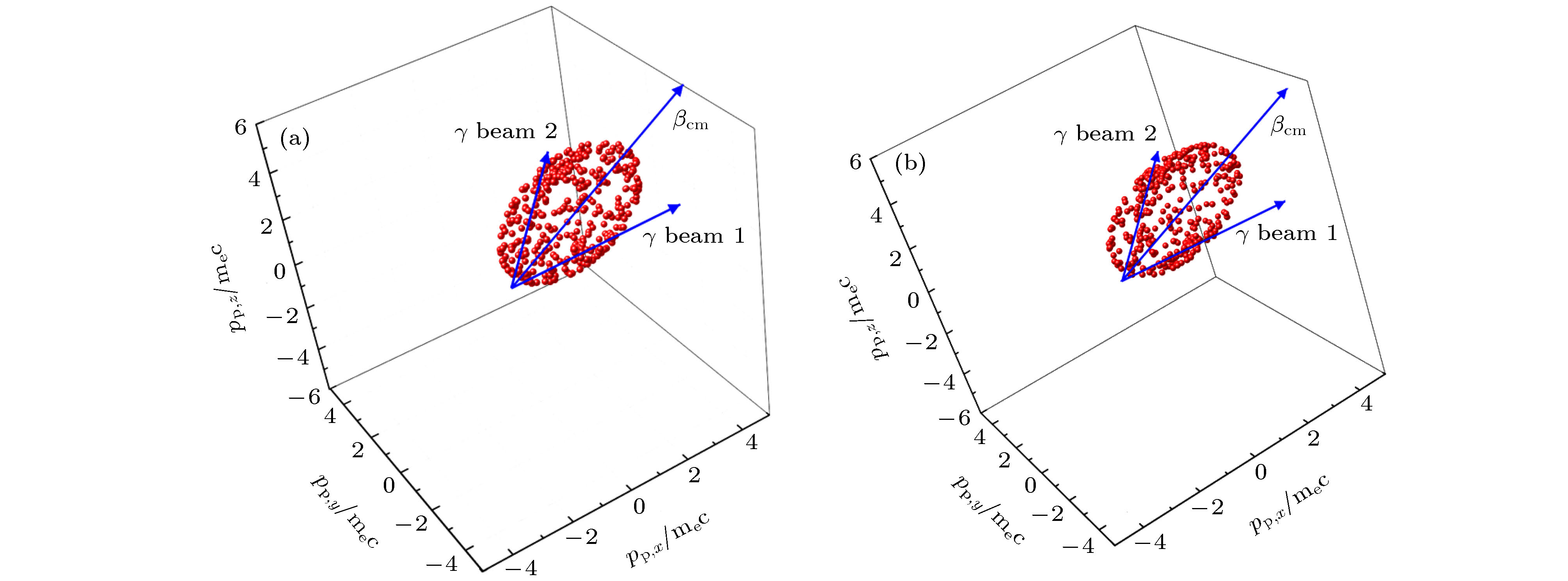
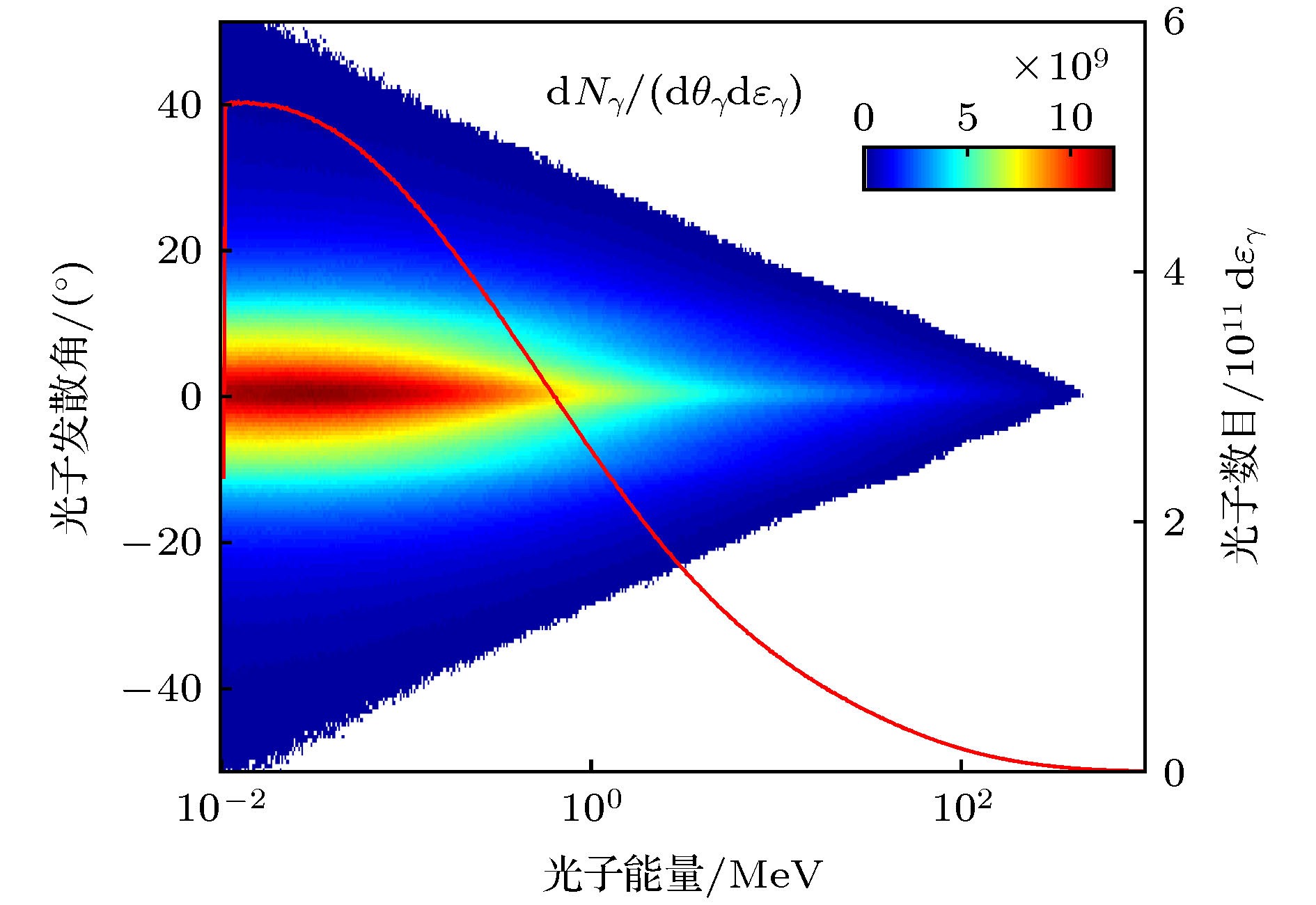
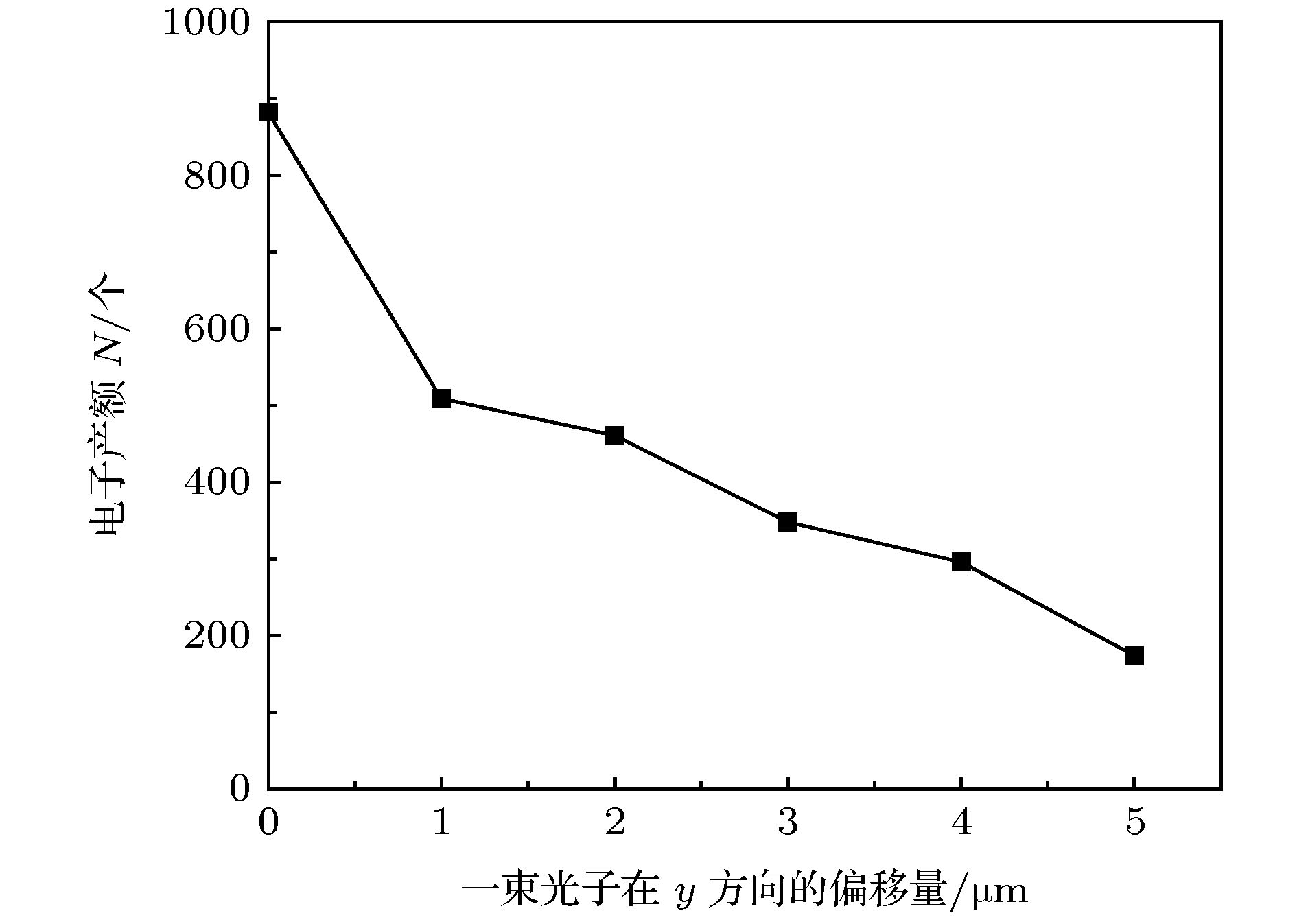
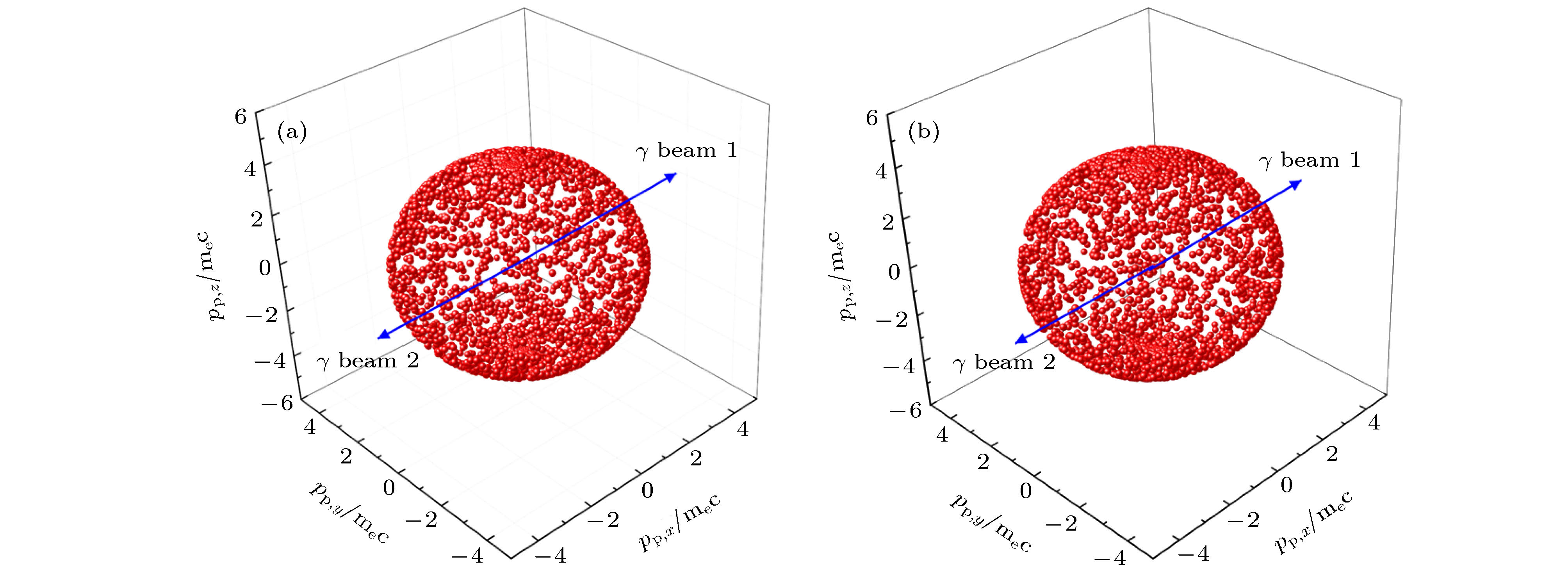
光子对撞产生正负电子对的Breit-Wheeler过程, 是由能量直接产生物质的过程, 在物质的起源与光子物理理论的研究中有着极为重要的作用. 随着激光与物质作用产生γ光源品质的提升, 使得在实验室首次观测双光子对撞的Breit-Wheeler过程成为可能. 针对光子对撞机的数值模拟方法, 本文提出了一种基于严格的双光子对撞动力学过程的计算电子产额与动力学参数的数值方法. 在对Breit-Wheeler过程的模拟中, 根据光子的运动规律将光子划分为定量的区块, 检测区块的对撞, 然后在区块内部以动力学原理检测光子是否发生对撞, 该方法可以有效提升计算模拟的效率. 同时, 该方法与已经发表的理论结果进行了比较, 发现该计算结果与理论结果高度一致. 应用这一数值方法, 能够为Breit-Wheeler过程给出较为精确的模拟结果, 也可以为未来γγ对撞机的实验设计提供参照.

关键词:

Abstract

The creation of positron and electron pairs through photon-photon collision, named Breit-Wheeler process, has been well understood in the theories of quantum electrodynamics for nearly 100 years. The photon-photon collision, which is one of the most basic processes of matter generation in the universe, has not been observed yet. The study on photon-photon collision can promote the development of two-photon physics, quantum electrodynamics theories and high energy physics. To observe photon-photon collision in the laboratory, one needs to collimate a huge number of energetic γ-ray photons into a very small spot. Recently, the development of highly collomated source generated by 10 PW laser makes photon-photon collider much more possible than before. In photon-photon collider, the study of numerical simulation plays a critical role since no experiment has achieved such a process. In this paper, a new numerical method is developed to handle the two-photon Breit-Wheeler process. This method is based on the exact two-photon collision dynamic principle, including energy threshold condition, cross-section condition, Lorentz transformation, etc. In the method, the photons are divided into quantitative photon blocks based on the spatial coordinates. Firstly, one needs to find the collision blocks according to the spatial motion law. Secondly, the ergodic method is used to look up the photons that satisfy the energy threshold condition and the cross-section condition from the blocks. Then, one can calculate the electron yield of the photon collision, and the kinetic parameters of the positrons and electrons. This method rigorously follows the physical principle so it has high precision. On the other hand, this method determines the collision of the block in advance, which can reduce the computational requirement a lot. A series of tests is carried out to confirm the accuracy and feasibility of this numerical method by calculating the collision between mono-energetic photon beams. In the tests, the collision angle is assumed to 180° and 60° separately, the results of pair momentum distribution are discussed. We also simulate the collision of the γ-ray beams generated through the interaction between ultra-intense laser and narrow tube targets. In the simulations, the collision angle is changed from 170° to 30° to see its effect on pair production. It is found that the yield of electron-positron pairs decreases with collision angle increasing, which has also been reported in previous work. Therefore, this numerical method can be efficiently used for modeling photon-photon collider, and provide theoretical reference and suggestion to the future experimental design of γ-ray collision.

Keywords:

作者及机构信息

1.
海军工程大学核科学技术学院, 武汉　430033

2.
北京大学物理学院, 核物理与核技术国家重点实验室, 北京　100871

通信作者: 余金清, jinqing.yu@hnu.edu.cn

Authors and contacts

1.
College of Nuclear Science and Technology, Naval University of Engineering, Wuhan 430033, China

2.
State Key Laboratory of Nuclear Physics and Technology, School of Physics, Peking University, Beijing 100871, China

Corresponding author: Yu Jin-Qing, jinqing.yu@hnu.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Marklund M, Shukla P K 2006 Rev. Mod. Phys. 78 591 Google Scholar
[2]	Ehlotzky F, Krajewska K, Kamiński J 2009 Rep. Prog. Phys. 72 046401 Google Scholar
[3]	Piazza A D, Müller C, Hatsagortsyan K Z, Keitel C H 2012 Rev. Mod. Phys. 84 1177 Google Scholar
[4]	黄金书, 罗鹏晖, 鲁公儒 2009 58 12 Huang J S, Luo P H, Lu G R 2009 Acta Phys. Sin. 58 12
[5]	Burke D L, Field R C, Smith G H, Spencer J E, Walz D 1997 Phys. Rev. Lett. 79 1626 Google Scholar
[6]	Breit G, Wheeler J A 1934 Phys. Rev. 46 1087 Google Scholar
[7]	Yu J Q, Lu H Y, Takahashi T, Hu R H, Gong Z, Ma W J, Huang Y S, Chen C E, Yan X Q 2019 Phys. Rev. Lett. 122 014802 Google Scholar
[8]	周美林, 颜学庆 2015 物理 44 281 Google Scholar Zhou M L, Yan X Q 2015 Physics 44 281 Google Scholar
[9]	Brady C S, Ridgers C, Arber T, Bell A R 2013 Plasma. Phys. Controlled Fusion 55 124016 Google Scholar
[10]	Yu J Q, Hu R H, Gong Z, Ting A, Najmudin Z, Wu D, Lu H Y, Ma W J, Yan X Q 2018 Appl. Phys. Lett. 112 204103 Google Scholar
[11]	Yu T P, Pukhov A, Sheng Z M, Liu F, Shvets G 2013 Phys. Rev. Lett. 110 045001 Google Scholar
[12]	Stark D J, Toncian T, Arefiev A V 2016 Phys. Rev. Lett. 116 185003 Google Scholar
[13]	Capdessus R, Humi`eres E, Tikhonchuk V T 2013 Phys. Rev. Lett. 110 215003 Google Scholar
[14]	Brady C S, Ridgers C P, Arber T D, Bell A R, Kirk J G 2012 Phys. Rev. Lett. 109 245006 Google Scholar
[15]	Nakamura T, Koga J K, Esirkepov T Z, Kando M, Korn G, Bulanov S V 2012 Phys. Rev. Lett. 108 195001 Google Scholar
[16]	Yi L, Pukhov A, Thanh P L, Shen B 2016 Phys. Rev. Lett. 116 115001 Google Scholar
[17]	Ji L L, Snyder J, Pukhov A, Freeman R R, Akli K U 2016 Sci. Rep. 6 23256 Google Scholar
[18]	Zhu X L, Yu T P, Sheng Z M, Yin Y, Turcu I C E, Pukhov A 2016 Nat. Commun. 7 13686 Google Scholar
[19]	Liu J X, Ma Y Y, Yu T P, Zhao J, Yang X H, Zou D B, Zhang G B, Zhao Y, Yang J K, Li H Z, Zhuo H B, Shao F Q, Kawata S 2017 Chin. Phys. B 26 035202 Google Scholar
[20]	Geng P F, Lv W J, Li X L, Tang R A, Xue J K 2018 Chin. Phys. B 27 035201 Google Scholar
[21]	Zhang G B, Hafz N A M, Ma Y Y, Qian L J, Shao F Q, Sheng Z M 2016 Chin. Phys. Lett. 33 095202 Google Scholar
[22]	Zhu X L, Yin Y, Yu T P, Shao F Q, Ge Z Y, Wang W Q, Liu J J 2015 New J. Phys. 17 053039 Google Scholar
[23]	Liu J J, Yu T P, Yin Y, Zhu X L, Shao F Q 2016 Opt. Express 24 14
[24]	Yu T P, Hu L X, Yin Y, Shao F Q, Zhuo H B, Ma Y Y, Yang X H, Luo W, Pukhov A 2014 Appl. Phys. Lett. 105 114101 Google Scholar
[25]	Luo W, Zhu Y B, Zhuo H B, Ma Y Y, Song Y M, Zhu Z C, Wang X D, Li X H, Turcu I, Chen M 2015 Phys. Plasmas 22 063112 Google Scholar
[26]	Luo W, Wu S D, Liu W Y, Ma Y Y, Li F Y, Yuan T, Yu J Y, Chen M, Sheng Z M 2018 Plasma Phys. Controlled Fusion 60 095006 Google Scholar
[27]	Chen L M, Yan W C, Li D Z, Hu Z D, Zhang L, Wang W M, Hafz N, Mao J Y, Huang K, Ma Y, Zhao J R, Ma J L, Li Y T, Lu X, Sheng Z M, Wei Z Y, Gao J, Zhang J 2013 Sci. Rep. 3 1912 Google Scholar
[28]	Wang W M, Sheng Z M, Gibbon P, Chen L M, Li Y T, Zhang J 2018 Proc. Natl. Acad. Sci. U.S.A. 115 9911 Google Scholar
[29]	Wang W M, Gibbon P, Sheng Z M, Li Y T, Zhang J 2017 Phys. Rev. E 96 013201 Google Scholar
[30]	Chen M, Luo J, Li F Y, Liu F, Sheng Z M, Zhang J 2016 Light-Sci. Appl. 5 e16015 Google Scholar
[31]	Liu J B, Yu J Q, Shou Y R, Wang D H, Hu R H, Tang Y H, Wang P J, Cao Z X, Mei Z S, Lin C, Lu H Y, Zhao Y Y, Zhu K, Yan X Q, Ma W J 2019 Phys. Plasmas 26 033109 Google Scholar
[32]	Gong Z, Hu R H, Lu H Y, Yu J Q, Wang D H, Fu E G, Chen C E, He X T, Yan X Q 2018 Plasma Phys. Controlled Fusion 60 044004 Google Scholar
[33]	H X Chang, B Qiao, Y X Zhang, Z Xu, W P Yao, C T Zhou, X T He 2017 Phys. Plasmas 24 043111 Google Scholar
[34]	Cristoforetti G, Londrillo P, Singh P K et al. 2017 Phys. Plasmas 7 1479 Google Scholar
[35]	Huang T, Zhou C, Zhang H, Wu S, Qiao B, He X, Ruan S 2017 Appl. Phys. Lett. 110 021102 Google Scholar
[36]	Shen B, Bu Z, Xu J, Xu T, Ji L, Li R, Xu Z 2018 Plasma Phys. Controlled Fuison 60 044002 Google Scholar
[37]	Ribeyre X, d’Humi`eres E, Jansen O, Jequier S, Tikhonchuk V T, Lobet M 2016 Phys. Rev. E 93 013201 Google Scholar
[38]	Jansen O, d’Humi`eres E, Ribeyre X, Jequier S, Tikhonchuk V T 2018 J. Comput. Phys. 355 582
[39]	Pike O J, Mackenroth F, Hill E G, Rose S J 2014 Nat. Photonics 8 434 Google Scholar
[40]	Ribeyre X, d’Humi`eres E, Jansen O, Jequier S, Tikhonchuk V T 2017 Plasma Phys. Controlled Fusion 59 014024 Google Scholar

施引文献

图 1 单能光子180°对撞时　(a)电子动量分布; (b)正电子动量分布

Fig. 1. (a) Electron momentum distribution; (b) positron momentum distribution of 180° collision of single-energy photons.

下载: 全尺寸图片幻灯片

图 2 单能光子60°对撞时　(a)电子动量分布; (b)正电子动量分布

Fig. 2. (a) Electron momentum distribution; (b) positron momentum distribution from 60° collision of single-energy photons.

下载: 全尺寸图片幻灯片

图 3 粒子模拟程序得到的光子束角-谱分布^[7,10]

Fig. 3. Angle-spectral distribution of photon beams from particle simulator^[7,10].

下载: 全尺寸图片幻灯片

图 4 10⁶光子170°对撞电子动量极角分布　(a)区块分法一; (b)区块分法二

Fig. 4. Polar angular distribution of electron momentum from 170° collision of 10⁶ photons: (a) the first block division; (b) the second block division.

下载: 全尺寸图片幻灯片

图 5 电子产额随光子束对撞角的变化趋势

Fig. 5. The trend of electronic yield with the collision angle of photon beam.

下载: 全尺寸图片幻灯片

图 6 电子产额随光子束偏移量的变化趋势

Fig. 6. The trend of electronic yield with the offset of photon beam.

下载: 全尺寸图片幻灯片

map

[1]	Marklund M, Shukla P K 2006 Rev. Mod. Phys. 78 591 Google Scholar
[2]	Ehlotzky F, Krajewska K, Kamiński J 2009 Rep. Prog. Phys. 72 046401 Google Scholar
[3]	Piazza A D, Müller C, Hatsagortsyan K Z, Keitel C H 2012 Rev. Mod. Phys. 84 1177 Google Scholar
[4]	黄金书, 罗鹏晖, 鲁公儒 2009 58 12 Huang J S, Luo P H, Lu G R 2009 Acta Phys. Sin. 58 12
[5]	Burke D L, Field R C, Smith G H, Spencer J E, Walz D 1997 Phys. Rev. Lett. 79 1626 Google Scholar
[6]	Breit G, Wheeler J A 1934 Phys. Rev. 46 1087 Google Scholar
[7]	Yu J Q, Lu H Y, Takahashi T, Hu R H, Gong Z, Ma W J, Huang Y S, Chen C E, Yan X Q 2019 Phys. Rev. Lett. 122 014802 Google Scholar
[8]	周美林, 颜学庆 2015 物理 44 281 Google Scholar Zhou M L, Yan X Q 2015 Physics 44 281 Google Scholar
[9]	Brady C S, Ridgers C, Arber T, Bell A R 2013 Plasma. Phys. Controlled Fusion 55 124016 Google Scholar
[10]	Yu J Q, Hu R H, Gong Z, Ting A, Najmudin Z, Wu D, Lu H Y, Ma W J, Yan X Q 2018 Appl. Phys. Lett. 112 204103 Google Scholar
[11]	Yu T P, Pukhov A, Sheng Z M, Liu F, Shvets G 2013 Phys. Rev. Lett. 110 045001 Google Scholar
[12]	Stark D J, Toncian T, Arefiev A V 2016 Phys. Rev. Lett. 116 185003 Google Scholar
[13]	Capdessus R, Humi`eres E, Tikhonchuk V T 2013 Phys. Rev. Lett. 110 215003 Google Scholar
[14]	Brady C S, Ridgers C P, Arber T D, Bell A R, Kirk J G 2012 Phys. Rev. Lett. 109 245006 Google Scholar
[15]	Nakamura T, Koga J K, Esirkepov T Z, Kando M, Korn G, Bulanov S V 2012 Phys. Rev. Lett. 108 195001 Google Scholar
[16]	Yi L, Pukhov A, Thanh P L, Shen B 2016 Phys. Rev. Lett. 116 115001 Google Scholar
[17]	Ji L L, Snyder J, Pukhov A, Freeman R R, Akli K U 2016 Sci. Rep. 6 23256 Google Scholar
[18]	Zhu X L, Yu T P, Sheng Z M, Yin Y, Turcu I C E, Pukhov A 2016 Nat. Commun. 7 13686 Google Scholar
[19]	Liu J X, Ma Y Y, Yu T P, Zhao J, Yang X H, Zou D B, Zhang G B, Zhao Y, Yang J K, Li H Z, Zhuo H B, Shao F Q, Kawata S 2017 Chin. Phys. B 26 035202 Google Scholar
[20]	Geng P F, Lv W J, Li X L, Tang R A, Xue J K 2018 Chin. Phys. B 27 035201 Google Scholar
[21]	Zhang G B, Hafz N A M, Ma Y Y, Qian L J, Shao F Q, Sheng Z M 2016 Chin. Phys. Lett. 33 095202 Google Scholar
[22]	Zhu X L, Yin Y, Yu T P, Shao F Q, Ge Z Y, Wang W Q, Liu J J 2015 New J. Phys. 17 053039 Google Scholar
[23]	Liu J J, Yu T P, Yin Y, Zhu X L, Shao F Q 2016 Opt. Express 24 14
[24]	Yu T P, Hu L X, Yin Y, Shao F Q, Zhuo H B, Ma Y Y, Yang X H, Luo W, Pukhov A 2014 Appl. Phys. Lett. 105 114101 Google Scholar
[25]	Luo W, Zhu Y B, Zhuo H B, Ma Y Y, Song Y M, Zhu Z C, Wang X D, Li X H, Turcu I, Chen M 2015 Phys. Plasmas 22 063112 Google Scholar
[26]	Luo W, Wu S D, Liu W Y, Ma Y Y, Li F Y, Yuan T, Yu J Y, Chen M, Sheng Z M 2018 Plasma Phys. Controlled Fusion 60 095006 Google Scholar
[27]	Chen L M, Yan W C, Li D Z, Hu Z D, Zhang L, Wang W M, Hafz N, Mao J Y, Huang K, Ma Y, Zhao J R, Ma J L, Li Y T, Lu X, Sheng Z M, Wei Z Y, Gao J, Zhang J 2013 Sci. Rep. 3 1912 Google Scholar
[28]	Wang W M, Sheng Z M, Gibbon P, Chen L M, Li Y T, Zhang J 2018 Proc. Natl. Acad. Sci. U.S.A. 115 9911 Google Scholar
[29]	Wang W M, Gibbon P, Sheng Z M, Li Y T, Zhang J 2017 Phys. Rev. E 96 013201 Google Scholar
[30]	Chen M, Luo J, Li F Y, Liu F, Sheng Z M, Zhang J 2016 Light-Sci. Appl. 5 e16015 Google Scholar
[31]	Liu J B, Yu J Q, Shou Y R, Wang D H, Hu R H, Tang Y H, Wang P J, Cao Z X, Mei Z S, Lin C, Lu H Y, Zhao Y Y, Zhu K, Yan X Q, Ma W J 2019 Phys. Plasmas 26 033109 Google Scholar
[32]	Gong Z, Hu R H, Lu H Y, Yu J Q, Wang D H, Fu E G, Chen C E, He X T, Yan X Q 2018 Plasma Phys. Controlled Fusion 60 044004 Google Scholar
[33]	H X Chang, B Qiao, Y X Zhang, Z Xu, W P Yao, C T Zhou, X T He 2017 Phys. Plasmas 24 043111 Google Scholar
[34]	Cristoforetti G, Londrillo P, Singh P K et al. 2017 Phys. Plasmas 7 1479 Google Scholar
[35]	Huang T, Zhou C, Zhang H, Wu S, Qiao B, He X, Ruan S 2017 Appl. Phys. Lett. 110 021102 Google Scholar
[36]	Shen B, Bu Z, Xu J, Xu T, Ji L, Li R, Xu Z 2018 Plasma Phys. Controlled Fuison 60 044002 Google Scholar
[37]	Ribeyre X, d’Humi`eres E, Jansen O, Jequier S, Tikhonchuk V T, Lobet M 2016 Phys. Rev. E 93 013201 Google Scholar
[38]	Jansen O, d’Humi`eres E, Ribeyre X, Jequier S, Tikhonchuk V T 2018 J. Comput. Phys. 355 582
[39]	Pike O J, Mackenroth F, Hill E G, Rose S J 2014 Nat. Photonics 8 434 Google Scholar
[40]	Ribeyre X, d’Humi`eres E, Jansen O, Jequier S, Tikhonchuk V T 2017 Plasma Phys. Controlled Fusion 59 014024 Google Scholar

[1]	李传可, 林南省, 周鲜鲜, 江淼, 李英骏. 双振荡场产生正负电子对的理论研究. , 2024, 73(4): 044201. doi: 10.7498/aps.73.20230432
[2]	叶全兴, 何广朝, 王倩. 正负电子对撞中类底夸克偶素的线形. , 2023, 72(20): 201401. doi: 10.7498/aps.72.20230908
[3]	罗蕙一, 江淼, 徐妙华, 李英骏. 不同频率的组合振荡场下产生正负电子对. , 2023, 72(2): 021201. doi: 10.7498/aps.72.20221660
[4]	牟家连, 吕军光, 孙希磊, 兰小飞, 黄永盛. 环形正负电子对撞机带电粒子鉴别的飞行时间探测器. , 2023, 72(12): 122901. doi: 10.7498/aps.72.20222271
[5]	谢柏松, 李烈娟, 麦丽开·麦提斯迪克, 王莉. 频率啁啾对强场下真空正负电子对产生的增强效应. , 2022, 71(13): 131201. doi: 10.7498/aps.71.20220148
[6]	范佳锟, 王洁, 高勇, 游志明, 王盛, 张静, 胡耀程, 许章炼, 王斌. 超级质子-质子对撞机中束流热屏的热-结构耦合模拟分析. , 2021, 70(1): 012901. doi: 10.7498/aps.70.20200830
[7]	游志明, 王洁, 高勇, 范佳锟, 张静, 胡耀程, 王盛, 许章炼, 张琦. 超级质子-质子对撞机束屏内气体密度演化规律研究. , 2021, 70(16): 166802. doi: 10.7498/aps.70.20201594
[8]	朱兴龙, 王伟民, 余同普, 何峰, 陈民, 翁苏明, 陈黎明, 李玉同, 盛政明, 张杰. 极强激光场驱动超亮伽马辐射和正负电子对产生的研究进展. , 2021, 70(8): 085202. doi: 10.7498/aps.70.20202224
[9]	孙婷, 王宇, 郭任彤, 卢知为, 栗建兴. 强激光驱动高能极化正负电子束与偏振伽马射线的研究进展. , 2021, 70(8): 087901. doi: 10.7498/aps.70.20210009
[10]	江淼, 郑晓冉, 林南省, 李英骏. 正负电子对产生过程中不同外场宽度下的多光子跃迁效应. , 2021, 70(23): 231202. doi: 10.7498/aps.70.20202101
[11]	董旭, 黄永盛, 唐光毅, 陈姗红, 司梅雨, 张建勇. 基于微波-电子康普顿背散射的环形正负电子对撞机束流能量测量方案. , 2021, 70(13): 131301. doi: 10.7498/aps.70.20202081
[12]	吴广智, 王强, 周沧涛, 傅立斌. 双势阱产生正负电子对过程中的正电子波干涉与克莱因隧穿现象. , 2017, 66(7): 070301. doi: 10.7498/aps.66.070301
[13]	王晓晖, 常本康, 钱芸生, 高频, 张益军, 乔建良, 杜晓晴. 透射式负电子亲和势GaN光电阴极的光谱响应研究. , 2011, 60(5): 057902. doi: 10.7498/aps.60.057902
[14]	付小倩, 常本康, 李飙, 王晓晖, 乔建良. 负电子亲和势GaN光电阴极的研究进展. , 2011, 60(3): 038503. doi: 10.7498/aps.60.038503
[15]	乔建良, 常本康, 钱芸生, 高频, 王晓晖, 徐源. 负电子亲和势GaN真空面电子源研究进展. , 2011, 60(10): 107901. doi: 10.7498/aps.60.107901
[16]	乔建良, 常本康, 钱芸生, 杜晓晴, 张益军, 高频, 王晓晖, 郭向阳, 牛军, 高有堂. 负电子亲和势GaN光电阴极光谱响应特性研究. , 2010, 59(5): 3577-3582. doi: 10.7498/aps.59.3577
[17]	乔建良, 田思, 常本康, 杜晓晴, 高频. 负电子亲和势GaN光电阴极激活机理研究. , 2009, 58(8): 5847-5851. doi: 10.7498/aps.58.5847
[18]	杜晓晴, 常本康. 负电子亲和势光电阴极量子效率公式的修正. , 2009, 58(12): 8643-8650. doi: 10.7498/aps.58.8643
[19]	黄金书, 罗鹏晖, 鲁公儒. 关于光子对撞机上底夸克对产生的研究. , 2009, 58(12): 8166-8173. doi: 10.7498/aps.58.8166
[20]	罗辽复, 陆埮. 高能正负电子对的湮没与超窄共振ψ粒子的作用. , 1975, 24(2): 145-150. doi: 10.7498/aps.24.145

计量

文章访问数: 8951
PDF下载量: 150
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

光子对撞机产生正负电子对的数值方法