-
In the conventional quark model, meson is made of one quark and one antiquark, and baryon is made of three quarks. Since the observation of the
${\rm{X}}(3872)$ in 2003 by Belle collaboration, numerous exotic candidates beyond the conventional quark model have been observed. Most of them are located in heavy quarkonium energy region. Several interpretations, e.g. compact multiquarks, hadronic molecules, hybrids, etc, are proposed to understand their internal structures. Hadronic molecules are based on the fact that most of exotic candidates have nearby thresholds, which makes them analogies of deuteron made of one proton and one neutron. Whether two or more hadrons can be form a hadronic molecule or not depends on their interactions. In this work, we study the${\rm{P}}$ -wave${\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)}$ interactions based on the${\rm{e^+e^-}}\to {\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)}$ cross sections from Belle-II experiment to study whether their interaction can form vector bottomonium-like states or not. As${\rm{B}}^{(*)}$ and$\bar{{\rm{B}}}^{(*)}$ mesons have bottom and antibottom quark, respectively, we work in the heavy quark limit, which respects both heavy quark spin symmetry and heavy quark flavor symmetry. In this framework, we construct effective contact potentials for$J^{{\rm{PC}}}=1^{--}$ ${\rm{P}}$ -wave${\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)}$ interactions, by decomposing the${\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)}$ dynamic channels into heavy-light basis. That, in the heavy quark limit, heavy and light degrees of freedoms are conserved individually makes the contact potentials in a very simple form. After solving the corresponding Lippmann-Schwinger equation, one can obtain the${\rm{e^+e^-}}\to {\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)}$ scattering amplitudes. With these scattering amplitudes, we can deduce the corresponding cross sections,which can be compared with the experimental data directly. By fitting to the data, we find that the mass shifts of the considered bottomonia are small due to their small couplings to the${\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)}$ continuum channels. As the result, the$\Upsilon(4{\rm{S}})$ ,$\Upsilon(3{\rm{D}})$ ,$\Upsilon(5{\rm{S}})$ and$\Upsilon(6{\rm{S}})$ vector bottomonia express theirselves as peaks at$10.58\; {\rm{GeV}}$ ,$10.87\; {\rm{GeV}}$ ,$11.03\; {\rm{GeV}}$ . The peak at$10.87\; {\rm{GeV}}$ is the interference between$\Upsilon(3{\rm{D}})$ and$\Upsilon(5{\rm{S}})$ . As there are only two data points around$10.63\; {\rm{GeV}}$ , we cannot obtain a very clear conclusion about the peak around this energy point. To further explore its nature, both detailed scan around this energy region in experiment and improved formula in theory are needed.-
Keywords:
- heavy quarkonia /
- exotic mesons /
- heavy quark effective theory
[1] Gell-Mann M 1964 Phys. Lett. 8 214
Google Scholar
[2] Zweig G 1964 An SU(3) model for strong interaction symmetry and its breaking CM-P0004288
[3] Choi S K, Olsen S L, Abe K, et al. 2003 Phys. Rev. Lett. 91 262001
Google Scholar
[4] Chen H X, Chen W, Liu X, Zhu S L 2016 Phys. Rep. 639 1
Google Scholar
[5] Chen H X, Chen W, Liu X, Liu Y R, Zhu S L 2017 Rep. Prog. Phys. 80 076201
Google Scholar
[6] Dong Y, Faessler A, Lyubovitskij V E 2017 Prog. Part. Nucl. Phys. 94 282
Google Scholar
[7] Lebed R F, Mitchell R E, Swanson E S 2017 Prog. Part. Nucl. Phys. 93 143
Google Scholar
[8] Guo F K, Hanhart C, Meißner U G, Wang Q, Zhao Q, Zou B S 2018 Rev. Mod. Phys. 90 015004
Google Scholar
[9] Liu Y R, Chen H X, Chen W, Liu X, Zhu S L 2019 Prog. Part. Nucl. Phys. 107 237
Google Scholar
[10] Albuquerque R M, Dias J M, Khemchandani K P, Torres A M, Navarra F S, Nielsen M, Zanetti C M 2019 J. Phys. G 46 093002
Google Scholar
[11] Yamaguchi Y, Hosaka A, Takeuchi S, Takizawa M 2020 J. Phys. G 47 053001
Google Scholar
[12] Guo F K, Liu X H, Sakai S 2020 Prog. Part. Nucl. Phys. 112 103757
Google Scholar
[13] Brambilla N, Eidelman S, Hanhart C, Nefediev A, Shen C P, Thomas C E, Vairo A, Yuan C Z 2020 Phys. Rep. 873 1
Google Scholar
[14] Zou B S 2021 Sci. Bull. 66 1258
Google Scholar
[15] Wang Q, Hanhart C, Zhao Q 2013 Phys. Rev. Lett. 111 132003
Google Scholar
[16] Guo F K, Hanhart C, Meißner U G, Wang Q, Zhao Q 2013 Phys. Lett. B 725 127
Google Scholar
[17] Cleven M, Wang Q, Guo F K, Hanhart C, Meißner U G, Zhao Q 2014 Phys. Rev. D 90 074039
Google Scholar
[18] Wang Q, Cleven M, Guo F K, Hanhart C, Meißner U G, Wu X G, Zhao Q 2014 Phys. Rev. D 89 034001
Google Scholar
[19] Wu X G, Hanhart C, Wang Q, Zhao Q 2014 Phys. Rev. D 89 054038
Google Scholar
[20] Chen Y H, Dai L Y, Guo F K, Kubis B 2019 Phys. Rev. D 99 074016
Google Scholar
[21] Xue S R, Jing H J, Guo F K, Zhao Q 2018 Phys. Lett. B 779 402
Google Scholar
[22] Lu Y, Anwar M N, Zou B S 2017 Phys. Rev. D 96 114022
Google Scholar
[23] Qin W, Xue S R, Zhao Q 2017 JPS Conf. Proc. 13 020022
Google Scholar
[24] Cleven M, Zhao Q 2017 Phys. Lett. B 768 52
Google Scholar
[25] Qin W, Xue S R, Zhao Q 2016 Phys. Rev. D 94 054035
Google Scholar
[26] Li G, An C S, Li P Y, Liu D, Zhang X, Zhou Z 2015 Chin. Phys. C 39 063102
Google Scholar
[27] Li G, Liu X H 2013 Phys. Rev. D 88 094008
Google Scholar
[28] Li X, Voloshin M B 2013 Phys. Rev. D 88 034012
Google Scholar
[29] Dong X K, Lin Y H, Zou B S 2020 Phys. Rev. D 101 076003
Google Scholar
[30] Cao Z, Zhao Q 2019 Phys. Rev. D 99 014016
Google Scholar
[31] Sanchez M, Geng L S, Lu J X, Hyodo T, Valderrama M P 2018 Phys. Rev. D 98 054001
Google Scholar
[32] Wang Q 2014 Phys. Rev. D 89 114013
Google Scholar
[33] Ji T, Dong X K, Guo F K, Zou B S 2022 Phys. Rev. Lett. 129 102002
Google Scholar
[34] Mizuk R, Bondar A, Adachi I, et al. 2021 JHEP 06 137
Google Scholar
[35] Du M L, Meißner U G, Wang Q 2016 Phys. Rev. D 94 096006
Google Scholar
[36] Voloshin M B 2012 Phys. Rev. D 85 034024
Google Scholar
[37] Du M L, Baru V, Guo F K, Hanhart C, Meißner U G, Oller J A, Wang Q 2020 Phys. Rev. Lett. 124 072001
Google Scholar
[38] Du M L, Baru V, Guo F K, Hanhart C, Meißner U G, Oller J A, Wang Q 2021 JHEP 08 157
Google Scholar
[39] Baru V, Epelbaum E, Filin A A, Hanhart C, Nefediev A V, Wang Q 2019 Phys. Rev. D 99 094013
Google Scholar
[40] Wang Q, Baru V, Filin A A, Hanhart C, Nefediev A V, Wynen J L 2018 Phys. Rev. D 98 074023
Google Scholar
[41] Workman R L, Burkert V D, Crede V, et al. 2022 PTEP 2022 083C
Google Scholar
[42] Mizuk R, Bondar A, Adachi I, et al. 2019 JHEP 10 220
Google Scholar
[43] Wang Q, Liu X H, Zhao Q 2011 Phys. Rev. D 84 014007
Google Scholar
-
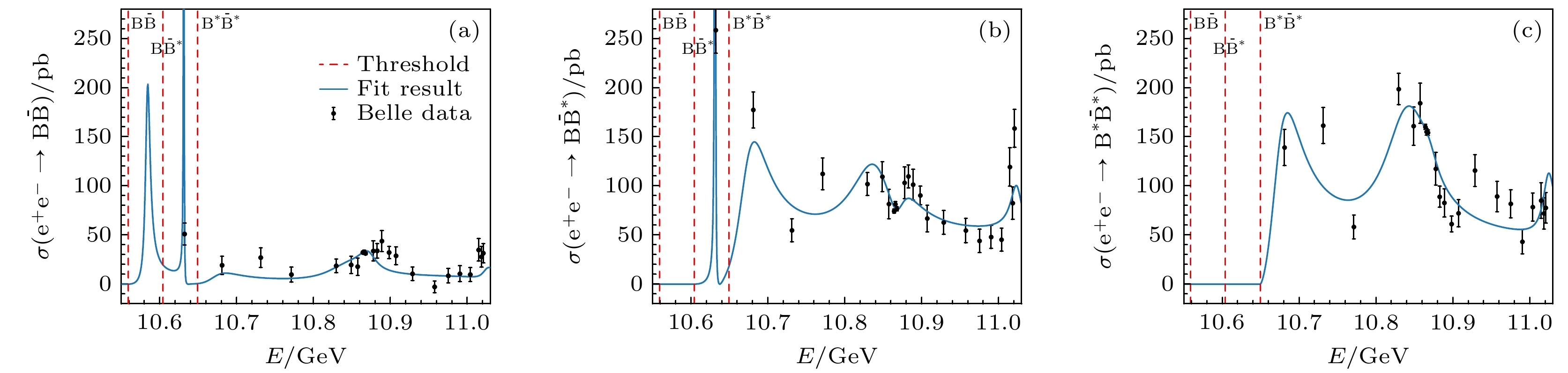
图 1 质心能量在
$ [10.55, 11.03]\; {\rm{GeV}} $ 之间$ {\rm{e^+e^-}} \rightarrow {\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)} $ 的散射截面. 实验数据点来自BelleII合作组[34]. 蓝色实线是理论计算的截面. 3条垂直的红色虚线从低到高分别是$ {\rm{B}}\bar{{\rm{B}}} $ ,$ {\rm{B}}\bar{{\rm{B}}}^* $ ,$ {\rm{B}}^*\bar{{\rm{B}}}^* $ 的阈值. 其中$ {\rm{e^+e^-}}\to {\rm{B}}^*\bar{{\rm{B}}}^* $ 过程的截面是第3个道和第4个道贡献的总和Figure 1. The cross sections of the
$ {\rm{e^+e^-}} \rightarrow {\rm{B}}^{(*)}\bar{{\rm{B}}}^{(*)} $ in the center of mass energy region$ [10.55, 11.03]\; {\rm{GeV}} $ . The blue solid curves are the theoretical results. The vertical red dashed lines are the$ {\rm{B}}\bar{{\rm{B}}} $ ,$ {\rm{B}}\bar{{\rm{B}}}^* $ ,$ {\rm{B}}^*\bar{{\rm{B}}}^* $ thresholds. The cross section of the$ {\rm{e^+e^-}}\to {\rm{B}}^*\bar{{\rm{B}}}^* $ process is the sum of that of the third and forth channels表 1 拟合参数和约化卡方
Table 1. Fitted parameters and the corresponding reduced
$ \chi ^2 $ 参数名 参数值 单位 $ C_0 $ $ 0.160\pm 0.149 $ $ {\rm{GeV}}^{-2} $ $ C_1 $ $ 1.669\pm 0.003 $ $ {\rm{GeV}}^{-2} $ $ C_2 $ $ -1.785\pm 2.677 $ $ {\rm{GeV}}^{-2} $ $ g_{4{\rm{S}}} $ $ -2.377\pm 0.180 $ $ {\rm{GeV}}^{0} $ $ g_{3{\rm{D}}} $ $ 0.966\pm 0.430 $ $ {\rm{GeV}}^{0} $ $ g_{5{\rm{S}}} $ $ -0.571\pm 0.073 $ $ {\rm{GeV}}^{0} $ $ g_{6{\rm{S}}} $ $ 0.252\pm 0.102 $ $ {\rm{GeV}}^{0} $ $ f_{{\rm{S}}}^0 $ $ 1.040\pm 0.097 $ $ {\rm{GeV}}^{0} $ $ f_{D}^0 $ $ -1.543\pm 1.535 $ $ {\rm{GeV}}^{0} $ $ m_{4{\rm{S}}} $ $ 10.468\pm 0.043 $ $ {\rm{GeV}} $ $ m_{3{\rm{D}}} $ $ 10.856\pm 0.004 $ $ {\rm{GeV}} $ $ m_{5{\rm{S}}} $ $ 10.830\pm 0.011 $ $ {\rm{GeV}} $ $ m_{6{\rm{S}}} $ $ 11.024\pm 0.008 $ $ {\rm{GeV}} $ $ \mit \Lambda $ $ 2.448\pm 0.001 $ $ {\rm{GeV}} $ $ \mit \Gamma_1 $ $ 0.029\pm 0.017 $ $ {\rm{GeV}} $ $ \mit \Gamma_2 $ $ 0.033\pm 0.010 $ $ {\rm{GeV}} $ $ \mit \Gamma_3 $ $ 0.139\pm 0.025 $ $ {\rm{GeV}} $ $ \mit \Gamma_4 $ $ 0.027\pm 0.015 $ $ {\rm{GeV}} $ $ \dfrac{\chi^2}{{\rm{d.o.f}}} $ 3.37 $ - $ 
DownLoad: CSV
表 2 物理黎曼面
$ R_{+++} $ , 离物理黎曼面近的黎曼面$ R_{-++}, R_{–+}, R_{---} $ 上的极点(第2列)和主要耦合道及其有效耦合常数(第3列)Table 2. Poles on the physical sheet
$ R_{+++} $ , those$ R_{-++}, R_{-+}, R_{---} $ close to the physical one (the second column), the dominant channel with the corresponding effective coupling (the third column)黎曼面 极点/GeV D.C.($ g^{\rm{eff}} $/$ {\rm{MeV}}^{-1/2} $) $ R_{+++} $ $ 10.638-0.000 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=0} $ [0.52] $ 10.871-0.014 {\rm{i}} $ $ {\rm{B}}\bar{{\rm{B}}}^* $ [0.05] $ 11.024-0.009 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=2} $ [0.06] $ R_{-++} $ $ 10.876-0.016 {\rm{i}} $ (${\rm{B}}^*\bar{{\rm{B}}}^*)^{s=2} $ [0.03] $ 11.024-0.008 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=2} $ [0.05] $ R_{--+} $ $ 10.873-0.021 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=2} $ [0.01] $ 11.018-0.008 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=0} $ [0.00] $ R_{---} $ $ 10.587-0.00 {\rm{i}} $ $ {\rm{B}}\bar{{\rm{B}}}^* $ [0.01] $ 10.635-0.033 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=2} $ [0.01] $ 10.846-0.090 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=0} $ [0.00] $ 10.871-0.020 {\rm{i}} $ ($ {\rm{B}}^*\bar{{\rm{B}}}^*)^{s=2} $ [0.01]
DownLoad: CSV
-
[1] Gell-Mann M 1964 Phys. Lett. 8 214
Google Scholar
[2] Zweig G 1964 An SU(3) model for strong interaction symmetry and its breaking CM-P0004288
[3] Choi S K, Olsen S L, Abe K, et al. 2003 Phys. Rev. Lett. 91 262001
Google Scholar
[4] Chen H X, Chen W, Liu X, Zhu S L 2016 Phys. Rep. 639 1
Google Scholar
[5] Chen H X, Chen W, Liu X, Liu Y R, Zhu S L 2017 Rep. Prog. Phys. 80 076201
Google Scholar
[6] Dong Y, Faessler A, Lyubovitskij V E 2017 Prog. Part. Nucl. Phys. 94 282
Google Scholar
[7] Lebed R F, Mitchell R E, Swanson E S 2017 Prog. Part. Nucl. Phys. 93 143
Google Scholar
[8] Guo F K, Hanhart C, Meißner U G, Wang Q, Zhao Q, Zou B S 2018 Rev. Mod. Phys. 90 015004
Google Scholar
[9] Liu Y R, Chen H X, Chen W, Liu X, Zhu S L 2019 Prog. Part. Nucl. Phys. 107 237
Google Scholar
[10] Albuquerque R M, Dias J M, Khemchandani K P, Torres A M, Navarra F S, Nielsen M, Zanetti C M 2019 J. Phys. G 46 093002
Google Scholar
[11] Yamaguchi Y, Hosaka A, Takeuchi S, Takizawa M 2020 J. Phys. G 47 053001
Google Scholar
[12] Guo F K, Liu X H, Sakai S 2020 Prog. Part. Nucl. Phys. 112 103757
Google Scholar
[13] Brambilla N, Eidelman S, Hanhart C, Nefediev A, Shen C P, Thomas C E, Vairo A, Yuan C Z 2020 Phys. Rep. 873 1
Google Scholar
[14] Zou B S 2021 Sci. Bull. 66 1258
Google Scholar
[15] Wang Q, Hanhart C, Zhao Q 2013 Phys. Rev. Lett. 111 132003
Google Scholar
[16] Guo F K, Hanhart C, Meißner U G, Wang Q, Zhao Q 2013 Phys. Lett. B 725 127
Google Scholar
[17] Cleven M, Wang Q, Guo F K, Hanhart C, Meißner U G, Zhao Q 2014 Phys. Rev. D 90 074039
Google Scholar
[18] Wang Q, Cleven M, Guo F K, Hanhart C, Meißner U G, Wu X G, Zhao Q 2014 Phys. Rev. D 89 034001
Google Scholar
[19] Wu X G, Hanhart C, Wang Q, Zhao Q 2014 Phys. Rev. D 89 054038
Google Scholar
[20] Chen Y H, Dai L Y, Guo F K, Kubis B 2019 Phys. Rev. D 99 074016
Google Scholar
[21] Xue S R, Jing H J, Guo F K, Zhao Q 2018 Phys. Lett. B 779 402
Google Scholar
[22] Lu Y, Anwar M N, Zou B S 2017 Phys. Rev. D 96 114022
Google Scholar
[23] Qin W, Xue S R, Zhao Q 2017 JPS Conf. Proc. 13 020022
Google Scholar
[24] Cleven M, Zhao Q 2017 Phys. Lett. B 768 52
Google Scholar
[25] Qin W, Xue S R, Zhao Q 2016 Phys. Rev. D 94 054035
Google Scholar
[26] Li G, An C S, Li P Y, Liu D, Zhang X, Zhou Z 2015 Chin. Phys. C 39 063102
Google Scholar
[27] Li G, Liu X H 2013 Phys. Rev. D 88 094008
Google Scholar
[28] Li X, Voloshin M B 2013 Phys. Rev. D 88 034012
Google Scholar
[29] Dong X K, Lin Y H, Zou B S 2020 Phys. Rev. D 101 076003
Google Scholar
[30] Cao Z, Zhao Q 2019 Phys. Rev. D 99 014016
Google Scholar
[31] Sanchez M, Geng L S, Lu J X, Hyodo T, Valderrama M P 2018 Phys. Rev. D 98 054001
Google Scholar
[32] Wang Q 2014 Phys. Rev. D 89 114013
Google Scholar
[33] Ji T, Dong X K, Guo F K, Zou B S 2022 Phys. Rev. Lett. 129 102002
Google Scholar
[34] Mizuk R, Bondar A, Adachi I, et al. 2021 JHEP 06 137
Google Scholar
[35] Du M L, Meißner U G, Wang Q 2016 Phys. Rev. D 94 096006
Google Scholar
[36] Voloshin M B 2012 Phys. Rev. D 85 034024
Google Scholar
[37] Du M L, Baru V, Guo F K, Hanhart C, Meißner U G, Oller J A, Wang Q 2020 Phys. Rev. Lett. 124 072001
Google Scholar
[38] Du M L, Baru V, Guo F K, Hanhart C, Meißner U G, Oller J A, Wang Q 2021 JHEP 08 157
Google Scholar
[39] Baru V, Epelbaum E, Filin A A, Hanhart C, Nefediev A V, Wang Q 2019 Phys. Rev. D 99 094013
Google Scholar
[40] Wang Q, Baru V, Filin A A, Hanhart C, Nefediev A V, Wynen J L 2018 Phys. Rev. D 98 074023
Google Scholar
[41] Workman R L, Burkert V D, Crede V, et al. 2022 PTEP 2022 083C
Google Scholar
[42] Mizuk R, Bondar A, Adachi I, et al. 2019 JHEP 10 220
Google Scholar
[43] Wang Q, Liu X H, Zhao Q 2011 Phys. Rev. D 84 014007
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2243
- PDF Downloads: 79
- Cited By: 0
