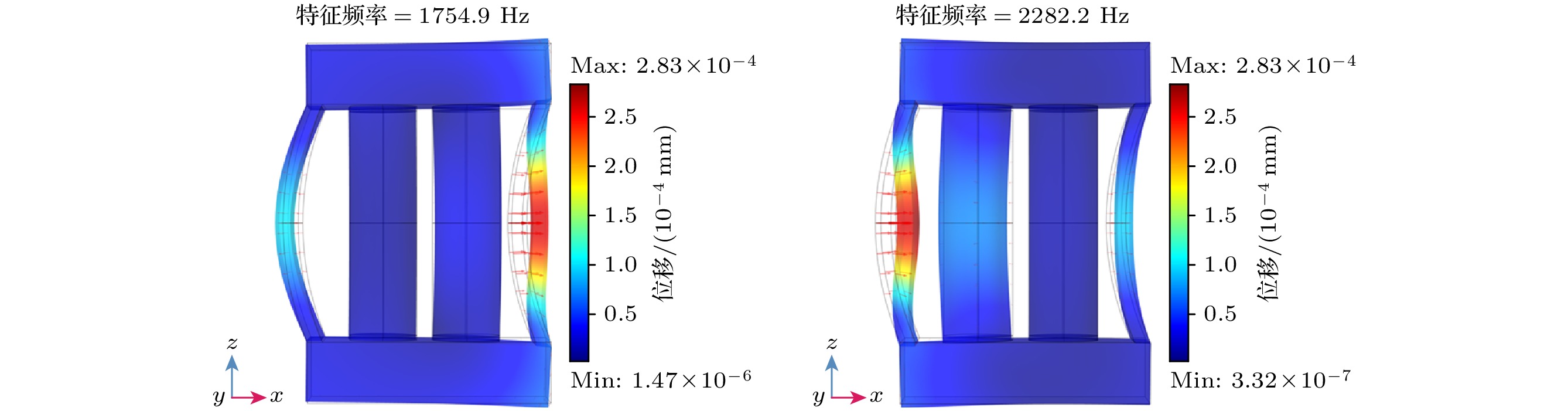
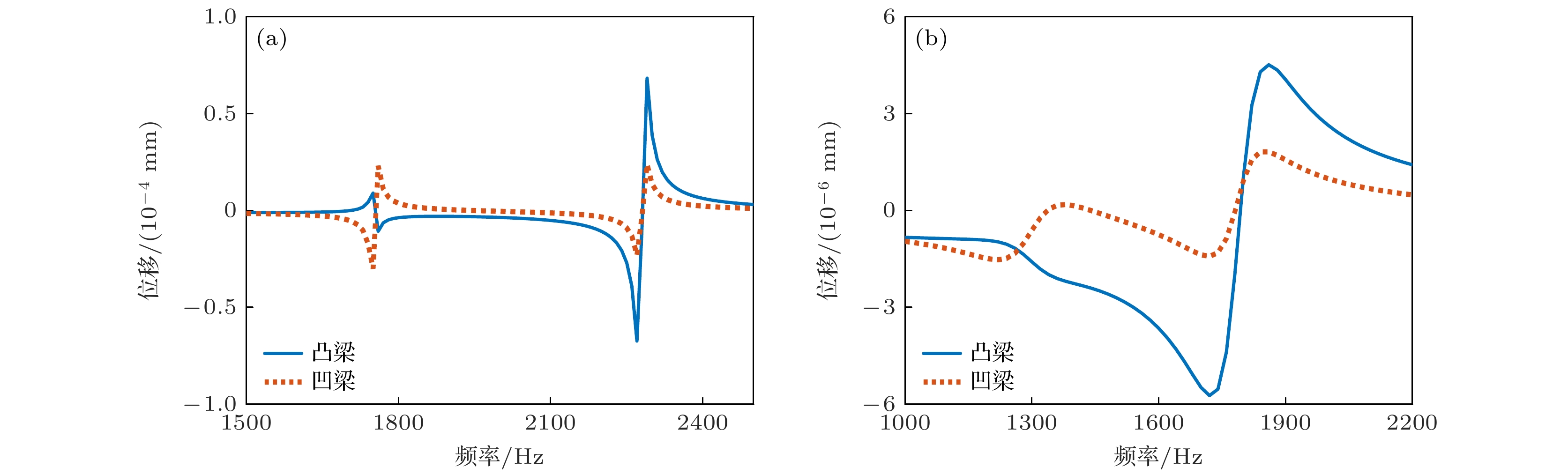
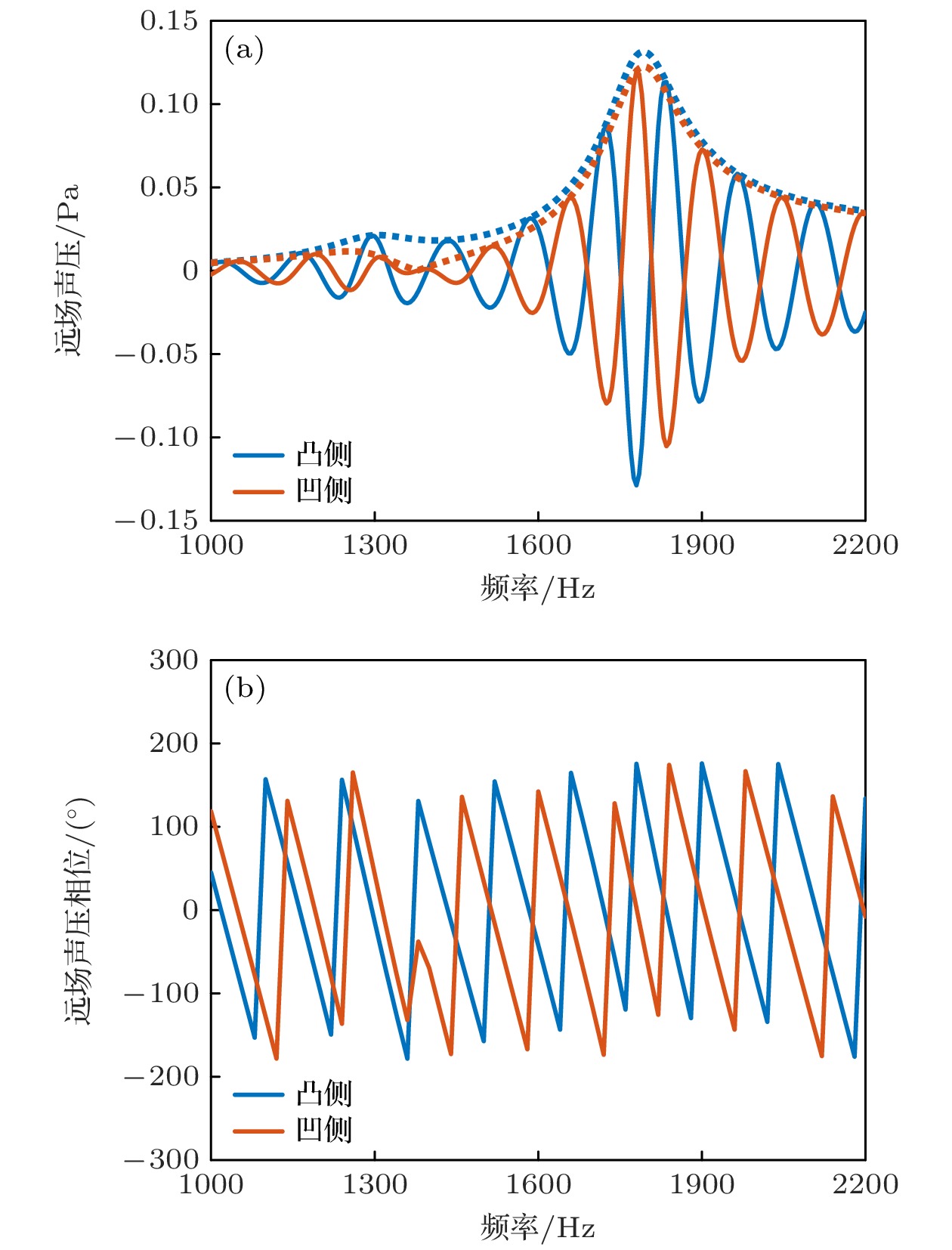
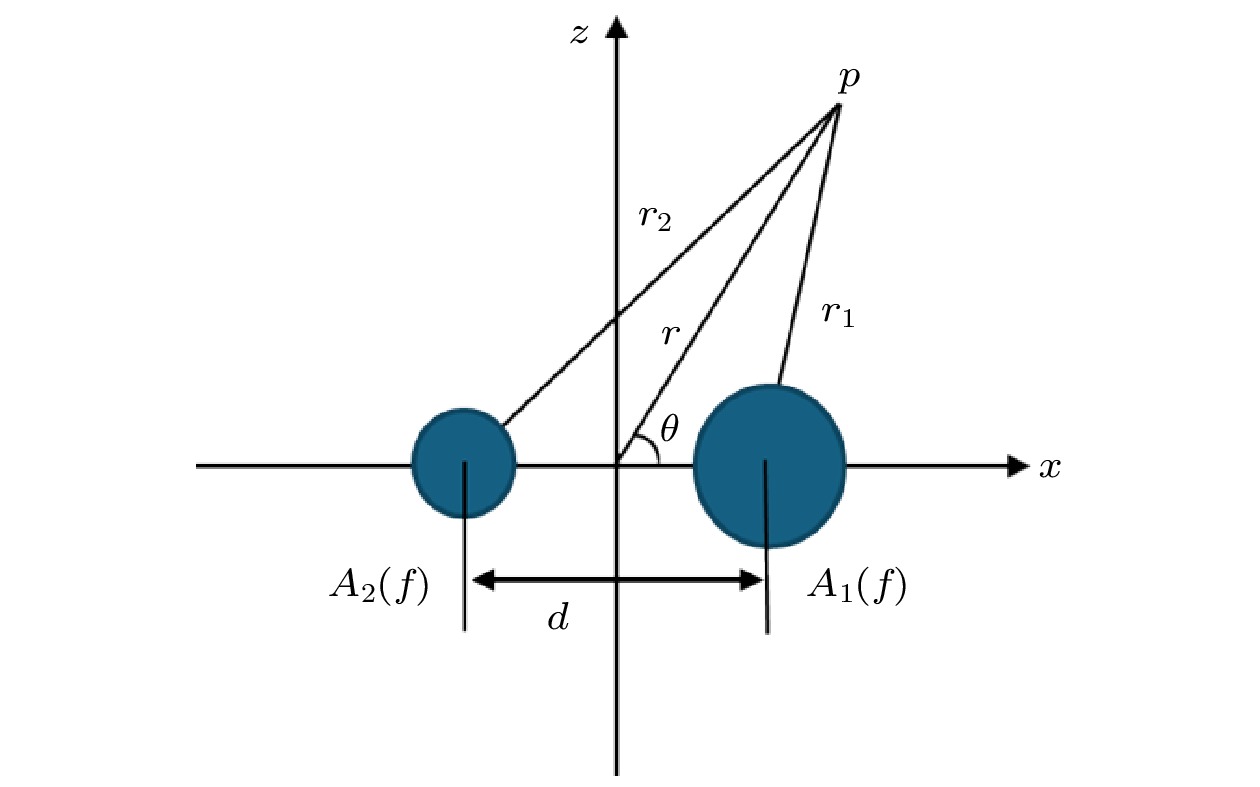
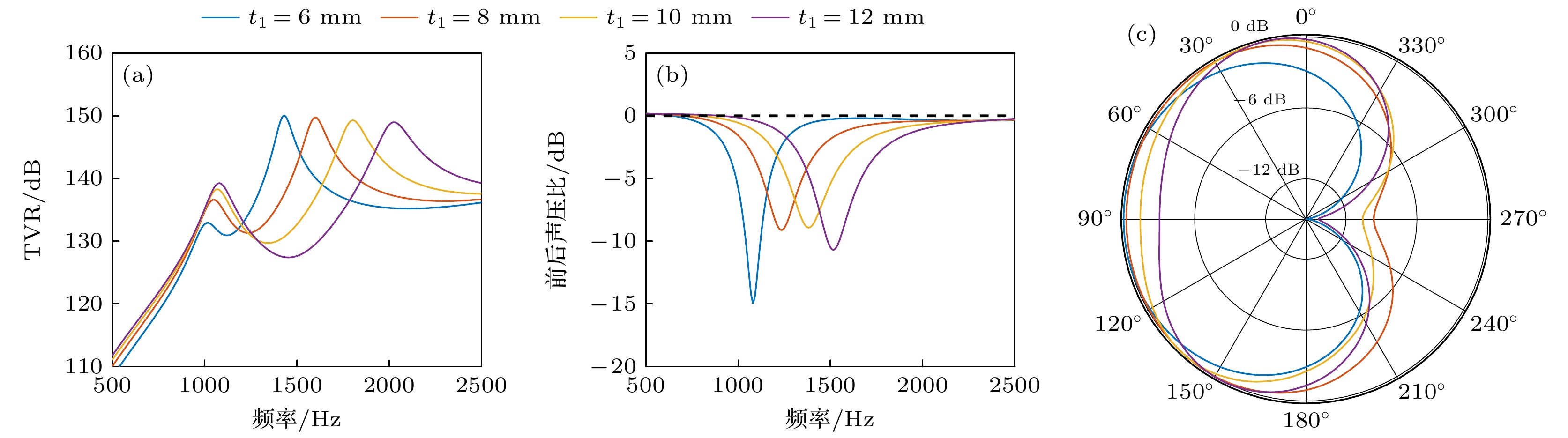
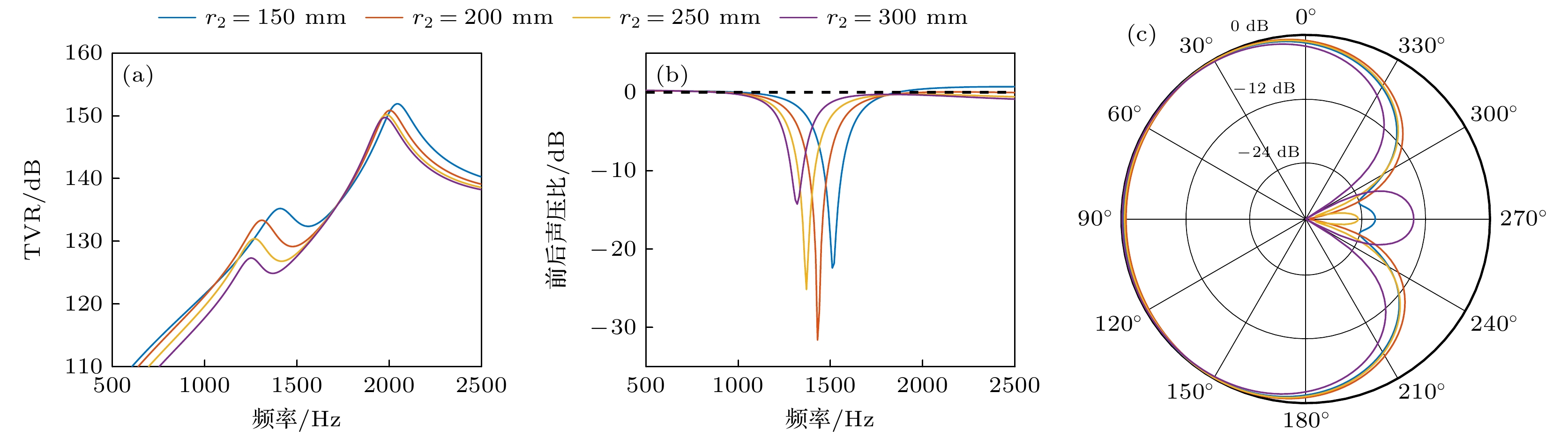
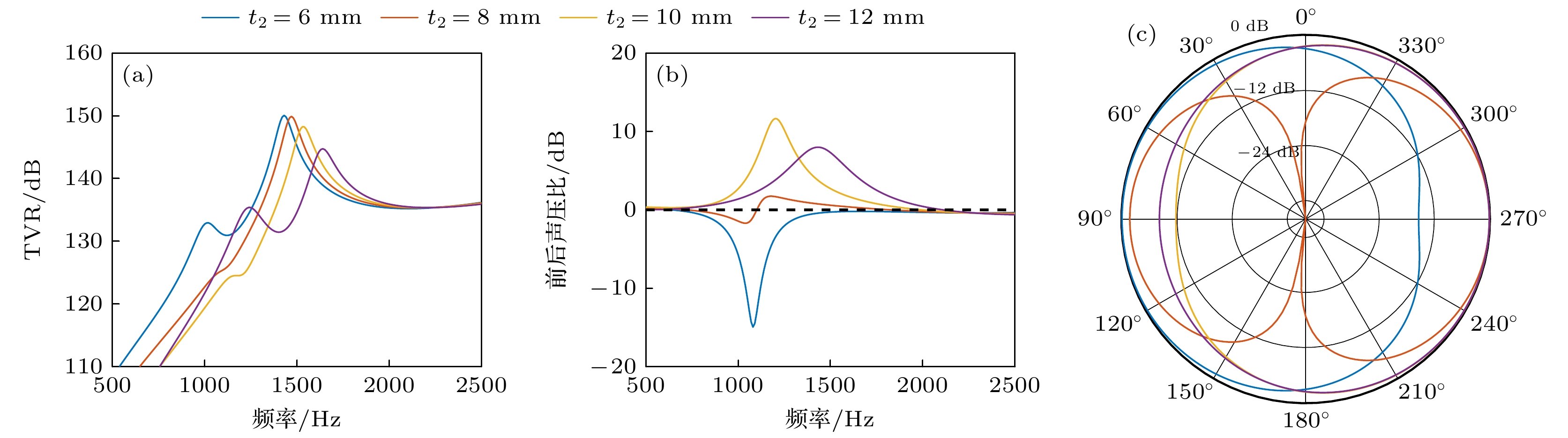
-
The dimensions of flextensional transducers are much smaller than the wavelength, thereby hindering the generation of directional beams by compact underwater acoustic transducers. To address the complexities of amplitude and phase modulation in circuit-driven traditional directional flextensional transducers, a directional flextensional transducer structure is proposed in this work. By implementing an asymmetric composite shell configuration combining concave and convex curved beams, the low-frequency directional radiation is achieved while simplifying peripheral driving circuits, thereby improving the operational convenience and cost-effectiveness. Through an analysis of the vibration characteristics and radiation mechanisms, this study elucidates the principle of directional generation. The concave and convex beams of the flextensional transducer exhibit an intrinsic operational characteristic of opposite-phase normal displacement in their vibration modes. By adjusting structural parameters, the amplitude output from the two beams under a single actuator drive can satisfy a specific differential relationship, effectively resulting in the modal superposition of a monopole and a dipole, thereby achieving directional radiation. By using a Lorentzian resonance fitting function and a linear fitting function, the relationship between the frequency-dependent amplitude ratio and phase difference of sound pressure for the concave and convex beams is established, forming an unequal amplitude, unequal phase dual-spherical source radiation model for the transducer, thereby providing a theoretical framework for controlling the directivity of the transducer. Through numerical simulations, the effects of the transducer sidewall parameters, as well as the thicknesses and curvature radii of the concave and convex beams, on the transducer’s resonance frequency, transmitting voltage response, front-to-back sound pressure ratio, and directivity are analyzed. Sensitivity ranking of the structural parameters is also presented. Finally, the optimization of transducer’s performance is discussed and compared with that in other existing research, showing the advantages of this design. Specifically, the transducer achieves a maximum transmitting voltage response of 145.9 dB within the operating frequency band from 1240 Hz to 1660 Hz. Under single-circuit drive, a cardioid-shaped directional beam with a maximum front-to-back sound pressure ratio of 27 dB is produced. Furthermore, the shear stress on the active material is significantly reduced, effectively preventing fatigue failure of the active material during high-power emission. This provides a more convenient method for achieving low-frequency underwater acoustic directional emission.
-
Keywords:
- flextensional transducer /
- low-frequency directional beam /
- cardioid directivity /
- modal coupling
[1] Fan X D, Zhu Y F, Liang B, Cheng J C, Zhang L K 2018 Phys. Rev. Appl. 9 034035
Google Scholar
[2] 刘永平, 莫喜平, 柴勇, 张运强, 崔斌 2019 声学学报 6 1060
Liu Y P, Mo X P, Chai Y, Zhang Y Q, Cui B 2019 Acta Acust. 6 1060
[3] Moosad K P B, Chandrashekar G, Joseph M J, Sharma D, Kumar N 2011 Appl. Acoust. 72 127
Google Scholar
[4] Butler S C 2010 160th Meeting Acoustical Society of America Cancun, Mexico, November 15–19, 2010 p030001
[5] Zhang J, Hladky-Hennion A C, Hughes W J, Newnham R E 2001 Ultrasonics 39 91
Google Scholar
[6] Zhang J, Newnham R E 2003 US Patent 6 614 143
[7] Wang Q M, Fan J, Lan Y, Zhou T F 2022 J. Acoust. Soc. Am. 151 2223
Google Scholar
[8] 蓝宇, 王秋木, 李宽 2017 中国专利 107452365A
Lan Y, Wang Q M, Li K 2017 CN Patent 107452365A
[9] 李宽 2015 硕士学位论文 (哈尔滨: 哈尔滨工程大学)
Li K 2015 M. S. Thesis (Harbin: Harbin Engineering University
[10] 莫喜平 2020 哈尔滨工程大学学报 41 1500
Google Scholar
Mo X P 2020 J. Harbin Eng. Univ. 41 1500
Google Scholar
[11] 夏铁坚, 范进良, 刘强, 周利生, 王照霞 2005 中国声学学会2005年青年学术会议论文集 中国杭州, 2005 第588页
Xia T J, Fan J L, Liu Q, Zhou L S, Wang Z X 2005 Proceedings of the CYCA'05 Hangzhou, China, 2005 p588
[12] Zhang X Z, Wu C F, Gong W, Wang K, Mo X P, Chai Y 2024 Appl. Phys. Lett. 124 022901
Google Scholar
[13] 滕舵 2016 水声换能器基础 第113页
Teng D 2016 Fundamentals of Hydroacoustic Transducers (Northwestern Polytechnical University Press) p113
[14] Butler S C, Butler A L, Butler J L, Cavanagh G H 1997 J. Acoust. Soc. Am. 102 308
Google Scholar
[15] Butler S C, Butler A L 1992 J. Acoust. Soc. Am. 92 2977
Google Scholar
[16] Butler J L, Butler A L 2003 J. Acoust. Soc. Am. 115 658
[17] 李杰, 顾磊, 吉辰 2024 舰船电子工程 44 214
Google Scholar
Li J, Gu L, Ji C 2024 Ship Electron. Eng. 44 214
Google Scholar
[18] 赵智勇, 王祖杰 2009 水雷与战舰防护 17 15
Zhao Z Y, Wang Z J 2009 J. Underwater Acoust. 17 15
[19] Zhang X Z, Chai Y, Mo X P 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications Nanjing, China, October 11-14, 2022 p691
[20] 张海澜 2012 理论声学(北京: 高等教育出版社) 第410页
Zhang H L 2012 Theoretical Acoustics (Beijing: Higher Education Press) p410
[21] 胡久龄 2009 硕士学位论文 (哈尔滨: 哈尔滨工程大学)
Hu J L 2009 M. S. Thesis (Harbin: Harbin Engineering University
[22] Moosad K P B, Krishnakumar P, Chandrashekar G, Vishnubhatla R M R 2007 Appl. Acoust. 68 1280
[23] 刘慧生, 张运强, 崔斌 2017 声学与电子工程 1 33
Google Scholar
Liu H S, Zhang Y Q, Cui B 2017 Acoust. Electron. Eng. 1 33
Google Scholar
[24] 李志强, 莫喜平, 张运强, 崔斌, 潘耀宗, 李鹏 2015 声学技术 6 566
Li Z Q, Mo X P, Zhang Y Q, Cui B, Pan Y Z, Li P 2015 Acoustical Technology 6 566
[25] 卢苇, 叶皓棠 2025 声学学报 50 149
Google Scholar
Lu W, Ye H T 2025 Acta Acust. 50 149
Google Scholar
-
图 1 换能器结构与主要尺寸参数
Figure 1. Transducer Structure and main dimensional parameters.
图 2 前二阶模态位移矢量图
Figure 2. Displacement vectors of the first two-order modes.
图 3 换能器在(a)空气中和(b)水中的凹凸梁辐射面中心点法向位移
Figure 3. Normal displacement at the center of the radiating surface of the arched beam for the transducer in (a) air and (b) water.
图 4 换能器水中凹侧和凸侧距离声中心10 m处的(a)声压及(b)相位频响曲线
Figure 4. (a) Sound pressure and (b) phase frequency response curves at 10 m from the acoustic center for the concave and convex sides of the transducer in water.
图 5 凹凸梁型低频指向性弯张换能器等效双球源模型
Figure 5. Equivalent dual-spherical source model of the concave-convex beam low-frequency directional flextensional transducer.
图 6 侧壁长度$ l $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性
Figure 6. Effect of sidewall length $ l $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 7 侧壁宽度$ w $对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性
Figure 7. Effect of sidewall width $ w $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 8 侧壁高度 $ h $对换能器的影响 (a) TVR, (b) FBR; (c) 最大指向性
Figure 8. Effect of sidewall height $ h $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 9 凸梁曲率半径$ {r}_{1} $对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性
Figure 9. Effect of convex beam curvature radius $ {r}_{1} $on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 10 凸梁厚度 $ {t}_{1} $对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性
Figure 10. Effect of convex beam thickness $ {t}_{1} $on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 11 凹梁曲率半径$ {r}_{2} $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性
Figure 11. Effect of concave beam curvature radius $ {r}_{2} $on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 12 凹梁厚度 $ {t}_{2} $对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性
Figure 12. Effect of concave beam thickness $ {t}_{2} $on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
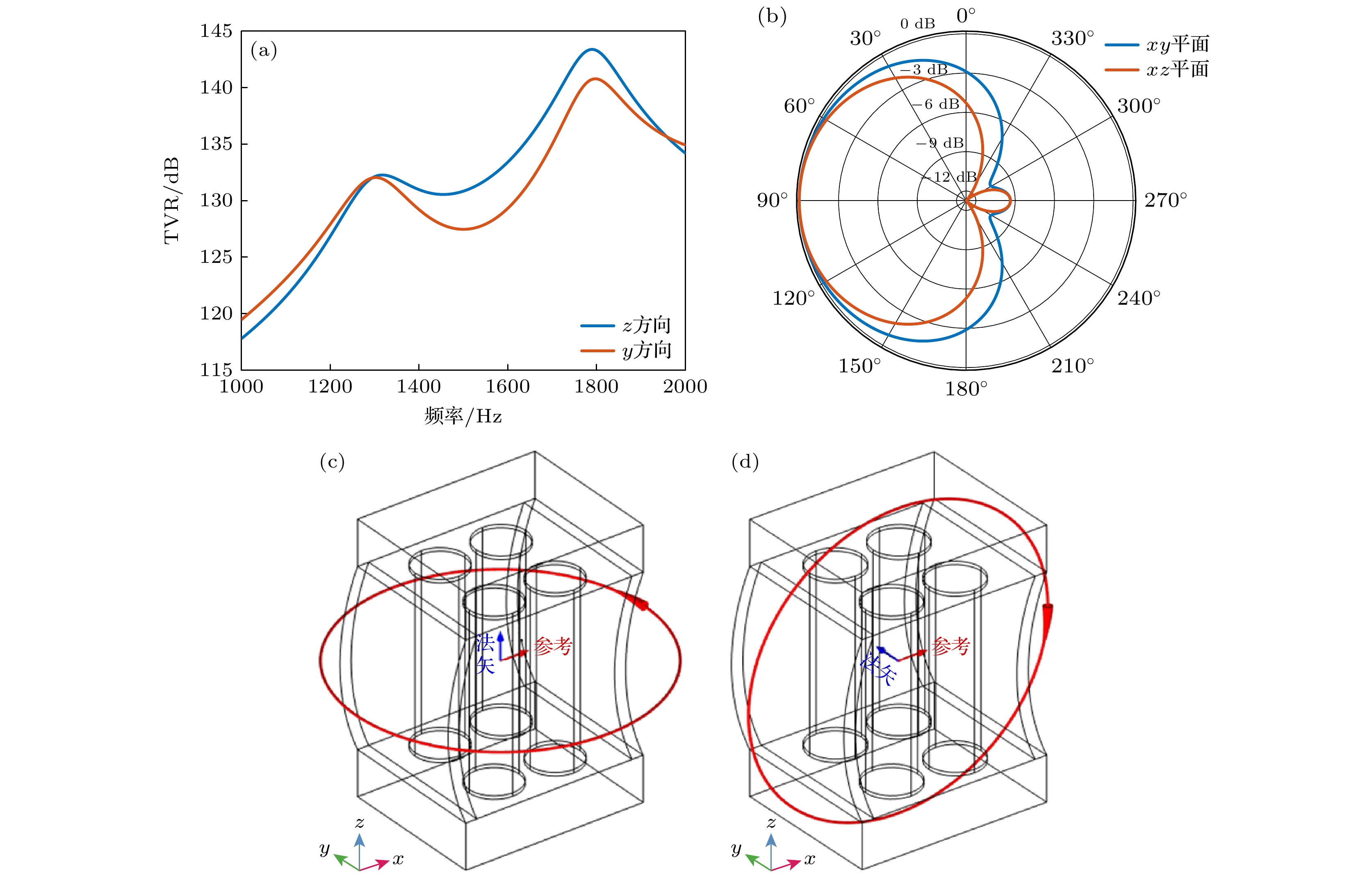
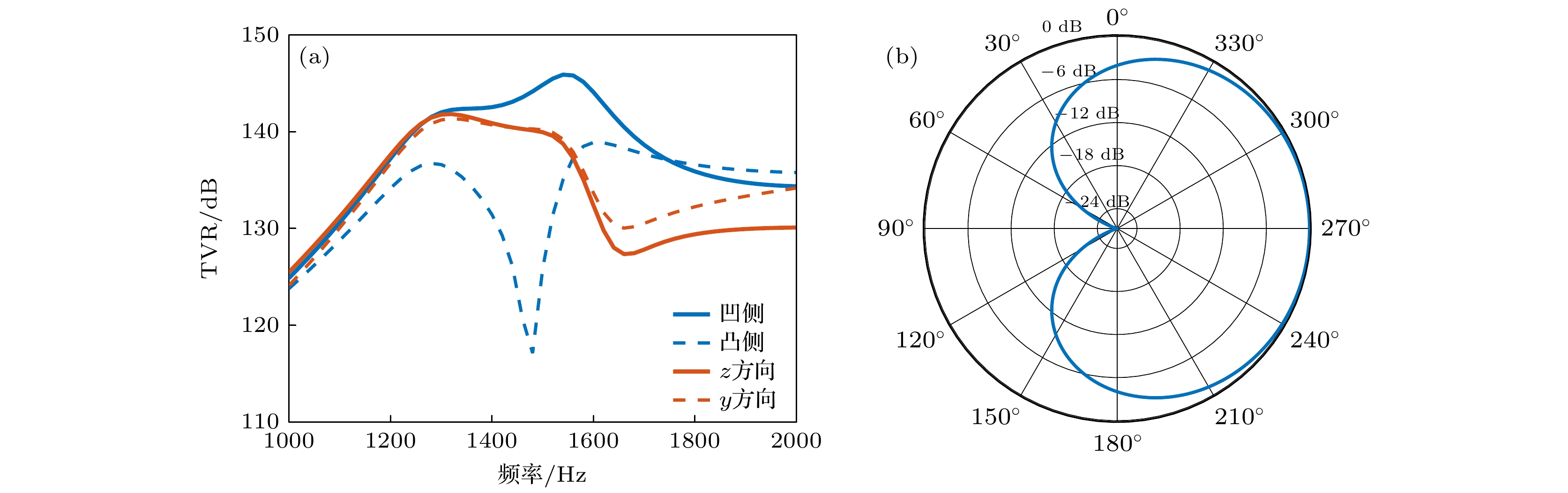
图 13 (a) 换能器z方向和y方向的TVR曲线对比; (b) 换能器在1480 Hz处的xy平面和xz平面指向性图; (c) 换能器xy平面示意图; (d) 换能器xz平面示意图
Figure 13. (a) Comparison of TVR curves in the z-direction and y-direction of the transducer; (b) directivity patterns in the xy-plane and xz-plane at 1480 Hz; (c) schematic diagram of the xy-plane of the transducer; (d) schematic diagram of the xz-plane of the transducer.
图 14 (a) 优化后的换能器凹侧、凸侧、z方向、y方向的TVR曲线; (b) 1480 Hz处的指向性图
Figure 14. (a) TVR curves of the concave side, convex side, z-, and y-directions of the optimized transducer; (b) directivity pattern at 1480 Hz.
图 15 (a) 优化后的换能器空气中导纳曲线; (b) 优化后的换能器水中导纳曲线
Figure 15. (a) Admittance curve of the optimized transducer in air; (b) admittance curve of the optimized transducer in water.
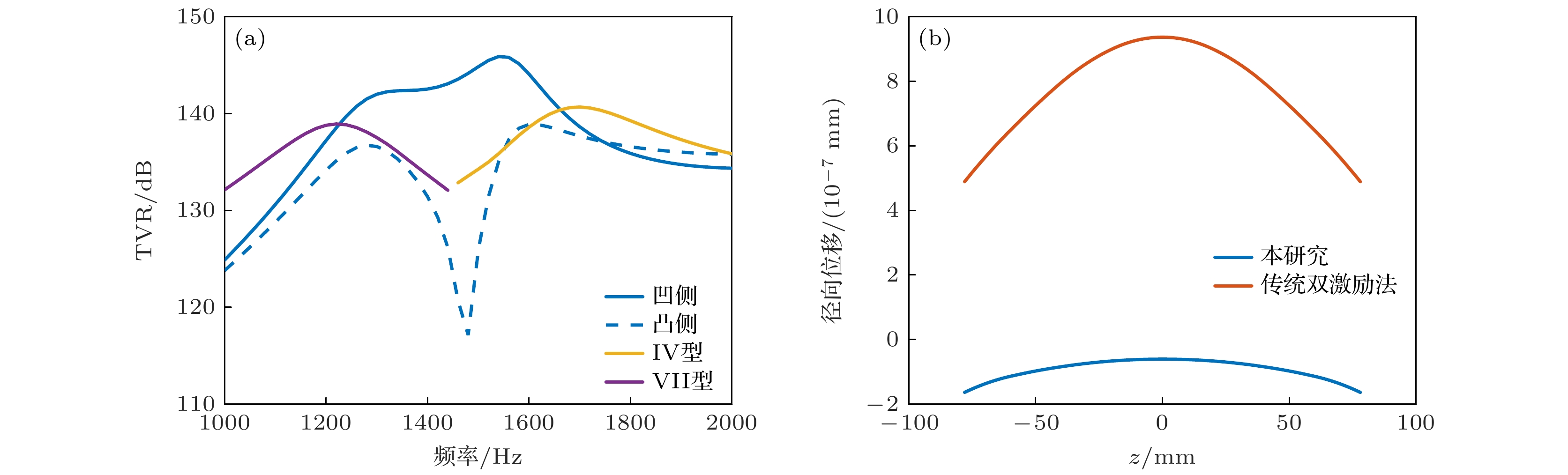
图 16 (a) 优化后的换能器和传统Ⅳ型、Ⅶ型弯张换能器的TVR对比; (b)优化后的换能器和传统采用双激励法实现低频指向性的Ⅳ型弯张换能器的压电振子径向位移对比
Figure 16. (a) Comparison of TVR between the optimized transducer and traditional Class IV and Class VII flextensional transducers; (b) comparison of radial displacement of piezoelectric vibrators between the optimized transducer and the traditional Class IV flextensional transducer achieving low-frequency directivity using dual-drive excitation.
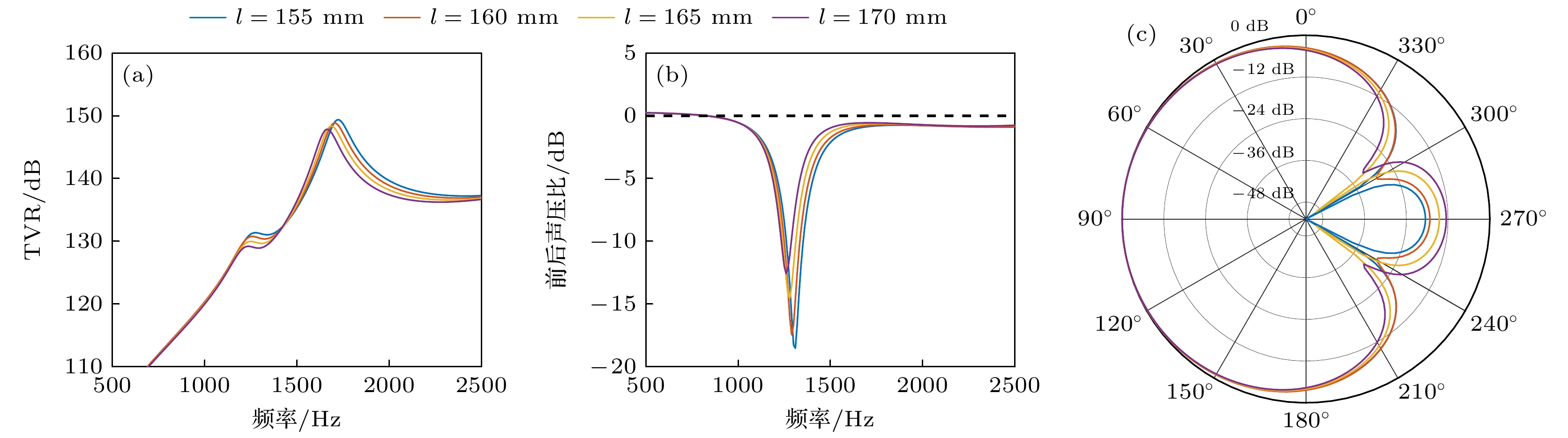
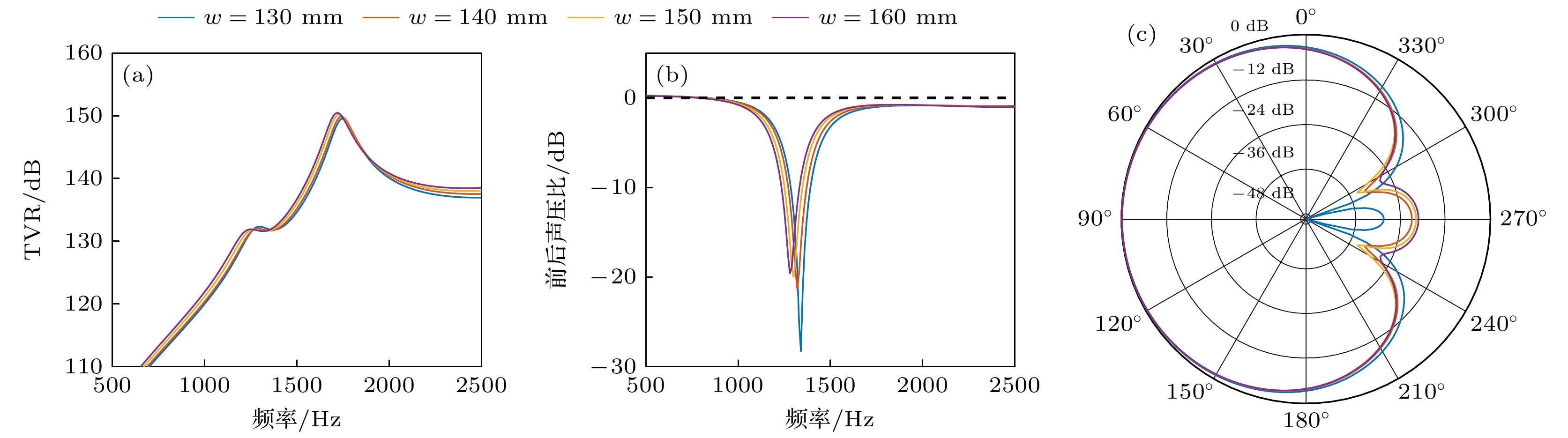
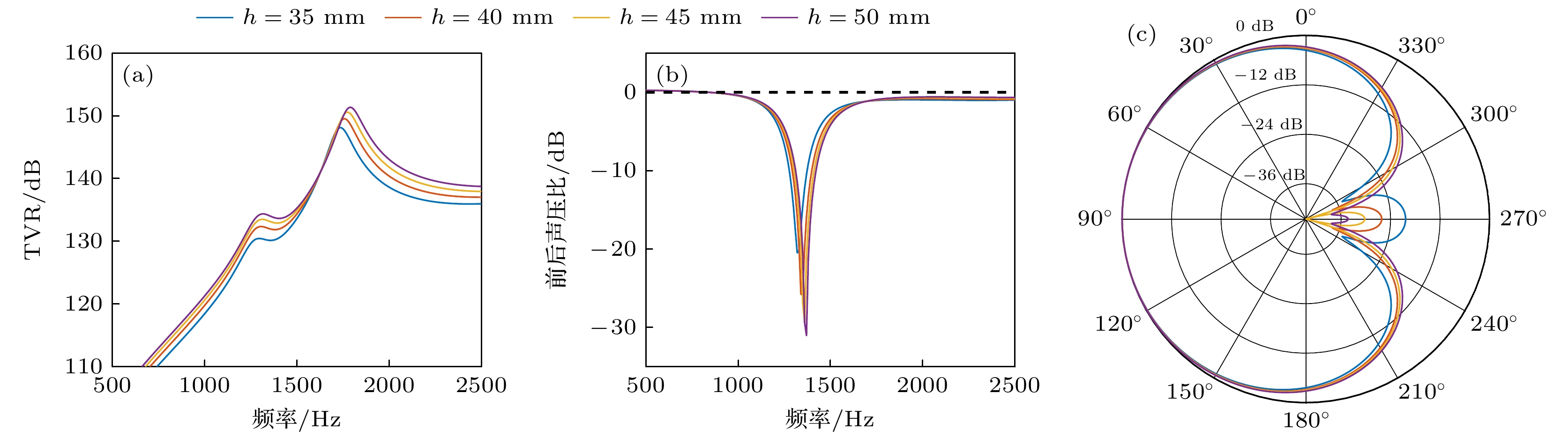
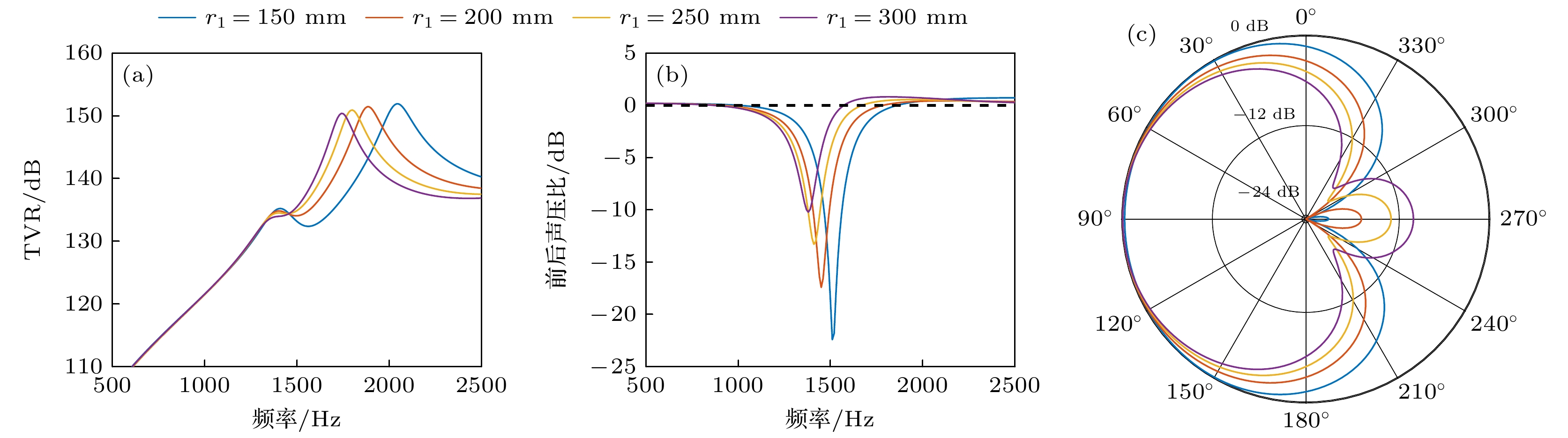
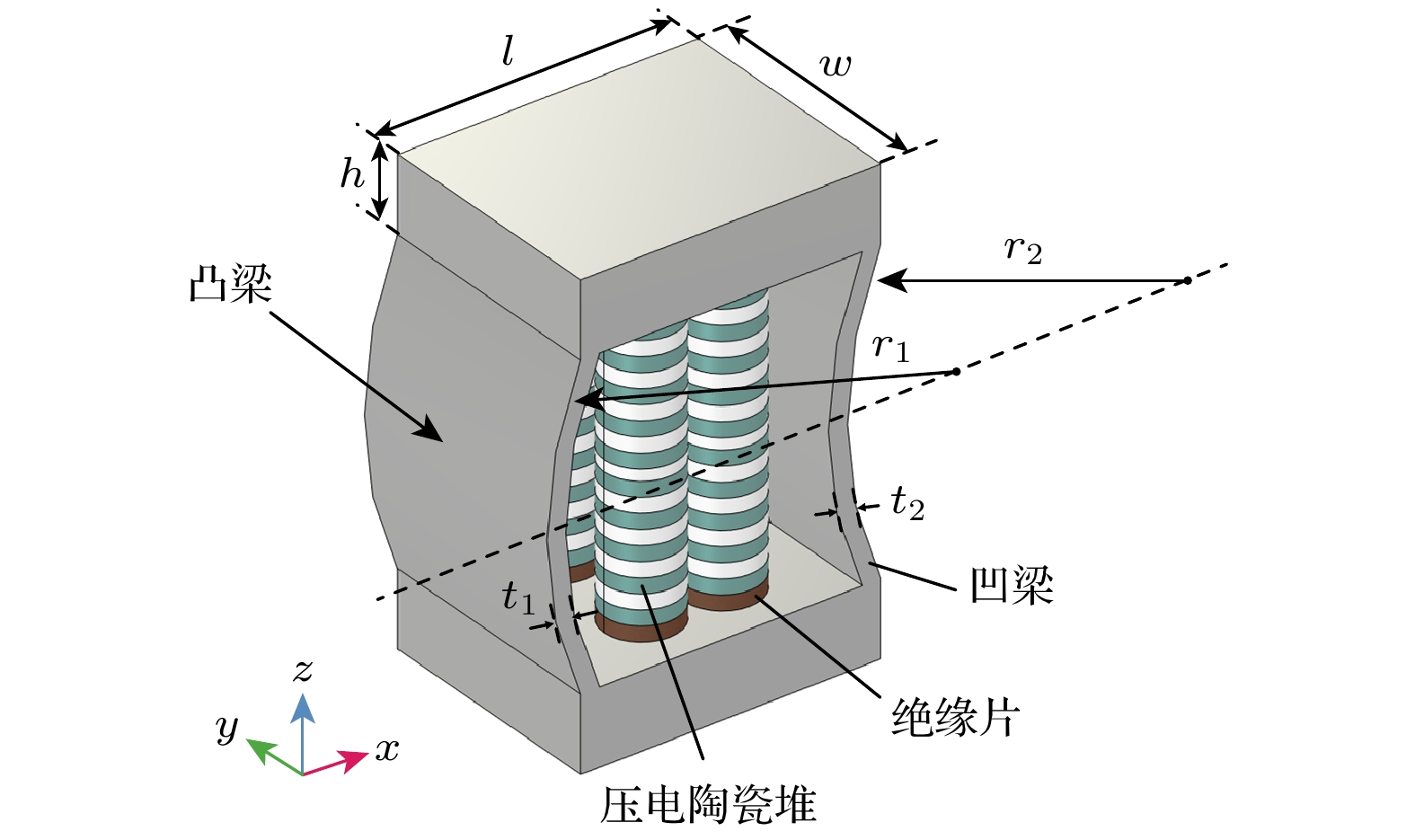
表 1 换能器结构参数优化范围
Table 1. Optimization range of the transducer structure parameters.
参数 取值范围/mm 步长/mm $ l $ 155—170 5 $ w $ 130—160 10 $ h $ 35—50 5 $ {r}_{1} $ 150—300 50 $ {t}_{1} $ 6—12 2 $ {r}_{2} $ 150—300 50 $ {t}_{2} $ 6—12 2 
DownLoad: CSV
表 2 换能器优化后的结构参数
Table 2. Structural parameters of the transducer after optimization.
参数 值/mm 参数 值/mm $ l $ 160 $ {t}_{1} $ 7 $ w $ 160 $ {r}_{2} $ 300 $ h $ 40 $ {t}_{2} $ 13 $ {r}_{1} $ 200 换能器总高度 236
DownLoad: CSV
-
[1] Fan X D, Zhu Y F, Liang B, Cheng J C, Zhang L K 2018 Phys. Rev. Appl. 9 034035
Google Scholar
[2] 刘永平, 莫喜平, 柴勇, 张运强, 崔斌 2019 声学学报 6 1060
Liu Y P, Mo X P, Chai Y, Zhang Y Q, Cui B 2019 Acta Acust. 6 1060
[3] Moosad K P B, Chandrashekar G, Joseph M J, Sharma D, Kumar N 2011 Appl. Acoust. 72 127
Google Scholar
[4] Butler S C 2010 160th Meeting Acoustical Society of America Cancun, Mexico, November 15–19, 2010 p030001
[5] Zhang J, Hladky-Hennion A C, Hughes W J, Newnham R E 2001 Ultrasonics 39 91
Google Scholar
[6] Zhang J, Newnham R E 2003 US Patent 6 614 143
[7] Wang Q M, Fan J, Lan Y, Zhou T F 2022 J. Acoust. Soc. Am. 151 2223
Google Scholar
[8] 蓝宇, 王秋木, 李宽 2017 中国专利 107452365A
Lan Y, Wang Q M, Li K 2017 CN Patent 107452365A
[9] 李宽 2015 硕士学位论文 (哈尔滨: 哈尔滨工程大学)
Li K 2015 M. S. Thesis (Harbin: Harbin Engineering University
[10] 莫喜平 2020 哈尔滨工程大学学报 41 1500
Google Scholar
Mo X P 2020 J. Harbin Eng. Univ. 41 1500
Google Scholar
[11] 夏铁坚, 范进良, 刘强, 周利生, 王照霞 2005 中国声学学会2005年青年学术会议论文集 中国杭州, 2005 第588页
Xia T J, Fan J L, Liu Q, Zhou L S, Wang Z X 2005 Proceedings of the CYCA'05 Hangzhou, China, 2005 p588
[12] Zhang X Z, Wu C F, Gong W, Wang K, Mo X P, Chai Y 2024 Appl. Phys. Lett. 124 022901
Google Scholar
[13] 滕舵 2016 水声换能器基础 第113页
Teng D 2016 Fundamentals of Hydroacoustic Transducers (Northwestern Polytechnical University Press) p113
[14] Butler S C, Butler A L, Butler J L, Cavanagh G H 1997 J. Acoust. Soc. Am. 102 308
Google Scholar
[15] Butler S C, Butler A L 1992 J. Acoust. Soc. Am. 92 2977
Google Scholar
[16] Butler J L, Butler A L 2003 J. Acoust. Soc. Am. 115 658
[17] 李杰, 顾磊, 吉辰 2024 舰船电子工程 44 214
Google Scholar
Li J, Gu L, Ji C 2024 Ship Electron. Eng. 44 214
Google Scholar
[18] 赵智勇, 王祖杰 2009 水雷与战舰防护 17 15
Zhao Z Y, Wang Z J 2009 J. Underwater Acoust. 17 15
[19] Zhang X Z, Chai Y, Mo X P 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications Nanjing, China, October 11-14, 2022 p691
[20] 张海澜 2012 理论声学(北京: 高等教育出版社) 第410页
Zhang H L 2012 Theoretical Acoustics (Beijing: Higher Education Press) p410
[21] 胡久龄 2009 硕士学位论文 (哈尔滨: 哈尔滨工程大学)
Hu J L 2009 M. S. Thesis (Harbin: Harbin Engineering University
[22] Moosad K P B, Krishnakumar P, Chandrashekar G, Vishnubhatla R M R 2007 Appl. Acoust. 68 1280
[23] 刘慧生, 张运强, 崔斌 2017 声学与电子工程 1 33
Google Scholar
Liu H S, Zhang Y Q, Cui B 2017 Acoust. Electron. Eng. 1 33
Google Scholar
[24] 李志强, 莫喜平, 张运强, 崔斌, 潘耀宗, 李鹏 2015 声学技术 6 566
Li Z Q, Mo X P, Zhang Y Q, Cui B, Pan Y Z, Li P 2015 Acoustical Technology 6 566
[25] 卢苇, 叶皓棠 2025 声学学报 50 149
Google Scholar
Lu W, Ye H T 2025 Acta Acust. 50 149
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 317
- PDF Downloads: 7
- Cited By: 0
