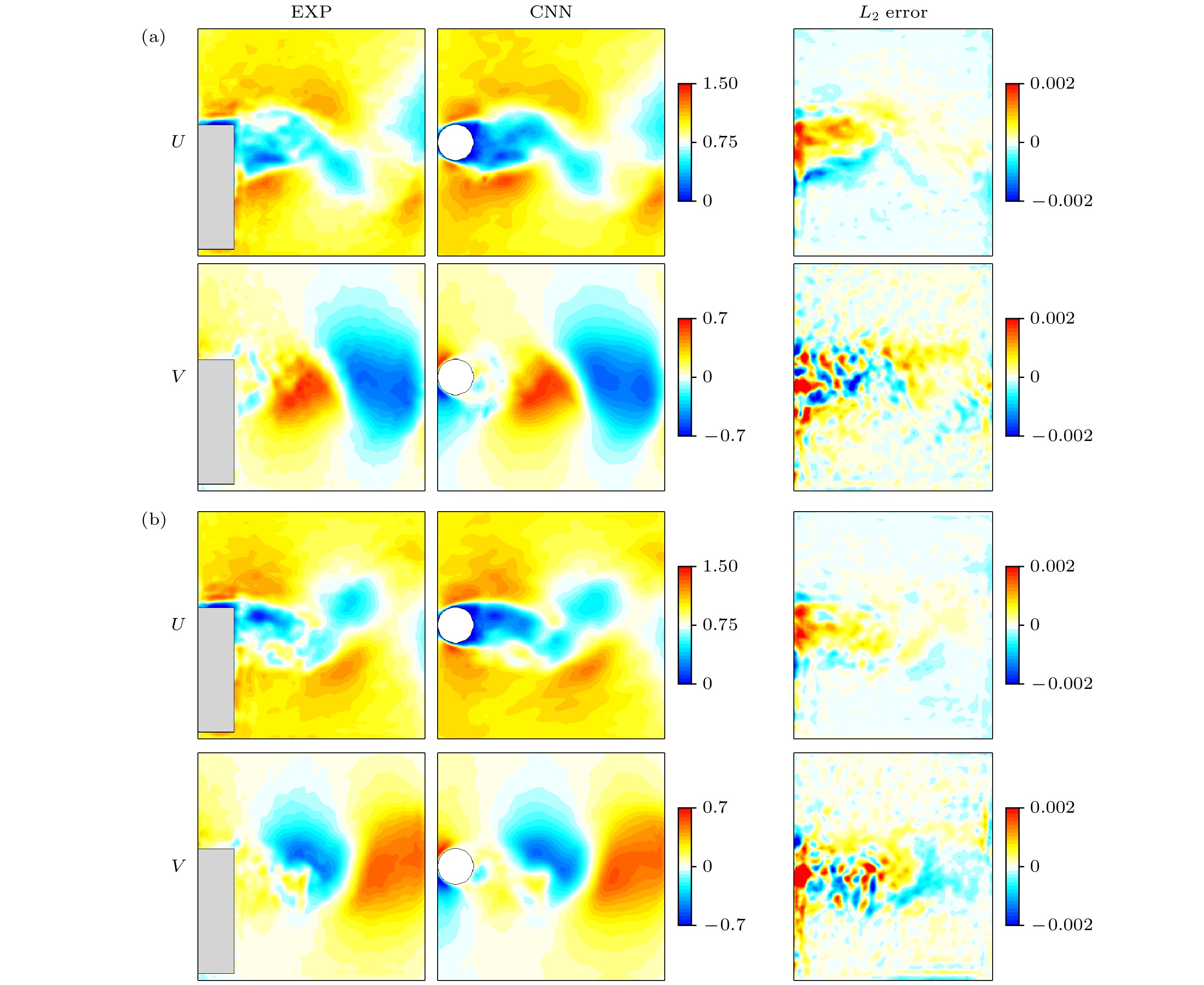
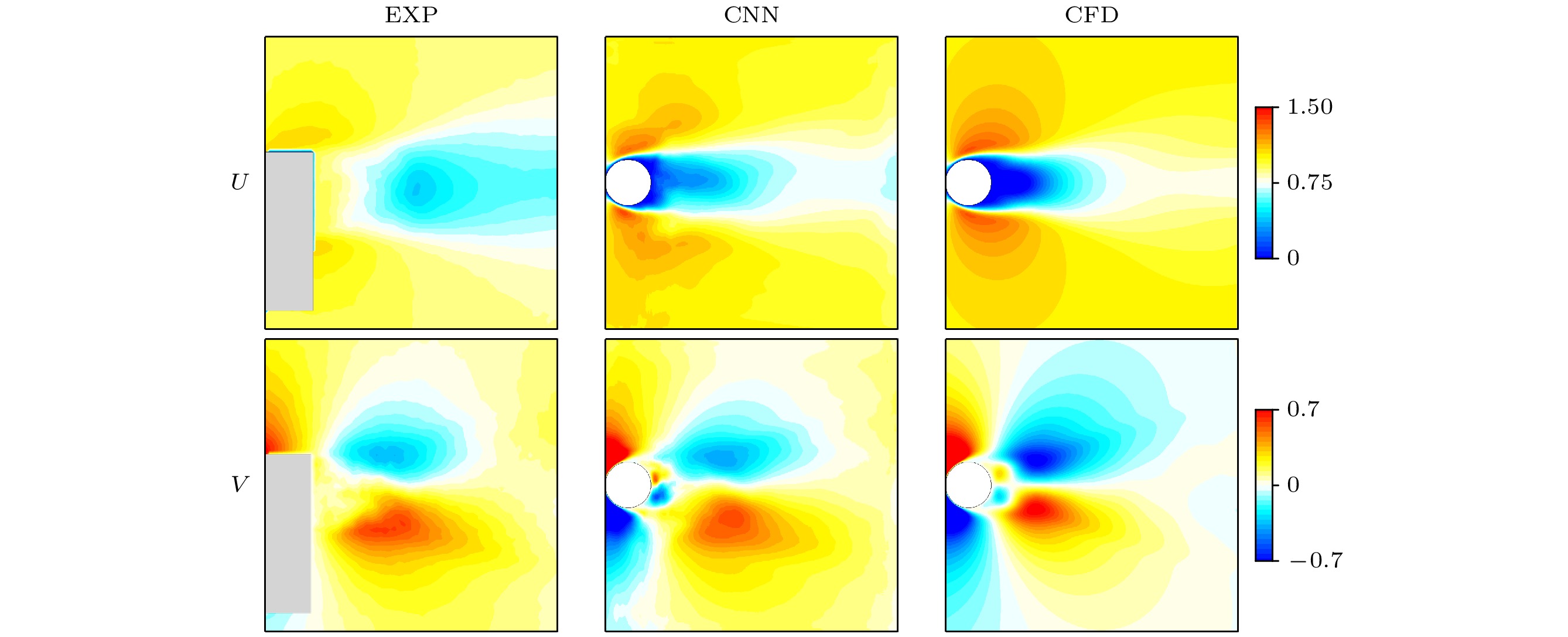
-
The prerequisite for accurate prediction and effective control of flow phenomena lies in the understanding of flow dynamics, and experimental studies provide essential data to support this process. Particle image velocimetry (PIV), as one of the important methods of measuring flow fields, plays a critical role in experimental investigations such as flow passing through a circular cylinder. PIV is a non-contact laser-optical measurement technique, however, it often faces challenges in obtaining complete and accurate flow field data when the optical path is obstructed. Particularly in PIV experiments involving flow passing through a circular cylinder, the presence of the cylinder itself and the supporting structure can significantly obscure the optical path, making it highly challenging to acquire complete PIV data. To solve this problem, we propose a deep learning-based flow field data reconstruction method, in which a deep learning framework centered on convolutional neural networks (CNNs) is used. The method aims to solve the reconstruction problem of gappy regions in flow field data by establishing a mapping relationship between flow fields with gappy regions and complete flow fields. First, the influence of gappy regions with different characteristics on the reconstruction accuracy of numerically simulated flow fields is investigated. The reconstructed flow fields are carefully compared with ground truth data through multi-dimensional assessments of instantaneous flow fields and velocity time statistics. The results indicate that the maximum L2 error between the reconstructed flow field and the ground truth is still about 0.02. Furthermore, it is observed that as the size of the gappy region increases along the flow direction, the difficulty in reconstructing flow field increases significantly. In contrast, changes in the size of the gappy region perpendicular to the flow direction have minimum influence on the accuracy of flow field reconstruction. Additionally, the robustness of the proposed deep neural network against noise is systematically evaluated. When clean numerical simulation data are used for training, test data are generated by artificially introducing varying levels of Gaussian noise to assess the network performance under noisy conditions. The results demonstrate that the error between the reconstructed data and the ground truth increases exponentially as the noise level rises. Finally, the proposed deep neural network model is applied to real PIV experimental data, with the training data remaining clean and numerically simulated. Both instantaneous flow fields and time-averaged statistics are analyzed and compared. The results show that the network model successfully reconstructs velocity information in the missing regions and effectively corrects data errors caused by measurement inaccuracies in the backflow zones. The reconstructed experimental results show closer statistical agreement with numerical simulation data, demonstrating that the model proposed in this work, when trained solely on numerical simulation data, is capable of reconstructing missing physical information in PIV experiments. This method provides a novel approach for addressing the challenge of data reconstructionin PIV experiments.
-
Keywords:
- deep learning /
- gappy data /
- flow past a circular cylinder
[1] Ragni D, Ashok A, van Oudheusden B W, Scarano F 2009 Meas. Sci. Technol. 20 074005
Google Scholar
[2] Gunes H, Rist U 2008 Phys. Fluids 20 104109
Google Scholar
[3] Tan B T, Damodaran M, Willcox K E 2004 AIAA J. 42 1505
Google Scholar
[4] 李天一, Buzzicotti Michele, Biferale Luca, 万敏平, 陈十一 2021 力学学报 53 2703
Google Scholar
Li T Y, Buzzicotti M, Biferale L, Wan M P, Chen S Y 2021 Chin. J. Mech. 53 2703
Google Scholar
[5] Sciacchitano A, Dwight R P, Scarano F 2012 Exp. Fluids 53 1421
Google Scholar
[6] Zimmermann R, Vendl A 2014 AIAA J. 52 255
Google Scholar
[7] Ruscher C J, Dannenhoffer J F, Glauser M N 2017 AIAA J. 55 255
Google Scholar
[8] Deng Z W, He C X, Wen X, Liu Y Z 2018 J. Vis. 21 1043
Google Scholar
[9] Li T X, He C X, Wen X, Liu Y Z 2023 J. Vis. 26 815
Google Scholar
[10] 何创新, 邓志文, 刘应征 2021 航空学报 42 524704
He C X, Deng Z W, Liu Y Z 2021 Acta Aeronautica et Astronautica Sinica 42 524704
[11] 袁昊, 寇家庆, 张伟伟 2024 力学学报 56 2799
Google Scholar
Yuan H, Kou J Q, Zhang W W 2024 Chin. J. Mech. 56 2799
Google Scholar
[12] 张伟伟, 王旭, 寇家庆 2023 力学进展 53 433
Google Scholar
Zhang W W, Wang X, Kou J Q 2023 Adv. Mech. 53 433
Google Scholar
[13] 任峰, 高传强, 唐辉 2021 航空学报 42 524686
Ren F, Gao C Q, Tang H 2021 Acta Aeronautica et Astronautica Sinica 42 524686
[14] Vinuesa R, Brunton S L, McKeon B J 2023 Nat. Rev. Phys 5 536
Google Scholar
[15] Brunton S L 2021 Acta Mech. Sin. 37 1718
Google Scholar
[16] Wen Z K, Shu W P, Zhang H, Liu S B, Zhang L Q, Liu L, Wang T, Zhang Q J, Li S 2024 Space Sci. Technol. 4 0080
Google Scholar
[17] 徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 69 014209
Google Scholar
Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209
Google Scholar
[18] Taira K, Hemati M S, Brunton S L, Sun Y Y, Duraisamy K, Bagheri S, Dawson S T M, Yeh C A 2020 AIAA J. 58 998
Google Scholar
[19] 郑天韵, 王圣业, 王光学, 邓小刚 2020 69 204701
Google Scholar
Zheng T Y, Wang S Y, Wang G X, Deng X G 2020 Acta Phys. Sin. 69 204701
Google Scholar
[20] Wang H P, Yang Z X, Li B L, Wang S Z 2020 Phys. Fluids 32 115105
Google Scholar
[21] Morimoto M, Fuakmi K, Fukagata K 2021 Phys. Fluids 33 087121
Google Scholar
[22] Zhang F, Hu H B, Ren F, Zhang H, Du P 2022 Phys. Fluids 34 127117
Google Scholar
[23] Luo Z H, Wang L Y, Xu J, Wang Z L, Chen M, Yuan J P 2023 Phys. Fluids 35 085115
Google Scholar
[24] Luo Z H, Wang L Y, Xu J, Yuan J P, Chen M, Li Y, Andy C T 2024 Ocean Eng. 293 116605
Google Scholar
[25] Zheng Q M, Li T Y, Ma B T, Fu L, Li X M 2024 Phys. Rev. Fluids 9 024608
Google Scholar
[26] Muharrem H A, Ilker G, Murat I, Abdullah C 2023 Phys. Fluids 35 114110
Google Scholar
[27] He K M, Zhang X Y, Ren S Q, Sun J 2016 ICCV Santiago, Chile, December 13–16, 2015 p1026
[28] Szegedy C, Ioffe S, Vanhoucke V, Alemi A 2017 AAAI California, USA, February 4–9, 2017 p1
[29] Lin M, Chen Q, Yan S C 2013 arXiv: 13124400 [cs.NE]
[30] He K M, Zhang X Y, Ren S Q, Sun J 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Las Vegas, USA, June 26–July 1, 2016 p770
[31] Zhang F, Hu H B, Zhang H, Zhang M, Song J, Meng Y Z 2024 Ocean Eng. 309 118578
Google Scholar
[32] 陈蒋力, 丁海艳, 胡海豹, 张帆, 文俊 2024 实验流体力学 39 1
Google Scholar
Chen J L, Ding H Y, Hu H B, Zhang F, Wen J 2024 Experimental Fluid Mechanics 39 1
Google Scholar
-
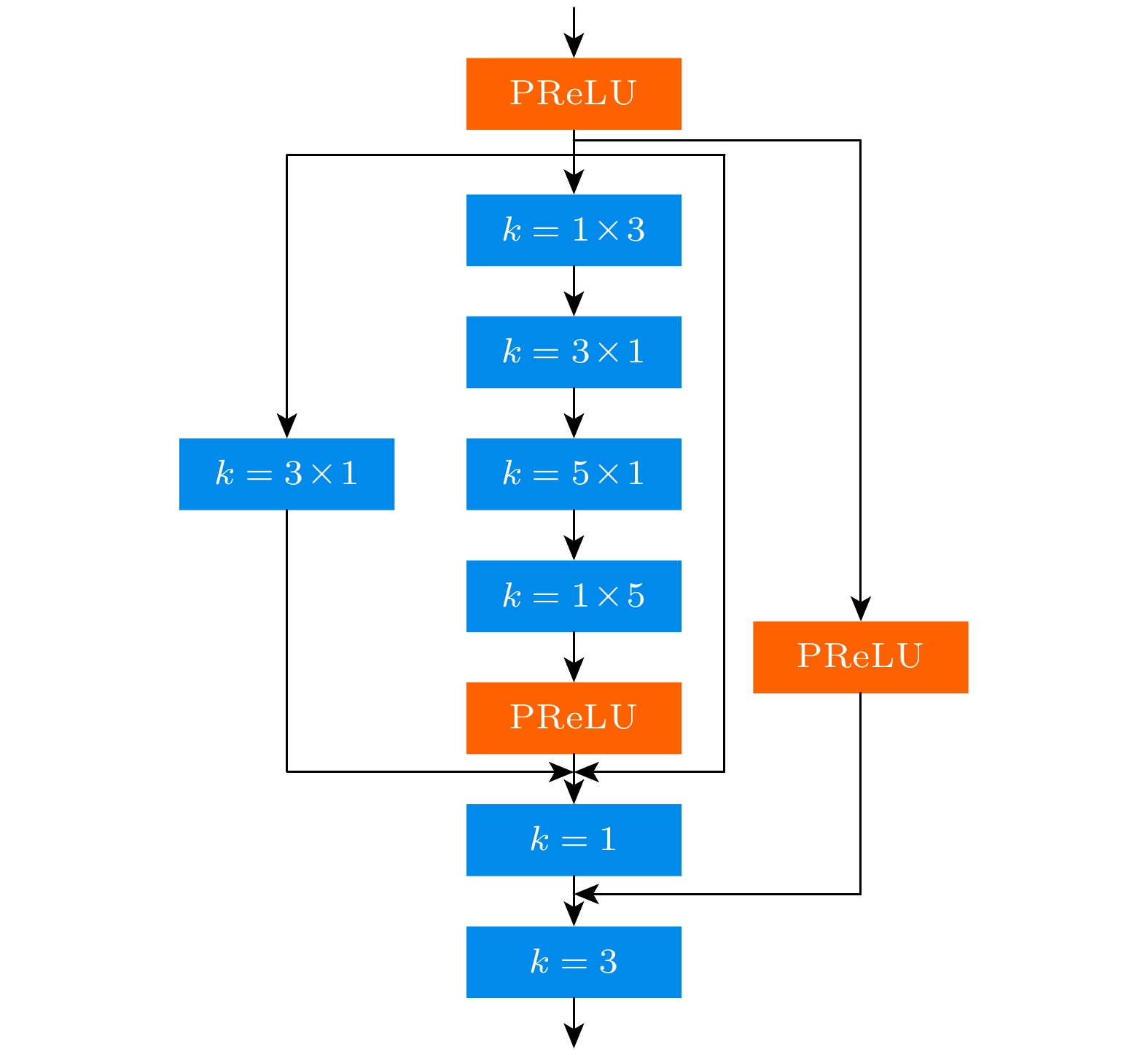
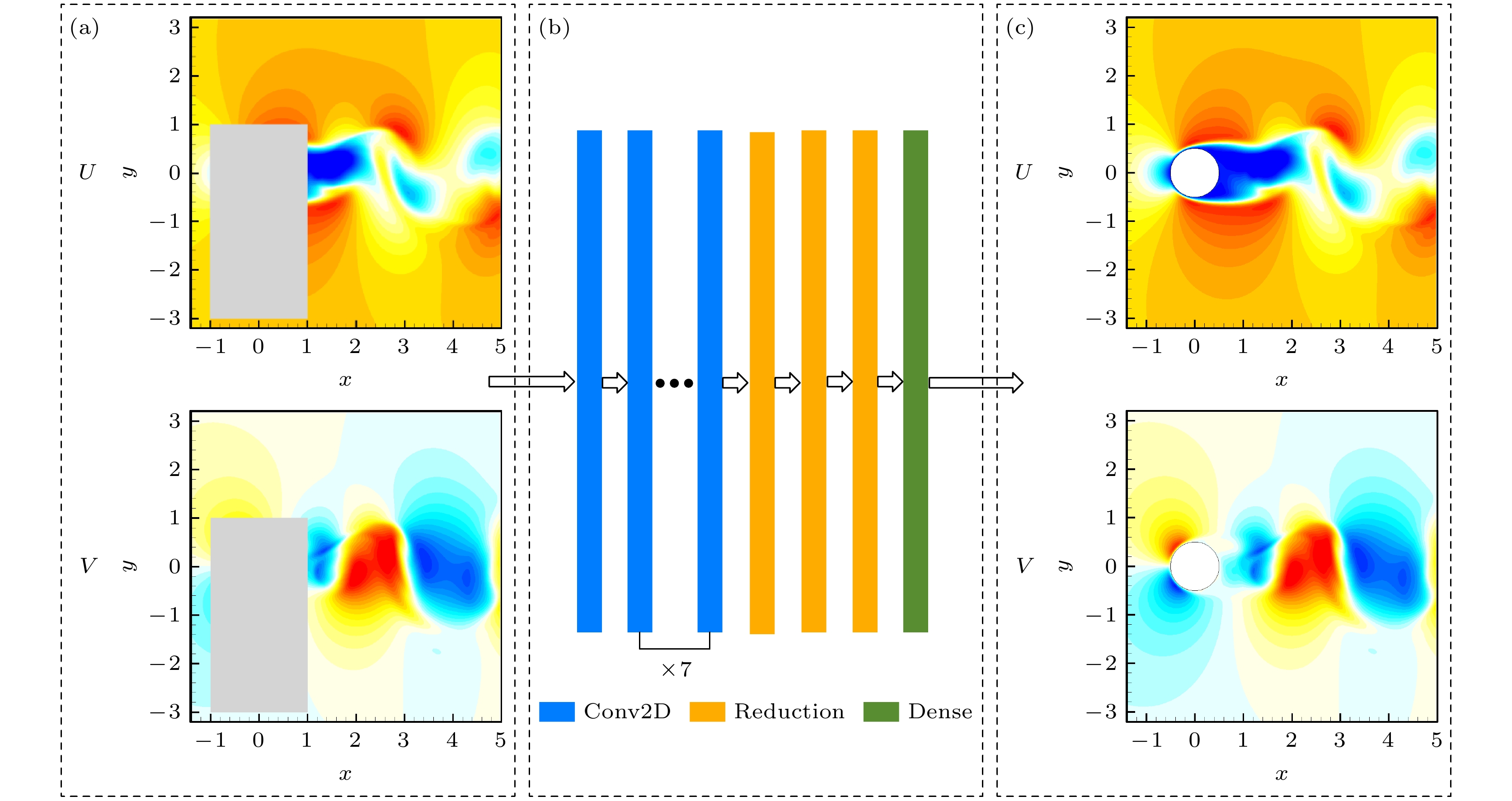
图 1 使用深度神经网络模型将圆柱绕流不完整的速度场重构为完整速度场 (a) 有缺失区域的速度场; (b) 本文使用的卷积神经网络模型; (c) 完整的速度场
Figure 1. A deep neural network model is used to reconstruct the incomplete velocity field of a flow past a cylinder into the complete one: (a) The velocity field with gappy area; (b) the CNN model used in this work; (c) the complete velocity field.
图 2 本文使用的神经网络模型中的Reduction模块
Figure 2. Reduction block in the neural network used in this work.
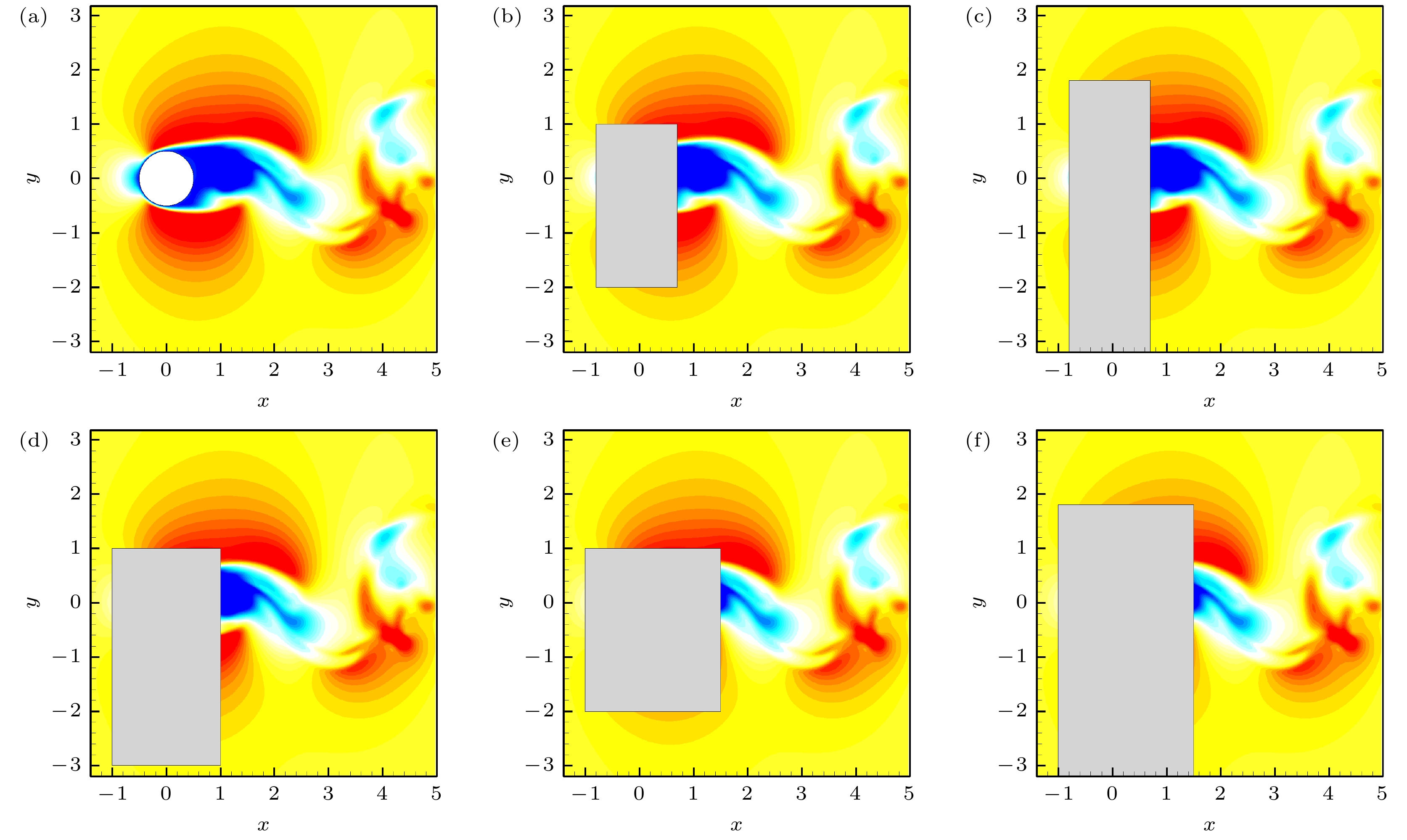
图 3 几种不同的数据缺失区域 (a) 无缺失的流场; (b) 缺失区域为$ 60\times 120 $; (c) 缺失区域为$ 60\times 200 $; (d) 缺失区域为$ 80\times 160 $; (e) 缺失区域为$ 100\times 120 $; (f) 缺失区域为$ 100\times 200 $
Figure 3. Gappy regions of several different areas: (a) The complete flow filed; (b) gappy region of $ 60\times 120 $; (c) gappy region of $ 60\times 200 $; (d) gappy region of $ 80\times 160 $; (e) gappy region of $ 100\times 120 $; (f) gappy region of $ 100\times 200 $.
图 4 不同的缺失区域对于训练误差收敛的影响
Figure 4. The influence of gappy regions on training loss convergence.
图 5 不同缺失区域的速度重构瞬时流场对比
Figure 5. The instantaneous reconstruction flow fields of different gappy regions.
图 6 不同缺失区域对尾流中线流向速度重构结果对比 (a)流向速度统计; (b)流向速度绝对误差
Figure 6. Comparison of reconstruction results of midline wake flow velocity of different gappy areas: (a) Streamwise velocity statistics; (b) absolute error of streamwise velocity.
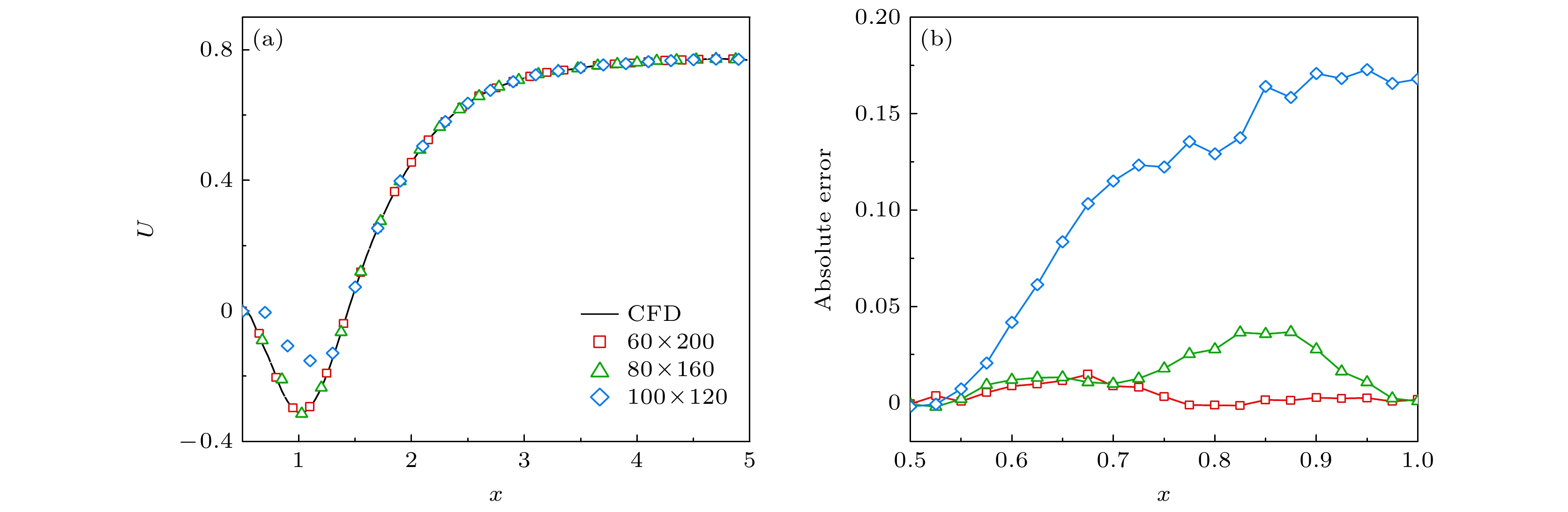
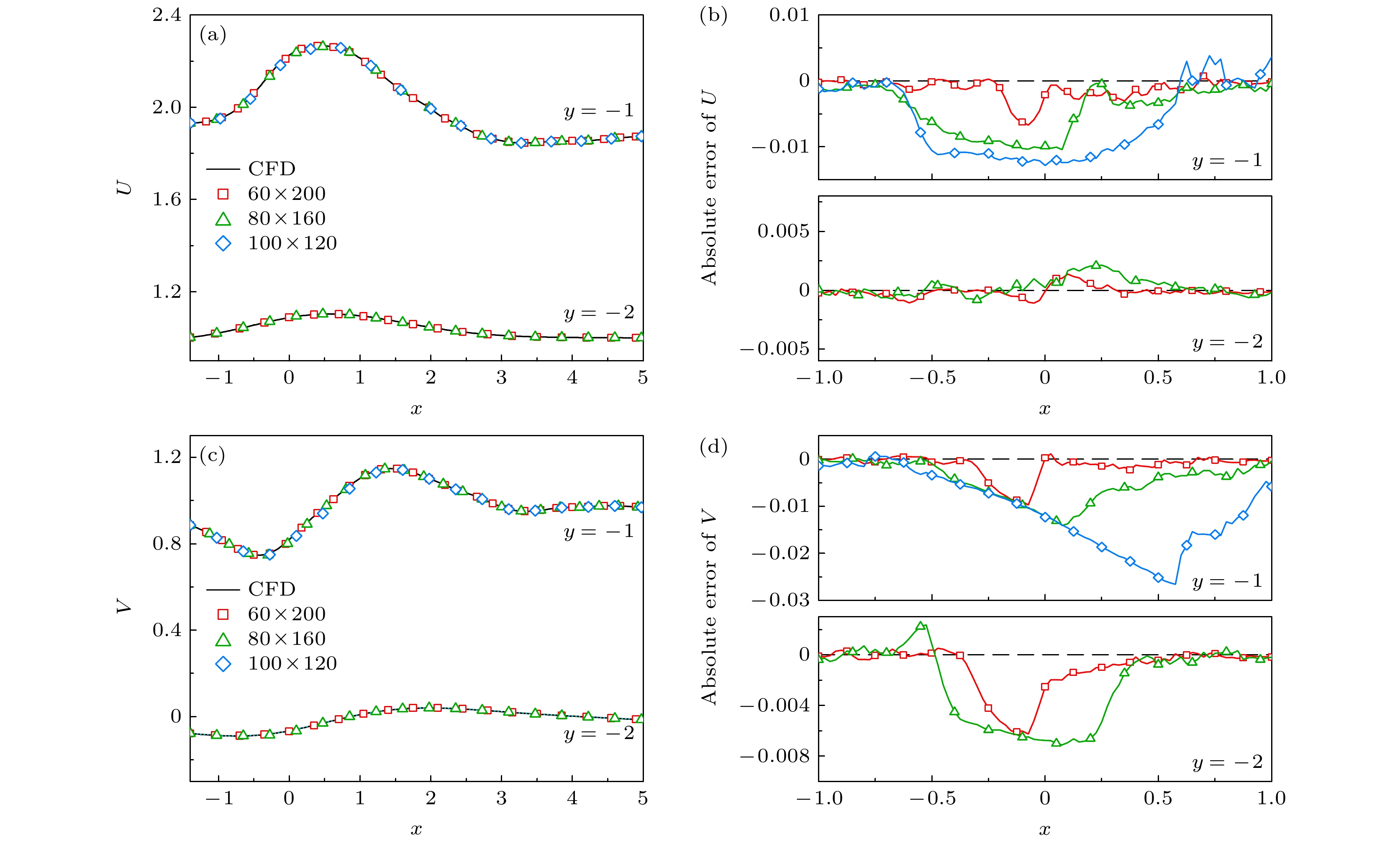
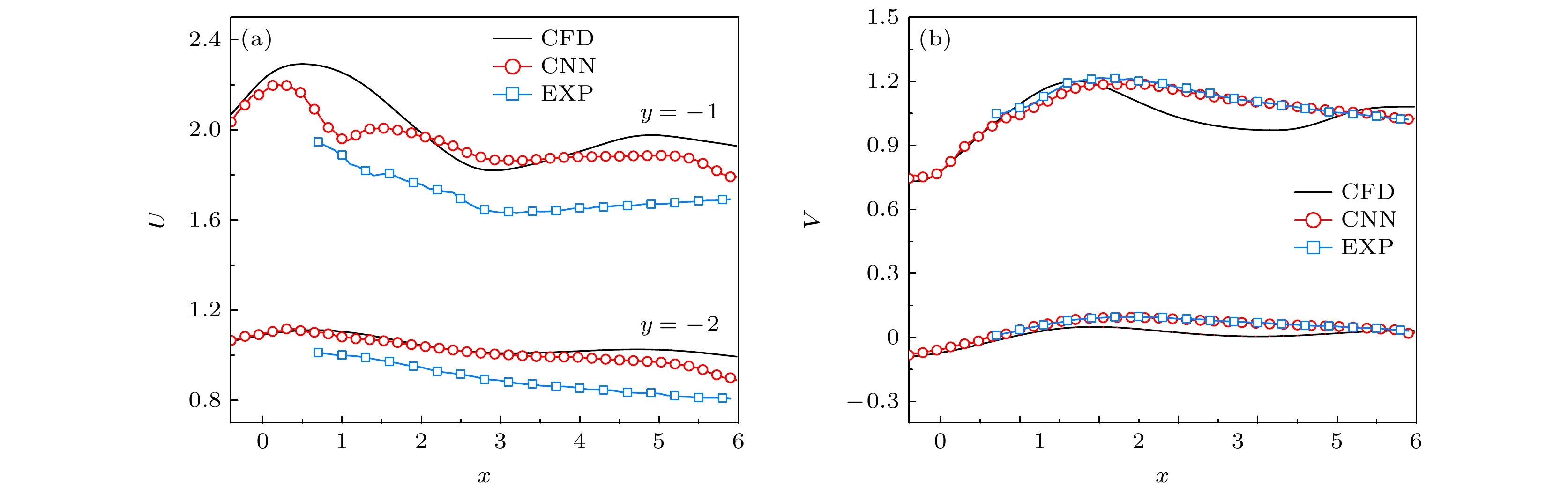
图 7 不同缺失区域对圆柱下方$ y=-1 $和$ y=-2 $处速度重构结果对比 (a)流向速度统计; (b)流向速度绝对误差; (c)法向速度统计; (d)法向速度绝对误差
Figure 7. Comparison of reconstruction results at y = –1 and y = –2 below the cylinder of different gappy regions: (a) Streamwise velocity stcatistics; (b) absolute error of streamwise velocity; (c) normal velocity stcatistics; (d) absolute error of normal velocity.
图 8 不同缺失区域的重构结果的POD结果对比 (a)流向速度; (b)法向速度
Figure 8. Comparison of POD of flow of different gappy regions: (a) Streamwise velocity; (b) normal velocity.
图 9 噪声等级对重构结果的影响 (a)平均$ L_2 $误差随噪声等级的变化; (b)几个不同噪声等级的重构结果对比
Figure 9. Effect of noise level on reconstruction results: (a) The mean $ L_2 $ error varies with noise level; (b) comparison of reconstruction results of several different noise levels.
图 10 实验中获得的PIV粒子图像
Figure 10. An image of PIV particles obtained in the experiment.
图 11 两个不同瞬时时刻的实验数据重构结果
Figure 11. Reconstruction results of experimental data at two different times.
图 12 实验、神经网络重构和数值计算的时均流场对比
Figure 12. Comparison of experimental, neural network reconstruction and numerically time-averaged flow fields.
图 13 圆柱下方$ y=-1 $和$ y=-2 $处实验、神经网络重构和数值仿真结果对比 (a)流向速度统计; (b)法向速度统计
Figure 13. Comparison of reconstruction results at y = –1 and y = –2 below the cylinder of different gappy regions: (a) Streamwise velocity stcatistics; (b) normal velocity stcatistics.
-
[1] Ragni D, Ashok A, van Oudheusden B W, Scarano F 2009 Meas. Sci. Technol. 20 074005
Google Scholar
[2] Gunes H, Rist U 2008 Phys. Fluids 20 104109
Google Scholar
[3] Tan B T, Damodaran M, Willcox K E 2004 AIAA J. 42 1505
Google Scholar
[4] 李天一, Buzzicotti Michele, Biferale Luca, 万敏平, 陈十一 2021 力学学报 53 2703
Google Scholar
Li T Y, Buzzicotti M, Biferale L, Wan M P, Chen S Y 2021 Chin. J. Mech. 53 2703
Google Scholar
[5] Sciacchitano A, Dwight R P, Scarano F 2012 Exp. Fluids 53 1421
Google Scholar
[6] Zimmermann R, Vendl A 2014 AIAA J. 52 255
Google Scholar
[7] Ruscher C J, Dannenhoffer J F, Glauser M N 2017 AIAA J. 55 255
Google Scholar
[8] Deng Z W, He C X, Wen X, Liu Y Z 2018 J. Vis. 21 1043
Google Scholar
[9] Li T X, He C X, Wen X, Liu Y Z 2023 J. Vis. 26 815
Google Scholar
[10] 何创新, 邓志文, 刘应征 2021 航空学报 42 524704
He C X, Deng Z W, Liu Y Z 2021 Acta Aeronautica et Astronautica Sinica 42 524704
[11] 袁昊, 寇家庆, 张伟伟 2024 力学学报 56 2799
Google Scholar
Yuan H, Kou J Q, Zhang W W 2024 Chin. J. Mech. 56 2799
Google Scholar
[12] 张伟伟, 王旭, 寇家庆 2023 力学进展 53 433
Google Scholar
Zhang W W, Wang X, Kou J Q 2023 Adv. Mech. 53 433
Google Scholar
[13] 任峰, 高传强, 唐辉 2021 航空学报 42 524686
Ren F, Gao C Q, Tang H 2021 Acta Aeronautica et Astronautica Sinica 42 524686
[14] Vinuesa R, Brunton S L, McKeon B J 2023 Nat. Rev. Phys 5 536
Google Scholar
[15] Brunton S L 2021 Acta Mech. Sin. 37 1718
Google Scholar
[16] Wen Z K, Shu W P, Zhang H, Liu S B, Zhang L Q, Liu L, Wang T, Zhang Q J, Li S 2024 Space Sci. Technol. 4 0080
Google Scholar
[17] 徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 69 014209
Google Scholar
Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209
Google Scholar
[18] Taira K, Hemati M S, Brunton S L, Sun Y Y, Duraisamy K, Bagheri S, Dawson S T M, Yeh C A 2020 AIAA J. 58 998
Google Scholar
[19] 郑天韵, 王圣业, 王光学, 邓小刚 2020 69 204701
Google Scholar
Zheng T Y, Wang S Y, Wang G X, Deng X G 2020 Acta Phys. Sin. 69 204701
Google Scholar
[20] Wang H P, Yang Z X, Li B L, Wang S Z 2020 Phys. Fluids 32 115105
Google Scholar
[21] Morimoto M, Fuakmi K, Fukagata K 2021 Phys. Fluids 33 087121
Google Scholar
[22] Zhang F, Hu H B, Ren F, Zhang H, Du P 2022 Phys. Fluids 34 127117
Google Scholar
[23] Luo Z H, Wang L Y, Xu J, Wang Z L, Chen M, Yuan J P 2023 Phys. Fluids 35 085115
Google Scholar
[24] Luo Z H, Wang L Y, Xu J, Yuan J P, Chen M, Li Y, Andy C T 2024 Ocean Eng. 293 116605
Google Scholar
[25] Zheng Q M, Li T Y, Ma B T, Fu L, Li X M 2024 Phys. Rev. Fluids 9 024608
Google Scholar
[26] Muharrem H A, Ilker G, Murat I, Abdullah C 2023 Phys. Fluids 35 114110
Google Scholar
[27] He K M, Zhang X Y, Ren S Q, Sun J 2016 ICCV Santiago, Chile, December 13–16, 2015 p1026
[28] Szegedy C, Ioffe S, Vanhoucke V, Alemi A 2017 AAAI California, USA, February 4–9, 2017 p1
[29] Lin M, Chen Q, Yan S C 2013 arXiv: 13124400 [cs.NE]
[30] He K M, Zhang X Y, Ren S Q, Sun J 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Las Vegas, USA, June 26–July 1, 2016 p770
[31] Zhang F, Hu H B, Zhang H, Zhang M, Song J, Meng Y Z 2024 Ocean Eng. 309 118578
Google Scholar
[32] 陈蒋力, 丁海艳, 胡海豹, 张帆, 文俊 2024 实验流体力学 39 1
Google Scholar
Chen J L, Ding H Y, Hu H B, Zhang F, Wen J 2024 Experimental Fluid Mechanics 39 1
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 537
- PDF Downloads: 13
- Cited By: 0
