-
针对经典圆柱绕流问题, 采用深度强化学习方法, 提出了基于壁面压力反馈的圆柱绕流减阻闭环主动控制方法, 并比较分析了施加控制前后圆柱阻力系数、升力系数及流场的差异. 控制系统中, 以圆柱壁面上均匀分布的压力探针测得的信号作为反馈, 利用多层感知机建立压强信号与吹/吸射流及控制效果的映射关系, 即控制策略; 通过在圆柱上下表面狭缝施加连续可调的吹/吸射流来进行主动控制. 同时, 利用深度强化学习中的近端策略优化方法, 在大量的学习过程中对该控制策略进行不断调整和优化, 以实现稳定减阻效果. 在圆柱绕流流动环境搭建方面, 采用格子Boltzmann方法建立与深度强化学习模型之间的交互式框架, 模拟提取非定常流场条件下圆柱表面的压强信号, 并计算实时调整吹/吸射流强度时圆柱表面升力、阻力数据, 以评估所选控制策略的优劣. 研究表明: 雷诺数为100时, 主动控制策略能减少约4.2%的圆柱阻力, 同时减少约49%升力幅度; 同时施加主动控制后圆柱的减阻效果与圆柱回流区长度呈现强相关趋势. 此外, 不同雷诺数下智能体习得的策略减阻效果不同, 雷诺数为200和400时, 该主动控制策略能依次减小圆柱阻力17.3%和31.6%. 本研究可为后续开展基于壁面压力反馈的圆柱流动主动控制实验以及其他复杂环境下钝体流动智能控制提供参考.Focusing on the typical problem of flow around a circular cylinder, we propose an active flow control method of reducing drag of a circular cylinder, in which a deep reinforcement learning (DRL) method is used to establish the closed-loop control strategy with pressure sensors providing feedback signals. The detailed comparisons of the lift, drag, and flow fields with and without control are conducted. In the control system, pressure sensors evenly distributed on the cylinder surface are used to provide feedback signals for the controller. The multilayer perceptron is adopted to establish the mapping relationship between the sensors and the blowing/suction jets, i.e. the control strategy. A pair of continuously adjustable synthetic jets that exert transverse force mainly on the top and bottom edge of the cylinder is implemented. Based on the state-of-the-art proximal policy optimization algorithm, the control strategy is explored and optimized during a large number of learning episodes, thus achieving an effective, efficient, and robust drag reduction strategy. To build up the high-fidelity numerical environment, we adopt the lattice Boltzmann method as a core solver, which, together with the DRL agent, establishes an interactive framework. Furthermore, the surface pressure signals are extracted during the unsteady simulation to adjust the real-time blowing/suction jets intensity. The lift information and the drag information are recorded to evaluate the performance of the current control strategy. Results show that the active control strategy learnt by the DRL agent can reduce the drag by about 4.2% and the lift amplitude by about 49% at Reynolds number 100. A strong correlation between the drag reduction effect of the cylinder and the elongated recirculation bubble is noted. In addition, the drag reduction rate varies over a range of Reynolds numbers. The active control strategy is able to reduce the drag by 17.3% and 31.6% at Reynolds number 200 and 400, respectively. Owing to the fact that wall pressure signals are easy to measure in realistic scenarios, this study provides valuable reference for experimentally designing the active flow control of a circular cylinder based on wall pressure signals and intelligent control in more complicated flow environments.
-
Keywords:
- active flow control /
- flow past a circular cylinder /
- deep reinforcement learning /
- wall pressure feedback
[1] 任峰, 高传强, 唐辉 2021 航空学报 42 524686
Google Scholar
Ren F, Gao C Q, Tang H 2021 Acta Aeronaut. Astronaut. Sin 42 524686
Google Scholar
[2] Brunton S L, Noack B R 2015 Appl. Mech. Rev. 67 050801
Google Scholar
[3] Li R, Noack B R, Cordier L, Borée J 2017 Exp. Fluids 58 1
Google Scholar
[4] Schoppa W, Hussain F 1998 Phys. Fluids 10 1049
Google Scholar
[5] Duriez T, Brunton S L, Noack B R 2017 Machine learning control-taming nonlinear dynamics and turbulence (Cham, Switzerland: Springer International Publishing) pp1–229
[6] Ren F, Hu H B, Tang H 2020 J. Hydrodyn. 32 247
Google Scholar
[7] Rabault J, Kuchta M, Jensen A, Réglade U, Cerardi N 2019 J. Fluid Mech. 865 281
Google Scholar
[8] Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O 2017 arXiv: 1707.06347
[9] Paris R, Beneddine S, Dandois J 2021 J. Fluid Mech. 913 A25
Google Scholar
[10] Ren F, Rabault J, Tang H 2021 Phys. Fluids 33 037121
Google Scholar
[11] Ren F, Song B, Zhang Y, Hu H 2018 Comput. Fluids. 173 29
Google Scholar
[12] Rabault J, Kuhnle A 2019 Phys. Fluids 31 094105
Google Scholar
[13] 郭照立 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第9—14页
Guo Z L, Zhen C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) pp 9–14 (In Chinese)
[14] 何雅玲, 王勇, 李庆 2009 格子 Boltzmann 方法的理论及应用 (北京: 科学出版社) 第5—79页
He Y L, Wang Y, Li Q 2009 Lattice Boltzmann Method: Theory and Application (Beijing: Science Press) pp5–79 (In Chinese)
[15] Qian Y H, D'Humières D, Lallemand P 1992 Europhys. Lett 17 479
Google Scholar
[16] D'Humières D 1992 AIAA J. 159 450
[17] D'Humières D, Ginzburg I, Krafczyk M, Lallemand P, Luo L S 2002 Philos. Trans. Roy. Soc. A 360 437
Google Scholar
[18] He X, Luo L S 1997 J. Stat. Phys. 88 927
Google Scholar
[19] Guo Z L, Zhen C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[20] Ziegler D P 1993 J. Stat. Phys. 71 1171
Google Scholar
[21] Yu D, Mei R, Luo L S, Shyy W 2003 Prog. Aeosp. Sci 39 329
Google Scholar
[22] Chen Y, Cai Q, Xia Z, Wang M, Chen S 2013 Phys. Rev. E 88 013303
Google Scholar
[23] Tang H, Rabault J, Kuhnle A, Kuhnle A, Wang Y, Wang T 2020 Phys. Fluids 32 053605
Google Scholar
[24] Schäfer M, Turek S, Durst F, Krause E 1997 Flow Simulation with High-Performance Computers II (Wiesbaden: Vieweg+Teubner Verlag) pp547–566
[25] Van Hasselt H, Guez A, Silver D 2016 Proceedings of the AAAI conference on artificial intelligence Phoenix, Germany, February 12–17, 2016 p2094
[26] Tiwari A, Vanka S P 2012 Int. J. Numer. Methods Fluids 69 481
Google Scholar
[27] Protas B, Wesfreid J 2002 Phys. Fluids 14 810
Google Scholar
[28] Bergmann M, Cordier L, Brancher J P 2005 Phys. Fluids 17 097101
Google Scholar
[29] Coutanceau M, Bouard R 1977 J. Fluid Mech. 79 231
Google Scholar
-
图 3 控制前后阻力系数(CD)随时间变化图
Fig. 3. Temporal variations of drag coefficient (CD) with and without active flow control.
图 4 压力探针位置图 (a) 6个压力探针; (b) 14个压力探针; (c) 30个压力探针
Fig. 4. Schematics of the pressure sensors position: (a) 6 pressure sensors; (b) 14 pressure sensors; (c) 30 pressure sensors.
图 5 圆柱压力分布曲线, Re = 20
Fig. 5. Pressure distribution curve along the cylinder surface, Re = 20.
图 7 主动控制和无控制下圆柱的阻力系数(CD), 升力系数(CL)和射流速度(Ujet)变化曲线, Re = 100
Fig. 7. Temporal variations of drag coefficient (CD), lift coefficient (CL), and jet velocity (Ujet) with and without active control, Re = 100.
图 8 Re = 100时的瞬时流场云图(a1)—(d1)无控制下流向速度, 横向速度, 压力及涡量云图; (a2)—(d2)主动控制下流向速度, 横向速度, 压力及涡量云图
Fig. 8. Instantaneous contours of flow fields at Re = 100: (a1)–(d1) Contours of streamwise velocity, transverse velocity, pressure, and vorticity without active control; (a2)–(d2) contours of streamwise velocity, transverse velocity, pressure, and vorticity with active control.
图 9 Re = 100时的时均流场云图 (a1)—(c1)无控制下流向速度, 横向速度及压力云图; (a2)—(c2)主动控制下流向速度, 横向速度及压力云图
Fig. 9. Time-averaged contours of flow fields at Re = 100: (a1)–(c1) Contours of streamwise velocity, spanwise velocity, pressure, and vorticity without active control; (a2)–(c2) contours of streamwise velocity, spanwise velocity, and pressure with active control.
图 10 主动控制与无控制下的圆柱阻力系数(CD), 升力系数(CL)和射流速度(Ujet)变化曲线
Fig. 10. Time-resolved value of drag coefficient (CD), lift coefficient (CL), and jet velocity (Ujet) with and without control.
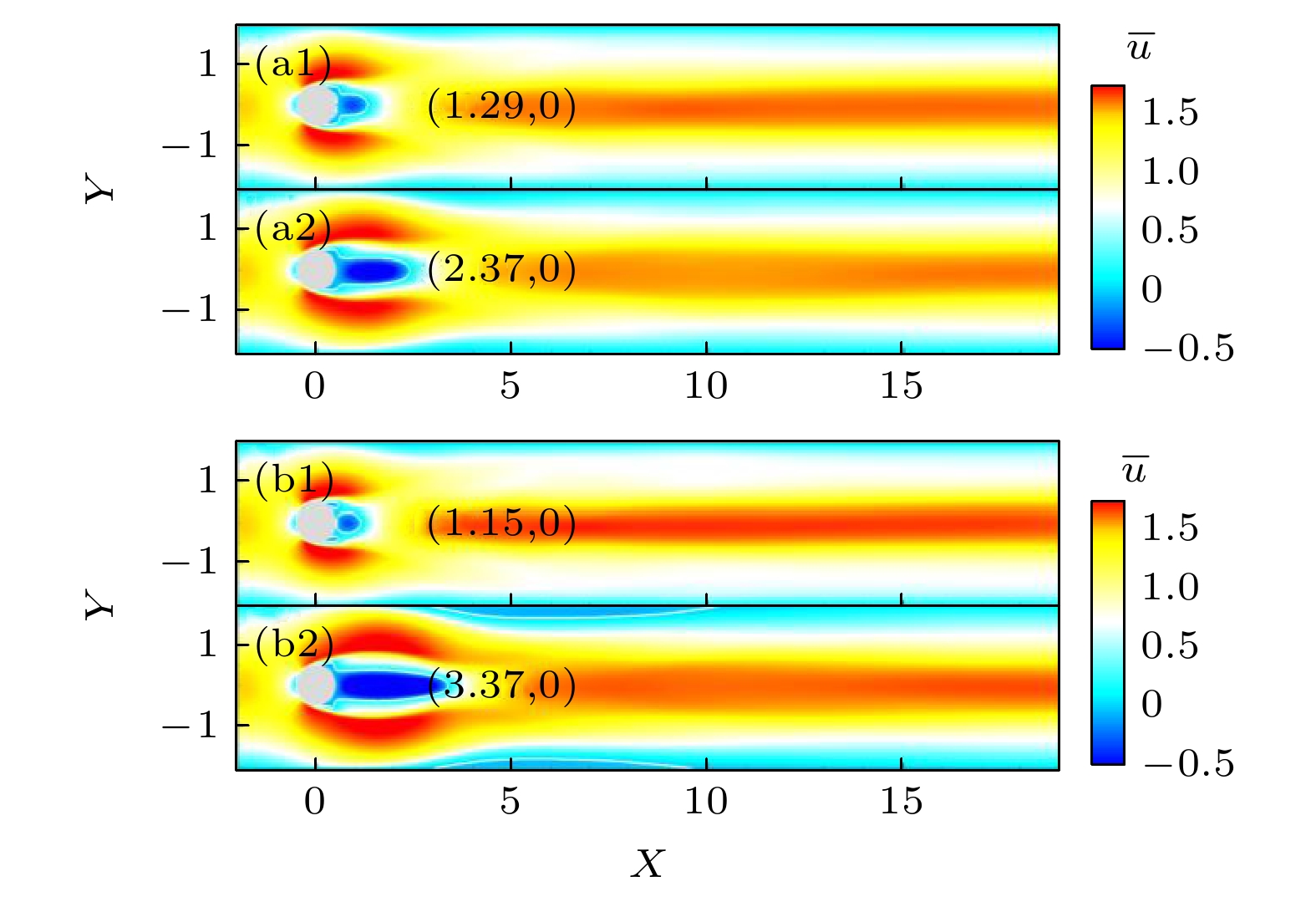
图 11 无控制下和施加主动控制下的时均流向速度云图 (a1) Re = 200, 无控制; (a2) Re = 200, 施加控制; (b1) Re = 400, 无控制; (B2) Re = 400, 施加控制
Fig. 11. Time-averaged streamwise velocity fields without control and with active control: (a1) Re = 200, without control; (a2) Re = 200, with control; (b1) Re = 400, without control; (b2) Re = 400, with control.
表 1 无关性验证(Re = 100)
Table 1. Validation and convergence study (Re = 100).
Mesh T/δt $ \overline {{C_{\text{D}}}} $ $ \overline {\left| {{C_{\text{L}}}} \right|} $ Sr Ⅰ 768×144 1000 3.192 0.612 0.3026 Ⅱ 1536×288 2000 3.201 0.639 0.3019 Ⅲ 3072×576 4000 3.201 0.640 0.3012 
下载: 导出CSV
表 2 Re = 100时最大升阻力系数CD,max, CL,max与Sr对比
Table 2. Comparison of CD,max, CL,max and Sr at Re = 100
下载: 导出CSV
-
[1] 任峰, 高传强, 唐辉 2021 航空学报 42 524686
Google Scholar
Ren F, Gao C Q, Tang H 2021 Acta Aeronaut. Astronaut. Sin 42 524686
Google Scholar
[2] Brunton S L, Noack B R 2015 Appl. Mech. Rev. 67 050801
Google Scholar
[3] Li R, Noack B R, Cordier L, Borée J 2017 Exp. Fluids 58 1
Google Scholar
[4] Schoppa W, Hussain F 1998 Phys. Fluids 10 1049
Google Scholar
[5] Duriez T, Brunton S L, Noack B R 2017 Machine learning control-taming nonlinear dynamics and turbulence (Cham, Switzerland: Springer International Publishing) pp1–229
[6] Ren F, Hu H B, Tang H 2020 J. Hydrodyn. 32 247
Google Scholar
[7] Rabault J, Kuchta M, Jensen A, Réglade U, Cerardi N 2019 J. Fluid Mech. 865 281
Google Scholar
[8] Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O 2017 arXiv: 1707.06347
[9] Paris R, Beneddine S, Dandois J 2021 J. Fluid Mech. 913 A25
Google Scholar
[10] Ren F, Rabault J, Tang H 2021 Phys. Fluids 33 037121
Google Scholar
[11] Ren F, Song B, Zhang Y, Hu H 2018 Comput. Fluids. 173 29
Google Scholar
[12] Rabault J, Kuhnle A 2019 Phys. Fluids 31 094105
Google Scholar
[13] 郭照立 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第9—14页
Guo Z L, Zhen C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) pp 9–14 (In Chinese)
[14] 何雅玲, 王勇, 李庆 2009 格子 Boltzmann 方法的理论及应用 (北京: 科学出版社) 第5—79页
He Y L, Wang Y, Li Q 2009 Lattice Boltzmann Method: Theory and Application (Beijing: Science Press) pp5–79 (In Chinese)
[15] Qian Y H, D'Humières D, Lallemand P 1992 Europhys. Lett 17 479
Google Scholar
[16] D'Humières D 1992 AIAA J. 159 450
[17] D'Humières D, Ginzburg I, Krafczyk M, Lallemand P, Luo L S 2002 Philos. Trans. Roy. Soc. A 360 437
Google Scholar
[18] He X, Luo L S 1997 J. Stat. Phys. 88 927
Google Scholar
[19] Guo Z L, Zhen C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
[20] Ziegler D P 1993 J. Stat. Phys. 71 1171
Google Scholar
[21] Yu D, Mei R, Luo L S, Shyy W 2003 Prog. Aeosp. Sci 39 329
Google Scholar
[22] Chen Y, Cai Q, Xia Z, Wang M, Chen S 2013 Phys. Rev. E 88 013303
Google Scholar
[23] Tang H, Rabault J, Kuhnle A, Kuhnle A, Wang Y, Wang T 2020 Phys. Fluids 32 053605
Google Scholar
[24] Schäfer M, Turek S, Durst F, Krause E 1997 Flow Simulation with High-Performance Computers II (Wiesbaden: Vieweg+Teubner Verlag) pp547–566
[25] Van Hasselt H, Guez A, Silver D 2016 Proceedings of the AAAI conference on artificial intelligence Phoenix, Germany, February 12–17, 2016 p2094
[26] Tiwari A, Vanka S P 2012 Int. J. Numer. Methods Fluids 69 481
Google Scholar
[27] Protas B, Wesfreid J 2002 Phys. Fluids 14 810
Google Scholar
[28] Bergmann M, Cordier L, Brancher J P 2005 Phys. Fluids 17 097101
Google Scholar
[29] Coutanceau M, Bouard R 1977 J. Fluid Mech. 79 231
Google Scholar
下载:
计量
- 文章访问数: 5968
- PDF下载量: 112
- 被引次数: 0
