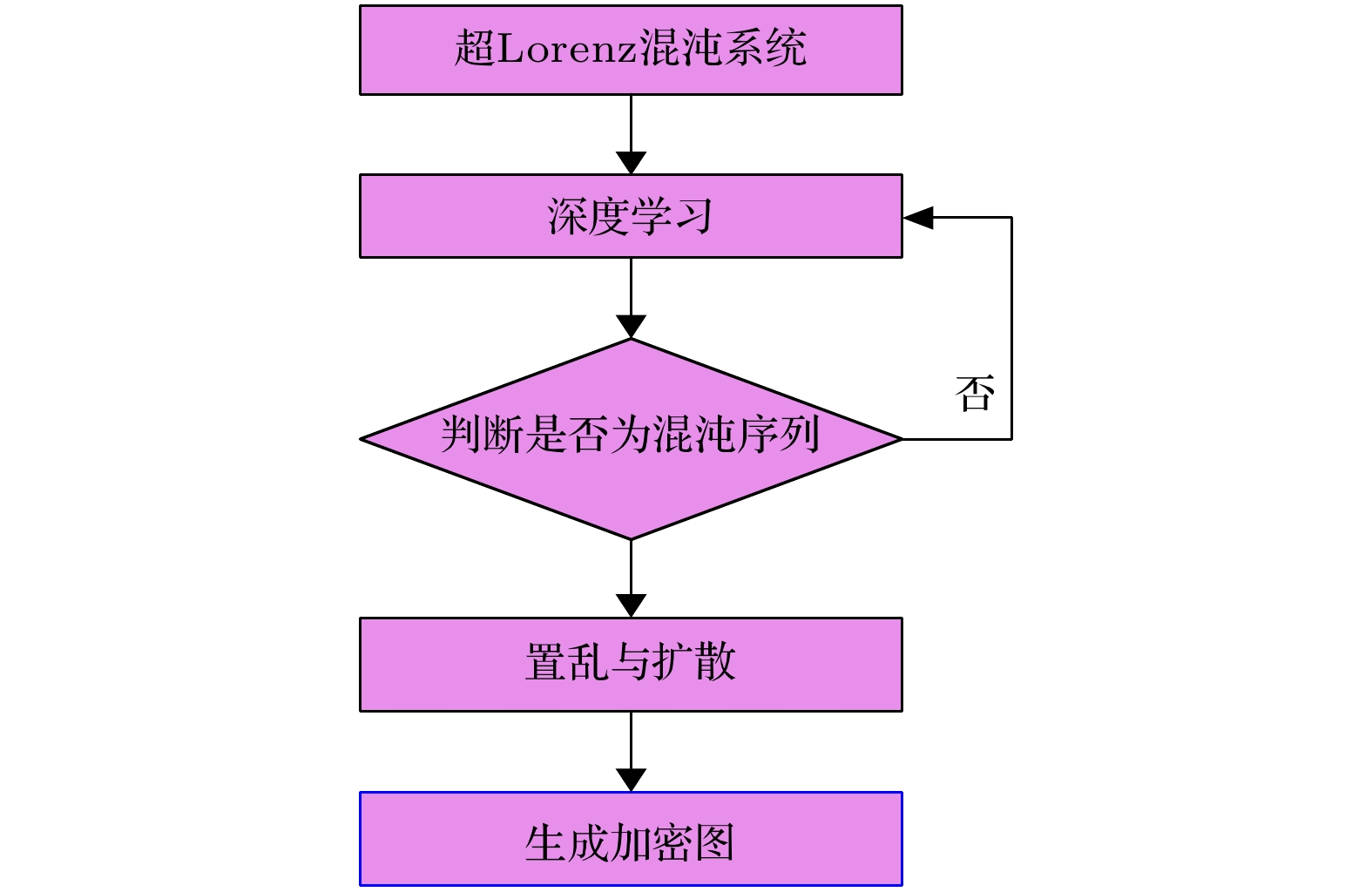
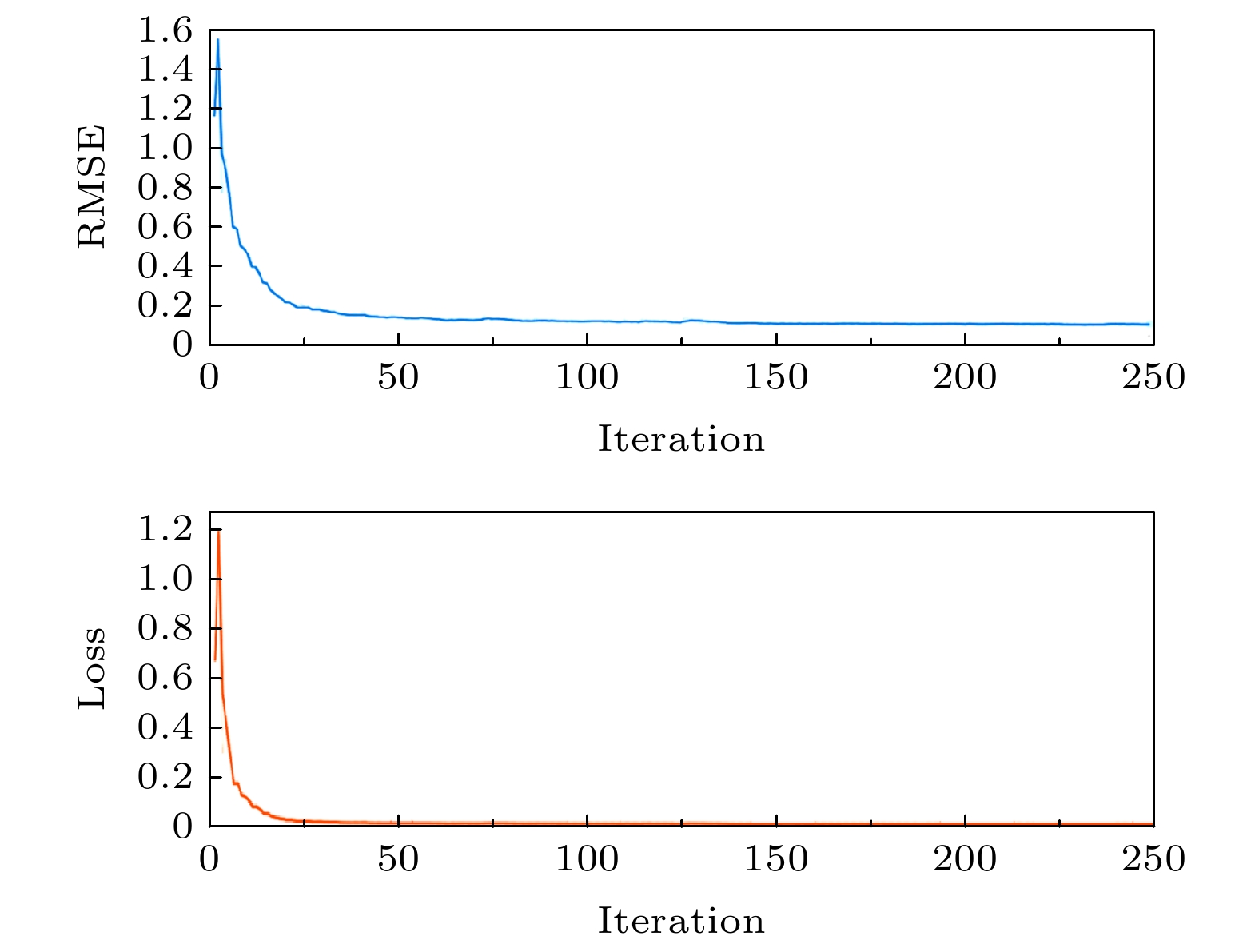
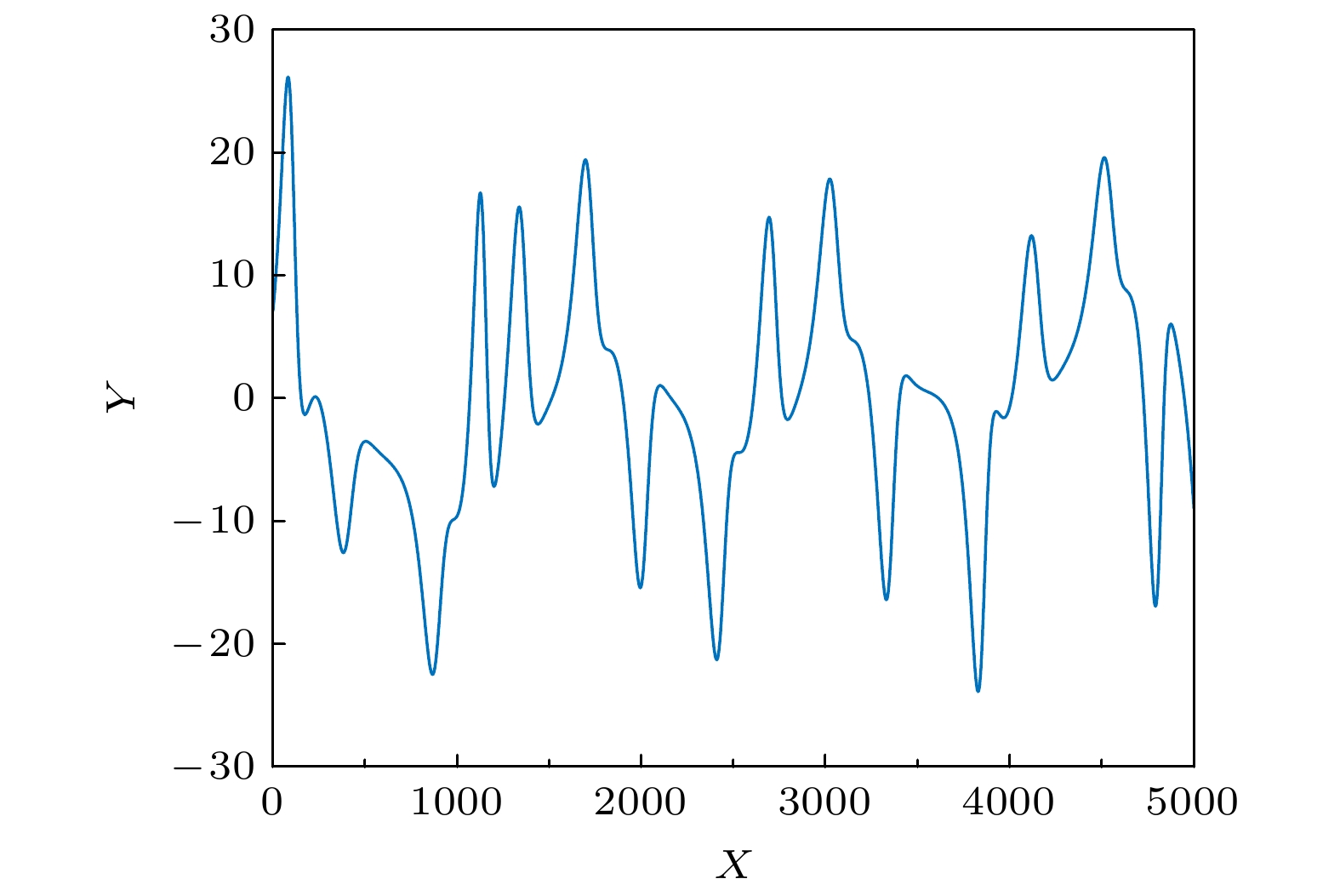
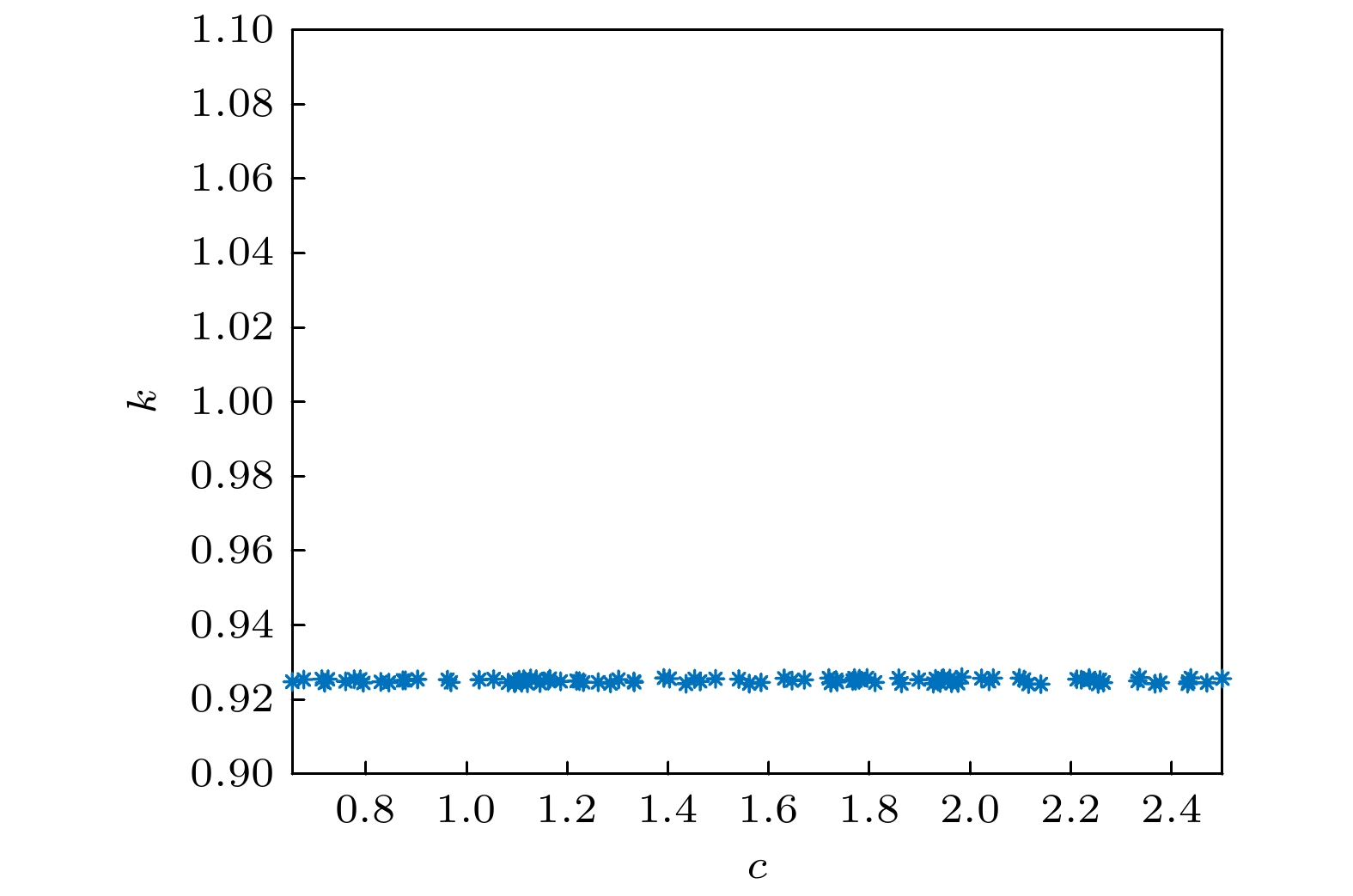
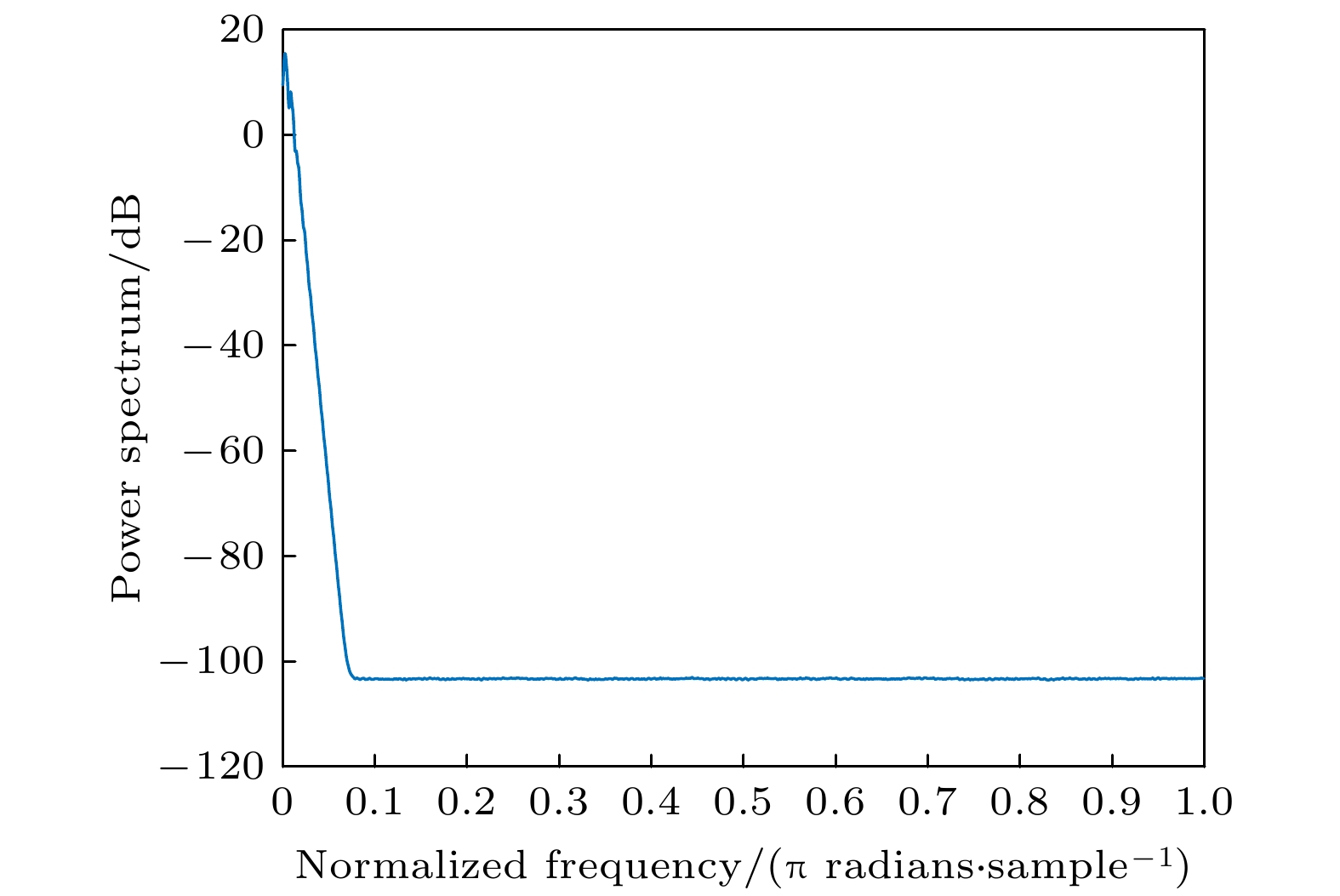
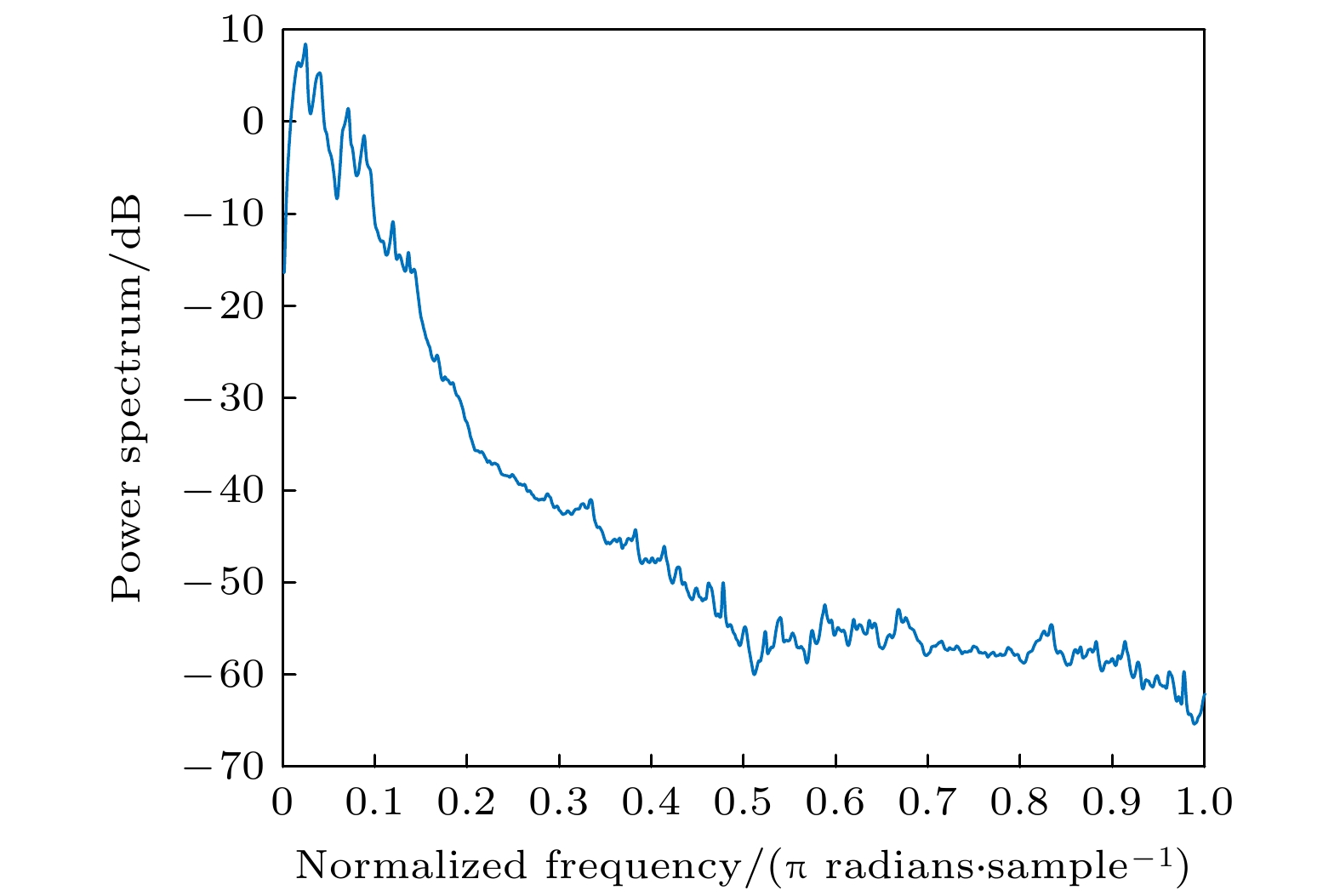
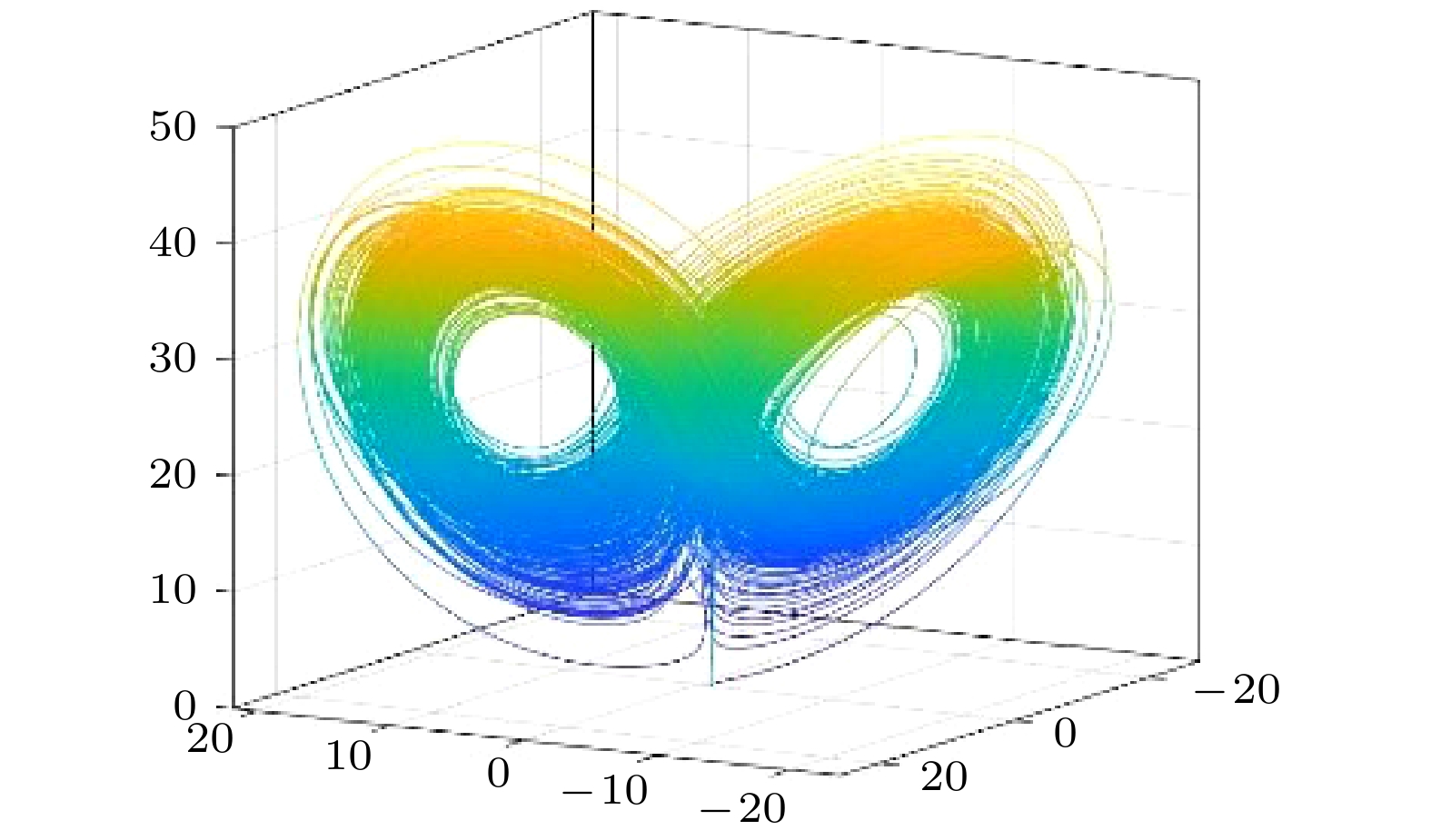
-
为提高单一混沌系统图像加密的安全性, 本文提出了基于深度学习的图像加密算法. 首先, 利用超混沌Lorenz系统产生混沌序列. 其次, 利用长短期记忆人工神经网络(long-short term memory, LSTM)复杂的网络结构模拟混沌特征构造新的混沌信号. 然后, 利用最大Lyapunov指数, 0-1测试, 功率谱分析、相图以及NIST测试对新信号的动力学特征进行分析. 最后, 将新信号应用到图像加密中. 由于该方法生成的新信号不同于原有混沌信号, 而且加密系统具有很高的复杂结构和非线性特征, 故很难被攻击者攻击. 仿真实验结果表明, 本文提出的图像加密算法相比其他一些传统方法具有更高的安全性, 能够抵抗常见的攻击方式.To improve the security of image encryption in singular chaotic systems, an encryption algorithm based on deep-learning is proposed in this paper. To begin with, the chaos sequence is generated by using a hyperchaotic Lorenz system, prior to creating new chaotic signals based on chaotic characteristics obtained from he simulations of the powerful complex network structure of long-short term memory artificial neural network (LSTM-ANN). Then, dynamic characteristics of the new signals are analyzed with the largest Lyapunov exponent, 0-1 test, power spectral analysis, phase diagrams and NIST test. In the end, the new signals are applied to image encryption, the results of which verify the expected increased difficulty in attacking the encrypted system. This is attributable to the differences of the new signals generated using the proposed method from the original chaotic signals, as well as arises from the high complexity and nonlinearity of the system. Considering its ability to withstand common encryption attacks, it is hence reasonable to conclude that the proposed method exhibits higher safety and security than other traditional methods.
-
Keywords:
- chaotic system /
- image encryption /
- deep learning
[1] Wang X Y, Teng L, Qin X 2012 Signal Pro. 92 1101
Google Scholar
[2] Liu W H, Sun K H, Zhu C X 2016 Optics Lasers Eng. 84 26
Google Scholar
[3] Wu X J, Kan H C, Kurths J 2015 Appl. Soft Comput. 37 24
Google Scholar
[4] Hua Z Y, Zhou Y C, Pun C M, Chen C. L. P 2015 Inf. Sci. 297 80
Google Scholar
[5] 郑洪英, 李琳, 肖迪 2021 信息网络安全 21 10
Google Scholar
Zheng H Y, Li L, Xiao D 2021 Net Inf. Security 21 10
Google Scholar
[6] Dharavathu K, Mosa A 2020 Int. J. Commun. Syst. 33 e4369
[7] Zhao J F, Wang S Y, Chang Y X, Li X F 2015 Nonlinear Dyn. 80 1721
Google Scholar
[8] Khan M 2015 Nonlinear Dyn. 82 527
Google Scholar
[9] Chai X L, Gan Z H, Yuan K, Yang L Chen Y R 2017 Chin. Phys. B 26 020504
Google Scholar
[10] Chai X L, Fu J Y, Zhang J T, Han D J, Gan Z H 2021 Neural Comput. Appl. 33 10271
Google Scholar
[11] Ran Q W, Yuan L, Zhao T Y 2015 Opt. Commun. 348 43
Google Scholar
[12] Kaur M, Kumar V 2018 Int. J. Bifurcat. Chaos 28 1850132
Google Scholar
[13] Yasser I, Khalifa F, Mohamed M A, Samrah A S 2020 Complexity 2020 9597619
Google Scholar
[14] Wu J H, Liao X F, Yang B 2017 Signal Pro. 141 109
Google Scholar
[15] Wang X Y, Feng L, Zhao H Y 2019 Inf. Sci. 486 340
Google Scholar
[16] Wang X Y, Li Z M 2019 Optics Lasers Engin. 115 107
Google Scholar
[17] Zhang Y 2018 Multimed. Tools Appl. 77 21589
Google Scholar
[18] Bansal R, Gupta S, Sharma G 2017 Multimed. Tools. Appl. 76 16529
Google Scholar
[19] Hua Z Y, Zhou Y C, Huang H J 2019 Inf. Sci. 480 403
Google Scholar
[20] Wang X Y, Yang J J 2021 Inf. Sci. 569 217
Google Scholar
[21] Mandal M K, Kar M, Singh S K, Barnwal V K 2014 Secur. Commun. Netw. 7 2145
Google Scholar
[22] Wang X Y, Gao S 2020 Inf. Sci. 539 195
Google Scholar
[23] Wang M X, Wang X Y, Zhao T T, Zhang C, Xia Z Q, Yao N M 2021 Inf. Sci. 544 1
Google Scholar
[24] Wang X Y, Wang T, Xu D H, Chen F 2014 Int. J. Modern Phys. B 28 1450023
Google Scholar
[25] Zhou S, Wang X Y, Wang M X, Zhang Y Q 2020 Chaos Solitons & Fract. 141 110225
Google Scholar
[26] Wang X Y, Gao S 2020 Inf. Sci. 507 16
Google Scholar
[27] Wang X Y, Liu C, Jiang D H 2021 Inf. Sci. 574 505
Google Scholar
[28] Zhang Y Q, Wang X Y 2015 Appl. Soft Comput. 26 10
Google Scholar
[29] Zhang Y Q, Jia Y R, Wang X Y, Niu Q, Chen N D 2020 IEEE Access 8 213296
Google Scholar
[30] He Y, Zhang Y Q, Wang X Y 2020 Neural Comput. Appl. 32 247
Google Scholar
[31] Zhang Y Q, Wang X Y, Liu L Y, Liu J 2018 Int. J. Bifurcat. Chaos 28 1850020
Google Scholar
[32] Zhang Y Q, He Y, Wang X Y 2018 Physica A 490 148
Google Scholar
[33] Zhou S, Wang X Y, Zhang Y Q, Ge B, Wang M X, Gao S 2021 Multimed. Syst. (Published Online)
Google Scholar
[34] 张勇 2016 混沌数字图像加密 (北京: 清华大学出版社) 第106—205页
Zhang Y 2016 Chaotic Digital Image Cryptosystem (Beijing: Tsinghua University Press) pp106–205 (in Chinese)
[35] 刘树堂, 孙福艳 2009 中国科学(G辑: 物理学 力学 天文学) 39 387
Liu S T, Sun F Y 2009 Sci. Sin-Phys. Mech. Astron. 39 387
[36] May R M 1976 Nature 261 459
Google Scholar
[37] Kanso A 2011 Commun. Nonlinear Sci. Numer. Simul. 16 822
Google Scholar
[38] Chinese) [李石磊, 刘崇新, 胡晓宇, 倪骏康 2017 西安交通大学学报 51 35
Li S L, Liu C X, Hu X Y, Ni J K 2017 J. Xi'an Jiaotong Univ. 51 35 (in
[39] Kaneko K 1989 Physica D 34 1
Google Scholar
[40] Sinha S 2002 Phys. Rev. E 66 016209
Google Scholar
[41] Zhang Y Q 2015 Ph. D. Dissertation (Dalian: Dalian University of Technology) (in Chinese)
[42] 石航, 王丽丹 2019 68 200501
Google Scholar
Shi H, Wang L D 2019 Acta Phys. Sin. 68 200501
Google Scholar
[43] 庄志本, 李军, 刘静漪, 陈世强 2020 69 040502
Google Scholar
Zhuang Z B, Li J, Liu J Y, Chen S Q 2020 Acta Phys. Sin. 69 040502
Google Scholar
[44] Zhang Q, Wei X P 2013 IETE Techn. Re. 30 404
[45] Zhang Y Q, Wang X Y 2014 Inf. Sci. 273 329
Google Scholar
[46] 陈炜, 郭媛, 敬世伟 2020 69 240502
Google Scholar
Chen W, Guo Y, Jing S W 2020 Acta Phys. Sin. 69 240502
Google Scholar
[47] He Y, Zhang Y Q, He X, Wang X Y 2021 Sci. Rep. 11 6398
Google Scholar
[48] 葛钊成, 胡汉平 2021 密码学报 8 215
Google Scholar
Ge Z C, Hu H P 2021 Cryptol. Res. 8 215
Google Scholar
[49] 熊有成, 赵鸿 2019 中国科学: 物理学 力学 天文学 49 92
Google Scholar
Xiong Y C, Zhao H 2019 Sci. Sin-Phys. Mech. Astron. 49 92
Google Scholar
[50] Sangiorgio M, Dercole F 2020 Chaos, Solitons Fract. 139 110045
Google Scholar
[51] 黄伟建, 李永涛, 黄远 2021 70 010501
Google Scholar
Huang W J, Li Y T, Huang Y 2021 Acta Phys. Sin. 70 010501
Google Scholar
[52] 王兴元, 王明军 2007 56 5136
Google Scholar
Wang X Y, Wang M J 2007 Acta Phys. Sin. 56 5136
Google Scholar
[53] Hochreiter S, Schmidhuber J 1997 Neural Comput. 9 1735
Google Scholar
[54] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Phys. D:Nonlinear Phenomena 16 285
Google Scholar
[55] Gottwald G A, Melbourne I 2009 SIAM J. Appl. Dyn. Syst. 8 129
Google Scholar
[56] Gottwald G A, Melbourne I 2004 P. Roy. Soc. A-Math. Phy. 460 603
Google Scholar
[57] Wu Y, Noonan J P, Agaian S 2011 Cyber J. 1 31
[58] Nepomuceno E G, Nardo L G, Arias-Garcia J, Butusov D N, Tutueva A 2019 Chaos 29 061101
Google Scholar
[59] Zhou M J, Wang C H 2020 Signal Pro. 171 107484
Google Scholar
[60] Xian Y J, Wang X Y 2021 Inf. Sci. 547 1154
Google Scholar
[61] Wang X Y, Xue W H, An J B 2020 Chaos, Solitons Fract. 141 110309
Google Scholar
[62] Boriga R, Dăscălescu A C, Priescu I 2014 Signal Processing: Image Communication 29 887
[63] Abolfazl Y N, Mohammad H M, Masood N T 2017 Optics Lasers Eng. 90 225
Google Scholar
-
图 1 超混沌Lorenz相图三维投影
Fig. 1. Three dimensional projection of hyperchaotic Lorenz phase diagram.
图 5
$ \left\{ {y_i'} \right\} $ LSTM模型训练过程Fig. 5. LSTM model training process of
$ \left\{ {y_i'} \right\} $ .
图 8 Wolf方法求
$ \left\{ {y_i'} \right\} $ 最大Lyapunov指数过程图Fig. 8. Using wolf method to find the largest Lyapunov exponent process of
$ \left\{ {y_i'} \right\} $ .
图 13 序列
$ \left\{ {y_i'} \right\} $ 的相图Fig. 13. Phase diagram of
$ \left\{ {y_i'} \right\} $ .
图 14 序列
$ \left\{ {{y_i}} \right\} $ 的相图Fig. 14. Phase diagram of
$ \left\{ {{y_i}} \right\} $ .
图 15 数字图像加密解密实验图 (a)鸟(256 × 256)原图; (b)鸟(256 × 256)加密图; (c)鸟(256 × 256)解密图; (d)辣椒(256 × 256)原图; (e)辣椒(256 × 256)加密图; (f)辣椒(256 × 256)解密图; (g)Lena(512 × 512)原图; (h) Lena(512 × 512)加密图; (i) Lena(512 × 512)解密图; (j) 液体泼洒(512 × 512)原图; (k) 液体泼洒(512 × 512)加密图; (l) 液体泼洒(512 × 512)解密图; (m)机场(1024 × 1024)原图; (n) 机场(1024 × 1024)加密图; (o) 机场(1024 × 1024)解密图; (p)飞机(1024 × 1024)原图; (q)飞机(1024 × 1024)加密图; (r)飞机(1024 × 1024)解密图
Fig. 15. Experimental picture of digital image encryption and decryption: (a) Original bird image; (b) encrypted bird image; (c) decrypted bird image; (d) original pepper (256 × 256) image; (e) encrypted pepper (256 × 256) image; (f) decrypted pepper (256 × 256) image; (g) original Lena (512 × 512) image; (h) encrypted Lena (512 × 512) image; (i) decrypted Lena (512 × 512) image; (j) original splash (512 × 512) image; (k) encrypted splash (512 × 512) image; (l) decrypted splash (512 × 512) image; (m) original airport (1024 × 1024) image; (n) encrypted airport (1024 × 1024) image; (o) decrypted airport (1024 × 1024) image; (p) original airplane (1024 × 1024) image; (q) encrypted airplane (1024 × 1024) image; (r) decrypted airplane (1024 × 1024) image.
图 16 密钥敏感性 (a)明文图像; (b)密文用
$ x_0' $ 解密结果; (c)密文用$ \left\{ {{y_i}} \right\} $ 解密结果Fig. 16. Sensitivity of secret key: (a) Original image; (b) error key
$ x_0' $ restoring diagram; (c) error key$ \left\{ {{y_i}} \right\} $ restoring diagram.
图 17 加密解密图像直方图 (a)鸟(256 × 256)原图与明文直方图; (b)鸟(256 × 256)加密图和密图直方图; (c)辣椒(256 × 256)原图与明文直方图; (d)辣椒(256 × 256)加密图和密图直方图; (e) Lena(512 × 512)原图与明文直方图; (f) Lena(512 × 512)加密图和密图直方图; (g)水滴泼洒(512 × 512)原图与明文直方图; (h)水滴泼洒(512 × 512)加密图和密图直方图; (i)机场(1024 × 1024)原图与明文直方图; (j)机场(1024 × 1024)加密图和密图直方图; (k)飞机(1024 × 1024)原图与明文直方图; (l)飞机(1024 × 1024)加密图和密图直方图
Fig. 17. Histograms of plain images and ciphered images: (a) Original image and histogram of bird (256 × 256); (b)cipher image and histogram of bird (256 × 256); (c) original image and histogram of pepper (256 × 256); (d) cipher image and histogram of pepper(256 × 256); (e) original image and histogram of Lena (512 × 512); (f) cipher image and histogram of Lena (512 × 512); (g) original image and histogram of splash (512 × 512); (h) cipher image and histogram of splash (512 × 512); (i) original image and histogram of airport (1024 × 1024); (j) cipher image and histogram of airport (1024 × 1024); (k) original image and histogram of airplane (1024 × 1024); (l) cipher image and histogram of airplane (1024 × 1024).
图 18 Lena图相关性分析 (a)明文; (b)密图
Fig. 18. Correlation coefficients of Lena: (a) Original image; (b) encrypted image
图 19 抗攻击性检验 (a) 10%剪切; (b) 30%剪切; (c) 80%剪切; (d) 0.001高斯白噪声攻击; (e) 0.01高斯白噪声攻击; (f) 0.1高斯白噪声攻击
Fig. 19. Anti attack test: (a) 10% data missed; (b) 30% date missed; (c) 80% data missed; (d) attack of 0.001 Gaussian white noise; (e) attack of 0.01 Gaussian white noise; (f) attack of 0.1 Gaussian white noise.
图 20 全黑全白图加密解密图像
Fig. 20. Encryption and decryption image of all black and all white image.
表 1 新混沌时间序列NIST测试
Table 1. NIST test of the new chotic time series
统计测试 p 值 结果 单比特频率测试 0.8752 通过 块内频率测试 0.8523 通过 游程测试 0.6121 通过 块内最长1游程测试 0.0828 通过 二进制矩阵秩测试 0.1445 通过 离散傅里叶(谱)测试 0.8152 通过 非重叠模板匹配测试 0.3527 通过 重叠模板匹配测试 0.4305 通过 Maurer通用统计测试 0.4214 通过 线性复杂度测试 0.2341 通过 序列测试 0.3053 通过 近似熵测试 0.1568 通过 累加和测试 0.3257 通过 随机旅行测试 0.1523 通过 随机旅行变种测试 0.1057 通过 
下载: 导出CSV
表 2 超混沌Lorenz混沌序列NIST测试
Table 2. NIST test of the hyperchaotic Lorenz time series.
统计测试 p 值 结果 单比特频率测试 0.8815 通过 块内频率测试 0.7253 通过 游程测试 0.5986 通过 块内最长1游程测试 0.0823 通过 二进制矩阵秩测试 0.1263 通过 离散傅里叶(谱)测试 0.8164 通过 非重叠模板匹配测试 0.3580 通过 重叠模板匹配测试 0.5216 通过 Maurer通用统计测试 0.4418 通过 线性复杂度测试 0.5052 通过 序列测试 0.6015 通过 近似熵测试 0.1435 通过 累加和测试 0.4863 通过 随机旅行测试 0.3997 通过 随机旅行变种测试 0.2265 通过
下载: 导出CSV
表 3 混沌信号统计参数对比
Table 3. Comparison of statistical parameters of chaotic signals.
信号来源 最大Lyapunov
指数0-1
测试功率谱
分析相图 NIST
测试超混沌Lorenz 0.3381[52] 0.7937 混沌 混沌 随机 深度学习 2.6002 0.9250 混沌 混沌 随机
下载: 导出CSV
表 4 NPCR和UACI
Table 4. NPCR and UACI.
图片 改变$ P(256, 256) $ NPCR/% UACI/% Bird ($ 256 \times 256 $) 99.56 33.35 Cameraman ($ 256 \times 256 $) 99.63 33.30 Pepper ($ 256 \times 256 $) 99.62 33.39 House ($ 256 \times 256 $) 99.63 33.37 Lena ($ 512 \times 512 $) 99.58 33.38 Airplane ($ 512 \times 512 $) 99.59 33.42 Tank ($ 512 \times 512 $) 99.61 33.49 Splash ($ 512 \times 512 $) 99.64 33.54 Truck ($ 512 \times 512 $) 99.60 33.47 Airport ($ 1024 \times 1024 $) 99.62 33.48 Airplane ($ 1024 \times 1024 $) 99.60 33.47
下载: 导出CSV
表 5 NPCR和UACI的平均值与其他加密算法的比较
Table 5. The average of NPCR and UACI and comparison with other algorithms.
下载: 导出CSV
表 6 图像相关系数
Table 6. Correlation coefficients of images.
图片 明文 密文 水平 垂直 对角 反对角 水平 垂直 对角 反对角 Lena 0.9844 0.9668 0.9620 0.9790 –0.0016 0.0014 –0.0014 –0.0010 Bird 0.9889 0.9826 0.9713 0.9519 0.0114 0.0103 0.0104 –0.0031 Cameraman 0.9591 0.9335 0.9101 0.9377 –0.0099 0.0141 –0.0165 –0.0028 Pepper 0.9638 0.9585 0.9368 0.9339 –0.0127 –0.0014 –0.0079 0.0134 Airport 0.9066 0.9072 0.8446 0.8752 –0.0091 0.0088 –0.0014 –0.0054 Splash 0.9925 0.9850 0.9797 0.9507 0.0082 0.0016 0.0039 –0.0060 Airplane 0.9476 0.9664 0.9418 0.9299 –0.0278 –0.0105 0.0013 –0.0083 House 0.9549 0.9780 0.9399 0.9027 0.0141 –0.0115 –0.0176 0.0005 Tank 0.8678 0.8815 0.8414 0.7949 –0.0036 0.0003 –0.0098 –0.0065 Truck 0.9258 0.9561 0.9114 0.8194 0.0028 –0.0041 0.0018 0.0074
下载: 导出CSV
表 8 信息熵
Table 8. Information entropy of images.
图片 图片大小 信息熵 House $ 256 \times 256 $ 7.9969 Cameraman $ 256 \times 256 $ 7.9971 Bird $ 256 \times 256 $ 7.9968 Pepper $ 256 \times 256 $ 7.9971 Lena $ 512 \times 512 $ 7.9993 Splash $ 512 \times 512 $ 7.9993 Airplane $ 512 \times 512 $ 7.9993 Tank $ 512 \times 512 $ 7.9994 Truck $ 512 \times 512 $ 7.9993 Airport $ 1024 \times 1024 $ 7.9998 Airplane $ 1024 \times 1024 $ 7.9998
下载: 导出CSV
表 9 全黑全白图的统计分析
Table 9. The statistical analysis of all-black image and all-white image.
NPCR UACI 信息熵 相关系数 水平 垂直 对角 全黑图 0.9958 0.3332 7.9970 0.0016 0.0003 0.0036 全白图 0.9961 0.3351 7.9971 0.0070 0.0004 0.0070
下载: 导出CSV
-
[1] Wang X Y, Teng L, Qin X 2012 Signal Pro. 92 1101
Google Scholar
[2] Liu W H, Sun K H, Zhu C X 2016 Optics Lasers Eng. 84 26
Google Scholar
[3] Wu X J, Kan H C, Kurths J 2015 Appl. Soft Comput. 37 24
Google Scholar
[4] Hua Z Y, Zhou Y C, Pun C M, Chen C. L. P 2015 Inf. Sci. 297 80
Google Scholar
[5] 郑洪英, 李琳, 肖迪 2021 信息网络安全 21 10
Google Scholar
Zheng H Y, Li L, Xiao D 2021 Net Inf. Security 21 10
Google Scholar
[6] Dharavathu K, Mosa A 2020 Int. J. Commun. Syst. 33 e4369
[7] Zhao J F, Wang S Y, Chang Y X, Li X F 2015 Nonlinear Dyn. 80 1721
Google Scholar
[8] Khan M 2015 Nonlinear Dyn. 82 527
Google Scholar
[9] Chai X L, Gan Z H, Yuan K, Yang L Chen Y R 2017 Chin. Phys. B 26 020504
Google Scholar
[10] Chai X L, Fu J Y, Zhang J T, Han D J, Gan Z H 2021 Neural Comput. Appl. 33 10271
Google Scholar
[11] Ran Q W, Yuan L, Zhao T Y 2015 Opt. Commun. 348 43
Google Scholar
[12] Kaur M, Kumar V 2018 Int. J. Bifurcat. Chaos 28 1850132
Google Scholar
[13] Yasser I, Khalifa F, Mohamed M A, Samrah A S 2020 Complexity 2020 9597619
Google Scholar
[14] Wu J H, Liao X F, Yang B 2017 Signal Pro. 141 109
Google Scholar
[15] Wang X Y, Feng L, Zhao H Y 2019 Inf. Sci. 486 340
Google Scholar
[16] Wang X Y, Li Z M 2019 Optics Lasers Engin. 115 107
Google Scholar
[17] Zhang Y 2018 Multimed. Tools Appl. 77 21589
Google Scholar
[18] Bansal R, Gupta S, Sharma G 2017 Multimed. Tools. Appl. 76 16529
Google Scholar
[19] Hua Z Y, Zhou Y C, Huang H J 2019 Inf. Sci. 480 403
Google Scholar
[20] Wang X Y, Yang J J 2021 Inf. Sci. 569 217
Google Scholar
[21] Mandal M K, Kar M, Singh S K, Barnwal V K 2014 Secur. Commun. Netw. 7 2145
Google Scholar
[22] Wang X Y, Gao S 2020 Inf. Sci. 539 195
Google Scholar
[23] Wang M X, Wang X Y, Zhao T T, Zhang C, Xia Z Q, Yao N M 2021 Inf. Sci. 544 1
Google Scholar
[24] Wang X Y, Wang T, Xu D H, Chen F 2014 Int. J. Modern Phys. B 28 1450023
Google Scholar
[25] Zhou S, Wang X Y, Wang M X, Zhang Y Q 2020 Chaos Solitons & Fract. 141 110225
Google Scholar
[26] Wang X Y, Gao S 2020 Inf. Sci. 507 16
Google Scholar
[27] Wang X Y, Liu C, Jiang D H 2021 Inf. Sci. 574 505
Google Scholar
[28] Zhang Y Q, Wang X Y 2015 Appl. Soft Comput. 26 10
Google Scholar
[29] Zhang Y Q, Jia Y R, Wang X Y, Niu Q, Chen N D 2020 IEEE Access 8 213296
Google Scholar
[30] He Y, Zhang Y Q, Wang X Y 2020 Neural Comput. Appl. 32 247
Google Scholar
[31] Zhang Y Q, Wang X Y, Liu L Y, Liu J 2018 Int. J. Bifurcat. Chaos 28 1850020
Google Scholar
[32] Zhang Y Q, He Y, Wang X Y 2018 Physica A 490 148
Google Scholar
[33] Zhou S, Wang X Y, Zhang Y Q, Ge B, Wang M X, Gao S 2021 Multimed. Syst. (Published Online)
Google Scholar
[34] 张勇 2016 混沌数字图像加密 (北京: 清华大学出版社) 第106—205页
Zhang Y 2016 Chaotic Digital Image Cryptosystem (Beijing: Tsinghua University Press) pp106–205 (in Chinese)
[35] 刘树堂, 孙福艳 2009 中国科学(G辑: 物理学 力学 天文学) 39 387
Liu S T, Sun F Y 2009 Sci. Sin-Phys. Mech. Astron. 39 387
[36] May R M 1976 Nature 261 459
Google Scholar
[37] Kanso A 2011 Commun. Nonlinear Sci. Numer. Simul. 16 822
Google Scholar
[38] Chinese) [李石磊, 刘崇新, 胡晓宇, 倪骏康 2017 西安交通大学学报 51 35
Li S L, Liu C X, Hu X Y, Ni J K 2017 J. Xi'an Jiaotong Univ. 51 35 (in
[39] Kaneko K 1989 Physica D 34 1
Google Scholar
[40] Sinha S 2002 Phys. Rev. E 66 016209
Google Scholar
[41] Zhang Y Q 2015 Ph. D. Dissertation (Dalian: Dalian University of Technology) (in Chinese)
[42] 石航, 王丽丹 2019 68 200501
Google Scholar
Shi H, Wang L D 2019 Acta Phys. Sin. 68 200501
Google Scholar
[43] 庄志本, 李军, 刘静漪, 陈世强 2020 69 040502
Google Scholar
Zhuang Z B, Li J, Liu J Y, Chen S Q 2020 Acta Phys. Sin. 69 040502
Google Scholar
[44] Zhang Q, Wei X P 2013 IETE Techn. Re. 30 404
[45] Zhang Y Q, Wang X Y 2014 Inf. Sci. 273 329
Google Scholar
[46] 陈炜, 郭媛, 敬世伟 2020 69 240502
Google Scholar
Chen W, Guo Y, Jing S W 2020 Acta Phys. Sin. 69 240502
Google Scholar
[47] He Y, Zhang Y Q, He X, Wang X Y 2021 Sci. Rep. 11 6398
Google Scholar
[48] 葛钊成, 胡汉平 2021 密码学报 8 215
Google Scholar
Ge Z C, Hu H P 2021 Cryptol. Res. 8 215
Google Scholar
[49] 熊有成, 赵鸿 2019 中国科学: 物理学 力学 天文学 49 92
Google Scholar
Xiong Y C, Zhao H 2019 Sci. Sin-Phys. Mech. Astron. 49 92
Google Scholar
[50] Sangiorgio M, Dercole F 2020 Chaos, Solitons Fract. 139 110045
Google Scholar
[51] 黄伟建, 李永涛, 黄远 2021 70 010501
Google Scholar
Huang W J, Li Y T, Huang Y 2021 Acta Phys. Sin. 70 010501
Google Scholar
[52] 王兴元, 王明军 2007 56 5136
Google Scholar
Wang X Y, Wang M J 2007 Acta Phys. Sin. 56 5136
Google Scholar
[53] Hochreiter S, Schmidhuber J 1997 Neural Comput. 9 1735
Google Scholar
[54] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Phys. D:Nonlinear Phenomena 16 285
Google Scholar
[55] Gottwald G A, Melbourne I 2009 SIAM J. Appl. Dyn. Syst. 8 129
Google Scholar
[56] Gottwald G A, Melbourne I 2004 P. Roy. Soc. A-Math. Phy. 460 603
Google Scholar
[57] Wu Y, Noonan J P, Agaian S 2011 Cyber J. 1 31
[58] Nepomuceno E G, Nardo L G, Arias-Garcia J, Butusov D N, Tutueva A 2019 Chaos 29 061101
Google Scholar
[59] Zhou M J, Wang C H 2020 Signal Pro. 171 107484
Google Scholar
[60] Xian Y J, Wang X Y 2021 Inf. Sci. 547 1154
Google Scholar
[61] Wang X Y, Xue W H, An J B 2020 Chaos, Solitons Fract. 141 110309
Google Scholar
[62] Boriga R, Dăscălescu A C, Priescu I 2014 Signal Processing: Image Communication 29 887
[63] Abolfazl Y N, Mohammad H M, Masood N T 2017 Optics Lasers Eng. 90 225
Google Scholar
下载:
计量
- 文章访问数: 10647
- PDF下载量: 403
- 被引次数: 0
