-
The max-cut problem (MCP) is a classic problem in the field of combinatorial optimization and has important applications in various fields, including statistical physics and image processing. However, except for some special cases, the MCP still encounters a non-deterministic polynomial complete problem (an NP-complete problem), and there is currently no known efficient classical algorithm that can solve it in polynomial time. The quantum approximate optimization algorithm (QAOA), as a pivotal algorithm in the noisy intermediate-scale quantum (NISQ) computing era, has shown significant potential for solving the MCP. However, due to the lack of quantum error correction, the reliability of computations in NISQ systems sharply declines as the circuit depth of the algorithm increases. Therefore, designing an efficient, shallow-depth, and low-complexity QAOA for the MCP is a critical challenge in demonstrating the advantages of quantum computing in the NISQ era.In this paper, according to the standard QAOA algorithm, we introduce Pauli Y rotation gates into the target Hamiltonian circuit for the MCP. By enhancing the flexibility of quantum trial functions and improving the efficiency of Hilbert space exploration within a single iteration, we significantly improve the performance of QAOA on the MCP.We conduct extensive numerical simulations using the MindSpore quantum platform, and compare the proposed RY-layer-assisted QAOA with standard QAOA and its existing variants, including MA-QAOA and QAOA+. The experiments are performed on various graph types, including complete graphs, 3-regular graphs, 4-regular graphs, and random graphs with edge probabilities between 0.3 and 0.5. Our results show that the RY-layer-assisted QAOA achieves higher approximation ratios in all graph types, particularly in regular and random graphs, where traditional QAOA variants are difficult to implement. Moreover, the proposed method exhibits strong robustness as the graph size increases, and can maintain high performance even for larger graphs. Importantly, the RY-layer-assisted QAOA requires fewer CNOT gates and has a lower circuit depth than the standard QAOA and its variants, making it more suitable for NISQ devices with limited coherence times and high error rates.In conclusion, the RY-layer-assisted QAOA provides a promising approach for solving MCP in the NISQ era. By improving the approximation ratio while reducing circuit complexity, this method demonstrates significant potential for practical quantum computing applications, thus paving the way for developing more efficient and reliable quantum optimization algorithms.
-
Keywords:
- quantum approximate optimization algorithm /
- max-cut /
- quantum computing /
- quantum circuit
[1] Adjiman C S, Schweiger C A, Floudas C A1998 Mixed-Integer Nonlinear Optimization in Process Synthesis // Du D Z, Pardalos P M Handbook of Combinatorial Optimization (Boston: Springer) pp1–12
[2] Håstad J 2001 JACM 48 798
Google Scholar
[3] Goemans M X, Williamson D P 1995 JACM 42 1115
Google Scholar
[4] Preskill J 2018 Quantum 2 79
Google Scholar
[5] Cruz D, Fournier R, Gremion F, et al. 2019 Adv. Quantum Technol. 2 1900015
Google Scholar
[6] Zhang J, Hegde S S, Suter D 2020 Phys. Rev. Lett. 125 030501
Google Scholar
[7] Wernsdorfer W, Godfrin C, Balestro F 2019 Bulletin of the American Physical Society Boston, USA, pS36
[8] Borle A, Elfving V, Lomonaco S J 2021 SciPost Phys. Core 4 031
Google Scholar
[9] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [quant-ph]
[10] Guerreschi G G, Matsuura A Y 2019 Sci. Rep. 9 6903
Google Scholar
[11] Herrman R, Ostrowski J, Humble T S, Siopsis G 2021 Quantum Inf. Process. 20 1
Google Scholar
[12] Wurtz J, Lykov D 2021 Phys. Rev. A 104 052419
Google Scholar
[13] Akshay V, Philathong H, Morales M E, Biamonte J D 2020 Phys. Rev. Lett. 124 090504
Google Scholar
[14] Wurtz J, Love P 2021 Phys. Rev. A 103 042612
Google Scholar
[15] Farhi E, Gamarnik D, Gutmann S 2020 arXiv: 2005.08747 [quant-ph]
[16] Xue C, Chen Z Y, Wu Y C, Guo G P 2021 Chin. Phys. Lett. 38 030302
Google Scholar
[17] Wang S, Fontana E, Cerezo M, Sharma K, Sone A, Cincio L, Coles P J 2021 Nat. Commun. 12 6961
Google Scholar
[18] Marshall J, Wudarski F, Hadfield S, Hogg T 2020 IOPSN 1 025208
Google Scholar
[19] Alam M, Ash-Saki A, Ghosh S 2019 arXiv: 1907.09631[quant-ph]
[20] Chandarana P, Hegade N N, Paul K, Albarrán-Arriagada F, Solano E, Del Campo A, Chen X 2022 Phys. Rev. Res. 4 013141
Google Scholar
[21] Magann A B, Rudinger K M, Grace M D, Sarovar M 2022 Phys. Rev. Lett. 129 250502
Google Scholar
[22] Chalupnik M, Melo H, Alexeev Y, Galda A 2022 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) Broomfield, USA, Sept. 18–23, 2022 p97
[23] Sun Z H, Wang Y Y, Cui J, Fan H 2023 NJP 25 013015
Google Scholar
[24] Wurtz J, Love P J 2021 TQE 2 1
Google Scholar
[25] Wang Z D, Zheng P L, Wu B, Zhang Y 2023 Phys. Rev. Research 5 023171
Google Scholar
[26] Herrman R, Lotshaw P C, Ostrowski J, Humble T S, Siopsis G 2022 Sci. Rep. 12 6781
Google Scholar
[27] Xu X, Cui J, Cui Z, et al. 2024 arXiv: 2406.17248[quant-ph]
[28] AbuGhanem M 2024 arXiv: 2410.00916[quant-ph]
-
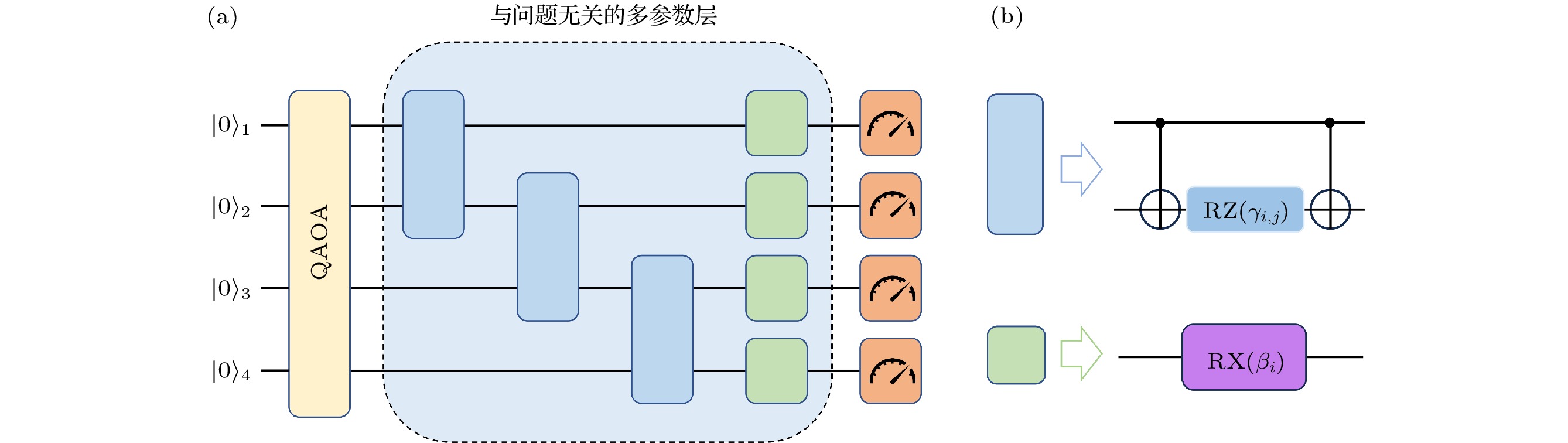
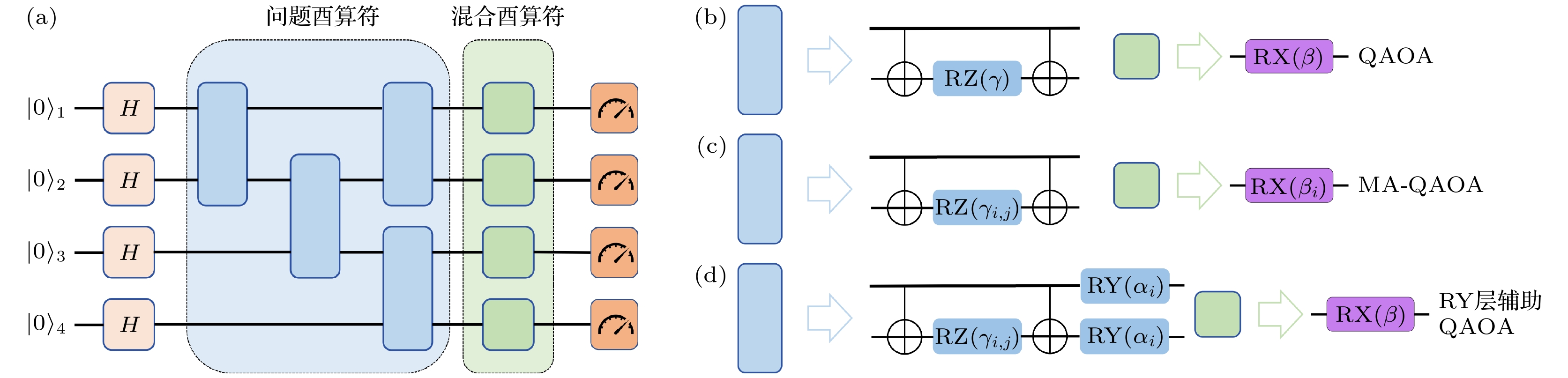
图 1 (a) 由问题酉算符和混合酉算符构成的单层QAOA量子线路框图; (b)标准QAOA的问题酉算符(蓝色)和混合酉算符(紫色)的分解; (c) MA-QAOA问题酉算符(蓝色)和混合酉算符(紫色)的分解; (d) RY层辅助QAOA问题酉算符(蓝色)和混合酉算符(紫色)的分解
Figure 1. (a) Single-layer QAOA quantum circuit diagram composed of problem and mixing operators; (b) decomposition of the problem operator (blue) and mixing operator (purple) in standard QAOA; (c) decomposition of the problem operator (blue) and mixing operator (purple) in MA-QAOA; (d) decomposition of the problem operator (blue) and mixing operator (purple) in RY-layer-assisted QAOA
图 3 实验采用的四类图 (a)完全图; (b) 3-正则图; (c) 4-正则图; (d)边概率在0.3—0.5之间的随机图
Figure 3. The four types of graphs adopted in the experiments: (a) Complete graphs; (b) 3-regular graphs; (c) 4-regular graphs; (d) random graphs with edge probabilities between 0.3 and 0.5
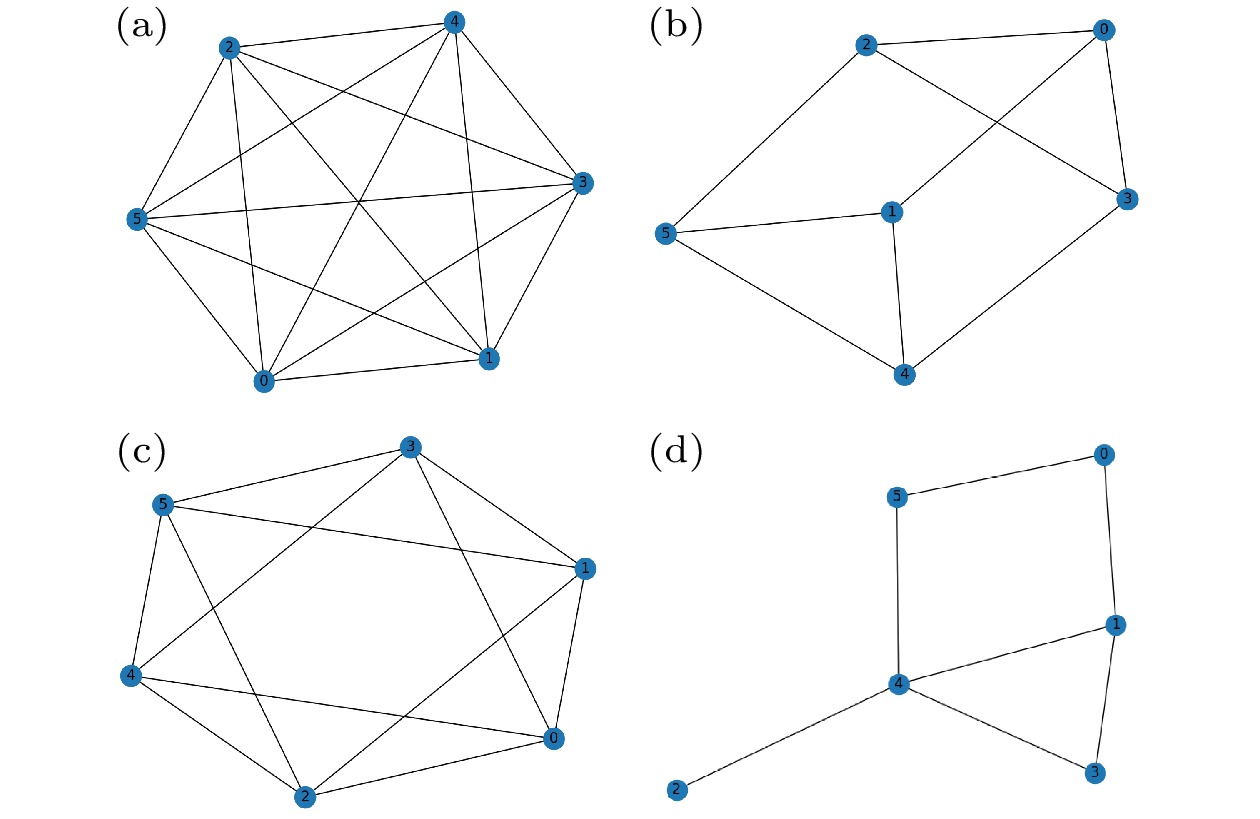
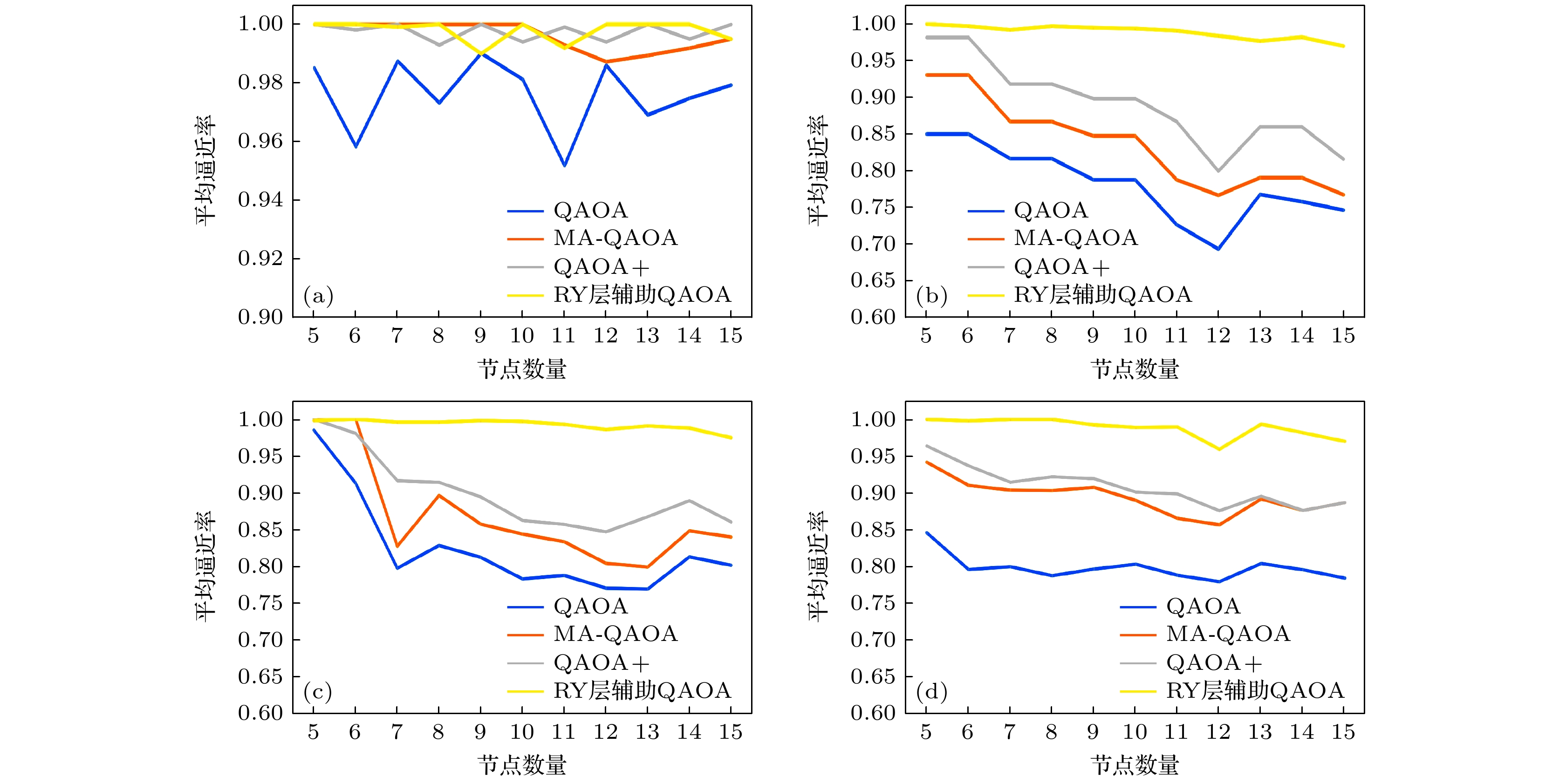
图 4 单层QAOA, MA-QAOA, QAOA+和RY层辅助QAOA分别在四类图上的平均逼近率 (a)完全图; (b) 3-regular图; (c) 4-regular图; (d)随机图. 这里的问题图由NetworkX库随机生成
Figure 4. Average approximation ratios of single-layer QAOA, MA-QAOA, QAOA+, and RY-layer-assisted QAOA on the four types of graphs: (a) Complete graphs; (b) 3-regular graphs; (c) 4-regular graphs; (d) random graphs. The problem instances are randomly generated using the NetworkX library
图 5 标准QAOA(包括单层和双层)及其各变体在8节点各类型图上的资源消耗及性能表现
Figure 5. Resource consumption and performance of standard QAOA (including single-layer and double-layer) and its variants on 8-node graphs of various types.
图 6 噪声条件下, 标准QAOA(双层)及RY层辅助QAOA在5—10节点4-正则图上的平均逼近率
Figure 6. Average approximation ratios of standard QAOA (two-layer) and RY-layer-assisted QAOA on 4-regular graphs with 5 to 10 nodes under noisy conditions.
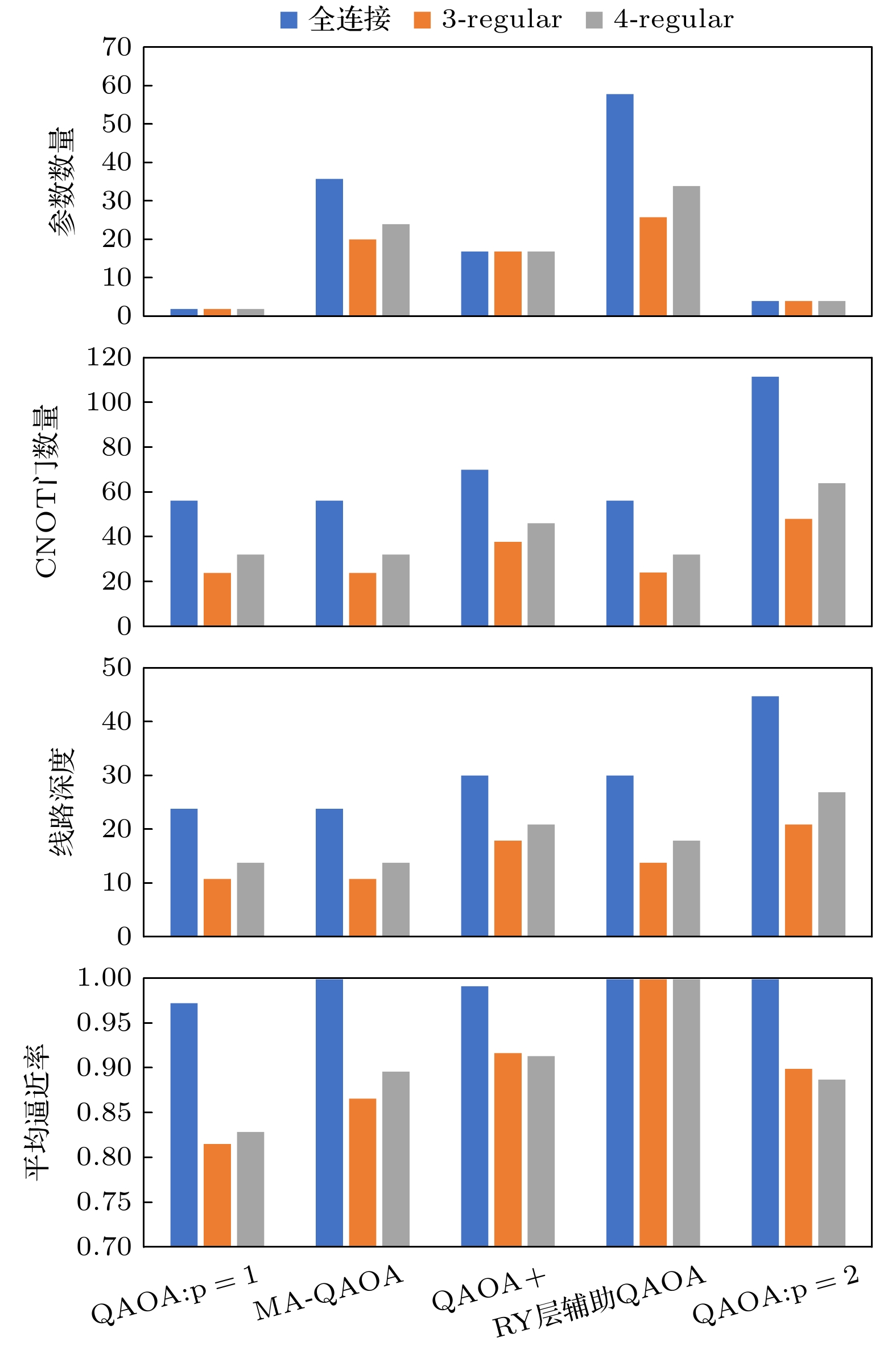
表 1 100个8节点随机问题图上, 各变体达到0.9的逼近率需要的平均线路深度、参数数量及CNOT门数
Table 1. The average circuit depth, number of parameters, and number of CNOT gates required for each variant to achieve an approximation ratio of 0.9 on 100 random 8-node problem graphs.
变体 线路深度 参数数量 CNOT门数量 QAOA 61.09 7.54 104.96 MA-QAOA 31.76 84.61 53.73 QAOA+ 50.09 38.52 89.54 RY层辅助QAOA 21.92 29.84 27.84 
DownLoad: CSV
-
[1] Adjiman C S, Schweiger C A, Floudas C A1998 Mixed-Integer Nonlinear Optimization in Process Synthesis // Du D Z, Pardalos P M Handbook of Combinatorial Optimization (Boston: Springer) pp1–12
[2] Håstad J 2001 JACM 48 798
Google Scholar
[3] Goemans M X, Williamson D P 1995 JACM 42 1115
Google Scholar
[4] Preskill J 2018 Quantum 2 79
Google Scholar
[5] Cruz D, Fournier R, Gremion F, et al. 2019 Adv. Quantum Technol. 2 1900015
Google Scholar
[6] Zhang J, Hegde S S, Suter D 2020 Phys. Rev. Lett. 125 030501
Google Scholar
[7] Wernsdorfer W, Godfrin C, Balestro F 2019 Bulletin of the American Physical Society Boston, USA, pS36
[8] Borle A, Elfving V, Lomonaco S J 2021 SciPost Phys. Core 4 031
Google Scholar
[9] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [quant-ph]
[10] Guerreschi G G, Matsuura A Y 2019 Sci. Rep. 9 6903
Google Scholar
[11] Herrman R, Ostrowski J, Humble T S, Siopsis G 2021 Quantum Inf. Process. 20 1
Google Scholar
[12] Wurtz J, Lykov D 2021 Phys. Rev. A 104 052419
Google Scholar
[13] Akshay V, Philathong H, Morales M E, Biamonte J D 2020 Phys. Rev. Lett. 124 090504
Google Scholar
[14] Wurtz J, Love P 2021 Phys. Rev. A 103 042612
Google Scholar
[15] Farhi E, Gamarnik D, Gutmann S 2020 arXiv: 2005.08747 [quant-ph]
[16] Xue C, Chen Z Y, Wu Y C, Guo G P 2021 Chin. Phys. Lett. 38 030302
Google Scholar
[17] Wang S, Fontana E, Cerezo M, Sharma K, Sone A, Cincio L, Coles P J 2021 Nat. Commun. 12 6961
Google Scholar
[18] Marshall J, Wudarski F, Hadfield S, Hogg T 2020 IOPSN 1 025208
Google Scholar
[19] Alam M, Ash-Saki A, Ghosh S 2019 arXiv: 1907.09631[quant-ph]
[20] Chandarana P, Hegade N N, Paul K, Albarrán-Arriagada F, Solano E, Del Campo A, Chen X 2022 Phys. Rev. Res. 4 013141
Google Scholar
[21] Magann A B, Rudinger K M, Grace M D, Sarovar M 2022 Phys. Rev. Lett. 129 250502
Google Scholar
[22] Chalupnik M, Melo H, Alexeev Y, Galda A 2022 2022 IEEE International Conference on Quantum Computing and Engineering (QCE) Broomfield, USA, Sept. 18–23, 2022 p97
[23] Sun Z H, Wang Y Y, Cui J, Fan H 2023 NJP 25 013015
Google Scholar
[24] Wurtz J, Love P J 2021 TQE 2 1
Google Scholar
[25] Wang Z D, Zheng P L, Wu B, Zhang Y 2023 Phys. Rev. Research 5 023171
Google Scholar
[26] Herrman R, Lotshaw P C, Ostrowski J, Humble T S, Siopsis G 2022 Sci. Rep. 12 6781
Google Scholar
[27] Xu X, Cui J, Cui Z, et al. 2024 arXiv: 2406.17248[quant-ph]
[28] AbuGhanem M 2024 arXiv: 2410.00916[quant-ph]
DownLoad:
Catalog
Metrics
- Abstract views: 407
- PDF Downloads: 15
- Cited By: 0
