Non-abelian statistics of Majorana modes and the applications to topological quantum computation

He Ying-Ping; Hong Jian-Song; Liu Xiong-Jun

doi:10.7498/aps.69.20200812

Abstract

Since their prediction as fundamental particles in 1937, Majorana fermions have drawn lots of interests in particle physics and dark matter. Their counterparts in condensed matter physics, Majorana zero-Modes (MZMs), have attracted remarkable attention in condensed matter for their potential in building a fault-tolerant quantum computer. Due to the relentless effort, lots of important progress has been made in Majorana physics in the past two decades, as introduced in several excellent review articles. This review focuses on the non-Abelian statistics of MZMs and their application to quantum computation. In the first section of this work, the theoretical progress in searching for MZM is briefly reviewed and the latest experimental progresses are summarized. We next introduce the basic concepts of non-Abelian statistics of MZMs and explain how they can be applied to quantum computation. We then discuss two key experiments to implementing quantum computers in the MZM platform: MZM braiding and MZM qubit readout. In this part, several representative proposals for the Majorana braiding and MZM qubit readout are elaborated. Finally, we introduce a latest concept, the symmetry-protected non-Abelian braiding of Majorana Kramers pairs in time-reversal invariant topological superconductors.

Keywords:

Authors and contacts

1.
International Center for Quantum Materials, School of Physics, Peking University, Beijing 100871, China
2.
Collaborative Innovation Center of Quantum Matter, Beijing 100871, China
3.
Beijing Academy of Quantum Information Science, Beijing 100193, China
4.
CAS Center for Excellence in Topological Quantum Computation, University of Chinese Academy of Sciences, Beijing 100190, China

Corresponding author: Liu Xiong-Jun, xiongjunliu@pku.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11825401, 11761161003, 11921005), the Major Project of the Ministry of Science and Technology of China (Grant No. 2016 YFA0301604), and the Strategic Priority Research Program of Chinese Academy of Sciences, China (Grant No. XDB28000000)

FullText HTML

References

[1]	Majorana E 1937 Nuovo Cim. 14 171 Google Scholar
[2]	Schechter J, Valle J W F 1982 Phys. Rev. D 25 2951 Google Scholar
[3]	Keung W Y, Senjanović G 1983 Phys. Rev. Lett. 50 1427 Google Scholar
[4]	Atre A, Han T, Pascoli S, Zhang B 2009 J. High Energy Phys. 2009 030 Google Scholar
[5]	Rodejohann W 2011 Inter. J. Mod. Phys. E 20 1833 Google Scholar
[6]	de Gouvêa A, Vogel P 2013 Progress in Particle and Nuclear Physics 71 75 Google Scholar
[7]	Kitaev A Y 2001 Physics-Uspekhi 44 131 Google Scholar
[8]	Alicea J 2012 Rep. Prog. Phys. 75 076501 Google Scholar
[9]	Elliott S R, Franz M 2015 Rev. Mod. Phys. 87 137 Google Scholar
[10]	Leijnse M, Flensberg K 2012 Semiconductor Science and Technology 27 124003 Google Scholar
[11]	Wilczek F 2009 Nature Physics 5 614 Google Scholar
[12]	Franz M 2013 Nat. Nanotechnol. 8 149 Google Scholar
[13]	Read N, Green D 2000 Phys. Rev. B 61 10267 Google Scholar
[14]	Ivanov D A 2001 Phys. Rev. Lett. 86 268 Google Scholar
[15]	Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083 Google Scholar
[16]	Freedman M, Kitaev A, Larsen M, Wang Z 2003 Bulletin of the American Mathematical Society 40 31 Google Scholar
[17]	Das Sarma S, Freedman M, Nayak C 2005 Phys. Rev. Lett. 94 166802 Google Scholar
[18]	Sarma S D, Freedman M, Nayak C 2006 Phys. Today 59 32 Google Scholar
[19]	Kitaev A 2003 Ann. Phys. 303 2 Google Scholar
[20]	Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407 Google Scholar
[21]	Sau J D, Lutchyn R M, Tewari S, Das Sarma S 2010 Phys. Rev. Lett. 104 040502 Google Scholar
[22]	Alicea J 2010 Phys. Rev. B 81 125318 Google Scholar
[23]	Lutchyn R M, Sau J D, Das Sarma S 2010 Phys. Rev. Lett. 105 077001 Google Scholar
[24]	Oreg Y, Refael G, von Oppen F 2010 Phys. Rev. Lett. 105 177002 Google Scholar
[25]	Hosur P, Ghaemi P, Mong R S K, Vishwanath A 2011 Phys. Rev. Lett. 107 097001 Google Scholar
[26]	Pientka F, Keselman A, Berg E, Yacoby A, Stern A, Halperin B I 2017 Phys. Rev. X 7 021032 Google Scholar
[27]	Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 1003 Google Scholar
[28]	Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602 Google Scholar
[29]	Sun H H, Zhang K W, Hu L H, et al. 2016 Phys. Rev. Lett. 116 257003 Google Scholar
[30]	He Q L, Pan L, Stern A L, et al. 2017 Science 357 294 Google Scholar
[31]	Zhang P, Yaji K, Hashimoto T, et al. 2018 Science 360 182 Google Scholar
[32]	Wang D, Kong L, Fan P, Chen H, Zhu S, Liu W, Cao L, Sun Y, Du S, Schneeloch J, Zhong R, Gu G, Fu L, Ding H, Gao H J 2018 Science 362 333 Google Scholar
[33]	Fornieri A, Whiticar A M, Setiawan F, Portolés E, Drachmann A C C, Keselman A, Gronin S, Thomas C, Wang T, Kallaher R, et al. 2019 Nature 569 89 Google Scholar
[34]	Ren H, Pientka F, Hart S, et al. 2019 Nature 569 93 Google Scholar
[35]	Jäck B, Xie Y, Li J, Jeon S, Bernevig B A, Yazdani A 2019 Science 364 1255 Google Scholar
[36]	van Heck B, Akhmerov A R, Hassler F, Burrello M, Beenakker C W J 2012 New J. Phys. 14 035019 Google Scholar
[37]	Aasen D, Hell M, Mishmash R V, Higginbotham A, Danon J, Leijnse M, Jespersen T S, Folk J A, Marcus C M, Flensberg K, Alicea J 2016 Phys. Rev. X 6 031016 Google Scholar
[38]	Vijay S, Fu L 2016 Phys. Rev. B 94 235446 Google Scholar
[39]	Karzig T, Knapp C, Lutchyn R M, Bonderson P, Hastings M B, Nayak C, Alicea J, Flensberg K, Plugge S, Oreg Y, Marcus C M, Freedman M H 2017 Phys. Rev. B 95 235305 Google Scholar
[40]	Schrade C, Fu L 2018. arXiv: 1807.06620 [cond-mat.mes-hall]
[41]	Stern A, Berg E 2019 Phys. Rev. Lett. 122 107701 Google Scholar
[42]	Wang Z 2010 Topological Quantum Computation (Santa Barbara: American Mathematical Soc.)
[43]	Zhang L, Liu X J 2018 Spin-orbit Coupling and Topological Phases for Ultracold Atoms (Chap. 1) (Singapore: World Scientific) pp1–87
[44]	Sau J D, Tewari S, Lutchyn R M, Stanescu T D, Das Sarma S 2010 Phys. Rev. B 82 214509 Google Scholar
[45]	Potter A C, Lee P A 2011 Phys. Rev. B 83 184520 Google Scholar
[46]	Sau J D, Tewari S, Das Sarma S 2012 Phys. Rev. B 85 064512 Google Scholar
[47]	Deng M T, Yu C L, Huang G Y, Larsson M, Caroff P, Xu H Q 2012 Nano Lett. 12 6414 Google Scholar
[48]	Das A, Ronen Y, Most Y, Oreg Y, Heiblum M, Shtrikman H 2012 Nat. Phys. 8 887 Google Scholar
[49]	Finck A D K, Van Harlingen D J, Mohseni P K, Jung K, Li X 2013 Phys. Rev. Lett. 110 126406 Google Scholar
[50]	Churchill H O H, Fatemi V, Grove-Rasmussen K, Deng M T, Caroff P, Xu H Q, Marcus C M 2013 Phys. Rev. B 87 241401 Google Scholar
[51]	Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001 Google Scholar
[52]	Flensberg K 2010 Phys. Rev. B 82 180516 Google Scholar
[53]	Wimmer M, Akhmerov A R, Dahlhaus J P, Beenakker C W J 2011 New J. Phys. 13 053016 Google Scholar
[54]	Lutchyn R M, Bakkers E P A M, Kouwenhoven L P, Krogstrup P, Marcus C M, Oreg Y 2018 Nat. Rev.s Mater. 3 52 Google Scholar
[55]	Liu X J, Lobos A M 2013 Phys. Rev. B 87 060504 Google Scholar
[56]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[57]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[58]	Fu L, Kane C L 2009 Phys. Rev. B 79 161408 Google Scholar
[59]	Scharf B, Pientka F, Ren H, Yacoby A, Hankiewicz E M 2019 Phys. Rev. B 99 214503 Google Scholar
[60]	Setiawan F, Stern A, Berg E 2019 Phys. Rev. B 99 220506 Google Scholar
[61]	Stone M, Roy R 2004 Physical Review B 69 184511 Google Scholar
[62]	Fu L, Kane C L, Mele E J 2007 Phys. Rev. Lett. 98 106803 Google Scholar
[63]	Fu L, Kane C L 2009 Phys. Rev. Lett. 102 216403 Google Scholar
[64]	Akhmerov A R, Nilsson J, Beenakker C W J 2009 Phys. Rev. Lett. 102 216404 Google Scholar
[65]	Tanaka Y, Yokoyama T, Nagaosa N 2009 Phys. Rev. Lett. 103 107002 Google Scholar
[66]	Linder J, Tanaka Y, Yokoyama T, Sudbø A, Nagaosa N 2010 Phys. Rev. B 81 184525 Google Scholar
[67]	Zhang C, Tewari S, Lutchyn R M, Das Sarma S 2008 Phys. Rev. Lett. 101 160401 Google Scholar
[68]	Sato M, Takahashi Y, Fujimoto S 2009 Phys. Rev. Lett. 103 020401 Google Scholar
[69]	Wang M X, Liu C, Xu J P, et al. 2012 Science 336 52 Google Scholar
[70]	He J J, Ng T K, Lee P A, Law K T 2014 Phys. Rev. Lett. 112 037001 Google Scholar
[71]	Xu J P, Liu C, Wang M X, Ge J, Liu Z L, Yang X, Chen Y, Liu Y, Xu Z A, Gao C L, Qian D, Zhang F C, Jia J F 2014 Phys. Rev. Lett. 112 217001 Google Scholar
[72]	Xu J P, Wang M X, Liu Z L, Ge J F, Yang X, Liu C, Xu Z A, Guan D, Gao C L, Qian D, Liu Y, Wang Q H, Zhang F C, Xue Q K, Jia J F 2015 Phys. Rev. Lett. 114 017001 Google Scholar
[73]	Wang Z, Zhang P, Xu G, Zeng L K, Miao H, Xu X, Qian T, Weng H, Richard P, Fedorov A V, Ding H, Dai X, Fang Z 2015 Phys. Rev. B 92 115119 Google Scholar
[74]	Xu G, Lian B, Tang P, Qi X L, Zhang S C 2016 Phys. Rev. Lett. 117 047001 Google Scholar
[75]	Kong L, Zhu S, Papaj M, et al. 2019 Nat. Phys. 15 1181 Google Scholar
[76]	König E J, Coleman P 2019 Phys. Rev. Lett. 122 207001 Google Scholar
[77]	Zhang P, Wang Z, Wu X, Yaji K, Ishida Y, Kohama Y, Dai G, Sun Y, Bareille C, Kuroda K, et al. 2018 Nat. Phys. 15 41 Google Scholar
[78]	Zhou X, Gordon K N, Jin K H, Li H, Narayan D, Zhao H, Zheng H, Huang H, Cao G, Zhigadlo N D, Liu F, Dessau D S 2019 Phys. Rev. B 100 184511 Google Scholar
[79]	Machida T, Sun Y, Pyon S, Takeda S, Kohsaka Y, Hanaguri T, Sasagawa T, Tamegai T 2019 Nat. Mater. 18 811 Google Scholar
[80]	Yan Z, Bi R, Wang Z 2017 Phys. Rev. Lett. 118 147003 Google Scholar
[81]	Chan C, Zhang L, Poon T F J, He Y P, Wang Y Q, Liu X J 2017 Phys. Rev. Lett. 119 047001 Google Scholar
[82]	Teo J C Y, Kane C L 2010 Phys. Rev. B 82 115120 Google Scholar
[83]	Chan C, Liu X J 2017 Phys. Rev. Lett. 118 207002 Google Scholar
[84]	Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 82 184516 Google Scholar
[85]	Chung S B, Qi X L, Maciejko J, Zhang S C 2011 Phys. Rev. B 83 100512 Google Scholar
[86]	Wang J, Zhou Q, Lian B, Zhang S C 2015 Phys. Rev. B 92 064520 Google Scholar
[87]	Lian B, Wang J, Zhang S C 2016 Phys. Rev. B 93 161401 Google Scholar
[88]	Kayyalha M, Xiao D, Zhang R, Shin J, Jiang J, Wang F, Zhao Y F, Xiao R, Zhang L, Fijalkowski K M, Mandal P, Winnerlein M, Gould C, Li Q, Molenkamp L W, Chan M H W, Samarth N, Chang C Z 2020 Science 367 64 Google Scholar
[89]	Deng M T, Vaitiekenas S, Hansen E B, Danon J, Leijnse M, Flensberg K, Nygård J, Krogstrup P, Marcus C M 2016 Science 354 1557 Google Scholar
[90]	Nichele F, Drachmann A C, Whiticar A M, et al. 2017 Phys. Rev. Lett. 119 136803 Google Scholar
[91]	Gül O, Zhang H, Bommer J D S, et al. 2018 Nat. Nanotechnol. 13 192 Google Scholar
[92]	Feldman B E, Randeria M T, Li J, Jeon S, Xie Y, Wang Z, Drozdov I K, Bernevig B A, Yazdani A 2017 Nat. Phys. 13 286 Google Scholar
[93]	Jeon S, Xie Y, Li J, Wang Z, Bernevig B A, Yazdani A 2017 Science 358 772 Google Scholar
[94]	Laroche D, Bouman D, van Woerkom D J, et al. 2019 Nat. Commun. 10 245 Google Scholar
[95]	Rokhinson L P, Liu X, Furdyna J K 2012 Nat. Phys. 8 795 Google Scholar
[96]	Beenakker C W J 2019. arXiv: 1907.06497 [cond-mat]
[97]	Bonderson P, Gurarie V, Nayak C 2011 Phys. Rev. B 83 075303 Google Scholar
[98]	Teo J C Y, Kane C L 2010 Phys. Rev. Lett. 104 046401 Google Scholar
[99]	Freedman M, Hastings M B, Nayak C, Qi X L, Walker K, Wang Z 2011 Phys. Rev. B 83 115132 Google Scholar
[100]	Freedman M, Hastings M B, Nayak C, Qi X L 2011 Phys. Rev. B 84 245119 Google Scholar
[101]	Alicea J, Oreg Y, Refael G, von Oppen F, Fisher M P A 2011 Nat. Phys. 7 412 Google Scholar
[102]	Feynman R P 1982 Intern. J. Theoretical Phys. 21 467 Google Scholar
[103]	Shor P W 1994 In Proceedings 35th Annual Symposium on Foundations of Computer Science (Ieee), pp124–134
[104]	Grover L K 1997 Phys. Rev. Lett. 79 325 Google Scholar
[105]	Lloyd S 1996 Science 273 1073 Google Scholar
[106]	Deutsch D 1985 Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 400 97 Google Scholar
[107]	Lo H K, Spiller T, Popescu S 1998 Introduction to quantum computation and information (World Scientific)
[108]	DiVincenzo D P 2000 Fortschritte der Physik: Progress of Physics 48 771 Google Scholar
[109]	Sarma S D, Freedman M, Nayak C 2015 npj Quantum Information 1 15001 Google Scholar
[110]	Lahtinen V, Pachos J 2017 SciPost Physics 3 021 Google Scholar
[111]	Kitaev A Y 1997 Uspekhi Matematicheskikh Nauk 52 53 Google Scholar
[112]	Dawson C M, Nielsen M A 2005. arXiv: 0505030 [quant-ph]
[113]	Bravyi S, Kitaev A 2005 Phys. Rev. A 71 022316 Google Scholar
[114]	Bravyi S 2006 Phys. Rev. A 73 042313 Google Scholar
[115]	Freedman M, Nayak C, Walker K 2006 Phys. Rev. B 73 245307 Google Scholar
[116]	Bonderson P, Clarke D J, Nayak C, Shtengel K 2010 Phys. Rev. Lett. 104 180505 Google Scholar
[117]	Karzig T, Oreg Y, Refael G, Freedman M H 2016 Phys. Rev. X 6 031019 Google Scholar
[118]	Cheng M, Galitski V, Das Sarma S 2011 Phys. Rev. B 84 104529 Google Scholar
[119]	Bauer B, Karzig T, Mishmash R, Antipov A, Alicea J 2018 Sci. Post Phys. 5 004 Google Scholar
[120]	Sau J D, Clarke D J, Tewari S 2011 Phys. Rev. B 84 094505 Google Scholar
[121]	Clarke D J, Sau J D, Tewari S 2011 Phys. Rev. B 84 035120 Google Scholar
[122]	Halperin B I, Oreg Y, Stern A, Refael G, Alicea J, von Oppen F 2012 Phys. Rev. B 85 144501 Google Scholar
[123]	Amorim C S, Ebihara K, Yamakage A, Tanaka Y, Sato M 2015 Phys. Rev. B 91 174305 Google Scholar
[124]	Liu X, Li X, Deng D L, Liu X J, Das Sarma S 2016 Phys. Rev. B 94 014511 Google Scholar
[125]	Bonderson P, Freedman M, Nayak C 2008 Phys. Rev. Lett. 101 010501 Google Scholar
[126]	Bonderson P 2013 Phys. Rev. B 87 035113 Google Scholar
[127]	Preskill J 2004 http://www.theory.caltech.edu/preskill/ talks/Preskill Biedenharn4.pdf
[128]	Luo X J, He Y P, Poon T F J, Liu X, Liu X J 2018. arXiv: 1803.02173 [cond-mat.mes-hall]
[129]	Chiu C K, Das Sarma S 2019 Phys. Rev. B 99 035312 Google Scholar
[130]	Jiang L, Pekker D, Alicea J, Refael G, Oreg Y, von Oppen F 2011 Phys. Rev. Lett. 107 236401 Google Scholar
[131]	Yang G, Lyu Z, Zhang X, Qu F, Lu L 2019 Chin. Phys. B 28 127402 Google Scholar
[132]	Stenger J P T, Hatridge M, Frolov S M, Pekker D 2019 Phys. Rev. B 99 035307 Google Scholar
[133]	Plugge S, Rasmussen A, Egger R, Flensberg K 2017 New J. Phys. 19 012001 Google Scholar
[134]	Liu D E, Cheng M, Lutchyn R M 2015 Phys. Rev. B 91 081405 Google Scholar
[135]	Barthel C, Reilly D J, Marcus C M, Hanson M P, Gossard A C 2009 Phys. Rev. Lett. 103 160503 Google Scholar
[136]	Medford J, Beil J, Taylor J M, Bartlett S D, Doherty A C, Rashba E I, DiVincenzo D P, Lu H, Gossard A C, Marcus C M 2013 Nat. Nanotechnol. 8 654 Google Scholar
[137]	Eng K, Ladd T D, Smith A, Borselli M G, Kiselev A A, Fong B H, Holabird K S, Hazard T M, Huang B, Deelman P W, Milosavljevic I, Schmitz A E, Ross R S, Gyure M F, Hunter A T 2015 Sci. Advances 1 1500214 Google Scholar
[138]	Fu L 2010 Phys. Rev. Lett. 104 056402 Google Scholar
[139]	Schrade C, Fu L 2018 Phys. Rev. Lett. 121 267002 Google Scholar
[140]	Knapp C 2019 Ph.D. Dissertation (UC Santa Barbara)
[141]	Qi X L, Hughes T L, Raghu S, Zhang S C 2009 Phys. Rev. Lett. 102 187001 Google Scholar
[142]	Schnyder A P, Brydon P M R, Manske D, Timm C 2010 Phys. Rev. B 82 184508 Google Scholar
[143]	Beenakker C W J, Dahlhaus J P, Wimmer M, Akhmerov A R 2011 Phys. Rev. B 83 085413 Google Scholar
[144]	Deng S, Viola L, Ortiz G 2012 Phys. Rev. Lett. 108 036803 Google Scholar
[145]	Nakosai S, Tanaka Y, Nagaosa N 2012 Phys. Rev. Lett. 108 147003 Google Scholar
[146]	Wong C L M, Law K T 2012 Phys. Rev. B 86 184516 Google Scholar
[147]	Zhang F, Kane C L, Mele E J 2013 Phys. Rev. Lett. 111 056402 Google Scholar
[148]	Keselman A, Fu L, Stern A, Berg E 2013 Phys. Rev. Lett. 111 116402 Google Scholar
[149]	Kim Y, Liu D E, Gaidamauskas E, Paaske J, Flensberg K, Lutchyn R M 2016 Phys. Rev. B 94 075439 Google Scholar
[150]	Fang C, Gilbert M J, Bernevig B A 2014 Phys. Rev. Lett. 112 106401 Google Scholar
[151]	Liu X J, He J J, Law K T 2014 Phys. Rev. B 90 235141 Google Scholar
[152]	Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005 Google Scholar
[153]	Snyder R A, Trimble C J, Rong C C, Folkes P A, Taylor P J, Williams J R 2018 Phys. Rev. Lett. 121 097701 Google Scholar
[154]	Trifunovic L, Brouwer P W 2019 Phys. Rev. X 9 011012 Google Scholar
[155]	Liu X J, Wong C L M, Law K T 2014 Phys. Rev. X 4 021018 Google Scholar
[156]	Gao P, He Y P, Liu X J 2016 Phys. Rev. B 94 224509 Google Scholar
[157]	Wölms K, Stern A, Flensberg K 2014 Phys. Rev. Lett. 113 246401 Google Scholar
[158]	Wölms K, Stern A, Flensberg K 2016 Phys. Rev. B 93 045417 Google Scholar
[159]	McGinley M, Cooper N R 2018 Phys. Rev. Lett. 121 090401 Google Scholar
[160]	Zhang F, Kane C L 2014 Phys. Rev. B 90 020501 Google Scholar

Cited By

图 1 Kitaev链的两个拓扑相　(a)和(b) Majorana基矢下的哈密顿量示意图. 图(a)中$\mu\neq0, \varDelta=t=0$, 只有第一项$ (1+ {\rm{i}}\gamma_{x, B}\gamma_{x, A})$不为零, 每一个格点上的两个马约拉纳算符耦合在一起, 不存在空间分离的MZM. 图(b)中$\mu=0, \varDelta=t$, 只有第二项$\gamma_{x, B}\gamma_{x+1, A}$不为零, 相邻格点的两个马约拉纳算符耦合在一起, 超导链的两端各自剩下一个MZM. (c) $\varDelta=0$时的色散关系. (d) Kitaev链的拓扑相图. 当化学势穿过能带时, 体系处在拓扑相, 由(d) 中的橙色区域描述; 反之, 体系处在平庸相, 由(d)中的白色区域描述

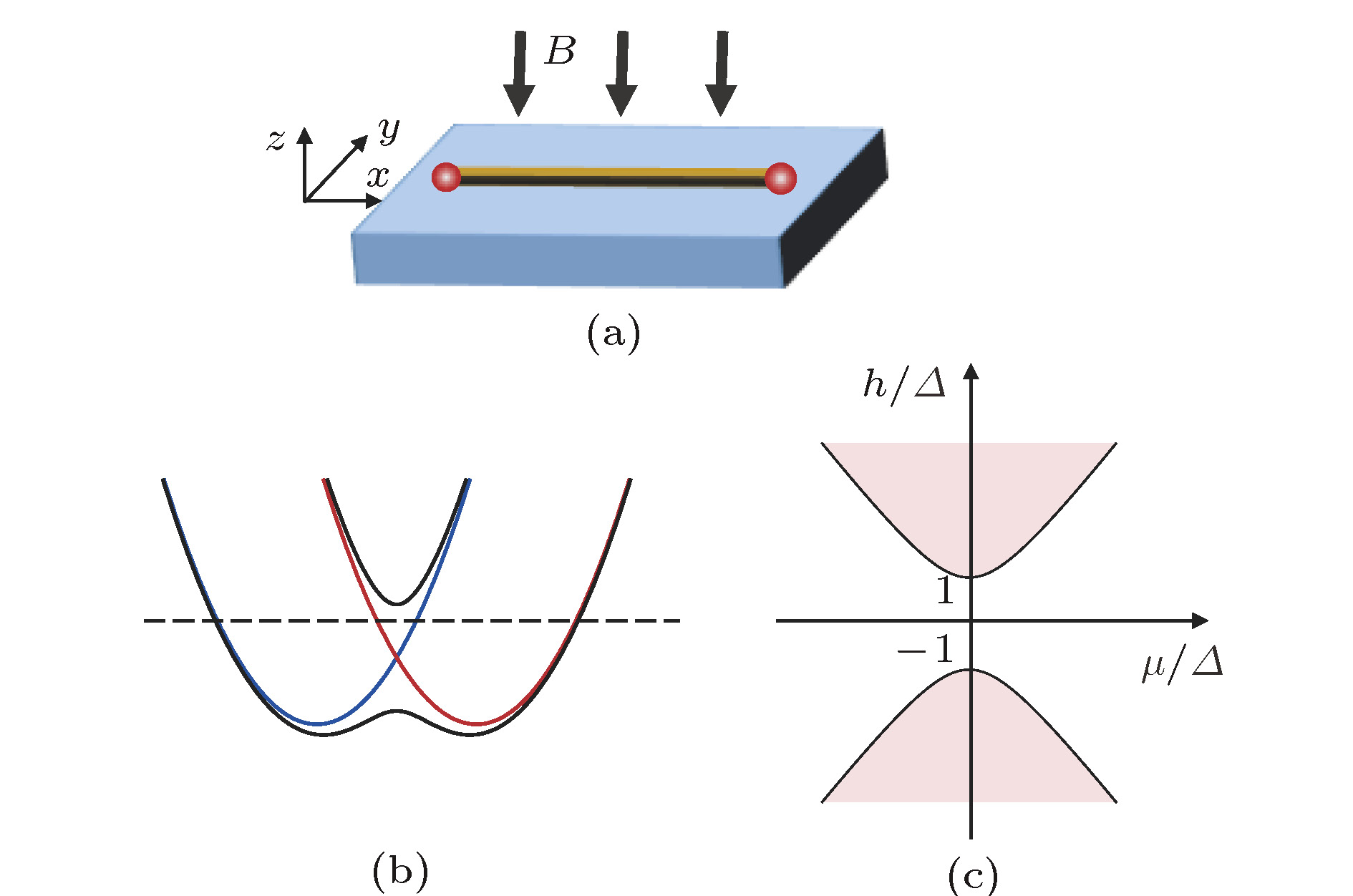
Figure 1. Two topological phases of the Kiteaev chain. (a) Sche-matic illustration of the Hamiltonian in Majorana basis. In (a) $\mu\neq0$, $\varDelta=t=0$, only the first term $(1+ {\rm{i}}\gamma_{x, B}\gamma_{x, A})$ survives thus Majoranas couple at the same site leaving no seperate MZMs left. In (b) $\mu=0, \varDelta=t$, only the second term $\gamma_{x, B}\gamma_{x+1, A}$ survives thus Majoranas couple at adjacent sites, leaving one MZM at each end of the chain. (c) Energy dispersion for $\varDelta=0$. (d) Topological phase diagram of Kitaev chain. When the chemical potential crosses the nomal spectrum the system is in topological phase, as described by the orange region in (d); otherwise the system is trivial, as described by the white region in (d).

DownLoad: Full-Size Img PowerPoint

图 2 在一维SOC纳米线中实现马约拉纳零模激发^[8]　(a)装置简图； (b)一维SOC纳米线的色散关系. 在无外加塞曼场时, 系统具有时间反演对称性, 体系有偶数个费米面(红色和蓝色曲线); 在外加塞曼场时, 时间反演对称性被破坏, $k=0$处被打开能隙(黑色曲线). 若化学势位于能隙中间, 该体系只有一个费米面, 其低能哈密顿量等效为Kitaev链. (c)体系的拓扑相图, 其中相边界由$h^{2}= \varDelta^{2}+\mu^{2}$给出, 橙色(白色)表示拓扑(平庸)区

Figure 2. Realizing MZMs in a 1D SOC nanowire^[8]. (a) Sketch of the basic setup. (b) Energy dispersion for the 1D SOC nanowire. When Zeeman field is absent, the system is time-reversal symmetric(TRS) and possesses even number of Fermi surfaces (red and blue curves); when Zeeman field is introduced, TRS is broken and a gap is opened at $k=0$(black curves). Given that the chemical potential lies within gap, the system possesses only one Fermi surface, and the low-energy Hamilitonian is equivalent to that of the Kitaev chain. (c) Topological phase diagram of the system with the phase boundary given by $h^{2}= \varDelta^{2}+ \mu^{2}$. Orange (white) denotes topological (trivial) region.

DownLoad: Full-Size Img PowerPoint

图 3 MZM交换示意图　(a)含有4个空间分离足够远的MZM$\gamma_{1, 2, 3, 4}$的体系, 其中$\gamma_{1}$和$\gamma_{2}$、$\gamma_{3}$和$\gamma_{4}$分别构成两个费米子. $\gamma_{2}$和$\gamma_{3}$顺时针交换一次, $\gamma_{2}$会跨越$\gamma_{3}$所在涡旋的相位割线获得一个负号, 而$\gamma_{3}$并未跨越$\gamma_{2}$所在涡旋的相位割线不获得负号. 因此结果是$\gamma_{2}\rightarrow-\gamma_{3}, \gamma_{3}\rightarrow\gamma_{2}$. (b)描述4个MZM的时间-空间(x; t)轨迹的世界线. $\gamma_{2}$和$\gamma_{3}$被编织一次, 因此它们的世界线缠绕一次. 系统由初态$|\varPhi_{\rm i}\rangle=|00\rangle$演化到$|\varPhi_{\rm f}\rangle=|00\rangle+ {\rm{i}}|11\rangle$

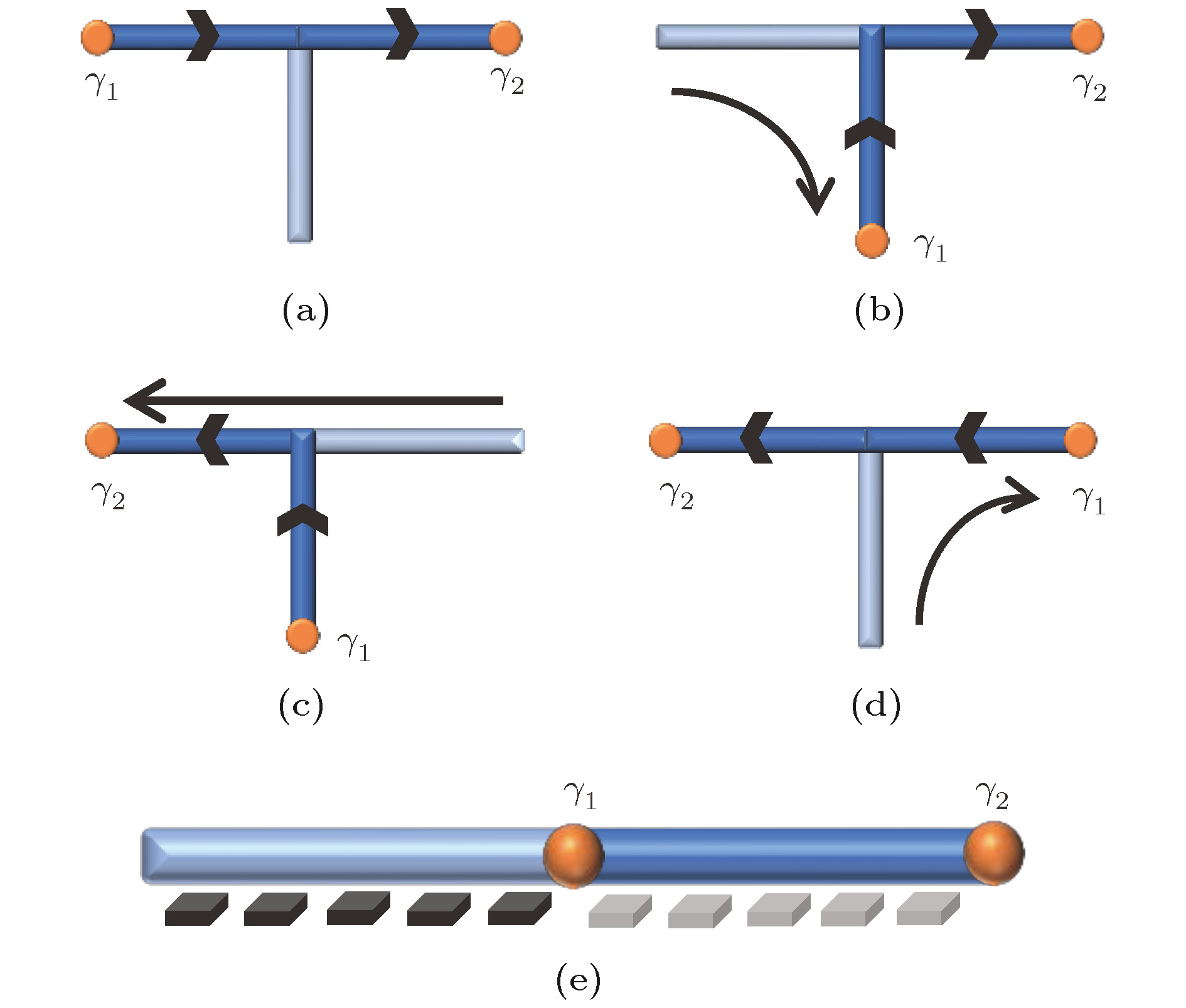
Figure 3. Skecth of a MZM braiding operation. (a) A system consists of 4 MZMs far enough apart, with $\gamma_{1}$ and $\gamma_{2}$, $\gamma_{3}$ and $\gamma_{4}$ forming 2 fermions $f_{1}$ and $f_{2}$. $\gamma_{2}$ and $\gamma_{3}$ are braided once clockwise. γ₂ crosses the branch cut of the votex hosting γ₃ and gains a minus sign, while γ₃ doesn't cross the branch cut of the votex hosting γ₂ and doesn't gain a minus sign. Hence the result is given by γ₂→ –γ₃, γ₃→ γ₂. (b) Worldlines in a space-time (x; t) diagram, describing four MZMs. $\gamma_{2}$ and $\gamma_{3}$ are braided once, hence their worldlines winds each other once. The initial state $|\varPhi_{\rm i}\rangle=|00\rangle$ evolves into $|\varPhi_{\rm f}\rangle=|00\rangle+ {\rm{i}}|11\rangle$.

DownLoad: Full-Size Img PowerPoint

图 4 通过MZM编织操作实现量子门^[110]　(a)−(d) 分别为实现单比特量子门H-门、Z-门、双比特门CNOT门和双比特门CZ门的编织操作示意图

Figure 4. Quantum gates realized by MZM braiding operations^[110]. (a)−(d) The elementary braids corresponding to the single-qubit gates H-, Z-gates on the first qubit as well as the 2-qubit CNOT and CZ gates.

DownLoad: Full-Size Img PowerPoint

图 5 T-型结进行编织操作以及键盘门的操作方式^[101]. T- 型结由两条水平链和一条竖直链组成, 深蓝色部分为拓扑相, 浅蓝色部分为平凡相, 超导体上向上和向右的箭头分别代表$\phi= \text{π}/2$和$\phi=0$, 用向左和向下的箭头代表$\phi=\text{π}$和$\phi=3\text{π}/2$. T-型结外的箭头代表MZM运动的方向. 黑色和灰色方块分别代表局域门的关闭和打开状态, 对应平凡相和拓扑相. (a)—(d) 给出$\gamma_{1}$先运动到竖直链上, 然后$\gamma_{2}$从水平链右端运动到左端, 最后$\gamma_{1}$运动到右端的过程, 过程结束后箭头反向. (e) 中局域门的存在可以保证在不关闭能隙的前提下逐渐移动MZM

Figure 5. A T-junction allows for braiding process and the keyboard gates^[101]. The T-junction consists of two horizontal segments and one vertical segment. Dark blue segments are in topological phase, and light blue lines trivial phase. $\phi=0$ or $\text{π}/2$ is represented with rightward or upward pointing arrows, while $\phi=\text{π}$ or $3\text{π}/2$ represents the leftward or downward pointing arrows. MZMs are transported according to the arrows around the T-junction. Black and gray blocks denote different states of tunable gates in accordance with trivial and topological phases. (a)–(d) sketch the process which $\gamma_{1}$ is transported to vertical line firstly, then $\gamma_{2}$ travels from the right end to the left end and at last $\gamma_{1}$ is transported to the right end. After this process, the arrow points to the opposite direction. Local gates in (e) ensure that the MZMs can be manipulated gradually without closing the gap.

DownLoad: Full-Size Img PowerPoint

图 6 通过转动铁磁体的磁化方向实现铁磁体两端的MZM^[128]　(a)交换世界带两次在拓扑上等价于世界带各自扭转$2\text{π}$. 箭头表示MZM的自旋; 世界带的红蓝边界标记MZM的内部自由度的时间演化. (b) SC/QSH/FI异质结装置中的MZM. 黄色(红色)箭头表示MZM的局域自旋方向(铁磁磁化方向). 下方的红色箭头转$\text{π}$角, $\gamma_{1}$和$\gamma_{2}$编织一次; 转$2\text{π}$角, $\gamma_{1}$和$\gamma_{2}$编织两次. 逆方向转动代表逆交换.

Figure 6. Braiding operation via winding FI magnetization^[128]. (a) The monodromy operator can be realized by either braiding two MZMs or twisting each worldribbons by $2\text{π}$. The arrows indicate the MZM spin. The blue and red edges of the ribbon denote the evolution of internal degree of freedom. (b) MZMs in the SC/QSH/FI hybrid system. The yellow (red) arrows represent the directions of local spin polari-zations for MZMs (FI magnetization). Winding the red arrow at the bottom by $\text{π}$, $\gamma_{1}$ and $\gamma_{2}$ are braided once; by $2\text{π}$ they are braided twice. A reverse rotation leads to an inverse braiding operation.

DownLoad: Full-Size Img PowerPoint

图 7 约瑟夫森结的量子比特读出装置^[129]　(a)为MZM约瑟夫森结的示意图. 结两端各自存在一个MZM. 蓝色区域为一维拓扑超导区, 绿色区域为绝缘体区. 拓扑区的长度足够长, 使得两个MZM通过拓扑区的耦合可以忽略. $\gamma_{1}$和$\gamma_{2}$通过足够短的绝缘区耦合起来, 形成一个能量非零的费米子. 通过改变通过线圈的磁场通量$\varPhi$可以改变结两端的超导相位差$\phi$. (b) 直流分数约瑟夫森电流随$\phi$的变化关系. 其中红色虚线代表空占据态$|0\rangle$, 蓝色实线代表占据态$|1\rangle$. 和传统的以$2{\text{π}}$周期的约瑟夫森电流不同的是, 分数约瑟夫森电流关于$\phi$的变化周期是$4{\text{π}}$. 量子比特$|0\rangle$和$|1\rangle$相对应的电流方向相反, 因此通过测量直流约瑟夫森电流可以读出MZM量子比特

Figure 7. Basic set-up for qubit readout using a Josephson junction(JJ)^[129]. (a) The schematic of a JJ with 2 MZMs residing at the junction. The blue region denotes 1d TSC and the green denoted trivial insulator. The TSC region should be long enough so that the coupling of the MZMs through TSC is negligible. $\gamma_{1}$ and $\gamma_{2}$ couple weakly at the junction, forming a non-zero energy fermion. The phase difference $\phi$ can be varied by changing the magnetic flux $\varPhi$. (b) The d.c. fractional Josephson current flowing across the junction versus$\phi$. Instead of conventional $2{\text{π}}$-periodic JJ current induced by Cooper pair tunneling, the fractional JJ current induced by MZMs exhibits $4{\text{π}}$ periodicity. The red dashed line denotes $|0\rangle$ and the blue solid line denotes $|1\rangle$. The direction of the current is inverse for the qubit $|0\rangle$ and $|1\rangle$, which enables the readout of the qubit by measuring the direct Josephson current.

DownLoad: Full-Size Img PowerPoint

图 8 MZM和量子点耦合的装置简图^[39]　 (a) , (b)分别是2个和4个MZM系统的装置; (c) 在调节量子点与MZM之间跃迁矩阵元的局域电平开关

Figure 8. Sketch of MZMs coupled to quantum dots^[39], with 2-MZM and 4-MZM system shown in (a) and (b), and in (c) the local gates controlling the coupling between MZMs and quantum dots are shown.

DownLoad: Full-Size Img PowerPoint

图 9 马约拉纳干涉仪装置^[38]　(a)电流从上方经过两个MZM也即一个拓扑量子比特, 从下方经过相位相干长度足够长的金属, 电路中间穿过可调节的磁通. 两条路径的相位差由电子的传输相移以及穿过线路的磁通决定. (b)通过测量干涉后的电导可以得到拓扑量子比特的宇称信息. 实线和虚线分别对应宇称为1和–1的量子比特的电导信号

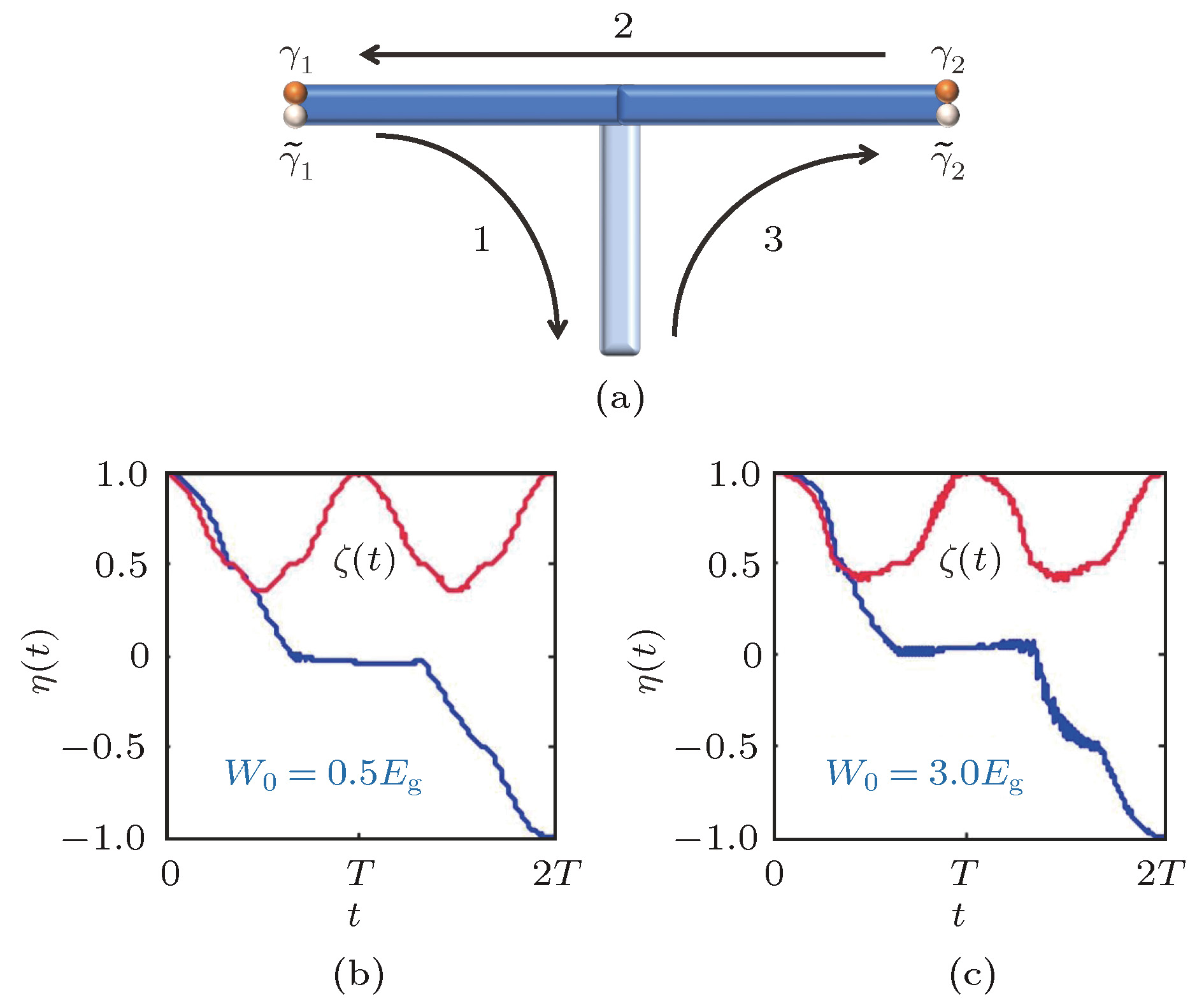
Figure 9. Majorana inferometry^[38]. (a) One path goes through two MZMs i.e. a topological qubit while the other path goes through a normal metal with a sufficiently long phase-coherence length. $\varPsi$ is the applied magnetic flux enclosed by the two paths. The phase difference of two paths is determined by the phase transition shift and the magnetic flux, which can be measured by the conductance. (b) Majorana interferometer provides a projective measurement of the fermion parity. Solid line and dotted line represent the conductance signals corresponding to qubits with parity 1 and –1 respectively.

DownLoad: Full-Size Img PowerPoint

图 10 时间反演对称性保护的编织过程及非阿贝尔统计的结果^[156]　(a) 时间反演不变的拓扑超导体两wlxb 端各有一对MZM, 以T-型结的方案完成编织. (b), (c) 不同的无序强度$W_{0}$下经过完整编织后MKP的演化结果, 在不同条件下均有$\eta(t)=\langle\gamma_{1}(0)|\gamma_{1}(t)\rangle|_{t=2 T}=-1$, 满足非阿贝尔统计. 经过一个周期后$\zeta(nT)=\displaystyle\sum\limits_{j=1, 2}[|\langle\gamma_{1}(nT) |\gamma_{j}(0)\rangle|^{2} + |\langle\gamma_{1}(nT)|\tilde{\gamma}_{j}(0)\rangle|^{2}]=1$给出绝热演化的条件

Figure 10. Time-reversal symmetry protected braiding process and the results of non-Abelian statistics^[156]. The TSC in (a) hosts a pair of MZMs at each end, and the braiding is fulfilled by the T-junction scheme. (b), (c) The evoluation of MKPs after the full braiding in the presence of different disorder strengh $W_{0}$. The non-Abelian statistics is confirmed by $\eta(t)=\langle\gamma_{1}(0)|\gamma_{1}(t)\rangle|_{t=2 T}=-1$. The adiabatic condition is satisfied in that $\zeta(nT)= \displaystyle\sum\limits_{j=1, 2}[|\langle\gamma_{1}(nT)|\gamma_{j}(0)\rangle|^{2} + |\langle\gamma_{1}(nT)|\tilde{\gamma}_{j}(0)\rangle|^{2}]=1$.

DownLoad: Full-Size Img PowerPoint

map

[1]	Majorana E 1937 Nuovo Cim. 14 171 Google Scholar
[2]	Schechter J, Valle J W F 1982 Phys. Rev. D 25 2951 Google Scholar
[3]	Keung W Y, Senjanović G 1983 Phys. Rev. Lett. 50 1427 Google Scholar
[4]	Atre A, Han T, Pascoli S, Zhang B 2009 J. High Energy Phys. 2009 030 Google Scholar
[5]	Rodejohann W 2011 Inter. J. Mod. Phys. E 20 1833 Google Scholar
[6]	de Gouvêa A, Vogel P 2013 Progress in Particle and Nuclear Physics 71 75 Google Scholar
[7]	Kitaev A Y 2001 Physics-Uspekhi 44 131 Google Scholar
[8]	Alicea J 2012 Rep. Prog. Phys. 75 076501 Google Scholar
[9]	Elliott S R, Franz M 2015 Rev. Mod. Phys. 87 137 Google Scholar
[10]	Leijnse M, Flensberg K 2012 Semiconductor Science and Technology 27 124003 Google Scholar
[11]	Wilczek F 2009 Nature Physics 5 614 Google Scholar
[12]	Franz M 2013 Nat. Nanotechnol. 8 149 Google Scholar
[13]	Read N, Green D 2000 Phys. Rev. B 61 10267 Google Scholar
[14]	Ivanov D A 2001 Phys. Rev. Lett. 86 268 Google Scholar
[15]	Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083 Google Scholar
[16]	Freedman M, Kitaev A, Larsen M, Wang Z 2003 Bulletin of the American Mathematical Society 40 31 Google Scholar
[17]	Das Sarma S, Freedman M, Nayak C 2005 Phys. Rev. Lett. 94 166802 Google Scholar
[18]	Sarma S D, Freedman M, Nayak C 2006 Phys. Today 59 32 Google Scholar
[19]	Kitaev A 2003 Ann. Phys. 303 2 Google Scholar
[20]	Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407 Google Scholar
[21]	Sau J D, Lutchyn R M, Tewari S, Das Sarma S 2010 Phys. Rev. Lett. 104 040502 Google Scholar
[22]	Alicea J 2010 Phys. Rev. B 81 125318 Google Scholar
[23]	Lutchyn R M, Sau J D, Das Sarma S 2010 Phys. Rev. Lett. 105 077001 Google Scholar
[24]	Oreg Y, Refael G, von Oppen F 2010 Phys. Rev. Lett. 105 177002 Google Scholar
[25]	Hosur P, Ghaemi P, Mong R S K, Vishwanath A 2011 Phys. Rev. Lett. 107 097001 Google Scholar
[26]	Pientka F, Keselman A, Berg E, Yacoby A, Stern A, Halperin B I 2017 Phys. Rev. X 7 021032 Google Scholar
[27]	Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 1003 Google Scholar
[28]	Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602 Google Scholar
[29]	Sun H H, Zhang K W, Hu L H, et al. 2016 Phys. Rev. Lett. 116 257003 Google Scholar
[30]	He Q L, Pan L, Stern A L, et al. 2017 Science 357 294 Google Scholar
[31]	Zhang P, Yaji K, Hashimoto T, et al. 2018 Science 360 182 Google Scholar
[32]	Wang D, Kong L, Fan P, Chen H, Zhu S, Liu W, Cao L, Sun Y, Du S, Schneeloch J, Zhong R, Gu G, Fu L, Ding H, Gao H J 2018 Science 362 333 Google Scholar
[33]	Fornieri A, Whiticar A M, Setiawan F, Portolés E, Drachmann A C C, Keselman A, Gronin S, Thomas C, Wang T, Kallaher R, et al. 2019 Nature 569 89 Google Scholar
[34]	Ren H, Pientka F, Hart S, et al. 2019 Nature 569 93 Google Scholar
[35]	Jäck B, Xie Y, Li J, Jeon S, Bernevig B A, Yazdani A 2019 Science 364 1255 Google Scholar
[36]	van Heck B, Akhmerov A R, Hassler F, Burrello M, Beenakker C W J 2012 New J. Phys. 14 035019 Google Scholar
[37]	Aasen D, Hell M, Mishmash R V, Higginbotham A, Danon J, Leijnse M, Jespersen T S, Folk J A, Marcus C M, Flensberg K, Alicea J 2016 Phys. Rev. X 6 031016 Google Scholar
[38]	Vijay S, Fu L 2016 Phys. Rev. B 94 235446 Google Scholar
[39]	Karzig T, Knapp C, Lutchyn R M, Bonderson P, Hastings M B, Nayak C, Alicea J, Flensberg K, Plugge S, Oreg Y, Marcus C M, Freedman M H 2017 Phys. Rev. B 95 235305 Google Scholar
[40]	Schrade C, Fu L 2018. arXiv: 1807.06620 [cond-mat.mes-hall]
[41]	Stern A, Berg E 2019 Phys. Rev. Lett. 122 107701 Google Scholar
[42]	Wang Z 2010 Topological Quantum Computation (Santa Barbara: American Mathematical Soc.)
[43]	Zhang L, Liu X J 2018 Spin-orbit Coupling and Topological Phases for Ultracold Atoms (Chap. 1) (Singapore: World Scientific) pp1–87
[44]	Sau J D, Tewari S, Lutchyn R M, Stanescu T D, Das Sarma S 2010 Phys. Rev. B 82 214509 Google Scholar
[45]	Potter A C, Lee P A 2011 Phys. Rev. B 83 184520 Google Scholar
[46]	Sau J D, Tewari S, Das Sarma S 2012 Phys. Rev. B 85 064512 Google Scholar
[47]	Deng M T, Yu C L, Huang G Y, Larsson M, Caroff P, Xu H Q 2012 Nano Lett. 12 6414 Google Scholar
[48]	Das A, Ronen Y, Most Y, Oreg Y, Heiblum M, Shtrikman H 2012 Nat. Phys. 8 887 Google Scholar
[49]	Finck A D K, Van Harlingen D J, Mohseni P K, Jung K, Li X 2013 Phys. Rev. Lett. 110 126406 Google Scholar
[50]	Churchill H O H, Fatemi V, Grove-Rasmussen K, Deng M T, Caroff P, Xu H Q, Marcus C M 2013 Phys. Rev. B 87 241401 Google Scholar
[51]	Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001 Google Scholar
[52]	Flensberg K 2010 Phys. Rev. B 82 180516 Google Scholar
[53]	Wimmer M, Akhmerov A R, Dahlhaus J P, Beenakker C W J 2011 New J. Phys. 13 053016 Google Scholar
[54]	Lutchyn R M, Bakkers E P A M, Kouwenhoven L P, Krogstrup P, Marcus C M, Oreg Y 2018 Nat. Rev.s Mater. 3 52 Google Scholar
[55]	Liu X J, Lobos A M 2013 Phys. Rev. B 87 060504 Google Scholar
[56]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[57]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[58]	Fu L, Kane C L 2009 Phys. Rev. B 79 161408 Google Scholar
[59]	Scharf B, Pientka F, Ren H, Yacoby A, Hankiewicz E M 2019 Phys. Rev. B 99 214503 Google Scholar
[60]	Setiawan F, Stern A, Berg E 2019 Phys. Rev. B 99 220506 Google Scholar
[61]	Stone M, Roy R 2004 Physical Review B 69 184511 Google Scholar
[62]	Fu L, Kane C L, Mele E J 2007 Phys. Rev. Lett. 98 106803 Google Scholar
[63]	Fu L, Kane C L 2009 Phys. Rev. Lett. 102 216403 Google Scholar
[64]	Akhmerov A R, Nilsson J, Beenakker C W J 2009 Phys. Rev. Lett. 102 216404 Google Scholar
[65]	Tanaka Y, Yokoyama T, Nagaosa N 2009 Phys. Rev. Lett. 103 107002 Google Scholar
[66]	Linder J, Tanaka Y, Yokoyama T, Sudbø A, Nagaosa N 2010 Phys. Rev. B 81 184525 Google Scholar
[67]	Zhang C, Tewari S, Lutchyn R M, Das Sarma S 2008 Phys. Rev. Lett. 101 160401 Google Scholar
[68]	Sato M, Takahashi Y, Fujimoto S 2009 Phys. Rev. Lett. 103 020401 Google Scholar
[69]	Wang M X, Liu C, Xu J P, et al. 2012 Science 336 52 Google Scholar
[70]	He J J, Ng T K, Lee P A, Law K T 2014 Phys. Rev. Lett. 112 037001 Google Scholar
[71]	Xu J P, Liu C, Wang M X, Ge J, Liu Z L, Yang X, Chen Y, Liu Y, Xu Z A, Gao C L, Qian D, Zhang F C, Jia J F 2014 Phys. Rev. Lett. 112 217001 Google Scholar
[72]	Xu J P, Wang M X, Liu Z L, Ge J F, Yang X, Liu C, Xu Z A, Guan D, Gao C L, Qian D, Liu Y, Wang Q H, Zhang F C, Xue Q K, Jia J F 2015 Phys. Rev. Lett. 114 017001 Google Scholar
[73]	Wang Z, Zhang P, Xu G, Zeng L K, Miao H, Xu X, Qian T, Weng H, Richard P, Fedorov A V, Ding H, Dai X, Fang Z 2015 Phys. Rev. B 92 115119 Google Scholar
[74]	Xu G, Lian B, Tang P, Qi X L, Zhang S C 2016 Phys. Rev. Lett. 117 047001 Google Scholar
[75]	Kong L, Zhu S, Papaj M, et al. 2019 Nat. Phys. 15 1181 Google Scholar
[76]	König E J, Coleman P 2019 Phys. Rev. Lett. 122 207001 Google Scholar
[77]	Zhang P, Wang Z, Wu X, Yaji K, Ishida Y, Kohama Y, Dai G, Sun Y, Bareille C, Kuroda K, et al. 2018 Nat. Phys. 15 41 Google Scholar
[78]	Zhou X, Gordon K N, Jin K H, Li H, Narayan D, Zhao H, Zheng H, Huang H, Cao G, Zhigadlo N D, Liu F, Dessau D S 2019 Phys. Rev. B 100 184511 Google Scholar
[79]	Machida T, Sun Y, Pyon S, Takeda S, Kohsaka Y, Hanaguri T, Sasagawa T, Tamegai T 2019 Nat. Mater. 18 811 Google Scholar
[80]	Yan Z, Bi R, Wang Z 2017 Phys. Rev. Lett. 118 147003 Google Scholar
[81]	Chan C, Zhang L, Poon T F J, He Y P, Wang Y Q, Liu X J 2017 Phys. Rev. Lett. 119 047001 Google Scholar
[82]	Teo J C Y, Kane C L 2010 Phys. Rev. B 82 115120 Google Scholar
[83]	Chan C, Liu X J 2017 Phys. Rev. Lett. 118 207002 Google Scholar
[84]	Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 82 184516 Google Scholar
[85]	Chung S B, Qi X L, Maciejko J, Zhang S C 2011 Phys. Rev. B 83 100512 Google Scholar
[86]	Wang J, Zhou Q, Lian B, Zhang S C 2015 Phys. Rev. B 92 064520 Google Scholar
[87]	Lian B, Wang J, Zhang S C 2016 Phys. Rev. B 93 161401 Google Scholar
[88]	Kayyalha M, Xiao D, Zhang R, Shin J, Jiang J, Wang F, Zhao Y F, Xiao R, Zhang L, Fijalkowski K M, Mandal P, Winnerlein M, Gould C, Li Q, Molenkamp L W, Chan M H W, Samarth N, Chang C Z 2020 Science 367 64 Google Scholar
[89]	Deng M T, Vaitiekenas S, Hansen E B, Danon J, Leijnse M, Flensberg K, Nygård J, Krogstrup P, Marcus C M 2016 Science 354 1557 Google Scholar
[90]	Nichele F, Drachmann A C, Whiticar A M, et al. 2017 Phys. Rev. Lett. 119 136803 Google Scholar
[91]	Gül O, Zhang H, Bommer J D S, et al. 2018 Nat. Nanotechnol. 13 192 Google Scholar
[92]	Feldman B E, Randeria M T, Li J, Jeon S, Xie Y, Wang Z, Drozdov I K, Bernevig B A, Yazdani A 2017 Nat. Phys. 13 286 Google Scholar
[93]	Jeon S, Xie Y, Li J, Wang Z, Bernevig B A, Yazdani A 2017 Science 358 772 Google Scholar
[94]	Laroche D, Bouman D, van Woerkom D J, et al. 2019 Nat. Commun. 10 245 Google Scholar
[95]	Rokhinson L P, Liu X, Furdyna J K 2012 Nat. Phys. 8 795 Google Scholar
[96]	Beenakker C W J 2019. arXiv: 1907.06497 [cond-mat]
[97]	Bonderson P, Gurarie V, Nayak C 2011 Phys. Rev. B 83 075303 Google Scholar
[98]	Teo J C Y, Kane C L 2010 Phys. Rev. Lett. 104 046401 Google Scholar
[99]	Freedman M, Hastings M B, Nayak C, Qi X L, Walker K, Wang Z 2011 Phys. Rev. B 83 115132 Google Scholar
[100]	Freedman M, Hastings M B, Nayak C, Qi X L 2011 Phys. Rev. B 84 245119 Google Scholar
[101]	Alicea J, Oreg Y, Refael G, von Oppen F, Fisher M P A 2011 Nat. Phys. 7 412 Google Scholar
[102]	Feynman R P 1982 Intern. J. Theoretical Phys. 21 467 Google Scholar
[103]	Shor P W 1994 In Proceedings 35th Annual Symposium on Foundations of Computer Science (Ieee), pp124–134
[104]	Grover L K 1997 Phys. Rev. Lett. 79 325 Google Scholar
[105]	Lloyd S 1996 Science 273 1073 Google Scholar
[106]	Deutsch D 1985 Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 400 97 Google Scholar
[107]	Lo H K, Spiller T, Popescu S 1998 Introduction to quantum computation and information (World Scientific)
[108]	DiVincenzo D P 2000 Fortschritte der Physik: Progress of Physics 48 771 Google Scholar
[109]	Sarma S D, Freedman M, Nayak C 2015 npj Quantum Information 1 15001 Google Scholar
[110]	Lahtinen V, Pachos J 2017 SciPost Physics 3 021 Google Scholar
[111]	Kitaev A Y 1997 Uspekhi Matematicheskikh Nauk 52 53 Google Scholar
[112]	Dawson C M, Nielsen M A 2005. arXiv: 0505030 [quant-ph]
[113]	Bravyi S, Kitaev A 2005 Phys. Rev. A 71 022316 Google Scholar
[114]	Bravyi S 2006 Phys. Rev. A 73 042313 Google Scholar
[115]	Freedman M, Nayak C, Walker K 2006 Phys. Rev. B 73 245307 Google Scholar
[116]	Bonderson P, Clarke D J, Nayak C, Shtengel K 2010 Phys. Rev. Lett. 104 180505 Google Scholar
[117]	Karzig T, Oreg Y, Refael G, Freedman M H 2016 Phys. Rev. X 6 031019 Google Scholar
[118]	Cheng M, Galitski V, Das Sarma S 2011 Phys. Rev. B 84 104529 Google Scholar
[119]	Bauer B, Karzig T, Mishmash R, Antipov A, Alicea J 2018 Sci. Post Phys. 5 004 Google Scholar
[120]	Sau J D, Clarke D J, Tewari S 2011 Phys. Rev. B 84 094505 Google Scholar
[121]	Clarke D J, Sau J D, Tewari S 2011 Phys. Rev. B 84 035120 Google Scholar
[122]	Halperin B I, Oreg Y, Stern A, Refael G, Alicea J, von Oppen F 2012 Phys. Rev. B 85 144501 Google Scholar
[123]	Amorim C S, Ebihara K, Yamakage A, Tanaka Y, Sato M 2015 Phys. Rev. B 91 174305 Google Scholar
[124]	Liu X, Li X, Deng D L, Liu X J, Das Sarma S 2016 Phys. Rev. B 94 014511 Google Scholar
[125]	Bonderson P, Freedman M, Nayak C 2008 Phys. Rev. Lett. 101 010501 Google Scholar
[126]	Bonderson P 2013 Phys. Rev. B 87 035113 Google Scholar
[127]	Preskill J 2004 http://www.theory.caltech.edu/preskill/ talks/Preskill Biedenharn4.pdf
[128]	Luo X J, He Y P, Poon T F J, Liu X, Liu X J 2018. arXiv: 1803.02173 [cond-mat.mes-hall]
[129]	Chiu C K, Das Sarma S 2019 Phys. Rev. B 99 035312 Google Scholar
[130]	Jiang L, Pekker D, Alicea J, Refael G, Oreg Y, von Oppen F 2011 Phys. Rev. Lett. 107 236401 Google Scholar
[131]	Yang G, Lyu Z, Zhang X, Qu F, Lu L 2019 Chin. Phys. B 28 127402 Google Scholar
[132]	Stenger J P T, Hatridge M, Frolov S M, Pekker D 2019 Phys. Rev. B 99 035307 Google Scholar
[133]	Plugge S, Rasmussen A, Egger R, Flensberg K 2017 New J. Phys. 19 012001 Google Scholar
[134]	Liu D E, Cheng M, Lutchyn R M 2015 Phys. Rev. B 91 081405 Google Scholar
[135]	Barthel C, Reilly D J, Marcus C M, Hanson M P, Gossard A C 2009 Phys. Rev. Lett. 103 160503 Google Scholar
[136]	Medford J, Beil J, Taylor J M, Bartlett S D, Doherty A C, Rashba E I, DiVincenzo D P, Lu H, Gossard A C, Marcus C M 2013 Nat. Nanotechnol. 8 654 Google Scholar
[137]	Eng K, Ladd T D, Smith A, Borselli M G, Kiselev A A, Fong B H, Holabird K S, Hazard T M, Huang B, Deelman P W, Milosavljevic I, Schmitz A E, Ross R S, Gyure M F, Hunter A T 2015 Sci. Advances 1 1500214 Google Scholar
[138]	Fu L 2010 Phys. Rev. Lett. 104 056402 Google Scholar
[139]	Schrade C, Fu L 2018 Phys. Rev. Lett. 121 267002 Google Scholar
[140]	Knapp C 2019 Ph.D. Dissertation (UC Santa Barbara)
[141]	Qi X L, Hughes T L, Raghu S, Zhang S C 2009 Phys. Rev. Lett. 102 187001 Google Scholar
[142]	Schnyder A P, Brydon P M R, Manske D, Timm C 2010 Phys. Rev. B 82 184508 Google Scholar
[143]	Beenakker C W J, Dahlhaus J P, Wimmer M, Akhmerov A R 2011 Phys. Rev. B 83 085413 Google Scholar
[144]	Deng S, Viola L, Ortiz G 2012 Phys. Rev. Lett. 108 036803 Google Scholar
[145]	Nakosai S, Tanaka Y, Nagaosa N 2012 Phys. Rev. Lett. 108 147003 Google Scholar
[146]	Wong C L M, Law K T 2012 Phys. Rev. B 86 184516 Google Scholar
[147]	Zhang F, Kane C L, Mele E J 2013 Phys. Rev. Lett. 111 056402 Google Scholar
[148]	Keselman A, Fu L, Stern A, Berg E 2013 Phys. Rev. Lett. 111 116402 Google Scholar
[149]	Kim Y, Liu D E, Gaidamauskas E, Paaske J, Flensberg K, Lutchyn R M 2016 Phys. Rev. B 94 075439 Google Scholar
[150]	Fang C, Gilbert M J, Bernevig B A 2014 Phys. Rev. Lett. 112 106401 Google Scholar
[151]	Liu X J, He J J, Law K T 2014 Phys. Rev. B 90 235141 Google Scholar
[152]	Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005 Google Scholar
[153]	Snyder R A, Trimble C J, Rong C C, Folkes P A, Taylor P J, Williams J R 2018 Phys. Rev. Lett. 121 097701 Google Scholar
[154]	Trifunovic L, Brouwer P W 2019 Phys. Rev. X 9 011012 Google Scholar
[155]	Liu X J, Wong C L M, Law K T 2014 Phys. Rev. X 4 021018 Google Scholar
[156]	Gao P, He Y P, Liu X J 2016 Phys. Rev. B 94 224509 Google Scholar
[157]	Wölms K, Stern A, Flensberg K 2014 Phys. Rev. Lett. 113 246401 Google Scholar
[158]	Wölms K, Stern A, Flensberg K 2016 Phys. Rev. B 93 045417 Google Scholar
[159]	McGinley M, Cooper N R 2018 Phys. Rev. Lett. 121 090401 Google Scholar
[160]	Zhang F, Kane C L 2014 Phys. Rev. B 90 020501 Google Scholar

[1]	Cui Na-Wei, Gao Jia-Xin, Dong Hui-Ru, Li Chuan-Qi, Luo Xiao-Bing, Xiao Jin-Peng. Topological superconducting phase competition in magnetic atomic rings. Acta Physica Sinica, 2024, 73(23): 237301. doi: 10.7498/aps.73.20241095
[2]	Chu Chun-Guang, Wang An-Qi, Liao Zhi-Min. Josephson effect in topological semimetal-superconductor heterojunctions. Acta Physica Sinica, 2023, 72(8): 087401. doi: 10.7498/aps.72.20230397
[3]	Yang Shuai, Zhang Hao, He Ke. Selective-area-epitaxied PbTe-superconductor hybrid nanowires: A new candidate system to realize topological quantum computing. Acta Physica Sinica, 2023, 72(23): 238101. doi: 10.7498/aps.72.20231603
[4]	Xu Lei, Li Pei-Ling, Lü Zhao-Zheng, Shen Jie, Qu Fan-Ming, Liu Guang-Tong, Lü Li. Detecting Majorana zero modes with transport measurements. Acta Physica Sinica, 2023, 72(17): 177401. doi: 10.7498/aps.72.20230951
[5]	Wang Chen-Xu, He Ran, Li Rui-Rui, Chen Yan, Fang Ding, Cui Jin-Ming, Huang Yun-Feng, Li Chuan-Feng, Guo Guang-Can. Advances in the study of ion trap structures in quantum computation and simulation. Acta Physica Sinica, 2022, 71(13): 133701. doi: 10.7498/aps.71.20220224
[6]	Zhou Zong-Quan. “Quantum memory” quantum computers and noiseless phton echoes. Acta Physica Sinica, 2022, 71(7): 070305. doi: 10.7498/aps.71.20212245
[7]	Wang Ning, Wang Bao-Chuan, Guo Guo-Ping. New progress of silicon-based semiconductor quantum computation. Acta Physica Sinica, 2022, 71(23): 230301. doi: 10.7498/aps.71.20221900
[8]	Su Fei-Fan, Yang Zhao-Hua, Zhao Shou-Kuan, Yan Hai-Sheng, Tian Ye, Zhao Shi-Ping. Fabrication of superconducting qubits and auxiliary devices with niobium base layer. Acta Physica Sinica, 2022, 71(5): 050303. doi: 10.7498/aps.71.20211865
[9]	Jiang Da, Yu Dong-Yang, Zheng Zhan, Cao Xiao-Chao, Lin Qiang, Liu Wu-Ming. Research progress of material, physics, and device of topological superconductors for quantum computing. Acta Physica Sinica, 2022, 71(16): 160302. doi: 10.7498/aps.71.20220596
[10]	Zhang Jie-Yin, Gao Fei, Zhang Jian-Jun. Research progress of silicon and germanium quantum computing materials. Acta Physica Sinica, 2021, 70(21): 217802. doi: 10.7498/aps.70.20211492
[11]	Zhang Shi-Hao, Zhang Xiang-Dong, Li Lü-Zhou. Research progress of measurement-based quantum computation. Acta Physica Sinica, 2021, 70(21): 210301. doi: 10.7498/aps.70.20210923
[12]	Wen Lian-Jun, Pan Dong, Zhao Jian-Hua. From high-quality semiconductor/superconductor nanowires to Majorana zero mode. Acta Physica Sinica, 2021, 70(5): 058101. doi: 10.7498/aps.70.20201750
[13]	Gu Kai-Yuan, Luo Tian-Chuang, Ge Jun, Wang Jian. Superconductivity in topological materials. Acta Physica Sinica, 2020, 69(2): 020301. doi: 10.7498/aps.69.20191627
[14]	Wang Jing. Chiral Majorana fermion. Acta Physica Sinica, 2020, 69(11): 117302. doi: 10.7498/aps.69.20200534
[15]	Kong Ling-Yuan, Ding Hong. Emergent vortex Majorana zero mode in iron-based superconductors. Acta Physica Sinica, 2020, 69(11): 110301. doi: 10.7498/aps.69.20200717
[16]	Liang Qi-Feng, Wang Zhi, Kawakami Takuto, Hu Xiao. Exploration of Majorana bound states in topological superconductors. Acta Physica Sinica, 2020, 69(11): 117102. doi: 10.7498/aps.69.20190959
[17]	Fan Heng. Quantum computation and quantum simulation. Acta Physica Sinica, 2018, 67(12): 120301. doi: 10.7498/aps.67.20180710
[18]	Zhao Shi-Ping, Liu Yu-Xi, Zheng Dong-Ning. Novel superconducting qubits and quantum physics. Acta Physica Sinica, 2018, 67(22): 228501. doi: 10.7498/aps.67.20180845
[19]	Zhao Na, Liu Jian-She, Li Tie-Fu, Chen Wei. Progress of coupled superconducting qubits. Acta Physica Sinica, 2013, 62(1): 010301. doi: 10.7498/aps.62.010301
[20]	Ye Bin, Gu Rui-Jun, Xu Wen-Bo. Robust quantum computation of the kicked Harper model and quantum chaos. Acta Physica Sinica, 2007, 56(7): 3709-3718. doi: 10.7498/aps.56.3709

Catalog

Vol. 69, Issue 11 - 2020-06-05

Metrics

Abstract views: 18759
PDF Downloads: 1356
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板