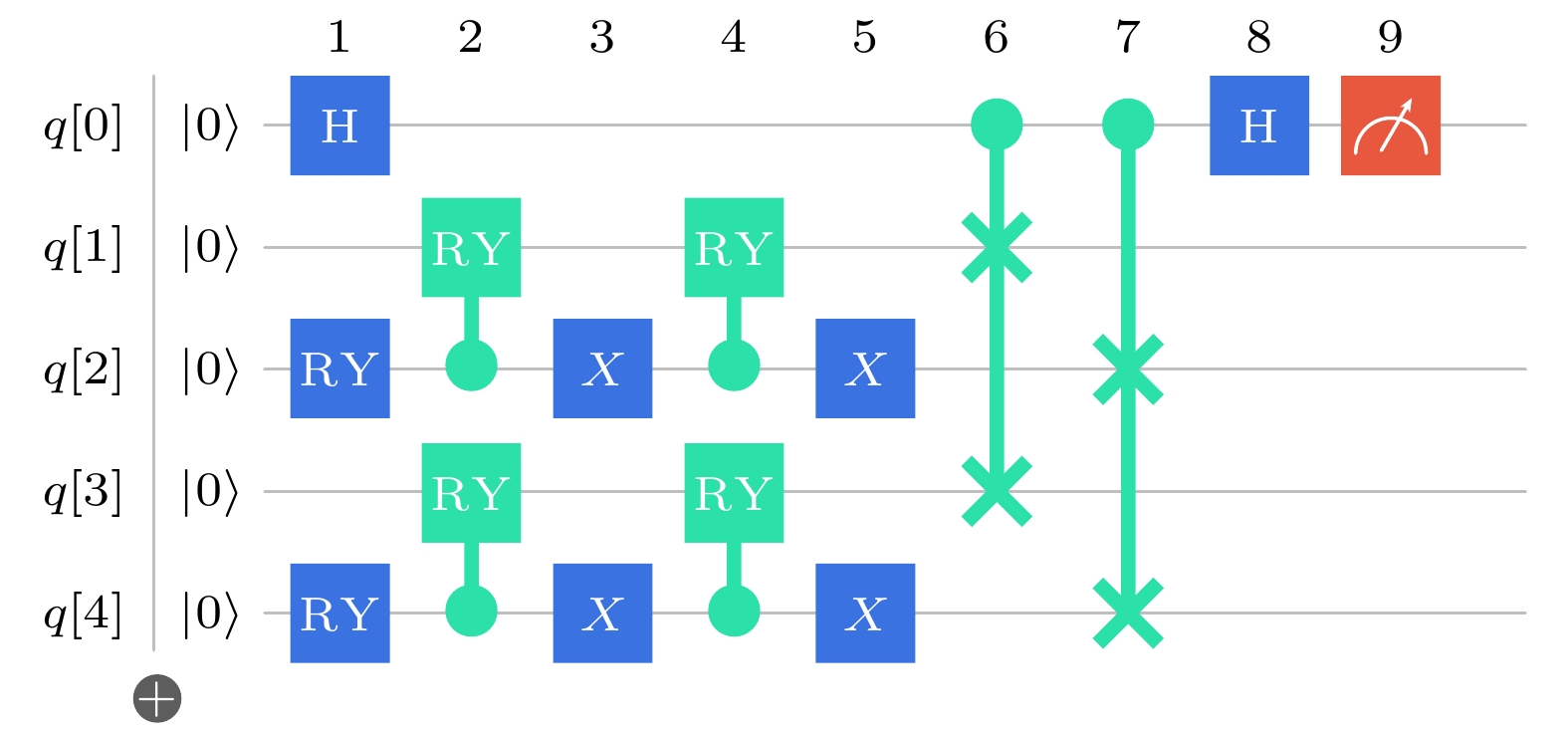
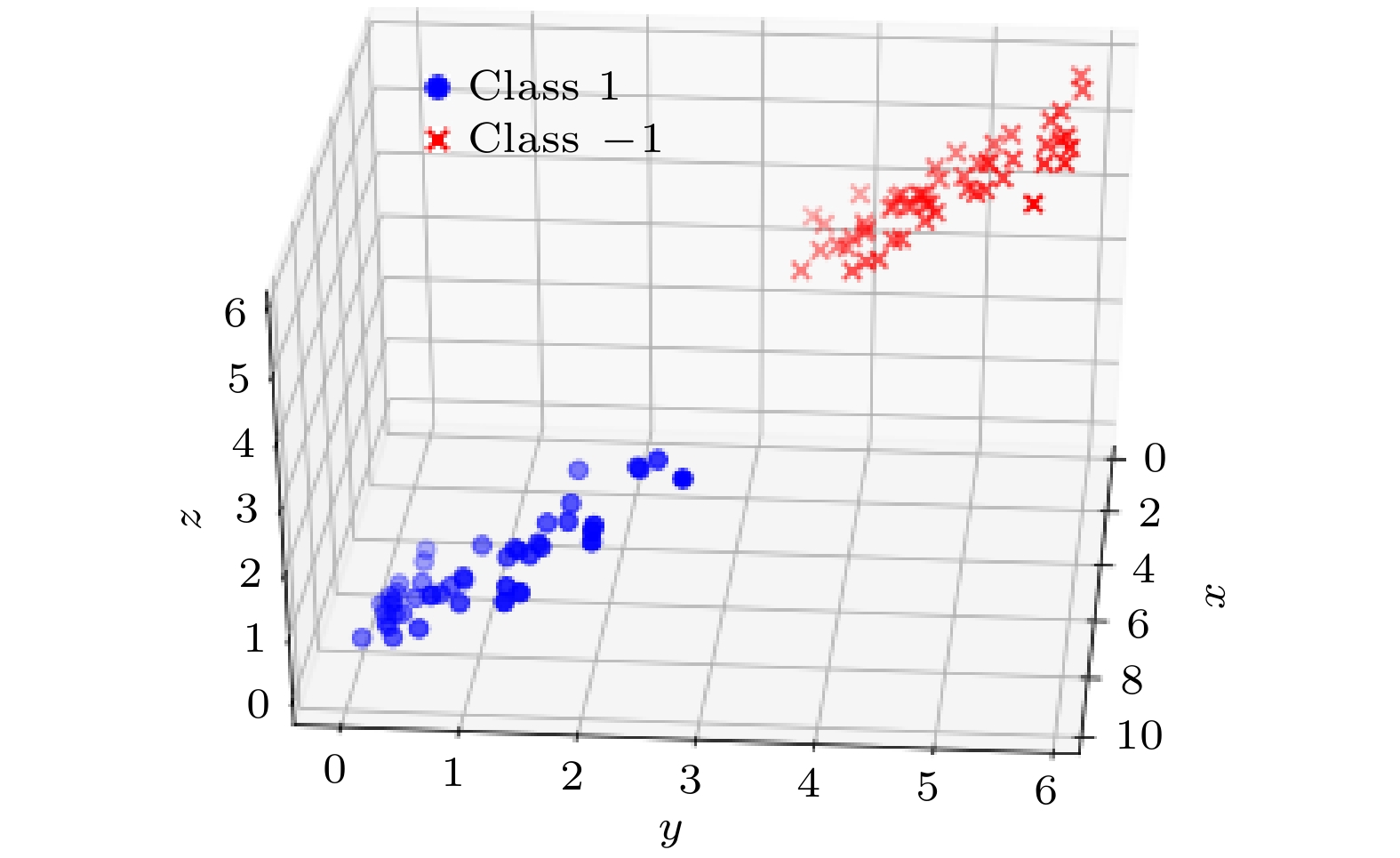
-
In order to improve the training efficiency of the support vector machine, a quantum circuit training scheme based on the inner product of the quantum state for the support vector machine is proposed in this work. Firstly, on the basis of the full analysis of the computational complexity of the classical support vector machine, the kernel function which is the main factor affecting the computational complexity of the algorithm is primarily analyzed. Based on quantum mechanics and quantum computing theory, the training sample elements in the kernel function are quantized to generate the corresponding quantum states. Secondly, according to the quantum states of the training sample elements, the types and quantities of the required quantum logic gates are derived and calculated, and the quantum circuit that can generate the corresponding quantum states of the training sample elements through the evolution of the quantum initial ground states and the quantum logic gates is designed. Then, in the light of the relationship between the inner product of the quantum state and the quantum logic gate SWAP, the quantum circuit is designed to complete the exchange operation of the corresponding quantum state amplitude. The inner product of the quantum state is realized by exchanging and evolving the amplitude of the quantum state in the quantum circuit. Finally, by measuring the quantum state of the controlling qubit, the inner product solution of the kernel function is obtained, and the acceleration effect of training support vector machine is realized. The verification results show that the scheme enables the support vector machine not only to complete the correct classification, but also to operate the quantum part of the scheme on the real quantum computer . Compared with the classical algorithm, the scheme reduces the time complexity of the algorithm for the polynomial degree, greatly shortens the training time of the model, and improves the efficiency of the algorithm. The scheme has certain feasibility, effectiveness and innovation, and expands the training idea of the support vector machine.
-
Keywords:
- quantum circuit /
- inner product /
- quantum state /
- support vector machine
[1] Cortes C, Vapnik V 1995 Mach. Learn. 20 273
[2] Sebastian S, Matthias S, Christian S 2021 ACM J. Exp. Algor. 26 1
[3] Vapnik V N 2000 The Nature of Statistical Learning Theory (New York: Springer-Verlag Press) pp25–314
[4] Jiang F, Lu Y, Chen Y, Cai D, Li G F 2020 Comput. Electron. Agr. 179 105824
Google Scholar
[5] Zhang Q, Liu J M, Tian Y 2022 Optik 260 168807
Google Scholar
[6] Okwuashi O, Ndehedehe C E, Olayinka D N, Eyoh A, Attai H 2021 Int. J. Remote Sens. 42 6502
[7] Kalaiarasi G, Maheswari S 2021 Neural Comput. Appl. 33 13391
Google Scholar
[8] Liu L M, Li P, Chu M X, Cai H B 2021 Int. J. Mach. Learn. Cyb. 12 2237
Google Scholar
[9] Reshma R, Pooja S, Suresh C 2018 Knowl. Based Syst. 139 64
Google Scholar
[10] Riyazuddin Y M, Basha S M, Reddy K K 2020 Int. J. Eng. Adv. Tech. 9 1336
[11] Ma W Z, Cao Y, Bao W Z, Yang B, Chen Y H 2020 Sci. Programming-Neth 20 1
[12] Cheng Y W, Fu L Y, Luo P, Ye Q L, Liu F, Zhu W 2020 Knowl. -Based Syst. 210 106488
Google Scholar
[13] Deen A J, Gyanchandani M 2020 Int. J. Adv. Comput. Sci. Appl. 11 187
[14] Kumaresan T, Palanisamy C 2017 Int. J. Bio-Inspire. Com. 9 142
Google Scholar
[15] Chen Y 2020 Comput. Commun. 154 278
Google Scholar
[16] Lu Y L, Li J T, Yang Z H, Ou X F, Xie W W 2021 J. Comput. Methods Sci. 21 435
[17] Tukan M, Baykal C, Feldman D, Rus D 2021 Theor. Comput. Sci. 890 171
Google Scholar
[18] Zhao J 2021 J. Phys. Conf. Ser. 1748 052006
Google Scholar
[19] Mangasarian O L, Wild E W 2006 IEEE T. Pattern Anal. 28 69
Google Scholar
[20] Zhang L, Suganthan P N 2015 IEEE T. Cybernetics 45 2165
Google Scholar
[21] Xu J, Tang Y Y, Zou B, Xu Z B, Li L Q, Lu Y, Zhang B C 2015 IEEE T. Cybernetics 45 1169
Google Scholar
[22] Zou B, Xu C, Lu Y, Tang Y Y, Xu J, You X G 2018 IEEE T. Neur. Net. Lear. 29 1328
Google Scholar
[23] Wu X H, Shi Z F, Xing H H, Xue Y S 2022 MATEC Web Conf. 355 03059
Google Scholar
[24] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[25] Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, Hu P, Yang Y X, Zhang W J, Li H, Li Y X, Jiang X, Gan L, Yang G W, You L X, Wang Z, Li L, Liu N L, Lu C Y, Pan J W 2020 Science 370 1460
Google Scholar
[26] Zhua Q L, Cao S R, Chen F S, et al. 2022 Sci. Bull. 67 240
Google Scholar
[27] Deshpande A, Mehta A, Vincent T, Quesada N, Hinsche M, Ioannou M, Madsen L, Lavoie J, Qi H Y, Eisert J, Hangleiter D, Fefferman B, Dhand I 2022 Sci. Adv. 8 eabi7894
Google Scholar
[28] Yuan X 2020 Science 369 1054
Google Scholar
[29] Zhang Y J, Mu X D, Liu X W, Wang X Y, Zhang X, Li K, Wu T Y, Zhao D, Dong C 2022 Appl. Soft Comput. 118 108554
Google Scholar
[30] Fan J N, Wu S X, Yu C S 2021 Quantum Inf. Process. 20 9
Google Scholar
[31] Huang S, Yin H L, Chen Z B, Wu S J 2022 arXiv: 2203.12884 v1
[32] Booth K E C, O'Gorman B, Marshall J, Hadfield S, Rieffel E 2021 Quantum 5 550
Google Scholar
[33] Rujuta V, Nagraj D, Rajesh K, Akash S 2021 Knowl. Based Syst. 219 106859
Google Scholar
[34] Chen J W, Qi X M, Chen L F, Chen F L, Cheng G H 2020 Knowl. Based Syst. 203 106167
Google Scholar
[35] Lloyd S, Mohseni M, Rebentrost P 2013 arXiv: 1307.0411 v1
[36] Rebentrost P, Mohseni M, Lloyd S 2014 Phys. Rev. Lett. 113 130503
Google Scholar
[37] Boser B E, Guyou I M, Vapnik V N 1992 Proceedings of the 5th Annual Workshop on Computational Learning Theory Pittsburgh Pennsylvania, USA, July 1–2, 1992 p144
[38] Osuna E, Frenud R, Girosi F 1997 Proceedings of the 1997 IEEE Signal Processing Society Workshop on Neural Networks for Signal Processing VII Amelia Island, FL, USA, September 24–26, 1997 p276
[39] Platt J C 1998 Advances in Kernel Methods-Support Vecotor Learning (Cambridge MA: MIT Press) pp41–65
[40] Ralaivola L, Alché-Buc F D' 2001 Proceedings of International Conference on Artificial Neural Networks Vienna, Austria, August 21–25, 2001 p322
-
图 1 制备量子态
$\left|\varphi \right\rangle$ 的量子线路简略图Fig. 1. The schematic diagram of the quantum circuit for preparing the quantum state
$\left|\varphi \right\rangle$ 
图 2 制备量子态
$\left|\varphi \right\rangle$ 和$\left|\phi \right\rangle$ 的量子线路Fig. 2. The quantum circuit for preparing the quantum states
$\left|\varphi \right\rangle$ and$\left|\phi\right\rangle$ 
图 5 5组数据用标准基态
$\left|0\right\rangle$ 和$\left|1\right\rangle$ 分别测量0和1的概率Fig. 5. The probability of 0 and 1 separately measured by standard ground state
$\left|0\right\rangle$ and$\left|1\right\rangle$ for five groups of data.
图 7 量子方案与经典方法训练效果对比
Fig. 7. Comparison of the training results between the IPQS-based quantum circuit solution scheme and the SMO-based method.
表 1 量子方案与经典方法求解内积结果对比
Table 1. Comparison of the inner product results between the quantum scheme and the classical method.
SN Data group Result of 0 Result of 1 Classical calculation Error rate/% Inner product value 1 (2.942485, 4.977398, 3.176513)(7.551510, 1.580030, 0.067732) 29.679279 29.679279 30.299795 2.05 2 (0.341367, 3.894998, 3.929515)(7.139979, 2.329896, 1.981083) 19.255815 19.255815 19.296989 0.21 3 (6.080573, 0.418886, 1.33507)(9.205805, 0.586480, 0.958476) 57.284265 57.284265 57.501870 0.38 4 (0.870296, 3.609952, 3.851484)(3.536555, 3.964960, 4.16744) 33.501898 33.501898 33.441993 0.18 5 (0.926310, 4.564359, 5.114204)(8.102154, 0.603875, 0.617218) 13.805552 13.805552 13.417987 2.89 
下载: 导出CSV
表 2 基于量子态内积的量子线路训练方案的伪代码
Table 2. The pseudo code of the IPQS-based quantum circuit solution scheme.
算法1. 基于量子态内积的量子线路训练方案 输入: 训练样本集数据. 输出: 支持向量机相关参数. 初始化训练样本数据M和数据特征数量N, 初始化目标函数和约束条件, 初始化量子线路运行环境$ {Q}_{r} $和量子比特数量$n\leftarrow \lceil{ {\rm{log} } }_{2}N\rceil$.1: 使用SMO算法求解拉格朗日乘子向量
$ \left({\alpha }_{1}, {\alpha }_{2}, \cdots , $$ {\alpha }_{M}\right) $;// 2.1节2: while 不满足停止条件时 do3: for $ i, j=1:M $ do4: 通过启发式策略选择一对 $ {\alpha }_{i} $ and $ {\alpha }_{j} $;// 2.1节5: 初始化量子态;6: 生成量子态制备对应的量子线路;// (23)式7: 生成量子态内积对应的量子线路;// (25)式8: 通过量子线路计算对应训练样本之间的内积;//
(19), (26) and (27) 式9: 计算 $ {\alpha }_{i}^{{\rm{n}}{\rm{e}}{\rm{w}}} $;// (10)式10: 计算 $ {\alpha }_{j}^{{\rm{n}}{\rm{e}}{\rm{w}}} $;// (11)式11: 计算 $ {b}_{i}^{{\rm{n}}{\rm{e}}{\rm{w}}} $;// (12)式12: 计算 $ {b}_{j}^{{\rm{n}}{\rm{e}}{\rm{w}}} $;// (13)式13: 更新$ {\alpha }_{i}, {\alpha }_{j}, b $的值;14: end for15: end while16: 输出$ \alpha $与b
下载: 导出CSV
-
[1] Cortes C, Vapnik V 1995 Mach. Learn. 20 273
[2] Sebastian S, Matthias S, Christian S 2021 ACM J. Exp. Algor. 26 1
[3] Vapnik V N 2000 The Nature of Statistical Learning Theory (New York: Springer-Verlag Press) pp25–314
[4] Jiang F, Lu Y, Chen Y, Cai D, Li G F 2020 Comput. Electron. Agr. 179 105824
Google Scholar
[5] Zhang Q, Liu J M, Tian Y 2022 Optik 260 168807
Google Scholar
[6] Okwuashi O, Ndehedehe C E, Olayinka D N, Eyoh A, Attai H 2021 Int. J. Remote Sens. 42 6502
[7] Kalaiarasi G, Maheswari S 2021 Neural Comput. Appl. 33 13391
Google Scholar
[8] Liu L M, Li P, Chu M X, Cai H B 2021 Int. J. Mach. Learn. Cyb. 12 2237
Google Scholar
[9] Reshma R, Pooja S, Suresh C 2018 Knowl. Based Syst. 139 64
Google Scholar
[10] Riyazuddin Y M, Basha S M, Reddy K K 2020 Int. J. Eng. Adv. Tech. 9 1336
[11] Ma W Z, Cao Y, Bao W Z, Yang B, Chen Y H 2020 Sci. Programming-Neth 20 1
[12] Cheng Y W, Fu L Y, Luo P, Ye Q L, Liu F, Zhu W 2020 Knowl. -Based Syst. 210 106488
Google Scholar
[13] Deen A J, Gyanchandani M 2020 Int. J. Adv. Comput. Sci. Appl. 11 187
[14] Kumaresan T, Palanisamy C 2017 Int. J. Bio-Inspire. Com. 9 142
Google Scholar
[15] Chen Y 2020 Comput. Commun. 154 278
Google Scholar
[16] Lu Y L, Li J T, Yang Z H, Ou X F, Xie W W 2021 J. Comput. Methods Sci. 21 435
[17] Tukan M, Baykal C, Feldman D, Rus D 2021 Theor. Comput. Sci. 890 171
Google Scholar
[18] Zhao J 2021 J. Phys. Conf. Ser. 1748 052006
Google Scholar
[19] Mangasarian O L, Wild E W 2006 IEEE T. Pattern Anal. 28 69
Google Scholar
[20] Zhang L, Suganthan P N 2015 IEEE T. Cybernetics 45 2165
Google Scholar
[21] Xu J, Tang Y Y, Zou B, Xu Z B, Li L Q, Lu Y, Zhang B C 2015 IEEE T. Cybernetics 45 1169
Google Scholar
[22] Zou B, Xu C, Lu Y, Tang Y Y, Xu J, You X G 2018 IEEE T. Neur. Net. Lear. 29 1328
Google Scholar
[23] Wu X H, Shi Z F, Xing H H, Xue Y S 2022 MATEC Web Conf. 355 03059
Google Scholar
[24] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[25] Zhong H S, Wang H, Deng Y H, Chen M C, Peng L C, Luo Y H, Qin J, Wu D, Ding X, Hu Y, Hu P, Yang Y X, Zhang W J, Li H, Li Y X, Jiang X, Gan L, Yang G W, You L X, Wang Z, Li L, Liu N L, Lu C Y, Pan J W 2020 Science 370 1460
Google Scholar
[26] Zhua Q L, Cao S R, Chen F S, et al. 2022 Sci. Bull. 67 240
Google Scholar
[27] Deshpande A, Mehta A, Vincent T, Quesada N, Hinsche M, Ioannou M, Madsen L, Lavoie J, Qi H Y, Eisert J, Hangleiter D, Fefferman B, Dhand I 2022 Sci. Adv. 8 eabi7894
Google Scholar
[28] Yuan X 2020 Science 369 1054
Google Scholar
[29] Zhang Y J, Mu X D, Liu X W, Wang X Y, Zhang X, Li K, Wu T Y, Zhao D, Dong C 2022 Appl. Soft Comput. 118 108554
Google Scholar
[30] Fan J N, Wu S X, Yu C S 2021 Quantum Inf. Process. 20 9
Google Scholar
[31] Huang S, Yin H L, Chen Z B, Wu S J 2022 arXiv: 2203.12884 v1
[32] Booth K E C, O'Gorman B, Marshall J, Hadfield S, Rieffel E 2021 Quantum 5 550
Google Scholar
[33] Rujuta V, Nagraj D, Rajesh K, Akash S 2021 Knowl. Based Syst. 219 106859
Google Scholar
[34] Chen J W, Qi X M, Chen L F, Chen F L, Cheng G H 2020 Knowl. Based Syst. 203 106167
Google Scholar
[35] Lloyd S, Mohseni M, Rebentrost P 2013 arXiv: 1307.0411 v1
[36] Rebentrost P, Mohseni M, Lloyd S 2014 Phys. Rev. Lett. 113 130503
Google Scholar
[37] Boser B E, Guyou I M, Vapnik V N 1992 Proceedings of the 5th Annual Workshop on Computational Learning Theory Pittsburgh Pennsylvania, USA, July 1–2, 1992 p144
[38] Osuna E, Frenud R, Girosi F 1997 Proceedings of the 1997 IEEE Signal Processing Society Workshop on Neural Networks for Signal Processing VII Amelia Island, FL, USA, September 24–26, 1997 p276
[39] Platt J C 1998 Advances in Kernel Methods-Support Vecotor Learning (Cambridge MA: MIT Press) pp41–65
[40] Ralaivola L, Alché-Buc F D' 2001 Proceedings of International Conference on Artificial Neural Networks Vienna, Austria, August 21–25, 2001 p322
下载:
计量
- 文章访问数: 3948
- PDF下载量: 76
- 被引次数: 0
