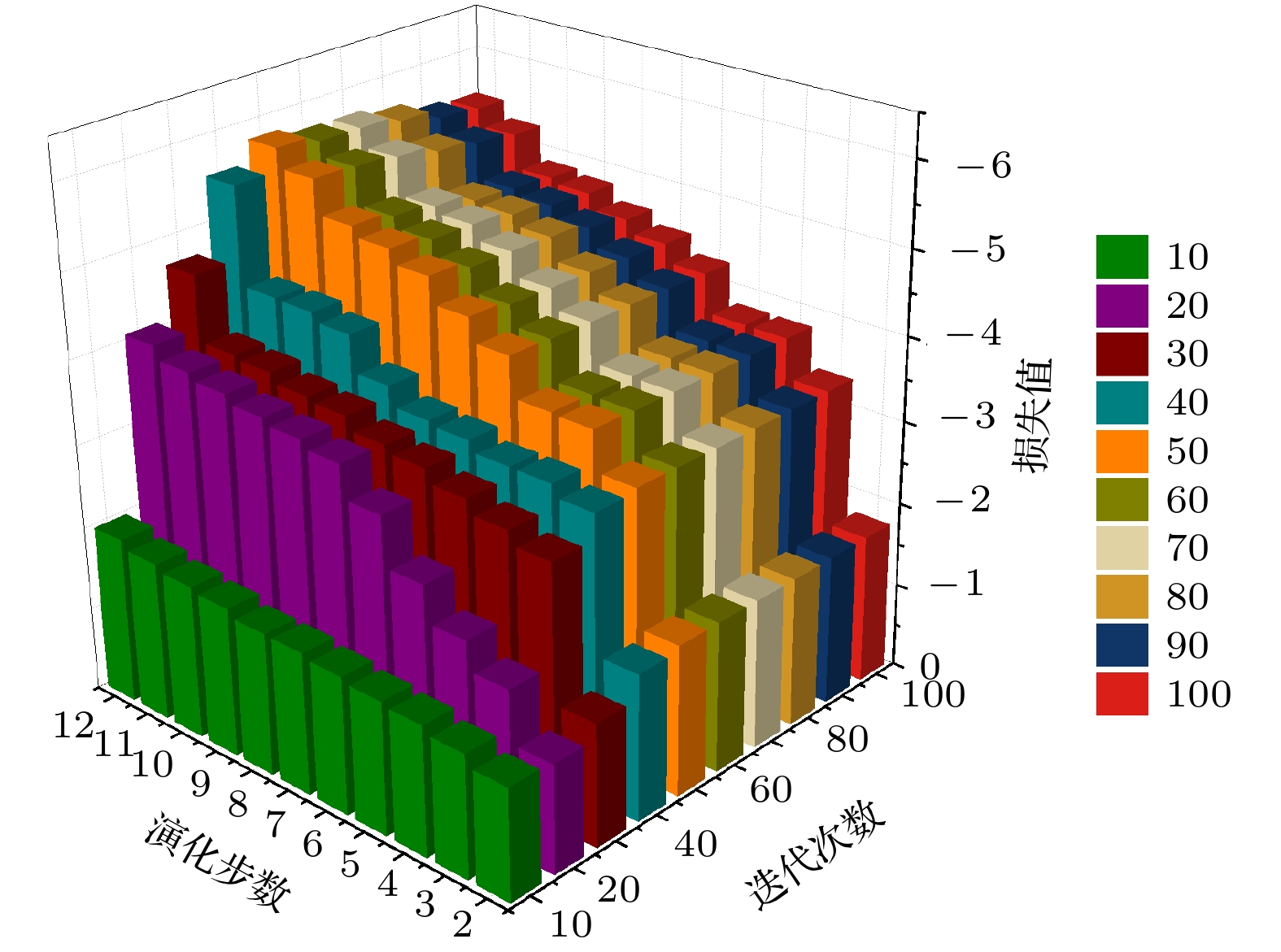
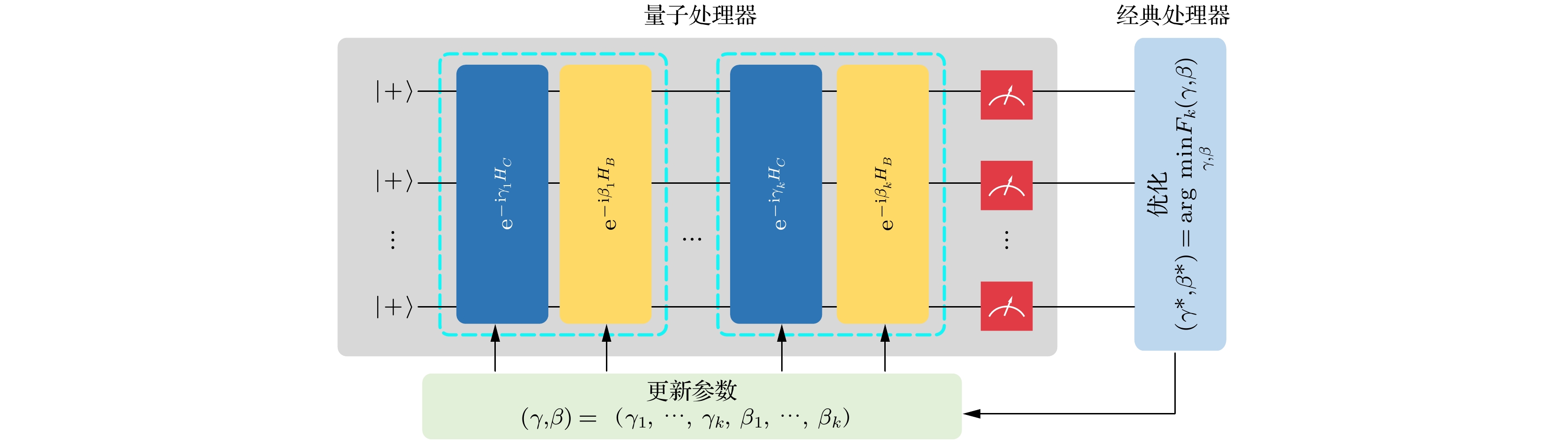
-
The mission planning problem in command and control organization can be mapped into a combinatorial optimization problem with many variables and is difficult to solve. The traditional heuristic list planning method faces the problems of high time complexity and poor real-time response. For the mission planning problem in command and control organization, a quantum circuit solution scheme is proposed based on quantum approximate optimization algorithm in this work. Firstly, the mission planning problem is transformed into a typical combinatorial optimization problem, the exact coverage problem. Then, by constructing the corresponding mathematical model, the final state Hamiltonian expression of the quantum approximate optimization algorithm for the exact coverage problem is derived. The quantum circuit based on the quantum approximate optimization algorithm is designed. Finally the parameters in the quantum logic gate are optimized by the momentum gradient descent algorithm, and the simulation experiment is carried out by using the quantum software development environment of the Origin Quantum Computing Company. The simulation results show that the quantum circuit scheme can be used to solve the mission planning problem, reduce the time complexity of the algorithm, and improve the resource utilization to a certain extent. This work lays the foundation for further application of quantum algorithm to solving the mission planning problem in command and control organization.
[1] 张杰勇, 姚佩阳, 周翔翔, 孙鹏 2012 火力与指挥控制 37 2293
Zhang J Y, Yao P Y, Zhou X X, Sun P 2012 Fire Control and Command Control 37 2293
[2] 张杰勇, 姚佩阳, 周翔翔, 王欣 2012 系统工程与电子技术 34 947
Google Scholar
Zhang J Y, Yao P Y, Zhou X X, Wang X 2012 Syst. Eng. Electron. 34 947
Google Scholar
[3] Sih G C, Lee E A 1993 IEEE Trans. Parallel Distrib. Syst. 4 175
Google Scholar
[4] Levchuk G M, Levchuk Y N, Luo J 2002 IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 32 346
Google Scholar
[5] 阳东升, 张维明, 刘忠, 等 2006 系统工程理论与实践 01 26
Google Scholar
Yang D S, Zhang W M, Liu Z, et al. 2006 Syst. Eng. Theor. Pract. 01 26
Google Scholar
[6] 鲁音隆, 阳东升, 刘忠, 等 2006 火力与指挥控制 31 12
Google Scholar
Lu Y L, Yang D S, Liu Z, et al. 2006 Fire Control and Command Control 31 12
Google Scholar
[7] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[8] Farhi E, Harrow A W 2019 arXiv: 1602.07674 v2 [quant-ph]
[9] Lin C Y Y, Zhu Y 2016 arXiv: 1601.01744 v1 [quant-ph]
[10] Wecker D, Hastings M B, Troyer M 2016 Phys. Rev. A 94 022309
Google Scholar
[11] Lechner W 2020 IEEE Trans. Quantum Eng. 1 3102206
[12] Yang Z C, Rahmani A, Shabani A, Neven H, Chamon C 2017 Phys. Rev. X 7 021027
[13] Zahedinejad E, Zaribafiyan A 2017 arXiv: 1708.05294 v1 [quant-ph]
[14] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 v1 [quant-ph]
[15] Albash T, Lidar D A 2018 Rev. Mod. Phys. 90 015002
Google Scholar
[16] Crooks G E 2018 arXiv: 1811.08419 v1[quant-ph]
[17] Guerreschi G G, Matsuura A Y 2019 Sci. Rep.s 9 6903
Google Scholar
[18] Wang Z, Hadfield S, Jiang Z, Rieffel E G 2018 Phys. Rev. A 97 022304
Google Scholar
[19] Farhi E, Goldstone J, Gutmann S, Lapan J, Lundgren A, Preda D 2001 Science 292 472
Google Scholar
[20] Young A P, Knysh S, Smelyanskiy V N 2010 Phys. Rev. Lett. 104 020502
Google Scholar
[21] Altshuler B, Krovi H, Rol J 2010 Proc. Natl.Acad. Sci. U. S. A. 107 12446
Google Scholar
[22] Choi V 2010 Comput. Sci. 108 7
[23] Wang H, Wu L A 2016 Sci. Rep. 6 22307
Google Scholar
[24] Graß T 2019 Phys. Rev. Lett. 123 120501
Google Scholar
[25] Lucas A 2014 Front.Phys. 2 5
[26] Fu Y, Anderson P W 1986 J. Phys. A 19 1605
Google Scholar
[27] Mézard M, Montanari A 2009 Information, Physics and Computation P35
[28] Vikstål P, Grönkvist M, Svensson M, et al. 2020 Phys. Rev. Appl. 14 034009
Google Scholar
[29] Broyden C G 1970 IMA J. Appl. Math. 6 76
Google Scholar
[30] Nelder J A, Mead R 1965 Comput. J. 7 308
Google Scholar
[31] Frazier P I 2018 arXiv: 1807.02811 v1 [stat.ML]
[32] Zhou L, Wang S T, Choi S, et al. 2020 Phys. Rev. X 10 021067
[33] 王培良, 张婷, 肖英杰 2020 69 080504
Google Scholar
Wang P L, Zhang T, Xiao Y J 2020 Acta Phys. Sin. 69 080504
Google Scholar
-
图 1 QAOA实现框架示意图
Figure 1. Schematic diagram of the QAOA implementation.
图 2 基于QAOA的4个量子比特量子线路图
Figure 2. Four-qubit quantum circuit based on QAOA.
图 3 不同迭代次数和演化步数对应的损失值
Figure 3. Loss values corresponding to different iterations and evolution steps.
图 4 演化步数为12, 迭代次数分别为50−100对应的损失值
Figure 4. The corresponding loss values with 12 evolution steps and 50−100 iterations, respectively.
图 5 迭代次数为50, 演化步数为2至12对应的问题正确解概率
Figure 5. The accuracy of the QAOA with 50 iterations and 2−12 evolution steps.
图 6 迭代次数为50, 演化步数为12对应的测量结果
Figure 6. Results with 50 iterations and 12 evolution steps.
表 1 平台对应可执行任务分配方案
Table 1. Platforms corresponding executable mission allocation.
平 台 1 2 3 4 5 6 平台可执
行的任务1,2,3 1,2,3,4 3,4,5,6 5,6,7,8 7,8,9,10 9,10,11,12 
DownLoad: CSV
-
[1] 张杰勇, 姚佩阳, 周翔翔, 孙鹏 2012 火力与指挥控制 37 2293
Zhang J Y, Yao P Y, Zhou X X, Sun P 2012 Fire Control and Command Control 37 2293
[2] 张杰勇, 姚佩阳, 周翔翔, 王欣 2012 系统工程与电子技术 34 947
Google Scholar
Zhang J Y, Yao P Y, Zhou X X, Wang X 2012 Syst. Eng. Electron. 34 947
Google Scholar
[3] Sih G C, Lee E A 1993 IEEE Trans. Parallel Distrib. Syst. 4 175
Google Scholar
[4] Levchuk G M, Levchuk Y N, Luo J 2002 IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 32 346
Google Scholar
[5] 阳东升, 张维明, 刘忠, 等 2006 系统工程理论与实践 01 26
Google Scholar
Yang D S, Zhang W M, Liu Z, et al. 2006 Syst. Eng. Theor. Pract. 01 26
Google Scholar
[6] 鲁音隆, 阳东升, 刘忠, 等 2006 火力与指挥控制 31 12
Google Scholar
Lu Y L, Yang D S, Liu Z, et al. 2006 Fire Control and Command Control 31 12
Google Scholar
[7] Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505
Google Scholar
[8] Farhi E, Harrow A W 2019 arXiv: 1602.07674 v2 [quant-ph]
[9] Lin C Y Y, Zhu Y 2016 arXiv: 1601.01744 v1 [quant-ph]
[10] Wecker D, Hastings M B, Troyer M 2016 Phys. Rev. A 94 022309
Google Scholar
[11] Lechner W 2020 IEEE Trans. Quantum Eng. 1 3102206
[12] Yang Z C, Rahmani A, Shabani A, Neven H, Chamon C 2017 Phys. Rev. X 7 021027
[13] Zahedinejad E, Zaribafiyan A 2017 arXiv: 1708.05294 v1 [quant-ph]
[14] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 v1 [quant-ph]
[15] Albash T, Lidar D A 2018 Rev. Mod. Phys. 90 015002
Google Scholar
[16] Crooks G E 2018 arXiv: 1811.08419 v1[quant-ph]
[17] Guerreschi G G, Matsuura A Y 2019 Sci. Rep.s 9 6903
Google Scholar
[18] Wang Z, Hadfield S, Jiang Z, Rieffel E G 2018 Phys. Rev. A 97 022304
Google Scholar
[19] Farhi E, Goldstone J, Gutmann S, Lapan J, Lundgren A, Preda D 2001 Science 292 472
Google Scholar
[20] Young A P, Knysh S, Smelyanskiy V N 2010 Phys. Rev. Lett. 104 020502
Google Scholar
[21] Altshuler B, Krovi H, Rol J 2010 Proc. Natl.Acad. Sci. U. S. A. 107 12446
Google Scholar
[22] Choi V 2010 Comput. Sci. 108 7
[23] Wang H, Wu L A 2016 Sci. Rep. 6 22307
Google Scholar
[24] Graß T 2019 Phys. Rev. Lett. 123 120501
Google Scholar
[25] Lucas A 2014 Front.Phys. 2 5
[26] Fu Y, Anderson P W 1986 J. Phys. A 19 1605
Google Scholar
[27] Mézard M, Montanari A 2009 Information, Physics and Computation P35
[28] Vikstål P, Grönkvist M, Svensson M, et al. 2020 Phys. Rev. Appl. 14 034009
Google Scholar
[29] Broyden C G 1970 IMA J. Appl. Math. 6 76
Google Scholar
[30] Nelder J A, Mead R 1965 Comput. J. 7 308
Google Scholar
[31] Frazier P I 2018 arXiv: 1807.02811 v1 [stat.ML]
[32] Zhou L, Wang S T, Choi S, et al. 2020 Phys. Rev. X 10 021067
[33] 王培良, 张婷, 肖英杰 2020 69 080504
Google Scholar
Wang P L, Zhang T, Xiao Y J 2020 Acta Phys. Sin. 69 080504
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5086
- PDF Downloads: 117
- Cited By: 0
