-
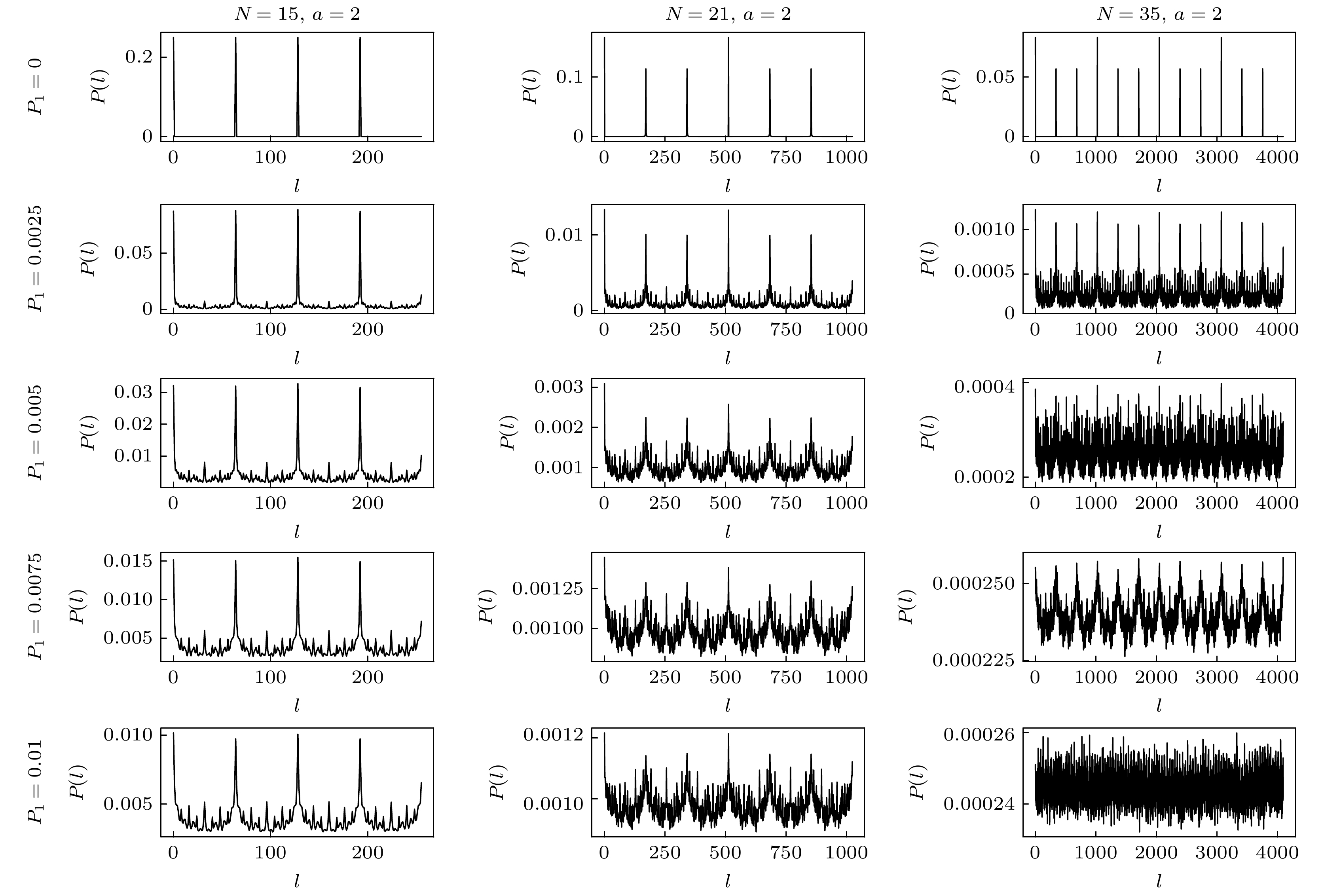
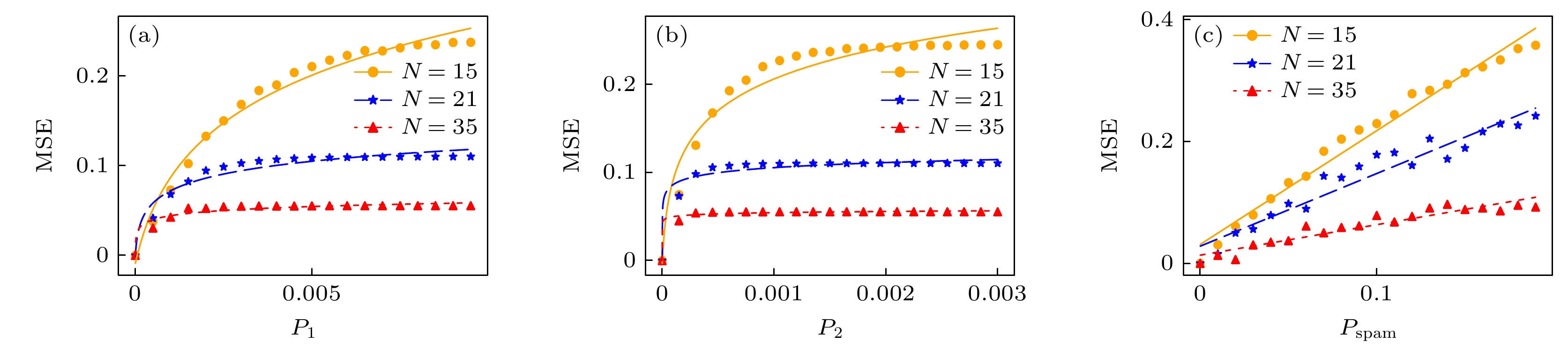
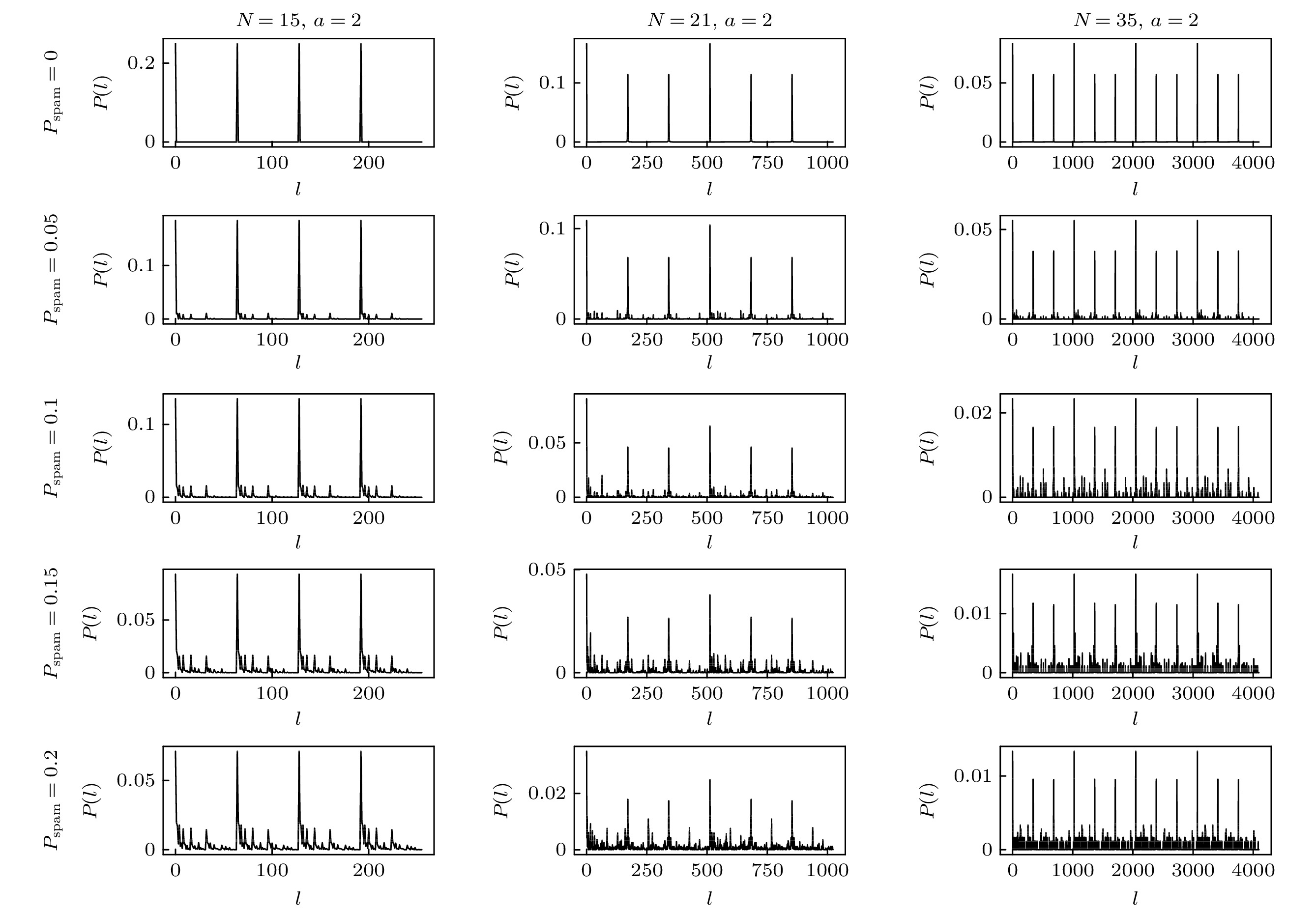
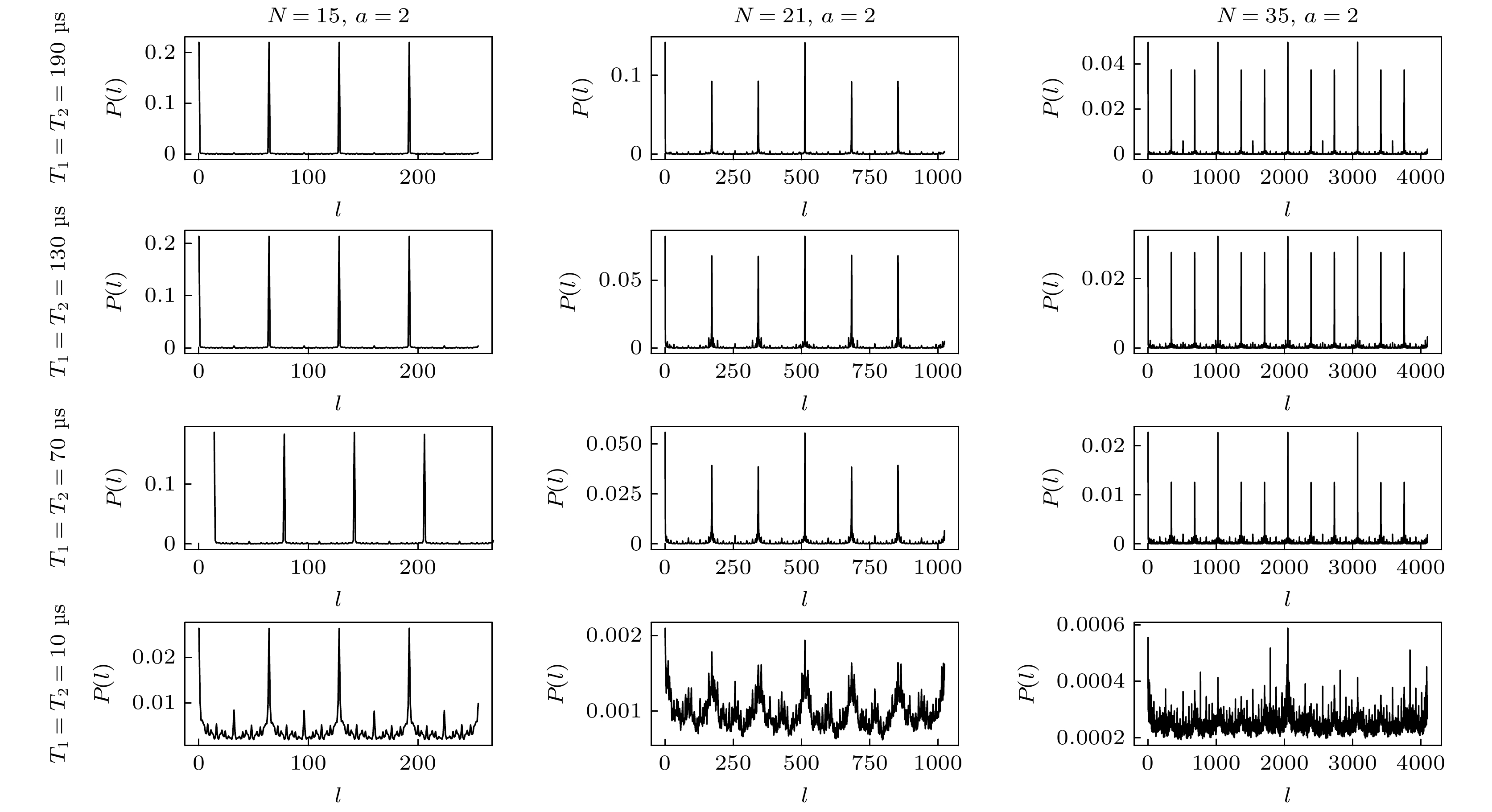
Shor’s quantum factoring algorithm (Shor’s algorithm) can solve factorization problem of large integers by using a fully-operational quantum computer with the complexity of polynomial-time level, thereby cracking a series of encryption algorithms (such as Rivest-Shamir-Adleman encryption algorithm, and Diffie-Hellman key exchange protocol) whose security is guaranteed by factorizing large integers, which is a difficult problem. We are currently in a noisy intermediate-scale quantum era, which means that we can only operate on quantum computers with a limited number of qubits and we have to take care of the effects of quantum noise. Quantum states on a quantum computer are prone to quantum noise caused by low-fidelity gates or interactions between qubits and the environment, which results in inaccurate measurements. We study the influence of quantum noise on Shor’s algorithm through 3 typical quantum noise channels: the depolarizing channel, the state preparation and measurement channel, and the thermal relaxation channel. We successfully simulate the factorization of the numbers 15, 21, and 35 into their corresponding prime factors by using the quantum circuit we have constructed on a classical computer. Then we simulate a running quantum circuit of Shor’s algorithm in a noisy environment with different level of noise for a certain type of noise channel and present numerical results. We can obtain precise measurements by calculating the state vector prior to measurement, instead of simulating and measuring expending much time, which contributes to higher efficiency. Each experiment is repeated 1000 times to reduce discrepancy. Our research indicates that Shor’s algorithm is easily affected by quantum noise. Successful rate of Shor’s algorithm decreases exponentially with the increase of noise level in the depolarizing channel, where the successful rate is an indicator we propose in this research to quantify the influence of noise on Shor’s algorithm, meanwhile the noise in the state preparation and measurement channel and the thermal relaxation channel can linearly affect the successful rate of Shor’s algorithm. There are
$O(n^4) $ quantum gates in the circuit, each of which is disrupted by noise in depolarizing channel during running the circuit, meanwhile there are only O(n) interruptions caused by noise in state preparation and measurement channel since we repeat the measurements only O(n) times in the circuit where n is the number of bits of the integer about to be factored. Linear relationship in thermal relaxation channel is mainly due to the large gap between quantum gate time and relaxation time even if each gate in the circuit is disrupted by noise in thermal relaxation channel such as depolarizing channel. The present research results can be used for correcting the subsequent errors, improving Shor’s algorithm, and providing guidance for the fidelity required in engineering implementation of Shor’s algorithm.-
Keywords:
- quantum computing /
- quantum algorithm /
- quantum noise /
- Shor’s algorithm
[1] Shor P W 1994 Proceedings of the 35th Annual Symposium on Foundations of Computer Science Washington DC, USA, November 20–22, 1994 p124
[2] Shor P W 1999 SIAM Rev. Soc. Ind. Appl. Math 41 303
[3] Lenstra A K, Hendrik Jr W 1993 The Development of the Number Field Sieve(Vol. 1554) (Heidelberg : Springer Science & Business Media) p5
[4] Lenstra A K, Lenstra Jr H W, Manasse M S, Pollard J M 1990 Proceedings of the Twenty-second Annual ACM Symposium on Theory of Computing Baltimore Maryland, USA, May 13–17, 1990 p564
[5] Buhler J P, Lenstra H W, Pomerance C 1993 The Development of the Number Field Sieve (Berlin Heidelberg: Springer) pp50–94
[6] Kleinjung T, Aoki K, Franke J, Lenstra A K, Thomé E, Bos J W, Gaudry P, Kruppa A, Montgomery P L, Osvik D A, Riele H T, Timofeev A, Zimmermann P 2010 Advances in Cryptology–CRYPTO 2010: 30th Annual Cryptology Conference Santa Barbara, CA, USA, August 15–19, 2010 p333
[7] Gidney C, Ekerå M 2021 Quantum 5 433
 Google Scholar
Google Scholar
[8] Preskill J 2018 Quantum 2 79
 Google Scholar
Google Scholar
[9] Harper R, Flammia S T, Wallman J J 2020 Nat. Phys. 16 1184
 Google Scholar
Google Scholar
[10] Georgopoulos K, Emary C, Zuliani P 2021 Phys. Rev. A 104 062432
 Google Scholar
Google Scholar
[11] Brown K R, Harrow A W, Chuang I L 2004 Phys. Rev. A 70 052318
 Google Scholar
Google Scholar
[12] Bassi A, Großardt A, Ulbricht H 2017 Classical Quantum Gravity 34 193002
 Google Scholar
Google Scholar
[13] Viola L, Knill E, Lloyd S 1999 Phys. Rev. Lett. 82 2417
 Google Scholar
Google Scholar
[14] Vedral V, Barenco A, Ekert A 1996 Phys. Rev. A 54 147
 Google Scholar
Google Scholar
[15] Draper T G 2000 arXiv: 0008033 v1[quant-ph
[16] Beauregard S 2002 arXiv: 0205095 v3[quant-ph
[17] Fowler A G, Mariantoni M, Martinis J M, Cleland A N 2012 Phys. Rev. A 86 032324
 Google Scholar
Google Scholar
[18] O’Gorman J, Campbell E T 2017 Phys. Rev. A 95 032338
 Google Scholar
Google Scholar
[19] Hwang Y, Kim T, Baek C, Choi B S 2020 Phys. Rev. Appl. 13 054033
 Google Scholar
Google Scholar
[20] Ha J, Lee J, Heo J 2022 Quantum Inf. Process. 21 60
 Google Scholar
Google Scholar
[21] Horsman D, Fowler A G, Devitt S, Van M R 2012 New J. Phys. 14 123011
 Google Scholar
Google Scholar
[22] Gidney C 2019 arXiv: 1905.07682 v1[quant-ph
[23] Xiao L, Qiu D, Luo L, Mateus P 2022 arXiv: 2207.05976 v1[quant-ph
[24] Rossi M, Asproni L, Caputo D, Rossi S, Cusinato A, Marini R, Agosti A, Magagnini M 2022 Quant. Mach. Intell. 4 18
 Google Scholar
Google Scholar
[25] Bogdanov Y I, Chernyavskiy A Y, Holevo A, Lukichev V F, Orlikovsky A A 2013 International Conference Micro-and Nano-Electronics Zvenigorod, Russian Federation, October 1–5, 2012 p404
[26] Nachman B, Urbanek M, de Jong W A, Bauer C W 2020 NPJ Quantum Inf. 6 84
 Google Scholar
Google Scholar
[27] Xue C, Chen Z Y, Wu Y C, Guo G P 2021 Chin. Phys. Lett. 38 030302
 Google Scholar
Google Scholar
[28] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 v1[quant-ph
[29] Wallman J J, Emerson J 2016 Phys. Rev. A 94 052325
 Google Scholar
Google Scholar
[30] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press) pp226–386
[31] Wilde M M 2013 Quantum Information Theory (Cambridge: Cambridge University Press) pp175–176
[32] Ji Z, Wang G, Duan R, Feng Y, Ying M 2008 IEEE Trans. Inf. Theory 54 5172
 Google Scholar
Google Scholar
[33] Ryan-Anderson C, Bohnet J G, Lee K, Gresh D, Hankin A, Gaebler J P, Stutz R P 2021 Phys. Rev. X 11 041058
[34] Aliferis P, Preskill J 2008 Phys. Rev. A 78 052331
 Google Scholar
Google Scholar
[35] Tuckett D K, Bartlett S D, Flammia S T 2018 Phys. Rev. Lett. 120 050505
 Google Scholar
Google Scholar
[36] Coppersmith D 2002 arXiv: 0201067 v1[quant-ph
[37] Ekert A, Jozsa R 1996 Rev. Mod. Phys. 68 733
 Google Scholar
Google Scholar
[38] Jozsa R 1998 Proc. R. Soc. London, Ser. A 454 323
 Google Scholar
Google Scholar
[39] Portugal R 2022 arXiv: 2201.10574 v5[quant-ph
[40] King C 2003 IEEE Trans. Inf. Theory 49 221
 Google Scholar
Google Scholar
[41] Resch S, Karpuzcu U R 2021 ACM Comput. Surv. 54 1
[42] Gottesman D 2009 arXiv: 0904.2557 v1[quant-ph
[43] Tomita Y, Svore K M 2014 Phys. Rev. A 90 062320
 Google Scholar
Google Scholar
[44] McKay D C, Alexander T, Bello L, et al. 2018 arXiv: 1809.03452 v1[quant-ph
-
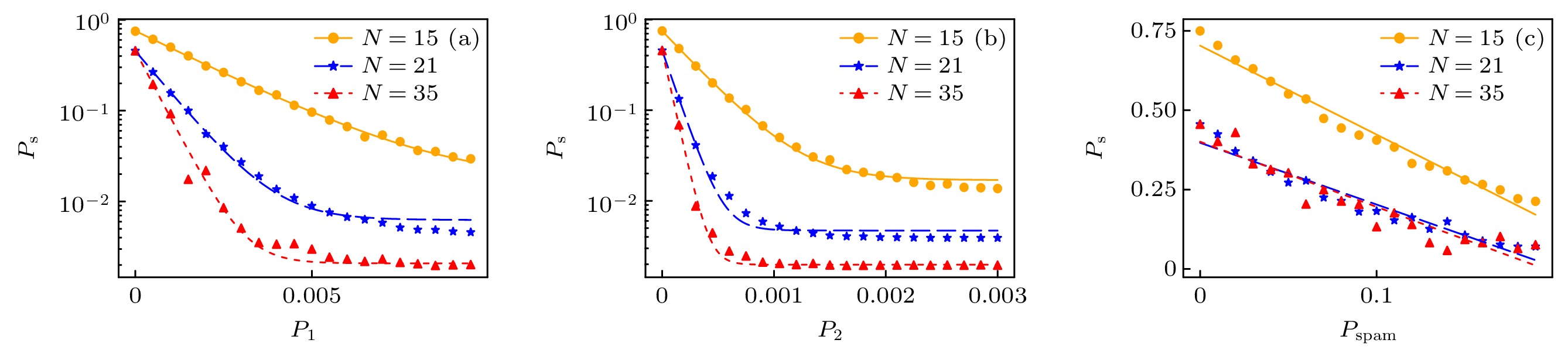
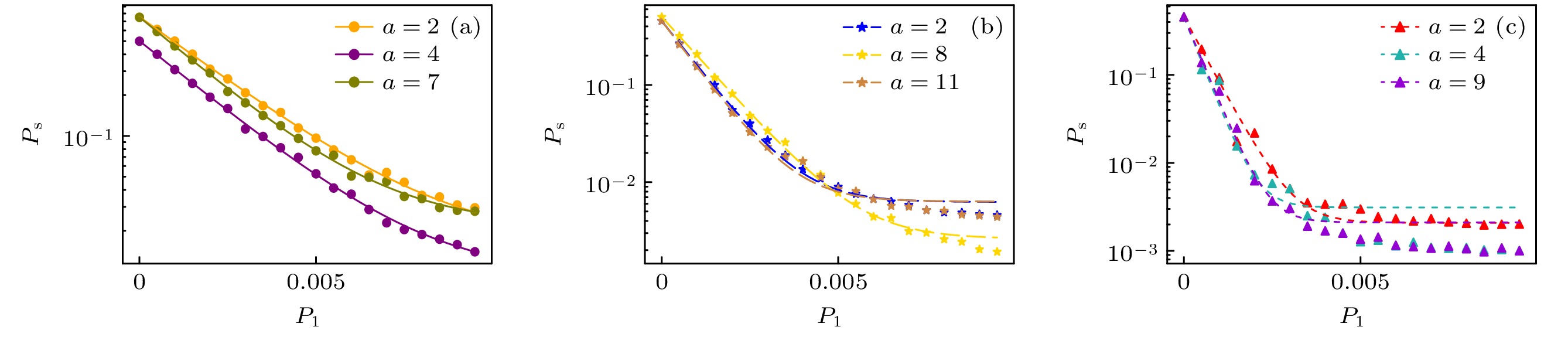
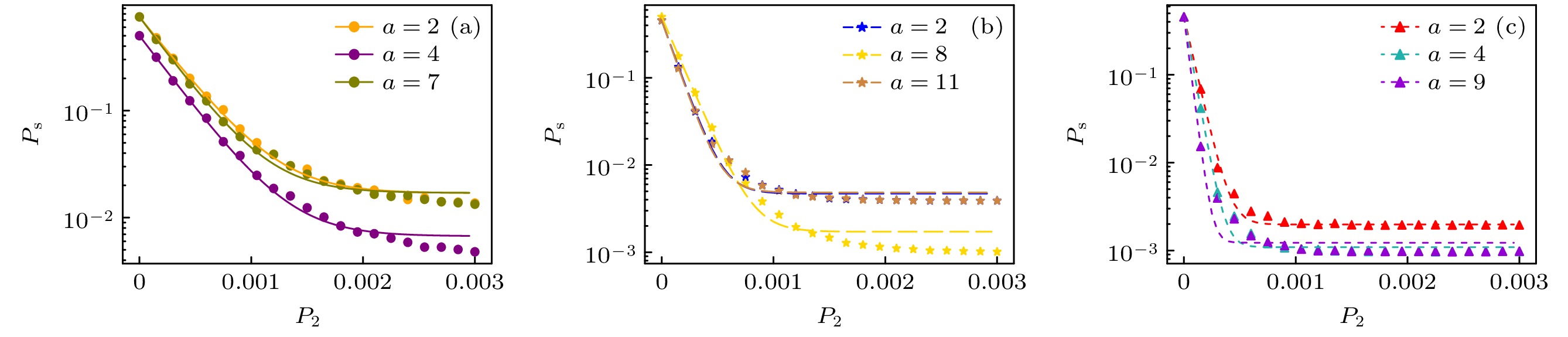
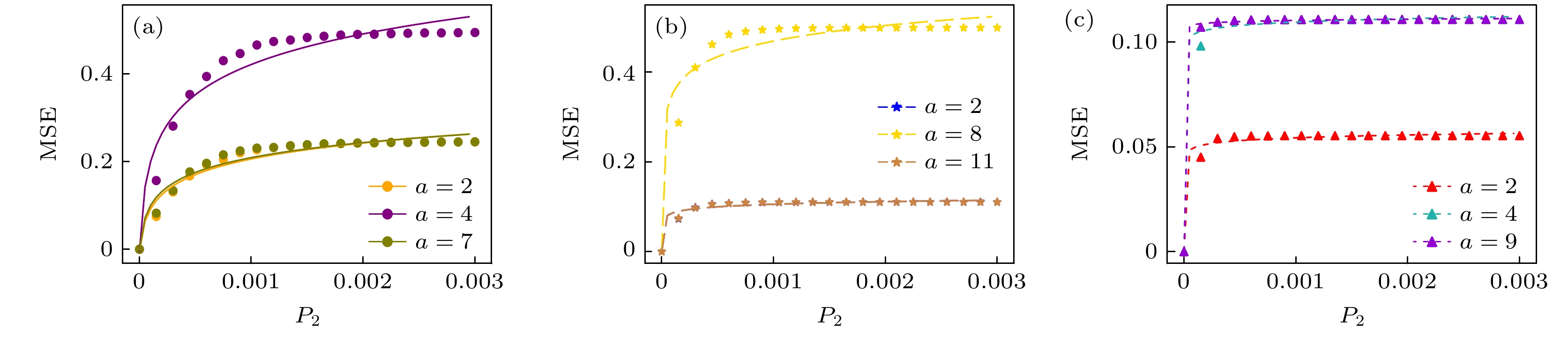
图 5 (a) $ P_{\mathrm{s}} $与去极化通道中单比特门噪声的关系; (b) $ P_{\mathrm{s}} $与去极化通道中双比特门噪声的关系; (c) $ P_{\mathrm{s}} $与状态制备与测量通道中噪声的关系
Figure 5. (a) Effect of one-qubit gate noise in DC on $ P_{\mathrm{s}} $; (b) effect of two-qubit gate noise in DC on $ P_{\mathrm{s}} $; (c) effect of noise in SPAM channel on $ P_{\mathrm{s}} $.
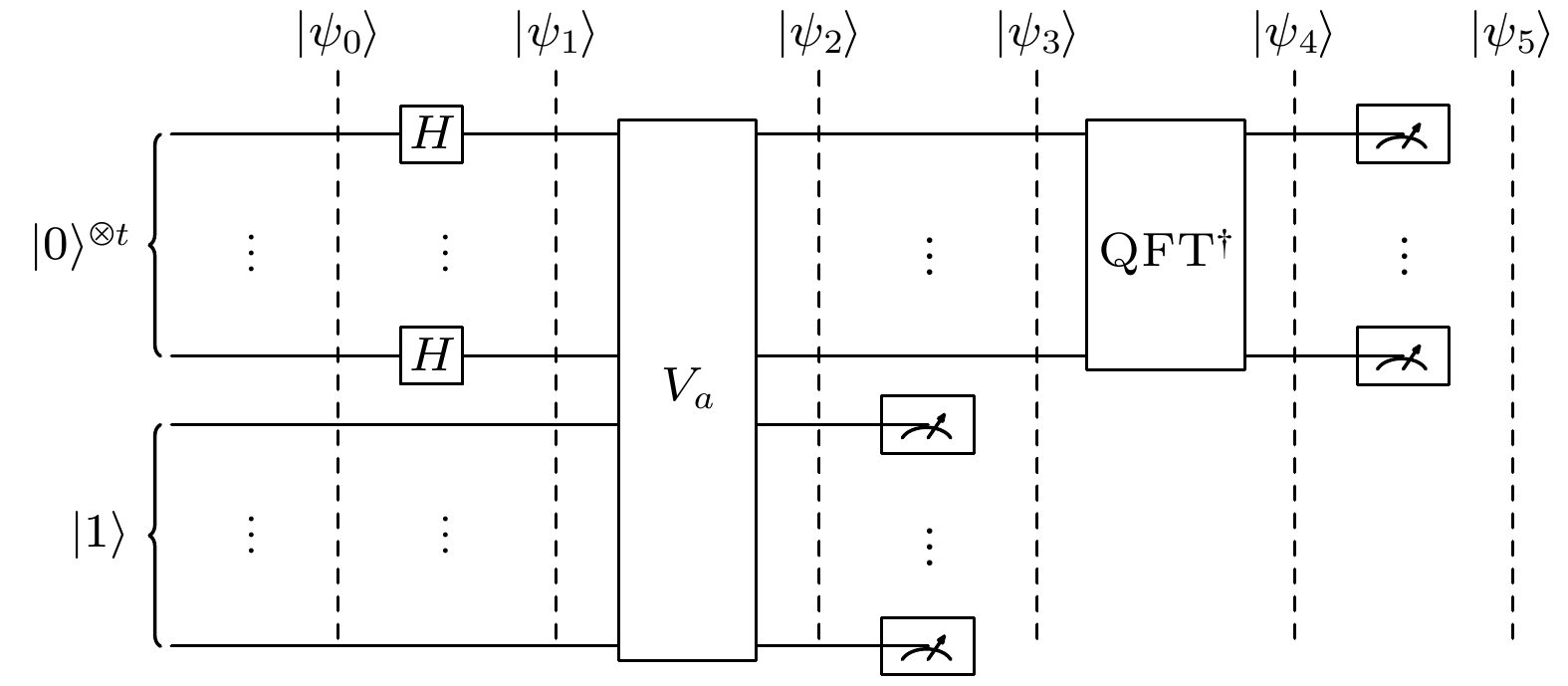
表 1 Shor算法流程
Table 1. Pseudo of Shor’s algorithm
算法 1 Shor算法 输入: 待分解的整数N 输出: N的非平凡素因子p, q 1: if N is even then 2: return $2, {N}/{2}$ 3: end if 4: if $N=p^k$, where $p$ is prime, $k > 0$ then 5: return $p$ 6: end if 7: select a random number a, where $1 < a < N$ 8: if $\mathrm{gcd}(a, N)>1$ then 9: return $\mathrm{gcd}(a, N)$, $ {N}/{{\rm{gcd}}(a, N)}$ 10: end if 11: excute quantum circuit, find minimal positive period of $f_a(x)=a^x\ {\rm{mod}}\ N$, denoted as r 12: if r is odd or $a^{\frac{r}{2}}\equiv -1\ ({\rm{mod}}\ N)$ then 13: GOTO 7 14: end if 15: calculate $p = \mathrm{gcd}(a^{\frac{r}{2}} - 1, N)$ and $q = \mathrm{gcd}(a^{\frac{r}{2}} + 1, N) $ 16: return $p, q$ 表 2 实验选择的待分解整数与随机数组合(N, a)
Table 2. Combination of integer about to be factored and random number (N, a).
N a 15 [2, 4, 7] 21 [2, 8, 11] 35 [2, 4, 9] 表 3 退相干通道中$T_1, T_2$的取值
Table 3. Choice of $T_1, T_2$ in TRC.
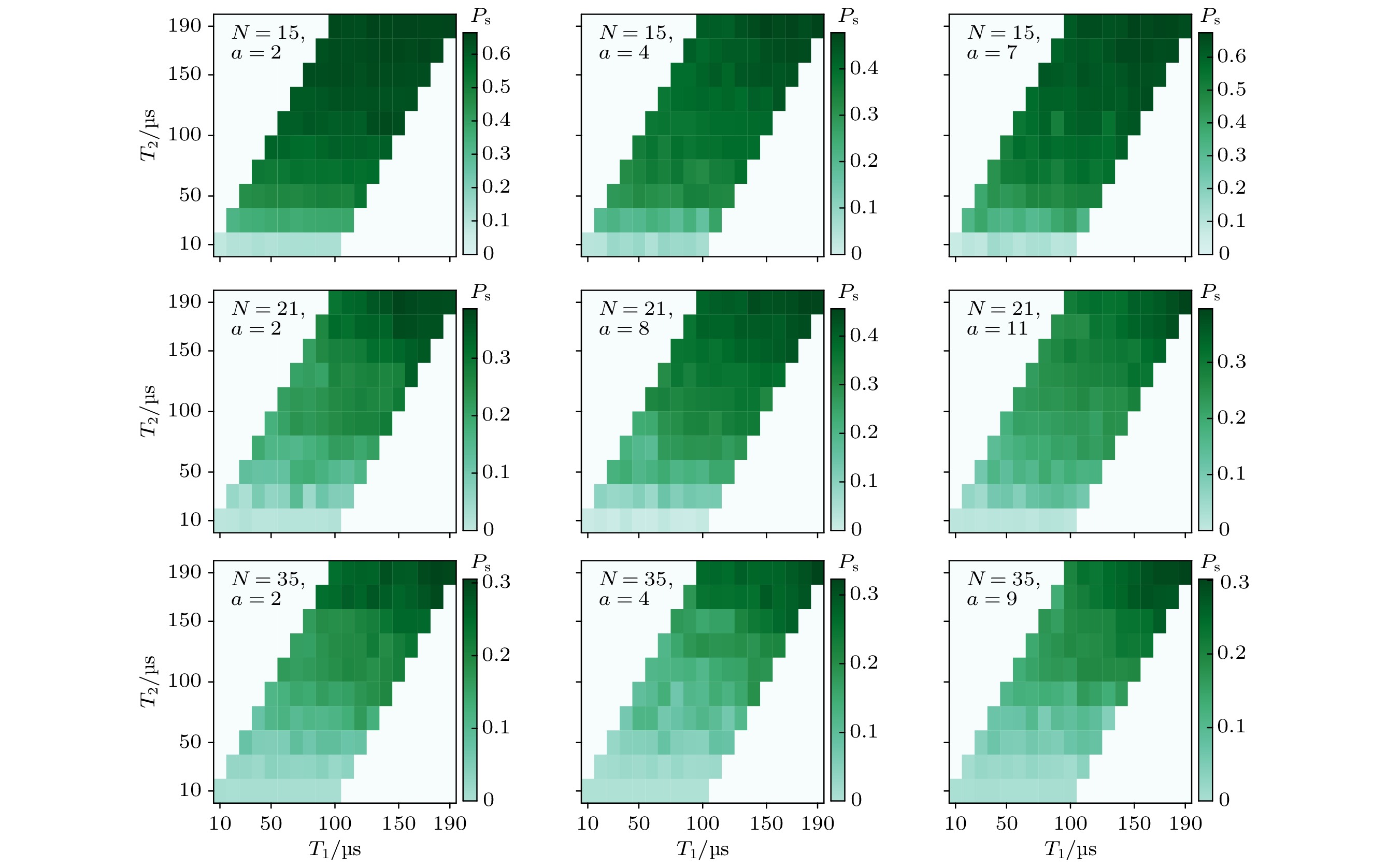
$T_1/\text{μ} {\rm{s}}$ $T_2/\text{μ} {\rm{s}}$ $[20, 30, \cdots, 90, 110]$ 30 $[30, 40, \cdots, 100, 120]$ 50 $[40, 50, \cdots, 110, 130]$ 70 $[50, 60, \cdots, 120, 140]$ 90 $[60, 70, \cdots, 130, 150]$ 110 $[70, 80, \cdots, 140, 160]$ 130 $[80, 90, \cdots, 150, 170]$ 150 $[90, 100, \cdots, 160, 180]$ 170 $[100, 110, \cdots, 170, 190]$ 190 表 B1 所有整数与随机数组合(N, a)在不同噪声的环境下的成功率
Table B1. Effect of different levels of noise in 3 channels on success rates of all (N, a) pairs.
N 15 21 35 a 2 4 7 2 8 11 2 4 9 单比特门数量 1584 2860 4680 双比特门数量 8476 17045 30594 线路深度 6432 12059 20565 线路宽度(量子比特数) 18 22 26 平均运行一次所需时间/s 1.15 11.89 142.34 理论成功率(无噪声) 0.75 0.5 0.75 0.4559 0.5 0.4559 0.4559 0.4559 0.4559 噪声环境中
的成功率$P_1=0.0025$ 0.2635 0.1593 0.2125 0.0408 0.0482 0.0327 0.0085 0.0058 0.0037 $P_1=0.005$ 0.0964 0.0526 0.0776 0.0089 0.0078 0.0085 0.0029 0.0013 0.0014 $P_1=0.0075$ 0.0455 0.0204 0.0358 0.0052 0.0031 0.0051 0.0021 0.0011 0.0011 $P_1=0.01$ 0.0295 0.0142 0.0278 0.0046 0.0019 0.0044 0.0020 0.0010 0.0010 $P_2=0.00075$ 0.1017 0.0512 0.0787 0.0073 0.0062 0.0082 0.0025 0.0012 0.0012 $P_2=0.0015$ 0.0284 0.0124 0.0255 0.0042 0.0015 0.0042 0.0019 0.0009 0.0010 $P_2=0.00225$ 0.0161 0.0064 0.0158 0.0039 0.0011 0.0039 0.0019 0.0008 0.0009 $P_2=0.003$ 0.0137 0.0048 0.0138 0.0038 0.0010 0.0038 0.0018 0.0008 0.0009 $P_{\rm{spam}}=0.05$ 0.5513 0.3441 0.5295 0.2721 0.3596 0.3373 0.3029 0.2739 0.3079 $P_{\rm{spam}}=0.1$ 0.4058 0.2354 0.4155 0.1823 0.1603 0.1438 0.1335 0.1223 0.1645 $P_{\rm{spam}}=0.15$ 0.2805 0.1812 0.2955 0.1066 0.1226 0.0758 0.0937 0.0427 0.0680 $P_{\rm{spam}}=0.2$ 0.2131 0.1193 0.2025 0.0705 0.0816 0.0721 0.0763 0.0125 0.0572 $T_1=T_2=10~{\text{μs}}$ 0.0792 0.0386 0.0646 0.0067 0.0041 0.0083 0.0029 0.0014 0.0016 $T_1=T_2=70~{\text{μs}}$ 0.5455 0.3444 0.5497 0.1556 0.2740 0.1963 0.1004 0.0722 0.1019 $T_1=T_2= 130~\text{μs}$ 0.6314 0.3992 0.6238 0.2714 0.3579 0.2811 0.2202 0.1972 0.2007 $T_1=T_2= 190\text{μs}$ 0.6603 0.4770 0.6513 0.3690 0.4521 0.3960 0.2998 0.3226 0.3014 -
[1] Shor P W 1994 Proceedings of the 35th Annual Symposium on Foundations of Computer Science Washington DC, USA, November 20–22, 1994 p124
[2] Shor P W 1999 SIAM Rev. Soc. Ind. Appl. Math 41 303
[3] Lenstra A K, Hendrik Jr W 1993 The Development of the Number Field Sieve(Vol. 1554) (Heidelberg : Springer Science & Business Media) p5
[4] Lenstra A K, Lenstra Jr H W, Manasse M S, Pollard J M 1990 Proceedings of the Twenty-second Annual ACM Symposium on Theory of Computing Baltimore Maryland, USA, May 13–17, 1990 p564
[5] Buhler J P, Lenstra H W, Pomerance C 1993 The Development of the Number Field Sieve (Berlin Heidelberg: Springer) pp50–94
[6] Kleinjung T, Aoki K, Franke J, Lenstra A K, Thomé E, Bos J W, Gaudry P, Kruppa A, Montgomery P L, Osvik D A, Riele H T, Timofeev A, Zimmermann P 2010 Advances in Cryptology–CRYPTO 2010: 30th Annual Cryptology Conference Santa Barbara, CA, USA, August 15–19, 2010 p333
[7] Gidney C, Ekerå M 2021 Quantum 5 433
 Google Scholar
Google Scholar
[8] Preskill J 2018 Quantum 2 79
 Google Scholar
Google Scholar
[9] Harper R, Flammia S T, Wallman J J 2020 Nat. Phys. 16 1184
 Google Scholar
Google Scholar
[10] Georgopoulos K, Emary C, Zuliani P 2021 Phys. Rev. A 104 062432
 Google Scholar
Google Scholar
[11] Brown K R, Harrow A W, Chuang I L 2004 Phys. Rev. A 70 052318
 Google Scholar
Google Scholar
[12] Bassi A, Großardt A, Ulbricht H 2017 Classical Quantum Gravity 34 193002
 Google Scholar
Google Scholar
[13] Viola L, Knill E, Lloyd S 1999 Phys. Rev. Lett. 82 2417
 Google Scholar
Google Scholar
[14] Vedral V, Barenco A, Ekert A 1996 Phys. Rev. A 54 147
 Google Scholar
Google Scholar
[15] Draper T G 2000 arXiv: 0008033 v1[quant-ph
[16] Beauregard S 2002 arXiv: 0205095 v3[quant-ph
[17] Fowler A G, Mariantoni M, Martinis J M, Cleland A N 2012 Phys. Rev. A 86 032324
 Google Scholar
Google Scholar
[18] O’Gorman J, Campbell E T 2017 Phys. Rev. A 95 032338
 Google Scholar
Google Scholar
[19] Hwang Y, Kim T, Baek C, Choi B S 2020 Phys. Rev. Appl. 13 054033
 Google Scholar
Google Scholar
[20] Ha J, Lee J, Heo J 2022 Quantum Inf. Process. 21 60
 Google Scholar
Google Scholar
[21] Horsman D, Fowler A G, Devitt S, Van M R 2012 New J. Phys. 14 123011
 Google Scholar
Google Scholar
[22] Gidney C 2019 arXiv: 1905.07682 v1[quant-ph
[23] Xiao L, Qiu D, Luo L, Mateus P 2022 arXiv: 2207.05976 v1[quant-ph
[24] Rossi M, Asproni L, Caputo D, Rossi S, Cusinato A, Marini R, Agosti A, Magagnini M 2022 Quant. Mach. Intell. 4 18
 Google Scholar
Google Scholar
[25] Bogdanov Y I, Chernyavskiy A Y, Holevo A, Lukichev V F, Orlikovsky A A 2013 International Conference Micro-and Nano-Electronics Zvenigorod, Russian Federation, October 1–5, 2012 p404
[26] Nachman B, Urbanek M, de Jong W A, Bauer C W 2020 NPJ Quantum Inf. 6 84
 Google Scholar
Google Scholar
[27] Xue C, Chen Z Y, Wu Y C, Guo G P 2021 Chin. Phys. Lett. 38 030302
 Google Scholar
Google Scholar
[28] Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 v1[quant-ph
[29] Wallman J J, Emerson J 2016 Phys. Rev. A 94 052325
 Google Scholar
Google Scholar
[30] Nielsen M A, Chuang I L 2010 Quantum Computation and Quantum Information (Cambridge: Cambridge University Press) pp226–386
[31] Wilde M M 2013 Quantum Information Theory (Cambridge: Cambridge University Press) pp175–176
[32] Ji Z, Wang G, Duan R, Feng Y, Ying M 2008 IEEE Trans. Inf. Theory 54 5172
 Google Scholar
Google Scholar
[33] Ryan-Anderson C, Bohnet J G, Lee K, Gresh D, Hankin A, Gaebler J P, Stutz R P 2021 Phys. Rev. X 11 041058
[34] Aliferis P, Preskill J 2008 Phys. Rev. A 78 052331
 Google Scholar
Google Scholar
[35] Tuckett D K, Bartlett S D, Flammia S T 2018 Phys. Rev. Lett. 120 050505
 Google Scholar
Google Scholar
[36] Coppersmith D 2002 arXiv: 0201067 v1[quant-ph
[37] Ekert A, Jozsa R 1996 Rev. Mod. Phys. 68 733
 Google Scholar
Google Scholar
[38] Jozsa R 1998 Proc. R. Soc. London, Ser. A 454 323
 Google Scholar
Google Scholar
[39] Portugal R 2022 arXiv: 2201.10574 v5[quant-ph
[40] King C 2003 IEEE Trans. Inf. Theory 49 221
 Google Scholar
Google Scholar
[41] Resch S, Karpuzcu U R 2021 ACM Comput. Surv. 54 1
[42] Gottesman D 2009 arXiv: 0904.2557 v1[quant-ph
[43] Tomita Y, Svore K M 2014 Phys. Rev. A 90 062320
 Google Scholar
Google Scholar
[44] McKay D C, Alexander T, Bello L, et al. 2018 arXiv: 1809.03452 v1[quant-ph
Catalog
Metrics
- Abstract views: 4339
- PDF Downloads: 169
- Cited By: 0















 DownLoad:
DownLoad: