Mirror buckling analysis of freestanding graphene membranes by coarse-grained molecular dynamics method

Xu Wen-Long; Kai Yue; Zhang Kai; Zheng Bai-Lin

doi:10.7498/aps.72.20231120

Abstract

Up to now, the analysis has rarely been conducted of thermal-mechanical mirror buckling behavior of freestanding graphene membranes discovered in scan tunneling microscope experiments. One of the potential applications of the out-of-plane deformational behavior of graphene membranes is energy harvesting system. Whether in the experiments or for energy harvesting systems, the size of graphene membrane needs to be down to micron scale. According to previous researches, traditional molecular dynamics method is a suitable method to characterize nano-scale mirror buckling. However, owing to the limit of algorithm, when dealing with micro size model by molecular dynamics method, two problems arise: low computational efficiency and too long calculation time. Therefore, for analyzing the mirror buckling of micro size graphene membranes, the coarse-grained molecular dynamics method is utilized in this work. Graphene membranes with a fan-shaped cross section and various depth-span ratios are under mechanical or thermal loads. Effects of each factor on the mirror buckling are investigated. The calculations indicate that for graphene membranes with various depth-span ratios under mechanical load mirror buckling can be observed. And the critical loading increases with the depth-span ratio increasing. Under thermal load graphene membranes only with low depth-span ratios can undergo complete flipping phenomenon. For high depth-span ratio graphene, the center height decreases with temperature rising. However, it is hard to flip over completely. The understanding of the effects of various factors on the mirror buckling phenomenon of graphene membranes can provide theoretical guidance for designing the energy harvesting systems.

Keywords:

Authors and contacts

1.
School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China
2.
School of Mathematics, Physics and Statistics, Center of Intelligent Computing and Applied Statistics, Shanghai University of Engineering Science, Shanghai 201620, China

Corresponding author: Zheng Bai-Lin, blzheng@tongji.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11872280).

FullText HTML : translate this paragraph

References

[1]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 Google Scholar
[2]	Lee C, Wei X, Kysar J W, Hone J 2008 Science 321 385 Google Scholar
[3]	Ma T, Li B, Chang T 2011 Appl. Phys. Lett. 99 201901 Google Scholar
[4]	Zhang Y, Pan C 2012 Diamond Relat. Mater. 24 1 Google Scholar
[5]	Galiotis C, Frank O, Koukaras E N, Sfyris D 2015 Annu. Rev. Chem. Biomol. 6 121 Google Scholar
[6]	李亮亮, 孟凡伟, 邹鲲, 黄瑶, 彭倚天 2021 70 086801 Google Scholar Li L L, Meng F W, Zou K, Huang Y, Peng Y T 2021 Acta Phys. Sin. 70 086801 Google Scholar
[7]	Faugeras C, Faugeras B, Orlita M, Potemski M, Nair R R, Geim A K 2010 ACS Nano 4 1889 Google Scholar
[8]	Chen L, Kumar S 2012 J. Appl. Phys. 112 043502 Google Scholar
[9]	Nan H Y, Ni Z H, Wang J, Zafar Z, Shi Z X, Wang Y Y 2013 J. Raman Spectrosc. 44 1018 Google Scholar
[10]	Renteria J D, Nika D L, Balandin A A 2014 Appl. Sci. 4 525 Google Scholar
[11]	Graf D, Molitor F, Ensslin K, Stampfer C, Jungen A, Hierold C, Wirtz L 2007 Nano Lett. 7 238 Google Scholar
[12]	Ferrari A C, Meyer J C, Scardaci V, Casiraghi C, Lazzeri M, Mauri F, Piscanec S, Jiang D, Novoselov K S, Roth S, Geim A K 2006 Phys. Rev. Lett. 97 187401 Google Scholar
[13]	Zhang Y, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201 Google Scholar
[14]	Bolotin K I, Sikes K J, Jiang Z, Klima M, Fudenberg G, Hone J, Kim P, Stormer H L 2008 Solid State Commun. 146 351 Google Scholar
[15]	Peres N M R 2009 Vacuum 83 1248 Google Scholar
[16]	Mogi M, Okamura Y, Kawamura M, Yoshimi R, Yasuda K, Tsukazaki A, Takahashi K S, Morimoto T, Nagaosa N, Kawasaki M, Takahashi Y, Tokura Y 2022 Nat. Phys. 18 390 Google Scholar
[17]	Xin N, Lourembam J, Kumaravadivel P, Kazantsev A E, Wu Z, Mullan C, Barrier J, Geim A A, Grigorieva I V, Mishchenko A, Principi A, Fal’ko V I, Ponomarenko L A, Geim A K, Berdyugin A I 2023 Nature 616 270 Google Scholar
[18]	López-Suárez M, Rurali R, Abadal G 2013 Microelectron. Eng. 111 122 Google Scholar
[19]	López-Suárez M, Rurali R, Gammaitoni L, Abadal G 2011 Phys. Rev. B 84 161401 Google Scholar
[20]	廖天军, 杨智敏, 林比宏 2021 70 227901 Google Scholar Liao T J, Yang Z M, Lin B H 2021 Acta Phys. Sin. 70 227901 Google Scholar
[21]	万震, 李成, 刘宇健, 宋学锋, 樊尚春 2022 71 126801 Google Scholar Wan Z, Li C, Liu Y J, Song X F, Fan S X 2022 Acta Phys. Sin. 71 126801 Google Scholar
[22]	Neek-Amal M, Xu P, Schoelz J K, Ackerman M L, Barber S D, Thibado P M, Sadeghi A, Peeters F M 2014 Nat. Commun. 5 4962 Google Scholar
[23]	Schoelz J K, Xu P, Meunier V, Kumar P, Neek-Amal M, Thibado P M, Peeters F M 2015 Phys. Rev. B 91 045413 Google Scholar
[24]	Ruiz-García M, Bonilla L L, Prados A 2016 Phys. Rev. B 94 205404 Google Scholar
[25]	Xu W, Kai Y, Zhang K, Zheng B 2022 Mater. Today Commun. 33 104230 Google Scholar
[26]	Lindahl N, Midtvedt D, Svensson J, Nerushev O A, Lindvall N, Isacsson A, Campbell E E 2012 Nano Lett. 12 3526 Google Scholar
[27]	Garaj S, Hubbard W, Reina A, Kong J, Branton D, Golovchenko J A 2010 Nature 467 190 Google Scholar
[28]	Chu Y, Ragab T, Basaran C 2014 Comput. Mater. Sci. 81 269 Google Scholar
[29]	Xu C, Xue T, Qiu W, Kang Y 2016 ACS Appl. Mater. Interfaces 8 27099 Google Scholar
[30]	Deng W, Li L, Hu Y, Wang X, Li X 2018 J. Therm. Stresses 41 1182 Google Scholar
[31]	Su R, Zhang X 2018 Appl. Therm. Eng. 144 488 Google Scholar
[32]	Ruiz L, Xia W, Meng Z, Keten S 2015 Carbon 82 103 Google Scholar
[33]	Li H, Zhang H, Cheng X 2017 Physica E 85 97 Google Scholar
[34]	Liu S, Duan K, Li L, Wang X, Hu Y 2021 Carbon 178 528 Google Scholar
[35]	Zhao Y, Zhao Y, Wu F, Zhao Y, Wang Y, Sui C, He X, Wang C, Tan H, Wang C 2021 Carbon 173 600 Google Scholar
[36]	Mangum J M, Harerimana F, Gikunda M N, Thibado P M 2021 Membranes 11 516 Google Scholar
[37]	Timoshenko S P 1936 Theory of Elastic Stability (New York: Dover Publication) pp320–324
[38]	Wang W D, Shen C L, Li S, Min J J, Yi C L 2014 AIP Adv. 4 200207 Google Scholar
[39]	https://www.lammps.org/[2023-7-9
[40]	https://www.ks.uiuc.edu/Research/vmd/ [2023-7-9

Cited By

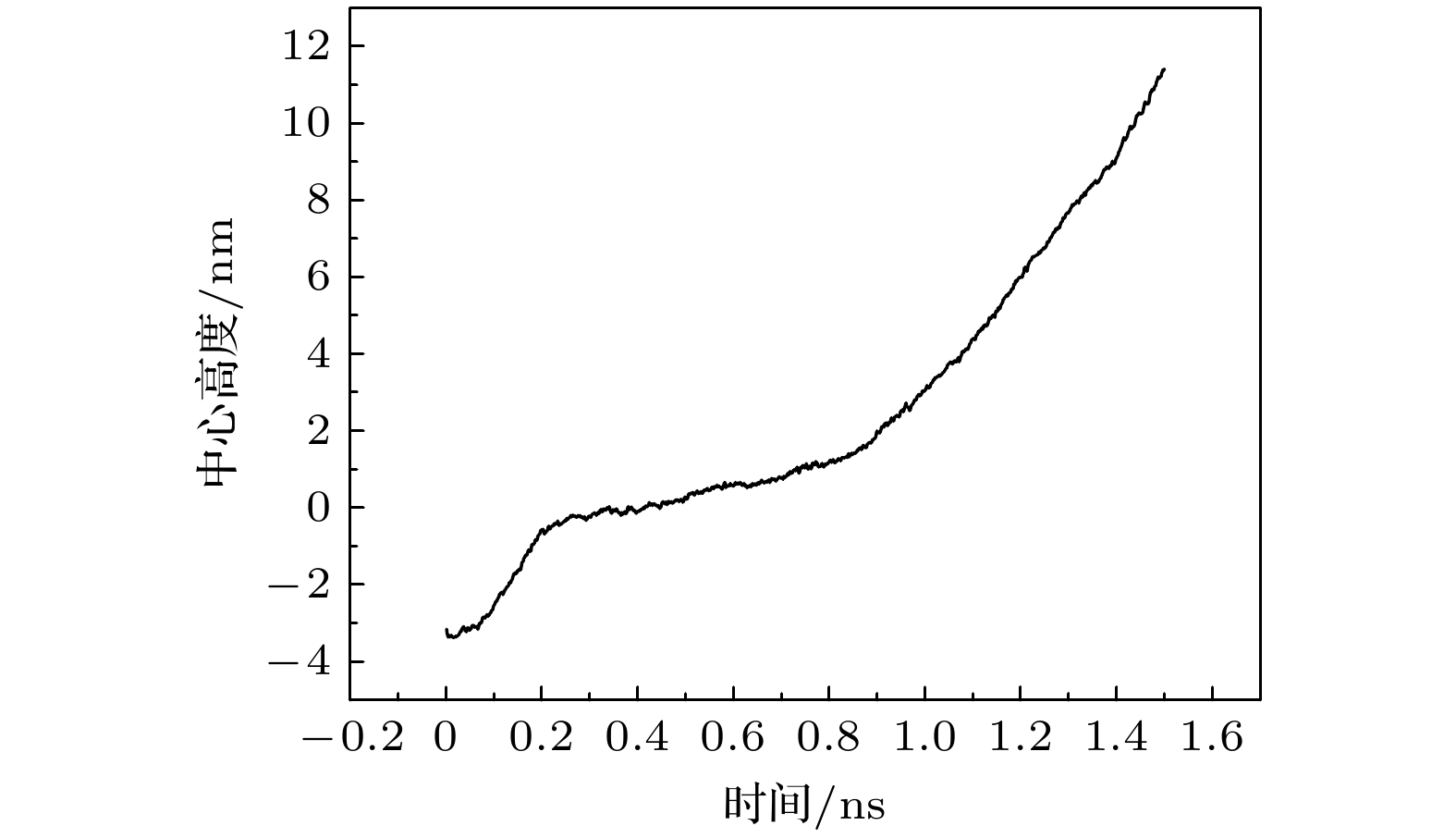
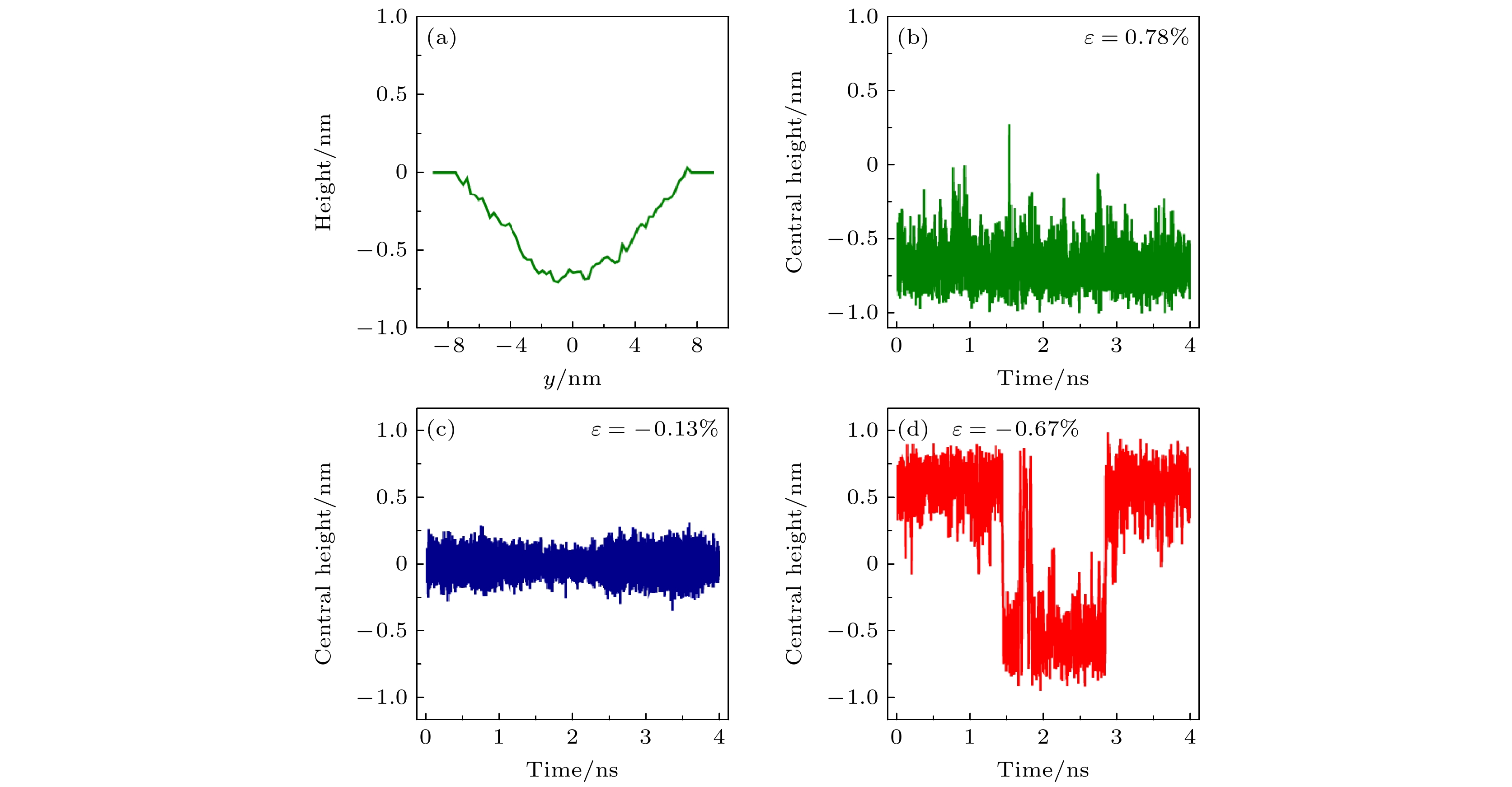
图 1 热镜面屈曲现象的实验观测——不同隧穿电流下石墨烯面外高度随电压变化曲线, 其中黑色曲线对应镜面屈曲现象^[22]

Figure 1. Experimental observation of thermal mirror buckling. Constant-current feedback-on, Z(V ) data sets on suspended graphene acquired using the labeled setpoint currents. The 4.0-nA curve (black) shows the mirror buckling phenomenon^[22].

DownLoad: Full-Size Img PowerPoint

图 2 CGMD模型示意图. 黑色圆点表示全粒子模型中的碳原子, 蓝色圆点表示CGMD模型中的珠子. 红色虚线区域表示碳原子与珠子的典型等效方式

Figure 2. Schematics of the CGMD model. The black dots indicate carbon atoms in the all-atom model. The blue dots indicate beads in the CGMD model. The region marked with rad dotted lines express a typical equivalent mode with carbon atoms and beads.

DownLoad: Full-Size Img PowerPoint

图 3 石墨烯粗粒化模型示意图, 其中黄色区域表示中心位置　(a)初始状态; (b)中心凹陷状态

Figure 3. Diagrams of CGMD graphene models, where the yellow region is located in the center: (a) Initial state; (b) concave region in the center.

DownLoad: Full-Size Img PowerPoint

图 4 CGMD计算得到石墨烯中心位置面外高度随时间的变化

Figure 4. Curve of the out-of-plane heights in the center region of the graphene via the time calculated by CGMD.

DownLoad: Full-Size Img PowerPoint

图 5 石墨烯膜扇形截面示意图

Figure 5. Diagram of the fan-shaped cross section of a graphene membrane.

DownLoad: Full-Size Img PowerPoint

图 6 石墨烯膜及加载方法示意图　(a) 机械载荷加载和边界条件; (b) 热载荷加载和边界条件

Figure 6. Diagrams of graphene membranes and loading forms: (a) The mechanical load form and boundary conditions; (b) the thermal load form and boundary conditions.

DownLoad: Full-Size Img PowerPoint

图 7 扇形截面石墨烯膜的最大挠度随机械载荷的变化

Figure 7. Maximum dimensionless deflections of the fan-shaped cross-sections of graphene membranes versus the mechanical force.

DownLoad: Full-Size Img PowerPoint

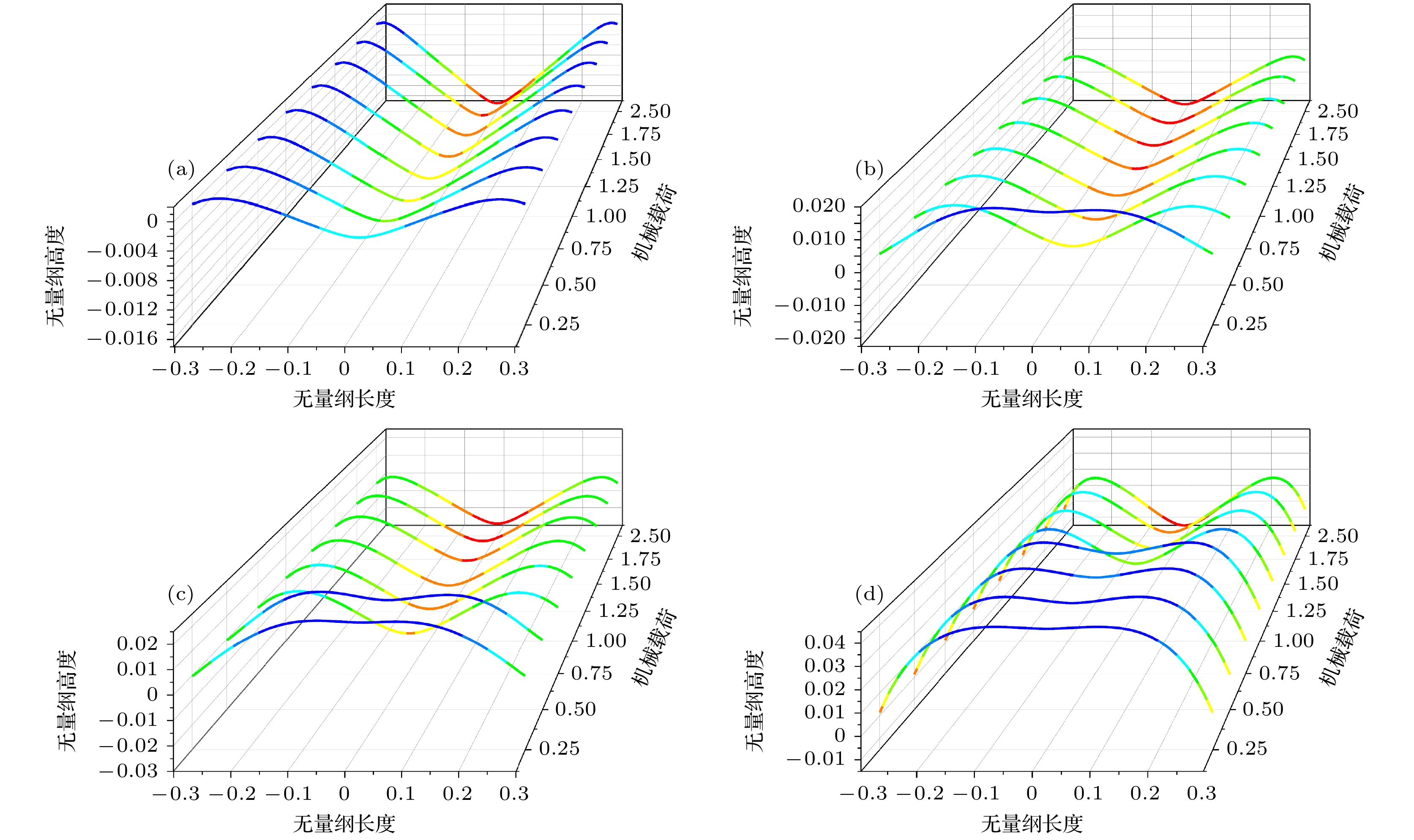
图 8 四种典型高跨比扇形截面石墨烯膜在不同机械载荷作用下, 最大挠度截面轮廓图　(a) λ = 2.5%; (b) λ = 5%; (c) λ = 10%; (d) λ = 20%

Figure 8. Cross-sectional profiles of maximum dimensionless deflections for the fan-shaped cross-sections of graphene membranes with the four typical depth-span ratio under different mechanical force: (a) λ = 2.5%; (b) λ = 5%; (c) λ = 10%; (d) λ = 20%.

DownLoad: Full-Size Img PowerPoint

图 9 扇形截面石墨烯膜的最大挠度随温度载荷的变化

Figure 9. Maximum dimensionless deflections of the fan-shaped cross-sections of graphene membranes versus the temperature.

DownLoad: Full-Size Img PowerPoint

图 10 四种典型高跨比扇形截面石墨烯膜在不同温度载荷作用下, 最大挠度截面轮廓图　(a) λ = 2.5%; (b) λ = 5%; (c) λ = 10%; (d) λ = 20%

Figure 10. Cross-sectional profiles of maximum dimensionless deflections for the fan-shaped cross-sections of graphene membranes with the four typical depth-span ratio at different temperature: (a) λ = 2.5%; (b) λ = 5%; (c) λ = 10%; (d) λ = 20%.

DownLoad: Full-Size Img PowerPoint

图 11 3000 K下应变对波纹的动态影响^[36]

Figure 11. Role of strain on ripple dynamics at 3000 K^[36].

DownLoad: Full-Size Img PowerPoint

表 1 CGMD化模型力场参数

Table 1. Parameters of the CGMD model force field

原子间相互作用形式	物理参数	数值
键长	$ {D_0} $/(kcal·mol^–1)	196.38
	$ \alpha $/Å^–1	1.55
	$ {k_{\text{b}}} $/(kcal·mol^–1·Å^–2)	470
键角	$ {k_\theta } $/(kcal·mol^–1·Å^–2)	409.4
键角	$ {\theta _0} $/(º)	120
二面角	$ {k_\phi } $/(kcal·mol^–1)	4.15
非成键	$ {\varepsilon}_{\text{LJ}} $/(kcal·mol^–1)	0.82
非成键	$ {\sigma _{{\text{LJ}}}} $/Å	3.46

DownLoad: CSV

表 2 高跨比及机械载荷和热载荷数据表

Table 2. Depth-span ratios and the magnitudes of mechanical and thermal loadings.

	高跨比λ/%	机械载荷大小/(10^–3 nN)	热载荷大小/K
1	2.5	–1.086	3
2	5	–2.171	50
3	7.5	–3.256	100
4	10	–4.341	150
5	20	–5.427	200
6	30	–6.512	250
7	—	–7.599	300
8	—	–10.86	350
9	—	—	400
10	—	—	450
11	—	—	500

DownLoad: CSV

map

[1]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 Google Scholar
[2]	Lee C, Wei X, Kysar J W, Hone J 2008 Science 321 385 Google Scholar
[3]	Ma T, Li B, Chang T 2011 Appl. Phys. Lett. 99 201901 Google Scholar
[4]	Zhang Y, Pan C 2012 Diamond Relat. Mater. 24 1 Google Scholar
[5]	Galiotis C, Frank O, Koukaras E N, Sfyris D 2015 Annu. Rev. Chem. Biomol. 6 121 Google Scholar
[6]	李亮亮, 孟凡伟, 邹鲲, 黄瑶, 彭倚天 2021 70 086801 Google Scholar Li L L, Meng F W, Zou K, Huang Y, Peng Y T 2021 Acta Phys. Sin. 70 086801 Google Scholar
[7]	Faugeras C, Faugeras B, Orlita M, Potemski M, Nair R R, Geim A K 2010 ACS Nano 4 1889 Google Scholar
[8]	Chen L, Kumar S 2012 J. Appl. Phys. 112 043502 Google Scholar
[9]	Nan H Y, Ni Z H, Wang J, Zafar Z, Shi Z X, Wang Y Y 2013 J. Raman Spectrosc. 44 1018 Google Scholar
[10]	Renteria J D, Nika D L, Balandin A A 2014 Appl. Sci. 4 525 Google Scholar
[11]	Graf D, Molitor F, Ensslin K, Stampfer C, Jungen A, Hierold C, Wirtz L 2007 Nano Lett. 7 238 Google Scholar
[12]	Ferrari A C, Meyer J C, Scardaci V, Casiraghi C, Lazzeri M, Mauri F, Piscanec S, Jiang D, Novoselov K S, Roth S, Geim A K 2006 Phys. Rev. Lett. 97 187401 Google Scholar
[13]	Zhang Y, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201 Google Scholar
[14]	Bolotin K I, Sikes K J, Jiang Z, Klima M, Fudenberg G, Hone J, Kim P, Stormer H L 2008 Solid State Commun. 146 351 Google Scholar
[15]	Peres N M R 2009 Vacuum 83 1248 Google Scholar
[16]	Mogi M, Okamura Y, Kawamura M, Yoshimi R, Yasuda K, Tsukazaki A, Takahashi K S, Morimoto T, Nagaosa N, Kawasaki M, Takahashi Y, Tokura Y 2022 Nat. Phys. 18 390 Google Scholar
[17]	Xin N, Lourembam J, Kumaravadivel P, Kazantsev A E, Wu Z, Mullan C, Barrier J, Geim A A, Grigorieva I V, Mishchenko A, Principi A, Fal’ko V I, Ponomarenko L A, Geim A K, Berdyugin A I 2023 Nature 616 270 Google Scholar
[18]	López-Suárez M, Rurali R, Abadal G 2013 Microelectron. Eng. 111 122 Google Scholar
[19]	López-Suárez M, Rurali R, Gammaitoni L, Abadal G 2011 Phys. Rev. B 84 161401 Google Scholar
[20]	廖天军, 杨智敏, 林比宏 2021 70 227901 Google Scholar Liao T J, Yang Z M, Lin B H 2021 Acta Phys. Sin. 70 227901 Google Scholar
[21]	万震, 李成, 刘宇健, 宋学锋, 樊尚春 2022 71 126801 Google Scholar Wan Z, Li C, Liu Y J, Song X F, Fan S X 2022 Acta Phys. Sin. 71 126801 Google Scholar
[22]	Neek-Amal M, Xu P, Schoelz J K, Ackerman M L, Barber S D, Thibado P M, Sadeghi A, Peeters F M 2014 Nat. Commun. 5 4962 Google Scholar
[23]	Schoelz J K, Xu P, Meunier V, Kumar P, Neek-Amal M, Thibado P M, Peeters F M 2015 Phys. Rev. B 91 045413 Google Scholar
[24]	Ruiz-García M, Bonilla L L, Prados A 2016 Phys. Rev. B 94 205404 Google Scholar
[25]	Xu W, Kai Y, Zhang K, Zheng B 2022 Mater. Today Commun. 33 104230 Google Scholar
[26]	Lindahl N, Midtvedt D, Svensson J, Nerushev O A, Lindvall N, Isacsson A, Campbell E E 2012 Nano Lett. 12 3526 Google Scholar
[27]	Garaj S, Hubbard W, Reina A, Kong J, Branton D, Golovchenko J A 2010 Nature 467 190 Google Scholar
[28]	Chu Y, Ragab T, Basaran C 2014 Comput. Mater. Sci. 81 269 Google Scholar
[29]	Xu C, Xue T, Qiu W, Kang Y 2016 ACS Appl. Mater. Interfaces 8 27099 Google Scholar
[30]	Deng W, Li L, Hu Y, Wang X, Li X 2018 J. Therm. Stresses 41 1182 Google Scholar
[31]	Su R, Zhang X 2018 Appl. Therm. Eng. 144 488 Google Scholar
[32]	Ruiz L, Xia W, Meng Z, Keten S 2015 Carbon 82 103 Google Scholar
[33]	Li H, Zhang H, Cheng X 2017 Physica E 85 97 Google Scholar
[34]	Liu S, Duan K, Li L, Wang X, Hu Y 2021 Carbon 178 528 Google Scholar
[35]	Zhao Y, Zhao Y, Wu F, Zhao Y, Wang Y, Sui C, He X, Wang C, Tan H, Wang C 2021 Carbon 173 600 Google Scholar
[36]	Mangum J M, Harerimana F, Gikunda M N, Thibado P M 2021 Membranes 11 516 Google Scholar
[37]	Timoshenko S P 1936 Theory of Elastic Stability (New York: Dover Publication) pp320–324
[38]	Wang W D, Shen C L, Li S, Min J J, Yi C L 2014 AIP Adv. 4 200207 Google Scholar
[39]	https://www.lammps.org/[2023-7-9
[40]	https://www.ks.uiuc.edu/Research/vmd/ [2023-7-9

[1]	Yu Xin-Xiu, Li Duo-Sheng, Ye Yin, Lang Wen-Chang, Liu Jun-Hong, Chen Jing-Song, Yu Shuang-Shuang. Molecular dynamics simulation of effect of nickel transition layer on deposition of carbon atoms and graphene growth on cemented carbide surfaces. Acta Physica Sinica, 2024, 73(23): 238701. doi: 10.7498/aps.73.20241170
[2]	Ding Ye-Zhang, Ye Yin, Li Duo-Sheng, Xu Feng, Lang Wen-Chang, Liu Jun-Hong, Wen Xin. Molecular dynamics simulation of graphene deposition and growth on WC-Co cemented carbides. Acta Physica Sinica, 2023, 72(6): 068703. doi: 10.7498/aps.72.20221332
[3]	Huang De-Rao, Song Jun-Jie, He Pi-Mo, Huang Kai-Kai, Zhang Han-Jie. Adsorption behavior of 9,9′-Dixanthylidene and moiré superstructure on Ru(0001). Acta Physica Sinica, 2022, 71(21): 216801. doi: 10.7498/aps.71.20221057
[4]	De-Rao Huang, Jun-Jie Song, Pi-Mo He, Kai-Kai Huang, Han-Jie Zhang. Adsorption Behavior of 9,9'-Dixanthylidene and Moiré Superstructure on Ru(0001). Acta Physica Sinica, 2022, 0(0): . doi: 10.7498/aps.7120221057
[5]	Wan Zhen, Li Cheng, Liu Yu-Jian, Song Xue-Feng, Fan Shang-Chun. Research progress of electromechanical graphene resonant sensors. Acta Physica Sinica, 2022, 71(12): 126801. doi: 10.7498/aps.71.20220215
[6]	Ming Zhi-Fei, Song Hai-Yang, An Min-Rong. Mechanical behavior of graphene magnesium matrix composites based on molecular dynamics simulation. Acta Physica Sinica, 2022, 71(8): 086201. doi: 10.7498/aps.71.20211753
[7]	Liu Qing-Yang, Xu Qing-Song, Li Rui. Effect of N-doping on tribological properties of graphene by molecular dynamics simulation. Acta Physica Sinica, 2022, 71(14): 146801. doi: 10.7498/aps.71.20212309
[8]	Cui Yan, Xia Cai-Juan, Su Yao-Heng, Zhang Bo-Qun, Zhang Ting-Ting, Liu Yang, Hu Zhen-Yang, Tang Xiao-Jie. Switching characteristics of anthraquinone molecular devices based on graphene electrodes. Acta Physica Sinica, 2021, 70(3): 038501. doi: 10.7498/aps.70.20201095
[9]	Bai Qing-Shun, Dou Yu-Hao, He Xin, Zhang Ai-Min, Guo Yong-Bo. Deposition and growth mechanism of graphene on copper crystal surface based on molecular dynamics simulation. Acta Physica Sinica, 2020, 69(22): 226102. doi: 10.7498/aps.69.20200781
[10]	Shi Chao, Lin Chen-Sen, Chen Shuo, Zhu Jun. Molecular dynamics simulation of characteristic water molecular arrangement on graphene surface and wetting transparency of graphene. Acta Physica Sinica, 2019, 68(8): 086801. doi: 10.7498/aps.68.20182307
[11]	Cui Yan, Xia Cai-Juan, Su Yao-Heng, Zhang Bo-Qun, Chen Ai-Min, Yang Ai-Yun, Zhang Ting-Ting, Liu Yang. Rectifying performances of oligo phenylene ethynylene molecular devices based on graphene electrodes. Acta Physica Sinica, 2018, 67(11): 118501. doi: 10.7498/aps.67.20180088
[12]	Qin Zhi-Hui. Recent progress of graphene-like germanene. Acta Physica Sinica, 2017, 66(21): 216802. doi: 10.7498/aps.66.216802
[13]	Zu Feng-Xia, Zhang Pan-Pan, Xiong Lun, Yin Yong, Liu Min-Min, Gao Guo-Ying. Design and electronic transport properties of organic thiophene molecular rectifier with the graphene electrodes. Acta Physica Sinica, 2017, 66(9): 098501. doi: 10.7498/aps.66.098501
[14]	Yang Wen-Long, Han Jun-Sheng, Wang Yu, Lin Jia-Qi, He Guo-Qiang, Sun Hong-Guo. Molecular dynamics simulation on the glass transition temperature and mechanical properties of polyimide/functional graphene composites. Acta Physica Sinica, 2017, 66(22): 227101. doi: 10.7498/aps.66.227101
[15]	Han Tong-Wei, Li Pan-Pan. Investigation on the large tensile deformation and mechanical behaviors of graphene kirigami. Acta Physica Sinica, 2017, 66(6): 066201. doi: 10.7498/aps.66.066201
[16]	Lu Xiao-Bo, Zhang Guang-Yu. Graphene/h-BN Moiré superlattice. Acta Physica Sinica, 2015, 64(7): 077305. doi: 10.7498/aps.64.077305
[17]	Qin Ye-Hong, Tang Chao, Zhang Chun-Xiao, Meng Li-Jun, Zhong Jian-Xin. Molecular dynamics study of ripples in graphene monolayer on silicon surface. Acta Physica Sinica, 2015, 64(1): 016804. doi: 10.7498/aps.64.016804
[18]	Yang Jing-Jing, Li Jun-Jie, Deng Wei, Cheng Cheng, Huang Ming. Transmission mode of a single layer graphene and its performance in the detection of the vibration spectrum of gas molecular. Acta Physica Sinica, 2015, 64(19): 198102. doi: 10.7498/aps.64.198102
[19]	Xu Zhi-Cheng, Zhong Wei-Rong. Transient kinetics of graphene bombarded by fullerene. Acta Physica Sinica, 2014, 63(8): 083401. doi: 10.7498/aps.63.083401
[20]	Han Tong-Wei, He Peng-Fei. Molecular dynamics simulation of relaxation properties of graphene sheets. Acta Physica Sinica, 2010, 59(5): 3408-3413. doi: 10.7498/aps.59.3408

Catalog

Vol. 72, Issue 24 - 2023-12-20

Metrics

Abstract views: 1903
PDF Downloads: 55
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板