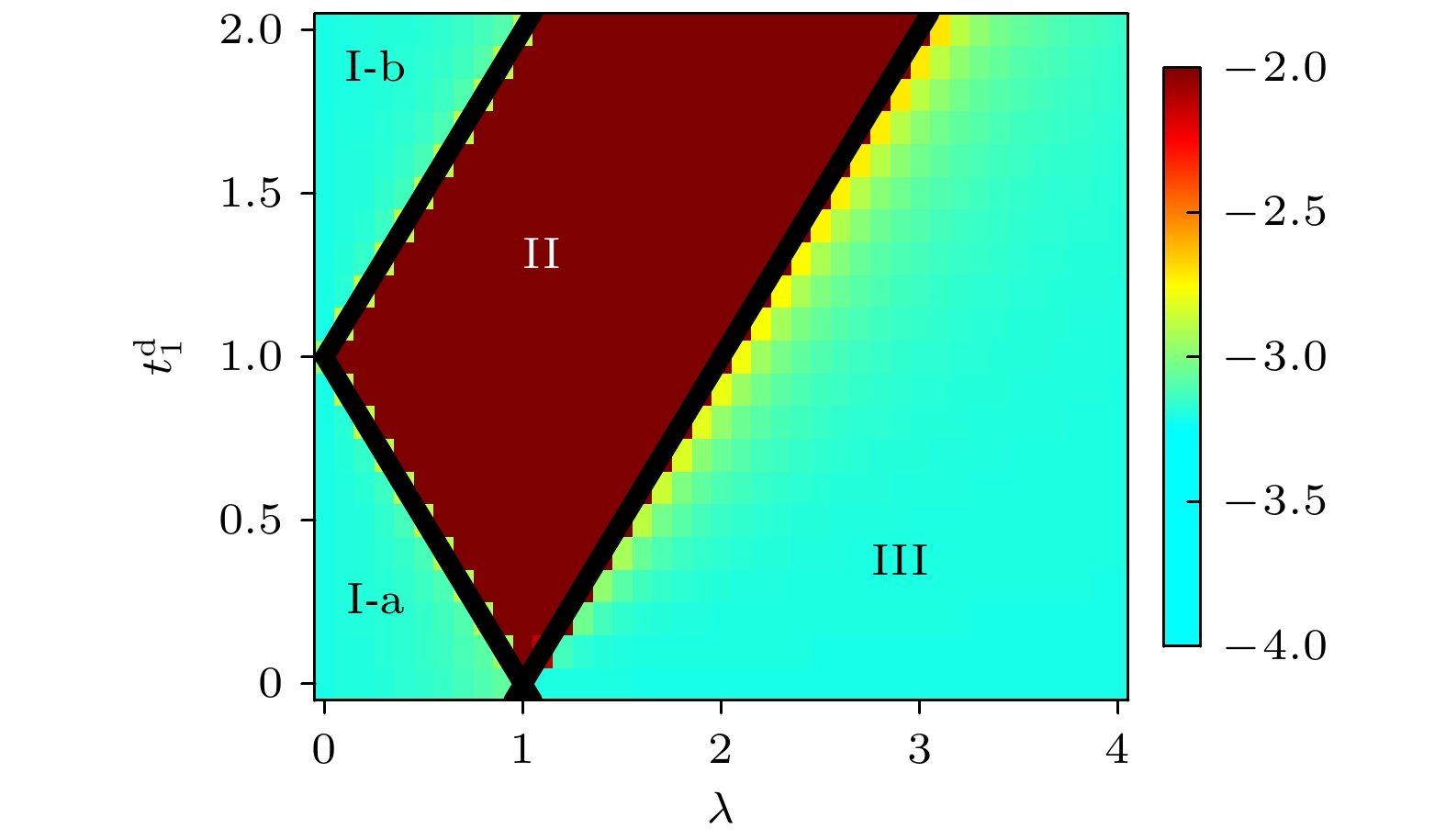
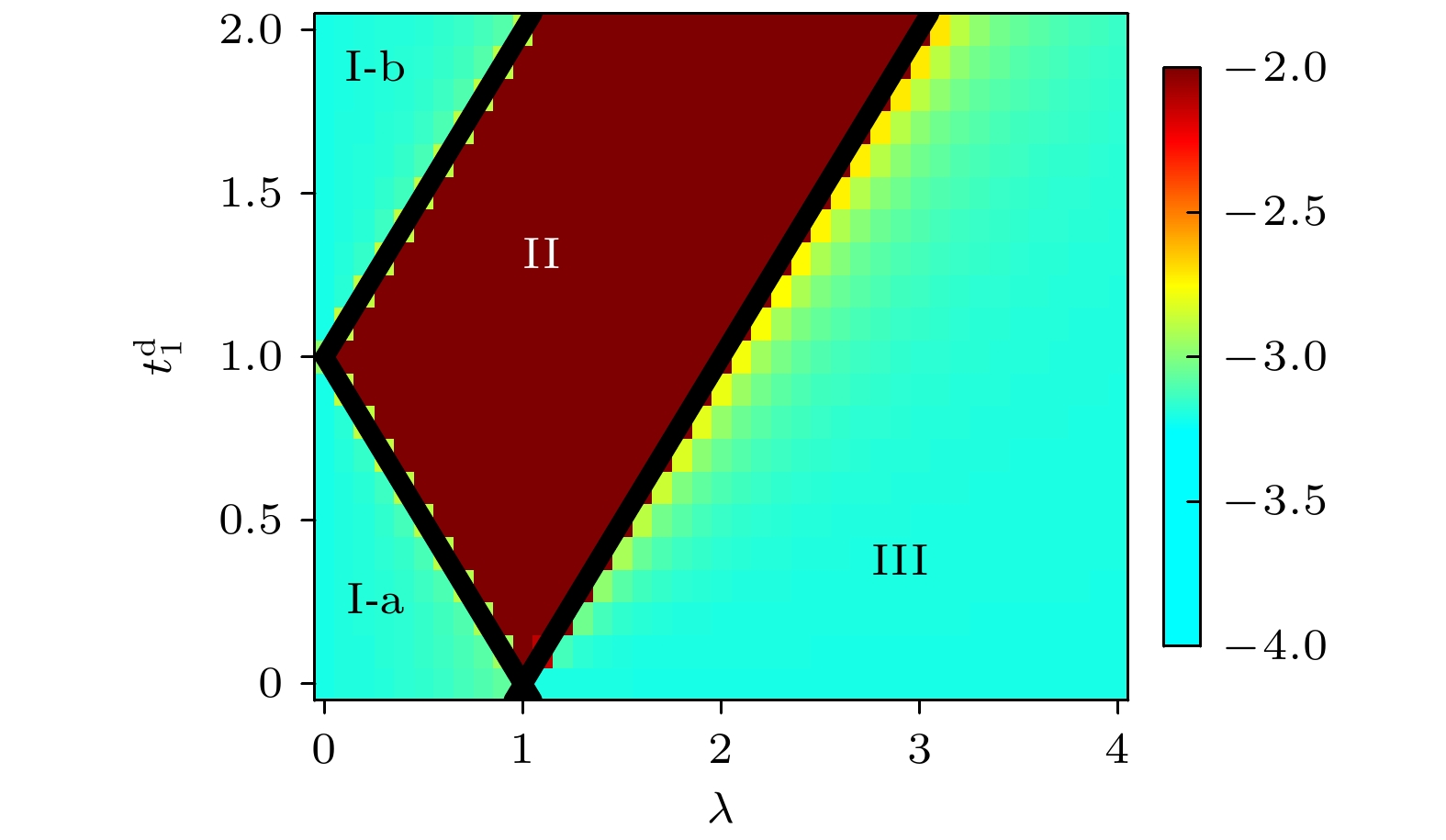
-
In this paper, we study the properties of a coupled chain modulated by the quasiperiodic complex potential. It is found that as the disorder strength increases, the system undergoes a localization transition from a fully extended phase to an intermediate phase, and then to a fully localized phase. The numerical solving of order parameters such as the average inverse participation ratio and the average normalized participation ratio, demonstrate that the fully extended phase, the intermediate phase with mobility edges, and the fully localized phase are all existent during the transition. The scalar analysis of the normalized participation ratio, confirms the stable existence of three different localization phases in the system. Moreover, the analytical derivation, shows that the localization transition from the extended phase to the intermediate phase and from the intermediate phase to the localized phase can be precisely determined. In addition, the local phase diagram of the system is also obtained by numerical calculation, as shown in Fig. (a). The regions for the extended, intermediate and localized phases are denoted by I-a (I-b), II, and III, respectively. The three black solid lines represent the localization transition points determined by the analytical results. One can see that the analytical results match the numerical results. Moreover, we discuss that the relationship between the real-complex spectrum transition and the localization transition. It is found that the energy spectrum of the system can undergo two real-to-complex transitions. Specifically, during the transition from the fully extended phase to the intermediate phase, the first real-complex transition occurs, where part of the energy spectrum changes from the real spectrum to the complex spectrum, while another part spectrum remains real. When the system transitions from the intermediate phase to the fully localized phase, the energy spectrum completely transforms into a complex spectrum. These research results provide a reference for the study of localization transitions and real-complex transitions in one-dimensional coupled chain systems, and also offer a new perspective for the study of localization.
-
Keywords:
- non-Hermitian /
- disorder /
- coupled chain
[1] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[2] Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891
Google Scholar
[3] Roati G, D’Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895
Google Scholar
[4] Schwartz T, Bartal G, Fishman S, Segev M 2007 Nature 446 52
Google Scholar
[5] Mott N 1987 J. Phys. C 20 3075
Google Scholar
[6] Lee P A, Ramakrishnan T V 1985 Rev. Mod. Phys. 57 287
Google Scholar
[7] Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
[8] Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355
Google Scholar
[9] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601
Google Scholar
[10] Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204
Google Scholar
[11] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601
Google Scholar
[12] Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134
Google Scholar
[13] Lin X S, Chen X M, Guo G C, Gong M 2023 Phys. Rev. B 108 174206
Google Scholar
[14] Ahmed A, Roy N, Sharma A 2023 Phys. Rev. B 107 245110
Google Scholar
[15] Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204
Google Scholar
[16] Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403
Google Scholar
[17] 陆展鹏, 徐志浩 2024 73 037202
Google Scholar
Lu Z P, Xu Z H 2024 Acta Phys. Sin. 73 037202
Google Scholar
[18] 吴瑾, 陆展鹏, 徐志浩, 郭利平 2022 71 113702
Google Scholar
Wu J, Lu Z P, Xu Z H, Guo L P 2022 Acta Phys. Sin. 71 113702
Google Scholar
[19] Xu Z H, Xia X, Chen S 2022 Sci. China-Phys. Mech. Astron. 65 227211
Google Scholar
[20] Longhi S 2019 Phys. Rev. Lett. 122 237601
Google Scholar
[21] Rossignolo M, DellÁnna L 2019 Phys. Rev. B 99 054211
Google Scholar
[22] Jazaeri A, Satija I I 2001 Phys. Rev. E 63 036222
Google Scholar
[23] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803
Google Scholar
[24] Li X, Sarma S D 2020 Phys. Rev. B 101 064203
Google Scholar
[25] Roy S, Chattopadhyay S, Mishra T, Basu S 2022 Phys. Rev. B 105 214203
Google Scholar
[26] Zuo Z W, Kang D 2022 Phys. Rev. A 106 013305
Google Scholar
[27] Liu T, Cheng S J 2023 Chin. Phys. B 32 027102
Google Scholar
[28] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[29] Budich J C, Bergholtz E J 2020 Phys. Rev. Lett. 125 180403
Google Scholar
[30] Longhi S 2019 Phys. Rev. B 100 125157
Google Scholar
-
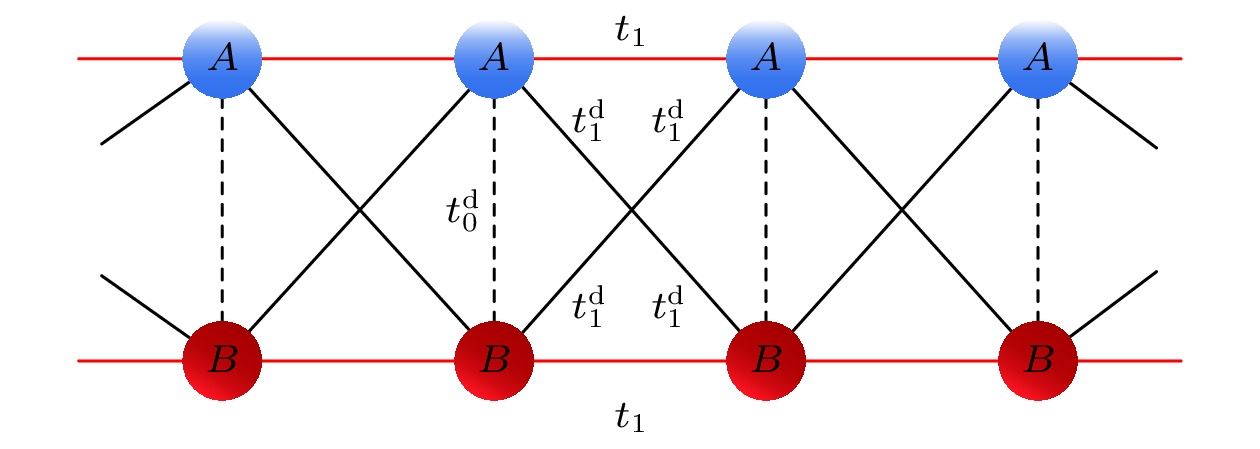
图 1 一维耦合链示意图, $ t_1 $代表相同原子链的最近邻跃迁, $ t_0^{\mathrm{d}} $代表不同原子链间的横向跃迁, $ t_1^{\mathrm{d}} $代表不同原子链间的交叉跃迁
Figure 1. Schematic diagram of the one-dimensional coupled chain, $ t_1 $ represents the nearest-neighbor hopping within the same atomic chain, $ t_0^{\mathrm{d}} $ represents the transverse hopping between different atomic chains, $ t_1^{\mathrm{d}} $ represents the cross hopping between different atomic chains.
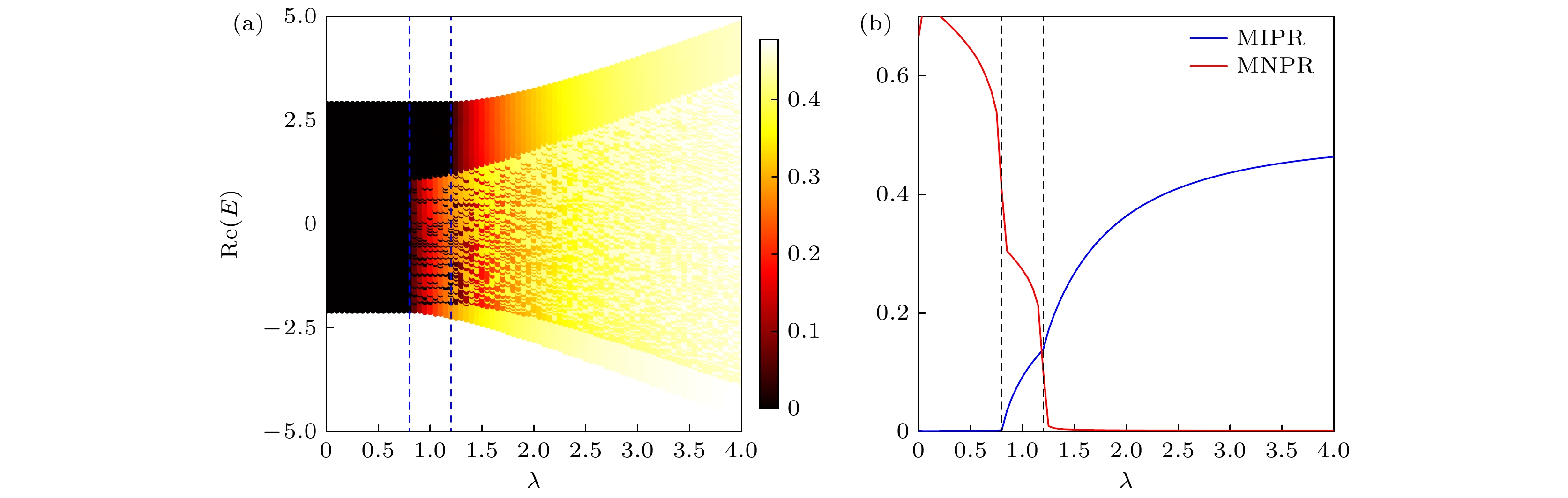
图 2 (a)当$ t_0^{\mathrm{d}}=0.5 $, $ t_1^{\mathrm{d}}=0.2 $和$ L=610 $时, 逆参与率(IPR)随着本征能量的实部$ ({\rm{Re}}(E)) $和无序强度λ的变化, 图中的颜色条代表逆参与率(IPR)的大小. (b)随着系统无序强度λ由小变大, MIPR和MNPR的变化趋势, 分别由蓝色和红色实线表示. 图(a), (b)中蓝色和黑色虚线代表由(10)式确定的系统的两个局域化转变点
Figure 2. (a) When $ t_0^{\mathrm{d}}=0.5 $, $ t_1^{\mathrm{d}}=0.2 $ and $ L=610 $, IPR varies with the real part of the eigenenergy $ ({\rm Re}{(E)}) $ and disorder strength λ, the colorbar represents the magnitude of IPR. (b) As the disorder strength λ of the system increases from weak to strong, the trends of MIPR and MNPR are represented by the blue and red solid lines, respectively; the blue and black dashed lines in Figs. (a) and (b) represent the two localization transition points of the system determined by Eq.(10).
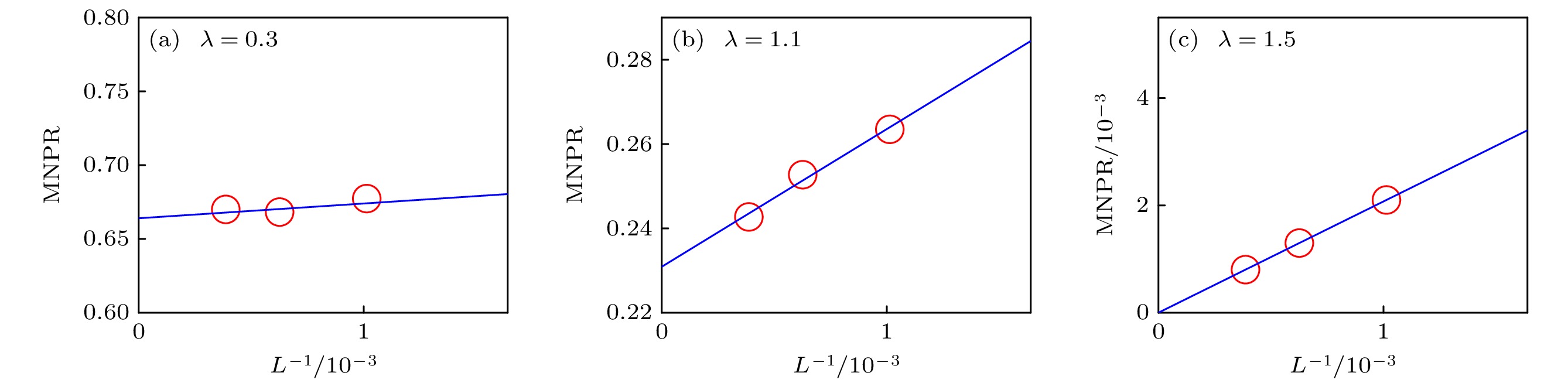
图 3 不同相区内MNPR的标度行为, 其中$ t_0^{\mathrm{d}}=0.5 $ 和$ t_1^{\mathrm{d}}=0.2 $ (a)扩展相区($ \lambda=0.3 $); (b)中间相区($ \lambda=1.1 $); (c)局域相区($ \lambda=1.5 $)
Figure 3. Scaling behavior of MNPR in different phases with $ t_0^{\mathrm{d}}=0.5 $ and $ t_1^{\mathrm{d}}=0.2 $: (a) The extended phase ($ \lambda=0.3 $); (b) the intermediate phase ($ \lambda=1.1 $); (c) the localized phase ($ \lambda=1.5 $).
图 4 $ t_1^{\mathrm{d}} \text-\lambda $参数平面内的局域化相图, 其中Ⅰ-a (Ⅰ-b)表示扩展相, Ⅱ代表具有迁移率边的中间相, Ⅲ表示局域相. 3条黑色实线是根据(10)式确定的局域化相变点, 颜色条代表序参量η的大小, 其中$ L=800 $, $ t_0^{\mathrm{d}}=0.5 $
Figure 4. Localization phase diagram in the $ t_1^{\mathrm{d}} \text-\lambda $ plane, and the regions for the extended, intermediate and localized phases are denoted by Ⅰ-a (Ⅰ-b), Ⅱ, and Ⅲ, respectively. Three black solid lines represent the localization transition points determined by Eq.(10), and the colorbar represents values of η. Here, $ L=800 $ and $ t_0^{\mathrm{d}}=0.5 $.
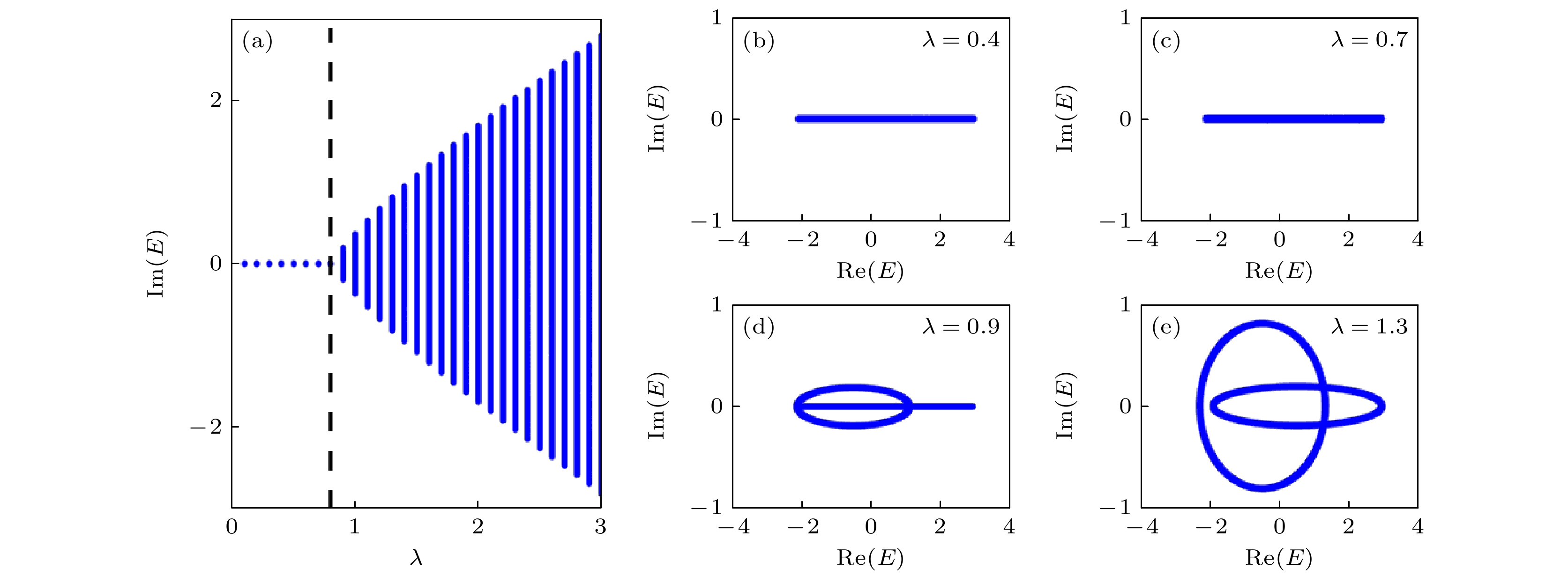
图 5 (a)本征能量的虚部Im(E)随着无序强度λ的变化, 其中黑色虚线由(10)式确定; (b)—(e)当无序强度$ \lambda=0.4, 0.7, 0.9 $ 和$ 1.3 $时, 系统的能谱. 其他参数为$ L=610 $, $ t_0^{\mathrm{d}}=0.5 $和$ t_1^{\mathrm{d}}=0.2 $
Figure 5. (a) The imaginary part of the energy Im(E) varies with disorder strength λ, where the black dashed line is given by Eq.(10); (b)–(e) the energy spectrum of the system for $ \lambda = 0.4, 0.7, 0.9 $ and $ 1.3 $. Other parameters: $ L=610 $, $ t_0^{\mathrm{d}}=0.5 $ and $ t_1^{\mathrm{d}}=0.2 $.
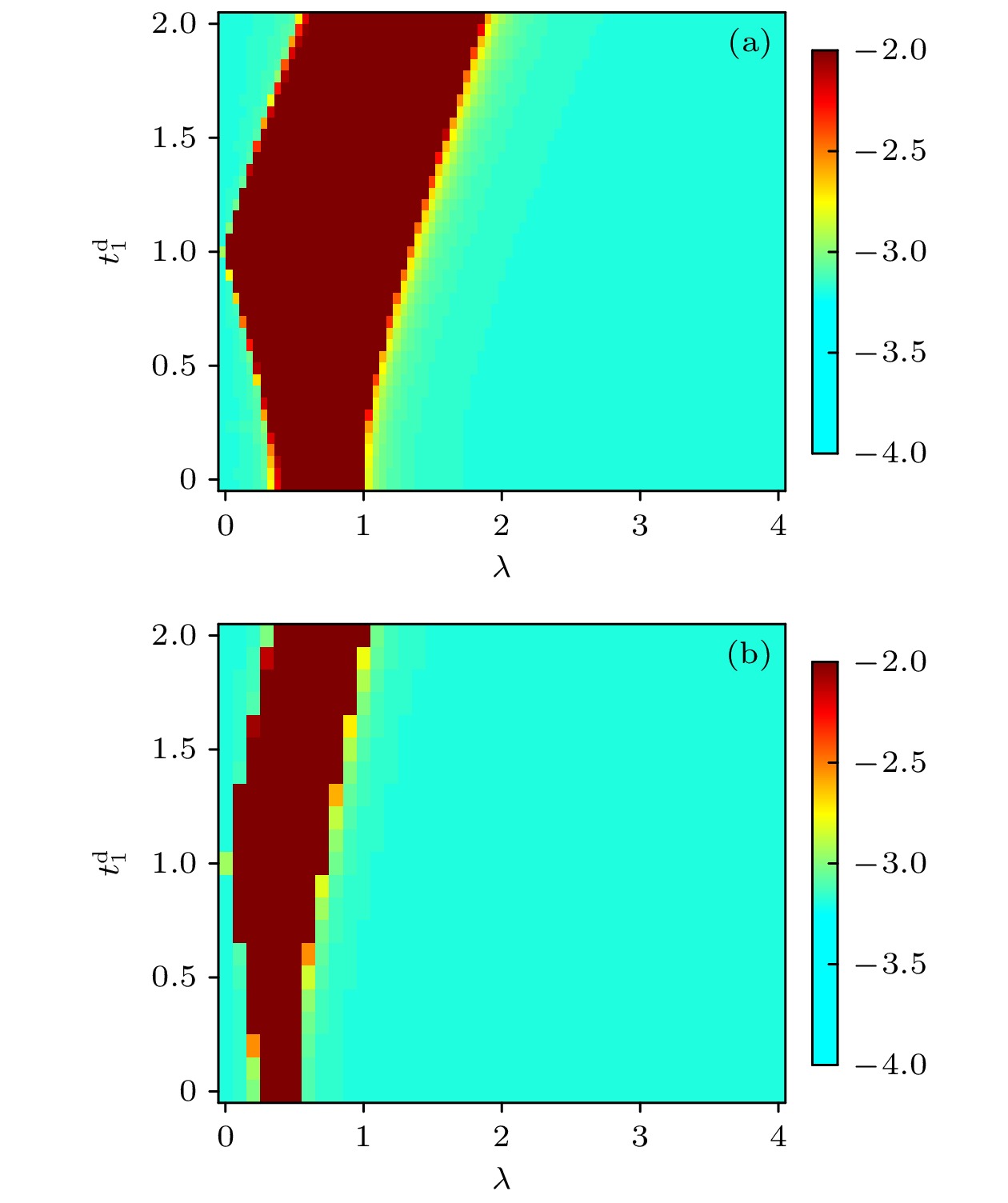
图 A1 $ t_1^{\mathrm{d}} \text-\lambda $参数空间中系统的局域化相图. 浅蓝色区域代表扩展相或者局域相, 棕色区域代表有迁移率边的中间相, 颜色条代表序参量η值, 其中$ L=800 $, $ t_0^{\mathrm{d}}=0.5 $ (a) $ \varepsilon_{A, n}=\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=3\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $; (b) $ \varepsilon_{A, n}=2\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=5\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $
Figure A1. Localization phase diagram in the $ t_1^{\mathrm{d}} \text-\lambda $ plane for (a)$ \varepsilon_{A, n}=\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=3\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $ and (b) $ \varepsilon_{A, n}= $$ 2\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=5\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $. The light blue region represents the extended phase or localized phase, while the brown region represents the intermediate phase with the mobility edges, the colorbar represents values of η, here, $ L=800 $ and $ t_0^{\mathrm{d}} =0.5 $.
-
[1] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[2] Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891
Google Scholar
[3] Roati G, D’Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895
Google Scholar
[4] Schwartz T, Bartal G, Fishman S, Segev M 2007 Nature 446 52
Google Scholar
[5] Mott N 1987 J. Phys. C 20 3075
Google Scholar
[6] Lee P A, Ramakrishnan T V 1985 Rev. Mod. Phys. 57 287
Google Scholar
[7] Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
[8] Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355
Google Scholar
[9] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601
Google Scholar
[10] Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204
Google Scholar
[11] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601
Google Scholar
[12] Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134
Google Scholar
[13] Lin X S, Chen X M, Guo G C, Gong M 2023 Phys. Rev. B 108 174206
Google Scholar
[14] Ahmed A, Roy N, Sharma A 2023 Phys. Rev. B 107 245110
Google Scholar
[15] Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204
Google Scholar
[16] Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403
Google Scholar
[17] 陆展鹏, 徐志浩 2024 73 037202
Google Scholar
Lu Z P, Xu Z H 2024 Acta Phys. Sin. 73 037202
Google Scholar
[18] 吴瑾, 陆展鹏, 徐志浩, 郭利平 2022 71 113702
Google Scholar
Wu J, Lu Z P, Xu Z H, Guo L P 2022 Acta Phys. Sin. 71 113702
Google Scholar
[19] Xu Z H, Xia X, Chen S 2022 Sci. China-Phys. Mech. Astron. 65 227211
Google Scholar
[20] Longhi S 2019 Phys. Rev. Lett. 122 237601
Google Scholar
[21] Rossignolo M, DellÁnna L 2019 Phys. Rev. B 99 054211
Google Scholar
[22] Jazaeri A, Satija I I 2001 Phys. Rev. E 63 036222
Google Scholar
[23] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803
Google Scholar
[24] Li X, Sarma S D 2020 Phys. Rev. B 101 064203
Google Scholar
[25] Roy S, Chattopadhyay S, Mishra T, Basu S 2022 Phys. Rev. B 105 214203
Google Scholar
[26] Zuo Z W, Kang D 2022 Phys. Rev. A 106 013305
Google Scholar
[27] Liu T, Cheng S J 2023 Chin. Phys. B 32 027102
Google Scholar
[28] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[29] Budich J C, Bergholtz E J 2020 Phys. Rev. Lett. 125 180403
Google Scholar
[30] Longhi S 2019 Phys. Rev. B 100 125157
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 757
- PDF Downloads: 42
- Cited By: 0
