-
Mobility edge as one of the most important concepts in a disordered system in which there exists an energy dependent conductor-to-insulator transition has aroused great interest. Unlike an arbitrarily small disorder inducing the Anderson localization in one-dimensional random potential, the well-known Aubry-André model presents a metal-to-insulator transition without mobility edges. Some generalized Aubry-André models are proposed whose the mobility edges in compactly analytic forms are found. However, the existence of the many-body mobility edges in thermodynamic limit for an interacting disordered system is still an open question due to the dimension of the Hilbert space beyond the numerical capacity. In this paper, we demonstrate the existence of the mobility edges of bosonic pairs trapped in one dimensional quasi-periodical lattices subjected to strongly interactions. We believe that our theory will provide a new insight into the studying of the many-body mobility edges. Two strongly interacting bosons are trapped in an incommensurate model, which is described as $\hat H = - J\sum\limits_j{} {\left( {\hat c_j^\dagger {{\hat c}_{j + 1}} + {\rm{h}}{\rm{.c}}{\rm{.}}} \right)} + 2\lambda \sum\limits_j{} {\dfrac{{\cos \left( {2{\text{π}}\alpha j} \right)}}{{1 - b\cos \left( {2{\text{π}}\alpha j} \right)}}} {\hat n_j} + \dfrac{U}{2}\sum\limits_j{} {{{\hat n}_j}\left( {{{\hat n}_j} - 1} \right)} ,$ where there exists no interaction, the system displays mobility edges at$b\varepsilon = 2(J - \lambda )$ , which separates the extended regime from the localized one and b = 0 is the standard Aubry-André model. By applying the perturbation method to the third order in a strong interaction case, we can induce an effective Hamiltonian for bosonic pairs. In the small b case, the bosonic pairs present the mobility edges in a simple closed expression form$b\left( {\dfrac{{{E^2}}}{U} - E - \dfrac{4}{E}} \right) = - 4\left(\dfrac{1}{E} + \lambda \right)$ , which is the central result of the paper. In order to identify our results numerically, we define a normalized participation ratio (NPR)$\eta (E)$ to discriminate between the extended properties of the many-body eigenvectors and the localized ones. In the thermodynamic limit, the NPR tends to 0 for a localized state, while it is finite for an extended state. The numerical calculations finely coincide with the analytic results for b = 0 and small b cases. Especially, for the b = 0 case, the mobility edges of the bosonic pairs are described as$\lambda = - 1/E$ . The extended regime and the one with the mobility edges will vanish with the interaction U increasing to infinity. We also study the scaling of the NPR with system size in both extended and localized regimes. For the extended state the NPR$\eta (E) \propto 1/L$ tends to a finite value with the increase of L and$L \to \infty $ , while for the localized case,$\eta (E) \propto {(1/L)^2}$ tends to zero when$L \to \infty $ . The$b \to 1$ limit is also considered. As the modulated potential approaches to a singularity when$b \to 1$ , the analytic expression does not fit very well. However, the numerical results indicate that the mobility edges of bosonic pairs still exist. We will try to consider the detection of the mobility edges of the bosonic pairs in the future.-
Keywords:
- Anderson localization /
- mobility edges /
- disorder
[1] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[2] Sarma S D, Song H, Xie X C 1988 Phys. Rev. L 61 2144
Google Scholar
[3] Hiramoto H, Kohmoto M 1989 Phys. Rev. B 40 8225
Google Scholar
[4] Sarma S D, Song He, Xie X C 1990 Phys. Rev. B 41 5544
Google Scholar
[5] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601
Google Scholar
[6] Biddle J, Wang B, Priour D J, Sarma S D 2009 Phys. Rev. A 80 021603(R)
Google Scholar
[7] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601
Google Scholar
[8] Hofstadter D R 1983 Phys. Rev. Lett. 51 1198
Google Scholar
[9] Lanini Y, Bromberg Y, Christodoulides D N, Silberberg Y 2010 Phys. Rev. Lett. 105 163905
Google Scholar
[10] Lanini Y, Avidan A, Pozzi F, Sorel M, Morandotti R, Christodoulides D N, Silberberg Y 2008 Phys. Rev. Lett. 100 013906
Google Scholar
[11] Schwartz T 2007 Nature 44 652
[12] Evers F, Mirlin A D 2007 Rev. Mod. Phys. 80 1355
[13] Lüschen H K, Scherg S, Kohlert T, Schreiber M 2018 Phys. Rev. Lett. 120 160404
Google Scholar
[14] McGehee W R, Kondov S S, Xu W, Zirbel J J, DeMarco B 2013 Phys. Rev. Lett. 111 145303
Google Scholar
[15] Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Sliberberg Y 2009 Phys. Rev. Lett. 103 013901
Google Scholar
[16] Aubry S, André G 1980 Ann. Isr.: Phys. Soc. 3 18
[17] Aulbach C 2004 New J. Phys. 3 70
[18] Eilmes A, Grimm U, Römer R A, Schreiber M 1999 Eur. Phys. J. B 8 547
[19] Wiater D, Sowiński T, Zakrzewski J 2017 Phys. Rev. A 96 043629
Google Scholar
[20] Barelli A, Bellissard J, Jacquod P, Shepelyansky D L 1996 Phys. Rev. Lett. 77 4752
Google Scholar
[21] Shepelyansky D L 1996 Phys. Rev. B 54 14896
Google Scholar
[22] Dufour D, Orso G 2012 Phys. Rev. Lett. 109 155306
Google Scholar
[23] Basko D M, Aleiner I L, Altshuler B L 2006 Ann. Phys. 321 1126
Google Scholar
[24] Lev Y B, Reichman D R 2014 Phys. Rev. B 89 220201(R)
Google Scholar
[25] Nag S, Garg A 2017 Phys. Rev. B 96 060203(R)
Google Scholar
[26] Wang Y C, Hu H P, Chen S 2016 Eur. Phys. J. B 89 77
Google Scholar
[27] Ponte P, Papić Z, Huveneers F 2015 Phys. Rev. B 751 55111
[28] Velhinho M T, Pimentel I R, 2000 Phys. Rev. B 61 1043
Google Scholar
[29] Macé N, Laflorencie N, Alet F 2018 arXiv: 1811.01912
[30] Li X P, Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 115 186601
Google Scholar
[31] Modak R, Mukerjee S 2015 Phys. Rev. Lett. 115 230401
Google Scholar
[32] Hsu Y T, Li X, Deng D L, Sarma S D 2018 Phys. Rev. Lett. 121 245701
Google Scholar
-
图 1
$b = 0$ 时,${\rm{NPR}}$ 在不同的相互作用强度$U$ 下随无序强度$\lambda $ 和能量本征值E的变化 (a)$U = - 15$ ; (b)$U = - 20$ ; (c)$U = - 40$ ; (d)$U = - 100$ ; 蓝色的实线对应迁移率边的表达式; 这里取$L = 150$ Figure 1. NPR varying with the disorder strengths
$\lambda $ and the energy eigenvalues E for$b = 0$ ,$L = 150$ and different U: (a) U = –15; (b) U = –20; (c) U = –40; (d) U = –100. The blue solid line represents the analytical expression of the mobility edges.
图 2 (a)
$b = 0,\;U = - 100,\;E = - 100.044$ 时,$\lambda $ 分别为$0.008$ 和$0.012$ 所对应本征态的密度分布; (b)$b = 0,\;U = - 100$ 时, 不同$\lambda $ 和$E$ 所对应的本征态的${\rm{NPR}}$ 随$1/L$ 的变化Figure 2. (a) Density distributions for
$b = 0,\;U = - 100,\;E = - 100.044$ ,$\lambda = 0.008$ and$0.012$ , respectively ; (b) NPR varying with$1/L$ for$b = 0,U = - 100$ and different$\lambda $ and$E$ .
图 3 (a) NPR在
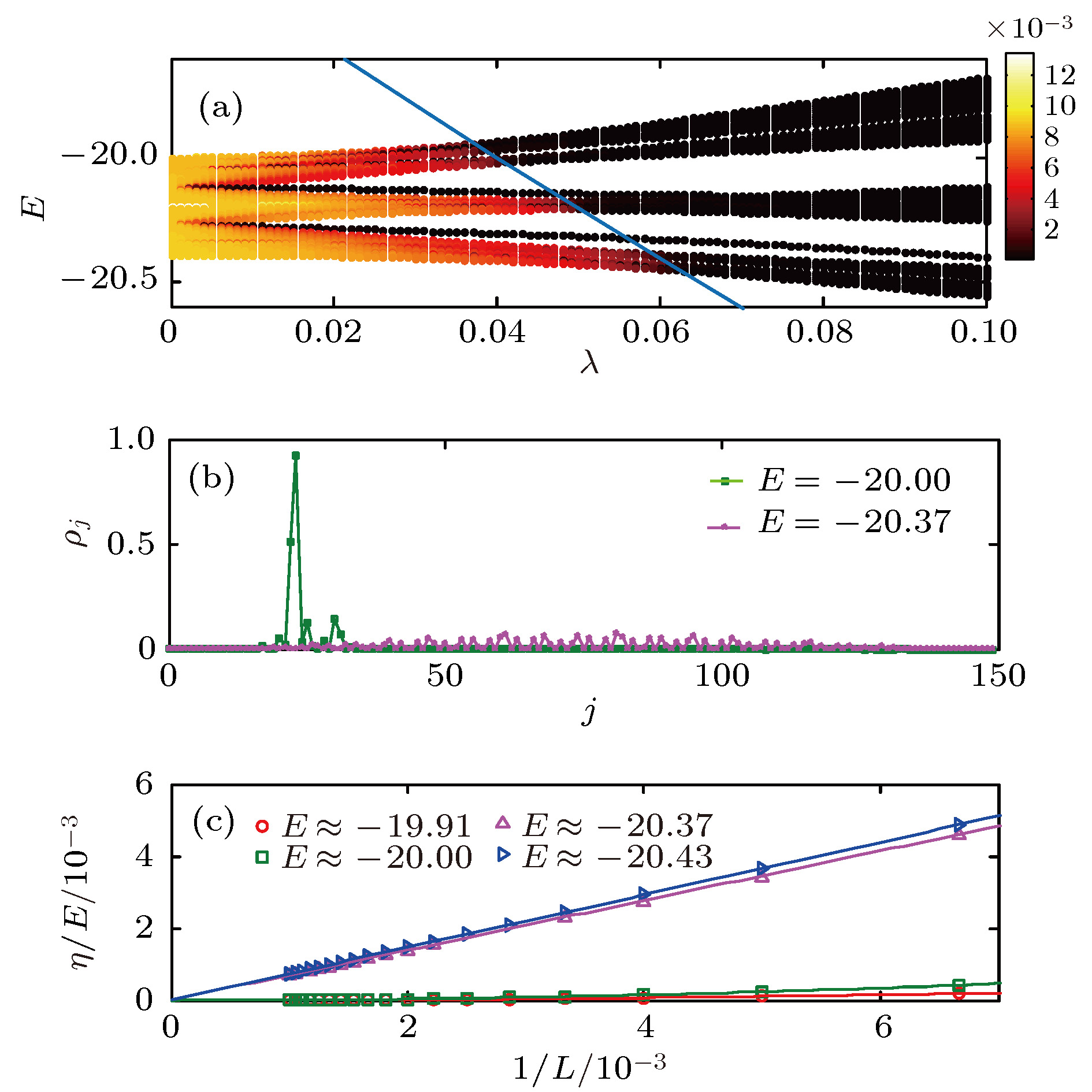
$L = 150$ 时随无序强度$\lambda $ 和能量本征值E的变化, 蓝色的实线对应迁移率边的表达式; (b)$\lambda =$ 0.048,$L = 150$ 时, 能量$E = - 20$ 和${\rm{ - }}20.37$ 所对应的密度分布; (c) 不同能量的NPR在$\lambda =0.048$ 时随$1/L$ 的变化. 这里我们选取$b = 0.2$ ,$U = - 20$ Figure 3. (a) NPR varying with the disorder strength
$\lambda $ and the eigenvalues$E$ with$L = 150$ , the blue solid line represents the analytical expression of the mobility edges; (b) density distributions for$\lambda = 0.048,L = 150$ and different$E = - 20$ and$ - 20.37$ ; (c) scaling of the NPR with system size for$\lambda = 0.048$ and different energies. Here, we choose$b = 0.2$ and$U = - 20$ .
图 4 (a), (b) 分别为
$\lambda = 0.08$ ,$b = 0.5,0.96$ 时,$\left| {2\lambda \left( j \right)} \right|$ 与$\left| {4\lambda {{\left( j \right)}^2}{\rm{/}}U} \right|$ 在格点上的分布情况; (c), (d)${\rm{NPR}}$ 在$L = 150$ 时随无序强度$\lambda $ 和能量本征值$E$ 的变化, 其参数与(a), (b)相同; 蓝色的实线对应迁移率边的表达式Figure 4. (a), (b)
$\left| {2\lambda (j)} \right|$ and$\left| {4\lambda {{(j)}^2}/U} \right|$ changing with different sites$j$ for$\lambda = 0.08,b = 0.5$ and$0.96$ , respectively; (c), (d) NPR varying with$\lambda $ and$E$ for$L = 150$ and with the same parameters as (a) and (b), respectively. The blue solid line represents the analytical expression of the mobility edges. -
[1] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[2] Sarma S D, Song H, Xie X C 1988 Phys. Rev. L 61 2144
Google Scholar
[3] Hiramoto H, Kohmoto M 1989 Phys. Rev. B 40 8225
Google Scholar
[4] Sarma S D, Song He, Xie X C 1990 Phys. Rev. B 41 5544
Google Scholar
[5] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601
Google Scholar
[6] Biddle J, Wang B, Priour D J, Sarma S D 2009 Phys. Rev. A 80 021603(R)
Google Scholar
[7] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601
Google Scholar
[8] Hofstadter D R 1983 Phys. Rev. Lett. 51 1198
Google Scholar
[9] Lanini Y, Bromberg Y, Christodoulides D N, Silberberg Y 2010 Phys. Rev. Lett. 105 163905
Google Scholar
[10] Lanini Y, Avidan A, Pozzi F, Sorel M, Morandotti R, Christodoulides D N, Silberberg Y 2008 Phys. Rev. Lett. 100 013906
Google Scholar
[11] Schwartz T 2007 Nature 44 652
[12] Evers F, Mirlin A D 2007 Rev. Mod. Phys. 80 1355
[13] Lüschen H K, Scherg S, Kohlert T, Schreiber M 2018 Phys. Rev. Lett. 120 160404
Google Scholar
[14] McGehee W R, Kondov S S, Xu W, Zirbel J J, DeMarco B 2013 Phys. Rev. Lett. 111 145303
Google Scholar
[15] Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Sliberberg Y 2009 Phys. Rev. Lett. 103 013901
Google Scholar
[16] Aubry S, André G 1980 Ann. Isr.: Phys. Soc. 3 18
[17] Aulbach C 2004 New J. Phys. 3 70
[18] Eilmes A, Grimm U, Römer R A, Schreiber M 1999 Eur. Phys. J. B 8 547
[19] Wiater D, Sowiński T, Zakrzewski J 2017 Phys. Rev. A 96 043629
Google Scholar
[20] Barelli A, Bellissard J, Jacquod P, Shepelyansky D L 1996 Phys. Rev. Lett. 77 4752
Google Scholar
[21] Shepelyansky D L 1996 Phys. Rev. B 54 14896
Google Scholar
[22] Dufour D, Orso G 2012 Phys. Rev. Lett. 109 155306
Google Scholar
[23] Basko D M, Aleiner I L, Altshuler B L 2006 Ann. Phys. 321 1126
Google Scholar
[24] Lev Y B, Reichman D R 2014 Phys. Rev. B 89 220201(R)
Google Scholar
[25] Nag S, Garg A 2017 Phys. Rev. B 96 060203(R)
Google Scholar
[26] Wang Y C, Hu H P, Chen S 2016 Eur. Phys. J. B 89 77
Google Scholar
[27] Ponte P, Papić Z, Huveneers F 2015 Phys. Rev. B 751 55111
[28] Velhinho M T, Pimentel I R, 2000 Phys. Rev. B 61 1043
Google Scholar
[29] Macé N, Laflorencie N, Alet F 2018 arXiv: 1811.01912
[30] Li X P, Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 115 186601
Google Scholar
[31] Modak R, Mukerjee S 2015 Phys. Rev. Lett. 115 230401
Google Scholar
[32] Hsu Y T, Li X, Deng D L, Sarma S D 2018 Phys. Rev. Lett. 121 245701
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7179
- PDF Downloads: 101
- Cited By: 0
