腔光子-自旋波量子耦合系统中各向异性奇异点的实验研究

张高见; 王逸璞

doi:10.7498/aps.69.20191632

摘要

通过耦合三维微波腔中光子和腔内钇铁石榴石单晶小球中的自旋波量子形成腔-自旋波量子的耦合系统, 并通过精确调节系统参数在该实验系统中观测到各向异性奇异点. 奇异点对应于非厄米系统中一种特殊状态, 在奇异点处, 耦合系统的本征值和本征矢均简并, 并且往往伴随着非平庸的物理性质. 以往大量研究主要集中在各向同性奇异点的范畴, 它的特征是在系统参数空间中沿着不同参数坐标趋近该奇异点时具有相同的函数关系. 在这篇文章中, 主要介绍实验上在腔光子-自旋波量子耦合系统中通过调节系统的耦合强度和腔的耗散衰减系数两条趋近奇异点的路径而实现了各向异性奇异点, 具体分别对应于在趋近奇异点时, 本征值的虚部的变化与耦合强度和腔的衰减系数的变化会有线性和平方根不同的行为. 各向异性奇异点的实现有助于基于腔光子-自旋波量子耦合系统的量子信息处理和精密探测器件的进一步研究.

关键词:

Abstract

We theoretically and experimentally demonstrate the anisotropic exceptional points (EPs) in the cavity magnonics system where magnons in a one millimeter-diameter yttrium iron garnet (YIG) sphere are coherently coupled with the microwave photons in a three-dimensional microwave cavity. The damping nature makes the cavity magnonics system inherently non-Hermitian. By solving the eigenvalues and eigenvectors of non-Hermitian Hamiltonian, a series of interesting and essential characteristics of the system can be obtained. Therefore, non-Hermitian physics has received more and more attention in both theory and experiment communities. Among them, exceptional points correspond to the non-Hermitian system’s degenerate states where the eigenvalues of the non-Hermitian system are identical, and the eigenvectors are parallel. The coupled cavity photon-magnon system has high tunability of coupling strength and cavity external damping rate, which is very suitable for studying EPs -related physics. Exceptional points (EPs) are crucial in all kinds of non-Hermitian physical systems, which have both fundamental and applicational importance. For instance, it can be used for sensitive detection by monitoring spectrum splitting of degenerate modes when a perturbation to be sensed occurs. The EPs can be anisotropic, which means that it has a different function relation when the system approaches the EPs along different parameter paths of the system. In this paper, by carefully designing the parameter space, we observe the anisotropic exceptional point in the coupled cavity photon-magnon system. It shows the linear and square-root behavior when the EPs are approached from different directions in the parameter space. One of the parameters is the position of the YIG sphere in the cavity, which determines the coherent coupling strength between the cavity mode and the magnon mode. Another parameter is the number of the gasket between the cavity signal loading port and the cavity external surface, which determines the external damping rate of the cavity mode. Both of these parameters can be easily and accurately adjusted experimentally. Our study paves the way for exploring anisotropic EPs based sensing technologies and more non-Hermitian related physics in the cavity magnonics system.

Keywords:

作者及机构信息

浙江大学, 浙江省量子技术与器件重点实验室, 杭州　310027

通信作者: 王逸璞, alex13@csrc.ac.cn

基金项目: 国家级-国家重点基础研究发展计划(批准号：2016YFA0301200)

Authors and contacts

Zhejiang Province Key Laboratory of Quantum Technology and Device, Zhejiang University, Hangzhou 310027, China

Corresponding author: Wang Yi-Pu, alex13@csrc.ac.cn

文章全文 : translate this paragraph

参考文献

[1]	Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623 Google Scholar
[2]	Kurizki G, Bertet P, Kubo Y, Mølmer K, Petrosyan D, Rabl P, Schmiedmayer J 2015 Proc. Natl. Acad. Sci. U.S.A. 112 3866 Google Scholar
[3]	Wallquist M, Hammerer K, Rabl P, Lukin M, Zoller P 2009 Phys. Scr. T137 014001 Google Scholar
[4]	Kimble H J 2008 Nature (London) 453 1023 Google Scholar
[5]	Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003 Google Scholar
[6]	Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603 Google Scholar
[7]	Zhang X, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401 Google Scholar
[8]	Goryachev M, Farr W G, Creedon D L, Fan Y, Kostylev M, Tobar M E 2014 Phys. Rev. Appl. 2 054002 Google Scholar
[9]	Bai L, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201 Google Scholar
[10]	Zhang D, Wang X M, Li T F, Luo X Q, Wu W, Nori F, You J Q 2015 npj Quantum Inf. 1 15014 Google Scholar
[11]	Soykal Ö O, Flatté M E 2010 Phys. Rev. Lett. 104 077202 Google Scholar
[12]	Rameshti B Z, Cao Y, Bauer G E W 2015 Phys. Rev. B 91 214430 Google Scholar
[13]	Cao Y, Yan P, Huebl H, Goennenwein S T B, Bauer G E W 2015 Phys. Rev. B 91 094423 Google Scholar
[14]	Bourhill J, Kostylev N, Goryachev M, Creedon D L, Tobar M E 2016 Phys. Rev. B 93 144420 Google Scholar
[15]	Kostylev N, Goryachev M, Tobar M E 2016 Appl. Phys. Lett. 108 062402 Google Scholar
[16]	Yao B M, Gui Y S, Xiao Y, Guo H, Chen X S, Lu W, Chien C L, Hu C M 2015 Phys. Rev. B 92 184407 Google Scholar
[17]	Zhang X, Zou C L, Jiang L, Tang H X 2016 Sci. Adv. 2 e1501286 Google Scholar
[18]	Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2015 Science 349 405 Google Scholar
[19]	Quirion D L, Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Nakamura Y 2017 Sci. Adv. 3 e1603150 Google Scholar
[20]	Osada A, Hisatomi R, Noguchi A, Tabuchi Y, Yamazaki R, Usami K, Sadgrove M, Yalla R, Nomura M, Nakamura Y 2016 Phys. Rev. Lett. 116 223601 Google Scholar
[21]	Hisatomi R, Osada A, Tabuchi Y, Ishikawa T, Noguchi A, Yamazaki R, Usami K, Nakamura Y 2016 Phys. Rev. B 93 174427 Google Scholar
[22]	Haigh J A, Langenfeld S, Lambert N J, Baumberg J J, Ramsay A J, Nunnenkamp A, Ferguson A J 2015 Phys. Rev. A 92 063845 Google Scholar
[23]	Zhang X, Zhu N, Zou C L, Tang H X 2016 Phys. Rev. Lett. 117 123605 Google Scholar
[24]	Liu T, Zhang X, Tang H X, Flatté M E 2016 Phys. Rev. B 94 060405 Google Scholar
[25]	Wang Y P, Zhang G Q, Zhang D, Luo X Q, Xiong W, Wang S P, Li T F, Hu C M, You J Q 2016 Phys. Rev. B 94 224410 Google Scholar
[26]	Sharma S, Blanter Y M, Bauer G E W 2017 Phys. Rev. B 96 094412 Google Scholar
[27]	Sharma S, Blanter Y M, Bauer G E W 2018 Phys. Rev. Lett. 121 087205 Google Scholar
[28]	Osada A, Gloppe A, Hisatomi R, Noguchi A, Yamazaki R, Nomura M, Nakamura Y, Usami K 2018 Phys. Rev. Lett. 120 133602 Google Scholar
[29]	Liu Z X, Wang B, Xiong H, Wu Y 2018 Opt. Lett. 43 3698 Google Scholar
[30]	Zhang X, Zou C L, Zhu N, Marquardt F, Jiang L, Tang H X 2015 Nat. Commun. 6 8914 Google Scholar
[31]	Lambert N J, Haigh J A, Langenfeld S, Doherty A C, Ferguson A J 2016 Phys. Rev. A 93 021803 Google Scholar
[32]	Bai L, Harder M, Hyde P, Zhang Z, Hu C M, Chen Y P, Xiao J Q 2017 Phys. Rev. Lett. 118 217201 Google Scholar
[33]	Wang Y P, Zhang G Q, Zhang D, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202 Google Scholar
[34]	Hyde P, Yao B M, Gui Y S, Zhang G Q, You J Q, Hu C M 2018 Phys. Rev. B 98 174423 Google Scholar
[35]	Harder M, Yang Y, Yao B M, Yu C H, Rao J W, Gui Y S, Stamps R L, Hu C M 2018 Phys. Rev. Lett. 21 137203 Google Scholar
[36]	Grigoryan V L, Shen K, Xia K 2018 Phys. Rev. B 98 024406 Google Scholar
[37]	Bhoi B, Kim B, Jang S H, Kim J, Yang J, Cho Y J, Kim S K 2019 Phys. Rev. B 99 134426 Google Scholar
[38]	Yang Y, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2019 Phys. Rev. Applied 11 054023 Google Scholar
[39]	Rao J W, Yu C H, Zhao Y T, Gui Y S, Fan X L, Xue D S, Hu C M 2019 New J. Phys. 21 065001 Google Scholar
[40]	Proskurin I, Macedo R, Stamps R L 2019 New J. Phys. 21 095003 Google Scholar
[41]	Yao B m, Yu T, Zhang X, Lu W, Gui Y S, Hu C M, Blanter Y M 2019 arXiv: 1906.12142 v2[cond-mat.mes-hall]
[42]	Yu W C, Wang J J, Yuan H Y, Xiao J 2019 Phys. Rev. Lett. 123 227201 Google Scholar
[43]	Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202 Google Scholar
[44]	Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601 Google Scholar
[45]	Li J, Zhu S Y, Agarwal G S 2019 Phys. Rev. A 99 021801(R)Google Scholar
[46]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[47]	陈增军, 宁西京 2003 52 2683 Google Scholar Chen Z J, Ning X J 2003 Acta Phys. Sin. 52 2683 Google Scholar
[48]	Gilbert T L 2004 IEEE Trans. Magn. 40 3443 Google Scholar
[49]	Stancil D D, Prabhakar A 2009 Spin Waves Theory and Applications (New York: Springer) pp263–296
[50]	Zhang D, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Commun. 8 1368 Google Scholar
[51]	Dembowski C, Gräf H D, Harney H L, Heine A, Heiss W D, Rehfeld H, Richter A 2001 Phys. Rev. Lett. 86 787 Google Scholar
[52]	Dembowski C, Dietz B, Gräf H D, Harney H L, Heine A, Heiss W D, Richter A 2003 Phys. Rev. Lett. 90 034101 Google Scholar
[53]	Gao T, Estrecho E, Bliokh K Y, Liew T C H, Fraser M D, Brodbeck S, Kamp M, Schneider C, Hfling S, Yamamoto Y, Nori F, Kivshar Y S, Truscott A G, Dall R G, Ostrovskaya E A 2015 Nature (London) 526 554 Google Scholar
[54]	Doppler J, Mailybaev A A, Böhm J, Kuhl U, Girschik A, Libisch F, Milburn T J, Rabl P, Moiseyev N, Rotter S 2016 Nature (London) 537 76 Google Scholar
[55]	Heiss W 2012 J. Phys. A 45 444016 Google Scholar
[56]	Ingrid R 2009 Journal Phys. A 42 153001
[57]	Eleuch H, Rotter I 2014 Eur. Phys. J. D 68 74 Google Scholar
[58]	Ding K, Ma G, Xiao M, Zhang Z Q, Chan C T 2016 Phys. Rev. X 6 021007 Google Scholar
[59]	Lu L, Joannopoulos J D, Soljacic M 2014 Nat. Photonics 8 821 Google Scholar
[60]	Zhou H, Peng C, Yoon Y, Hsu C W, Nelson K A, Fu L, Joannopoulos J D, Soljacic M, Zhen B 2018 Science 359 1009 Google Scholar
[61]	Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 Google Scholar
[62]	Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature (London) 548 187 Google Scholar
[63]	Lin Z, Pick A, Loncar M, Rodriguez A W 2016 Phys. Rev. Lett. 117 107402 Google Scholar
[64]	Jing H, Özdemir S K, Lu H, Nori F 2017 Sci. Rep. 7 3386 Google Scholar
[65]	Nada M Y, Othman M A K, Capolino F 2017 Phys. Rev. B 96 184304 Google Scholar
[66]	Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404 Google Scholar
[67]	Kato T 1966 Perturbation Theory for Linear Operators (Berlin: Springer-Verlag) p516
[68]	Ding K, Ma G, Zhang Z Q, Chan C T 2018 Phys. Rev. Lett. 121 085702 Google Scholar
[69]	Rotter I 2009 J. Phys. A 42 153001 Google Scholar
[70]	Eleuch H, Rotter I 2015 Eur. Phys. J. D 69 229 Google Scholar
[71]	Kittel C 1948 Phys. Rev. 73 155 Google Scholar

施引文献

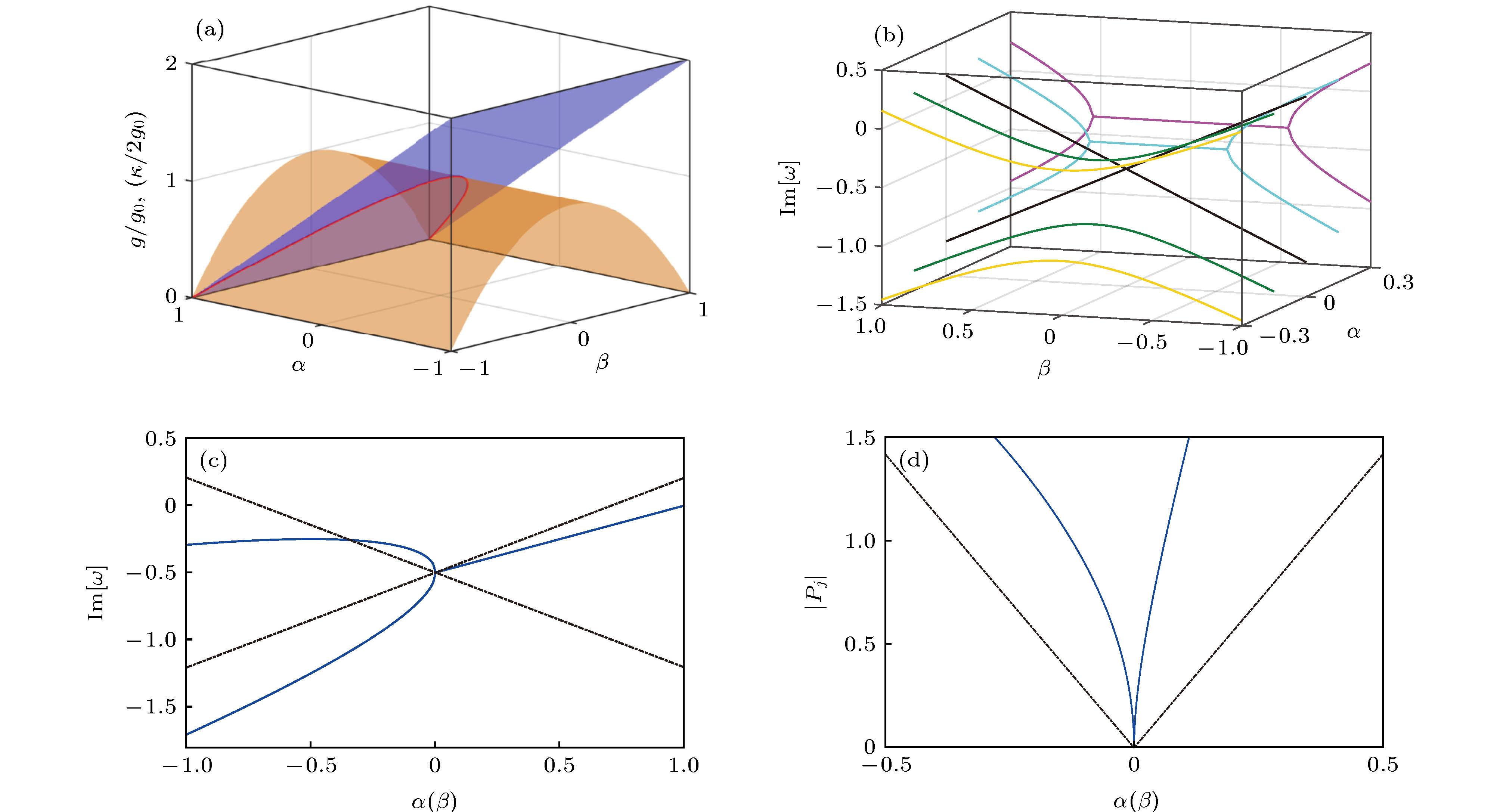
图 1 (a)归一化耦合常数$ g/g_0 $和归一化衰减系数差$ \Delta\kappa/(2 g_0) $在参数空间$ (\alpha, \beta) $ 中分别用黄色和绿色表示, 红色的实线表示的是奇异点连成的线; (b)系统本征频率在参数空间中的虚部, 黑色实线交叉的地方就是各向异性奇异点的位置; (c)表示本征频率的虚部分别沿着$ \alpha (\beta = 0) $(实线)和$ \beta(\alpha = 0) $ (虚线)方向; (d)表示的是态分别沿着$ \alpha (\beta = 0) $(实线)和$ \beta(\alpha = 0) $(虚线)方向的相位信息; 上面的参数为: $ \omega_0 = 1, \gamma_{\rm m} = 0, g_0 = 0.5 $

Fig. 1. (a) The normalized coupling constant $ g/g_0 $ and normalized loss difference $ \Delta\kappa/(2 g_0) $ in the parameter space $ (\alpha, \beta) $ are shown by the yellow and green surfaces, respectively. The solid red line corresponds to a line of EPs; (b) the imaginary part of the eigenfrequencies in the parameter space as a function of $ \beta $ and $ \alpha $, where the black solid line crossing is the position of the anisotropic EP; (c) imaginary part of the eigenfrequencies along $ \alpha (\beta = 0) $ adjusting direction (solid line) and $ \beta(\alpha = 0) $ adjusting direction (dotted line), respectively; (d) phase rigidity of the corresponding states along $ \alpha (\beta = 0) $ adjusting direction (solid line) and $ \beta(\alpha = 0) $ adjusting direction (dotted line), respectively. The parameters used are $ \omega_0 = 1, \gamma_{\rm m} = 0 $ and $ g_0 = 0.5 $.

下载: 全尺寸图片幻灯片

图 2 (a) 腔-自旋波量子系统的实验装置图, 把包含YIG 小球的3D腔放入一个室温可高精度调节的双轭双调型电磁铁产生的磁场中, 通过网络分析仪测出腔的透射谱; (b) 表示的是YIG小球黏在一根玻璃钢棒上, 通过一个4 mm的孔, 在腔的一侧插入到3D矩形腔内. 端口1和端口2用来得到腔模的传输谱; (c) 3D腔的透射谱, 横轴为电磁铁线圈的电流(既偏置磁场的大小), 纵轴为探测场的频率. 腔模和Kittle模共振时, 两子系统间的耦合强度最大为$ g_0/2{\text{π}}$ = 8.45 MHz

Fig. 2. Schematic of the experiment setup. The 3D cavity containing the YIG sphere is placed in the static magnetic field generated by a double-yoke double-tuned electromagnet which can be accurately adjusted at room temperature, and the transmission spectrum of the cavity is measured by network analyzer; (b) the YIG sphere is attached to a fiberglass reinforced plastic rod and inserted into a 3D rectangular cavity through a 4 mm hole on one side of the cavity. Ports 1 and 2 are used to obtain the transmission spectrum of cavity modes; (c) transmission spectrum of coupled system as a function of the current of the electromagnet coil(the magnitude of the biased magnetic field) and the probe field frequency. 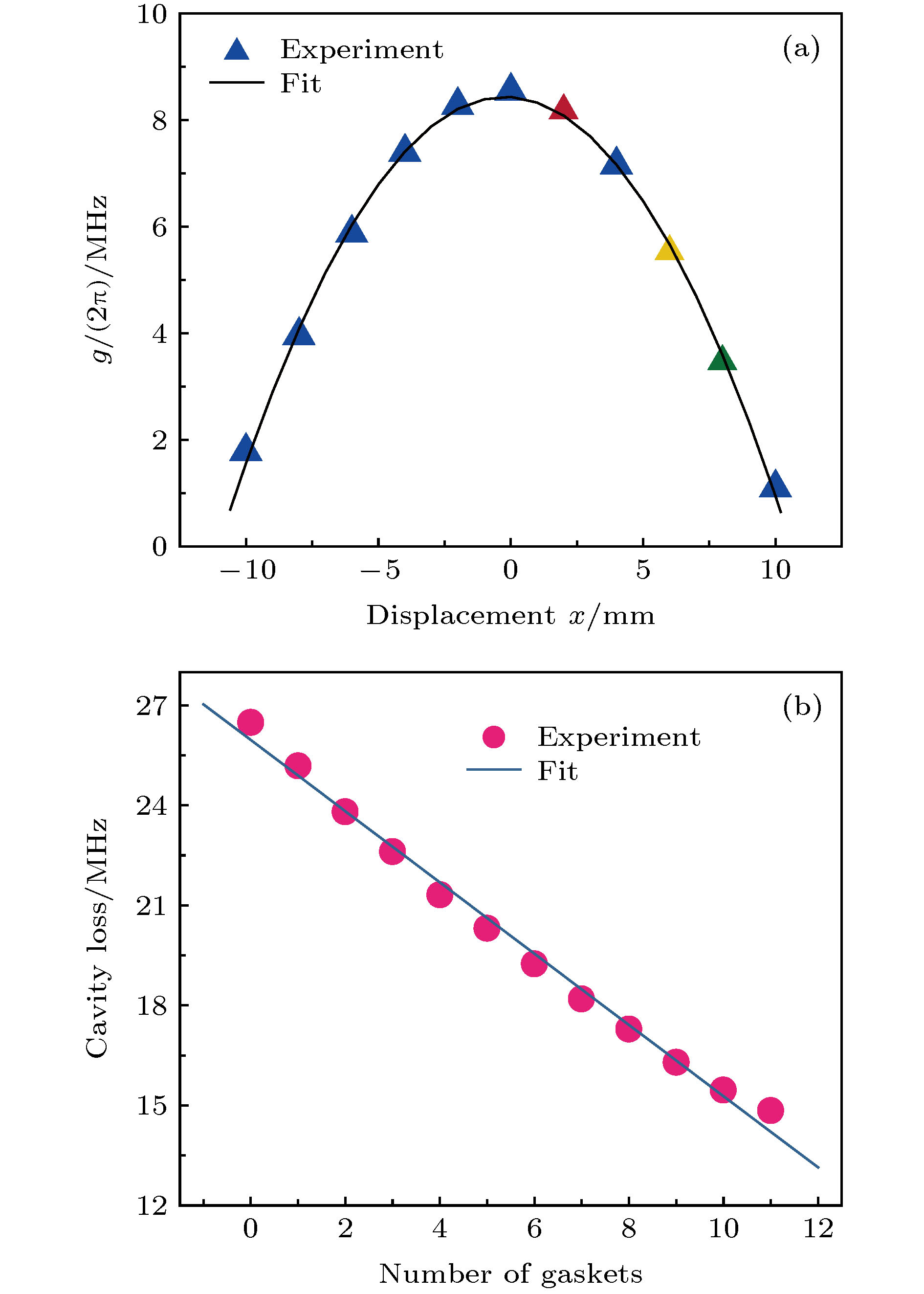When the cavity mode and Kittle mode are resonant, the normal mode splitting equals to $ 2 g_0/2{\text{π}} $ = 16.9 MHz.

下载: 全尺寸图片幻灯片

图 3 (a) 系统的耦合强度g和YIG小球在腔中位置x的二次函数关系, 三角形代表实验得到的结果. 黑色实抛物线线是理论拟合实验数据的结果. 其中深红、黄色和绿色分别表示耦合强度为 8.17, 5.54, 3.47 MHz; (b) 3D腔的衰减$ \kappa $和垫片数量y呈线性函数关系, 品红色原点代表实验测量的结果. 蓝色实线代表理论拟合的结果

Fig. 3. (a) The coherent coupling strength as a function of the position of the YIG sphere in the cavity, and the triangle dots the experimental results. The black solid curve is the result of theoretical fitting of experimental data. Among them, crimson, yellow and green dots indicate the coupling strengthes equal to: 8.17, 5.54 and 3.47 MHz, respectively; (b) the damping rate $ \kappa $ of the 3D cavity as a function of the number of gaskets y between the cavity and SMA connector, and the magenta dots represent the measured results. The solid blue line is the theoretical fitting curve.

下载: 全尺寸图片幻灯片

图 4 在腔的三种不同损耗下测得的传输谱. 所有实线表示应用图3中得到的系统的耦合强度和腔模的衰减系数实验值代入到输入- 输出理论中得到的, 腔模的衰减系数分别为15.64, 18.19和21.32 MHz

Fig. 4. (a)Transmission spectra measured under three different damping rates of the cavity. All the solid lines are calculated using the input-output theory. The damping rates of the cavity mode are 15.64, 18.19 and 21.32 MHz, respectively.

下载: 全尺寸图片幻灯片

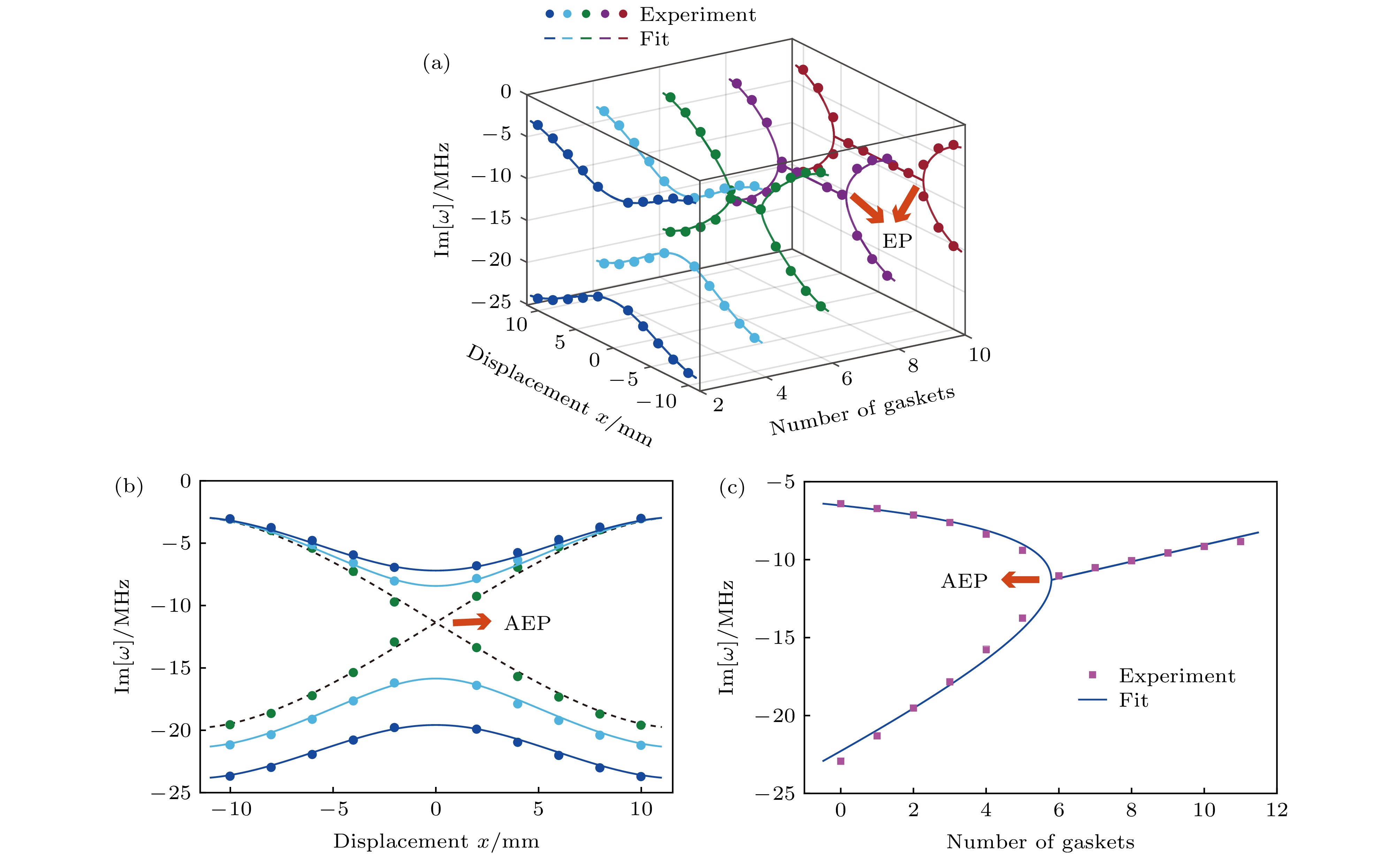
图 5 (a) 在不同腔模损耗下本征频率虚部关于YIG小球在腔中位置x的函数关系. 实线是利用前面实验得到的耦合强度和腔模的损耗(参见图3)计算得到的, 圆点是实验测得的数据; (b)本征频率虚部在垫片数量分别为6, 4, 2的时候并分别用点划线、靛青和蓝色实线表示, 点划线显示了线性交叉行为; (c) 当系统耦合强度$ g_0/2{\text{π}}$ = 8.45 MHz 时, 本征频率虚部关于腔的端口处垫片数量y(腔模损耗)的关系. 实线是理论计算的结果, 品红色方块是实验结果

Fig. 5. (a) Imaginary part of the eigenfrequencies as a function of the position x of the YIG sphere in the cavity with different number of gaskets. The solid curves are calculated using the coupling strengthes and the damping rates of the cavity modes obtained from the previous experiments (see Fig. 3), and the dots are obtained from the experimental data shown in Fig. 4; (b) imaginary part of the eigenfrequencies is plotted by black dotted line, indigo line and blue line when the number of gaskets are 6, 4 and 2, respectively. The black dotted line shows the linear crossing behavior; (c) when the coupling strength of the system is $ g_0/2{\text{π}}$ = 8.45 MHz, imaginary part of the eigenfrequencies are plotted as function of the gaskets y. The solid line is the result of theoretical calculation and the magenta square dots are the experimental results.

下载: 全尺寸图片幻灯片

map

[1]	Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623 Google Scholar
[2]	Kurizki G, Bertet P, Kubo Y, Mølmer K, Petrosyan D, Rabl P, Schmiedmayer J 2015 Proc. Natl. Acad. Sci. U.S.A. 112 3866 Google Scholar
[3]	Wallquist M, Hammerer K, Rabl P, Lukin M, Zoller P 2009 Phys. Scr. T137 014001 Google Scholar
[4]	Kimble H J 2008 Nature (London) 453 1023 Google Scholar
[5]	Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003 Google Scholar
[6]	Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603 Google Scholar
[7]	Zhang X, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401 Google Scholar
[8]	Goryachev M, Farr W G, Creedon D L, Fan Y, Kostylev M, Tobar M E 2014 Phys. Rev. Appl. 2 054002 Google Scholar
[9]	Bai L, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201 Google Scholar
[10]	Zhang D, Wang X M, Li T F, Luo X Q, Wu W, Nori F, You J Q 2015 npj Quantum Inf. 1 15014 Google Scholar
[11]	Soykal Ö O, Flatté M E 2010 Phys. Rev. Lett. 104 077202 Google Scholar
[12]	Rameshti B Z, Cao Y, Bauer G E W 2015 Phys. Rev. B 91 214430 Google Scholar
[13]	Cao Y, Yan P, Huebl H, Goennenwein S T B, Bauer G E W 2015 Phys. Rev. B 91 094423 Google Scholar
[14]	Bourhill J, Kostylev N, Goryachev M, Creedon D L, Tobar M E 2016 Phys. Rev. B 93 144420 Google Scholar
[15]	Kostylev N, Goryachev M, Tobar M E 2016 Appl. Phys. Lett. 108 062402 Google Scholar
[16]	Yao B M, Gui Y S, Xiao Y, Guo H, Chen X S, Lu W, Chien C L, Hu C M 2015 Phys. Rev. B 92 184407 Google Scholar
[17]	Zhang X, Zou C L, Jiang L, Tang H X 2016 Sci. Adv. 2 e1501286 Google Scholar
[18]	Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2015 Science 349 405 Google Scholar
[19]	Quirion D L, Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Nakamura Y 2017 Sci. Adv. 3 e1603150 Google Scholar
[20]	Osada A, Hisatomi R, Noguchi A, Tabuchi Y, Yamazaki R, Usami K, Sadgrove M, Yalla R, Nomura M, Nakamura Y 2016 Phys. Rev. Lett. 116 223601 Google Scholar
[21]	Hisatomi R, Osada A, Tabuchi Y, Ishikawa T, Noguchi A, Yamazaki R, Usami K, Nakamura Y 2016 Phys. Rev. B 93 174427 Google Scholar
[22]	Haigh J A, Langenfeld S, Lambert N J, Baumberg J J, Ramsay A J, Nunnenkamp A, Ferguson A J 2015 Phys. Rev. A 92 063845 Google Scholar
[23]	Zhang X, Zhu N, Zou C L, Tang H X 2016 Phys. Rev. Lett. 117 123605 Google Scholar
[24]	Liu T, Zhang X, Tang H X, Flatté M E 2016 Phys. Rev. B 94 060405 Google Scholar
[25]	Wang Y P, Zhang G Q, Zhang D, Luo X Q, Xiong W, Wang S P, Li T F, Hu C M, You J Q 2016 Phys. Rev. B 94 224410 Google Scholar
[26]	Sharma S, Blanter Y M, Bauer G E W 2017 Phys. Rev. B 96 094412 Google Scholar
[27]	Sharma S, Blanter Y M, Bauer G E W 2018 Phys. Rev. Lett. 121 087205 Google Scholar
[28]	Osada A, Gloppe A, Hisatomi R, Noguchi A, Yamazaki R, Nomura M, Nakamura Y, Usami K 2018 Phys. Rev. Lett. 120 133602 Google Scholar
[29]	Liu Z X, Wang B, Xiong H, Wu Y 2018 Opt. Lett. 43 3698 Google Scholar
[30]	Zhang X, Zou C L, Zhu N, Marquardt F, Jiang L, Tang H X 2015 Nat. Commun. 6 8914 Google Scholar
[31]	Lambert N J, Haigh J A, Langenfeld S, Doherty A C, Ferguson A J 2016 Phys. Rev. A 93 021803 Google Scholar
[32]	Bai L, Harder M, Hyde P, Zhang Z, Hu C M, Chen Y P, Xiao J Q 2017 Phys. Rev. Lett. 118 217201 Google Scholar
[33]	Wang Y P, Zhang G Q, Zhang D, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202 Google Scholar
[34]	Hyde P, Yao B M, Gui Y S, Zhang G Q, You J Q, Hu C M 2018 Phys. Rev. B 98 174423 Google Scholar
[35]	Harder M, Yang Y, Yao B M, Yu C H, Rao J W, Gui Y S, Stamps R L, Hu C M 2018 Phys. Rev. Lett. 21 137203 Google Scholar
[36]	Grigoryan V L, Shen K, Xia K 2018 Phys. Rev. B 98 024406 Google Scholar
[37]	Bhoi B, Kim B, Jang S H, Kim J, Yang J, Cho Y J, Kim S K 2019 Phys. Rev. B 99 134426 Google Scholar
[38]	Yang Y, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2019 Phys. Rev. Applied 11 054023 Google Scholar
[39]	Rao J W, Yu C H, Zhao Y T, Gui Y S, Fan X L, Xue D S, Hu C M 2019 New J. Phys. 21 065001 Google Scholar
[40]	Proskurin I, Macedo R, Stamps R L 2019 New J. Phys. 21 095003 Google Scholar
[41]	Yao B m, Yu T, Zhang X, Lu W, Gui Y S, Hu C M, Blanter Y M 2019 arXiv: 1906.12142 v2[cond-mat.mes-hall]
[42]	Yu W C, Wang J J, Yuan H Y, Xiao J 2019 Phys. Rev. Lett. 123 227201 Google Scholar
[43]	Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202 Google Scholar
[44]	Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601 Google Scholar
[45]	Li J, Zhu S Y, Agarwal G S 2019 Phys. Rev. A 99 021801(R)Google Scholar
[46]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[47]	陈增军, 宁西京 2003 52 2683 Google Scholar Chen Z J, Ning X J 2003 Acta Phys. Sin. 52 2683 Google Scholar
[48]	Gilbert T L 2004 IEEE Trans. Magn. 40 3443 Google Scholar
[49]	Stancil D D, Prabhakar A 2009 Spin Waves Theory and Applications (New York: Springer) pp263–296
[50]	Zhang D, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Commun. 8 1368 Google Scholar
[51]	Dembowski C, Gräf H D, Harney H L, Heine A, Heiss W D, Rehfeld H, Richter A 2001 Phys. Rev. Lett. 86 787 Google Scholar
[52]	Dembowski C, Dietz B, Gräf H D, Harney H L, Heine A, Heiss W D, Richter A 2003 Phys. Rev. Lett. 90 034101 Google Scholar
[53]	Gao T, Estrecho E, Bliokh K Y, Liew T C H, Fraser M D, Brodbeck S, Kamp M, Schneider C, Hfling S, Yamamoto Y, Nori F, Kivshar Y S, Truscott A G, Dall R G, Ostrovskaya E A 2015 Nature (London) 526 554 Google Scholar
[54]	Doppler J, Mailybaev A A, Böhm J, Kuhl U, Girschik A, Libisch F, Milburn T J, Rabl P, Moiseyev N, Rotter S 2016 Nature (London) 537 76 Google Scholar
[55]	Heiss W 2012 J. Phys. A 45 444016 Google Scholar
[56]	Ingrid R 2009 Journal Phys. A 42 153001
[57]	Eleuch H, Rotter I 2014 Eur. Phys. J. D 68 74 Google Scholar
[58]	Ding K, Ma G, Xiao M, Zhang Z Q, Chan C T 2016 Phys. Rev. X 6 021007 Google Scholar
[59]	Lu L, Joannopoulos J D, Soljacic M 2014 Nat. Photonics 8 821 Google Scholar
[60]	Zhou H, Peng C, Yoon Y, Hsu C W, Nelson K A, Fu L, Joannopoulos J D, Soljacic M, Zhen B 2018 Science 359 1009 Google Scholar
[61]	Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 Google Scholar
[62]	Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature (London) 548 187 Google Scholar
[63]	Lin Z, Pick A, Loncar M, Rodriguez A W 2016 Phys. Rev. Lett. 117 107402 Google Scholar
[64]	Jing H, Özdemir S K, Lu H, Nori F 2017 Sci. Rep. 7 3386 Google Scholar
[65]	Nada M Y, Othman M A K, Capolino F 2017 Phys. Rev. B 96 184304 Google Scholar
[66]	Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404 Google Scholar
[67]	Kato T 1966 Perturbation Theory for Linear Operators (Berlin: Springer-Verlag) p516
[68]	Ding K, Ma G, Zhang Z Q, Chan C T 2018 Phys. Rev. Lett. 121 085702 Google Scholar
[69]	Rotter I 2009 J. Phys. A 42 153001 Google Scholar
[70]	Eleuch H, Rotter I 2015 Eur. Phys. J. D 69 229 Google Scholar
[71]	Kittel C 1948 Phys. Rev. 73 155 Google Scholar

[1]	刘敬鹄, 徐志浩. 随机两体耗散诱导的非厄米多体局域化. , 2024, 73(7): 077202. doi: 10.7498/aps.73.20231987
[2]	古燕, 陆展鹏. 非厄米耦合链中的局域化转变. , 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[3]	钱黎明, 孙梦然, 郑改革. α相三氧化钼中各向异性双曲声子极化激元的耦合性质. , 2023, 72(7): 077101. doi: 10.7498/aps.72.20222144
[4]	彭皓, 任芮彬, 钟扬帆, 蔚涛. 三态噪声激励下分数阶耦合系统的随机共振现象. , 2022, 71(3): 030502. doi: 10.7498/aps.71.20211272
[5]	潘磊. 非厄米线性响应理论及其应用. , 2022, 71(17): 170305. doi: 10.7498/aps.71.20220862
[6]	曲登科, 范毅, 薛鹏. 高维宇称-时间对称系统中的信息恢复与临界性. , 2022, 0(0): . doi: 10.7498/aps.71.20220511
[7]	曲登科, 范毅, 薛鹏. 高维宇称-时间对称系统中的信息恢复与临界性. , 2022, 71(13): 130301. doi: 10.7498/aps.70.20220511
[8]	范辉颖, 罗杰. 非厄密电磁超表面研究进展. , 2022, 71(24): 247802. doi: 10.7498/aps.71.20221706
[9]	施婷婷, 张露丹, 张帅宁, 张威. 两量子比特系统中相互作用对高阶奇异点的影响. , 2022, 0(0): 0-0. doi: 10.7498/aps.71.20220716
[10]	施婷婷, 张露丹, 张帅宁, 张威. 两量子比特系统中相互作用对高阶奇异点的影响. , 2022, 71(13): 130303. doi: 10.7498/aps.70.20220716
[11]	唐原江, 梁超, 刘永椿. 宇称-时间对称与反对称研究进展. , 2022, 71(17): 171101. doi: 10.7498/aps.71.20221323
[12]	祝可嘉, 郭志伟, 陈鸿. 实验观测非厄米系统奇异点的手性翻转现象. , 2022, 71(13): 131101. doi: 10.7498/aps.71.20220842
[13]	彭皓, 任芮彬, 蔚涛. 三态噪声激励下分数阶耦合系统的随机共振现象研究. , 2021, (): . doi: 10.7498/aps.70.20211272
[14]	卢敏, 黄惠莲, 余冬海, 刘维清, 魏望和. 不同晶面银纳米晶高温熔化的各向异性. , 2015, 64(10): 106101. doi: 10.7498/aps.64.106101
[15]	周建美, 张烨, 汪宏年, 杨守文, 殷长春. 耦合势有限体积法高效模拟各向异性地层中海洋可控源的三维电磁响应. , 2014, 63(15): 159101. doi: 10.7498/aps.63.159101
[16]	白占国, 董丽芳, 李永辉, 范伟丽. 双层耦合Lengel-Epstein模型中的超点阵斑图. , 2011, 60(11): 118201. doi: 10.7498/aps.60.118201
[17]	凌瑞良, 冯进, 冯金福. 三维各向异性耦合谐振子体系的量子化能谱与精确波函数. , 2010, 59(12): 8348-8358. doi: 10.7498/aps.59.8348
[18]	周建华, 刘虹遥, 罗海陆, 文双春. 各向异性超常材料中倒退波的传播研究. , 2008, 57(12): 7729-7736. doi: 10.7498/aps.57.7729
[19]	林敏, 方利民, 朱若谷. 双频信号作用下耦合双稳系统的双共振特性. , 2008, 57(5): 2638-2642. doi: 10.7498/aps.57.2638
[20]	崔元顺. 介观多环耦合系统中的量子电流增强效应. , 2005, 54(4): 1799-1803. doi: 10.7498/aps.54.1799

计量

文章访问数: 8832
PDF下载量: 157
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

腔光子-自旋波量子耦合系统中各向异性奇异点的实验研究