具有平带的一维十字型晶格中重返局域化现象

陆展鹏; 徐志浩

doi:10.7498/aps.73.20231393

摘要

数值研究了在具有平带的一维十字型晶格中引入准周期调制所诱导的重返局域化现象. 当参数$ \varDelta\neq0$时, 此平带系统等价于存在一个双频率调制的行为. 通过数值求解分形维度、平均逆参与率、平均归一化参与率等序参量证明了在一维十字型晶格中随着调制强度的增加会经历2次局域转变, 即发生第1次局域化转变进入完全局域相后, 继续增加调制强度, 一些局域态重新恢复成了退局域化态, 进一步增加调制强度, 系统将再次进入完全局域化相. 最后给出了局域化相图. 当参数$ \varDelta=0$时, 此系统仅存在单频率调制. 通过解析和数值求解证明了, 系统存在解析的迁移率边, 但不存在重返局域化. 该研究结果为平带系统中重返局域化的研究提供了参考, 也为重返局域化的研究提供了新的视角.

关键词:

无序 /
迁移率边 /
局域化

Abstract

In this work, we numerically study the localization properties in a quasi-periodically modulated one-dimensional cross-stitch lattice with a flat band. When $\varDelta\neq0$, it is found that there are two different quasi-periodic modulation frequencies in the system after the local transformation, and the competing modulation by two frequencies may lead to the reentrant localization transition in the system. By numerically solving the fractal dimension, the average inverse participation ratio, and the average normalized participation ratio, we confirm that the system can undergo twice localization transitions. It means that the system first becomes localized as the disorder increases, at some critical points, some of the localized states go back to the delocalized ones, and as the disorder further increases, the system again becomes fully localized. By the scalar analysis of the normalized participation ratio, we confirm that reentrant localization stably exists in the system. And the local phase diagram is also obtained. From the local phase diagram, we find that when $1.6<\varDelta<1.9$, the system undergoes a cascade of delocalization-localization-delocalization-localization transition by increasing λ. When $\varDelta=0$, there exists only one quasi-periodic modulation frequency in the system. And we analytically obtain the expressions of the mobility edges, which are in consistence with the numerical studies by calculating the fractal dimension. And the system exhibits one localization transition. This work could expand the understanding of the reentrant localization in a flat band system and offers a new perspective on the research of the reentrant localization transition.

Keywords:

作者及机构信息

陆展鹏¹,
徐志浩^1,2

1.
山西大学理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

2.
山西大学极端光学协同创新中心, 太原　030006

通信作者: 徐志浩, xuzhihao@sxu.edu.cn

基金项目: 国家自然科学基金(批准号: 12375016)、山西省基础研究计划(批准号: 20210302123442)、北京凝聚态物理国家研究中心开放课题和山西省“1331工程”重点学科建设计划资助的课题.

Authors and contacts

Lu Zhan-Peng¹,
Xu Zhi-Hao^1,2

1.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Xu Zhi-Hao, xuzhihao@sxu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12375016), the Fundamental Research Program of Shanxi Province,China (Grant No. 20210302123442), the Open Research Fund of Beijing National Laboratory for Condensed Matter Physics, and the Fund for Shanxi “1331 Project” Key Subjects, China.

文章全文 : translate this paragraph

参考文献

[1]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar
[2]	Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 Google Scholar
[3]	Roati G, D'Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895 Google Scholar
[4]	Chabanov A A, Stoytchev M, Genack A Z 2000 Nature 404 850 Google Scholar
[5]	Pradhan P, Sridhar S 2000 Phys. Rev. Lett. 85 2360 Google Scholar
[6]	Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Silberberg Y 2009 Phys. Rev. Lett. 103 013901 Google Scholar
[7]	Mott N 1987 J. Phys. C 20 3075 Google Scholar
[8]	Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
[9]	Harper P G 1955 Proc. Phys. Soc. London Sect. A 68 874 Google Scholar
[10]	Longhi S 2019 Phys. Rev. Lett. 122 237601 Google Scholar
[11]	Longhi S 2019 Phys. Rev. B 100 125157 Google Scholar
[12]	Kraus Y E, Lahini Y, Ringel Z, Verbin M, Zilberberg O 2012 Phys. Rev. Lett. 109 106402 Google Scholar
[13]	Segev M, Silberberg Y, Christodoulides D N 2013 Nat. Photonics 7 197 Google Scholar
[14]	Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601 Google Scholar
[15]	Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601 Google Scholar
[16]	Wang Y C, Zhang L, Sun W, Poon T F J, Liu X J 2022 Phys. Rev. B 106 L140203 Google Scholar
[17]	Zhou X C, Zhou Y J, Poon T F J, Zhou Q, Liu X J 2023 Phys. Rev. Lett. 131 176401 Google Scholar
[18]	Roy N, Sharma A 2021 Phys. Rev. B 103 075124 Google Scholar
[19]	Ahmed A, Roy N, Sharma A 2021 Phys. Rev. B 104 155137 Google Scholar
[20]	Qi R, Cao J P, Jiang X P 2023 arXiv: 2306.03807 [cond-mat.dis-nn
[21]	Goblot V, Štrkalj A, Pernet N, Lado J L, Dorow C, Lemaître A, Gratiet L Le, Harouri A, Sagnes I, Ravets S, Amo A, Bloch J, Zilberberg O 2020 Nat. Phys. 16 832 Google Scholar
[22]	Zhai L J, Huang G Y, Yin S 2021 Phys. Rev. B 104 014202 Google Scholar
[23]	Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 Google Scholar
[24]	Padhan A, Giri M K, Mondal S, Mishra T 2022 Phys. Rev. B 105 L220201 Google Scholar
[25]	Zuo Z W, Kang D W 2022 Phys. Rev. A 106 013305 Google Scholar
[26]	Aditya S, Sengupta K, Sen D 2023 Phys. Rev. B 107 035402 Google Scholar
[27]	Roy S, Chattopadhyay S, Mishra T, Basu S 2022 Phys. Rev. B 105 214203 Google Scholar
[28]	Qi R, Cao J P, Jiang X P 2023 Phys. Rev. B 107 224201 Google Scholar
[29]	Nair P S, Joy D, Sanyal S 2023 arXiv: 2302.14053 [cond-mat.dis-nn
[30]	Li S Z, Li Z 2023 arXiv: 2304.11811 [cond-mat.dis-nn
[31]	Li S Z, Li Z 2023 arXiv: 2305.12321 [cond-mat.dis-nn
[32]	Wu C H, Fan J T, Chen G, Jia S T 2021 New J. Phys. 23 123048 Google Scholar
[33]	Jiang X P, Qiao Y, Cao J P 2021 Chin. Phys. B 30 097202 Google Scholar
[34]	Zhou L W, Han W Q 2022 Phys. Rev. B 106 054307 Google Scholar
[35]	Han W Q, Zhou L W 2022 Phys. Rev. B 105 054204 Google Scholar
[36]	Wang H Y, Zheng X H, Chen J, Xiao L T, Jia S T, Zhang L 2023 Phys. Rev. B 107 075128 Google Scholar
[37]	Flach S, Leykam D, Bodyfelt J D, Matthies P, Desyatnikov A S 2014 Europhys. Lett. 105 30001 Google Scholar
[38]	Wang H, Gao J H, Zhang F C 2013 Phys. Rev. B 87 155116 Google Scholar
[39]	Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 Google Scholar
[40]	Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204 Google Scholar
[41]	Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 Google Scholar
[42]	Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134 Google Scholar
[43]	Cheng S J, Liu T 2023 Chin. Phys. B 32 027102 Google Scholar
[44]	Gneiting C, Li Z, Nori F 2018 Phys. Rev. B 98 134203 Google Scholar
[45]	Han J, Gneiting C, Leykam D 2019 Phys. Rev. B 99 224201 Google Scholar
[46]	吴瑾, 陆展鹏, 徐志浩, 郭利平 2022 71 113702 Google Scholar Wu J, Lu Z P, Xu Z H, Guo L P 2022 Acta Phys. Sin. 71 113702 Google Scholar
[47]	Xu Z H, Huangfu H L, Zhang Y B, Chen S 2020 New J. Phys. 22 013036 Google Scholar
[48]	DeGottardi W, Thakurathi M, Vishveshwara S, Sen D 2013 Phys. Rev. B 88 165111 Google Scholar
[49]	Deng X, Ray S, Sinha S, Shlyapnikov G V, Santos L 2019 Phys. Rev. Lett. 123 025301 Google Scholar
[50]	Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204 Google Scholar

施引文献

图 1 一维十字型晶格示意图. 绿色虚线代表一个原胞. t代表胞内跃迁强度, J代表胞间跃迁强度

Fig. 1. Schematic diagram of the cross-stitch lattice. Each unit cell with two sublattices (A and B) is shown in the green dotted box. t and J are the intracell and intercell hopping amplitudes.

下载: 全尺寸图片幻灯片

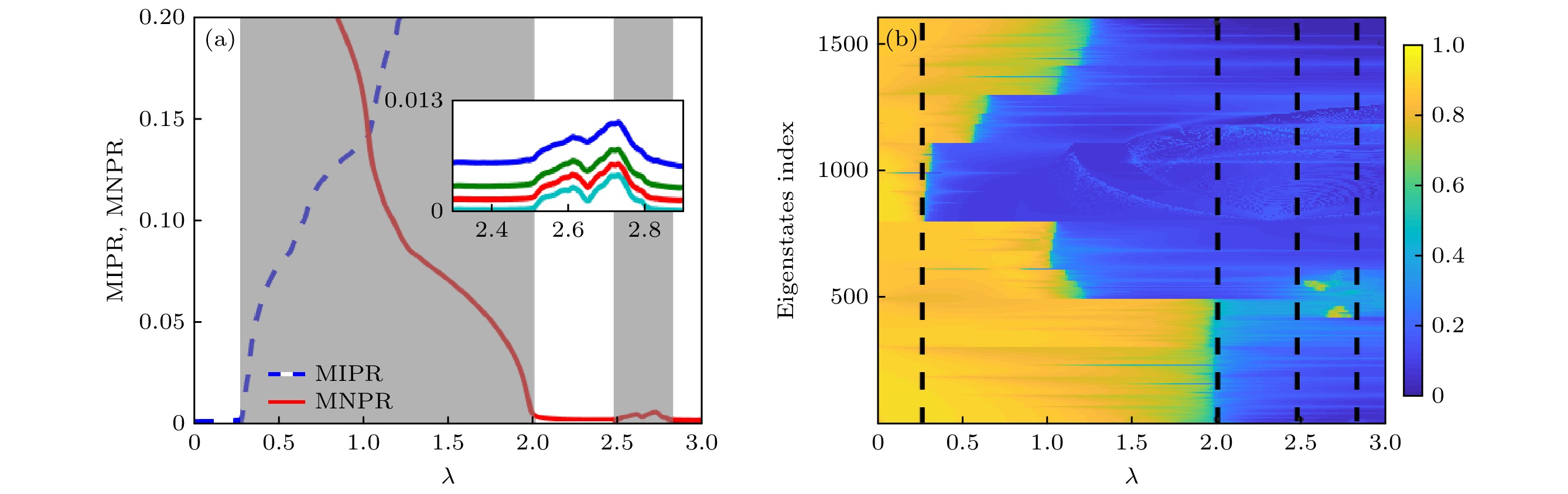
图 2 当$\varDelta=1.68$, $L=800$时, (a) ${\rm{MIPR}}$(蓝色虚线)和${\rm{MNPR}}$(红色实线)随着无序强度λ的变化, 灰色区域表示具有迁移率边的中间相区; 插图显示当$L=300$ (蓝色实线), 500 (深绿色实线), 800 (红色实线)和1500 (湖蓝色实线)时, ${\rm{MNPR}}$随无序强度λ的变化. (b)分形维度$\varGamma_{{i}}$随着本征态指标(eigenstates index)和无序强度λ的变化. 系统存在4个局域化转变点: $\lambda=0.27, $$ \; 2.01,\; 2.48$和2.83 (黑色虚线表示). 图中的颜色条代表分形维度$\varGamma_{{i}}$的大小

Fig. 2. (a) ${\rm{MIPR}}$ (blue dashed line) and ${\rm{MNPR}}$ (red solid line) as a function of the disorder strength λ. The shaded regions represent the intermediate regimes with the mobility edges. The inset shows the ${\rm{MNPR}}$ as a function of the disorder strength λ for L = 300, 500, 800, and 1500, which are marked by blue, bottle green, red and lake blue lines, respectively. (b) The fractal dimension ${\varGamma}_i$ associated with the eigenstate indices as a function of λ. The colorbar indicates the magnitude of ${\varGamma}_i$. There exist four localization transition points $\lambda=0.27,\; 2.01,\; 2.48, $ and 2.83, which marked by the black lines. Other parameters: $\varDelta=1.68$ and $L=800$.

下载: 全尺寸图片幻灯片

图 3 (a)$\lambda=0.1$, (b)$\lambda=2.32$, (c)$\lambda=2.72$时, ${\rm{MNPR}}$随$1/L$变化. 这里, $\varDelta=1.68$

Fig. 3. ${\rm{MNPR}}$ as a function of $1/L$ for (a)$\lambda=0.1$, (b) $\lambda=2.32$ and (c) $\lambda=2.72$, respectively. Here, $\varDelta=1.68$.

下载: 全尺寸图片幻灯片

图 4 $\varDelta{\text{-}}\lambda$参数平面内的局域化相图, 其中绿色区域表示完全扩展或局域相, 红蓝色区域表示具有迁移率边的中间相. 颜色条代表序参量η的大小. 这里$L=800$

Fig. 4. Localization Phase diagram in the $\varDelta{\text{-}}\lambda$ plane, where the green regions denote the full extended or localized phase and the red and blue regions represent the intermediate phase the mobility edges. The colorbar represents values of η. Here, $L=800$.

下载: 全尺寸图片幻灯片

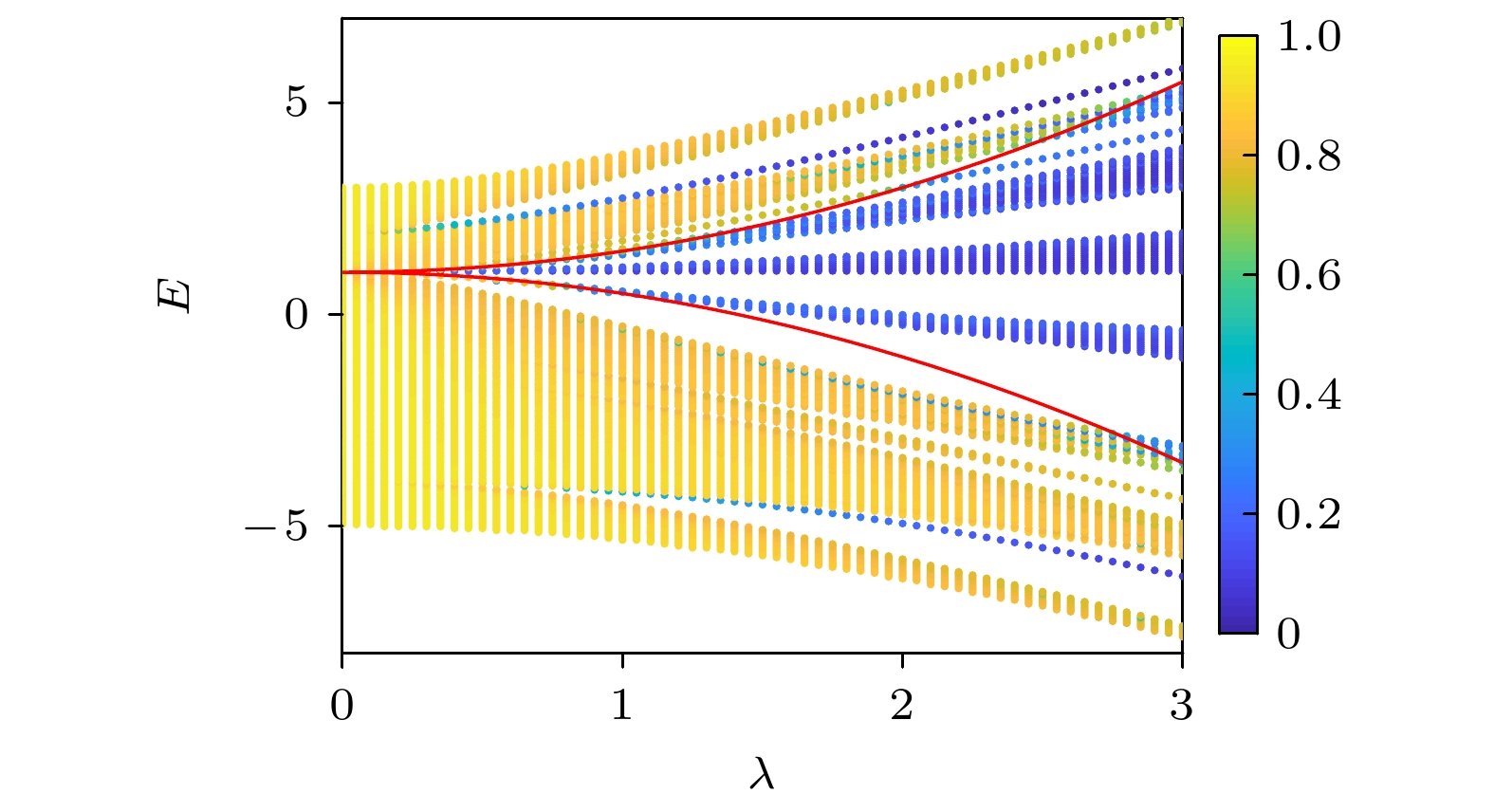
图 5 分形维度$\varGamma_{{i}}$随着调制强度λ和本征能量E的变化. 其中红色实线代表迁移率边的表达式(15). 图中的颜色条代表分形维度$\varGamma_{{i}}$的大小. 其他参数为: $L=800$, $t=1$

Fig. 5. The $\varGamma_{{i}}$ of the eigenstates as a function of he disorder strength λ and the eigen energy E. The red solid line represents the analytical expression (15) of the mobility edge. The colorbar represents the values of $\varGamma_{{i}}$. Here, $L=800$ and $t=1$.

下载: 全尺寸图片幻灯片

map

[1]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar
[2]	Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 Google Scholar
[3]	Roati G, D'Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895 Google Scholar
[4]	Chabanov A A, Stoytchev M, Genack A Z 2000 Nature 404 850 Google Scholar
[5]	Pradhan P, Sridhar S 2000 Phys. Rev. Lett. 85 2360 Google Scholar
[6]	Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Silberberg Y 2009 Phys. Rev. Lett. 103 013901 Google Scholar
[7]	Mott N 1987 J. Phys. C 20 3075 Google Scholar
[8]	Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
[9]	Harper P G 1955 Proc. Phys. Soc. London Sect. A 68 874 Google Scholar
[10]	Longhi S 2019 Phys. Rev. Lett. 122 237601 Google Scholar
[11]	Longhi S 2019 Phys. Rev. B 100 125157 Google Scholar
[12]	Kraus Y E, Lahini Y, Ringel Z, Verbin M, Zilberberg O 2012 Phys. Rev. Lett. 109 106402 Google Scholar
[13]	Segev M, Silberberg Y, Christodoulides D N 2013 Nat. Photonics 7 197 Google Scholar
[14]	Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601 Google Scholar
[15]	Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601 Google Scholar
[16]	Wang Y C, Zhang L, Sun W, Poon T F J, Liu X J 2022 Phys. Rev. B 106 L140203 Google Scholar
[17]	Zhou X C, Zhou Y J, Poon T F J, Zhou Q, Liu X J 2023 Phys. Rev. Lett. 131 176401 Google Scholar
[18]	Roy N, Sharma A 2021 Phys. Rev. B 103 075124 Google Scholar
[19]	Ahmed A, Roy N, Sharma A 2021 Phys. Rev. B 104 155137 Google Scholar
[20]	Qi R, Cao J P, Jiang X P 2023 arXiv: 2306.03807 [cond-mat.dis-nn
[21]	Goblot V, Štrkalj A, Pernet N, Lado J L, Dorow C, Lemaître A, Gratiet L Le, Harouri A, Sagnes I, Ravets S, Amo A, Bloch J, Zilberberg O 2020 Nat. Phys. 16 832 Google Scholar
[22]	Zhai L J, Huang G Y, Yin S 2021 Phys. Rev. B 104 014202 Google Scholar
[23]	Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 Google Scholar
[24]	Padhan A, Giri M K, Mondal S, Mishra T 2022 Phys. Rev. B 105 L220201 Google Scholar
[25]	Zuo Z W, Kang D W 2022 Phys. Rev. A 106 013305 Google Scholar
[26]	Aditya S, Sengupta K, Sen D 2023 Phys. Rev. B 107 035402 Google Scholar
[27]	Roy S, Chattopadhyay S, Mishra T, Basu S 2022 Phys. Rev. B 105 214203 Google Scholar
[28]	Qi R, Cao J P, Jiang X P 2023 Phys. Rev. B 107 224201 Google Scholar
[29]	Nair P S, Joy D, Sanyal S 2023 arXiv: 2302.14053 [cond-mat.dis-nn
[30]	Li S Z, Li Z 2023 arXiv: 2304.11811 [cond-mat.dis-nn
[31]	Li S Z, Li Z 2023 arXiv: 2305.12321 [cond-mat.dis-nn
[32]	Wu C H, Fan J T, Chen G, Jia S T 2021 New J. Phys. 23 123048 Google Scholar
[33]	Jiang X P, Qiao Y, Cao J P 2021 Chin. Phys. B 30 097202 Google Scholar
[34]	Zhou L W, Han W Q 2022 Phys. Rev. B 106 054307 Google Scholar
[35]	Han W Q, Zhou L W 2022 Phys. Rev. B 105 054204 Google Scholar
[36]	Wang H Y, Zheng X H, Chen J, Xiao L T, Jia S T, Zhang L 2023 Phys. Rev. B 107 075128 Google Scholar
[37]	Flach S, Leykam D, Bodyfelt J D, Matthies P, Desyatnikov A S 2014 Europhys. Lett. 105 30001 Google Scholar
[38]	Wang H, Gao J H, Zhang F C 2013 Phys. Rev. B 87 155116 Google Scholar
[39]	Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 Google Scholar
[40]	Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204 Google Scholar
[41]	Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 Google Scholar
[42]	Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134 Google Scholar
[43]	Cheng S J, Liu T 2023 Chin. Phys. B 32 027102 Google Scholar
[44]	Gneiting C, Li Z, Nori F 2018 Phys. Rev. B 98 134203 Google Scholar
[45]	Han J, Gneiting C, Leykam D 2019 Phys. Rev. B 99 224201 Google Scholar
[46]	吴瑾, 陆展鹏, 徐志浩, 郭利平 2022 71 113702 Google Scholar Wu J, Lu Z P, Xu Z H, Guo L P 2022 Acta Phys. Sin. 71 113702 Google Scholar
[47]	Xu Z H, Huangfu H L, Zhang Y B, Chen S 2020 New J. Phys. 22 013036 Google Scholar
[48]	DeGottardi W, Thakurathi M, Vishveshwara S, Sen D 2013 Phys. Rev. B 88 165111 Google Scholar
[49]	Deng X, Ray S, Sinha S, Shlyapnikov G V, Santos L 2019 Phys. Rev. Lett. 123 025301 Google Scholar
[50]	Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204 Google Scholar

[1]	冯曦曦, 陈文, 高先龙. 量子信息中的度量空间方法在准周期系统中的应用. , 2024, 73(4): 040501. doi: 10.7498/aps.73.20231605
[2]	古燕, 陆展鹏. 非厄米耦合链中的局域化转变. , 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[3]	刘敬鹄, 徐志浩. 随机两体耗散诱导的非厄米多体局域化. , 2024, 73(7): 077202. doi: 10.7498/aps.73.20231987
[4]	刘辉, 陆展鹏, 徐志浩. 一维非厄米十字晶格中的退局域-局域转变. , 2024, 73(13): 137201. doi: 10.7498/aps.73.20240510
[5]	任国梁, 申开波, 刘永佳, 刘英光. 类石墨烯氮化碳结构(C₃N)热传导机理研究. , 2023, 72(1): 013102. doi: 10.7498/aps.72.20221441
[6]	陈奇, 戴越, 李飞燕, 张彪, 李昊辰, 谭静柔, 汪潇涵, 何广龙, 费越, 王昊, 张蜡宝, 康琳, 陈健, 吴培亨. 5—10 µm波段超导单光子探测器设计与研制. , 2022, 71(24): 248502. doi: 10.7498/aps.71.20221594
[7]	刘佳琳, 庞婷方, 杨孝森, 王正岭. 无序非厄米Su-Schrieffer-Heeger中的趋肤效应. , 2022, 71(22): 227402. doi: 10.7498/aps.71.20221151
[8]	吴瑾, 陆展鹏, 徐志浩, 郭利平. 由超辐射引起的迁移率边和重返局域化. , 2022, 71(11): 113702. doi: 10.7498/aps.71.20212246
[9]	傅聪, 叶梦浩, 赵晖, 陈宇光, 鄢永红. 共轭聚合物链中光激发过程的无序效应. , 2021, 70(11): 117201. doi: 10.7498/aps.70.20201801
[10]	徐志浩, 皇甫宏丽, 张云波. 一维准周期晶格中玻色子对的迁移率边. , 2019, 68(8): 087201. doi: 10.7498/aps.68.20182218
[11]	刘通, 高先龙. 具有p波超流的一维非公度晶格中迁移率边研究. , 2016, 65(11): 117101. doi: 10.7498/aps.65.117101
[12]	侯碧辉, 刘凤艳, 岳明, 王克军. 纳米金属镝的传导电子定域化. , 2011, 60(1): 017201. doi: 10.7498/aps.60.017201
[13]	丁锐, 金亚秋, 小仓久直. 二维随机介质中柱面波传播及其局域性的随机泛函分析. , 2010, 59(6): 3674-3685. doi: 10.7498/aps.59.3674
[14]	李晓春, 高俊丽, 刘绍娥, 周科朝, 黄伯云. 无序对二维声子晶体平板负折射成像的影响. , 2010, 59(1): 376-380. doi: 10.7498/aps.59.376
[15]	曹永军, 杨旭, 姜自磊. 弹性波通过一维复合材料系统的透射性质. , 2009, 58(11): 7735-7740. doi: 10.7498/aps.58.7735
[16]	王慧琴, 刘正东, 王冰. 二维随机介质中的能量分布和频谱特性. , 2008, 57(9): 5550-5557. doi: 10.7498/aps.57.5550
[17]	王慧琴, 刘正东, 王冰. 同材质颗粒不同填充密度的随机介质中光场的空间分布. , 2008, 57(4): 2186-2191. doi: 10.7498/aps.57.2186
[18]	曹永军, 董纯红, 周培勤. 一维准周期结构声子晶体透射性质的研究. , 2006, 55(12): 6470-6475. doi: 10.7498/aps.55.6470
[19]	许兴胜, 陈弘达, 张道中. 非晶光子晶体中的光子局域化. , 2006, 55(12): 6430-6434. doi: 10.7498/aps.55.6430
[20]	刘小良, 徐慧, 马松山, 宋招权. 一维无序二元固体中电子局域性质的研究. , 2006, 55(6): 2949-2954. doi: 10.7498/aps.55.2949

计量

文章访问数: 2813
PDF下载量: 179
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

具有平带的一维十字型晶格中重返局域化现象