-
Linear response theory is the theoretical foundation of modern experiments. In particular, it plays a vital role in measuring quantum matters. Its main idea is to take the external probe signal of the physical system as a perturbation and use the correlation function in the unperturbed equilibrium state to depict the response to the observable in system. In recent half century, the linear response theory for the closed quantum system has achieved great success in experiments on quantum matters. In recent years, with the tremendous progress of the precise manipulation of the light-matter interaction, the ultracold atom experiments can precisely control dissipative quantum many-body systems. With the discovery of many novel phenomena, dissipative quantum systems and non-Hermitian physics have attracted extensive attention in theory and experiment. We developed a linear response theory, named non-Hermitian linear response theory, to deal with open quantum systems. This theory takes the non-Hermitian term and quantum noise, which are induced by dissipation, as an external perturbative input, to detect the properties of the quantum system, and relates the time evolution of the observable with the correlation function in the unperturbed state of the system. The non-Hermitian linear response theory provides a new method for distinguishing the exotic quantum phase from the normal phase. The theoretical predictions are highly consistent with the recent experimental results of cold atom systems. This paper will review the non-Hermitian linear response theory and discuss its applications in quantum many-body and time-reversal symmetric quantum systems.
-
Keywords:
- non-Hermitian /
- linear response theory /
- quantum many-body systems /
- time-reversal symmetry
[1] Barontini G, Labouvie R, Stubenrauch F, Vogler A, Guarrera V, Ott H 2013 Phys. Rev. Lett. 110 035302
[2] Patil Y S, Chakram S, Vengalattore M 2015 Phys. Rev. Lett. 115 140402
[3] Labouvie R, Santra B, Heun S, Ott H 2016 Phys. Rev. Lett. 116 235302
[4] Lüschen H P, Bordia P, Hodgman S S, Schreiber M, Sarkar S, Daley A J, Fischer M H, Altman E, Bloch I, Schneider U 2017 Phys. Rev. X 7 011034
[5] Tomita T, Nakajima S, Takasu Y, Takahashi Y 2019 Phys. Rev. A 99 031601(R
Google Scholar
[6] Tomita T, Nakajima S, Danshita S, Takasu S, Takahashi Y, 2017 Sci. Adv. 3 e1701513
[7] Sponselee K, Freystatzky L, Abeln B, Diem M, Hundt B, Kochanke A, Ponath T, Santra B, Mathey L, Sengstock K, Becker C 2018 Quantum Sci. Technol. 4 014002
Google Scholar
[8] Takasu Y, Yagami T, Ashida Y, Hamazaki R, Kuno Y, Takahashi Y 2020 Prog. Theor. Exp. Phys. 2020 12A110
Google Scholar
[9] Yan B, Moses S A, Gadway B, Covey J P, Hazzard K R, Rey A M, Jin D S, Ye J 2013 Nature 501 521
Google Scholar
[10] Schäfer F, Fukuhara T, Sugawa S, Takasu Y, Takahashi Y, 2020 Nat. Rev. Phys. 2 411
[11] Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005
[12] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
[13] Bouganne R, Aguilera M B, Ghermaoui A, Beugnon J, Gerbier F 2020 Nat. Phys. 16 21
Google Scholar
[14] Pan L, Chen X, Chen Y, Zhai H 2020 Nat. Phys. 16 767
Google Scholar
[15] Mahan G D 1981 Many Particle Physics (New York and London: Plenum Press)
[16] Coleman P 2015 Introduction to Many-Body Physics (Cambridge: Cambridge University Press)
[17] Kamenev A 2011 Field Theory for Non-equilibrium Systems (Cambridge: Cambridge University Press)
[18] Dalla Torre E G, DiehlS, Lukin M D, Sachdev S, Strack P 2013 Phys. Rev. A 87 023831
[19] Zhai H 2021 Ultracold Atomic Physics (Cambridge: Cambridge University Press)
[20] Purfath M 2014 The Non-Equilibrium Green’s Function Method for Nanoscale Device Simulation (Verlag Wien: Springer Press)
[21] Vale C J, Zwierlein M 2021 Nat. Phys 17 1305
Google Scholar
[22] Stewart J T, Gaebler J P, Jin D S 2008 Nature 454 744
Google Scholar
[23] Dao T L, Georges A, Dalibard J, Salomon C, Carusotto I 2007 Phys. Rev. Lett. 98 240402
Google Scholar
[24] Koschorreck M, Pertot D, Vogt E, Fröhlich B, Feld M, Kröhl M 2012 Nature 485 619
Google Scholar
[25] Brown P T, Guardado-Sanchez E, Spar B M, Huang E W, Devereaux T P, Bakr W S 2020 Nat. Phys. 16 26
[26] Sachdev S 2011 Quantum Phase Transitions (Cambridge: Cambridge University Press)
[27] Zinn-Justin J 2007 Phase Transitions and Renormalisation Group (Oxford: Oxford University Press)
[28] Debenedetti P G, Stillinger F H 2001 Nature 410 259
[29] Dyre J C 2006 Rev. Mod. Phys. 78 953
Google Scholar
[30] Witczak-Krempa W, Sørensen E S, Sachdev S 2014 Nat. Phys. 10 361
Google Scholar
[31] Giamarchi T 2004 Quantum Physics in One Dimension (New York: Oxford University Press)
[32] Lieb E H, Liniger W 1963 Phys. Rev. 130 1605
Google Scholar
[33] Imambekov A, Glazman L I 2008 Phys. Rev. Lett. 100 206805
Google Scholar
[34] Lieb E H 1963 Phys. Rev. 130 1616
Google Scholar
[35] Jiang Y Z, Chen Y Y, Guan X W 2015 Chin. Phys. B 24 050311
[36] Yang B, Chen Y Y, Zheng Y G, Sun H, Dai H N, Guan X W, Yuan Z S, Pan J W 2017 Phys. Rev. Lett. 119 165701
[37] Imambekov A, Schmidt T L, Glazman L I 2012 Rev. Mod. Phys. 84 1253
[38] Sticlet D, Dóra B, Moca C P 2022 Phys. Rev. Lett. 128 016802
[39] Dóra B, Moca C P 2020 Phys. Rev. Lett. 124 136802
[40] Bácsi Á, Moca C P, Dóra B 2020 Phys. Rev. Lett. 124 136401
[41] Bernier J S, Tan R, Guo C, Kollath C, Poletti D 2020 Phys. Rev. B 102 115156
[42] Chen Y 2021 J. High Energy Phys. 04 215
[43] Su K, Zhang P, Zhai H 2021 J. High Energy Phys. 06 156
[44] Wigner E P 1959 Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra (New York: Academic Press)
[45] Dimmock J O 1963 J. Math. Phys. 4 1307
[46] McGinley M, Cooper N R 2020 Nat. Phys. 16 1181
Google Scholar
[47] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
[48] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[49] Bernevig B A, Zhang S C 2006 Phys. Rev. Lett. 96 106802
Google Scholar
[50] König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L W, Qi X L, Zhang S C 2007 Science 318 766
Google Scholar
[51] Deng T S, Pan L, Chen Y, Zhai H 2021 Phys. Rev. Lett. 127 086801
Google Scholar
[52] Wu S, Fatemi V, Gibson Q D, Watanabe K, Taniguchi T, Cava R J, Jarillo-Herrero P 2018 Science 359 76
Google Scholar
[53] Schmidt T L, Rachel S, von Oppen F, Glazman L I 2012 Phys. Rev. Lett. 108 156402
Google Scholar
[54] Väyrynen J I, Goldstein M, Glazman L I 2013 Phys. Rev. Lett. 110 216402
Google Scholar
[55] Väyrynen J I, Pikulin D I, Alicea J 2018 Phys. Rev. Lett. 121 106601
Google Scholar
[56] Roth A, Brüne C, Buhmann H, Molenkamp L W, Maciejko J, Qi X L, Zhang S C 2009 Science 325 294
Google Scholar
[57] Du L, Knez I, Sullivan G, Du R R 2015 Phys. Rev. Lett. 114 096802
Google Scholar
[58] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133
Google Scholar
[59] Haldane F D M 1983 Phys. Lett. A 93 464
Google Scholar
[60] Haldane F D M 1983 Phys. Rev. Lett. 50 1153
[61] White S R, Huse D A 1993 Phys. Rev. B 48 3844
Google Scholar
[62] Kenzelmann M, Cowley R A, Buyers W J L, Tun Z, Coldea R, Enderle M 2002 Phys. Rev. B 66 024407
[63] Affleck I, Kennedy T, Lieb E H, Tasaki H 1987 Phys. Rev. Lett. 59 799
Google Scholar
[64] Pollmann F, Berg E, Turner A M, Oshikawa M 2012 Phys. Rev. B 85 075125
[65] Wang Z, Li Q, Li W, Cai Z 2021 Phys. Rev. Lett. 126 237201
Google Scholar
[66] Deng T S, Pan L 2021 Phys. Rev. B 104 094306
[67] Eigen C, Glidden J A, Lopes R, Cornell E A, Smith R P, Hadzibabic Z 2018 Nature 563 221
[68] Scheie A, Sherman N E, Dupont M, Nagler S E, Stone M B, Granroth G E, Moore J E, Tennant D A 2021 Nat. Phys. 17 726
[69] Jepsen P N, Amato-Grill J, Dimitrova I, Ho W W, Demler E, Ketterle W 2020 Nature 588 403
Google Scholar
[70] David D, Rubio-Abadal A, Ye B, Machado F, Kemp J, Srakaew K, Simon Hollerith S, Rui J, Gopalakrishnan S, Yao N Y, Bloch I, Zeiher J 2022 Science 376 716
-
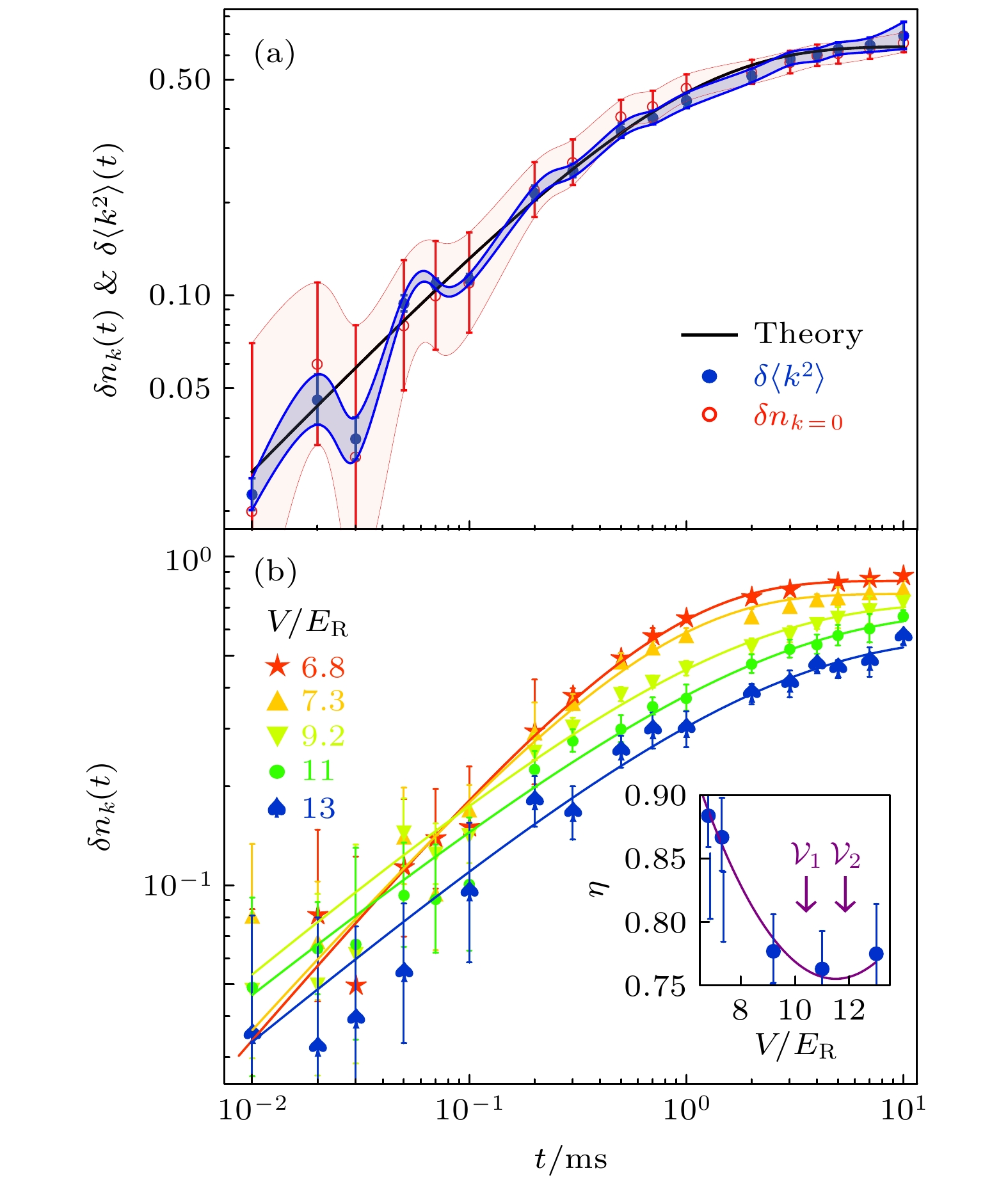
图 1 二维Bose-Hubbard模型耗散动力学实验[13]和理论对比图 (a) 在固定光晶格势阱深度下的动量分布的峰值和宽度随时间的改变, 实线是理论公式拟合的结果; (b) 在不同光晶格势阱深度下的动量峰值随时间的演化图(以
$ \delta n_{{\boldsymbol{ k}}=0}(0) $ 为单位). 实线是理论公式拟合结果, 插图画出了每条曲线对应不同的临界指数$ \eta $ , 其中误差棒来源于标准的拟合误差($ 95\% $ 的置信区间). 两个箭头标注的分别是填充因子$ \nu=1 $ 和$ \nu=2 $ 的超流-Mott绝缘体转变的临界值. 所有的实验数据(包括误差棒)均取自实验文章[13]Figure 1. Experimental data reported in Ref. [13] versus theory on dissipative two-dimensional Bose-Hubbard Model: (a) Two sets of data
$ \delta n_{{\boldsymbol{ k}}=0}(t) $ and$ \delta \langle k^2\rangle(t) $ perfectly coincide with each other by a properly chosen scaling factor. Solid line is fitting with our theory. (b) Fit experimental data of$ \delta n_{{\boldsymbol{ k}}=0}(t) $ (scaled by$ \delta n_{{\boldsymbol{ k}}=0}(0) $ ) at different lattice depths with our theory, which yields$ \eta $ for different lattice depths shown in the inset where the error bar comes from the standard fitting error ($ 95\% $ confidence interval). Two arrows label the critical value for superfluid-Mott insulator transition for filling number$ \nu=1 $ and$ \nu=2 $ , respectively. All experimental data are taken from Ref. [13]
图 2 一维相互作用玻色气体(Luttinger液体)中的动量分布
$ \delta n_{{\boldsymbol{ k}}}(t) $ 从弱相互作用极限(蓝线)到强相互作用极限(红线)的含时演化的理论预测. 这里所有的曲线均取$ \tau_0=1.0\;\rm{ms} $ . 插图表示的是临界指数$ \eta $ 随相互作用强度的变化曲线Figure 2. Prediction of
$ \delta n_{{\boldsymbol{ k}}}(t) $ for a one-dimensional Bose gas (Luttinger liquid) from the weakly interacting limit (blue line) to the Tonks limit (red line). Here$ \tau_0=1.0\;\rm{ms} $ is fixed for all plots. The inset shows how$ \eta $ changes with the one-dimensional interaction parameter$ g/n $ 
图 4 蜂窝格子上的Kane-Mele模型, 其中
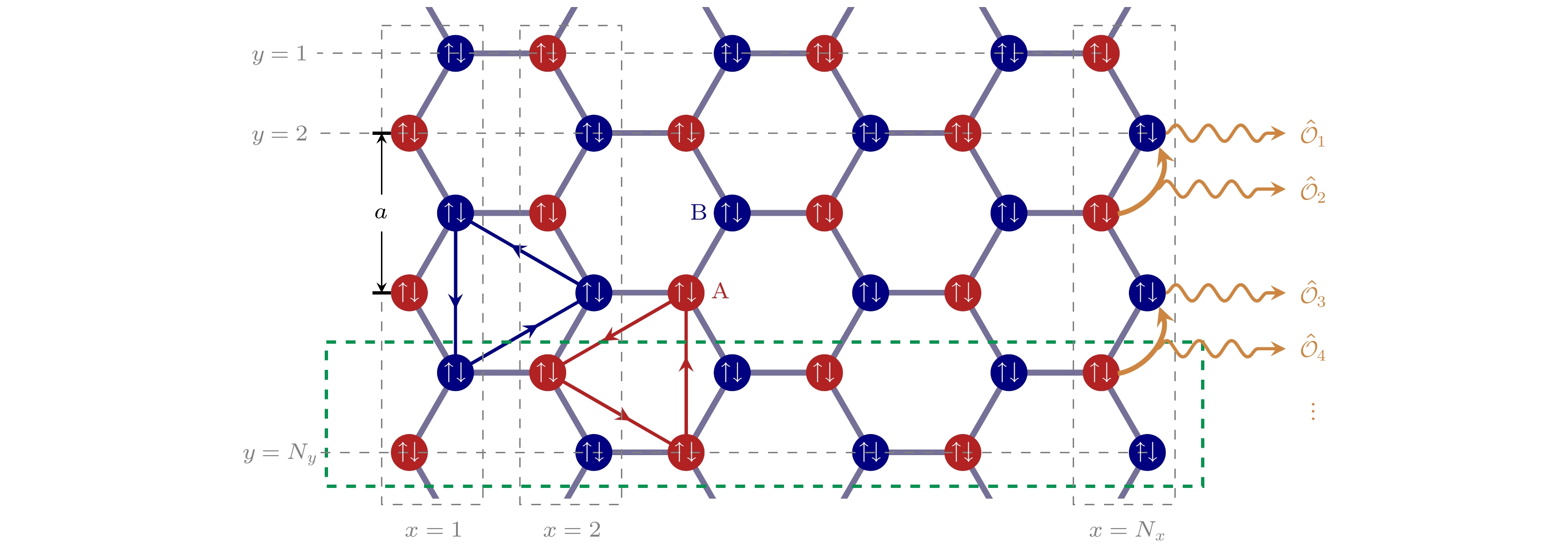
$ x $ 方向取开边界条件,$ y $ 方向上取周期边界条件. 系统尺寸为$ N_x\times N_y $ . 耗散耦合算符$ \hat{\boldsymbol{{{\cal{O}}}}}_m $ 位于右边界, 奇偶分别作用在连接和格点上Figure 4. Honeycomb lattice of the tight-binding Kane-Mele model with open boundary condition along
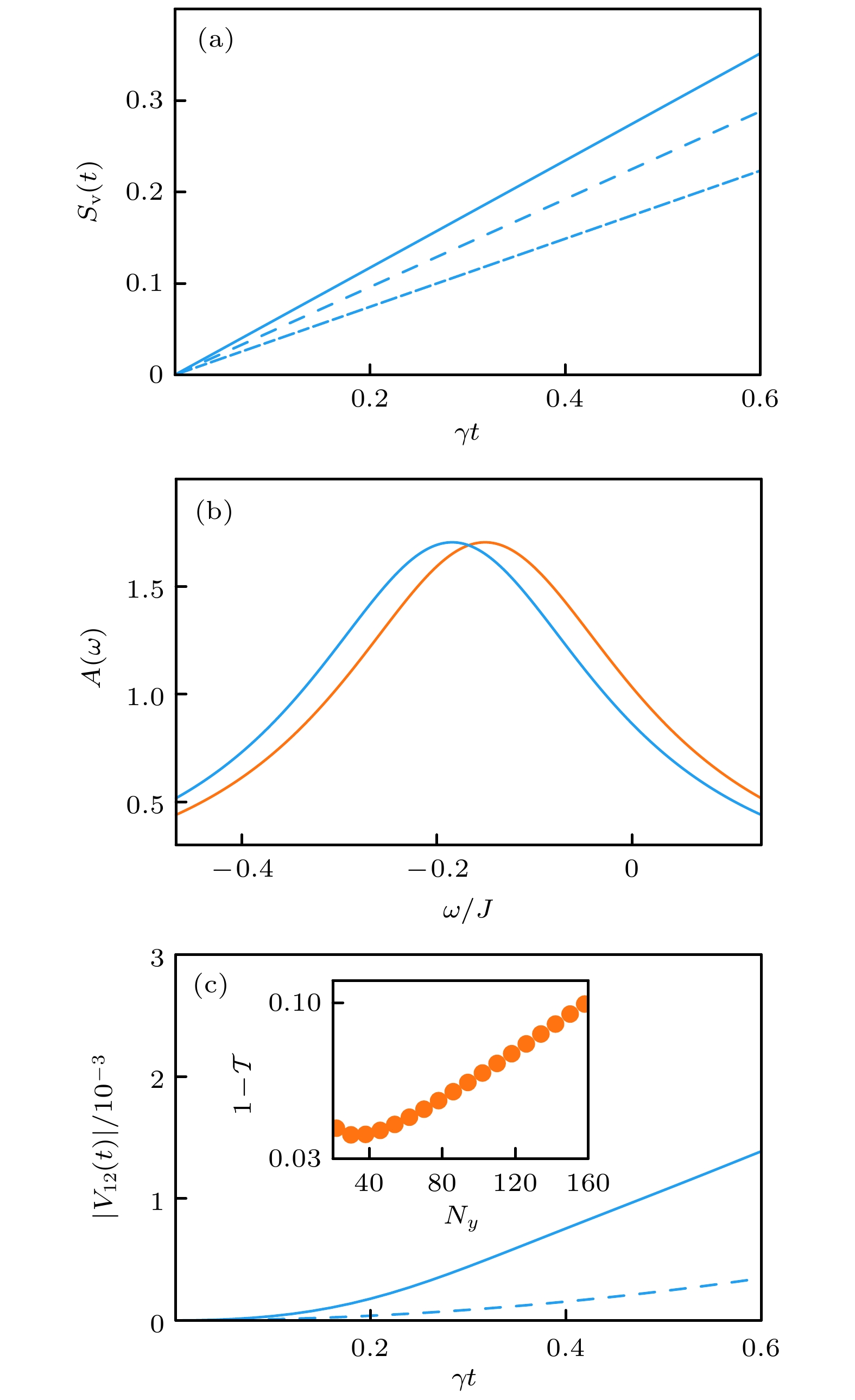
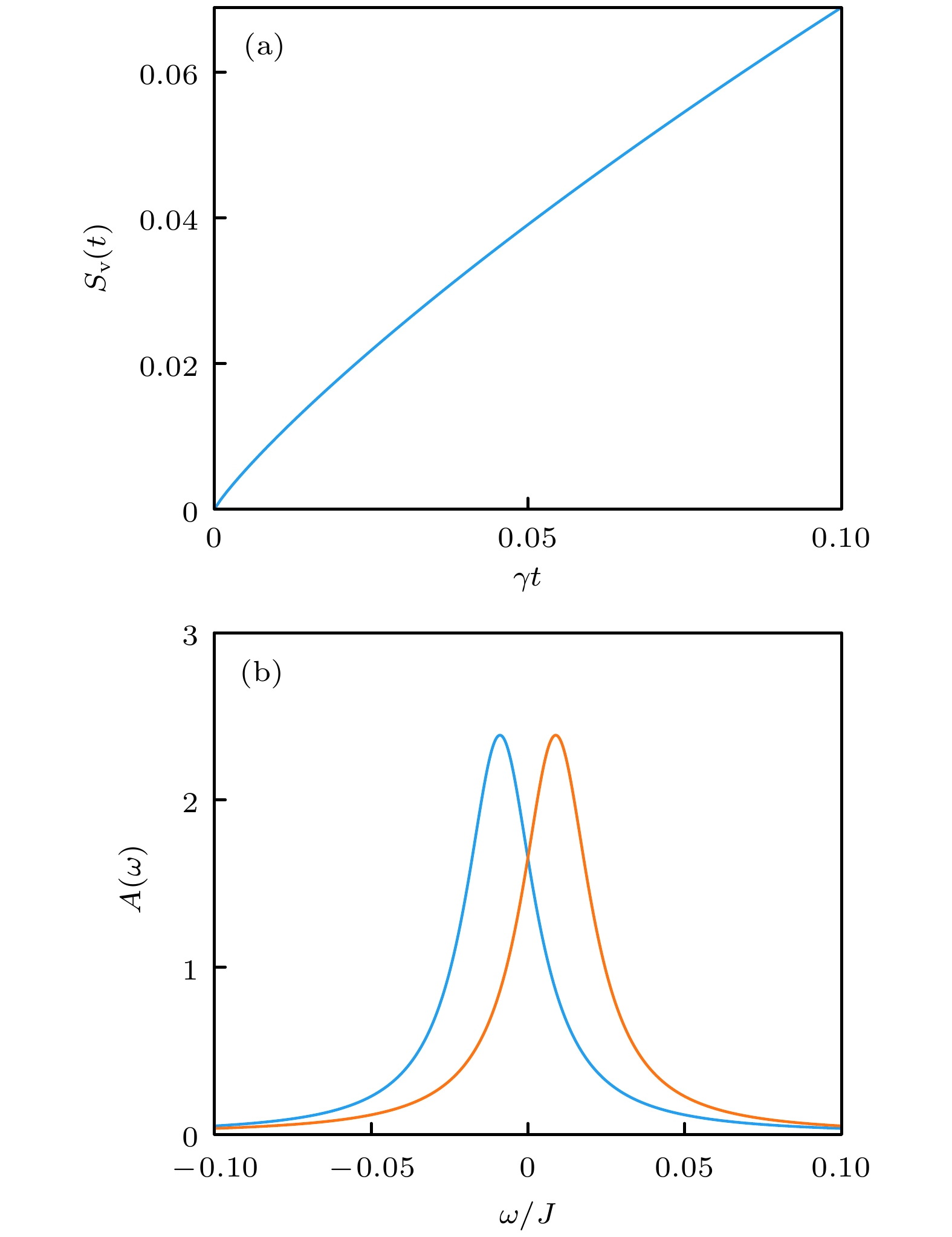
$ x $ -axis and with periodical boundary condition along$ y $ -axis. The sample size is$ N_x\times N_y $ . The coupling operators$ \hat{\boldsymbol{{{\cal{O}}}}}_m $ are located on the right edge, which are defined on links for odd$ m $ and defined on sites for even$ m $ 
图 5 (a) von Neumann熵随时间的变化, 三条曲线分别对应不同耗散耦合通道数目:
$ M=20 $ (实线),$ M=16 $ (虚线) 和$ M=12 $ (点虚线); (b) Kramers简并空间中的谱函数; (c) 杂质势的非对角元$ V_{12}(t) $ 随时间的变化, 实线包含所有态的贡献, 虚线仅包含边缘态的贡献($ M=20 $ ). 插图表示反射率随样品尺寸的变化. 耗散强度$ \gamma $ 大小为$ 0.2 J $ [51]Figure 5. (a) The von Neumann entropy
$ S_{\rm v}(t) $ as a function of time. Here we choosethe number of coupling operators as M = 20 (solid line), M = 16 (dashed line), and M = 12 (dotted dashedline), respectively. (b) The spectral function$ A(\omega) $ for two Kramers degenerate states with dissipation, with$ M=20 $ . (c) Time evolution of the matrix element of the impurity potential$ V_{12}(t) $ between two degenerate edge states with. The solid line includes contributions from all states and the dashed line only includes contributions from edge states. The inset shows the transmission coefficient as a function of$ N_y $ . The dissipation strength$ \gamma $ is taken as$ 0.2 J $ [51]
图 7 AKLT模型基态示意图. 其中每个格点上的自旋
$ S=1 $ (绿色椭圆)被分解成两个自旋$S={1}/{2}$ (蓝色圆点), 被黑色直线连接起来的两个蓝点表示两个自旋$S={1}/{2}$ 形成的自旋单态. 左右边界上的红色圆点表示自由的自旋$S={1}/{2}$ Figure 7. A schematic diagram for groundstate of the AKLT model. The spin
$ S=1 $ (green oval shape) at each site is split into two spin-half (blue dots), and two blue dots connected by black line represents the spin singlet formed by the two spin$ S=1/2 $ . The red dot at each boundary represents free spin-half.
图 8 (a) AKLT模型中的von Neumann熵随时间的变化; (b) 基态空间中的谱函数
Figure 8. (a) The von Neumann entropy as a function of time in the AKLT model; (b) the spectral function in groundstate subspace
-
[1] Barontini G, Labouvie R, Stubenrauch F, Vogler A, Guarrera V, Ott H 2013 Phys. Rev. Lett. 110 035302
[2] Patil Y S, Chakram S, Vengalattore M 2015 Phys. Rev. Lett. 115 140402
[3] Labouvie R, Santra B, Heun S, Ott H 2016 Phys. Rev. Lett. 116 235302
[4] Lüschen H P, Bordia P, Hodgman S S, Schreiber M, Sarkar S, Daley A J, Fischer M H, Altman E, Bloch I, Schneider U 2017 Phys. Rev. X 7 011034
[5] Tomita T, Nakajima S, Takasu Y, Takahashi Y 2019 Phys. Rev. A 99 031601(R
Google Scholar
[6] Tomita T, Nakajima S, Danshita S, Takasu S, Takahashi Y, 2017 Sci. Adv. 3 e1701513
[7] Sponselee K, Freystatzky L, Abeln B, Diem M, Hundt B, Kochanke A, Ponath T, Santra B, Mathey L, Sengstock K, Becker C 2018 Quantum Sci. Technol. 4 014002
Google Scholar
[8] Takasu Y, Yagami T, Ashida Y, Hamazaki R, Kuno Y, Takahashi Y 2020 Prog. Theor. Exp. Phys. 2020 12A110
Google Scholar
[9] Yan B, Moses S A, Gadway B, Covey J P, Hazzard K R, Rey A M, Jin D S, Ye J 2013 Nature 501 521
Google Scholar
[10] Schäfer F, Fukuhara T, Sugawa S, Takasu Y, Takahashi Y, 2020 Nat. Rev. Phys. 2 411
[11] Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005
[12] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
[13] Bouganne R, Aguilera M B, Ghermaoui A, Beugnon J, Gerbier F 2020 Nat. Phys. 16 21
Google Scholar
[14] Pan L, Chen X, Chen Y, Zhai H 2020 Nat. Phys. 16 767
Google Scholar
[15] Mahan G D 1981 Many Particle Physics (New York and London: Plenum Press)
[16] Coleman P 2015 Introduction to Many-Body Physics (Cambridge: Cambridge University Press)
[17] Kamenev A 2011 Field Theory for Non-equilibrium Systems (Cambridge: Cambridge University Press)
[18] Dalla Torre E G, DiehlS, Lukin M D, Sachdev S, Strack P 2013 Phys. Rev. A 87 023831
[19] Zhai H 2021 Ultracold Atomic Physics (Cambridge: Cambridge University Press)
[20] Purfath M 2014 The Non-Equilibrium Green’s Function Method for Nanoscale Device Simulation (Verlag Wien: Springer Press)
[21] Vale C J, Zwierlein M 2021 Nat. Phys 17 1305
Google Scholar
[22] Stewart J T, Gaebler J P, Jin D S 2008 Nature 454 744
Google Scholar
[23] Dao T L, Georges A, Dalibard J, Salomon C, Carusotto I 2007 Phys. Rev. Lett. 98 240402
Google Scholar
[24] Koschorreck M, Pertot D, Vogt E, Fröhlich B, Feld M, Kröhl M 2012 Nature 485 619
Google Scholar
[25] Brown P T, Guardado-Sanchez E, Spar B M, Huang E W, Devereaux T P, Bakr W S 2020 Nat. Phys. 16 26
[26] Sachdev S 2011 Quantum Phase Transitions (Cambridge: Cambridge University Press)
[27] Zinn-Justin J 2007 Phase Transitions and Renormalisation Group (Oxford: Oxford University Press)
[28] Debenedetti P G, Stillinger F H 2001 Nature 410 259
[29] Dyre J C 2006 Rev. Mod. Phys. 78 953
Google Scholar
[30] Witczak-Krempa W, Sørensen E S, Sachdev S 2014 Nat. Phys. 10 361
Google Scholar
[31] Giamarchi T 2004 Quantum Physics in One Dimension (New York: Oxford University Press)
[32] Lieb E H, Liniger W 1963 Phys. Rev. 130 1605
Google Scholar
[33] Imambekov A, Glazman L I 2008 Phys. Rev. Lett. 100 206805
Google Scholar
[34] Lieb E H 1963 Phys. Rev. 130 1616
Google Scholar
[35] Jiang Y Z, Chen Y Y, Guan X W 2015 Chin. Phys. B 24 050311
[36] Yang B, Chen Y Y, Zheng Y G, Sun H, Dai H N, Guan X W, Yuan Z S, Pan J W 2017 Phys. Rev. Lett. 119 165701
[37] Imambekov A, Schmidt T L, Glazman L I 2012 Rev. Mod. Phys. 84 1253
[38] Sticlet D, Dóra B, Moca C P 2022 Phys. Rev. Lett. 128 016802
[39] Dóra B, Moca C P 2020 Phys. Rev. Lett. 124 136802
[40] Bácsi Á, Moca C P, Dóra B 2020 Phys. Rev. Lett. 124 136401
[41] Bernier J S, Tan R, Guo C, Kollath C, Poletti D 2020 Phys. Rev. B 102 115156
[42] Chen Y 2021 J. High Energy Phys. 04 215
[43] Su K, Zhang P, Zhai H 2021 J. High Energy Phys. 06 156
[44] Wigner E P 1959 Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra (New York: Academic Press)
[45] Dimmock J O 1963 J. Math. Phys. 4 1307
[46] McGinley M, Cooper N R 2020 Nat. Phys. 16 1181
Google Scholar
[47] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
[48] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[49] Bernevig B A, Zhang S C 2006 Phys. Rev. Lett. 96 106802
Google Scholar
[50] König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L W, Qi X L, Zhang S C 2007 Science 318 766
Google Scholar
[51] Deng T S, Pan L, Chen Y, Zhai H 2021 Phys. Rev. Lett. 127 086801
Google Scholar
[52] Wu S, Fatemi V, Gibson Q D, Watanabe K, Taniguchi T, Cava R J, Jarillo-Herrero P 2018 Science 359 76
Google Scholar
[53] Schmidt T L, Rachel S, von Oppen F, Glazman L I 2012 Phys. Rev. Lett. 108 156402
Google Scholar
[54] Väyrynen J I, Goldstein M, Glazman L I 2013 Phys. Rev. Lett. 110 216402
Google Scholar
[55] Väyrynen J I, Pikulin D I, Alicea J 2018 Phys. Rev. Lett. 121 106601
Google Scholar
[56] Roth A, Brüne C, Buhmann H, Molenkamp L W, Maciejko J, Qi X L, Zhang S C 2009 Science 325 294
Google Scholar
[57] Du L, Knez I, Sullivan G, Du R R 2015 Phys. Rev. Lett. 114 096802
Google Scholar
[58] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133
Google Scholar
[59] Haldane F D M 1983 Phys. Lett. A 93 464
Google Scholar
[60] Haldane F D M 1983 Phys. Rev. Lett. 50 1153
[61] White S R, Huse D A 1993 Phys. Rev. B 48 3844
Google Scholar
[62] Kenzelmann M, Cowley R A, Buyers W J L, Tun Z, Coldea R, Enderle M 2002 Phys. Rev. B 66 024407
[63] Affleck I, Kennedy T, Lieb E H, Tasaki H 1987 Phys. Rev. Lett. 59 799
Google Scholar
[64] Pollmann F, Berg E, Turner A M, Oshikawa M 2012 Phys. Rev. B 85 075125
[65] Wang Z, Li Q, Li W, Cai Z 2021 Phys. Rev. Lett. 126 237201
Google Scholar
[66] Deng T S, Pan L 2021 Phys. Rev. B 104 094306
[67] Eigen C, Glidden J A, Lopes R, Cornell E A, Smith R P, Hadzibabic Z 2018 Nature 563 221
[68] Scheie A, Sherman N E, Dupont M, Nagler S E, Stone M B, Granroth G E, Moore J E, Tennant D A 2021 Nat. Phys. 17 726
[69] Jepsen P N, Amato-Grill J, Dimitrova I, Ho W W, Demler E, Ketterle W 2020 Nature 588 403
Google Scholar
[70] David D, Rubio-Abadal A, Ye B, Machado F, Kemp J, Srakaew K, Simon Hollerith S, Rui J, Gopalakrishnan S, Yao N Y, Bloch I, Zeiher J 2022 Science 376 716
DownLoad:
Catalog
Metrics
- Abstract views: 7081
- PDF Downloads: 473
- Cited By: 0
