-
Graphene, a two-dimensional material characterized by its honeycomb lattice structure, has demonstrated significant potential applications in electronic devices. The topological Anderson insulator (TAI) represents a novel phenomenon where a system transforms into a topological phase induced by disorder. In past studies, TAI is widely found in theoretical models such as the BHZ model and the Kane-Mele model. A common feature is that these models can open topological non-trivial gaps by changing their topological mass terms, but the rise of TAI is independent of the topological status of gaps. In order to investigate whether there is any difference in the disorder-induced phase between topologically trivial and topologically non-trivial cases of the Haldane model in the clean limit, the Haldane model in an infinitely long quasi-one-dimensional ZigZag-edged graphene ribbon is considered in this work. The Hamiltonian and band structure of it are analyzed, and the non-equilibrium Green's function theory is used to calculate the transport properties of ribbons under topologically trivial and non-trivial states versus disorder. The conductance, current density, transport coefficient and localisation length are calculated as parameters characterising the transmission properties. It is found from the analysis of the band structure that the system in either topological trivial or topological non-trivial state has edge states. When the Fermi energy lies in the conduction band, the conductance of the system decreases rapidly under weak disorder intensity and strong disorder intensity, regardless of whether the system is topologically non-trivial or not. At moderate disorder intensities, the conductance of topologically non-trivial systems keeps stable with a value of 1, indicating the appearance of the topological Anderson insulator phase in the system. Meanwhile, for topological trivial systems, the decrease of conductance noticeably slows down. The calculations of local current density show that both systems exhibit robust edge states, with topologically protected edge states showing greater robustness. The analysis of the transmission coefficients of edge state and bulk state indicates that the coexistence of bulk states and robust edge states is the basis for the phenomena observed in the Haldane model. Under weak disorder, bulk states are localized, and the transmission coefficient of edge states decreases due to scattering into the bulk states. Under strong disorder, edge states are localized, resulting in zero conductance. However, at moderate disorder strength, bulk states are annihilated while robust edge states persist, thereby reducing scattering from edge states to bulk states. This enhances the transport stability of the system. The fluctuation of conduction and localisation length reveal that the metal-TAI-normal insulator transition occurs in the Haldane model with topological non-trivial gap and if the system is of cylinder shape, there will be no edge states, the TAI will not occur. For the topological trivial gap case, only metal-normal insulator transition can be clearly identified. Therefore, topologically protected edge states are so robust that they generate a conductance plateau and it is demonstrated that the topologically trivial edge states are robust to a certain extent and can resist this level of disorder. The robustness of edge states is a crucial factor for the occurrence of the TAI phenomenon in the Haldane model.
-
Keywords:
- quantum anomalous Hall effect /
- disorder /
- topological Anderson insulator /
- quantum transport
-
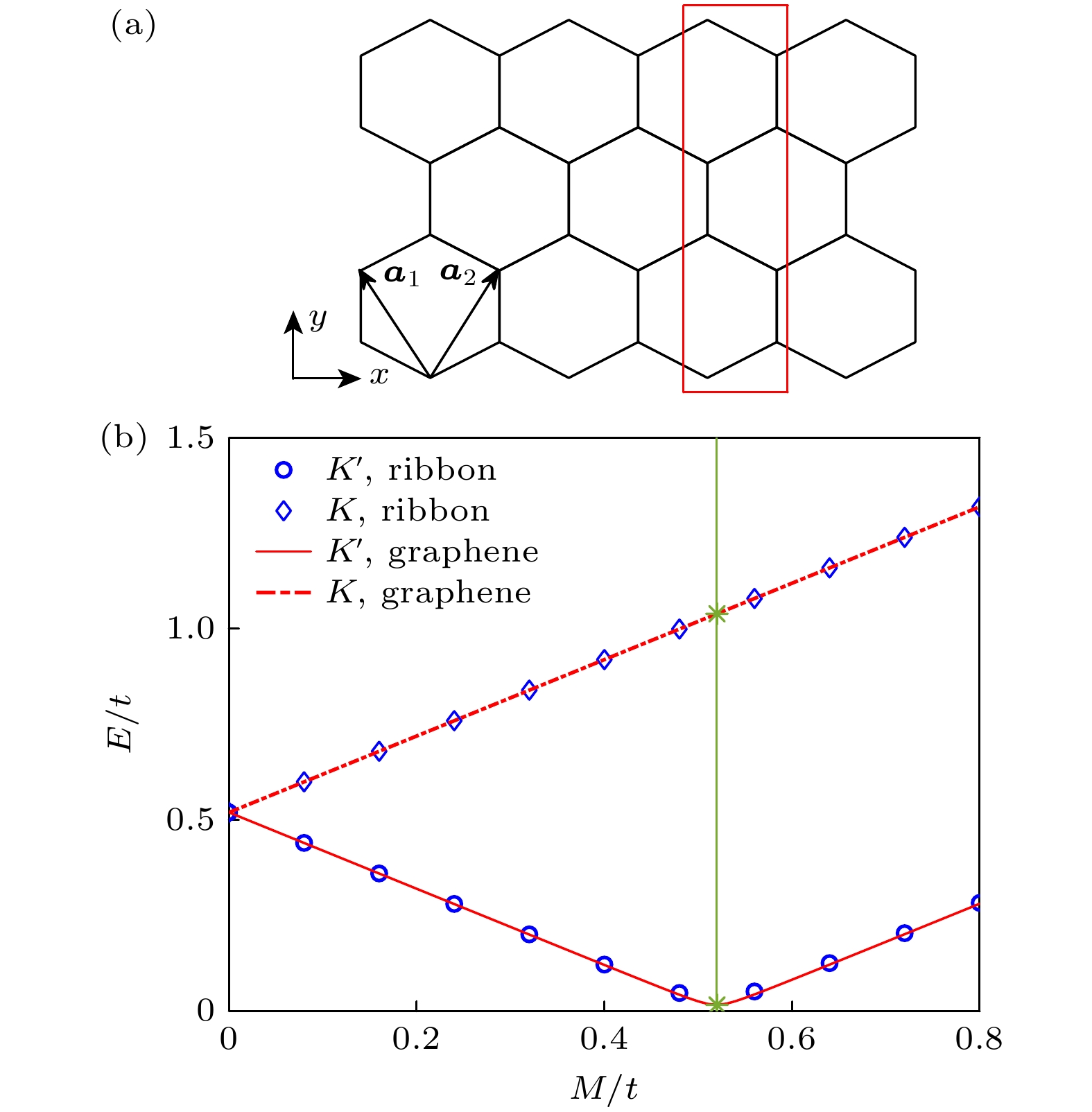
图 1 (a) 当Ny = 2, Nx =4时, ZigZag边界石墨烯条带几何结构图, 红色突出显示系统单位元, 即Nx =1, ${{\boldsymbol{a}}_1}, $${{\boldsymbol{a}}_2}$为格矢; (b) Ny = 80时, 无限大石墨烯平面及ZigZag边界石墨烯条带狄拉克点处带边位置随M 变化图, 图中由绿色线串联的两个绿色星号标记了系统拓扑转变点
Figure 1. (a) Geometry of ZigZag graphene ribbon when Ny = 2, Nx = 4, the red rectangles in the figure show the geometry of the unit cell, Nx = 1, ${{\boldsymbol{a}}_1}, $${{\boldsymbol{a}}_2}$arelattice vectors; (b) variation of band edges with M at Dirac points in the infinite graphene plane and ZigZag graphene ribbon for Ny = 80, green stars connected by a green line mark the system topology transition points.
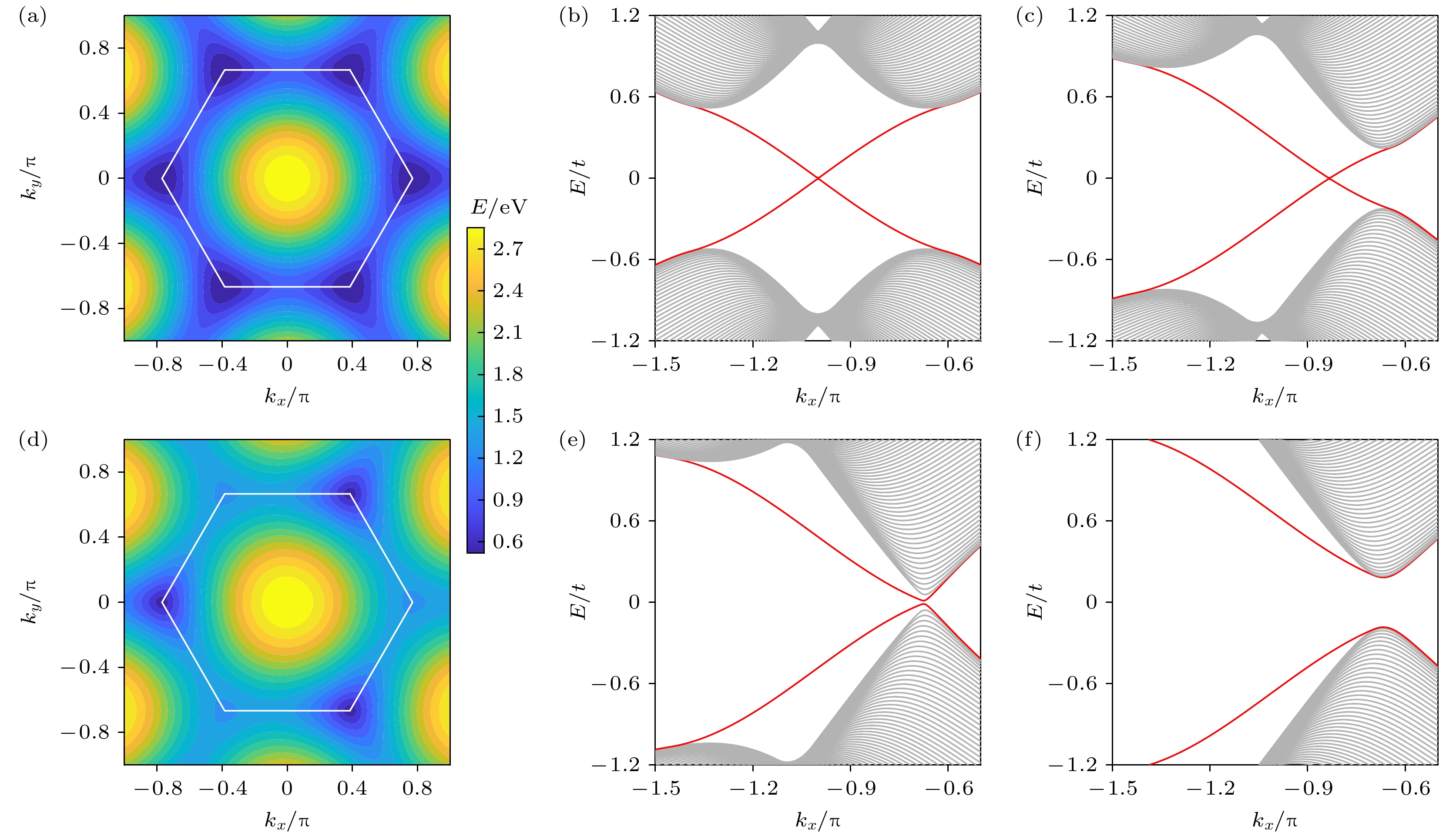
图 2 (a), (d)无限大石墨烯平面能带结构图, 白色六边形标注了第一布里渊区, 颜色条代表能量E的大小 (a) $M = 0$; (d) $M = $$ 0.52 t$. (b), (c), (e), (f)无限长ZigZag边石墨烯条带能带结构 (b) $M = 0$; (c) $M = 0.3 t$; (e) $M = 0.52 t$; (f) $M = 0.7 t$. 将$M$或$\phi $反号可以使能带的闭合位置转移至另外的狄拉克点
Figure 2. (a), (d) Band structure of two-dimensional infinite graphene surface, the first Brillouin zone is marked by the white hexagon in the figure, and the color bar represents the value of energy E: (a) $ M = 0 $; (d) $M = 0.52 t$. (b), (c), (e), (f) Band structure of infinitely long ZigZag-edge graphene ribbon: (b) $M = 0$; (c) $M = 0.3 t$; (e) $M = 0.52 t$; (f) $M = 0.7 t$. Inverting the sign of $M$or $\phi $ shifts the closure position of the energy band to the other Dirac point.
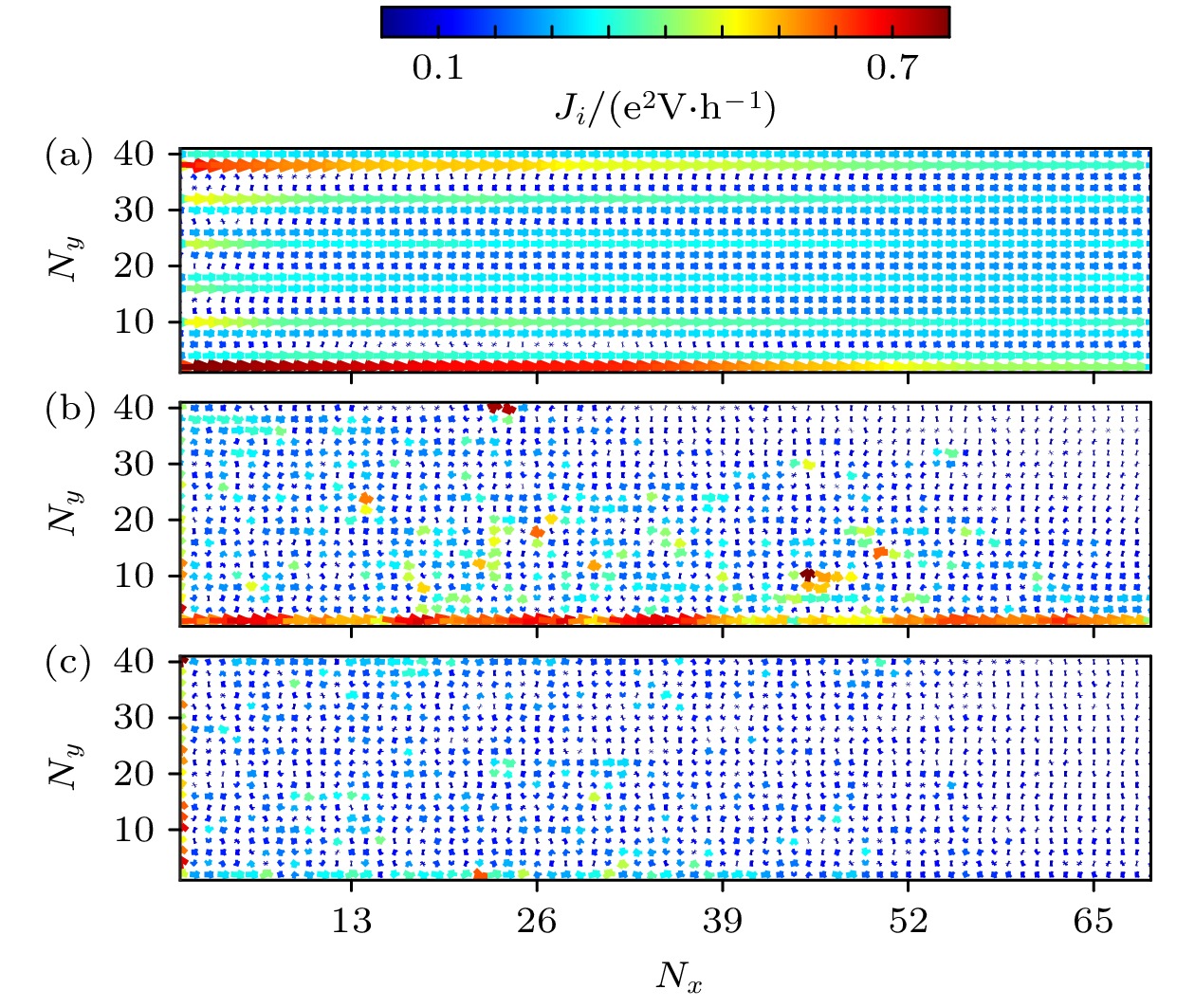
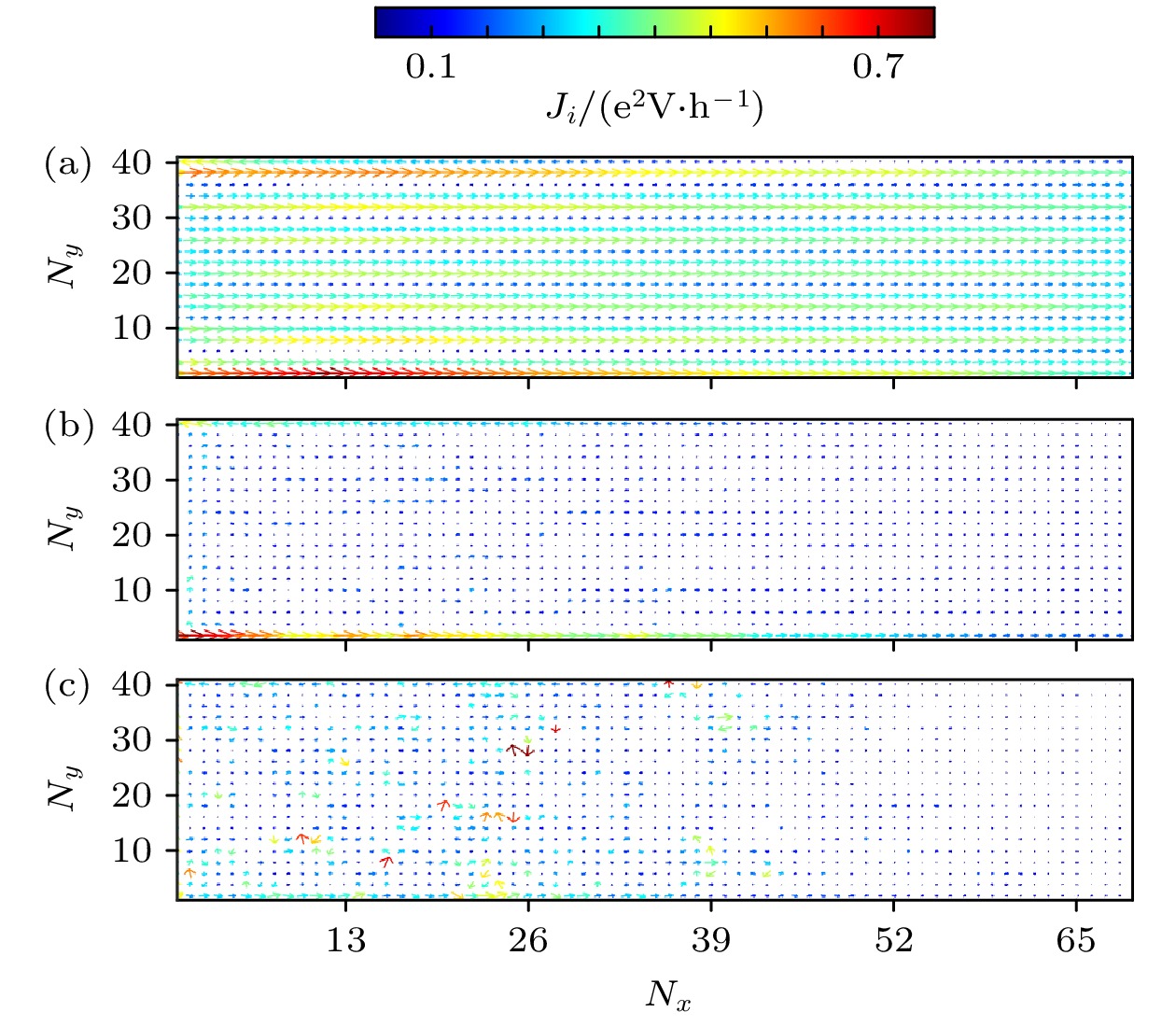
图 3 Ny = 40, Nx = 69, $ M = 0.3 t $, $ {E_{\text{F}}} = 0.25 t $时, 不同无序强度下体系的局域电流密度Ji分布图 (a) W = 0.8t; (b) W = 2.8t; (c) W = 5t
Figure 3. Local current density distribution of the system for different strength of the disorder with Ny = 40, Nx = 69, $ M = 0.3 t $, $ {E_{\text{F}}} = 0.25 t $: (a) W = 0.8t; (b) W = 2.8t; (c) W = 5t.
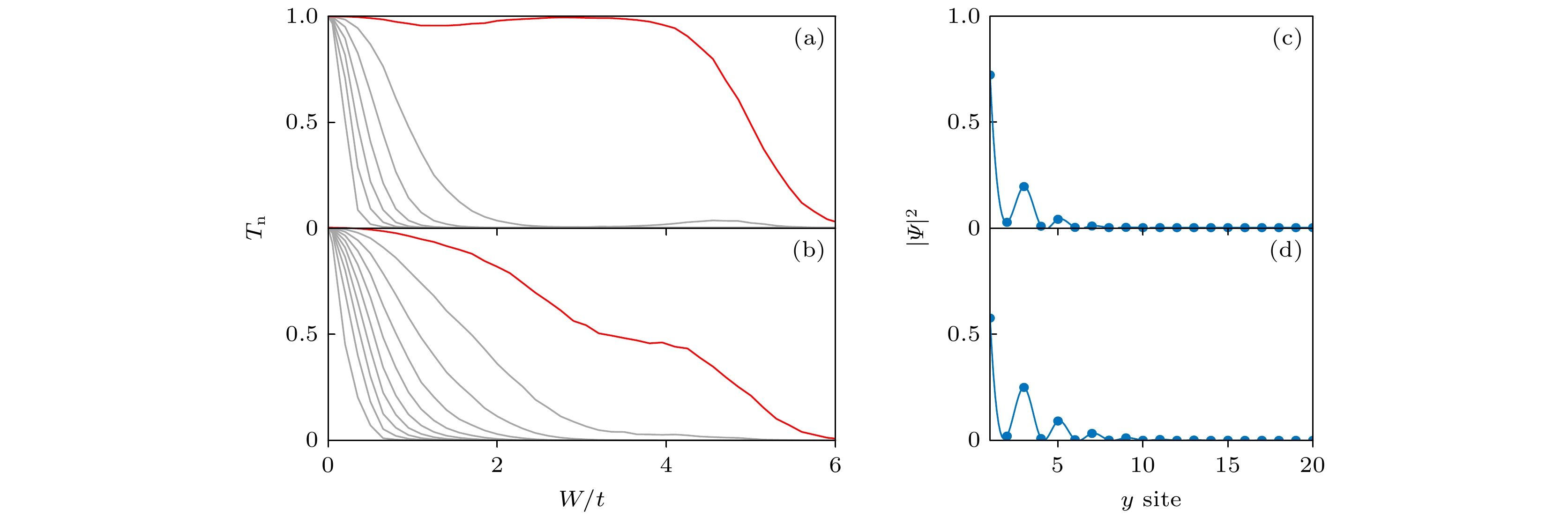
图 5 (a), (b)子带传输随无序的变化; (c), (d) 边缘态概率密度y方向分布图; (a), (c) $M = 0.3 t$, ${E_{\text{F}}} = 0.25 t$, Ny = 90, Nx = 156; (b), (d) $ M = 0.7 t $, ${E_{\text{F}}} = 0.25 t$, Ny = 90, Nx = 156
Figure 5. (a), (b) Transmissions of eigen channels vs. disorder; (c), (d) edge state probability distribution in y direction; (a), (c) $M = 0.3 t$, ${E_{\text{F}}} = 0.25 t$, Ny = 90, Nx = 156; (b), (d) $ M = 0.7 t $, ${E_{\text{F}}} = 0.25 t$, Ny = 90, Nx = 156.
图 6 电导、电导涨落及局域化长度随无序的变化. c代表圆筒形(cylinder)结构, r代表条带(ribbon)结构, 由红色点划线串联的星号代表系统相变点 (a)—(c) $ M = 0.3 t $, $ {E_{\text{F}}} = 0.15 t $; (d)—(f) $M = 0.3 t$, ${E_{\text{F}}} = 0.25 t$, 图(f)中实线代表Ny = 34, 虚线代表Ny = 60; (g)—(i) $M = 0.7 t$, ${E_{\text{F}}} = 0.25 t$
Figure 6. The conductance, fluctuation of the conductance and the localization length vs. disoder. The c denotes a cylindrical structure and r denotes a striped structure, stars in series by red dotted lines represent phase transition points: (a)–(c) $ M = 0.3 t $, $ {E_{\text{F}}} = 0.15 t $; (d)–(f) $M = 0.3 t$, ${E_{\text{F}}} = 0.25 t$, the solid lines represent Ny = 34 and the dotted lines represent Ny = 60 in panel (f); (g)–(i) $M = 0.7 t$, ${E_{\text{F}}} = 0.25 t$.
-
[1] Peres N M R 2010 Rev. Mod. Phys. 82 2673
Google Scholar
[2] Peres N M R, Castro Neto A H, Guinea F 2006 Phys. Rev. B 73 195411
Google Scholar
[3] Gusynin V P, Sharapov S G 2005 Phys. Rev. Lett. 95 146801
Google Scholar
[4] Geim A K 2009 Science 324 1530
Google Scholar
[5] Das Sarma S, Adam S, Hwang E H, Rossi E 2011 Rev. Mod. Phys. 83 407
Google Scholar
[6] Li T C, Lu S P 2008 Phys. Rev. B 77 085408
Google Scholar
[7] Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197
Google Scholar
[8] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[9] Slonczewski J C, Weiss P R 1958 Phys. Rev. 109 272
Google Scholar
[10] Semenoff G W 1984 Phys. Rev. Lett. 53 2449
Google Scholar
[11] Thonhauser T, Vanderbilt D 2006 Phys. Rev. B 74 235111
Google Scholar
[12] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[13] Aharonov Y, Bohm D 1959 Phys. Rev. 115 485
Google Scholar
[14] Anderson P W 1972 Science 177 393
Google Scholar
[15] Yu R, Zhang W, Zhang H J, Zhang S C, Dai X, Fang Z 2010 Science 329 61
Google Scholar
[16] Bernevig B A, Hughes T L 2013 Topological Insulators and Topological Superconductors (Princeton: Princeton University Press) pp72–77
[17] Chang Z W, Hao W C, Liu X 2022 J. Phys. : Condens. Matter 34 485502
Google Scholar
[18] Wen X G 1989 Phys. Rev. B 40 7387
[19] Sticlet D, Pindens. Matte Phys. Rev. B 87 115402
[20] Yakovenko V M 1990 Phys. Rev. Lett. 65 251
Google Scholar
[21] Zhao Y F, Zhang R, Mei R, Zhou L J, Yi H, Zhang Y Q, Yu J, Xiao R, Wang K, Samarth N, Chan M H W, Liu C X, Chang C Z 2020 Nature 588 419
Google Scholar
[22] Liu C X, Zhang S C, Qi X L 2016 Annu. Rev. Condens. Matter 7 301
Google Scholar
[23] Serlin M, Tschirhart C L, Polshyn H, Zhang Y, Zhu J, Watanabe K, Taniguchi T, Balents L, Young A F 2020 Science 367 900
Google Scholar
[24] Chang C Z, Liu C X, MacDonald A H 2023 Rev. Mod. Phys. 95 011002
Google Scholar
[25] Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature 515 237
Google Scholar
[26] Sompet P, Hirthe S, Bourgund D, Chalopin T, Bibo J, Koepsell J, Bojović P, Verresen R, Pollmann F, Salomon G, Gross C, Hilker T A, Bloch I 2022 Nature 606 484
Google Scholar
[27] Xu J J, Gu Q, Mueller E J 2018 Phys. Rev. Lett. 120 085301
Google Scholar
[28] Simon J 2014 Nature 515 202
Google Scholar
[29] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801
Google Scholar
[30] König M, Wiedmann S, Br J 2018 Chalopin T, Bibo J, Koepsell J, Bojović P, Verresen R Science 318 766
[31] Hsieh D, Qian D, Wray L, Xia Y, Hor Y S, Cava R J, Hasan M Z 2008 Nature 452 970
Google Scholar
[32] Xia Y, Qian D, Hsieh D, Wray L, Pal A, Lin H, Bansil A, Grauer D, Hor Y S, Cava R J, Hasan M Z 2009 Nat. Phys. 5 398
Google Scholar
[33] Li J, Chu R L, Jain J K, Shen S Q 2009 Phys. Rev. Lett. 102 136806
Google Scholar
[34] Yamakage A, Nomura K, Imura K I, Kuramoto Y 2011 J. Phys. Soc. Jpn. 80 053703
Google Scholar
[35] Guo H M, Rosenberg G, Refael G, Franz M 2010 Phys. Rev. Lett. 105 216601
Google Scholar
[36] Liu H, Xie B Y, Wang H N, Liu W W, Li Z C, Cheng H, Tian J G, Liu Z Y, Chen S Q 2023 Phys. Rev. B 108 L161410
Google Scholar
[37] Stützer S, Plotnik Y, Lumer Y, Titum P, Lindner N H, Segev M, Rechtsman M C, Szameit A 2018 Nature 560 461
Google Scholar
[38] Zhang Z Q, Wu B L, Song J, Jiang H 2019 Phys. Rev. B 100 184202
Google Scholar
[39] Chen R, Yi X X, Zhou B 2023 Phys. Rev. B 108 085306
Google Scholar
[40] Chen H, Liu Z R, Chen R, Zhou B 2023 Chin. Phys. B 33 017202
Google Scholar
[41] Groth C W, Wimmer M, Akhmerov A R, Tworzydło J, Beenakker C W J 2009 Phys. Rev. Lett. 103 196805
Google Scholar
[42] Orth C P, Sekera T, Bruder C, Schmidt T L 2016 Sci. Rep. 6 24007
Google Scholar
[43] 邢燕霞, 梁钰林 2022 山西大学学报(自然科学版) 3 672
Xing Y X, Lang Y L 2022 J. Shanxi. Univ. (Nat. Sci. Ed. ) 3 672
[44] Wei M, Zhou M, Zhang Y T, Xing Y 2020 Phys. Rev. B 101 155408
Google Scholar
[45] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[46] Caroli C, Combescot R, Nozieres P, Saint James D 1971 J. Phys. C: Solid State Phys. 4 916
Google Scholar
[47] Xing Y X, Wang J, Sun Q F 2010 Phys. Rev. B 81 165425
Google Scholar
[48] Jiang H, Wang L, Sun Q F, Xie X C 2009 Phys. Rev. B 80 165316
Google Scholar
[49] Zhang Y Y, Hu J P, Bernevig B A, Wang X R, Xie X C, Liu W M 2008 Phys. Rev. B 78 155413
Google Scholar
[50] Jauho A e, Wingreen N S, Meir Y 1994 Phys. Rev. B 50 5528
Google Scholar
[51] Nikolić B K, Zârbo L P, Souma S 2006 Phys. Rev. B 73 075303
Google Scholar
[52] Cresti A, Grosso G, Parravicini G P 2004 Phys. Rev. B 69 233313
Google Scholar
[53] 琚鑫, 郭健宏 2011 60 057302
Google Scholar
Ju X, Guo J H 2011 Acta Phys. Sin. 60 057302
Google Scholar
[54] Datta S 1995 Electronic Transport in Mesoscopic Systems (Ed. 1st) (United Kingdom: Cambridge University Press) pp57–65
[55] 许易, 许小言, 张薇, 欧阳滔, 唐超 2019 68 247202
Google Scholar
Xu Y, Xu X Y, Zhang W, Ouyang T, Tang C 2019 Acta Phys. Sin. 68 247202
Google Scholar
[56] 邢海英, 张子涵, 吴文静, 郭志英, 茹金豆 2023 72 038502
Google Scholar
Xing H Y, Zhang Z H, Wu W J, Guo Z Y, Ru J D 2023 Acta Phys. Sin. 72 038502
Google Scholar
[57] 闫婕, 魏苗苗, 邢燕霞 2019 68 227301
Google Scholar
Yan J, Wei M M, Xing Y X 2019 Acta Phys. Sin. 68 227301
Google Scholar
[58] MacKinnon A, Kramer B 1981 Phys. Rev. Lett. 47 1546
Google Scholar
[59] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[60] Chen C Z, Liu H, Xie X C 2019 Phys. Rev. Lett. 122 026601
Google Scholar
DownLoad:
Metrics
- Abstract views: 518
- PDF Downloads: 16
- Cited By: 0
