Skin effect in disordered non-Hermitian Su-Schrieffer-Heeger

Liu Jia-Lin; Pang Ting-Fang; Yang Xiao-Sen; Wang Zheng-Ling

doi:10.7498/aps.71.20221151

Abstract

In recent years, a large number of novel phenomena such as the breakdown of conventional bulk-boundary correspondence and non-Hermitian skin effect, have emerged in non-Hermitian systems. In this work, we investigate the localization of the eigenstates and the non-Hermitian skin effect of the disordered non-Hermitian Su-Schrieffer-Heeger (SSH) model by inverse participation rate (IPR) and average inverse participation rate (MIPR). We also investigate the bulk-boundary correspondence ratio of the system. Based on the above, we further investigate the effect of disorder on the non-Hermitian skin effect and the topological properties of the NH system. We find that the disorder does not destroy the localization of the topological edge state due to the protection from the topology of the system. But the eigenstates of bulk are greatly affected by the disorder. In the presence of disorder, the eigenstates of the bulk will rapidly extend into the bulk. Thus, the non-Hermitian skin effect is vulnerable to the disorder. When the disorder is enhanced, the non-Hermitian skin effect will be greatly suppressed. We also show that the disorder will reduce the energy gap and imaginary energy of the system. Our study contributes to the further understanding of the non-Hermitian skin effect.

Keywords:

Authors and contacts

Department of Physics, Jiangsu University, Zhenjiang 212013, China

Corresponding author: Wang Zheng-Ling, zlwang@ujs.edu.cn

FullText HTML : translate this paragraph

References

[1]	Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004 Google Scholar
[2]	Moore J E, Balents L 2007 Phys. Rev. B 75 121306 Google Scholar
[3]	Fu L, Kane C L, Mele E J 2007 Phys. Rev. Lett. 98 106803 Google Scholar
[4]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[5]	陈增军, 宁西京 2003 52 2683 Google Scholar Chen Z J, Ning X J 2003 Acta Phys. Sin. 52 2683 Google Scholar
[6]	Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005 Google Scholar
[7]	王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延锋 2019 68 224206 Google Scholar Wang H F, Xie B Y, Zhan P, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 224206 Google Scholar
[8]	孙孔浩, 易为 2021 70 230309 Google Scholar Sun K H, Yi W 2021 Acta Phys. Sin. 70 230309 Google Scholar
[9]	沈瑞昌, 张国强, 王逸璞, 游建强 2019 68 230305 Google Scholar Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305 Google Scholar
[10]	王学友, 王宇飞, 郑婉华 2020 69 024202 Google Scholar Wang X Y, Wang Y F, Zheng W H 2020 Acta Phys. Sin 69 024202 Google Scholar
[11]	Zhou L W, Han W Q 2021 Chin. Phys. B 30 100308 Google Scholar
[12]	Zhang S M, Jin L, Song Z 2022 Chin. Phys. B 31 010312 Google Scholar
[13]	Wang J H, Tao Y L, Xu Y 2022 Chin. Phys. Lett. 39 010301 Google Scholar
[14]	Cheng Z, Yu Z H 2021 Chin. Phys. Lett. 38 070302 Google Scholar
[15]	Li L, Lee C H, Mu S, Gong J 2020 Nat. Commun. 11 5491 Google Scholar
[16]	Lee C H, Li L, Thomale R, Gong J 2020 Phys. Rev. B 102 085151 Google Scholar
[17]	Liu J S, Han Y Z, Liu C S 2020 Chin. Phys. B 29 010302 Google Scholar
[18]	Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 Google Scholar
[19]	Longhi S 2019 Phys. Rev. Res. 1 023013 Google Scholar
[20]	Wang H, Ruan J, Zhang H 2019 Phys. Rev. B 99 075130 Google Scholar
[21]	Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 54301 Google Scholar
[22]	Zeng Q B, Xu Y 2020 Phys. Rev. Res. 2 033052 Google Scholar
[23]	Liu T, Zhang Y R, Ai Q, Gong Z, Kawabata K, Ueda M, Nori F 2019 Phys. Rev. Lett. 122 076801 Google Scholar
[24]	Lee C H, Longhi S 2020 Commun. Phys. 3 147 Google Scholar
[25]	Lee C H, Thomale R 2019 Phys. Rev. B 99 201103 Google Scholar
[26]	Deng T S, Yi W 2019 Phys. Rev. B 100 035102 Google Scholar
[27]	Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801 Google Scholar
[28]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
[29]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[30]	Longhi S 2020 Phys. Rev. Lett. 124 066602 Google Scholar
[31]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[32]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[33]	Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 Google Scholar
[34]	Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802 Google Scholar
[35]	Ghatak A, Das T 2019 J. Phys. Condens. Matter 31 263001 Google Scholar
[36]	Jin L, Song Z 2019 Phys. Rev. B 99 081103 Google Scholar
[37]	Kawabata K, Shiozaki K, Ueda M 2018 Phys. Rev. B 98 165148 Google Scholar
[38]	Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 Google Scholar
[39]	Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 Google Scholar
[40]	Cao P C, Peng Y G, Li Y, Zhu X F 2022 Chin. Phys. Lett. 39 057801 Google Scholar
[41]	Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005 Google Scholar
[42]	Araki H, Yoshida T, Hatsugai Y 2021 J. Phys. Soc. Jpn. 90 053703 Google Scholar
[43]	Luo X W, Zhang C 2019 Phys. Rev. Lett. 123 073601 Google Scholar
[44]	Yi Y, Yang Z 2020 Phys. Rev. Lett. 125 186802 Google Scholar
[45]	Fu Y, Hu J, Wan S 2021 Phys. Rev. B 103 045420 Google Scholar
[46]	Cao Y, Li Y, Yang X 2021 Phys. Rev. B 103 075126 Google Scholar
[47]	Hu Y M, Song F, Wang Z 2021 Acta Phys. Sin. 70 230307 Google Scholar
[48]	Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, Thomale R 2020 Nature Phys. 16 747 Google Scholar
[49]	Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311 Google Scholar
[50]	Gou W, Chen T, Xie D, Xiao T, Deng T S, Gadway B, Yi W, Yan B 2020 Phys. Rev. Lett. 124 070402 Google Scholar
[51]	Yoshida T, Mizoguchi T, Hatsugai Y 2020 Phys. Rev. Res. 2 022062 Google Scholar
[52]	Mandal S, Banerjee R, Ostrovskaya E A, Liew T C H 2020 Phys. Rev. Lett. 125 123902 Google Scholar
[53]	Gao P, Willatzen M, Christensen J 2020 Phys. Rev. Lett. 125 206402 Google Scholar
[54]	Zhu X, Wang H, Gupta S K, Zhang H, Xie B, Lu M, Chen Y 2020 Phys. Rev. Res. 2 013280 Google Scholar
[55]	Hofmann T, Helbig T, Schindler F, Salgo N, Brzezińska M, Greiter M, Kiessling T, Wolf D, Vollhardt A, Kabaši A, Lee C H, Bilusic A, Thomale R, Neupert T 2020 Phys. Rev. Res. 2 023265 Google Scholar
[56]	Brandenbourger M, Locsin X, Lerner E, Coulais C 2019 Nat. Commun. 10 4608 Google Scholar
[57]	Rosa M I N, Ruzzene M 2020 New J. Phys. 22 053004 Google Scholar
[58]	Zhong J, Wang K, Park Y, Asadchy V, Wojcik C C, Dutt A, Fan S 2021 Phys. Rev. B 104 125416 Google Scholar
[59]	Zhang L, Yang Y, Ge Y, Guan Y J, Chen Q, Yan Q, Chen F, Xi R, Li Y, Jia D, Yuan S Q, Sun H X, Chen H, Zhang B 2021 Nat. Commun. 12 6297 Google Scholar
[60]	Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 Google Scholar
[61]	Wu H, An J H 2020 Phys. Rev. B 102 041119 Google Scholar
[62]	Rudner M S, Lindner N H, Berg E, Levin M 2013 Phys. Rev. X 3 031005
[63]	Yao S, Yan Z, Wang Z 2017 Phys. Rev. B 96 195303 Google Scholar
[64]	Li T Y, Zhang Y S, Yi W 2021 Chin. Phys. Lett. 38 030301 Google Scholar
[65]	Zhai L J, Huang G Y, Yin S 2021 Phys. Rev. B 104 014202
[66]	Lee T E 2016 Phys. Rev. Lett. 116 133903 Google Scholar
[67]	Wang X R, Guo C X, Kou S P 2020 Phys. Rev. B 101 121116 Google Scholar
[68]	Wang X R, Guo C X, Du Q, Kou S P 2020 Chin. Phys. Lett. 37 117303 Google Scholar
[69]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar

Cited By

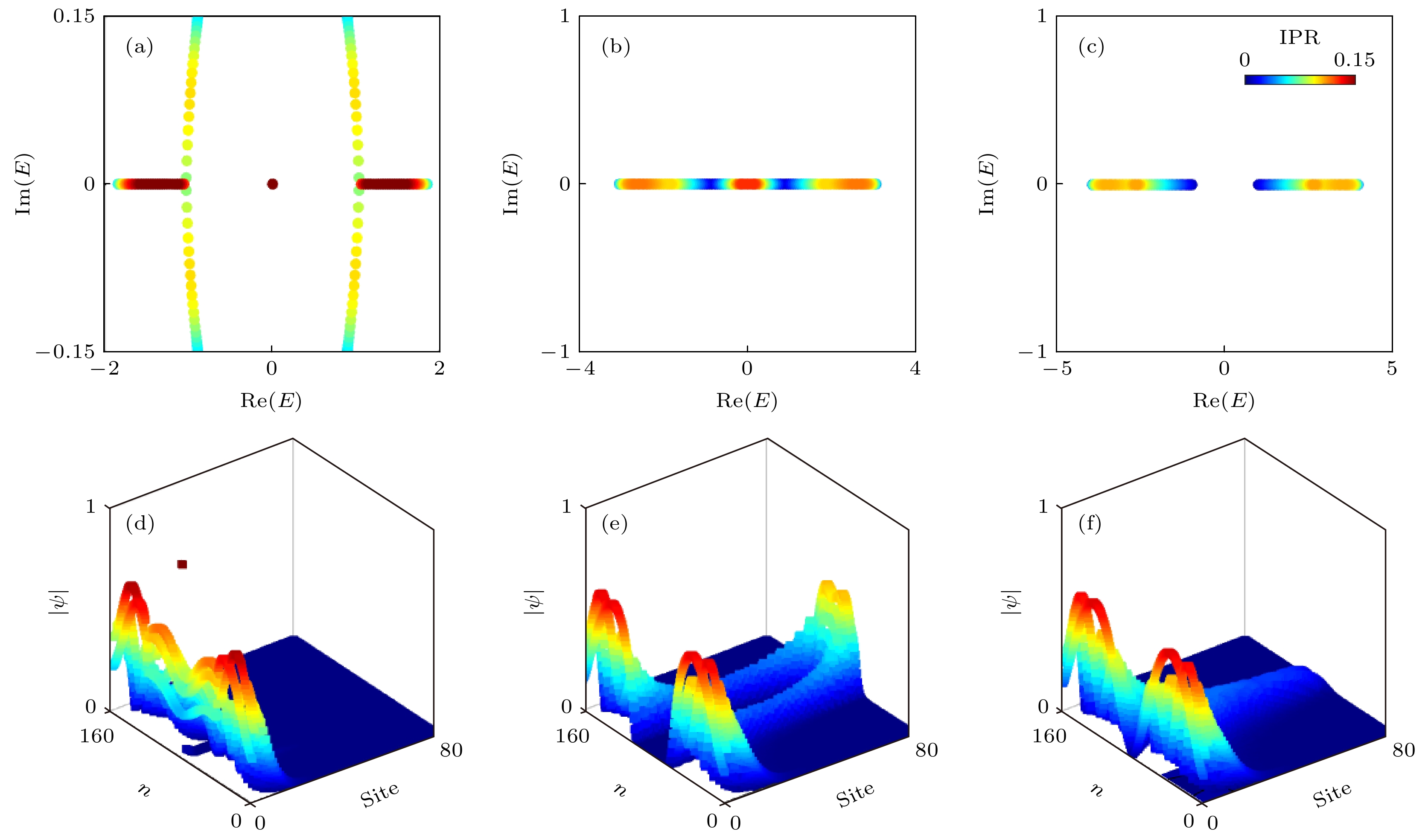
图 1 (a)—(c)拓扑非平凡态, 临界和拓扑平凡态的能谱. 颜色表示能量对应的波函数的IPR. 参数为 (a) $ {t_1} = 0.4 $; (b) ${t_1} = $$ 1.58$; (c) $ {t_1} = 2.5 $. (d)—(f) 分别对应图(a)—(c)中所有本征态在空间的分布. 其余的参数为: $\gamma = 0.4$, 系统的尺寸L为80

Figure 1. (a)–(c) The eigenenergies of topological nontrivial, critical and topological trivial phases with different parameters: (a) $ {t_1} = 0.4 $; (b) $ {t_1} = 1.58 $; (c) $ {t_1} = 2.5 $. The color denotes the IPR of the eigenstates corresponding to the eigenenergies. (d)–(f) The corresponding eigenstates in real space for Figure (a)–(c), respectively. The remaining parameter is $\gamma = 0.4$. The length of the lattice is 80.

DownLoad: Full-Size Img PowerPoint

图 2 (a) 平均逆参与率(MIPR)随参数${t_1}$变化. 参数为 $\gamma = 0.4$, $L = 80$. (b) 平均逆参与率与晶格尺寸L的标度. 绿色线对应${t_1} = 0.4$, $\gamma = 0$. 其他颜色的线分别对应不同的${t_1}$, $\gamma = 0.4$

Figure 2. (a) MIPR varies with $ {t_1} $, other parameters are$\gamma = 0.4$ and $L = 80$; (b) finite-size scaling of MIPR for different $ {t_1} $. The green line corresponds to ${t_1} = 0.4$, $\gamma = 0$, and the other lines correspond to different ${t_1}$with $\gamma = 0.4$.

DownLoad: Full-Size Img PowerPoint

图 3 (a) ${t_1} \text- \gamma$平面的相图. 红色为拓扑相区域, 体边对应率是0.5, 此时存在DES. (b) 体边对应率随微扰大小变化. 当微扰为零时, ${R_{\rm BBC}}$为0.5, 当微扰增大时, ${R_{\rm BBC}}$ 迅速增加到1. 其余参数为$ {t_1} = 0.4 $, $\gamma = 0.4$以及$L = 80$

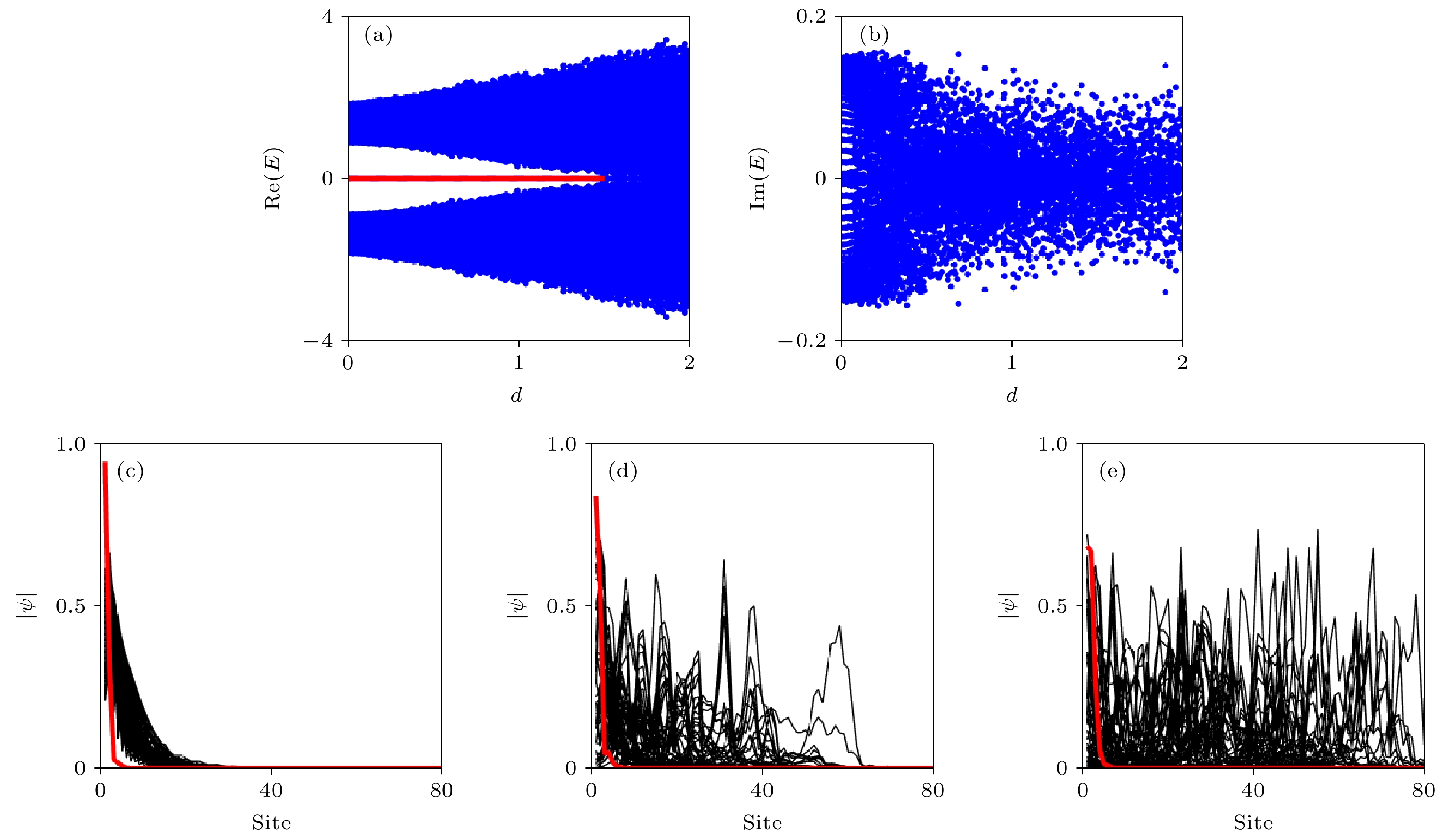
Figure 3. (a) Phase diagram in ${t_1} \text- \gamma$ plane. The phase is topological nontrivial in the red regions, where the value of BBC ratio is 0.5. And there exists DES. (b) ${R_{BBC}}$varies with the disturbance $\Delta $ . When the disturbance is zero, the value of ${R_{\rm BBC}}$is 0.5, and when the disturbance increases, the value of ${R_{\rm BBC}}$ jumps to 1. The remaining parameters are $ {t_1} = 0.4 $, $\gamma = 0.4$ and $L = 80$.

DownLoad: Full-Size Img PowerPoint

图 4 (a), (b) 开边界条件下的能谱. 红色点表示拓扑零能, 蓝色表示体态本征能量. (c)—(e) 不同无序强度d下的波函数. 黑色线表示体态的波函数, 红色线表示拓扑零能对应的拓扑边缘态的波函数. 无序强度分别为 (c)$ d = 0 $, (d) $ d = 0.5 $, (e)$ d = 1 $. 其余参数为 $ {t_1} = 0.4 $, $\gamma = 0.4$以及$L = 80$.

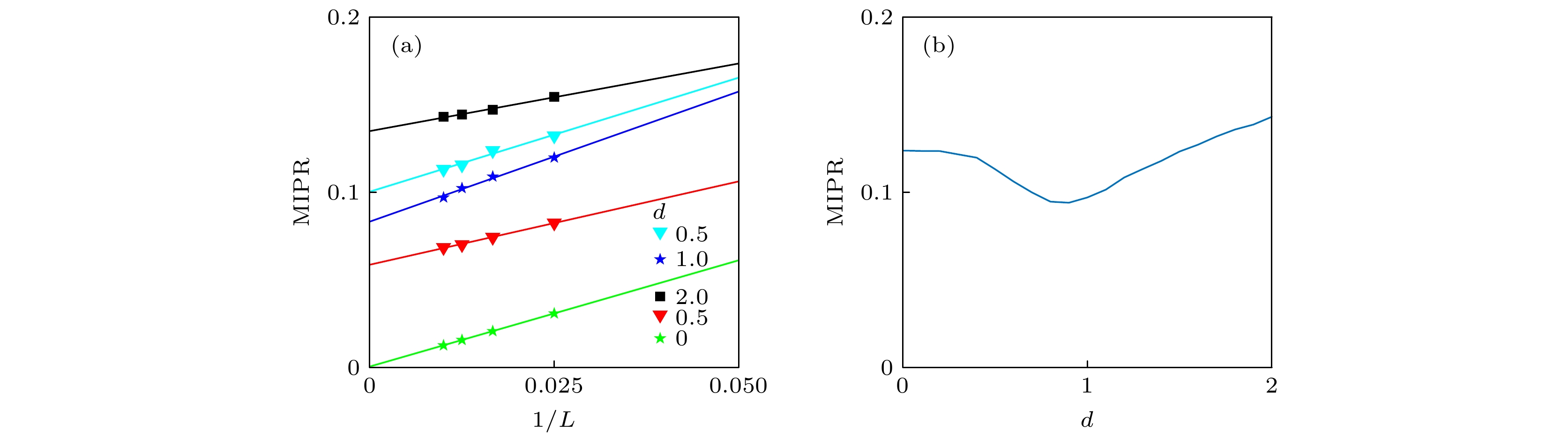
Figure 4. (a), (b) Energy spectra under the open boundary condition. The red dots are topological zero-mode. (c)–(e) The eigenstate wave functions with different disorders d. The black curves are the bulk-state wave functions and the red curves are the zero-mode wave functions. The disorder strength is: (c) d = 0, (d) d = 0.5, (e) d = 1. The remaining parameters are $ {t_1} $ = 0.4, $\gamma = 0.4$ and L = 80.

DownLoad: Full-Size Img PowerPoint

图 5 (a) 平均逆参与率与晶格尺寸L的标度. 所有线对应$ {t_1} = 0.4 $. 其中绿色线对应$d = 0$, $\gamma = 0$. 红色线对应$d = 0.5$, $\gamma = 0$. 其他颜色的线分别对应不同的$d$, $\gamma = 0.4$. (b) 平均逆参与率(MIPR)随无序强度$d$变化. 参数为$ {t_1} = 0.4 $, $\gamma = 0.4$, $L = 100$

Figure 5. (a) Finite-size scaling of MIPR for different $d$. All the lines correspond to ${t_1} = 0.4$.The green line corresponds to $d = 0$, $\gamma = 0$ and the red line corresponds to $d = 0.5$, $\gamma = 0$. The other lines correspond to different $d$with $\gamma = 0.4$. (b) MIPR varies with $d$, other parameters are$ {t_1} = 0.4 $, $\gamma = 0.4$ and $L = 100$.

DownLoad: Full-Size Img PowerPoint

map

[1]	Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004 Google Scholar
[2]	Moore J E, Balents L 2007 Phys. Rev. B 75 121306 Google Scholar
[3]	Fu L, Kane C L, Mele E J 2007 Phys. Rev. Lett. 98 106803 Google Scholar
[4]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[5]	陈增军, 宁西京 2003 52 2683 Google Scholar Chen Z J, Ning X J 2003 Acta Phys. Sin. 52 2683 Google Scholar
[6]	Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys. 88 035005 Google Scholar
[7]	王洪飞, 解碧野, 詹鹏, 卢明辉, 陈延锋 2019 68 224206 Google Scholar Wang H F, Xie B Y, Zhan P, Lu M H, Chen Y F 2019 Acta Phys. Sin. 68 224206 Google Scholar
[8]	孙孔浩, 易为 2021 70 230309 Google Scholar Sun K H, Yi W 2021 Acta Phys. Sin. 70 230309 Google Scholar
[9]	沈瑞昌, 张国强, 王逸璞, 游建强 2019 68 230305 Google Scholar Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305 Google Scholar
[10]	王学友, 王宇飞, 郑婉华 2020 69 024202 Google Scholar Wang X Y, Wang Y F, Zheng W H 2020 Acta Phys. Sin 69 024202 Google Scholar
[11]	Zhou L W, Han W Q 2021 Chin. Phys. B 30 100308 Google Scholar
[12]	Zhang S M, Jin L, Song Z 2022 Chin. Phys. B 31 010312 Google Scholar
[13]	Wang J H, Tao Y L, Xu Y 2022 Chin. Phys. Lett. 39 010301 Google Scholar
[14]	Cheng Z, Yu Z H 2021 Chin. Phys. Lett. 38 070302 Google Scholar
[15]	Li L, Lee C H, Mu S, Gong J 2020 Nat. Commun. 11 5491 Google Scholar
[16]	Lee C H, Li L, Thomale R, Gong J 2020 Phys. Rev. B 102 085151 Google Scholar
[17]	Liu J S, Han Y Z, Liu C S 2020 Chin. Phys. B 29 010302 Google Scholar
[18]	Okuma N, Kawabata K, Shiozaki K, Sato M 2020 Phys. Rev. Lett. 124 086801 Google Scholar
[19]	Longhi S 2019 Phys. Rev. Res. 1 023013 Google Scholar
[20]	Wang H, Ruan J, Zhang H 2019 Phys. Rev. B 99 075130 Google Scholar
[21]	Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 54301 Google Scholar
[22]	Zeng Q B, Xu Y 2020 Phys. Rev. Res. 2 033052 Google Scholar
[23]	Liu T, Zhang Y R, Ai Q, Gong Z, Kawabata K, Ueda M, Nori F 2019 Phys. Rev. Lett. 122 076801 Google Scholar
[24]	Lee C H, Longhi S 2020 Commun. Phys. 3 147 Google Scholar
[25]	Lee C H, Thomale R 2019 Phys. Rev. B 99 201103 Google Scholar
[26]	Deng T S, Yi W 2019 Phys. Rev. B 100 035102 Google Scholar
[27]	Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801 Google Scholar
[28]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
[29]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[30]	Longhi S 2020 Phys. Rev. Lett. 124 066602 Google Scholar
[31]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[32]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[33]	Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 Google Scholar
[34]	Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802 Google Scholar
[35]	Ghatak A, Das T 2019 J. Phys. Condens. Matter 31 263001 Google Scholar
[36]	Jin L, Song Z 2019 Phys. Rev. B 99 081103 Google Scholar
[37]	Kawabata K, Shiozaki K, Ueda M 2018 Phys. Rev. B 98 165148 Google Scholar
[38]	Shen H, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402 Google Scholar
[39]	Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 Google Scholar
[40]	Cao P C, Peng Y G, Li Y, Zhu X F 2022 Chin. Phys. Lett. 39 057801 Google Scholar
[41]	Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005 Google Scholar
[42]	Araki H, Yoshida T, Hatsugai Y 2021 J. Phys. Soc. Jpn. 90 053703 Google Scholar
[43]	Luo X W, Zhang C 2019 Phys. Rev. Lett. 123 073601 Google Scholar
[44]	Yi Y, Yang Z 2020 Phys. Rev. Lett. 125 186802 Google Scholar
[45]	Fu Y, Hu J, Wan S 2021 Phys. Rev. B 103 045420 Google Scholar
[46]	Cao Y, Li Y, Yang X 2021 Phys. Rev. B 103 075126 Google Scholar
[47]	Hu Y M, Song F, Wang Z 2021 Acta Phys. Sin. 70 230307 Google Scholar
[48]	Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, Thomale R 2020 Nature Phys. 16 747 Google Scholar
[49]	Weidemann S, Kremer M, Helbig T, Hofmann T, Stegmaier A, Greiter M, Thomale R, Szameit A 2020 Science 368 311 Google Scholar
[50]	Gou W, Chen T, Xie D, Xiao T, Deng T S, Gadway B, Yi W, Yan B 2020 Phys. Rev. Lett. 124 070402 Google Scholar
[51]	Yoshida T, Mizoguchi T, Hatsugai Y 2020 Phys. Rev. Res. 2 022062 Google Scholar
[52]	Mandal S, Banerjee R, Ostrovskaya E A, Liew T C H 2020 Phys. Rev. Lett. 125 123902 Google Scholar
[53]	Gao P, Willatzen M, Christensen J 2020 Phys. Rev. Lett. 125 206402 Google Scholar
[54]	Zhu X, Wang H, Gupta S K, Zhang H, Xie B, Lu M, Chen Y 2020 Phys. Rev. Res. 2 013280 Google Scholar
[55]	Hofmann T, Helbig T, Schindler F, Salgo N, Brzezińska M, Greiter M, Kiessling T, Wolf D, Vollhardt A, Kabaši A, Lee C H, Bilusic A, Thomale R, Neupert T 2020 Phys. Rev. Res. 2 023265 Google Scholar
[56]	Brandenbourger M, Locsin X, Lerner E, Coulais C 2019 Nat. Commun. 10 4608 Google Scholar
[57]	Rosa M I N, Ruzzene M 2020 New J. Phys. 22 053004 Google Scholar
[58]	Zhong J, Wang K, Park Y, Asadchy V, Wojcik C C, Dutt A, Fan S 2021 Phys. Rev. B 104 125416 Google Scholar
[59]	Zhang L, Yang Y, Ge Y, Guan Y J, Chen Q, Yan Q, Chen F, Xi R, Li Y, Jia D, Yuan S Q, Sun H X, Chen H, Zhang B 2021 Nat. Commun. 12 6297 Google Scholar
[60]	Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 Google Scholar
[61]	Wu H, An J H 2020 Phys. Rev. B 102 041119 Google Scholar
[62]	Rudner M S, Lindner N H, Berg E, Levin M 2013 Phys. Rev. X 3 031005
[63]	Yao S, Yan Z, Wang Z 2017 Phys. Rev. B 96 195303 Google Scholar
[64]	Li T Y, Zhang Y S, Yi W 2021 Chin. Phys. Lett. 38 030301 Google Scholar
[65]	Zhai L J, Huang G Y, Yin S 2021 Phys. Rev. B 104 014202
[66]	Lee T E 2016 Phys. Rev. Lett. 116 133903 Google Scholar
[67]	Wang X R, Guo C X, Kou S P 2020 Phys. Rev. B 101 121116 Google Scholar
[68]	Wang X R, Guo C X, Du Q, Kou S P 2020 Chin. Phys. Lett. 37 117303 Google Scholar
[69]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar

[1]	Huang Ze-Xin, Sheng Zong-Qiang, Cheng Le-Le, Cao San-Zhu, Chen Hua-Jun, Wu Hong-Wei. Steering non-Hermitian skin states by engineering interface in 1D nonreciprocal acoustic crystal. Acta Physica Sinica, 2024, 73(21): 214301. doi: 10.7498/aps.73.20241087
[2]	Gu Yan, Lu Zhan-Peng. Localization transition in non-Hermitian coupled chain. Acta Physica Sinica, 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[3]	Liu Jing-Hu, Xu Zhi-Hao. Random two-body dissipation induced non-Hermitian many-body localization. Acta Physica Sinica, 2024, 73(7): 077202. doi: 10.7498/aps.73.20231987
[4]	Liu Hui, Lu Zhan-Peng, Xu Zhi-Hao. Delocalization-localization transitions in 1D non-Hermitian cross-stitch lattices. Acta Physica Sinica, 2024, 73(13): 137201. doi: 10.7498/aps.73.20240510
[5]	Xu Can-Hong, Xu Zhi-Cong, Zhou Zi-Yu, Cheng En-Hong, Lang Li-Jun. Electrical circuit simulation of non-Hermitian lattice models. Acta Physica Sinica, 2023, 72(20): 200301. doi: 10.7498/aps.72.20230914
[6]	Yang Yan-Li, Duan Zhi-Lei, Xue Hai-Bin. Edge states and skin effect dependent electron transport properties of non-Hermitian Su-Schrieffer-Heeger chain. Acta Physica Sinica, 2023, 72(24): 247301. doi: 10.7498/aps.72.20231286
[7]	Chen Qi, Dai Yue, Li Fei-Yan, Zhang Biao, Li Hao-Chen, Tan Jing-Rou, Wang Xiao-Han, He Guang-Long, Fei Yue, Wang Hao, Zhang La-Bao, Kang Lin, Chen Jian, Wu Pei-Heng. Design and fabrication of superconducting single-photon detector operating in 5–10 μm wavelength band. Acta Physica Sinica, 2022, 71(24): 248502. doi: 10.7498/aps.71.20221594
[8]	Cheng En-Hong, Lang Li-Jun. Electrical circuit simulation of nonreciprocal Aubry-André models. Acta Physica Sinica, 2022, 71(16): 160301. doi: 10.7498/aps.71.20220219
[9]	Wu Jin, Lu Zhan-Peng, Xu Zhi-Hao, Guo Li-Ping. Mobility edges and reentrant localization induced by superradiance. Acta Physica Sinica, 2022, 71(11): 113702. doi: 10.7498/aps.71.20212246
[10]	Hou Bo, Zeng Qi-Bo. Non-Hermitian mosaic dimerized lattices. Acta Physica Sinica, 2022, 71(13): 130302. doi: 10.7498/aps.71.20220890
[11]	Chen Shu-Yue, Jiang Chuang, Ke Shao-Lin, Wang Bing, Lu Pei-Xiang. Suppression of non-Hermitian skin effect via Aharonov-Bohm cage. Acta Physica Sinica, 2022, 71(17): 174201. doi: 10.7498/aps.71.20220978
[12]	Deng Tian-Shu. Non-Hermitian skin effect in a domain-wall system. Acta Physica Sinica, 2022, 71(17): 170306. doi: 10.7498/aps.71.20221087
[13]	Hu Yu-Min, Song Fei, Wang Zhong. Generalized Brillouin zone and non-Hermitian band theory. Acta Physica Sinica, 2021, 70(23): 230307. doi: 10.7498/aps.70.20211908
[14]	Fu Cong, Ye Meng-Hao, Zhao Hui, Chen Yu-Guang, Yan Yong-Hong. Effects of intrachain disorder on photoexcitation in conjugated polymer chains. Acta Physica Sinica, 2021, 70(11): 117201. doi: 10.7498/aps.70.20201801
[15]	Xu Zhi-Hao, Huangfu Hong-Li, Zhang Yun-Bo. Mobility edges of bosonic pairs in one-dimensional quasi-periodical lattices. Acta Physica Sinica, 2019, 68(8): 087201. doi: 10.7498/aps.68.20182218
[16]	Wang Xiao, Chen Li-Chao, Liu Yan-Hong, Shi Yun-Long, Sun Yong. Effect of longitudinal mode on the transmission properties near the Dirac-like point of the photonic crystals. Acta Physica Sinica, 2015, 64(17): 174206. doi: 10.7498/aps.64.174206
[17]	Hou Bi-Hui, Liu Feng-Yan, Yue Ming, Wang Ke-Jun. Localization of conduction electrons in nanometer metal Dy. Acta Physica Sinica, 2011, 60(1): 017201. doi: 10.7498/aps.60.017201
[18]	Li Xiao-Chun, Gao Jun-Li, Liu Shao-E, Zhou Ke-Chao, Huang Bo-Yun. Disorder effect on the focus image of phononic crystal panel with negative refraction. Acta Physica Sinica, 2010, 59(1): 376-380. doi: 10.7498/aps.59.376
[19]	Liu Xiao-Liang, Xu Hui, Ma Song-Shan, Song Zhao-Quan. The localized properties of electronic states in one-dimensional disordered binary solid. Acta Physica Sinica, 2006, 55(6): 2949-2954. doi: 10.7498/aps.55.2949
[20]	Xu Xing-Sheng, Chen Hong-Da, Zhang Dao-Zhong. Photon localization in amorphous photonic crystal. Acta Physica Sinica, 2006, 55(12): 6430-6434. doi: 10.7498/aps.55.6430

Catalog

Vol. 71, Issue 22 - 2022-11-20

Metrics

Abstract views: 5297
PDF Downloads: 309
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板