随机两体耗散诱导的非厄米多体局域化

刘敬鹄; 徐志浩

doi:10.7498/aps.73.20231987

摘要

本文数值研究了在一维非厄米的硬核玻色模型中由随机两体耗散诱导的非厄米多体局域化现象. 随着无序强度的增强, 系统的能谱统计分布从AI^†对称类向二维泊松系综过渡, 多体本征态的归一化参与率展示了从有限值到接近零的转变, 半链纠缠熵服从体积律到面积律的转变, 动力学半链纠缠熵表现为从线性增长到对数增长的转变. 数值结果表明, 在该模型中由随机两体耗散诱导的非厄米多体局域化现象的鲁棒性. 该研究结果为非厄米系统中多体局域化的研究提供了新的视角.

关键词:

Abstract

Recent researches on disorder-driven many-body localization (MBL) in non-Hermitian quantum systems have aroused great interest. In this work, we investigate the non-Hermitian MBL in a one-dimensional hard-core Bose model induced by random two-body dissipation, which is described by　　　　　　　　　　　

$ \hat{H}=\displaystyle\sum\limits_{j}^{L-1}\left[ -J\left( \hat{b}_{j}^{\dagger}\hat{b}_{j+1}+\hat {b}_{j+1}^{\dagger}\hat{b}_{j}\right) +\frac{1}{2}\left( U-{\mathrm{i}}\gamma_{j}\right) \hat{n}_{j}\hat{n}_{j+1}\right] \notag,$

with the random two-body loss $\gamma_j\in\left[0,W\right]$. By the level statistics, the system undergoes a transition from the AI$^{\dagger}$ symmetry class to a two-dimensional Poisson ensemble with the increase of disorder strength. This transition is accompanied by the changing of the average magnitude (argument) $\overline{\left\langle {r}\right\rangle}$ ($\overline{-\left\langle \cos {\theta}\right\rangle }$) of the complex spacing ratio, shifting from approximately 0.722 (0.193) to about 2/3 (0). The normalized participation ratios of the majority of eigenstates exhibit finite values in the ergodic phase, gradually approaching zero in the non-Hermitian MBL phase, which quantifies the degree of localization for the eigenstates. For weak disorder, one can see that average half-chain entanglement entropy $\overline{\langle S \rangle}$ follows a volume law in the ergodic phase. However, it decreases to a constant independent of L in the deep non-Hermitian MBL phase, adhering to an area law. These results indicate that the ergodic phase and non-Hermitian MBL phase can be distinguished by the half-chain entanglement entropy, even in non-Hermitian system, which is similar to the scenario in Hermitian system. Finally, for a short time, the dynamic evolution of the entanglement entropy exhibits linear growth with the weak disorder. In strong disorder case, the short-time evolution of $\overline{S(t)}$ shows logarithmic growth. However, when $t\geqslant10^2$, $\overline{S(t)}$ can stabilize and tend to the steady-state half-chain entanglement entropy $\overline{ S_0 }$. The results of the dynamical evolution of $\overline{S(t)}$ imply that one can detect the occurrence of the non-Hermitian MBL by the short-time evolution of $\overline{S(t)}$, and the long-time behavior of $\overline{S(t)}$ signifies the steady-state information.

Keywords:

作者及机构信息

刘敬鹄¹,
徐志浩^1,2

1.
山西大学理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

2.
山西大学极端光学协同创新中心, 太原　030006

通信作者: 徐志浩, xuzhihao@sxu.edu.cn

基金项目: 国家自然科学基金(批准号: 12375016)、山西省基础研究计划(批准号: 20210302123442)、北京凝聚态物理国家研究中心开放课题和山西“1331工程”重点学科建设计划资助的课题.

Authors and contacts

Liu Jing-Hu¹,
Xu Zhi-Hao^1,2

1.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Xu Zhi-Hao, xuzhihao@sxu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12375016), the Fundamental Research Program of Shanxi Province, China (Grant No. 20210302123442), the Beijing National Laboratory for Condensed Matter Physics, China, and the Fund for Shanxi “1331Project” Key Subjects, China.

文章全文 : translate this paragraph

参考文献

[1]	Basko D M, Aleiner I L, Altshuler B L 2006 Ann. Phys. 321 1126 Google Scholar
[2]	Laumann C R, Pal A, Scardicchio A 2014 Phys. Rev. Lett. 113 200405 Google Scholar
[3]	Nandkishore R, Huse D A 2015 Annu. Rev. Condens. Matter Phys. 6 15 Google Scholar
[4]	Kjäll J A, Bardarson J H, Pollmann F 2014 Phys. Rev. Lett. 113 107204 Google Scholar
[5]	Bera S, Schomerus H, Heidrich-Meisner F, Bardarson J H 2015 Phys. Rev. Lett. 115 046603 Google Scholar
[6]	Rademaker L, Ortuño M 2016 Phys. Rev. Lett. 116 010404 Google Scholar
[7]	Khemani V, Sheng D N, Huse D A 2017 Phys. Rev. Lett. 119 075702 Google Scholar
[8]	Macé N, Alet F, Laflorencie N 2019 Phys. Rev. Lett. 123 180601 Google Scholar
[9]	Bar Lev Y, Cohen G, Reichman D R 2015 Phys. Rev. Lett. 114 100601 Google Scholar
[10]	Bairey E, Refael G, Lindner N H 2017 Phys. Rev. B 96 020201 Google Scholar
[11]	Decker K S C, Karrasch C, Eisert J, Kennes D M 2020 Phys. Rev. Lett. 124 190601 Google Scholar
[12]	Giamarchi T, Schulz H J 1988 Phys. Rev. B 37 325 Google Scholar
[13]	De Luca A, Altshuler B L, Kravtsov V E, Scardicchio A 2014 Phys. Rev. Lett. 113 046806 Google Scholar
[14]	Deutsch J M 2018 Rep. Prog. Phys. 81 082001 Google Scholar
[15]	De Luca A, Scardicchio A 2013 EPL 101 37003 Google Scholar
[16]	Bar Lev Y, Reichman D R 2014 Phys. Rev. B 89 220201
[17]	Luitz D J, Laflorencie N, Alet F 2016 Phys. Rev. B 93 060201
[18]	Abanin D A, Altman E, Bloch I, Serbyn M 2019 Rev. Mod. Phys. 91 021001 Google Scholar
[19]	Guhr T, Müller–Groeling A, Weidenmüller H A 1998 Phys. Rep. 299 189 Google Scholar
[20]	Atas Y Y, Bogomolny E, Giraud O, Roux G 2013 Phys. Rev. Lett. 110 084101 Google Scholar
[21]	Bardarson J H, Pollmann F, Moore J E 2012 Phys. Rev. Lett. 109 017202 Google Scholar
[22]	Serbyn M, Papić Z, Abanin D A 2013 Phys. Rev. Lett. 110 260601 Google Scholar
[23]	Bauer B, Nayak C 2013 J. Stat. Mech. 2013 P09005 Google Scholar
[24]	Serbyn M, Michailidis A A, Abanin D A, Papić Z 2016 Phys. Rev. Lett. 117 160601 Google Scholar
[25]	Guo Q, Cheng C, Sun Z H, et al. 2021 Nat. Phys. 17 234 Google Scholar
[26]	Guo Q, Cheng C, Li H, et al. 2021 Phys. Rev. Lett. 127 240502 Google Scholar
[27]	Ros V, Müller M, Scardicchio A 2015 Nucl. Phys. B 891 420 Google Scholar
[28]	Bertoni C, Eisert J, Kshetrimayum A, Nietner A, Thomson S J 2023 arXiv: 2208.14432 v4 [cond-mat.dis-nn]
[29]	Schreiber M, Hodgman S S, Bordia P, Lüschen H P, Fischer M H, Vosk R, Altman E, Schneider U, Bloch I 2015 Science 349 842 Google Scholar
[30]	Bordia P, Lüschen H P, Hodgman S S, Schreiber M, Bloch I, Schneider U 2016 Phys. Rev. Lett. 116 140401 Google Scholar
[31]	Kohlert T, Scherg S, Li X, Lüschen H P, Das Sarma S, Bloch I, Aidelsburger M 2019 Phys. Rev. Lett. 122 170403 Google Scholar
[32]	Smith J, Lee A, Richerme P, Neyenhuis B, Hess P W, Hauke P, Heyl M, Huse D A, Monroe C 2016 Nat. Phys. 12 907 Google Scholar
[33]	Roushan P, Neill C, Tangpanitanon J, et al. 2017 Science 358 1175 Google Scholar
[34]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[35]	Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
[36]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[37]	Zhang K, Yang Z, Fang C 2022 Nat. Commun. 13 2496 Google Scholar
[38]	Ou Z, Wang Y, Li L 2023 Phys. Rev. B 107 L161404 Google Scholar
[39]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[40]	Borgnia D S, Kruchkov A J, Slager R J 2020 Phys. Rev. Lett. 124 056802 Google Scholar
[41]	Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 Google Scholar
[42]	Wang Y C, You J S, Jen H H 2022 Nat. Commun. 13 4598 Google Scholar
[43]	Xu Z, Chen S 2020 Phys. Rev. B 102 035153 Google Scholar
[44]	Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 Google Scholar
[45]	Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 Google Scholar
[46]	Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384 Google Scholar
[47]	Hamazaki R, Kawabata K, Ueda M 2019 Phys. Rev. Lett. 123 090603 Google Scholar
[48]	Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 Google Scholar
[49]	Zhai L J, Yin S, Huang G Y 2020 Phys. Rev. B 102 064206 Google Scholar
[50]	Gong Z, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079
[51]	Tomita T, Nakajima S, Danshita I, Takasu Y, Takahashi Y 2017 Sci. Adv. 3 e1701513 Google Scholar
[52]	Sponselee K, Freystatzky L, Abeln B, et al. 2018 Quantum Sci. Technol. 4 014002 Google Scholar
[53]	Wang C, Liu C, Shi Z Y 2022 Phy. Rev. Lett. 129 203401 Google Scholar
[54]	Berry M V, Tabor M 1977 Proc. R. Soc. London, Ser. A 256 375
[55]	Bohigas O, Giannoni M J, Schmit C 1984 Phys. Rev. Lett. 52 1 Google Scholar
[56]	Casati G, Valz-Gris F, Guarnieri I 1980 Lett. Nuovo Cimento 28 279 Google Scholar
[57]	Rigol M, Dunjko V, Olshanii M 2008 Nature 452 854 Google Scholar
[58]	Hamazaki R, Kawabata K, Kura N, Ueda M 2020 Phys. Rev. Res. 2 023286 Google Scholar
[59]	Sá L, Ribeiro P, Prosen T 2020 Phys. Rev. X 10 021019
[60]	García-García A M, Sá L, Verbaarschot J J M 2022 Phys. Rev. X 12 021040
[61]	Ginibre J 1965 J. Math. Phys. 6 440 Google Scholar
[62]	Peron T, De Resende B M F, Rodrigues F A, Costa L D F, Méndez-Bermúdez J A 2020 Phys. Rev. E 102 062305 Google Scholar
[63]	Liu J, Xu Z 2023 Phys. Rev. B 108 184205 Google Scholar
[64]	Oganesyan V, Huse D A 2007 Phys. Rev. B 75 155111 Google Scholar
[65]	Ghosh S, Gupta S, Kulkarni M 2022 Phys. Rev. B 106 134202 Google Scholar
[66]	Li X, Ganeshan S, Pixley J H, Das Sarma S 2015 Phys. Rev. Lett. 115 186601 Google Scholar
[67]	Suthar K, Wang Y C, Huang Y P, Jen H H, You J S 2022 Phys. Rev. B 106 064208

施引文献

图 1 当L = 14时, 哈密顿量(1)式平均的最近邻能级间距s的统计分布　(a) W = 2; (b) W = 20. 黑色虚线、红色实线和绿色点线分别表示A, AI$^{\dagger}$类和二维泊松分布

Fig. 1. Mean unfolded nearest-level-spacing distributions of the Hamiltonian Eq. (1) with L = 14: (a) W = 2; (b) W = 20. Black dash, red solid, and green dotted lines represent A, AI${\mathrm{}}^{\dagger}$ classes, and two dimensional (2D)-Poisson distributions, respectively.

下载: 全尺寸图片幻灯片

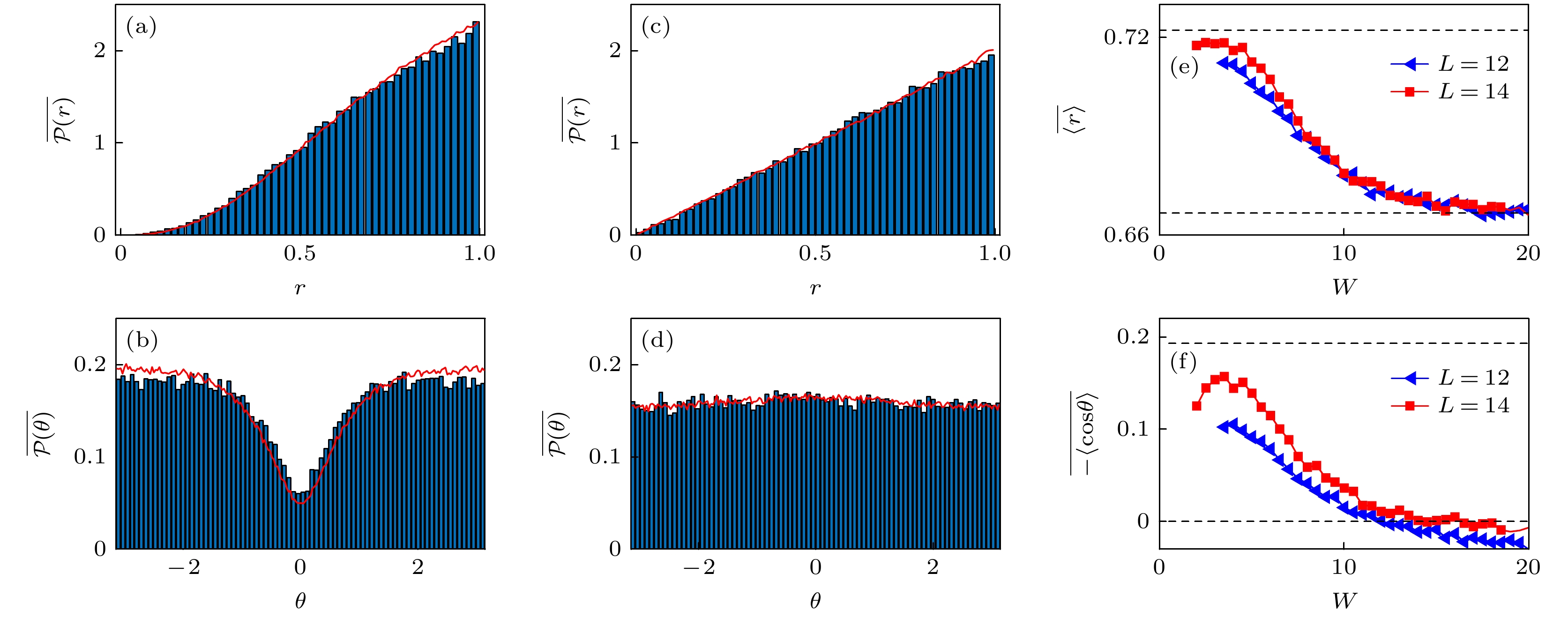
图 2 当$L=14$时, 平均的径向强度分布$\overline{\mathcal{P}(r)}$和相应的幅角分布$\overline{\mathcal{P} (\theta )}$　(a), (b) $W=2$; (c), (d) $W=20$. 红色实线是通过统计对应的随机矩阵($1000\times 1000$)的结果, 其无序次数选取为1000. (e), (f)径向强度的平均值$\overline{\left\langle {r}\right\rangle }$和相应的幅角的平均值$\overline{-\left\langle \cos{\theta}\right\rangle} $随无序强度变化曲线. 上(下)虚线对应于AI$^{\dagger}$对称类(2D-Poisson)统计极限值, $\overline{\langle {r}\rangle}_{{\text{AI}}^{\dagger}}\approx0.722$, $\overline{-\langle \cos{{\theta}} \rangle}_{{\text{AI}}^{\dagger}}\approx $$ 0.193$ $(\overline{\langle {r}\rangle}_{\text{Pois}}=2/3$, $\overline{-\langle \cos{{\theta}} \rangle}_{\text{Pois}}=0)$

Fig. 2. (a), (b) Mean marginal distributions $\overline{\mathcal{P}(r)}$ and $\overline{\mathcal{P} (\theta )}$ with $W=2$ for the complex energy spectrum for $L=14$; (c), (d) the marginal distributions $\overline{\mathcal{P}(r)}$ and $\overline{\mathcal{P} (\theta )}$ with $W=20$ for the complex energy spectrum. The red solid lines are obtained by calculating $\overline{\mathcal{P}(r)}$ and $\overline{\mathcal{P} (\theta )}$ of the $1000\times 1000$ random matrices with the corresponding random matrix ensembles averaged 1000 realizations. (e), (f) The averages $\overline{\left\langle {r}\right\rangle} $ and $\overline{-\left\langle \cos {\theta}\right\rangle }$ as a function of the disorder strength W. The upper (lower) dash line corresponds to the ${\mathrm{AI}}^{\dagger}$ symmetry class (2D-Poisson) expectation, $\overline{\langle {r}\rangle}_{{\text{AI}}^{\dagger}}\approx0.722$, $\overline{-\langle \cos{{\theta}} \rangle}_{{\text{AI}}^{\dagger}}\approx 0.193$ $(\overline{\langle {r}\rangle}_{\text{Pois}}=2/3$, $\overline{-\langle \cos{{\theta}} \rangle}_{\text{Pois}}=0)$

下载: 全尺寸图片幻灯片

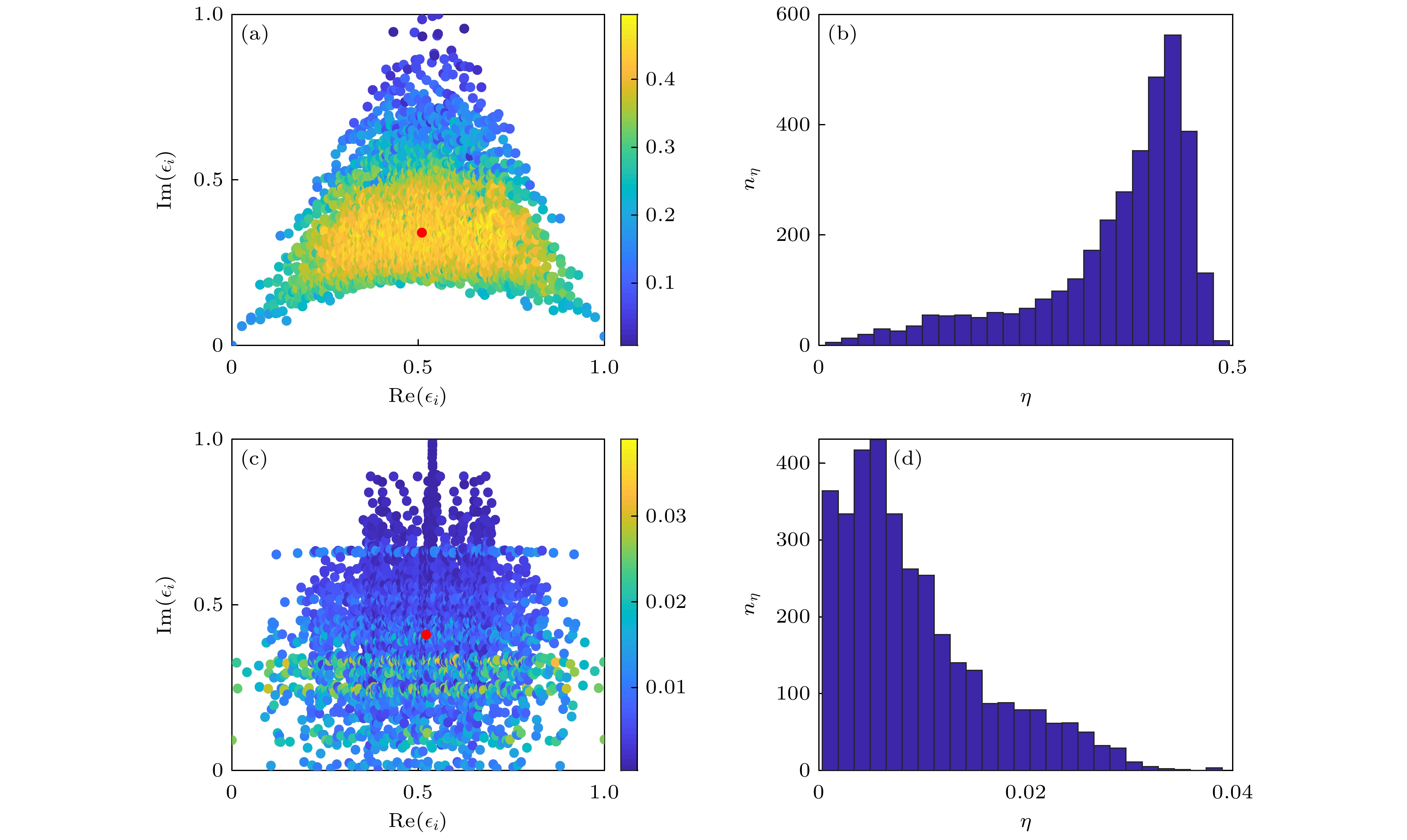
图 3 当$L=14$时, 在复平面上, 系统所有本征态的$\eta$随重整后能谱$\varepsilon_{i}$的分布情况(红点表示能谱的中心)　(a) $W=2$; (c) $W=20$. 归一化的参与率$\eta$统计直方图　(b) $W=2$; (d) $W=20$

Fig. 3. Distribution of $\eta$ for all eigenstates versus the rescaled spectrum $\varepsilon_{i}$ with $L=14$ (Red dots represent the center of the energy spectrum): (a) $W=2$; (c) $W=20$. Histogram of the normalized participation ratio $\eta$: (b) $W=2$; (d) $W=20$.

下载: 全尺寸图片幻灯片

图 4 (a)不同尺寸下, 平均半链纠缠熵$\overline{\left\langle {S}\right\rangle }$随无序强度的变化; (b)当$L=14$时, 不同无序强度W对应的$\overline{S\left( t\right) }$随时间的演化. 初态为$\left\vert \psi_{0} \right\rangle =\left\vert 1010\cdots\right\rangle $. 插图展示了平均稳态熵$\overline{S_{0}}$随无序强度的变化

Fig. 4. (a) Mean half-chain entanglement entropy $\overline{\left\langle {S}\right\rangle }$ as a function of the disorder strength W for different L; (b) the dynamics of the mean half-chain entanglement entropy $\overline{S\left( t\right) }$ for different W with $L=14$. The initial state is taken as $\left\vert \psi_{0} \right\rangle =\left\vert 1010\cdots\right\rangle $. The inset displays the mean steady-state entanglement entropy $\overline{S_{0}}$ as a function of W.

下载: 全尺寸图片幻灯片

map

[1]	Basko D M, Aleiner I L, Altshuler B L 2006 Ann. Phys. 321 1126 Google Scholar
[2]	Laumann C R, Pal A, Scardicchio A 2014 Phys. Rev. Lett. 113 200405 Google Scholar
[3]	Nandkishore R, Huse D A 2015 Annu. Rev. Condens. Matter Phys. 6 15 Google Scholar
[4]	Kjäll J A, Bardarson J H, Pollmann F 2014 Phys. Rev. Lett. 113 107204 Google Scholar
[5]	Bera S, Schomerus H, Heidrich-Meisner F, Bardarson J H 2015 Phys. Rev. Lett. 115 046603 Google Scholar
[6]	Rademaker L, Ortuño M 2016 Phys. Rev. Lett. 116 010404 Google Scholar
[7]	Khemani V, Sheng D N, Huse D A 2017 Phys. Rev. Lett. 119 075702 Google Scholar
[8]	Macé N, Alet F, Laflorencie N 2019 Phys. Rev. Lett. 123 180601 Google Scholar
[9]	Bar Lev Y, Cohen G, Reichman D R 2015 Phys. Rev. Lett. 114 100601 Google Scholar
[10]	Bairey E, Refael G, Lindner N H 2017 Phys. Rev. B 96 020201 Google Scholar
[11]	Decker K S C, Karrasch C, Eisert J, Kennes D M 2020 Phys. Rev. Lett. 124 190601 Google Scholar
[12]	Giamarchi T, Schulz H J 1988 Phys. Rev. B 37 325 Google Scholar
[13]	De Luca A, Altshuler B L, Kravtsov V E, Scardicchio A 2014 Phys. Rev. Lett. 113 046806 Google Scholar
[14]	Deutsch J M 2018 Rep. Prog. Phys. 81 082001 Google Scholar
[15]	De Luca A, Scardicchio A 2013 EPL 101 37003 Google Scholar
[16]	Bar Lev Y, Reichman D R 2014 Phys. Rev. B 89 220201
[17]	Luitz D J, Laflorencie N, Alet F 2016 Phys. Rev. B 93 060201
[18]	Abanin D A, Altman E, Bloch I, Serbyn M 2019 Rev. Mod. Phys. 91 021001 Google Scholar
[19]	Guhr T, Müller–Groeling A, Weidenmüller H A 1998 Phys. Rep. 299 189 Google Scholar
[20]	Atas Y Y, Bogomolny E, Giraud O, Roux G 2013 Phys. Rev. Lett. 110 084101 Google Scholar
[21]	Bardarson J H, Pollmann F, Moore J E 2012 Phys. Rev. Lett. 109 017202 Google Scholar
[22]	Serbyn M, Papić Z, Abanin D A 2013 Phys. Rev. Lett. 110 260601 Google Scholar
[23]	Bauer B, Nayak C 2013 J. Stat. Mech. 2013 P09005 Google Scholar
[24]	Serbyn M, Michailidis A A, Abanin D A, Papić Z 2016 Phys. Rev. Lett. 117 160601 Google Scholar
[25]	Guo Q, Cheng C, Sun Z H, et al. 2021 Nat. Phys. 17 234 Google Scholar
[26]	Guo Q, Cheng C, Li H, et al. 2021 Phys. Rev. Lett. 127 240502 Google Scholar
[27]	Ros V, Müller M, Scardicchio A 2015 Nucl. Phys. B 891 420 Google Scholar
[28]	Bertoni C, Eisert J, Kshetrimayum A, Nietner A, Thomson S J 2023 arXiv: 2208.14432 v4 [cond-mat.dis-nn]
[29]	Schreiber M, Hodgman S S, Bordia P, Lüschen H P, Fischer M H, Vosk R, Altman E, Schneider U, Bloch I 2015 Science 349 842 Google Scholar
[30]	Bordia P, Lüschen H P, Hodgman S S, Schreiber M, Bloch I, Schneider U 2016 Phys. Rev. Lett. 116 140401 Google Scholar
[31]	Kohlert T, Scherg S, Li X, Lüschen H P, Das Sarma S, Bloch I, Aidelsburger M 2019 Phys. Rev. Lett. 122 170403 Google Scholar
[32]	Smith J, Lee A, Richerme P, Neyenhuis B, Hess P W, Hauke P, Heyl M, Huse D A, Monroe C 2016 Nat. Phys. 12 907 Google Scholar
[33]	Roushan P, Neill C, Tangpanitanon J, et al. 2017 Science 358 1175 Google Scholar
[34]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[35]	Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
[36]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[37]	Zhang K, Yang Z, Fang C 2022 Nat. Commun. 13 2496 Google Scholar
[38]	Ou Z, Wang Y, Li L 2023 Phys. Rev. B 107 L161404 Google Scholar
[39]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[40]	Borgnia D S, Kruchkov A J, Slager R J 2020 Phys. Rev. Lett. 124 056802 Google Scholar
[41]	Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 Google Scholar
[42]	Wang Y C, You J S, Jen H H 2022 Nat. Commun. 13 4598 Google Scholar
[43]	Xu Z, Chen S 2020 Phys. Rev. B 102 035153 Google Scholar
[44]	Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 Google Scholar
[45]	Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 Google Scholar
[46]	Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384 Google Scholar
[47]	Hamazaki R, Kawabata K, Ueda M 2019 Phys. Rev. Lett. 123 090603 Google Scholar
[48]	Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 Google Scholar
[49]	Zhai L J, Yin S, Huang G Y 2020 Phys. Rev. B 102 064206 Google Scholar
[50]	Gong Z, Ashida Y, Kawabata K, Takasan K, Higashikawa S, Ueda M 2018 Phys. Rev. X 8 031079
[51]	Tomita T, Nakajima S, Danshita I, Takasu Y, Takahashi Y 2017 Sci. Adv. 3 e1701513 Google Scholar
[52]	Sponselee K, Freystatzky L, Abeln B, et al. 2018 Quantum Sci. Technol. 4 014002 Google Scholar
[53]	Wang C, Liu C, Shi Z Y 2022 Phy. Rev. Lett. 129 203401 Google Scholar
[54]	Berry M V, Tabor M 1977 Proc. R. Soc. London, Ser. A 256 375
[55]	Bohigas O, Giannoni M J, Schmit C 1984 Phys. Rev. Lett. 52 1 Google Scholar
[56]	Casati G, Valz-Gris F, Guarnieri I 1980 Lett. Nuovo Cimento 28 279 Google Scholar
[57]	Rigol M, Dunjko V, Olshanii M 2008 Nature 452 854 Google Scholar
[58]	Hamazaki R, Kawabata K, Kura N, Ueda M 2020 Phys. Rev. Res. 2 023286 Google Scholar
[59]	Sá L, Ribeiro P, Prosen T 2020 Phys. Rev. X 10 021019
[60]	García-García A M, Sá L, Verbaarschot J J M 2022 Phys. Rev. X 12 021040
[61]	Ginibre J 1965 J. Math. Phys. 6 440 Google Scholar
[62]	Peron T, De Resende B M F, Rodrigues F A, Costa L D F, Méndez-Bermúdez J A 2020 Phys. Rev. E 102 062305 Google Scholar
[63]	Liu J, Xu Z 2023 Phys. Rev. B 108 184205 Google Scholar
[64]	Oganesyan V, Huse D A 2007 Phys. Rev. B 75 155111 Google Scholar
[65]	Ghosh S, Gupta S, Kulkarni M 2022 Phys. Rev. B 106 134202 Google Scholar
[66]	Li X, Ganeshan S, Pixley J H, Das Sarma S 2015 Phys. Rev. Lett. 115 186601 Google Scholar
[67]	Suthar K, Wang Y C, Huang Y P, Jen H H, You J S 2022 Phys. Rev. B 106 064208

[1]	陆展鹏, 徐志浩. 具有平带的一维十字型晶格中重返局域化现象. , 2024, 73(3): 037202. doi: 10.7498/aps.73.20231393
[2]	刘辉, 陆展鹏, 徐志浩. 一维非厄米十字晶格中的退局域-局域转变. , 2024, 73(13): 137201. doi: 10.7498/aps.73.20240510
[3]	古燕, 陆展鹏. 非厄米耦合链中的局域化转变. , 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[4]	陈奇, 戴越, 李飞燕, 张彪, 李昊辰, 谭静柔, 汪潇涵, 何广龙, 费越, 王昊, 张蜡宝, 康琳, 陈健, 吴培亨. 5—10 µm波段超导单光子探测器设计与研制. , 2022, 71(24): 248502. doi: 10.7498/aps.71.20221594
[5]	曲登科, 范毅, 薛鹏. 高维宇称-时间对称系统中的信息恢复与临界性. , 2022, 0(0): . doi: 10.7498/aps.71.20220511
[6]	曲登科, 范毅, 薛鹏. 高维宇称-时间对称系统中的信息恢复与临界性. , 2022, 71(13): 130301. doi: 10.7498/aps.70.20220511
[7]	唐原江, 梁超, 刘永椿. 宇称-时间对称与反对称研究进展. , 2022, 71(17): 171101. doi: 10.7498/aps.71.20221323
[8]	吴瑾, 陆展鹏, 徐志浩, 郭利平. 由超辐射引起的迁移率边和重返局域化. , 2022, 71(11): 113702. doi: 10.7498/aps.71.20212246
[9]	刘佳琳, 庞婷方, 杨孝森, 王正岭. 无序非厄米Su-Schrieffer-Heeger中的趋肤效应. , 2022, 71(22): 227402. doi: 10.7498/aps.71.20221151
[10]	潘磊. 非厄米线性响应理论及其应用. , 2022, 71(17): 170305. doi: 10.7498/aps.71.20220862
[11]	傅聪, 叶梦浩, 赵晖, 陈宇光, 鄢永红. 共轭聚合物链中光激发过程的无序效应. , 2021, 70(11): 117201. doi: 10.7498/aps.70.20201801
[12]	张高见, 王逸璞. 腔光子-自旋波量子耦合系统中各向异性奇异点的实验研究. , 2020, 69(4): 047103. doi: 10.7498/aps.69.20191632
[13]	徐志浩, 皇甫宏丽, 张云波. 一维准周期晶格中玻色子对的迁移率边. , 2019, 68(8): 087201. doi: 10.7498/aps.68.20182218
[14]	韩华, 吴翎燕, 宋宁宁. 基于随机矩阵的金融网络模型. , 2014, 63(13): 138901. doi: 10.7498/aps.63.138901
[15]	侯碧辉, 刘凤艳, 岳明, 王克军. 纳米金属镝的传导电子定域化. , 2011, 60(1): 017201. doi: 10.7498/aps.60.017201
[16]	徐赞新, 王钺, 司洪波, 冯振明. 基于随机矩阵理论的城市人群移动行为分析. , 2011, 60(4): 040501. doi: 10.7498/aps.60.040501
[17]	李晓春, 高俊丽, 刘绍娥, 周科朝, 黄伯云. 无序对二维声子晶体平板负折射成像的影响. , 2010, 59(1): 376-380. doi: 10.7498/aps.59.376
[18]	李蓉, 颜平兰, 陈健, 李俊, 李金, 张凯旺, 钟建新. 随机矩阵理论在肺癌基因网络识别中的应用. , 2009, 58(10): 6703-6708. doi: 10.7498/aps.58.6703
[19]	许兴胜, 陈弘达, 张道中. 非晶光子晶体中的光子局域化. , 2006, 55(12): 6430-6434. doi: 10.7498/aps.55.6430
[20]	刘小良, 徐慧, 马松山, 宋招权. 一维无序二元固体中电子局域性质的研究. , 2006, 55(6): 2949-2954. doi: 10.7498/aps.55.2949

计量

文章访问数: 2055
PDF下载量: 99
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

随机两体耗散诱导的非厄米多体局域化