-
The acoustic radiation force allows acoustic tweezers to suspend and move tiny particles. The horizontal movement is one of the common forms in which acoustic tweezers manipulate particles. In this paper, the direct relationship between acoustic radiation force and sound pressure is derived theoretically. The results show that there is a corresponding relationship between the maximum point of sound pressure (focus point) and the minimum point of acoustic radiation force potential energy. A model for focused acoustic field in acoustic tweezers is established based on the principle of phase modulating. In the numerical simulation, taking the double-sided 16-element acoustic tweezers device for example, the method of controlling the horizontal movement of particles and its stability are analyzed. Owing to the influence of gravity, the balance in the vertical direction must be considered in the horizontal movement of particles. Horizontal movement shows different stabilities at different positions in acoustic filed. The closer to the center of the array the particle is, the more stably it moves. The step length (accuracy) also has an important influence on the moving stability. In general, the shorter the step size is, the higher the stability is. In this model, when moving step length is reduced by one-half, the stability is improved by nearly 40%. The research results have theoretical significance for designing acoustic tweezers, planning particle movement paths, and promoting the application of acoustic tweezers technology.
[1] Lee J, Post R, Ishii H 2011 UIST 2011: Proceedings of the 24th Annual ACM symposium on User Interface Software and Technology Santa Barbara, USA, 2011 p327
[2] Baudoin M, Thomas J L 2020 Annu. Rev. Fluid Mech. 52 205
Google Scholar
[3] Baresch D, Thomas J L, Marchiano R 2016 Phys. Rev. Lett. 116 024301
Google Scholar
[4] Xie W J, Cao C D, Lue Y J, Hong Z Y, Wei B 2006 Appl. Phys. Lett. 89 214102
Google Scholar
[5] Polimeno P, Magazzu A, Iati M A, Patti F, Saija R, Boschi C D, Donato M G, Gucciardi P G, Jones P H, Volpe G, Marago O M 2018 J. Quant. Spectrosc. Ra. 218 131
Google Scholar
[6] Hanson A R, Domich E G, Adams H S 1964 Rev. Sci. Instrum. 35 1031
Google Scholar
[7] Wu J R 1990 J. Acoust. Soc. Am. 88 S167
Google Scholar
[8] Wu D, Yin D Y, Xiao Z Y, Shi Q F 2019 Chin. Phys. Lett. 36 094301
Google Scholar
[9] Norasikin M A, Plasencia D M, Polychronopoulos S, Memoli G, Tokuda Y, Subramanian S 2018 UIST 2018: Proceedings of the 31st Annual ACM Symposium on User Interface Software and Technology Berlin, Germany, October 14–17, 2018 p247
[10] Guo F, Mao Z M, Chen Y C 2016 P. Natl. Acad. Sci. USA 113 1522
Google Scholar
[11] Marzo A, Seah S A, Drinkwater B W, Sahoo D R, Long B, Subramanian S 2015 Nat. Commun. 6 8661
Google Scholar
[12] Foresti D, Nabavi M, Klingauf M, Ferrari A, Poulikakos D A 2013 P. Natl. Acad. Sci. USA 110 12549
Google Scholar
[13] Courtney C R P, Ong C K, Drinkwater B W, Wilcox P D, Demore C, Cochran S, Glynne-Jones P, Hill M 2010 J. Acoust. Soc. Am. 128 EL195
Google Scholar
[14] Ochiai Y, Hoshi T, Rekimoto J 2014 ACM T. Graphic. 33 85
Google Scholar
[15] Marzo A, Drinkwater B W 2019 P. Natl. Acad. Sci. USA 116 84
Google Scholar
[16] Omirou T, Marzo A, Seah S A, Subramanian S 2015 CHI 2015: Proceedings of the 33rd Annual CHI Conference on Human Factors in Computing Systems Seoul, South Korea, April 18–23, 2015 p309
[17] Gor’Kov L P 1961 Doklady Akademii Nauk SSSR 140 88
Google Scholar
[18] 程建春 2012 声学原理 (北京: 科学出版社) 第794, 799页
Cheng J C 2012 Principles for Acoustics (Beijing: Science Press) pp794, 799 (in Chinese)
[19] 钱祖文 2009 非线性声学 (第二版) (北京: 科学出版社) 第23, 24页
Qian Z W 2009 Non-linear Acoustics (2nd Ed.) (Beijing: Science Press) pp23, 24 (in Chinese)
[20] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础 (第三版) (南京: 南京大学出版社) 第223−225页
Du G H, Zhu Z M, Gong X F 2012 Fundamentals of Acoustics (3rd Ed.) (Nanjing: Nanjing University Press) pp223−225 (in Chinese)
[21] 郭木铎 2014 硕士学位论文 (哈尔滨: 哈尔滨工业大学)
Guo M D 2014 M. S. Thesis (Harbin: Harbin Institute of Technology) (in Chinese)
[22] Bruus H. 2012 Lab Chip 12 1014
Google Scholar
-
图 1 换能器与焦点之间的几何关系. 坐标原点位于下方阵列的中心处, x轴和y轴分别平行于方形阵列的两个边. 这里将换能器与聚焦点之间的距离视为换能器表面中心与聚焦点之间的距离, z轴垂直指向上方阵列. 图中, 某换能器中心到聚焦点在该阵元平面上的投影点之间的距离为
$ d $ , 上下阵列平面之间的距离为H, 换能器与聚焦点间的距离为$ r $ ,$ d $ 与$ r $ 之间所夹锐角记为$ \xi $ Figure 1. Geometric relationship between the transducer and the focal point. Origin of the coordinate is located at the center of the lower array, and the x-axis and y-axis are parallel to the two sides of the square array. Here, the distance between the transducer and the focus point is regarded as the distance between the center of the transducer surface and the focusing point, and the z-axis points vertically to the upper array. In the figure, the distance between the center of a certain transducer and the projection point of the focal point on the array plane is
$ d $ , the distance between the upper and lower array planes is H, and the distance between the transducer and the focal point is$ r $ . The acute angle in between$ d $ and$ r $ is recorded as$ \xi $ 
图 2 (a)−(c)微粒在平面内移动过程的俯视示意图, 其中(a)微粒被束缚在聚焦点处, 黑色箭头代表力的分布; (b)聚焦点移动后微粒与力的汇聚区相对位置示意图, 黑色箭头代表微粒所受力的方向; (c)微粒回到聚焦点; (d), (e)力的汇聚区移动的示意图. 上下两块正对的正方形区域为换能器阵列所在平面, 上嵌的圆圈代表换能器, 不同颜色代表不同的相位. 力的汇聚区以红色虚线圆圈表示, 黑色虚线簇代表声线, 黑色实线为辅助线, 用以标明力的汇聚区位置, 粉色虚线为力的汇聚区移动轨迹所在直线
Figure 2. (a)−(c) Schematic top views of the movement of particles in a plane: (a) Particles are bounded at the focus point, and the black arrow represents the distribution of acoustic radiation force (ARF); (b) schematic diagram of the relative position of the particle and the convergent area of the force after the focus point moves, with a black arrow representing the direction of the force acting on the particle; (c) particle returning to the focus point. (d), (e) Schematic diagrams of the movement of the force convergence area. The upper and lower two square areas facing each other are the planes where the transducers are located. The circles embedded on the planes represent the transducers, and different colors represent different phases. The force convergence area is represented by a red dashed circle. The black clusters of dashed lines represent acoustic rays. The black solid line is an auxiliary line to indicate the location of the force convergence area, and the pink dashed line is the straight line where the trajectory lies.
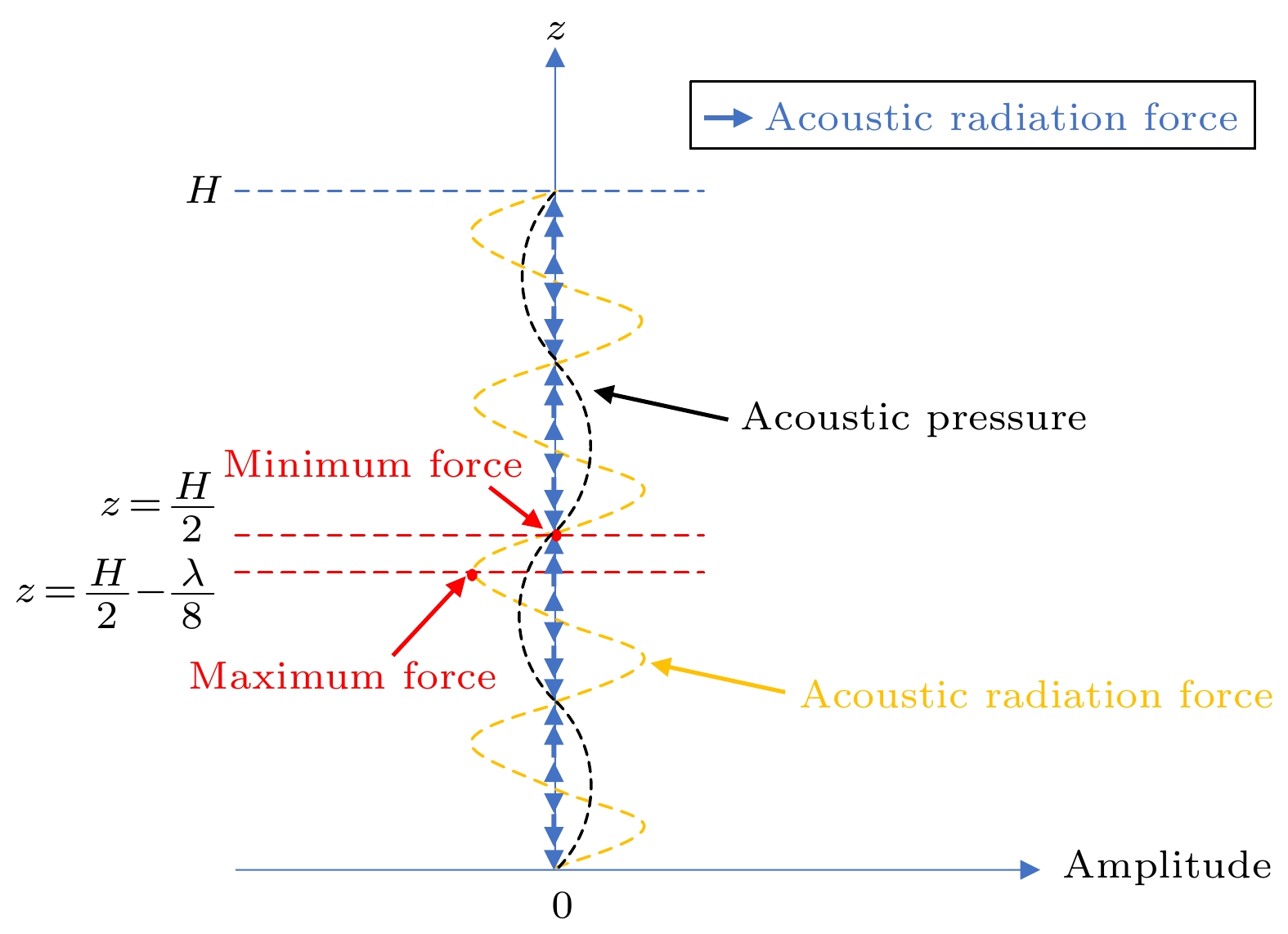
图 3 某对换能器在垂直方向产生的驻波声场中的相关元素示意图. 黑色虚线为声压的垂向分布, 黄色虚线为声辐射力的垂向分布, 蓝色箭头的长短和方向代表声辐射力的大小和方向. z轴上的H/2高度处应为力的汇聚点, 其下方1/8个波长处应为相邻的1个力的极大值对应的高度
Figure 3. Schematic diagram of the relevant elements in the standing wave acoustic field generated by a pair of transducers in the vertical direction. The black dashed line is the vertical distribution of acoustic pressure, the yellow dashed line is the vertical distribution of the ARF. The length and direction of the blue arrow represent the magnitude and direction of the ARF. The height of H/2 on the z axis should be the convergence point of the force, and the one-eighth of the wavelength below it should be the height corresponding to the adjacent maximum force.
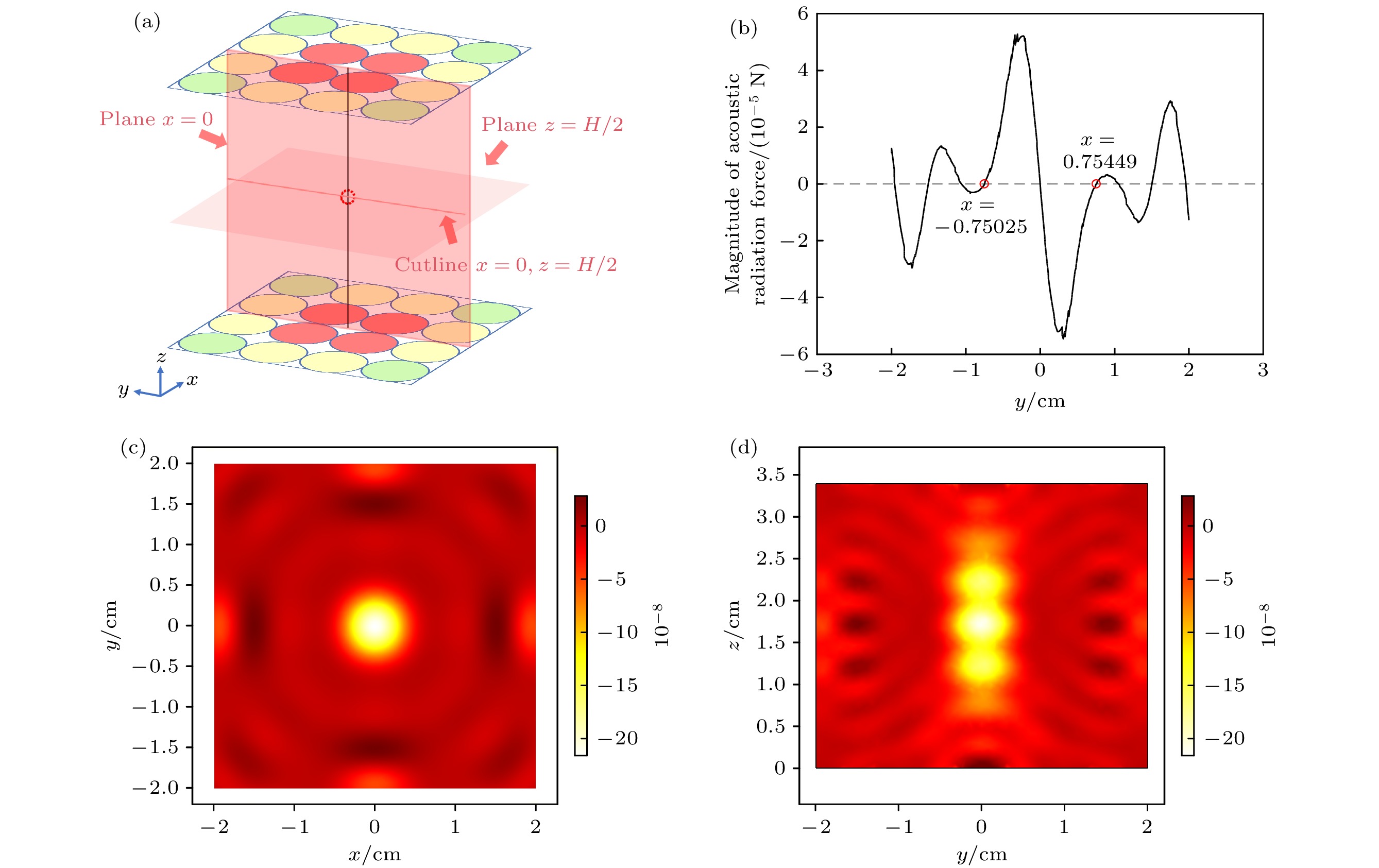
图 4 聚焦点在中心时声辐射力势能的分布 (a)聚焦点在中心时的相位分布示意以及截面z = H/2、截面x = 0、截线x = 0、截线z = H/2所在位置; (b)截线x = 0, z = H/2上声辐射力在y方向的分量; (c)平面z = H/2上的声辐射力势能的分布; (d)平面x = 0上的声辐射力势能分布
Figure 4. Distribution of ARF potential energy when the focal point is at the center: (a) Phase distribution diagram when the focal point is at the center and the position of section z = H/2, section x = 0 and section line x = 0, z = H/2; (b) component of the ARF in the y direction on the section line x = 0, z = H/2; (c) distribution of ARF potential energy on the plane z = H/2; (d) distribution of ARF potential energy on the plane x = 0.
图 5 (a)格点化操控表面以及部分聚焦位置. 根据对称性将所有点归类为图中的10个实线蓝圈所标出的点, 3个虚线蓝圈标出的点为补充遗漏路径需要绘制的点. 经线从中心向外围以递增数字1−4标注, 纬线自上而下以A, B, C, D标注. 这样任意一点可以以字母与数字的组合命名, 字母在前数字在后, 如中心处的点为D1点. (b)聚焦点在C3处时, y = 0截面上声辐射力势能的分布. 横坐标为x轴刻度, 纵坐标为z轴刻度. 图中标注出了D2和D4处的垂直截线. 当聚焦点位于C3时, 取D2, D4, C3这3个位置处的3条垂直截线, 绘制了沿其分布的垂向声辐射力于(c)图中, 正负代表方向, 红色虚线标注出高度z = 1.715 cm
Figure 5. (a) Grid on the manipulation plane and part of the focus position. According to symmetry, all points are represented as the points marked by the 10 solid blue circles in the figure, and the points marked by the 3 dashed blue circles are the points that need to be drawn to supplement the missing path. Longitude lines are marked with increasing numbers 1−4 from the center to the periphery, and latitude lines are marked with A, B, C, and D from top to bottom. In this way, any point can be named with a combination of letters and numbers, with letters in the front and numbers in the back, for example, the point at the center is the D1 point. (b) Distribution of the ARF potential energy on the y = 0 section when the focal point is at C3. The coordinates of x axis and z axis are recorded on abscissa and ordinate respectively. The positions of D2 and D4 are marked in the figure. The distribution of vertical ARF along three vertical cutlines D2, D4, C3 are depicted in panel (c) when focusing point is located at C3. The signs of ARF represent their directions. Red dashed line marks the latitude of z = 1.715 cm.
图 6 (a)细化后的格点平面图, 图中的红点区域为囊括所有移动情形的最小研究区域, 格点的命名法则与之前的粗格点相同. (b)聚焦点位于细格点平面F5处(粗格点平面C3处)时, 格点F5 (C3), G4以及粗格点平面中D2处垂直截线上垂向声辐射力随高度的分布情况. 红色虚线标出1.715 cm高度. (c)红色箭头代表不稳定移动的路径, 绿色箭头代表稳定移动的路径. 黑色虚线右下方为稳定移动的区域, 左上方为不稳定移动的区域. (d)绿色区域为可稳定操控微粒的区域; 紫色区域内跨对角线向中心移动是不稳定的; 黄色区域内斜跨对角线向中心和向外移动是不稳定的; 红色区域内沿网格线向中心移动不稳定; 橙色区域为红、黄交叠区域, 深紫色区域为红、黄、紫交叠区域. (e), (f)聚焦点分别位于H7和B7处时, 操控平面上声辐射力势能的分布
Figure 6. (a) Refined grid plane. The red dot area in the figure is the smallest research area that includes all moving situations. The nomenclature of the points is the same as the previous coarse grid points. (b) Distribution of vertical ARF along 3 vertical cutlines located at F5 (C3 in the coarse grid), G4 and D2 (the coarse grid) respectively. Red dashed line marks the height of 1.715 cm. The red arrows in panel (c) represent the path of unstable movement, and the green arrows represent the path of stable movement. Below the black dotted line is the stable moving area, and the rest part is the unstable moving area. The green area in panel (d) is the area where the particles can be stably manipulated. The purple, yellow and red area are areas where movement along diagonal of grids towards the center, movement along diagonal of grids towards and away from the center, movement along grid line towards the center are ubstable; orange area is the superposition of red area and yellow area, dark purple area is the superposition of red, yellow and purple area. (e), (f) Distribution of ARF potential energy on manipulation plane when the focus points are located at H7 and B7.
-
[1] Lee J, Post R, Ishii H 2011 UIST 2011: Proceedings of the 24th Annual ACM symposium on User Interface Software and Technology Santa Barbara, USA, 2011 p327
[2] Baudoin M, Thomas J L 2020 Annu. Rev. Fluid Mech. 52 205
Google Scholar
[3] Baresch D, Thomas J L, Marchiano R 2016 Phys. Rev. Lett. 116 024301
Google Scholar
[4] Xie W J, Cao C D, Lue Y J, Hong Z Y, Wei B 2006 Appl. Phys. Lett. 89 214102
Google Scholar
[5] Polimeno P, Magazzu A, Iati M A, Patti F, Saija R, Boschi C D, Donato M G, Gucciardi P G, Jones P H, Volpe G, Marago O M 2018 J. Quant. Spectrosc. Ra. 218 131
Google Scholar
[6] Hanson A R, Domich E G, Adams H S 1964 Rev. Sci. Instrum. 35 1031
Google Scholar
[7] Wu J R 1990 J. Acoust. Soc. Am. 88 S167
Google Scholar
[8] Wu D, Yin D Y, Xiao Z Y, Shi Q F 2019 Chin. Phys. Lett. 36 094301
Google Scholar
[9] Norasikin M A, Plasencia D M, Polychronopoulos S, Memoli G, Tokuda Y, Subramanian S 2018 UIST 2018: Proceedings of the 31st Annual ACM Symposium on User Interface Software and Technology Berlin, Germany, October 14–17, 2018 p247
[10] Guo F, Mao Z M, Chen Y C 2016 P. Natl. Acad. Sci. USA 113 1522
Google Scholar
[11] Marzo A, Seah S A, Drinkwater B W, Sahoo D R, Long B, Subramanian S 2015 Nat. Commun. 6 8661
Google Scholar
[12] Foresti D, Nabavi M, Klingauf M, Ferrari A, Poulikakos D A 2013 P. Natl. Acad. Sci. USA 110 12549
Google Scholar
[13] Courtney C R P, Ong C K, Drinkwater B W, Wilcox P D, Demore C, Cochran S, Glynne-Jones P, Hill M 2010 J. Acoust. Soc. Am. 128 EL195
Google Scholar
[14] Ochiai Y, Hoshi T, Rekimoto J 2014 ACM T. Graphic. 33 85
Google Scholar
[15] Marzo A, Drinkwater B W 2019 P. Natl. Acad. Sci. USA 116 84
Google Scholar
[16] Omirou T, Marzo A, Seah S A, Subramanian S 2015 CHI 2015: Proceedings of the 33rd Annual CHI Conference on Human Factors in Computing Systems Seoul, South Korea, April 18–23, 2015 p309
[17] Gor’Kov L P 1961 Doklady Akademii Nauk SSSR 140 88
Google Scholar
[18] 程建春 2012 声学原理 (北京: 科学出版社) 第794, 799页
Cheng J C 2012 Principles for Acoustics (Beijing: Science Press) pp794, 799 (in Chinese)
[19] 钱祖文 2009 非线性声学 (第二版) (北京: 科学出版社) 第23, 24页
Qian Z W 2009 Non-linear Acoustics (2nd Ed.) (Beijing: Science Press) pp23, 24 (in Chinese)
[20] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础 (第三版) (南京: 南京大学出版社) 第223−225页
Du G H, Zhu Z M, Gong X F 2012 Fundamentals of Acoustics (3rd Ed.) (Nanjing: Nanjing University Press) pp223−225 (in Chinese)
[21] 郭木铎 2014 硕士学位论文 (哈尔滨: 哈尔滨工业大学)
Guo M D 2014 M. S. Thesis (Harbin: Harbin Institute of Technology) (in Chinese)
[22] Bruus H. 2012 Lab Chip 12 1014
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4940
- PDF Downloads: 133
- Cited By: 0
