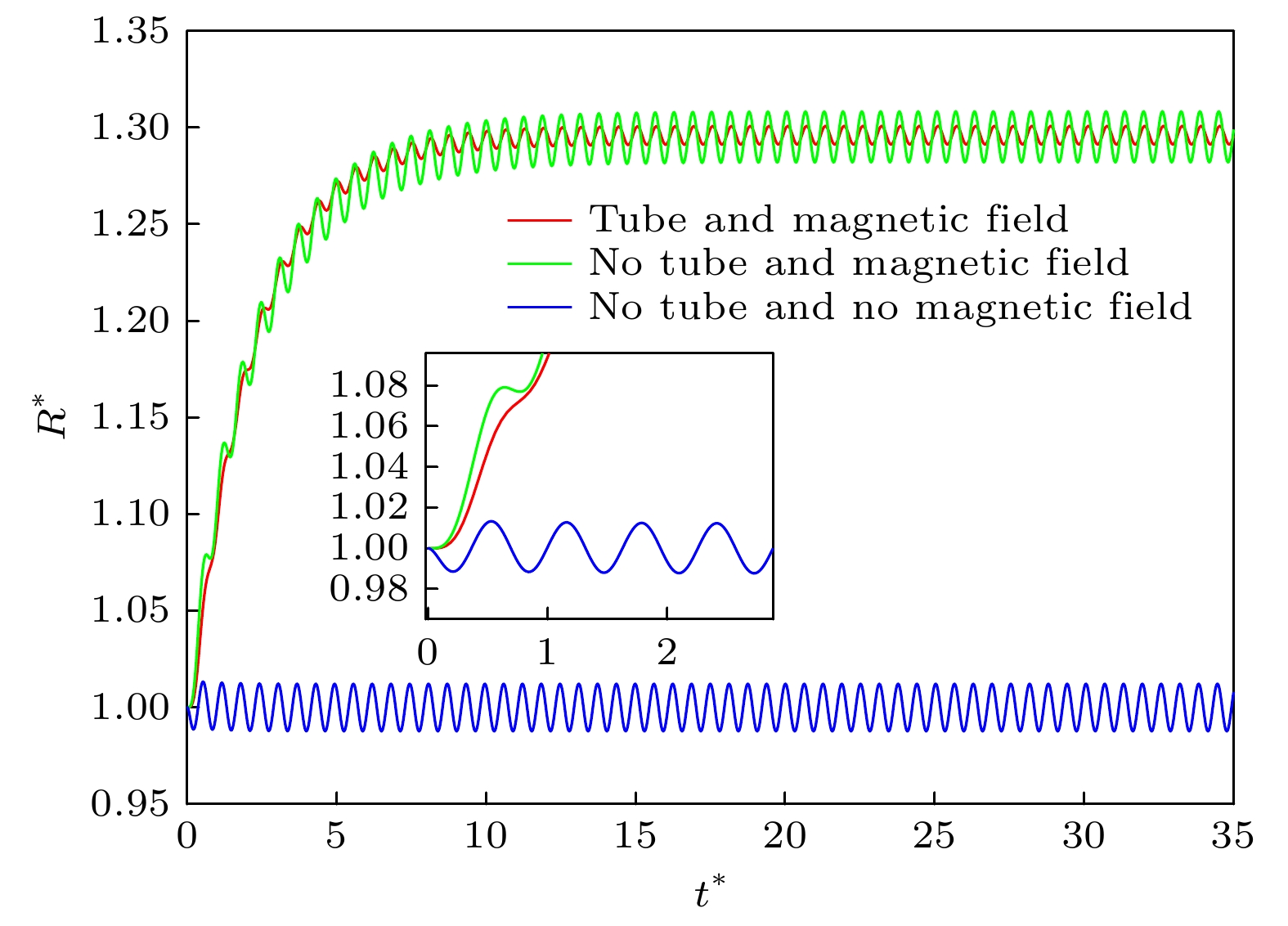
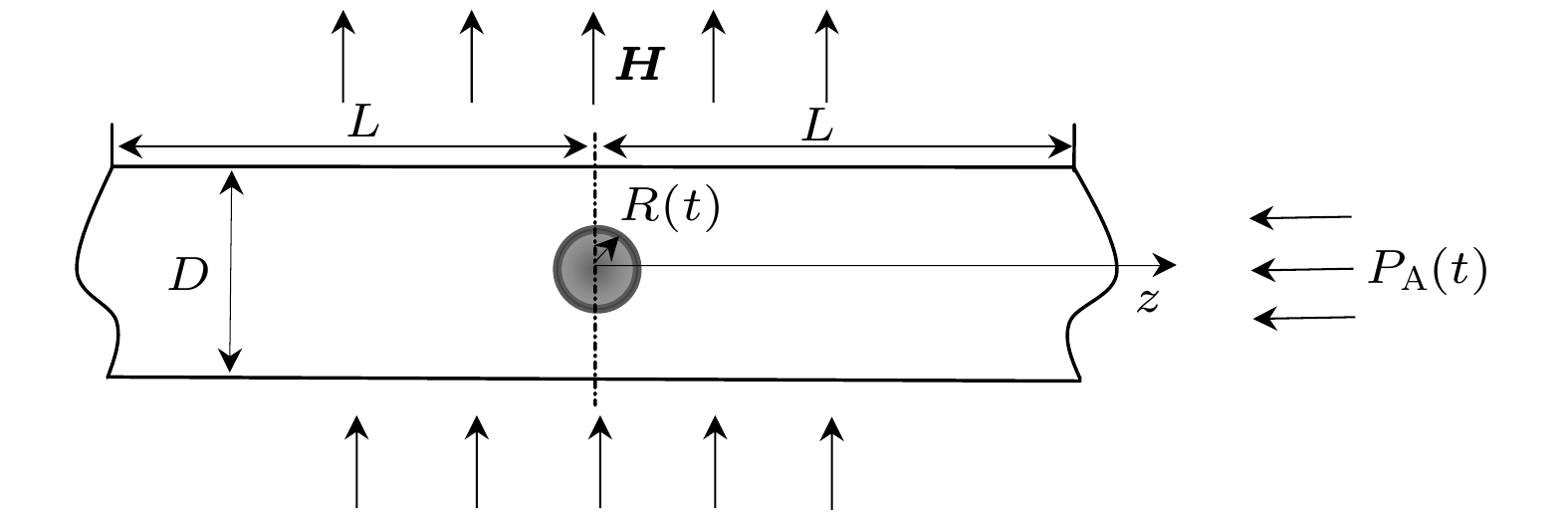
-
The dynamic behavior of coated microbubble in a magneto-acoustic field is very significant for its application to therapy. In this paper, the radial vibration equation of microbubble is derived by placing the coated-microbubbles in a tube filled with magnetic fluid and considering the magnetic pressure on the magnetic fluid under the magneto-acoustic field. The dynamic equation is nondimensionalized by using characteristic quantities such as Weber number and Reynolds number. The effects of magnetic-acoustic field parameters and magnetofluid characteristics on the vibration behavior of the vibration system are analyzed by the Runge-Kutta method. The results show that the magnetic field can prevent the collapse and make bubble oscillate stably. When the acoustic field is constant, the magnetic field can stabilize the oscillation of the microbubble and increase the equilibrium radius of the oscillating microbubble. The stronger the magnetic field is, the more obvious the influence of magnetofluid magnetisability χm on the vibration of the microbubble is and the stronger the nonlinear of the transient response of the microbubble is when the magnetic field is larger. In addition, the larger acoustic field parameters will enhance the response of oscillating microbubble to magnetic field. The larger the magnetic field is, the weaker the influence of acoustic parameters on the oscillations of microbubble is. Also, the transient response of microbubble is obviously nonlinear, but the steady-state response keeps the reciprocating oscillation with small amplitude. It can be seen that the adjusting of the magneto-acoustic field is beneficial to realizing the stable oscillation of microbubble in the blood vessel and avoiding collapse.
-
Keywords:
- magnetic-acoustic composite field /
- finite tube /
- coated microbubble /
- vibration
[1] Michalakis A A, Matthew F B, Jeffry E P, Paul S S, Peter N B 2020 Ultrasound Med. Bio. 46 498
Google Scholar
[2] Wischhusen J, Padilla F 2018 IRBM 40 10
Google Scholar
[3] Pysz M A, Foygel K, Rosenberg J, Gambhir S S, Schneider M, Willmann J K 2010 Radiology 256 519
Google Scholar
[4] Bekeredjian R, Grayburn P, Shohet R 2005 Am. Coll. Cardiol. 45 329
Google Scholar
[5] Hernot S, Klibanov A 2008 Adv. Drug Deliv. Rev. 60 1153
Google Scholar
[6] Martin M J, Chung E M L, Goodall A H 2008 J. Vasc. Surg. 47 1371
Google Scholar
[7] Owen J, Pankhurst Q, Stride E 2012 Int. J. Hyperthermia 28 362
Google Scholar
[8] Yvonn H, Staffan H, Alexandra H, Bernhard G, Martina A, Dietmar E, Daniela W, Alexander P, Markus W, Florian K, Ulrich P, Hanna M 2017 Theranostics 7 295
Google Scholar
[9] Iwanaga K, Tominaga K, Yamamoto K, Habu M, Maeda H, Akifusa S, Tsujisawa T, Okinaga T, Fukuda J, Nishihara T 2007 Cancer Gene Ther. 14 354
Google Scholar
[10] Fan C H, Cheng Y H, Ting C Y, Ho Y J, Hsu P H, Liu H L, Yeh C K 2016 Theranostics 6 1542
Google Scholar
[11] de Saint V M, Carugo D, Barnsley L C, Owen J, Coussios C-C, Stride E 2017 Phys. Med. Biol. 62 7451
Google Scholar
[12] Bi F, Zhang J, Su Y J, Chun Y J, Tang Ya, Liu J N 2009 Biomaterials 30 5125
Google Scholar
[13] Mulvana H, Eckersley R J, Tang M X, Pankhurst Q, Stride E 2012 Ultrasound Med. Biol. 38 864
Google Scholar
[14] Yan L P, Miao W, Li D D 2020 J. Nanotechno. 20 6087
Google Scholar
[15] Lind, Steven J 2014 Phys. Fluids 6 26
Google Scholar
[16] Malvar S, Gontijo R G, Cunha F R 2018 J. Eng. Math. 108 143
Google Scholar
[17] Church C C 1995 J. Acoust. Soc. Am. 97 1510
Google Scholar
[18] 赵丽霞, 王成会, 莫润阳 2021 70 014301
Google Scholar
Zhao L X, Wang C H, Mo R Y 2021 Acta Phys. Sin. 70 014301
Google Scholar
[19] Sassaroli E, Hynynen K 2005 Phys. Med. Biol. 50 5293
Google Scholar
[20] Ni B Y, Zhang A M, Wang Q X, Wang B 2012 Acta. Mechanica Sinica. 28 1248
Google Scholar
[21] Fan Y Z, Li H S, Daniel F 2020 Phys. Week 102 013105
Google Scholar
[22] Qin S P, Ferrara K W 2006 Phys. Med. Biol. 51 5065
Google Scholar
[23] Owen J, Rademeyer P, Chung D, Cheng Q, Holroyd D, Coussios C, Friend P, Pankhurst Q A, Stride E 2015 Interface Focus 5 20150001
Google Scholar
[24] Beguin E, Gray M D, Logan K A, Nesbitt H, Sheng Y J, Kamila S, Barnsley L C, Bau L, McHale A P, Callan J F, Stride E 2020 J. Controlled Release 317 23
Google Scholar
[25] Zhang B H, Kim H, Jiang X N 2019 Ultrasonics 98 62
Google Scholar
[26] Droste D W 2008 Eur. Neurol. 1 2
Google Scholar
[27] 莫润阳, 吴临燕, 詹思楠, 张引红 2015 64 124301
Google Scholar
Mo R Y, Wu L Y, Zhan S N, Zhang Y H 2015 Acta Phys. Sin. 64 124301
Google Scholar
[28] Zudin Y B, Isakov N S, Zenin V V 2014 J. Eng. Thermophys. 87 1487
Google Scholar
[29] Stride E 2008 Philos. T. R. Soc. A 366 2103
Google Scholar
[30] Stride E, Porter C, Prieto A G, Pankhurst Q 2009 Ultrasound Med. Biol. 35 861
Google Scholar
[31] 毕勤成, 施东晓, 何永清, 邱晟华 2010 热科学与技术 9 189
Bi Q C, Shi D X, He Y Q, Qiu S H 2010 J. Ther. Sci. Techno. 9 189
[32] 陈杰, 张杰, 莫润阳, 王成会, 胡静 2020 磁性材料及器件 51 9
Chen J, Zhang J, Mo R Y, Wang C H, Hu J 2020 J. Magn. Mater. Device 51 9
[33] Owen J, Grove P, Rademeyer P, Stride E 2014 J. R. Soc. Interface 11 20140622
Google Scholar
[34] Victor M S, Crake C, Coussios C C, Stride E 2014 Expert Opin. Drug Del. 11 87
Google Scholar
-
图 1 管内包膜微泡在磁声混合场作用下的几何模型
Figure 1. Geometric model of the microbubble in a tube under magneto-acoustic mixing field.
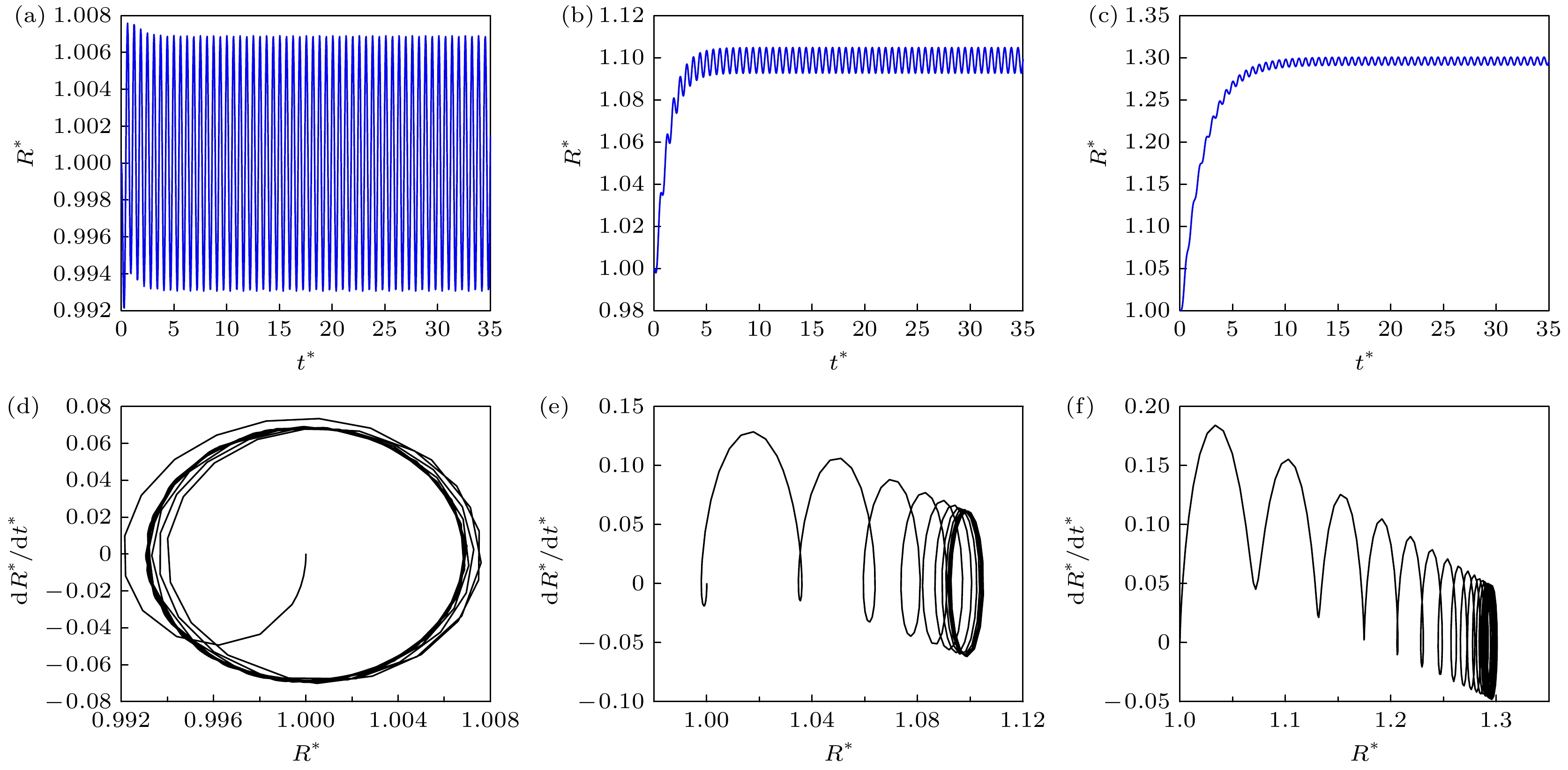
图 2 无磁场存在(Remag→
$ {\infty } $ )时, 管内微泡在声场驱动下的振荡特性 (a) R*-t*图; (b) PG/P0-t*图; (c) 振动相图 (We = 5, a = 2, ω = 1)Figure 2. When magnetic field is absent (Remag→
$ {\infty } $ ), the oscillation characteristics of the microbubble in a tube driven by acoustic field(We = 5, a = 2, ω = 1): (a) R*-t* plot; (b) PG/P0-t* plot; (c) the vibration phase diagram (We = 5, a = 2, ω = 1).
图 3 振荡微泡的磁场响应, 其中包括(a)—(c) R*-t*图及对应(d)—(f)相图(We = 5, a = 2, ω = 1, χm = 0.1) (a), (d) Remag = 10; (b), (e) Remag = 1; (c), (f) Remag = 0.5
Figure 3. Magnetic field response of the oscillating microbubble (We = 5, a = 2, ω = 1, χm = 0.1), including (a)−(c) R*-t* plot and corresponding (d)−(f) phase diagram: (a), (d) Remag = 10; (b), (e) Remag = 1; (c), (f) Remag = 0.5.
图 4 磁化率χm不同的磁流体中振荡微泡的磁场响应, 其中包括(a)—(c) R*−t*图及相应(d)—(f)相图(We = 5, a = 2, ω = 1) (a), (d) Remag = 10; (b), (e) Remag = 1; (c), (f) Remag = 0.5
Figure 4. Magnetic field response of the oscillating microbubble in the magnetic fluid with different susceptibility χm (We = 5, a = 2, ω = 1), including (a)−(c) R*−t* plot and corresponding (d)−(f) phase diagram: (a), (d) Remag = 10; (b), (e) Remag = 1; (c), (f) Remag = 0.5
图 5 ω = 5时振荡微泡的磁响应, 其中包括(a)—(c) R*-t*图及相应(d)—(f)相图(We =10, a = 2, χm = 1) (a), (d) Remag →
$ {\infty } $ ; (b), (e) Remag = 1; (c), (f) Remag = 0.5Figure 5. Magnetic response of the oscillating microbubble at ω = 5 (We = 10, a = 2, χm = 1), including (a)−(c) R*-t* plot and corresponding (d)−(f) phase diagram: (a), (d) Remag→
$ {\infty } $ ; (b), (e) Remag = 1; (c), (f) Remag = 0.5.
图 6 ω = 10时振荡微泡的磁响应, 其中包括(a)—(c) R*-t*图及相应(d)—(f)相图(We = 10, a = 2, χm = 1) (a), (d) Remag→
$ {\infty } $ ; (b), (e) Remag = 1; (c), (f) Remag = 0.5Figure 6. Magnetic response of the oscillating microbubble at ω = 10 (We = 10, a = 2, χm = 1), including (a)−(c) R*-t* plot and corresponding (d)−(f) phase diagram: (a), (d) Remag→
$ {\infty } $ ; (b), (e) Remag = 1; (c), (f) Remag = 0.5.
图 7 声压幅值不同时振荡微泡的磁响应R*-t*图 (We = 10, χm = 1) (a)—(c) 磁雷诺数Remag分别为
$ {\infty } $ , 1和0.5; (d)—(f)声压幅值a分别为2, 1和0.5Figure 7. Magnetic response of the oscillating microbubble with different acoustic pressure amplitudes (We = 10, χm = 1): (a)−(c) magnetic Reynolds number Remag is
$ {\infty } $ , 1 and 0.5, respectively; (d)−(f) acoustic pressure a is 2, 1 and 0.5, respectively.
图 8 不同环境条件下微泡的振动响应R*-t*图 (Remag = 0.5)
Figure 8. Vibration response of the microbubble under different environmental conditions (Remag = 0.5)
-
[1] Michalakis A A, Matthew F B, Jeffry E P, Paul S S, Peter N B 2020 Ultrasound Med. Bio. 46 498
Google Scholar
[2] Wischhusen J, Padilla F 2018 IRBM 40 10
Google Scholar
[3] Pysz M A, Foygel K, Rosenberg J, Gambhir S S, Schneider M, Willmann J K 2010 Radiology 256 519
Google Scholar
[4] Bekeredjian R, Grayburn P, Shohet R 2005 Am. Coll. Cardiol. 45 329
Google Scholar
[5] Hernot S, Klibanov A 2008 Adv. Drug Deliv. Rev. 60 1153
Google Scholar
[6] Martin M J, Chung E M L, Goodall A H 2008 J. Vasc. Surg. 47 1371
Google Scholar
[7] Owen J, Pankhurst Q, Stride E 2012 Int. J. Hyperthermia 28 362
Google Scholar
[8] Yvonn H, Staffan H, Alexandra H, Bernhard G, Martina A, Dietmar E, Daniela W, Alexander P, Markus W, Florian K, Ulrich P, Hanna M 2017 Theranostics 7 295
Google Scholar
[9] Iwanaga K, Tominaga K, Yamamoto K, Habu M, Maeda H, Akifusa S, Tsujisawa T, Okinaga T, Fukuda J, Nishihara T 2007 Cancer Gene Ther. 14 354
Google Scholar
[10] Fan C H, Cheng Y H, Ting C Y, Ho Y J, Hsu P H, Liu H L, Yeh C K 2016 Theranostics 6 1542
Google Scholar
[11] de Saint V M, Carugo D, Barnsley L C, Owen J, Coussios C-C, Stride E 2017 Phys. Med. Biol. 62 7451
Google Scholar
[12] Bi F, Zhang J, Su Y J, Chun Y J, Tang Ya, Liu J N 2009 Biomaterials 30 5125
Google Scholar
[13] Mulvana H, Eckersley R J, Tang M X, Pankhurst Q, Stride E 2012 Ultrasound Med. Biol. 38 864
Google Scholar
[14] Yan L P, Miao W, Li D D 2020 J. Nanotechno. 20 6087
Google Scholar
[15] Lind, Steven J 2014 Phys. Fluids 6 26
Google Scholar
[16] Malvar S, Gontijo R G, Cunha F R 2018 J. Eng. Math. 108 143
Google Scholar
[17] Church C C 1995 J. Acoust. Soc. Am. 97 1510
Google Scholar
[18] 赵丽霞, 王成会, 莫润阳 2021 70 014301
Google Scholar
Zhao L X, Wang C H, Mo R Y 2021 Acta Phys. Sin. 70 014301
Google Scholar
[19] Sassaroli E, Hynynen K 2005 Phys. Med. Biol. 50 5293
Google Scholar
[20] Ni B Y, Zhang A M, Wang Q X, Wang B 2012 Acta. Mechanica Sinica. 28 1248
Google Scholar
[21] Fan Y Z, Li H S, Daniel F 2020 Phys. Week 102 013105
Google Scholar
[22] Qin S P, Ferrara K W 2006 Phys. Med. Biol. 51 5065
Google Scholar
[23] Owen J, Rademeyer P, Chung D, Cheng Q, Holroyd D, Coussios C, Friend P, Pankhurst Q A, Stride E 2015 Interface Focus 5 20150001
Google Scholar
[24] Beguin E, Gray M D, Logan K A, Nesbitt H, Sheng Y J, Kamila S, Barnsley L C, Bau L, McHale A P, Callan J F, Stride E 2020 J. Controlled Release 317 23
Google Scholar
[25] Zhang B H, Kim H, Jiang X N 2019 Ultrasonics 98 62
Google Scholar
[26] Droste D W 2008 Eur. Neurol. 1 2
Google Scholar
[27] 莫润阳, 吴临燕, 詹思楠, 张引红 2015 64 124301
Google Scholar
Mo R Y, Wu L Y, Zhan S N, Zhang Y H 2015 Acta Phys. Sin. 64 124301
Google Scholar
[28] Zudin Y B, Isakov N S, Zenin V V 2014 J. Eng. Thermophys. 87 1487
Google Scholar
[29] Stride E 2008 Philos. T. R. Soc. A 366 2103
Google Scholar
[30] Stride E, Porter C, Prieto A G, Pankhurst Q 2009 Ultrasound Med. Biol. 35 861
Google Scholar
[31] 毕勤成, 施东晓, 何永清, 邱晟华 2010 热科学与技术 9 189
Bi Q C, Shi D X, He Y Q, Qiu S H 2010 J. Ther. Sci. Techno. 9 189
[32] 陈杰, 张杰, 莫润阳, 王成会, 胡静 2020 磁性材料及器件 51 9
Chen J, Zhang J, Mo R Y, Wang C H, Hu J 2020 J. Magn. Mater. Device 51 9
[33] Owen J, Grove P, Rademeyer P, Stride E 2014 J. R. Soc. Interface 11 20140622
Google Scholar
[34] Victor M S, Crake C, Coussios C C, Stride E 2014 Expert Opin. Drug Del. 11 87
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3434
- PDF Downloads: 49
- Cited By: 0
