-
Objective With the development of optical technology, the investigation of light-field-particle interactions has gained significant momentum. Such studies find widespread applications in optical manipulation, precision laser ranging, laser gas spectroscopy, and related fields. In optical manipulation techniques, employing two or more laser beams proves more effective for capturing and manipulating particles than using a single beam alone. In addition, with the increasing demand for manipulating particles with complex structures, it is necessary to conduct in-depth research on the radiation force characteristics of double Gaussian beams on non-uniform chiral particles. This research aims to deepen our understanding of how optical fields influence particles, thereby offering fresh perspectives in manipulating and utilizing non-uniform chiral layered particles on both a microscale and a nanoscale. Method Based on the generalized Lorentz-Mie theory (GLMT) and spherical vector wave functions (SVWFs), the total incident field of a double Gaussian beam can be expanded by using the coordinate addition theorem. The incident field coefficient and scattering coefficient of each region of the multilayer chiral sphere are obtained by enforcing boundary continuity and employing multilayer sphere scattering theory. The radiation force acting on non-uniform chiral layered particles within a double Gaussian beam is then derived through application of the electromagnetic momentum conservation theorem. Results and Discussions The theory and programs in this paper is compared with those in existing literature. The influence of various parameters on the radiation force is analyzed in detail, such as the incident angle, polarization angle, beam waist width, beam center position, and internal and external chiral parameters. These results indicate that compared with a single Gaussian beam, counter-propagating Gaussian standing waves exhibit significant advantages in capturing or confining inhomogeneous chiral layered particles, offering enhanced particle manipulation capabilities. Additionally, by selecting an appropriate polarization state of the incident light, a delicate balance can be achieved among these parameters, effectively stabilizing the capture of inhomogeneous chiral particles. Conclusions This study employs the generalized Lorenz-Mie theory and the principle of electromagnetic momentum conservation to derive analytical expressions for the transverse and axial radiation forces exerted by dual Gaussian beams on multi-layered chiral particles propagating in arbitrary directions. The research provides an in-depth analysis of how standing wave beams affect the radiation force behavior of non-uniform chiral particles. Numerical analysis reveals significant influences of beam waist, particle size, chiral parameters, polarization angle and mode, as well as particle refractive index on both transverse and axial radiation forces. This research is important in analyzing and understanding the optical properties of complex-shaped multilayer biological cells and realizing the applications in the micromanipulation of multilayer biological structures. [1] Ashkin A 1970 Phys. Rev. Lett. 24 156
Google Scholar
[2] Ashkin A 1980 Science 210 1081
Google Scholar
[3] Leach J, Howard D, Roberts S, Gibson G, Gothard D, Cooper J, Buttery L 2009 J. Mod. Optic. 56 448
Google Scholar
[4] Molloy J E, Dholakia K, Padgett M J 2003 J. Mod. Optic. 50 1501
Google Scholar
[5] Parlatan U, Başar G, Başar G 2019 J. Mod. Optic. 66 228
Google Scholar
[6] Jordan P, Clare H, Flendrig L, Leach J, Cooper J, Padgett M 2004 J. Mod. Optic. 51 627
Google Scholar
[7] Tang Q, Liu P Z, Tang S 2022 Chin. Phys. B 31 044301
Google Scholar
[8] Barton J P, Alexander D R, Schaub S A 1989 J. Appl. Phys. 66 4594
Google Scholar
[9] Yang A H, Moore S D, Schmidt B S, Klug M, Lipson M, Erickson D 2009 Nature 457 71
Google Scholar
[10] Padgett M, Bowman R 2011 Nat. Photon. 5 343
Google Scholar
[11] Wang Z L, Yin J P 2008 Chin. Phys. B 17 2466
Google Scholar
[12] Kiselev A D, Plutenko D O 2016 Phys. Rev. A 94 013804
Google Scholar
[13] Zang Y C, Lin W J, Su C, Wu P F 2021 Chin. Phys. B 30 044301
Google Scholar
[14] Dong F B, Chang C H, Jun F H, Yi W 2009 Chin. Phys. B 18 2853
Google Scholar
[15] Ng J, Lin Z F, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[16] Liu X Y, Sun C, Deng D M 2021 Chin. Phys. B 30 024202
Google Scholar
[17] 王焱, 彭妙, 程伟, 彭政, 成浩, 臧圣寅, 刘浩, 任孝东, 帅雨贝, 黄承志, 吴加贵, 杨俊波 2023 72 027801
Google Scholar
Wang Y, Peng M, Cheng W, Peng Z, Cheng H, Zang S Y, Liu H, Ren X D, Shuai Y B, Huang C Z, Wu J G, Yang J B 2023 Acta Phys. Sin. 72 027801
Google Scholar
[18] 殷杰, 陶超, 刘晓峻 2015 64 098102
Google Scholar
Yin J, Tao C, Liu X J 2015 Acta Phys. Sin. 64 098102
Google Scholar
[19] Ashkin A, Dziedzic J M 1971 Appl. Phys. Lett. 19 283
Google Scholar
[20] Zemánek P, Jonáš A, Šrámek L, Liška M 1998 Opt. Commun. 151 273
Google Scholar
[21] Zemánek P, Jonáš A, Liška M 2002 J. Opt. Soc. Am. A 19 1025
Google Scholar
[22] Gauthier R C, Frangioudakis A 2000 Appl. Opt. 39 26
Google Scholar
[23] Ren K F, Greha G, Gouesbet G 1994 Opt. Commun. 108 343
Google Scholar
[24] Gouesbet G, Lock J A 1994 J. Opt. Soc. Am. A 11 2516
Google Scholar
[25] Zemánek P, Jonáš A, Jákl P, Šerý M, Liška M 2003 Opt. Commun. 220 401
Google Scholar
[26] Cizmar T, Garces-Chavez V, Dholakia K, Zemanek P 2004 Opt. Trap. Micro. 5514 643
Google Scholar
[27] Van der Horst A, van Oostrum P D J, Moroz A, van Blaaderen A, Dogterom M 2008 Appl. Opt. 47 3196
Google Scholar
[28] Zhao L, Li Y, Qi J, Xu J, Sun Q 2010 Opt. Express 18 5724
Google Scholar
[29] Zhang T, Mahdy M R C, Dewan S S, Hossain M N, Rivy H M, Masud N, Jony Z R 2018 arXiv: 1811.01874 [physics. optics]
[30] Li Z J, Li S, Li H Y, Qu T, Shang Q C 2021 J. Opt. Soc. Am. A 38 616
Google Scholar
[31] Wang S L, Liu X, Mourdikoudis S, Chen J, Fu W W, Sofer Z, Zhang Y, Zhang S P, Zheng G C 2022 ACS Nano. 16 19789
Google Scholar
[32] 马晓亮, 李雄, 郭迎辉, 赵泽宇, 罗先刚 2017 66 147802
Google Scholar
Ma X L, Li X, Guo Y H, Zhao Z Y, Luo X G 2017 Acta Phys. Sin. 66 147802
Google Scholar
[33] Rohrbach A, Stelzer E H K 2001 J. Opt. Soc. Am. A 18 839
Google Scholar
[34] 史书姝, 肖姗, 许秀来 2022 71 067801
Google Scholar
Shi S S, Xiao S, Xu X L 2022 Acta Phys. Sin. 71 067801
Google Scholar
[35] 王志全, 施卫 2022 71 188704
Google Scholar
Wang Z Q, Shi W 2022 Acta Phys. Sin. 71 188704
Google Scholar
[36] Habashi A, Ghobadi C, Nourinia J, R Naderali 2023 Opt. Commun. 547 129840
Google Scholar
[37] 米利, 周宏伟, 孙祉伟, 刘丽霞, 徐升华 2013 62 134704
Google Scholar
Mi L, Zhou H W, Sun Z W, Liu L X, Xu S H 2013 Acta Phys. Sin. 62 134704
Google Scholar
[38] Worasawate D, Mautz J R, Arvas E 2003 IEEE Trans. Antennas Propag. 51 1077
Google Scholar
[39] Yuceer M, Mautz J R, Arvas E 2005 IEEE Trans. Antennas Propag. 53 1163
Google Scholar
[40] Demir V, Elsherbeni A Z, Arvas E 2005 IEEE Trans. Antennas Propag. 53 3374
Google Scholar
[41] Kuzu L, Demir V, Elsherbeni A Z, Arvas E 2007 Prog. Electromagn. Res. 67 1
Google Scholar
[42] Cooray M F R, Ciric I R 1993 J. Opt. Soc. Am. A 10 1197
Google Scholar
[43] Ermutlu M E, Sihvola A H 1994 Prog. Electromagn. Res. 9 87
Google Scholar
[44] Jaggard D L, Liu J C 1999 IEEE Trans. Antennas Propag. 47 1201
Google Scholar
[45] Yan B, Liu C H, Zhang H Y, Shi Y 2015 Opt. Commun. 338 261
Google Scholar
[46] Wang W J, Sun Y F, Zhang H Y 2017 Opt. Commun. 385 54
Google Scholar
[47] Gao X, Zhang H 2017 Optik 129 43
Google Scholar
[48] Zheng M, Zhang H Y, Sun Y F, Wang Z G 2015 J. Quant. Spectrosc. Ra. 151 192
Google Scholar
[49] Li L W, Dan Y, Leong M S, Kong J A 1999 Prog. Electromagn. Res. 23 239
Google Scholar
[50] Shang Q C, Wu Z S, Qu T, Li Z J, Bai L 2016 J. Quant. Spectrosc. Ra. 173 72
Google Scholar
[51] Qu T, Wu Z S, Shang Q C, Wu J, Bai L 2018 J. Quant. Spectrosc. Ra. 217 363
Google Scholar
[52] Bai J, Liu X, Ge C X, Li Z J, Xiao C, Wu Z S, Shang Q C 2024 Opt. Commun. 554 130136
Google Scholar
[53] Edmonds A R, Mendlowitz H 1958 Phys. Today 11 34
Google Scholar
[54] Gouesbet G, Gréhan G 1999 J Opt. A-Pure. Appl. Opt. 1 706
Google Scholar
[55] Geng Y L, Wu X B, Li L W, Guan B R 2004 Phys. Rev. E 70 056609
Google Scholar
[56] Lock J A, Gouesbet G 1994 J. Opt. Soc. Am. A 11 2503
Google Scholar
[57] Gouesbet G, Gréhan G, Maheu B 1990 J. Opt. Soc. Am. A 7 998
Google Scholar
[58] Doicu A, Wriedt T 1997 Appl. Opt. 36 2971
Google Scholar
[59] Brown A J 2014 J. Opt. Soc. Am. A 31 2789
Google Scholar
[60] Edmonds A R 1957 Angular Momentum in Quantum Mechanics (Princeton: Princeton University Press) pp24−37
[61] Lakhtakia A 1994 Beltrami Fields in Chiral Media (World Scientific Pub. Co. Inc. ) pp5−26
[62] Sarkar D, Halas N J 1997 Phys. Rev. E 56 1102
Google Scholar
[63] Aden A L, Kerker M 1951 J. Appl. Phys. 22 1242
Google Scholar
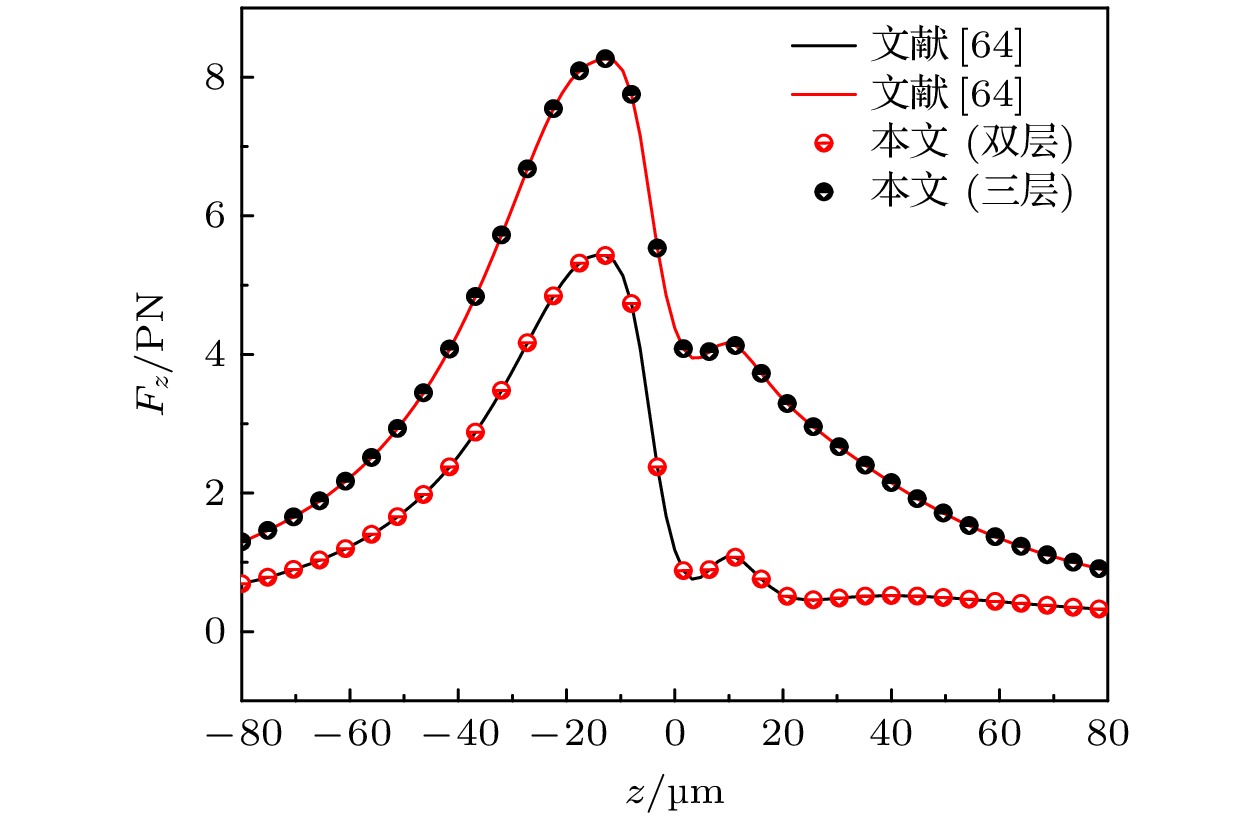
[64] Shang Q C, Wu Z S, Qu T, Li Z J, Bai L 2013 Opt. Express 21 8677
Google Scholar
-
图 1 两束高斯波束照射多层手性粒子示意图
Figure 1. Structure plan of nonuniform chiral layered particles irradiated by DGBS
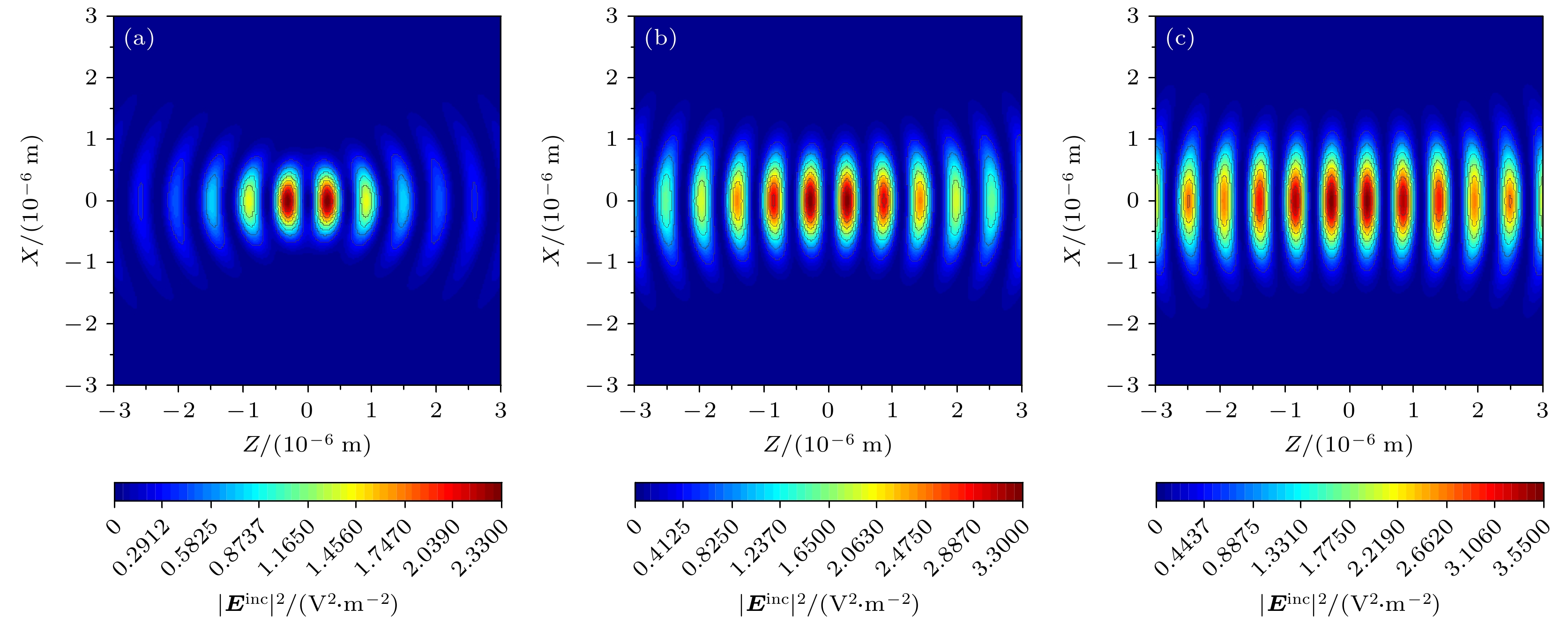
图 2 具有相同偏振角的反向传播双高斯波束$zox$平面强度分布图 (a)${w_{01}}\ ( {w_{02}} ) = 1.7\lambda $; (b)${w_{01}} ({w_{02}}) = 1.8\lambda $; (c) ${w_{01}}({w_{02}}) = 1.9\lambda $
Figure 2. Intensity distribution of counter propagating DGBs in $zox$ plane with different $ {w_1},\; {w_2} $: (a) ${w_{01}}({w_{02}}) = 1.7\lambda $; (b) ${w_{01}}({w_{02}}) = 1.8\lambda $; (c) ${w_{01}}({w_{02}}) = 1.9\lambda $.
图 3 与图2相比具有不同偏振角的反向传播双高斯波束$zox$平面强度分布图 (a)${w_{01}}({w_{02}}) = 1.7\lambda $; (b)${w_{01}}({w_{02}}) = 1.8\lambda $; (c) ${w_{01}}({w_{02}}) = 1.9\lambda $
Figure 3. Intensity distribution of counter propagating DGBs in $zox$ plane with different ${\beta _1}$, ${\beta _2}$ compared with Fig. 2: (a) ${w_{01}}({w_{02}}) = 1.7\lambda $; (b) ${w_{01}}({w_{02}}) = 1.8\lambda $; (c) ${w_{01}}({w_{02}}) = 1.9\lambda $.
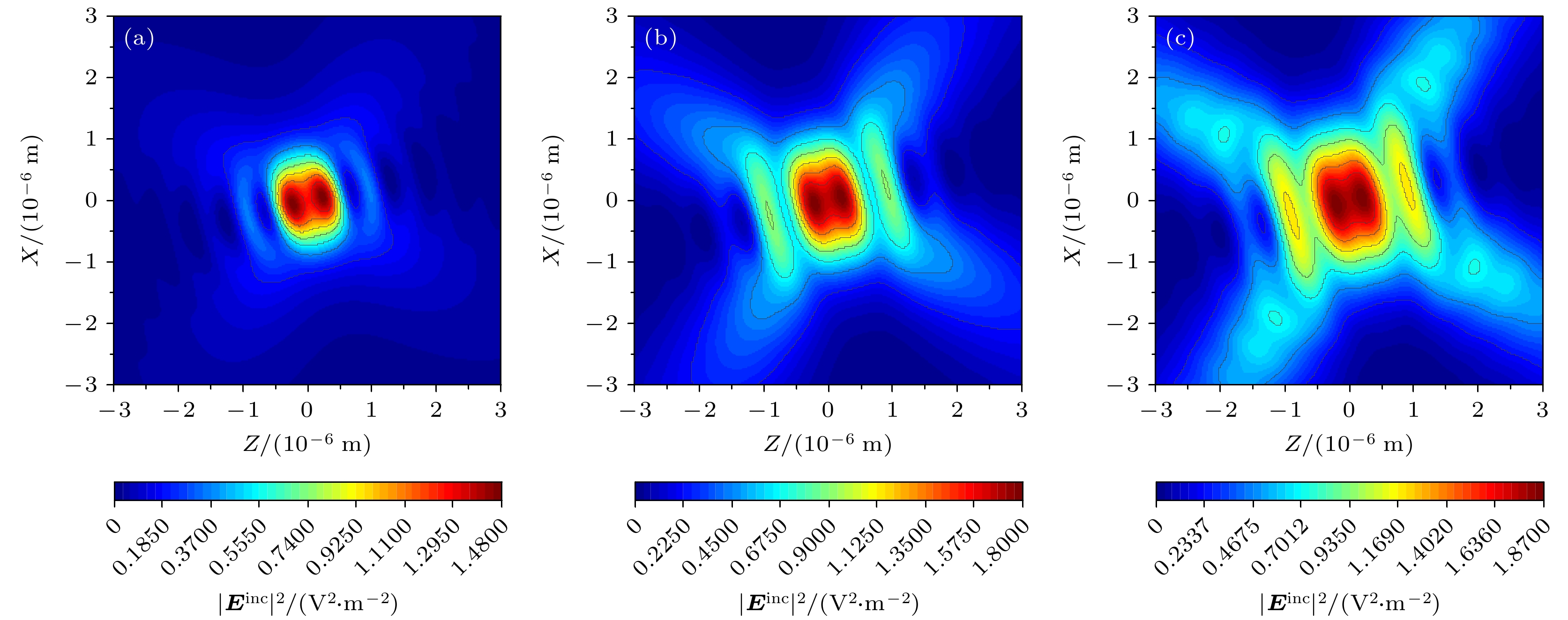
图 4 与图2相比具有不同入射角度的双高斯波束$zox$平面强度分布图 (a) ${w_{01}}({w_{02}}) = 1.7\lambda $; (b)${w_{01}}({w_{02}}) = 1.8\lambda $; (c)${w_{01}}({w_{02}}) = 1.9\lambda $
Figure 4. Intensity distribution of counter propagating DGBs in $zox$ plane with different ${\alpha _1},\; {\alpha _2}$ compared with Fig. 2: (a) ${w_{01}}({w_{02}}) = 1.7\lambda $; (b) ${w_{01}}({w_{02}}) = 1.8\lambda $; (c) ${w_{01}}({w_{02}}) = 1.9\lambda $.
图 5 多层手性粒子对单高斯光束轴向辐射力与文献结果进行对比
Figure 5. Comparison of radiative force results for multilayer chiral spherical particles with a single Gaussian beam.
图 6 双高斯波束对各向同性介质球的轴向辐射力
Figure 6. Axial radiation force of DGBS on isotropic particle.
图 7 不同束腰半径下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$;(b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$
Figure 7. Radiative force of DGBS in different girdle radii on double-layer chiral sphere: (a) z-axis radiative force ${F_z}$; (b) x-axis radiative force ${F_x}$; (c) y-axis radiative force ${F_y}$.
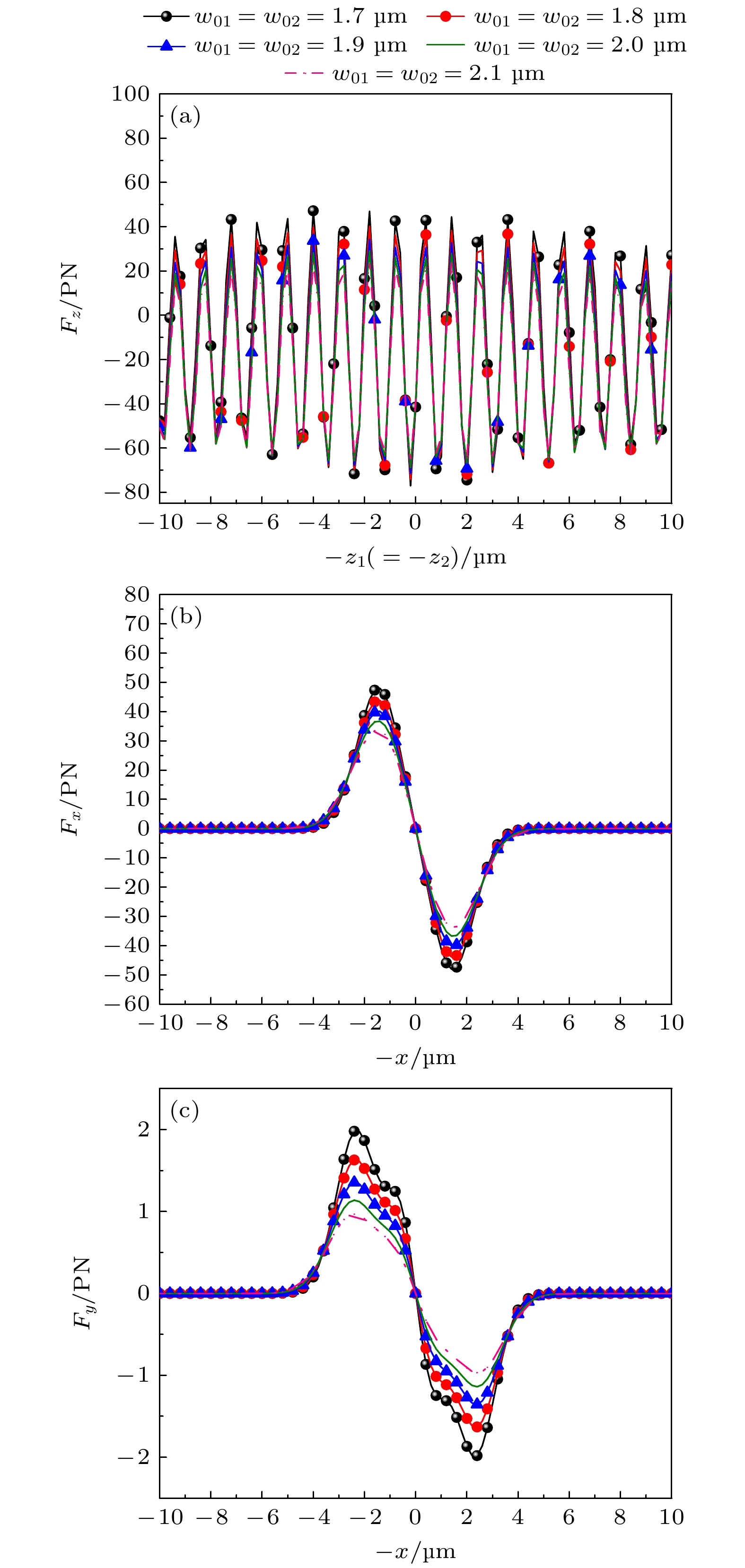
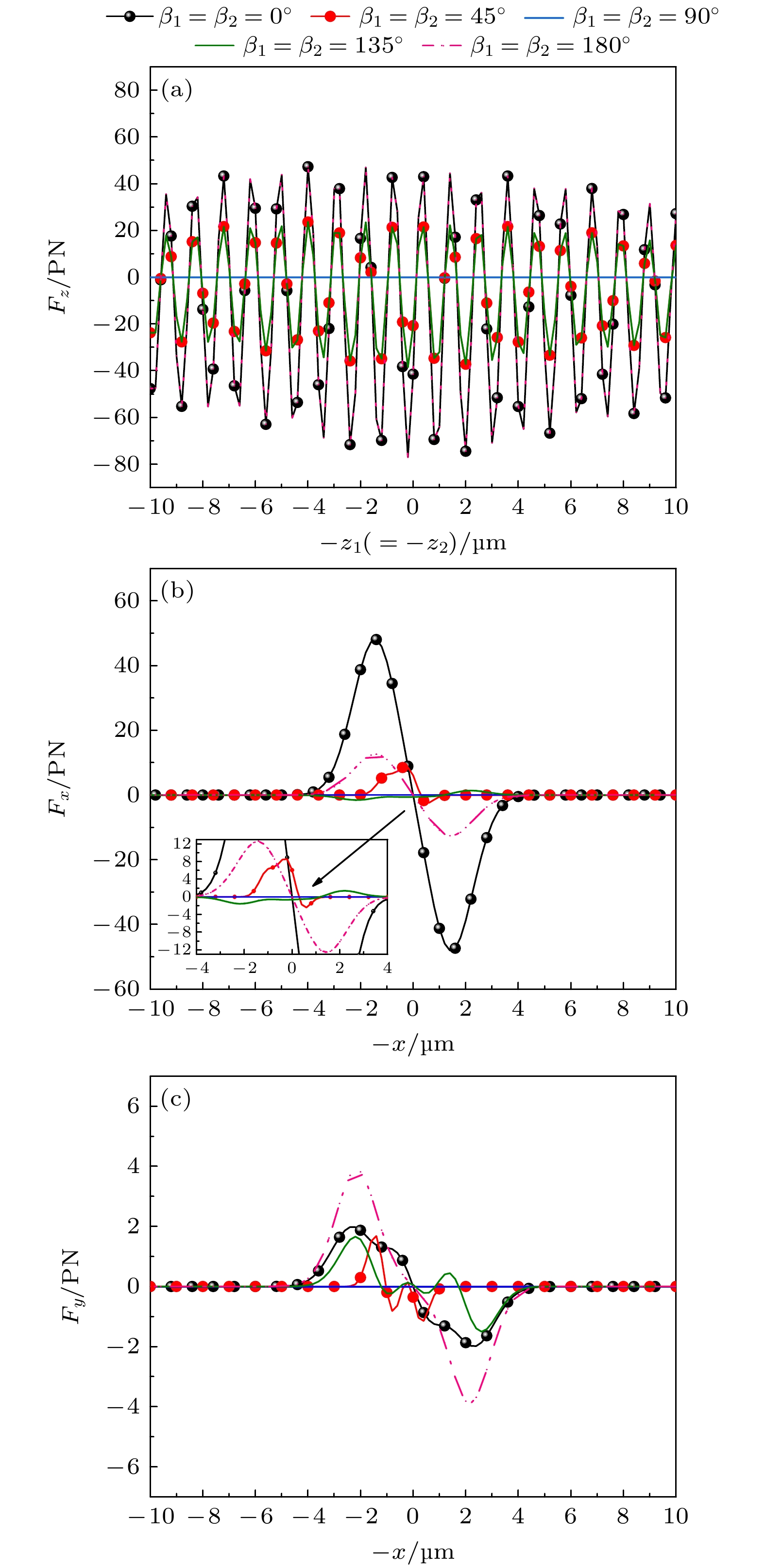
图 8 不同偏振角下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$;(b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$
Figure 8. Radiative force of DGBS in different polarization angles on double-layer chiral sphere; (a) Radiative force along the z-axis ${F_z}$; (b) radiative force along the x-axis ${F_x}$; (c) radiative force along the y-axis ${F_y}$.
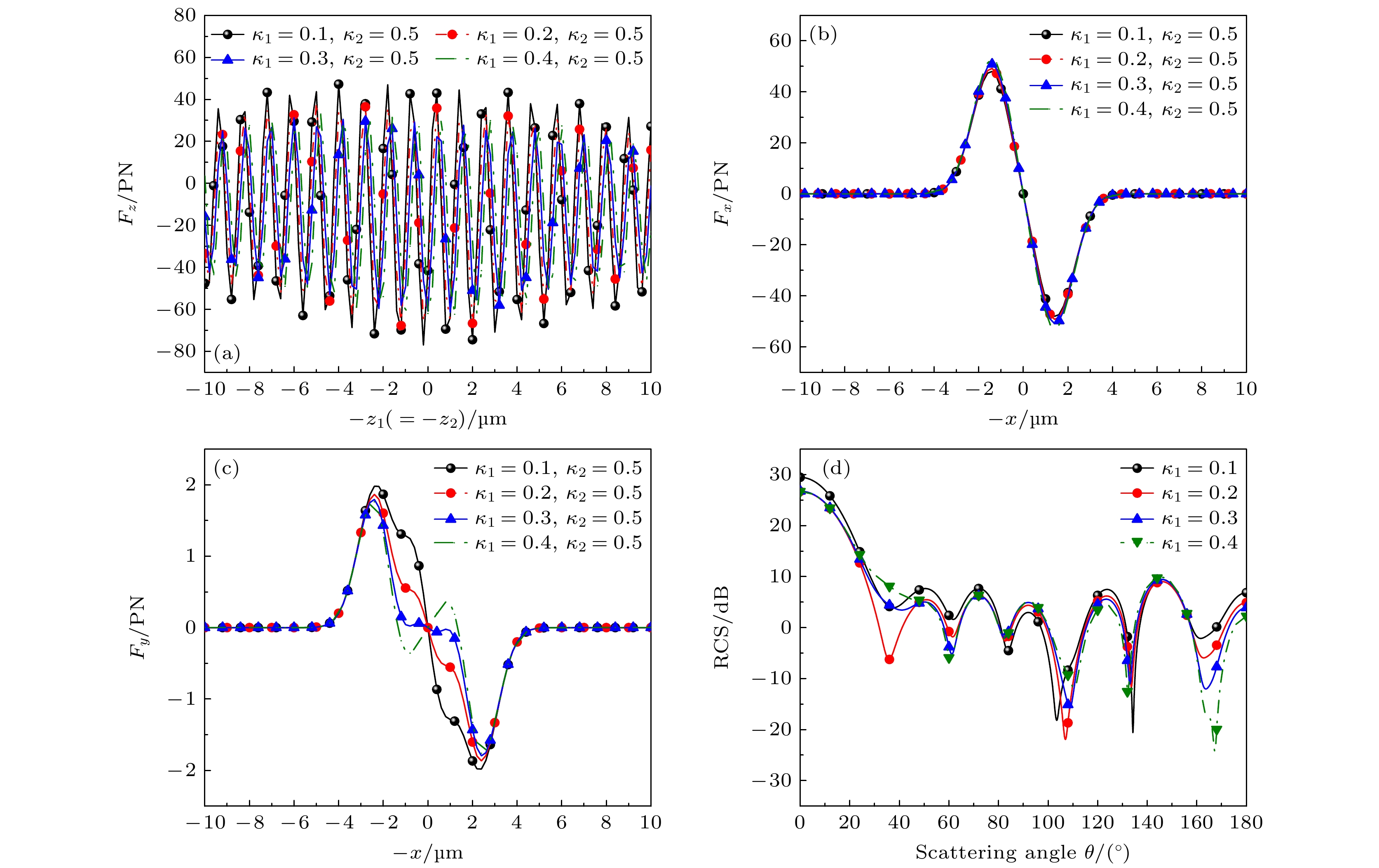
图 9 不同内层手性下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$; (b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$; (d)双高斯波束对双层手性球远场散射RCS
Figure 9. Radiative force of DGBS in different inner layer chiral on double-layer chiral sphere: (a) z-axis radiative force ${F_z}$; (b) x-axis radiative force ${F_x}$; (c) y-axis radiative force ${F_y}$; (d) the RCS of dual Gaussian beams scattering double-layer chiral sphere.
图 10 不同外层手性下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$; (b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$
Figure 10. Radiative force of DGBS in different outer layer chiral on double-layer chiral sphere: (a) z-axis radiative force ${F_z}$; (b) x-axis radiative force ${F_x}$; (c) y-axis radiative force ${F_y}$.
图 11 不同球内层半径下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$; (b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$
Figure 11. Radiative force of DGBS in different radii of the inner layers on double-layer chiral sphere: (a) z-axis radiative force ${F_z}$; (b) x-axis radiative force ${F_x}$; (c) y-axis radiative force ${F_y}$.
图 12 不同球外层半径下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$; (b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$
Figure 12. Radiative force of DGBS in different radii of the outer layers on double-layer chiral sphere: (a) z-axis radiative force ${F_z}$; (b) x-axis radiative force ${F_x}$; (c) y-axis radiative force ${F_y}$.
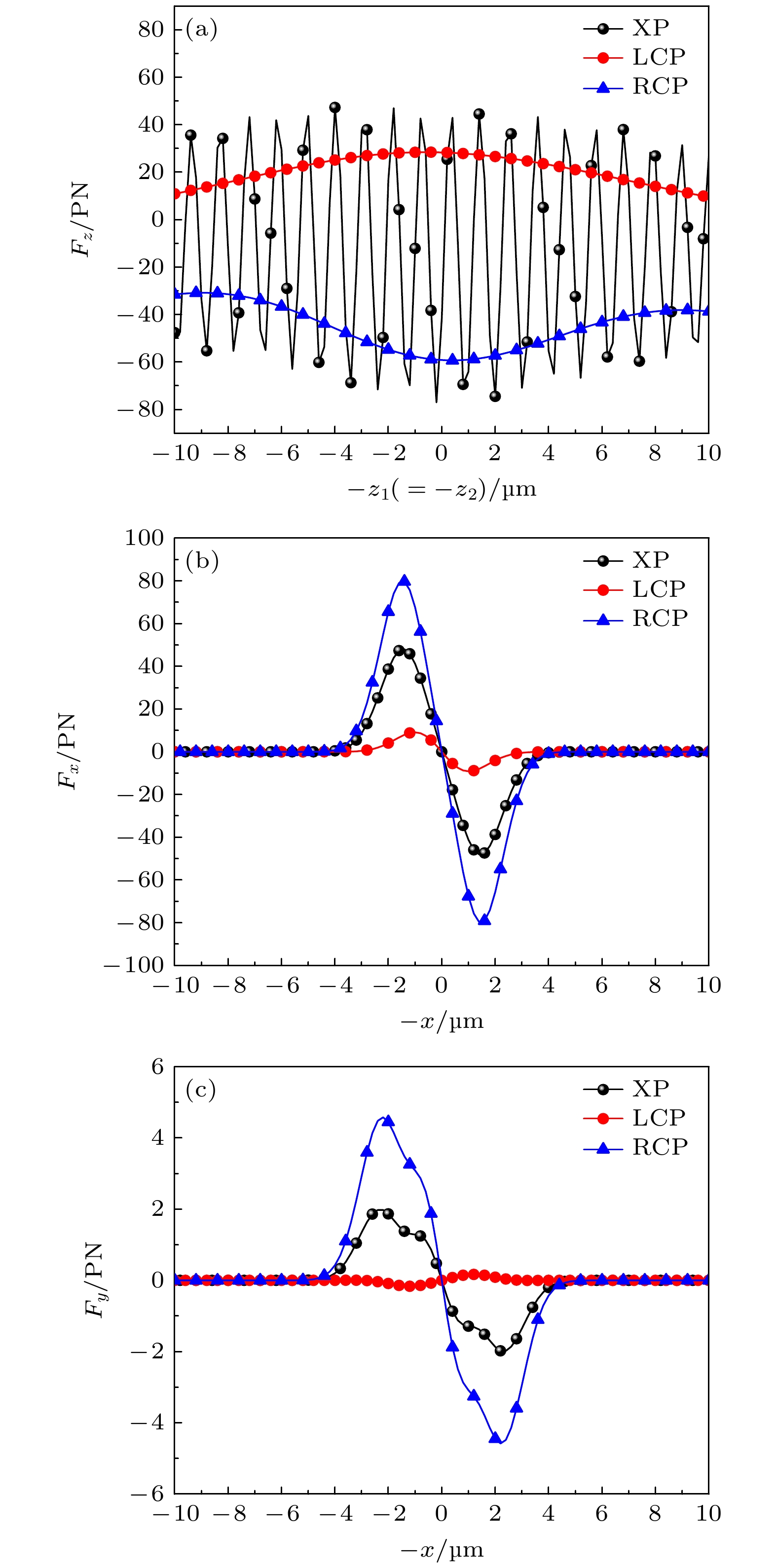
图 13 不同偏振状态下, 双高斯波束入射双层手性球的辐射力随轴(横)向位置的变化曲线 (a)沿z轴辐射力${F_z}$; (b)沿x轴辐射力${F_x}$; (c)沿y轴辐射力${F_y}$
Figure 13. Radiative force of DGBS in different polarization states on double-layer chiral sphere: (a) z-axis radiative force ${F_z}$; (b) x-axis radiative force ${F_x}$; (c) y-axis radiative force ${F_y}$.
图 14 折射率由内向外逐层减小时, 辐射力随轴向位置变化曲线
Figure 14. Curves of radiative force when refractive index decreases layer by layer from inside to outside.
图 15 折射率由内向外逐层增大时, 辐射力随轴向位置变化曲线
Figure 15. Curves of radiative force when refractive index increases layer by layer from inside to outside.
-
[1] Ashkin A 1970 Phys. Rev. Lett. 24 156
Google Scholar
[2] Ashkin A 1980 Science 210 1081
Google Scholar
[3] Leach J, Howard D, Roberts S, Gibson G, Gothard D, Cooper J, Buttery L 2009 J. Mod. Optic. 56 448
Google Scholar
[4] Molloy J E, Dholakia K, Padgett M J 2003 J. Mod. Optic. 50 1501
Google Scholar
[5] Parlatan U, Başar G, Başar G 2019 J. Mod. Optic. 66 228
Google Scholar
[6] Jordan P, Clare H, Flendrig L, Leach J, Cooper J, Padgett M 2004 J. Mod. Optic. 51 627
Google Scholar
[7] Tang Q, Liu P Z, Tang S 2022 Chin. Phys. B 31 044301
Google Scholar
[8] Barton J P, Alexander D R, Schaub S A 1989 J. Appl. Phys. 66 4594
Google Scholar
[9] Yang A H, Moore S D, Schmidt B S, Klug M, Lipson M, Erickson D 2009 Nature 457 71
Google Scholar
[10] Padgett M, Bowman R 2011 Nat. Photon. 5 343
Google Scholar
[11] Wang Z L, Yin J P 2008 Chin. Phys. B 17 2466
Google Scholar
[12] Kiselev A D, Plutenko D O 2016 Phys. Rev. A 94 013804
Google Scholar
[13] Zang Y C, Lin W J, Su C, Wu P F 2021 Chin. Phys. B 30 044301
Google Scholar
[14] Dong F B, Chang C H, Jun F H, Yi W 2009 Chin. Phys. B 18 2853
Google Scholar
[15] Ng J, Lin Z F, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[16] Liu X Y, Sun C, Deng D M 2021 Chin. Phys. B 30 024202
Google Scholar
[17] 王焱, 彭妙, 程伟, 彭政, 成浩, 臧圣寅, 刘浩, 任孝东, 帅雨贝, 黄承志, 吴加贵, 杨俊波 2023 72 027801
Google Scholar
Wang Y, Peng M, Cheng W, Peng Z, Cheng H, Zang S Y, Liu H, Ren X D, Shuai Y B, Huang C Z, Wu J G, Yang J B 2023 Acta Phys. Sin. 72 027801
Google Scholar
[18] 殷杰, 陶超, 刘晓峻 2015 64 098102
Google Scholar
Yin J, Tao C, Liu X J 2015 Acta Phys. Sin. 64 098102
Google Scholar
[19] Ashkin A, Dziedzic J M 1971 Appl. Phys. Lett. 19 283
Google Scholar
[20] Zemánek P, Jonáš A, Šrámek L, Liška M 1998 Opt. Commun. 151 273
Google Scholar
[21] Zemánek P, Jonáš A, Liška M 2002 J. Opt. Soc. Am. A 19 1025
Google Scholar
[22] Gauthier R C, Frangioudakis A 2000 Appl. Opt. 39 26
Google Scholar
[23] Ren K F, Greha G, Gouesbet G 1994 Opt. Commun. 108 343
Google Scholar
[24] Gouesbet G, Lock J A 1994 J. Opt. Soc. Am. A 11 2516
Google Scholar
[25] Zemánek P, Jonáš A, Jákl P, Šerý M, Liška M 2003 Opt. Commun. 220 401
Google Scholar
[26] Cizmar T, Garces-Chavez V, Dholakia K, Zemanek P 2004 Opt. Trap. Micro. 5514 643
Google Scholar
[27] Van der Horst A, van Oostrum P D J, Moroz A, van Blaaderen A, Dogterom M 2008 Appl. Opt. 47 3196
Google Scholar
[28] Zhao L, Li Y, Qi J, Xu J, Sun Q 2010 Opt. Express 18 5724
Google Scholar
[29] Zhang T, Mahdy M R C, Dewan S S, Hossain M N, Rivy H M, Masud N, Jony Z R 2018 arXiv: 1811.01874 [physics. optics]
[30] Li Z J, Li S, Li H Y, Qu T, Shang Q C 2021 J. Opt. Soc. Am. A 38 616
Google Scholar
[31] Wang S L, Liu X, Mourdikoudis S, Chen J, Fu W W, Sofer Z, Zhang Y, Zhang S P, Zheng G C 2022 ACS Nano. 16 19789
Google Scholar
[32] 马晓亮, 李雄, 郭迎辉, 赵泽宇, 罗先刚 2017 66 147802
Google Scholar
Ma X L, Li X, Guo Y H, Zhao Z Y, Luo X G 2017 Acta Phys. Sin. 66 147802
Google Scholar
[33] Rohrbach A, Stelzer E H K 2001 J. Opt. Soc. Am. A 18 839
Google Scholar
[34] 史书姝, 肖姗, 许秀来 2022 71 067801
Google Scholar
Shi S S, Xiao S, Xu X L 2022 Acta Phys. Sin. 71 067801
Google Scholar
[35] 王志全, 施卫 2022 71 188704
Google Scholar
Wang Z Q, Shi W 2022 Acta Phys. Sin. 71 188704
Google Scholar
[36] Habashi A, Ghobadi C, Nourinia J, R Naderali 2023 Opt. Commun. 547 129840
Google Scholar
[37] 米利, 周宏伟, 孙祉伟, 刘丽霞, 徐升华 2013 62 134704
Google Scholar
Mi L, Zhou H W, Sun Z W, Liu L X, Xu S H 2013 Acta Phys. Sin. 62 134704
Google Scholar
[38] Worasawate D, Mautz J R, Arvas E 2003 IEEE Trans. Antennas Propag. 51 1077
Google Scholar
[39] Yuceer M, Mautz J R, Arvas E 2005 IEEE Trans. Antennas Propag. 53 1163
Google Scholar
[40] Demir V, Elsherbeni A Z, Arvas E 2005 IEEE Trans. Antennas Propag. 53 3374
Google Scholar
[41] Kuzu L, Demir V, Elsherbeni A Z, Arvas E 2007 Prog. Electromagn. Res. 67 1
Google Scholar
[42] Cooray M F R, Ciric I R 1993 J. Opt. Soc. Am. A 10 1197
Google Scholar
[43] Ermutlu M E, Sihvola A H 1994 Prog. Electromagn. Res. 9 87
Google Scholar
[44] Jaggard D L, Liu J C 1999 IEEE Trans. Antennas Propag. 47 1201
Google Scholar
[45] Yan B, Liu C H, Zhang H Y, Shi Y 2015 Opt. Commun. 338 261
Google Scholar
[46] Wang W J, Sun Y F, Zhang H Y 2017 Opt. Commun. 385 54
Google Scholar
[47] Gao X, Zhang H 2017 Optik 129 43
Google Scholar
[48] Zheng M, Zhang H Y, Sun Y F, Wang Z G 2015 J. Quant. Spectrosc. Ra. 151 192
Google Scholar
[49] Li L W, Dan Y, Leong M S, Kong J A 1999 Prog. Electromagn. Res. 23 239
Google Scholar
[50] Shang Q C, Wu Z S, Qu T, Li Z J, Bai L 2016 J. Quant. Spectrosc. Ra. 173 72
Google Scholar
[51] Qu T, Wu Z S, Shang Q C, Wu J, Bai L 2018 J. Quant. Spectrosc. Ra. 217 363
Google Scholar
[52] Bai J, Liu X, Ge C X, Li Z J, Xiao C, Wu Z S, Shang Q C 2024 Opt. Commun. 554 130136
Google Scholar
[53] Edmonds A R, Mendlowitz H 1958 Phys. Today 11 34
Google Scholar
[54] Gouesbet G, Gréhan G 1999 J Opt. A-Pure. Appl. Opt. 1 706
Google Scholar
[55] Geng Y L, Wu X B, Li L W, Guan B R 2004 Phys. Rev. E 70 056609
Google Scholar
[56] Lock J A, Gouesbet G 1994 J. Opt. Soc. Am. A 11 2503
Google Scholar
[57] Gouesbet G, Gréhan G, Maheu B 1990 J. Opt. Soc. Am. A 7 998
Google Scholar
[58] Doicu A, Wriedt T 1997 Appl. Opt. 36 2971
Google Scholar
[59] Brown A J 2014 J. Opt. Soc. Am. A 31 2789
Google Scholar
[60] Edmonds A R 1957 Angular Momentum in Quantum Mechanics (Princeton: Princeton University Press) pp24−37
[61] Lakhtakia A 1994 Beltrami Fields in Chiral Media (World Scientific Pub. Co. Inc. ) pp5−26
[62] Sarkar D, Halas N J 1997 Phys. Rev. E 56 1102
Google Scholar
[63] Aden A L, Kerker M 1951 J. Appl. Phys. 22 1242
Google Scholar
[64] Shang Q C, Wu Z S, Qu T, Li Z J, Bai L 2013 Opt. Express 21 8677
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 769
- PDF Downloads: 20
- Cited By: 0
