零阶Bessel驻波场中任意粒子声辐射力和力矩的Born近似

臧雨宸; 苏畅; 吴鹏飞; 林伟军

doi:10.7498/aps.71.20212251

摘要

声辐射力和声辐射力矩的计算是实现粒子精准操控的重要基础. 基于经典声散射理论的偏波级数展开法较难直接用于复杂模型的研究, 而纯数值的方法则不利于进行系统的参数化分析. 基于Born近似的基本原理, 推导了低频情况下零阶Bessel驻波场中心任意粒子的声辐射力和力矩表达式. 在此基础上, 以球形粒子、椭球形粒子和柱形粒子为例进行详细地计算, 并考虑声参数的非均匀性对声辐射力和力矩的影响. 仿真结果表明, 在低频范围内Born近似具有很高的精度, 随着频率的增加和粒子与流体的阻抗匹配变差, Born近似的精度逐渐下降. 对于倾斜放置于零阶Bessel驻波场中的椭球形粒子和柱形粒子, 非对称性会导致其受到声辐射力矩的作用. 在粒子尺寸远小于波长的情况下, 声辐射力特性与粒子的具体形状几乎无关, 但声辐射力矩不然. 最后, 引入周围流体的黏滞效应并对声辐射力的表达式进行了修正. 该研究预期可以为生物医学、材料科学等领域利用驻波场声镊子实现微小粒子的精准操控提供一定的理论指导.

关键词:

Abstract

The calculation of acoustic radiation force and acoustic radiation torque is an important basis for the precise manipulation of particles. It is difficult to directly apply the partial-wave series expansion method based on the classical acoustic scattering theory to the study of complicated models, while pure numerical methods are not conducive to the parametric analyses of the system. Based on the basic principle of Born approximation, the expressions of acoustic radiation force and torque acting on an arbitrary particle located in the center of a zero-order Bessel standing wave field are derived at low frequencies. On this basis, the numerical simulations are systematically performed by taking spherical, spheroidal and cylindrical particles as examples. The effects of inhomogeneity on the acoustic radiation force and torque are also investigated. The simulation results show that the Born approximation method has a high accuracy in the low frequency range. As the frequency increases and the impedance matching between the particle and the fluid becomes worse, the accuracy of Born approximation will gradually decrease. An acoustic radiation torque caused by asymmetry will be exerted on spheroidal and cylindrical particles obliquely positioned in a zero-order Bessel standing wave field. When the particle size is much smaller than the wavelength, the acoustic radiation force is nearly independent of the particle shape, but this is not the case for acoustic radiation torque. Finally, viscous effect of the surrounding fluid is introduced and the expression of acoustic radiation force is corrected accordingly. The study is expected to provide a theoretical guide for the precise manipulation of small particles using standing wave acoustic tweezers in biomedicine and material sciences.

Keywords:

作者及机构信息

1.
中国科学院声学研究所, 北京　100190

2.
中国科学院大学, 北京　100049

3.
北京市海洋深部钻探测量工程技术研究中心, 北京　100190

通信作者: 苏畅, suchang@mail.ioa.ac.cn

基金项目: 国家自然科学基金 (批准号: 81527901)、国家重点研发计划 (批准号: 2018YFC0114900)、中国科学院声学研究所自主部署“目标导向”类项目(批准号: MBDX202113)和中国科学院青年创新促进会项目(批准号: 2019024)资助的课题

Authors and contacts

1.
Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China

2.
University of Chinese Academy of Sciences, Beijing 100049, China

3.
Beijing Deep See Drilling Measurement Engineering Technology Research Center, Beijing 100190, China

Corresponding author: Su Chang, suchang@mail.ioa.ac.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 81527901), the National Key R&D Program of China (Grant No. 2018YFC0114900), the Goal-oriented Project Deployed by Institute of Acoustics, Chinese Academy of Sciences, China (Grant No. MBDX202113) and the Youth Innovation Promotion Association, Chinese Academy of Sciences, China (Grant No. 2019024).

文章全文 : translate this paragraph

参考文献

[1]	Wu J R 1991 J. Acoust. Soc. Am. 89 2140 Google Scholar
[2]	Lee J W, Ha K L, Shung K K 2005 J. Acoust. Soc. Am. 117 3273 Google Scholar
[3]	Lee J W, Shung K K 2006 J. Acoust. Soc. Am. 120 1084 Google Scholar
[4]	黄先玉, 蔡飞燕, 李文成, 郑海荣, 何兆剑, 邓科, 赵鹤平 2017 66 044301 Google Scholar Huang X Y, Cai F Y, Li W C, Zheng H R, He Z J, Deng K, Zhao H P 2017 Acta Phys. Sin. 66 044301 Google Scholar
[5]	Ozcelik A, Rufo J, Guo F, Guo Y Y, Li P, Lata J, Huang T J 2018 Nat. Methods. 15 1021 Google Scholar
[6]	Baudoin M, Thomas J L 2020 Annu. Rev. Fluid Mech. 52 205 Google Scholar
[7]	Lierke E G 1996 Acustica 82 220
[8]	Yarin A L, Pfaffenlehner M, Tropea C 1998 J. Fluid Mech. 356 65 Google Scholar
[9]	King L V 1934 Proc. Roya. Soc. London, Ser. A 147 212 Google Scholar
[10]	Awatani J 1953 J. Acous. Soc. Jpn. 9 140
[11]	Yosioka K, Kawasima Y 1955 Acta Acust. United Ac. 5 167
[12]	Hasegawa T, Yosioka K 1969 J. Acoust. Soc. Am. 46 1139 Google Scholar
[13]	Hasegawa T, Watanabe Y 1978 J. Acoust. Soc. Am. 63 1733 Google Scholar
[14]	Hasegawa T 1979 J. Acoust. Soc. Am. 65 32 Google Scholar
[15]	Hasegawa T 1979 J. Acoust. Soc. Am. 65 41 Google Scholar
[16]	Hasegawa T, Saka K, Inoue N, Matsuzawa K 1988 J. Acoust. Soc. Am. 83 1770 Google Scholar
[17]	Silva G T, Lobo T P, Mitri F G 2012 EPL 97 54003 Google Scholar
[18]	Gong Z X, M. Baudoin 2020 J. Acoust. Soc. Am. 148 3131 Google Scholar
[19]	Hasegawa T, Hino Y, Annou A, Noda H, Kato M, Inoue N 1993 J. Acoust. Soc. Am. 93 154 Google Scholar
[20]	Mitri F G 2005 Ultrasonics 43 681 Google Scholar
[21]	Mitri F G 2006 Ultrasonics 44 244 Google Scholar
[22]	Wang Y Y, Yao J, Wu X W, Wu D J, Liu X J 2017 J. Appl. Phys. 122 094902 Google Scholar
[23]	Peng X J, He W, Xin F X, Genin G M, Lu T J 2020 Ultrasonics 108 106205 Google Scholar
[24]	Peng X J, He W, Xin F X, Genin G M, Lu T J 2020 J. Mech. Phys. Solids 145 104134 Google Scholar
[25]	Wu R R, Cheng K X, Liu X Z, Liu J H, Mao Y W, Gong X F, Li Y F 2014 J. Appl. Phys. 116 144903 Google Scholar
[26]	Wang H B, Liu X Z, Gao S, Cui J, Liu J H, He A J, Zhang G T 2018 Chin. Phys. B 27 034302 Google Scholar
[27]	Zang Y C, Lin W J 2020 Results Phys. 16 102847 Google Scholar
[28]	Mitri F G 2020 Chin. Phys. B 29 114302 Google Scholar
[29]	Mitri F G 2021 Chin. Phys. B 30 024302 Google Scholar
[30]	Mitri F G 2006 New J. Phys. 8 138 Google Scholar
[31]	Aglyamov S R, Karpiouk A B, Ilinskii Y A, Zabolotskaya E A, Emelianov S Y 2007 J. Acoust. Soc. Am. 122 1927 Google Scholar
[32]	Nikolaeva A V, Kryzhanovsky M A, Tsysar S A, Kreider, W, Sapozhnikov O A 2015 AIP Conference Proceedings 1685 040009
[33]	Garbin A, Leibacher I, Hahn P, Le Ferrand H, Studart A R, Dual J 2015 J. Acoust. Soc. Am. 138 2759 Google Scholar
[34]	Johnson K A, Vormohr H R, Doinikov A A, Bouakaz A, Shields C W, Lopez G P, Dayton P A 2016 Phys Rev. E 93 053109 Google Scholar
[35]	Qiao Y P, Gong M Y, Wang H B, Lan J, Liu T, Liu J H, Mao Y W, He A J, Liu X Z 2021 Phys. Fluids 33 047107 Google Scholar
[36]	Wijaya F B, Lim K M 2015 Acta Acust. 101 531 Google Scholar
[37]	Glynne-Jones P, Mishra P P, Boltryk R J, Hill M 2013 J. Acoust. Soc. Am. 133 1885 Google Scholar
[38]	Wei W, Thiessen D B, Marston P L 2004 J. Acoust. Soc. Am. 116 201 Google Scholar
[39]	Hasheminejad S M, Sanaei R 2007 J. Comput. Acoust. 15 377 Google Scholar
[40]	Marston P L, Wei W, Thiessen D B 2006 AIP Conf. Proc. 838 495 Google Scholar
[41]	Mitri F G 2016 Ultrasonics 66 27 Google Scholar
[42]	Mitri F G 2015 J. Appl. Phys. 118 214903 Google Scholar
[43]	Mitri F G 2015 Wave Motion 57 231 Google Scholar
[44]	Mitri F G 2015 EPL 112 34002 Google Scholar
[45]	Mitri F G 2017 Ultrasonics 74 62 Google Scholar
[46]	Silva G T, Drinkwater B W 2018 J. Acoust. Soc. Am. 144 EL453 Google Scholar
[47]	Jerome T S, Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2020 J. Acoust. Soc. Am. 148 2403 Google Scholar
[48]	Jerome T S, Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2021 J. Acoust. Soc. Am. 149 2081 Google Scholar
[49]	Marston P L 2006 J. Acoust. Soc. Am. 120 3518 Google Scholar
[50]	Marston P L 2009 J. Acoust. Soc. Am. 125 3539 Google Scholar
[51]	Mitri F G 2008 Ann. Phys. 323 1604 Google Scholar
[52]	Mitri F G 2009 Ultrasonics 49 794 Google Scholar
[53]	Mitri F G 2009 IEEE UFFC 56 1059 Google Scholar
[54]	Mitri F G 2009 J. Phys. A, Math. Theor. 42 245202 Google Scholar
[55]	Mitri F G 2009 Eur. Phys. J. E 28 469 Google Scholar
[56]	Zhang L K, Marston P L 2011 J. Acoust. Soc. Am. 129 1679 Google Scholar
[57]	Zhang L K, Marston P L 2011 Phys. Rev. E 84 065601 Google Scholar
[58]	Zhang L K, Marston P L 2011 J. Acoust. Soc. Am. 129 2381
[59]	Zhang L K 2018 Phys. Rev. Appl. 10 034039 Google Scholar
[60]	Gong Z X, Marston P L 2019 Phys. Rev. Appl. 11 064022 Google Scholar
[61]	Jerome T S, Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2019 J. Acoust. Soc. Am. 145 36 Google Scholar
[62]	Jerome T S, Hamilton M F 2020 Proc. Meet. Acoust. 39 045007
[63]	Jerome T S, Hamilton M F 2021 J. Acoust. Soc. Am. 150 3417 Google Scholar
[64]	Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2012 AIP Conf. Proc. 1474 255
[65]	Sapozhnikov O A, Bailey M R 2013 J. Acoust. Soc. Am. 133 661 Google Scholar
[66]	Ilinskii Yu A, Zabolotskaya E A, Treweek B C, Hamilton M F 2018 J. Acoust. Soc. Am. 144 568 Google Scholar
[67]	Durnin J 1987 J. Opt. Soc. Am. A 4 651 Google Scholar
[68]	Rayleigh L 1884 Philos. Trans. R. Soc. London 175 1
[69]	Landau L D, Lifshitz E M 1993 Fluid Mechanics (2nd Ed.) (Vol. 6) Course of Theoretical Physics (Oxford: Pergamon)
[70]	Settnes M, Bruus H 2012 Phys. Rev. E 85 016327 Google Scholar

施引文献

图 1 倾斜放置于零阶Bessel驻波场中心的任意轴对称粒子

Fig. 1. An arbitrary object with axisymmetric geometry obliquely positioned in a zero-order standing Bessel beam.

下载: 全尺寸图片幻灯片

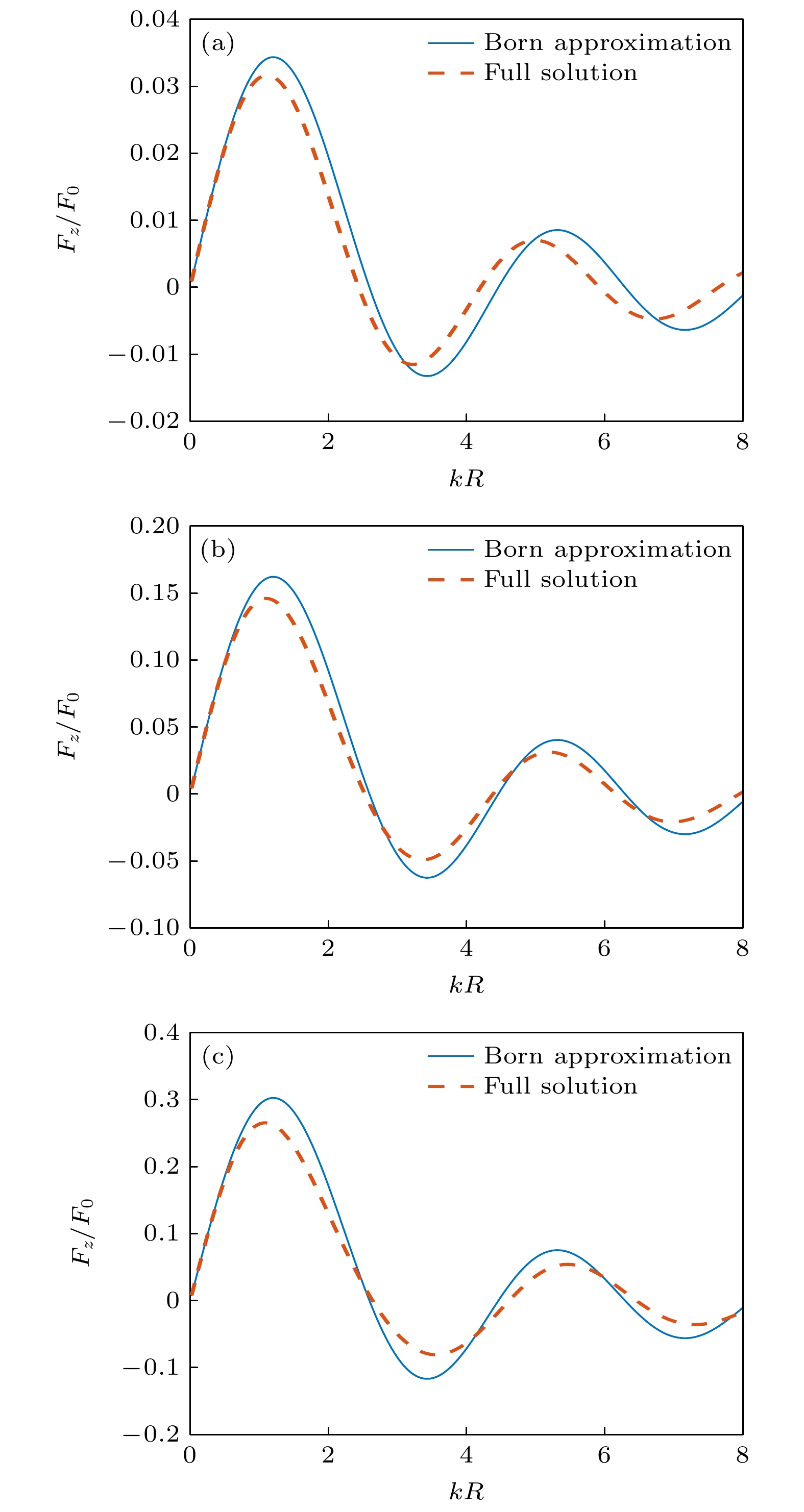
图 2 零阶Bessel驻波场中心均匀球形粒子受到的归一化声辐射力随kR的变化(β = π/6, k_zh = π /4, ρ_m/ρ₀ = 1)　(a) c_m/c₀ = 1.01; (b) c_m/c₀ = 1.05; (c) c_m/c₀ = 1.1

Fig. 2. The dimensionless acoustic radiation force plots for a homogeneous sphere versus kR in a zero-order standing Bessel beam (β = π/6, k_zh = π/4, ρ_m/ρ₀ = 1): (a) c_m/c₀ = 1.01; (b) c_m/c₀ = 1.05; (c) c_m/c₀ = 1.1.

下载: 全尺寸图片幻灯片

图 3 零阶Bessel驻波场中心均匀球形粒子受到的归一化声辐射力随β的变化(kR = 0.5, k_zh = π/4, ρ_m/ρ₀ = 1)

Fig. 3. The dimensionless acoustic radiation force plots for a homogeneous sphere versus β in a zero-order standing Bessel beam (kR = 0.5, k_zh = π/4, ρ_m/ρ₀ = 1).

下载: 全尺寸图片幻灯片

图 4 零阶Bessel驻波场中心非均匀球形粒子受到的归一化声辐射力随kR的变化(f_A = f_C = 0, β = π/6, k_zh = π/4)

Fig. 4. The dimensionless acoustic radiation force plots for an inhomogeneous sphere versus kR in a zero-order standing Bessel beam (f_A = f_C = 0, β = π/6, k_zh = π/4).

下载: 全尺寸图片幻灯片

图 5 零阶Bessel驻波场中心非均匀球形粒子受到的归一化声辐射力随β的变化(f_A = f_C = 0, kR = 0.5, k_zh = π/4)

Fig. 5. The dimensionless acoustic radiation force plots for an inhomogeneous sphere versus β in a zero-order standing Bessel beam (f_A = f_C = 0, kR = 0.5, k_zh = π/4).

下载: 全尺寸图片幻灯片

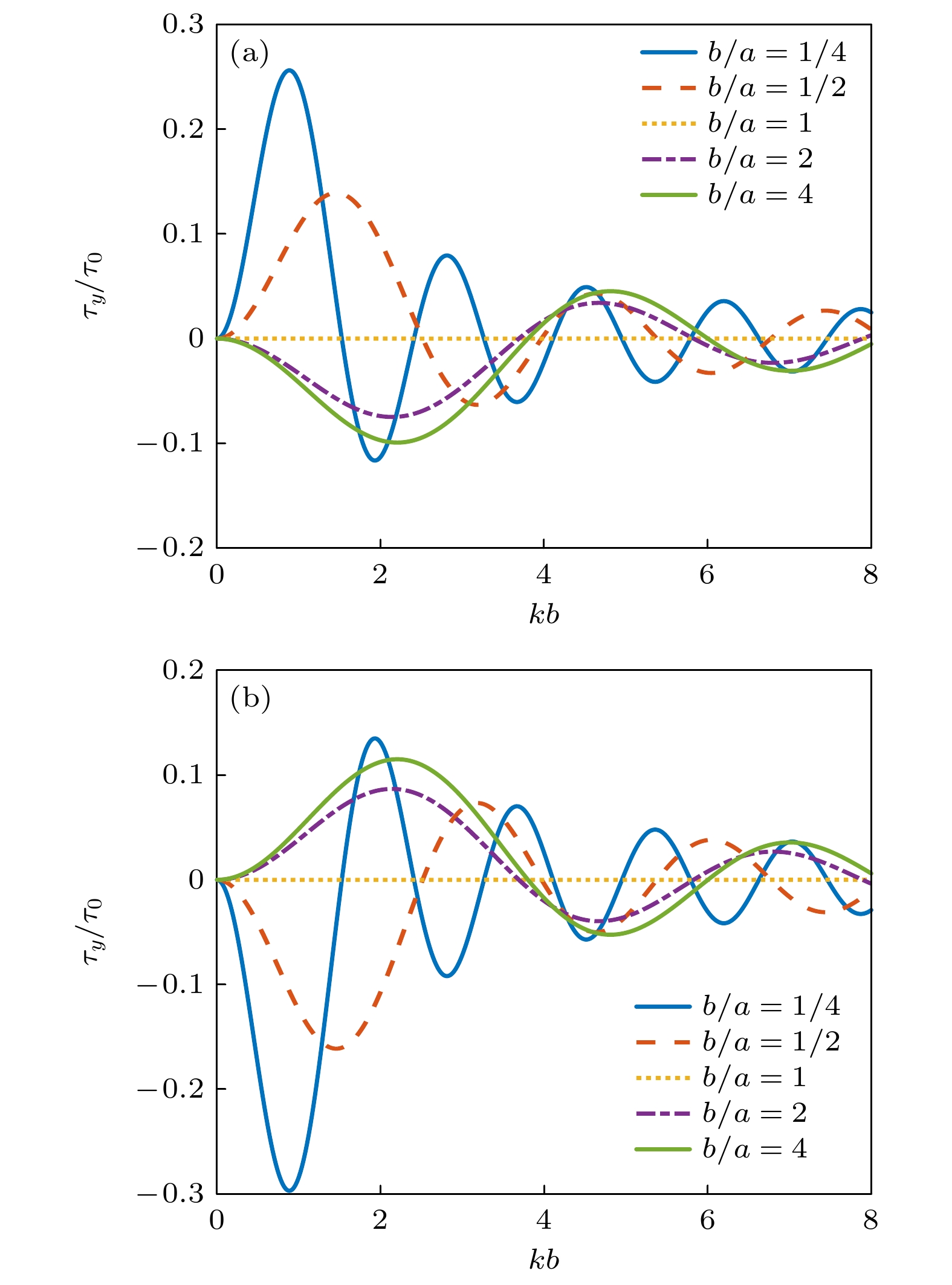
图 6 零阶Bessel驻波场中心均匀椭球形粒子受到的归一化声辐射力和力矩随kb的变化(β = π/6, θ_s = π/6, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05)　(a)归一化声辐射力(k_zh = π/4); (b)归一化声辐射力矩(k_zh = 0)

Fig. 6. The dimensionless acoustic radiation force and torque plots for a homogeneous spheroid versus kb in a zero-order standing Bessel beam (β = π/6, θ_s = π/6, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05): (a) Dimensionless acoustic radiation force (k_zh = π/4); (b) dimensionless acoustic radiation torque (k_zh = 0).

下载: 全尺寸图片幻灯片

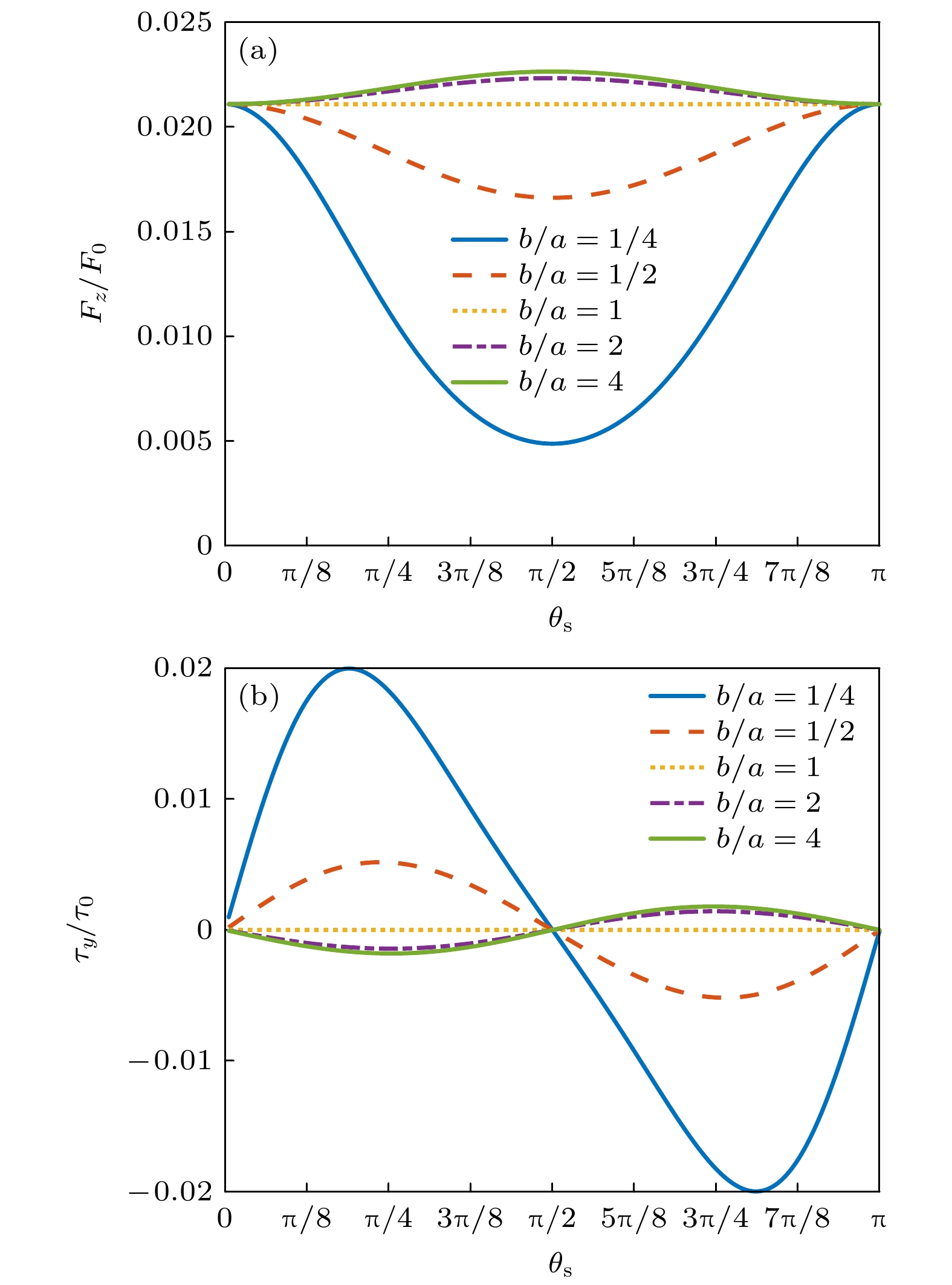
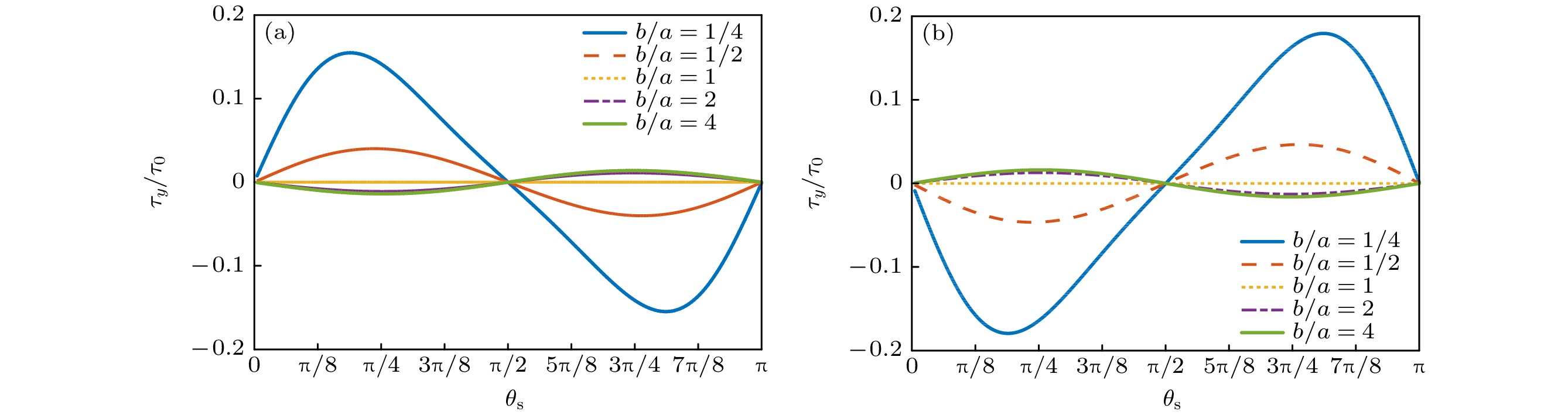
图 7 零阶Bessel驻波场中心均匀椭球形粒子受到的归一化声辐射力和力矩随θ_s的变化(kb = 0.5, β = π/6, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05)　(a)归一化声辐射力(k_zh = π/4); (b)归一化声辐射力矩(k_zh = 0)

Fig. 7. The dimensionless acoustic radiation force and torque plots for a homogeneous spheroid versus θ_s in a zero-order standing Bessel beam (kb = 0.5, β = π/6, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05): (a) Dimensionless acoustic radiation force (k_zh = π/4); (b) dimensionless acoustic radiation torque (k_zh = 0).

下载: 全尺寸图片幻灯片

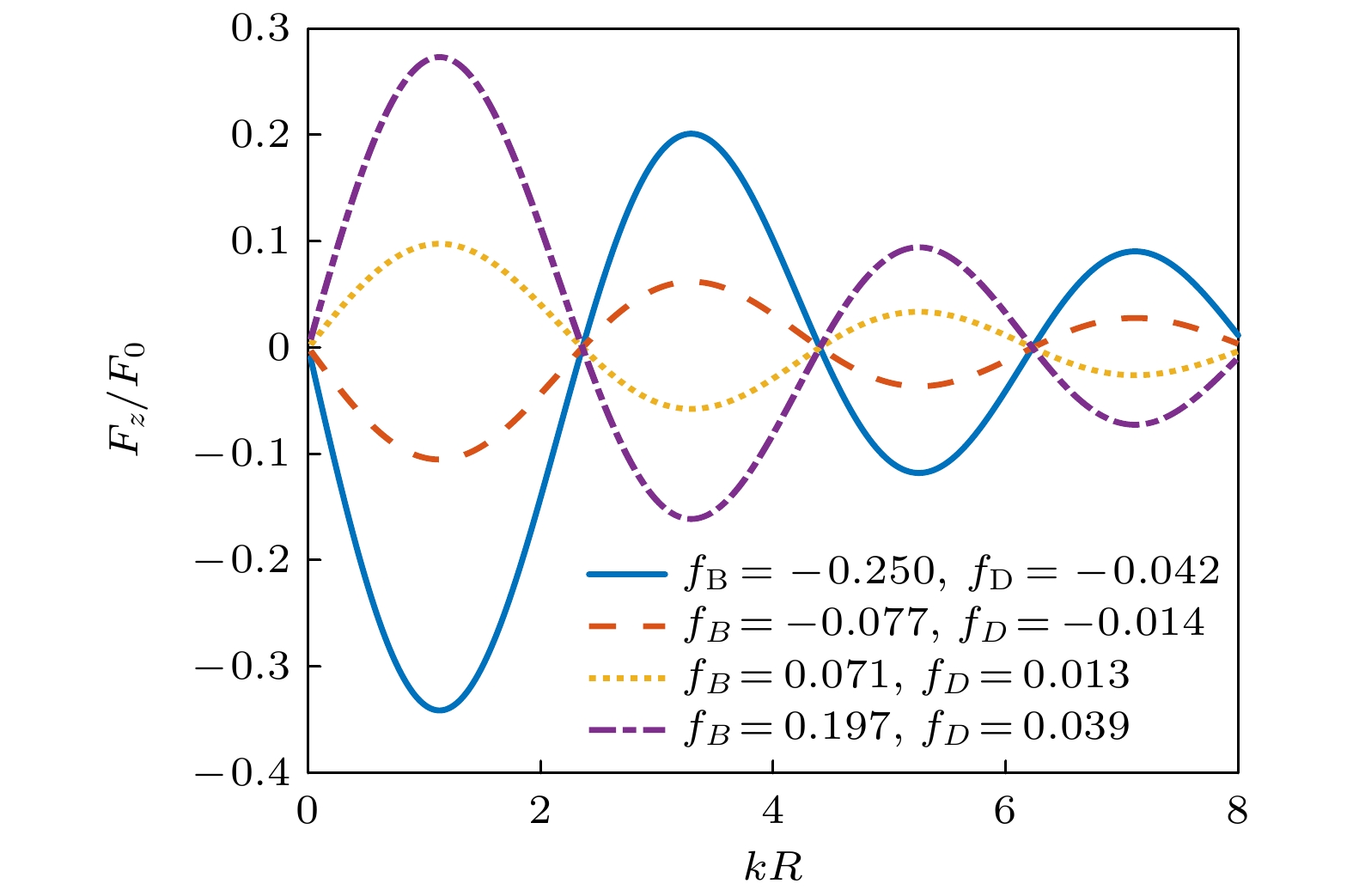
图 8 零阶Bessel驻波场中心非均匀椭球形粒子受到的归一化声辐射力随kb的变化(β = π/6, θ_s = π/6, k_zh = π/4):　(a) f_A = 0.137, f_B = 0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056

Fig. 8. The dimensionless acoustic radiation force plots for an inhomogeneous spheroid versus kb in a zero-order standing Bessel beam (β = π/6, θ_s = π/6, k_zh = π/4): (a) f_A = 0.137, f_B = 0.254, f_C=0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056

下载: 全尺寸图片幻灯片

图 9 零阶Bessel驻波场中心非均匀椭球形粒子受到的归一化声辐射力矩随kb的变化(β = π/6, θ_s = π/6, k_zh = 0)　(a) f_A = 0.137, f_B = 0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056

Fig. 9. The dimensionless acoustic radiation torque plots for an inhomogeneous spheroid versus kb in a zero-order standing Bessel beam (β = π/6, θ_s = π/6, k_zh = 0): (a) f_A = 0.137, f_B = 0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056.

下载: 全尺寸图片幻灯片

图 10 零阶Bessel驻波场中心非均匀椭球形粒子受到的归一化声辐射力随θ_s的变化(kb = 0.5, β = π/6, k_zh = π/4)　(a) f_A = 0.137, f_B = 0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056

Fig. 10. The dimensionless acoustic radiation force plots for an inhomogeneous spheroid versus θ_s in a zero-order standing Bessel beam (kb = 0.5, β = π/6, k_zh = π/4): (a) f_A = 0.137, f_B = 0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056.

下载: 全尺寸图片幻灯片

图 11 零阶Bessel驻波场中心非均匀椭球形粒子受到的归一化声辐射力矩随θ_s的变化(kb = 0.5, β = π/6, k_zh = 0)　(a) f_A = 0.137, f_B = 0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056

Fig. 11. The dimensionless acoustic radiation torque plots for an inhomogeneous spheroid versus θ_s in a zero-order standing Bessel beam (kb = 0.5, β = π/6, k_zh = 0): (a) f_A = 0.137, f_B=0.254, f_C = 0.026, f_D = 0.051; (b) f_A = –0.160, f_B = –0.349, f_C = –0.027, f_D = –0.056.

下载: 全尺寸图片幻灯片

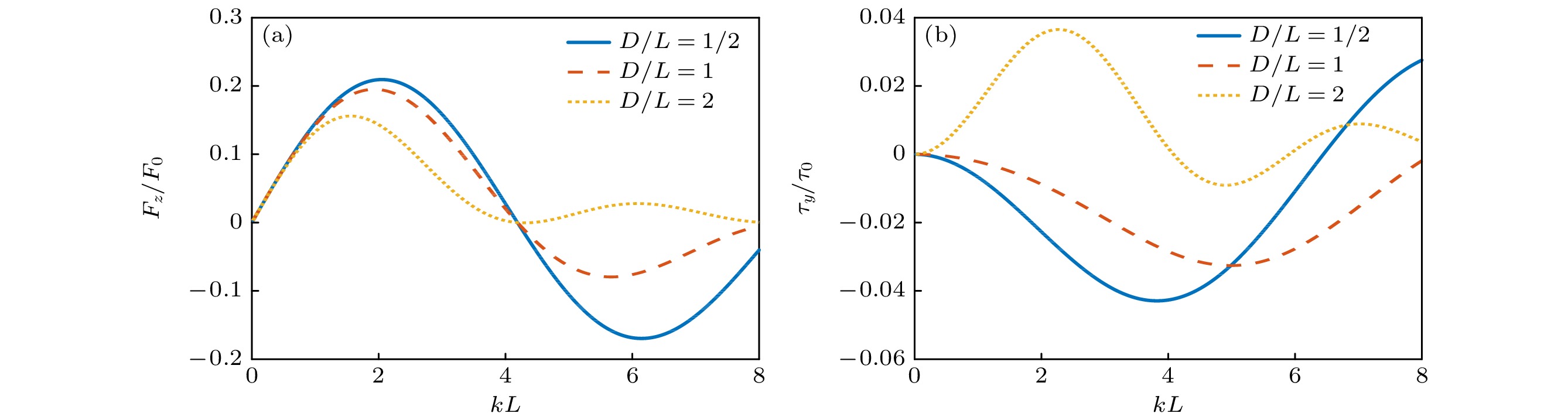
图 12 零阶Bessel驻波场中心均匀柱形粒子受到的归一化声辐射力和力矩随kL的变化(β=π/6, θ_s = π/6, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05)　(a)归一化声辐射力(k_zh = π/4); (b)归一化声辐射力矩(k_zh = 0)

Fig. 12. The dimensionless acoustic radiation force and torque plots for a homogeneous cylinder versus kL in a zero-order standing Bessel beam (β = π/6, θ_s = π/6, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05): (a) Dimensionless acoustic radiation force (k_zh = π/4); (b) dimensionless acoustic radiation torque (k_zh = 0).

下载: 全尺寸图片幻灯片

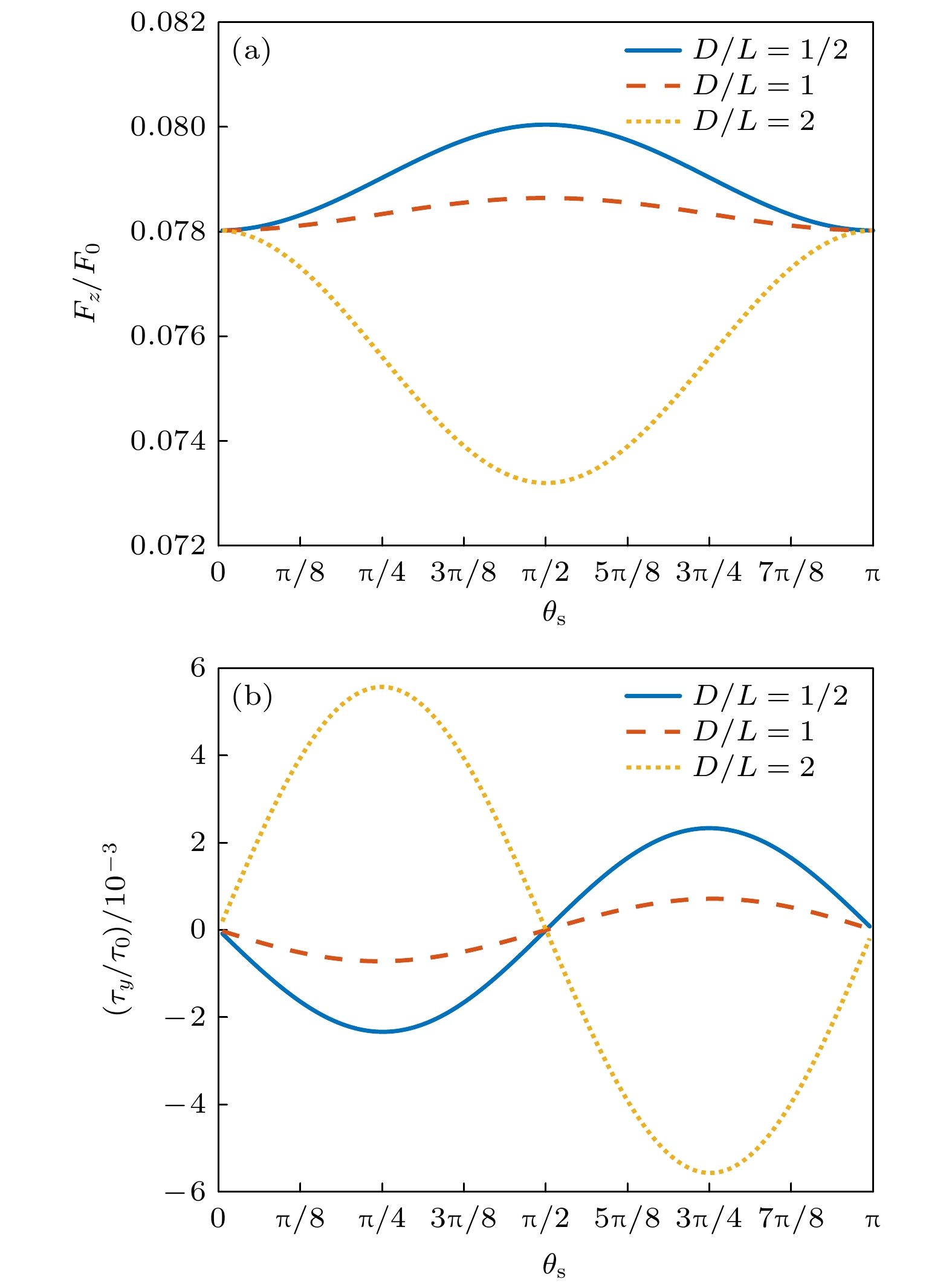
图 13 零阶Bessel驻波场中心均匀柱形粒子受到的归一化声辐射力和力矩随θ_s的变化(β = π/6, kL = 0.5, ρ_m/ρ₀ = 1, c_m/c₀ = 1.05)　(a)归一化声辐射力(k_zh = π/4); (b)归一化声辐射力矩(k_zh = 0)

Fig. 13. The dimensionless acoustic radiation force and torque plots for a homogeneous cylinder versus θ_s in a zero-order standing Bessel beam (β = π/6, kL = 0.5, ρ_m/ρ₀=1, c_m/c₀=1.05): (a) Dimensionless acoustic radiation force (k_zh = π/4); (b) dimensionless acoustic radiation torque (k_zh = 0).

下载: 全尺寸图片幻灯片

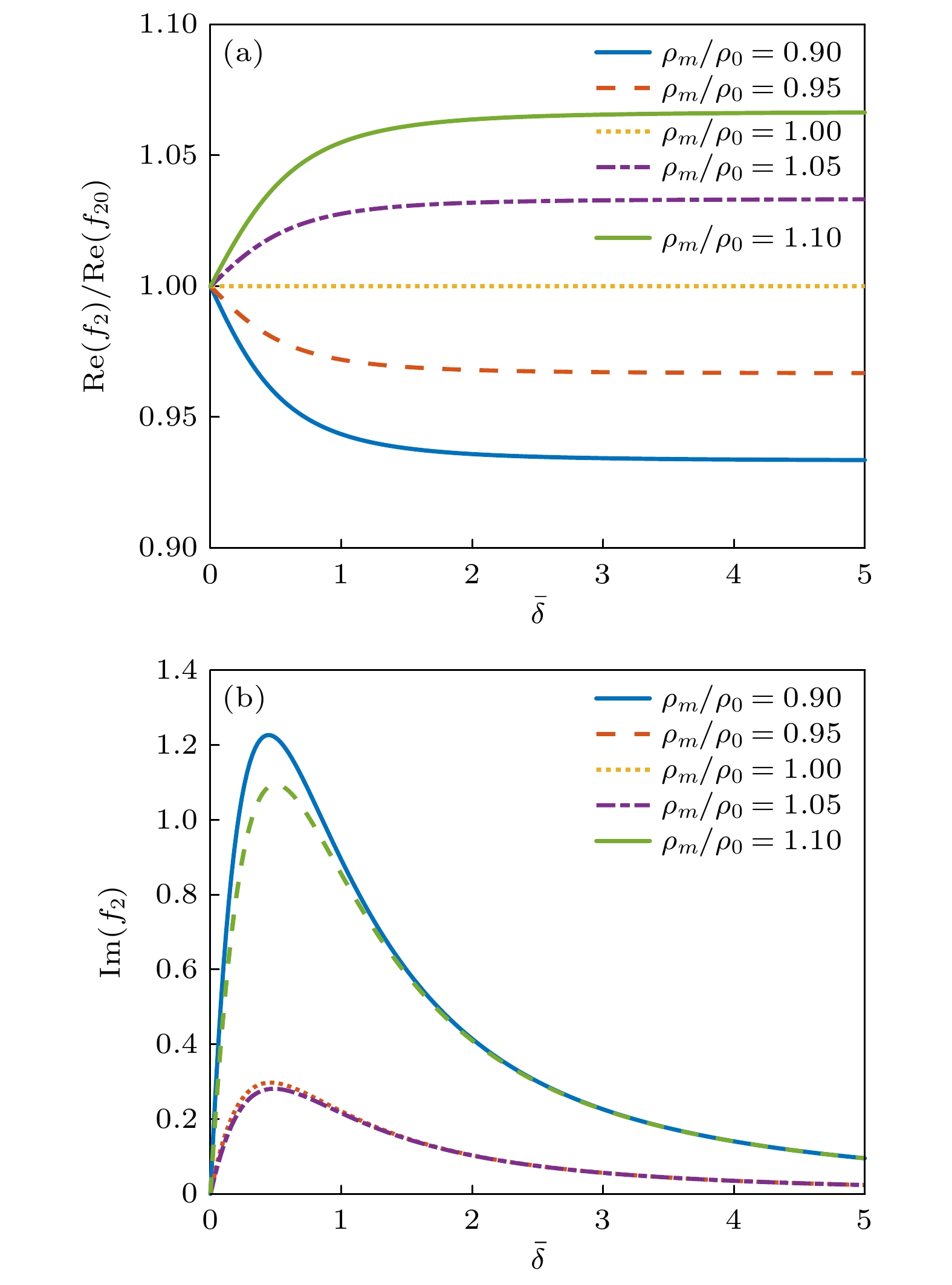
图 14 均匀球形粒子的偶极散射系数f₂随$ \bar \delta $的变化　(a) ${\rm {Re}} ( {{f_2}})/{\rm {Re}} ( {{f_{20}}} )$; (b) $ {\rm {Im}} \left( {{f_2}} \right) $

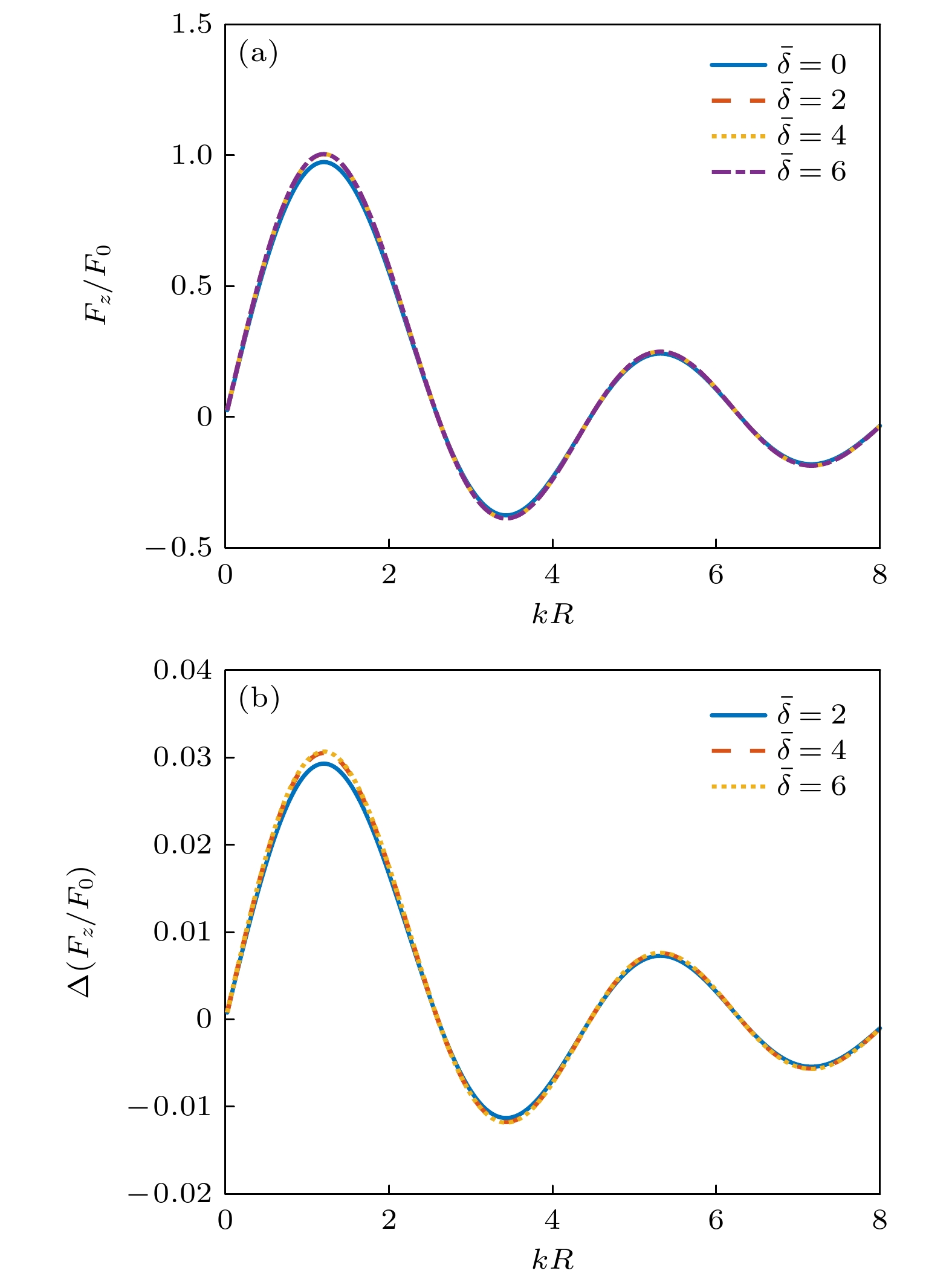
Fig. 14. The dipole scattering coefficient f₂ plots for a homogeneous sphere versus $ \bar \delta $ (a) ${\rm {Re}} ( {{f_2}})/{\rm {Re}} ( {{f_{20}}} )$; (b) ${\rm {Im}} ({{f_2}})$

下载: 全尺寸图片幻灯片

图 15 零阶Bessel驻波场中心均匀球形粒子受到的归一化声辐射力随kR的变化(β = π/6, k_zh = π/4, ρ_m/ρ₀ = 1.2, c_m/c₀ = 1.1)　(a) 归一化声辐射力; (b) 黏性流体与理想流体中归一化声辐射力的差值

Fig. 15. The dimensionless acoustic radiation force plots for a homogeneous sphere versus kR in a zero-order standing Bessel beam (β = π/6, k_zh = π/4, ρ_m/ρ₀ = 1.1, c_m/c₀ = 1.1): (a) Dimensionless acoustic radiation force; (b) difference of dimensionless acoustic radiation force in a viscous fluid and in an ideal fluid

下载: 全尺寸图片幻灯片

map

[1]	Wu J R 1991 J. Acoust. Soc. Am. 89 2140 Google Scholar
[2]	Lee J W, Ha K L, Shung K K 2005 J. Acoust. Soc. Am. 117 3273 Google Scholar
[3]	Lee J W, Shung K K 2006 J. Acoust. Soc. Am. 120 1084 Google Scholar
[4]	黄先玉, 蔡飞燕, 李文成, 郑海荣, 何兆剑, 邓科, 赵鹤平 2017 66 044301 Google Scholar Huang X Y, Cai F Y, Li W C, Zheng H R, He Z J, Deng K, Zhao H P 2017 Acta Phys. Sin. 66 044301 Google Scholar
[5]	Ozcelik A, Rufo J, Guo F, Guo Y Y, Li P, Lata J, Huang T J 2018 Nat. Methods. 15 1021 Google Scholar
[6]	Baudoin M, Thomas J L 2020 Annu. Rev. Fluid Mech. 52 205 Google Scholar
[7]	Lierke E G 1996 Acustica 82 220
[8]	Yarin A L, Pfaffenlehner M, Tropea C 1998 J. Fluid Mech. 356 65 Google Scholar
[9]	King L V 1934 Proc. Roya. Soc. London, Ser. A 147 212 Google Scholar
[10]	Awatani J 1953 J. Acous. Soc. Jpn. 9 140
[11]	Yosioka K, Kawasima Y 1955 Acta Acust. United Ac. 5 167
[12]	Hasegawa T, Yosioka K 1969 J. Acoust. Soc. Am. 46 1139 Google Scholar
[13]	Hasegawa T, Watanabe Y 1978 J. Acoust. Soc. Am. 63 1733 Google Scholar
[14]	Hasegawa T 1979 J. Acoust. Soc. Am. 65 32 Google Scholar
[15]	Hasegawa T 1979 J. Acoust. Soc. Am. 65 41 Google Scholar
[16]	Hasegawa T, Saka K, Inoue N, Matsuzawa K 1988 J. Acoust. Soc. Am. 83 1770 Google Scholar
[17]	Silva G T, Lobo T P, Mitri F G 2012 EPL 97 54003 Google Scholar
[18]	Gong Z X, M. Baudoin 2020 J. Acoust. Soc. Am. 148 3131 Google Scholar
[19]	Hasegawa T, Hino Y, Annou A, Noda H, Kato M, Inoue N 1993 J. Acoust. Soc. Am. 93 154 Google Scholar
[20]	Mitri F G 2005 Ultrasonics 43 681 Google Scholar
[21]	Mitri F G 2006 Ultrasonics 44 244 Google Scholar
[22]	Wang Y Y, Yao J, Wu X W, Wu D J, Liu X J 2017 J. Appl. Phys. 122 094902 Google Scholar
[23]	Peng X J, He W, Xin F X, Genin G M, Lu T J 2020 Ultrasonics 108 106205 Google Scholar
[24]	Peng X J, He W, Xin F X, Genin G M, Lu T J 2020 J. Mech. Phys. Solids 145 104134 Google Scholar
[25]	Wu R R, Cheng K X, Liu X Z, Liu J H, Mao Y W, Gong X F, Li Y F 2014 J. Appl. Phys. 116 144903 Google Scholar
[26]	Wang H B, Liu X Z, Gao S, Cui J, Liu J H, He A J, Zhang G T 2018 Chin. Phys. B 27 034302 Google Scholar
[27]	Zang Y C, Lin W J 2020 Results Phys. 16 102847 Google Scholar
[28]	Mitri F G 2020 Chin. Phys. B 29 114302 Google Scholar
[29]	Mitri F G 2021 Chin. Phys. B 30 024302 Google Scholar
[30]	Mitri F G 2006 New J. Phys. 8 138 Google Scholar
[31]	Aglyamov S R, Karpiouk A B, Ilinskii Y A, Zabolotskaya E A, Emelianov S Y 2007 J. Acoust. Soc. Am. 122 1927 Google Scholar
[32]	Nikolaeva A V, Kryzhanovsky M A, Tsysar S A, Kreider, W, Sapozhnikov O A 2015 AIP Conference Proceedings 1685 040009
[33]	Garbin A, Leibacher I, Hahn P, Le Ferrand H, Studart A R, Dual J 2015 J. Acoust. Soc. Am. 138 2759 Google Scholar
[34]	Johnson K A, Vormohr H R, Doinikov A A, Bouakaz A, Shields C W, Lopez G P, Dayton P A 2016 Phys Rev. E 93 053109 Google Scholar
[35]	Qiao Y P, Gong M Y, Wang H B, Lan J, Liu T, Liu J H, Mao Y W, He A J, Liu X Z 2021 Phys. Fluids 33 047107 Google Scholar
[36]	Wijaya F B, Lim K M 2015 Acta Acust. 101 531 Google Scholar
[37]	Glynne-Jones P, Mishra P P, Boltryk R J, Hill M 2013 J. Acoust. Soc. Am. 133 1885 Google Scholar
[38]	Wei W, Thiessen D B, Marston P L 2004 J. Acoust. Soc. Am. 116 201 Google Scholar
[39]	Hasheminejad S M, Sanaei R 2007 J. Comput. Acoust. 15 377 Google Scholar
[40]	Marston P L, Wei W, Thiessen D B 2006 AIP Conf. Proc. 838 495 Google Scholar
[41]	Mitri F G 2016 Ultrasonics 66 27 Google Scholar
[42]	Mitri F G 2015 J. Appl. Phys. 118 214903 Google Scholar
[43]	Mitri F G 2015 Wave Motion 57 231 Google Scholar
[44]	Mitri F G 2015 EPL 112 34002 Google Scholar
[45]	Mitri F G 2017 Ultrasonics 74 62 Google Scholar
[46]	Silva G T, Drinkwater B W 2018 J. Acoust. Soc. Am. 144 EL453 Google Scholar
[47]	Jerome T S, Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2020 J. Acoust. Soc. Am. 148 2403 Google Scholar
[48]	Jerome T S, Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2021 J. Acoust. Soc. Am. 149 2081 Google Scholar
[49]	Marston P L 2006 J. Acoust. Soc. Am. 120 3518 Google Scholar
[50]	Marston P L 2009 J. Acoust. Soc. Am. 125 3539 Google Scholar
[51]	Mitri F G 2008 Ann. Phys. 323 1604 Google Scholar
[52]	Mitri F G 2009 Ultrasonics 49 794 Google Scholar
[53]	Mitri F G 2009 IEEE UFFC 56 1059 Google Scholar
[54]	Mitri F G 2009 J. Phys. A, Math. Theor. 42 245202 Google Scholar
[55]	Mitri F G 2009 Eur. Phys. J. E 28 469 Google Scholar
[56]	Zhang L K, Marston P L 2011 J. Acoust. Soc. Am. 129 1679 Google Scholar
[57]	Zhang L K, Marston P L 2011 Phys. Rev. E 84 065601 Google Scholar
[58]	Zhang L K, Marston P L 2011 J. Acoust. Soc. Am. 129 2381
[59]	Zhang L K 2018 Phys. Rev. Appl. 10 034039 Google Scholar
[60]	Gong Z X, Marston P L 2019 Phys. Rev. Appl. 11 064022 Google Scholar
[61]	Jerome T S, Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2019 J. Acoust. Soc. Am. 145 36 Google Scholar
[62]	Jerome T S, Hamilton M F 2020 Proc. Meet. Acoust. 39 045007
[63]	Jerome T S, Hamilton M F 2021 J. Acoust. Soc. Am. 150 3417 Google Scholar
[64]	Ilinskii Yu A, Zabolotskaya E A, Hamilton M F 2012 AIP Conf. Proc. 1474 255
[65]	Sapozhnikov O A, Bailey M R 2013 J. Acoust. Soc. Am. 133 661 Google Scholar
[66]	Ilinskii Yu A, Zabolotskaya E A, Treweek B C, Hamilton M F 2018 J. Acoust. Soc. Am. 144 568 Google Scholar
[67]	Durnin J 1987 J. Opt. Soc. Am. A 4 651 Google Scholar
[68]	Rayleigh L 1884 Philos. Trans. R. Soc. London 175 1
[69]	Landau L D, Lifshitz E M 1993 Fluid Mechanics (2nd Ed.) (Vol. 6) Course of Theoretical Physics (Oxford: Pergamon)
[70]	Settnes M, Bruus H 2012 Phys. Rev. E 85 016327 Google Scholar

[1]	白靖, 马文浩, 葛城显, 吴振森, 许彤. 驻波场中非均匀手征分层粒子的辐射力特性. , 2024, 73(18): 184201. doi: 10.7498/aps.73.20240842
[2]	王俊, 蔡飞燕, 张汝钧, 李永川, 周伟, 李飞, 邓科, 郑海荣. 基于压电声子晶体板波声场的微粒操控. , 2024, 73(7): 074302. doi: 10.7498/aps.73.20231886
[3]	陈聪, 张若钦, 李锋, 李志远. 基于亚波长管道增强的漩涡声场悬浮操控微粒和液滴的实验研究. , 2023, 72(12): 124302. doi: 10.7498/aps.72.20230383
[4]	王燕萍, 蔡飞燕, 李飞, 张汝钧, 李永川, 王金萍, 张欣, 郑海荣. 基于二维声子晶体板共振声场的微粒操控. , 2023, 72(14): 144207. doi: 10.7498/aps.72.20230099
[5]	齐绍富, 蔡飞燕, 田振, 黄先玉, 周娟, 王金萍, 李文成, 郑海荣, 邓科. 基于一维声栅共振场的大规模微粒并行排列的实验研究. , 2023, 72(2): 024301. doi: 10.7498/aps.72.20221793
[6]	潘瑞琪, 李凡, 杜芷玮, 胡静, 莫润阳, 王成会. 平面波声场中内置偏心液滴的弹性球壳声辐射力. , 2023, 72(5): 054302. doi: 10.7498/aps.72.20222155
[7]	朱纪霖, 高东宝, 曾新吾. 基于相位变换声镊的单个微粒平面移动操控. , 2021, 70(21): 214302. doi: 10.7498/aps.70.20210981
[8]	臧雨宸, 林伟军, 苏畅, 吴鹏飞. Gauss声束对离轴椭圆柱的声辐射力矩. , 2021, 70(8): 084301. doi: 10.7498/aps.70.20201635
[9]	黄先玉, 蔡飞燕, 李文成, 郑海荣, 何兆剑, 邓科, 赵鹤平. 空气中一维声栅对微粒的声操控. , 2017, 66(4): 044301. doi: 10.7498/aps.66.044301
[10]	沈壮志. 声驻波场中空化泡的动力学特性. , 2015, 64(12): 124702. doi: 10.7498/aps.64.124702
[11]	毕欣, 黄林, 杜劲松, 齐伟智, 高扬, 荣健, 蒋华北. 脉冲微波辐射场空间分布的热声成像研究. , 2015, 64(1): 014301. doi: 10.7498/aps.64.014301
[12]	汪拓, 吴锋, 李端勇, 陈浩, 林杰. 驻波热声系统的自激振荡机理. , 2015, 64(4): 044301. doi: 10.7498/aps.64.044301
[13]	王磊, 范宜仁, 黄瑞, 韩玉娇, 巫振观, 邢东辉, 李炜. 各向异性介质多分量感应测井三维Born几何因子理论研究. , 2015, 64(23): 239301. doi: 10.7498/aps.64.239301
[14]	聂永发, 朱海潮. 利用源强密度声辐射模态重建声场. , 2014, 63(10): 104303. doi: 10.7498/aps.63.104303
[15]	张立民, 贾昌春, 王琦, 陈长进. 共面双对称条件下电子碰撞Ar原子单电离的一阶扭曲波Born近似. , 2014, 63(15): 153401. doi: 10.7498/aps.63.153401
[16]	蒋云峰, 陆璇辉, 赵承良. 高度聚焦的余弦高斯光束对瑞利粒子的辐射力分析. , 2010, 59(6): 3959-3964. doi: 10.7498/aps.59.3959
[17]	张碧星, 汪承灏, Anders Bostr?m. 压电条SH声辐射场研究. , 2005, 54(5): 2111-2117. doi: 10.7498/aps.54.2111
[18]	卢新培, 潘垣, 张寒虹. 水中脉冲放电的电特性与声辐射特性研究. , 2002, 51(7): 1549-1553. doi: 10.7498/aps.51.1549
[19]	胡宁, 章德海, 丁浩刚. 双星放射引力辐射的阻尼力. , 1981, 30(8): 1003-1010. doi: 10.7498/aps.30.1003
[20]	钱祖文. 计算线源声参量阵辐射场的新方法. , 1981, 30(11): 1479-1487. doi: 10.7498/aps.30.1479

计量

文章访问数: 5162
PDF下载量: 97
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

零阶Bessel驻波场中任意粒子声辐射力和力矩的Born近似