-
声波可以非接触、无损伤地操控微粒, 其在细胞操纵、材料组装等领域具有广阔的应用前景. 然而, 如何高通量、灵活且快速操控微粒仍然面临挑战. 在本工作中, 利用二维声子晶体板的周期局域梯度场实现了大规模微粒的并行操控. 其主要机制是由于黄铜平板刻蚀周期分布的正方体凸起构成的二维声子晶体板可激发板子固有的Lamb波零阶反对称模式; 其周期局域梯度场在平行于声子晶体板表面为驻波声场、在垂直于声子晶体板表面为局域梯度声场; 该周期分布的局域声场可以对微粒产生平行于表面的声停驻力、垂直于表面的声吸引力. 我们进一步构建了操控实验装置, 利用压电陶瓷片激励二维声子晶体板, 在实验中观察到了玻璃微球的捕获和排列现象, 实现了大规模微粒的二维排列操控. 该工作为高通量、快速、灵活操控微粒和细胞等提供了物理基础和技术支持.Acoustic waves can manipulate particles without contact or damage, and has received increasing attention due to their potential applications in various fields, such as cell sorting, organoid construction, and material assembly. In general, high-throughput manipulation of microparticles relies on a large number of active transducers and phase-shifting circuits to create standing wave patterns, thus significantly inducing system complexity. Recently, we realized the parallel manipulation of microparticles by using an acoustic field modulated by a one-dimensional phononic crystal plate. The concept is based on the fact that phononic crystal plate can resonantly excite the zero-order asymmetric (A0) Lamb wave, inducing highly localized periodic radiation force on the particles. In this paper, we further show that by using a two-dimensional phononic crystal plate (TDPCP), parallel manipulation of massive particles can be achieved only with a single transducer. The A0 Lamb wave can be excited by a TDPCP, forming a two-dimensional periodic localized field, and then particles can suffer negative vertical force and stable zero horizontal force, inducing two-dimensional periodic trapping on the surface of the plate. Combining a PZT source with a TDPCP consisting of a brass plate patterned with periodical brass stubs, we observe the capture and arrangement of glass microspheres, achieving two-dimensional arrangement manipulation of particles on the TDPCP. This system represents a significant advancement in developing high-throughput, rapid, and flexible devices for particles and cell manipulation.
-
Keywords:
- phononic crystal /
- acoustic radiation force /
- particle manipulation
[1] Meng L, Cai F, Li F, Zhou W, Niu L, Zheng H 2019 J. Phys. D: Appl. Phys. 52 273001
Google Scholar
[2] Olson R J, Shalapyonok A, Kalb D J, Graves S W, Sosik H M 2017 Limnol. Oceanogr. Methods 15 867
Google Scholar
[3] Meng L, Cai F, Jiang P, Deng Z, Li F, Niu L, Chen Y, Wu J, Zheng H 2014 Appl. Phys. Lett. 104 073701
Google Scholar
[4] Meng L, Cai F, Chen J, Niu L, Li Y, Wu J, Zheng H 2012 Appl. Phys. Lett. 100 173701
Google Scholar
[5] Ding X, Lin S C S, Kiraly B, Yue H, Li S, Chiang I K, Shi J, Benkovic S J, Huang T J 2012 Proc. Natl. Acad. Sci. U.S.A. 109 11105
Google Scholar
[6] Meng L, Cai F, Zhang Z, Niu L, Jin Q, Yan F, Wu J, Wang Z, Zheng H 2011 Biomicrofluidics 5 044104
Google Scholar
[7] Marzo A, Drinkwater B W 2019 Proc. Natl. Acad. Sci. U.S.A. 116 84
Google Scholar
[8] Tian Z, Yang S, Huang P H, Wang Z, Zhang P, Gu Y, Bachman H, Chen C, Wu M, Xie Y 2019 Sci. Adv. 5 6062
Google Scholar
[9] Jiang X, Li Y, Liang B, Cheng J C, Zhang L 2016 Phys. Rev. Lett. 117 034301
Google Scholar
[10] Xia X, Cai F, Li F, Meng L, Ma T, Zhou H, Ke M, Qiu C, Liu Z, Zheng H 2018 Adv. Mater. 4 1800542
[11] Li Y, Assouar M B 2015 Sci. Rep. 5 17612
Google Scholar
[12] Li Y, Shen C, Xie Y, Li J, Wang W, Cummer S A, Jing Y 2017 Phys. Rev. Lett. 119 035501
Google Scholar
[13] Xia X, Li Y, Cai F, Zhou H, Ma T, Zheng H 2020 Appl. Phys. Lett. 117 021904
Google Scholar
[14] Melde K, Mark A G, Qiu T, Fischer P 2016 Nature 537 518
Google Scholar
[15] Huang J, Ren X, Zhou Q, Zhou J, Xu Z 2023 Ultrasonics 128 106865
Google Scholar
[16] Memoli G, Caleap M, Asakawa M, Sahoo D R, Drinkwater B W, Subramanian S 2017 Nat. Commun. 8 14608
Google Scholar
[17] Wang T, Ke M, Xu S, Feng J, Qiu C, Liu Z 2015 Appl. Phys. Lett. 106 163504
Google Scholar
[18] Korozlu N, Bicer A, Sayarcan D, Adem Kaya O, Cicek A 2022 Ultrasonics 124 106777
Google Scholar
[19] Wang Y, Luo L, Ke M, Liu Z 2022 Phys. Rev. Appl. 17 014026
Google Scholar
[20] 黄先玉, 蔡飞燕, 李文成, 郑海荣, 何兆剑, 邓科, 赵鹤平 2017 66 044301
Google Scholar
Huang X Y, Cai F Y, Li W C, Zheng H R, He Z J, Deng K, Zhao H P 2017 Acta Phys. Sin. 66 044301
Google Scholar
[21] 齐绍富, 蔡飞燕, 田振, 黄先玉, 周娟, 王金萍, 李文成, 郑海荣, 邓科 2023 72 024301
Google Scholar
Qi S F, Cai F Y, Tian Z, Huang X Y, Zhou J, Wang J P, Li W C, Zheng H R, Deng K 2023 Acta Phys. Sin. 72 024301
Google Scholar
[22] Li F, Cai F, Liu Z, Meng L, Qian M, Wang C, Cheng Q, Qian M, Liu X, Wu J, Li J, Zheng H 2014 Phys. Rev. Appl. 1 051001
Google Scholar
[23] Li F, Cai F, Zhang L, Liu Z, Li F, Meng L, Wu J, Li J, Zhang X, Zheng H 2020 Phys. Rev. Appl. 13 044077
Google Scholar
[24] Li F, Yan F, Chen Z, Lei J, Yu J, Chen M, Zhou W, Meng L, Niu L, Wu J, Li J, Cai F, Zheng H 2018 Appl. Phys. Lett. 113 083701
Google Scholar
[25] Sweden S. https://cn.comsol.com/ [2023-1-18]
[26] He Z, Jia H, Qiu C, Peng S, Mei X, Cai F, Peng P, Ke M, Liu Z 2010 Phys. Rev. Lett. 105 074301
Google Scholar
[27] Sarvazyan A P, Rudenko O V, Nyborg W L 2010 Ultrasound Med. Biol. 36 1379
Google Scholar
[28] King L V 1934 Proc. R. Soc. London, Ser. A 147 212
Google Scholar
-
图 1 二维声子晶体板声学特性 (a) 二维声子晶体板单胞示意图; (b) 二维声子晶体板实验样品图; (c) 正入射时, 二维声子晶体板和厚度为0.38 mm的均匀黄铜板透射曲线; (d) 二维声子晶体板色散曲线(红色和蓝色圆圈), 被折叠在第一布里渊区的均匀板色散曲线(红色和蓝色实线)及水的色散曲线(黑色圆圈); (e) 在Γ点且频率为0.21 MHz处, 离均匀板表面距离为0.05 mm, 4阶简并模式的本征声场分布; (f) 在Γ点且频率为0.24 MHz附近, 离声子晶体板表面距离为0.05 mm, 4个模式的本征声场分布
Fig. 1. Acoustic characteristics of two-dimensional phononic crystal plate (TDPCP): (a) Schematic diagram of two-dimensional phononic crystal plate cell; (b) photograph of the TDPCP sample; (c) transmission spectrum at normal incidence versus frequency for the TDPCP and uniform brass plate with the height of 0.38 mm; (d) dispersion curves (red circles and blue circles) for the TDPCP immersed in water, accompanied with the water line (dark circles). For comparison, the simply folded dispersion curves for the uniform plate are plotted as lines with the same color; (e) the eigen pressure fields of four-order degenerate mode above the uniform brass plate with distance 0.05 mm at Γ with frequency of 0.21 MHz; (f) the eigen pressure field above the TDPCP with distance 0.05 mm at Γ with frequency around 0.24 MHz.
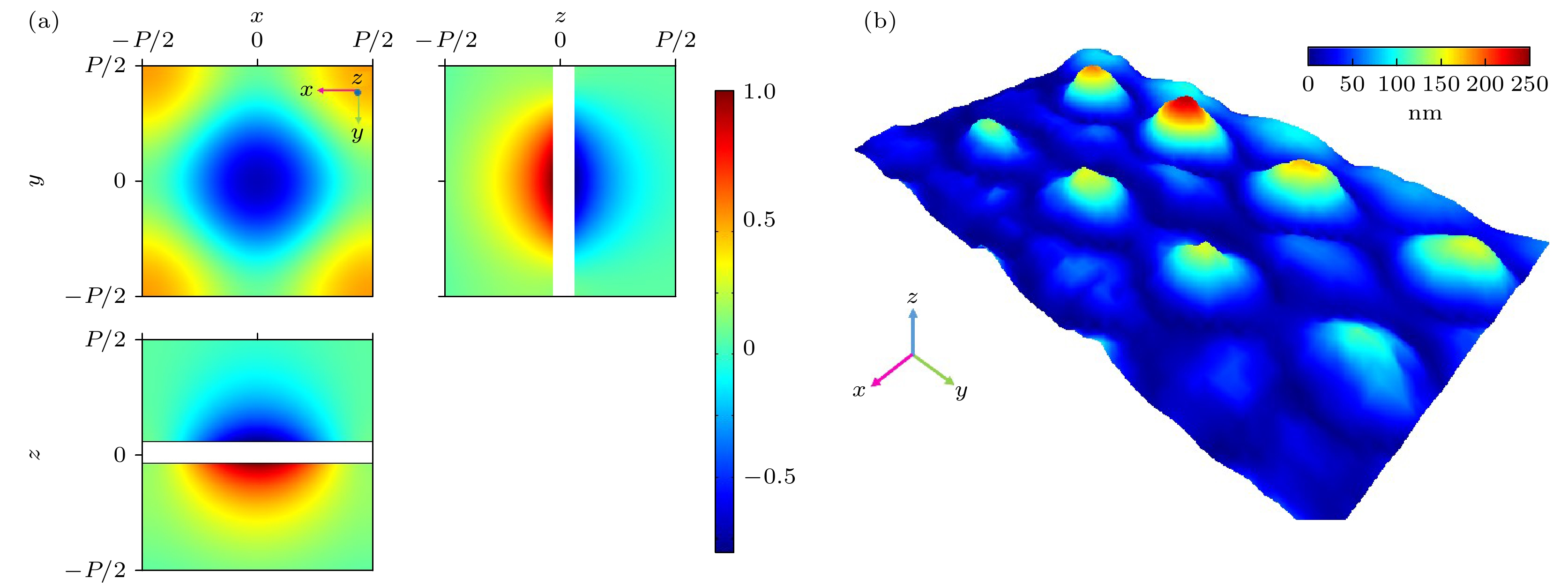
图 2 数值计算声压场与实验测量位移场 (a) 在共振频率0.24 MHz处声子晶体板单胞周围的声场分布(数值模拟); (b) 在共振频率处声子晶体板面的位移场分布(LDV实验测量)
Fig. 2. Calculated pressure field and measured displacement field at resonant frequency: (a) Calculated pressure field of unit cell around the TDPCP at resonance frequency; (b) measured displacement field at the surface of the TDPCP at resonant frequency by LDV.
图 3 共振频率处玻璃微球在二维声子晶体板表面受到的Gor’kov势(归一化)和声辐射力分布, 其中背景颜色表示Gor'kov势大小, 箭头长度和方向分别表示声辐射力的大小和方向
Fig. 3. Distribution of normalized Gor’kov potential and acoustic radiation force exerted on glass microspheres at the surface of TDPCP at resonance frequency, the color represents the magnitude of Gor’kov potential, the length and direction of the arrow represent the magnitude and direction of the acoustic radiation force, respectively.
图 4 微粒操控实验系统示意图及实验效果图 (a) 微粒操控实验系统示意图; (b) 超声开启前, 玻璃微球随机分布在声子晶体板表面; (c) 超声开启后, 玻璃微球二维周期捕获在声子晶体板表面
Fig. 4. Schematic diagram of the experimental system and experimental effect of particles manipulation: (a) Schematic diagram of the experimental system; (b) initially, glass spheres are randomly distributed on the surface of the TDPCP; (c) when ultrasonic wave is on, glass spheres are trapped and periodically arranged on the surface of the TDPCP.
-
[1] Meng L, Cai F, Li F, Zhou W, Niu L, Zheng H 2019 J. Phys. D: Appl. Phys. 52 273001
Google Scholar
[2] Olson R J, Shalapyonok A, Kalb D J, Graves S W, Sosik H M 2017 Limnol. Oceanogr. Methods 15 867
Google Scholar
[3] Meng L, Cai F, Jiang P, Deng Z, Li F, Niu L, Chen Y, Wu J, Zheng H 2014 Appl. Phys. Lett. 104 073701
Google Scholar
[4] Meng L, Cai F, Chen J, Niu L, Li Y, Wu J, Zheng H 2012 Appl. Phys. Lett. 100 173701
Google Scholar
[5] Ding X, Lin S C S, Kiraly B, Yue H, Li S, Chiang I K, Shi J, Benkovic S J, Huang T J 2012 Proc. Natl. Acad. Sci. U.S.A. 109 11105
Google Scholar
[6] Meng L, Cai F, Zhang Z, Niu L, Jin Q, Yan F, Wu J, Wang Z, Zheng H 2011 Biomicrofluidics 5 044104
Google Scholar
[7] Marzo A, Drinkwater B W 2019 Proc. Natl. Acad. Sci. U.S.A. 116 84
Google Scholar
[8] Tian Z, Yang S, Huang P H, Wang Z, Zhang P, Gu Y, Bachman H, Chen C, Wu M, Xie Y 2019 Sci. Adv. 5 6062
Google Scholar
[9] Jiang X, Li Y, Liang B, Cheng J C, Zhang L 2016 Phys. Rev. Lett. 117 034301
Google Scholar
[10] Xia X, Cai F, Li F, Meng L, Ma T, Zhou H, Ke M, Qiu C, Liu Z, Zheng H 2018 Adv. Mater. 4 1800542
[11] Li Y, Assouar M B 2015 Sci. Rep. 5 17612
Google Scholar
[12] Li Y, Shen C, Xie Y, Li J, Wang W, Cummer S A, Jing Y 2017 Phys. Rev. Lett. 119 035501
Google Scholar
[13] Xia X, Li Y, Cai F, Zhou H, Ma T, Zheng H 2020 Appl. Phys. Lett. 117 021904
Google Scholar
[14] Melde K, Mark A G, Qiu T, Fischer P 2016 Nature 537 518
Google Scholar
[15] Huang J, Ren X, Zhou Q, Zhou J, Xu Z 2023 Ultrasonics 128 106865
Google Scholar
[16] Memoli G, Caleap M, Asakawa M, Sahoo D R, Drinkwater B W, Subramanian S 2017 Nat. Commun. 8 14608
Google Scholar
[17] Wang T, Ke M, Xu S, Feng J, Qiu C, Liu Z 2015 Appl. Phys. Lett. 106 163504
Google Scholar
[18] Korozlu N, Bicer A, Sayarcan D, Adem Kaya O, Cicek A 2022 Ultrasonics 124 106777
Google Scholar
[19] Wang Y, Luo L, Ke M, Liu Z 2022 Phys. Rev. Appl. 17 014026
Google Scholar
[20] 黄先玉, 蔡飞燕, 李文成, 郑海荣, 何兆剑, 邓科, 赵鹤平 2017 66 044301
Google Scholar
Huang X Y, Cai F Y, Li W C, Zheng H R, He Z J, Deng K, Zhao H P 2017 Acta Phys. Sin. 66 044301
Google Scholar
[21] 齐绍富, 蔡飞燕, 田振, 黄先玉, 周娟, 王金萍, 李文成, 郑海荣, 邓科 2023 72 024301
Google Scholar
Qi S F, Cai F Y, Tian Z, Huang X Y, Zhou J, Wang J P, Li W C, Zheng H R, Deng K 2023 Acta Phys. Sin. 72 024301
Google Scholar
[22] Li F, Cai F, Liu Z, Meng L, Qian M, Wang C, Cheng Q, Qian M, Liu X, Wu J, Li J, Zheng H 2014 Phys. Rev. Appl. 1 051001
Google Scholar
[23] Li F, Cai F, Zhang L, Liu Z, Li F, Meng L, Wu J, Li J, Zhang X, Zheng H 2020 Phys. Rev. Appl. 13 044077
Google Scholar
[24] Li F, Yan F, Chen Z, Lei J, Yu J, Chen M, Zhou W, Meng L, Niu L, Wu J, Li J, Cai F, Zheng H 2018 Appl. Phys. Lett. 113 083701
Google Scholar
[25] Sweden S. https://cn.comsol.com/ [2023-1-18]
[26] He Z, Jia H, Qiu C, Peng S, Mei X, Cai F, Peng P, Ke M, Liu Z 2010 Phys. Rev. Lett. 105 074301
Google Scholar
[27] Sarvazyan A P, Rudenko O V, Nyborg W L 2010 Ultrasound Med. Biol. 36 1379
Google Scholar
[28] King L V 1934 Proc. R. Soc. London, Ser. A 147 212
Google Scholar
下载:
计量
- 文章访问数: 2972
- PDF下载量: 79
- 被引次数: 0
