-
In the deep ocean environment, the sound energy from the direct path is very hard to illuminate a target located in the shadow zone. To solve the problem, the bottom bouncing technique, in which the vertical transmitting beamforming and the bottom bouncing are used to illuminate the target in the shadow zone, provides a potential way. However, due to the sound field interference in the bottom bouncing area in the deep ocean environment, the sound energy in the bottom bouncing area is fluctuant, which produces several discrete detectable areas. In order to detect underwater targets in these areas when using an active sonar with a transmitting vertical linear array, the selecting of reasonable vertical transmitting beam angles is necessary. Therefore, the relationship between the discrete detectable area and the transmitting vertical angle in deep ocean is very important for the active sonar using a transmitting vertical linear array. In this paper, it is shown that the sound field fluctuation in the bottom bouncing area is due to the energy fluctuation of the rays having different grazing angles. And the active sonar can achieve high noise gain in a detectable area when the vertical transmitting angle is equal to the grazing angle of the sound ray with the peak energy. To obtain a high noise gain of the active sonar using the vertical transmitting array, an efficient method to estimate the grazing angle of sound rays with peak energy according to the sound field distribution of angle dimension is proposed, which is helpful for selecting a group of best vertical transmitting angles. Meanwhile, a transmitting signal which contains a group of subpulses is designed. Furthermore, each subpulse is applied to the whole transmitting array by using the vertical steering to illuminate a certain detectable area in the bottom bouncing area. By doing so, a subpulse steered to the previously selected vertical angle will ensure a high transmitting array gain in a detectable area, and all of pulses will illuminate the whole detectable areas with high array gains almost simultaneously. Numerical simulations show that the proposed method is stable and efficient, and has good noise gain in the shadow zone (where almost no direct path exists) in the deep ocean environment.
-
Keywords:
- active sonar /
- bottom bounce area /
- vertical beam pitch /
- angle dimension
[1] Udovydchenkov I A, Stephen R A, Duda T F, Bolmer S T, Worcester P F, Dzieciuch M A, Mercer J A, Andrew R K, Howe B M 2012 J. Acoust. Soc. Am. 132 2224
Google Scholar
[2] Chuprov S D, Maltsev N E 1981 Doklady Akademii Nauk SSSR 257 474
[3] 翁晋宝, 李风华, 郭永刚 2016 声学学报 41 330
Weng J B, Li F H, Guo Y G 2016 Acta Acustica 41 330
[4] 段睿 2016 博士学位论文 (西安: 西北工业大学)
Duan R 2016 Ph.D. Dissertation (Xi’an: Northwestern Polytechnical University) (in Chinese)
[5] 翁晋宝 2015 博士学位论文 (北京: 中国科学院大学)
Weng J B 2015 Ph.D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[6] Harrison C H 2011 J. Acoust. Soc. Am. 129 2863
Google Scholar
[7] Colosi J A, Duda T F, Morozov A K 2012 J. Acoust. Soc. Am. 131 1749
Google Scholar
[8] Finn B J, William A K, Michael B P, Henrik S 2000 Computational Ocean Acoustics (Vol. 2) (New York: AIP Press/Springer) p340
[9] 郭晓乐, 杨坤德, 马远良, 杨秋龙 2016 65 214302
Google Scholar
Guo X L, Yang K D, Ma Y L 2016 Acta Phys. Sin. 65 214302
Google Scholar
[10] 张仁和, 何怡, 刘红 1994 声学学报 9 1
Zhang R H, He Y, Liu H 1994 Acta Acustica 9 1
[11] Tindle C T, Guthrie K M 1974 J. Sound Vib. 34 291
Google Scholar
[12] Kamel A, Felsen L B 1982 J. Acoust. Soc. Am. 71 1445
Google Scholar
[13] 林巨, 赵越, 王欢, 陈鹏 2015 南京大学学报: 自然科学 51 1223
Lin J, Zhao Y, Wang H, Chen P 2015 J. Nanjing Univ. Nat. Sci. 51 1223
[14] 韩志斌, 彭朝晖, 刘扬 2019 应用声学 38 569
Google Scholar
Han Z B, Peng Z H, Liu Y 2019 Journal of Applied Acoustic 38 569
Google Scholar
[15] 吴俊楠, 周士弘, 张岩 2016 中国科学: 物理学 力学 天文学 46 094311
Google Scholar
Wu J N, Zhou S H, Zhang Y 2016 Sci. Sin. Phys. Mech. Astron. 46 094311
Google Scholar
[16] Wu J N, Zhou S H, Peng Z H, Zhang Y, Zhang R H 2016 Chin. Phys. B 25 124311
Google Scholar
[17] 刘伯胜, 雷家煜 1993 水声学原理 (哈尔滨: 哈尔滨工程大学出版社) 第106页
Liu B S, Lei J Y 1993 Principles of Underwater Sound (Haerbin: Haerbin Engineering University Press) p106 (in Chinese)
[18] 谢磊, 孙超, 刘雄厚, 蒋光禹 2016 65 144303
Google Scholar
Xie L, Sun C, Liu X H, Jiang G Y 2016 Acta Phys. Sin. 65 144303
Google Scholar
[19] 杨坤德, 孙超 2007 电声技术 31 4
Google Scholar
Yang K D, Sun C, 2007 Audio Eng. 31 4
Google Scholar
[20] 宋俊 2005 博士学位论文 (长沙: 国防科技大学)
Song J 2005 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
-
图 1 典型深海Munk声道下声传播损失随距离和接收深度变化情况
Figure 1. Transmission loss variety with the change of distance and receiver depth in Munk sound channel.
图 2 典型深海Munk声道下接收深度固定时声传播损失随距离的变化
Figure 2. Transmission loss variety with the change of distance in Munk sound channel when the receiver depth is fixed.
图 3 典型深海Munk声道下声场的角谱域分布
Figure 3. Acoustic field distribution of angle dimension in Munk sound channel.
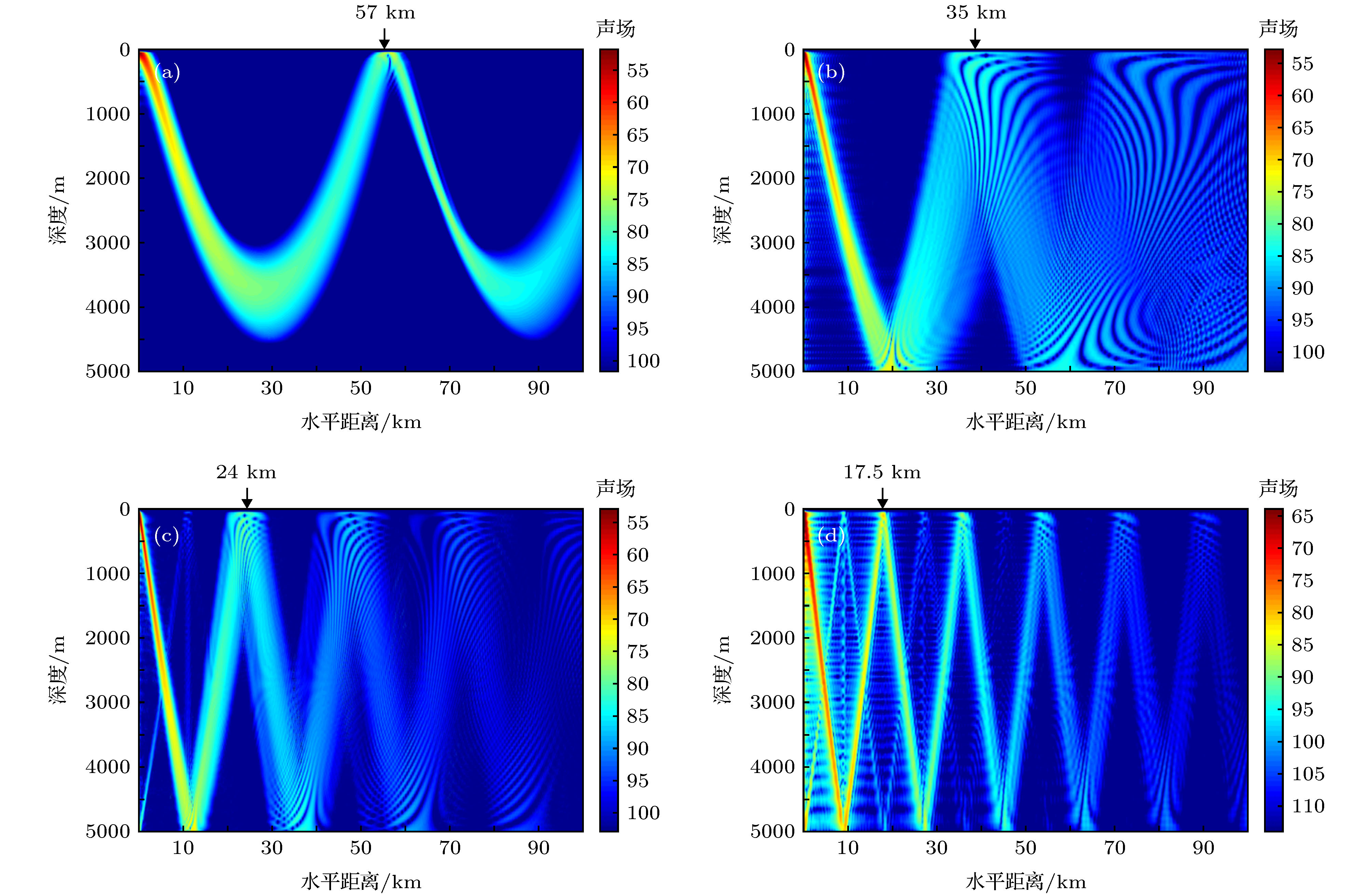
图 4 不同简正波(声线)簇形成的声场 (a) 1—120阶简正波(出射角0°—9.5°的声线)叠加声场; (b) 121—216阶简正波(出射角9.5°—18.2°的声线)叠加声场; (c) 217—314阶简正波(出射角18.2°—27.6°声线)叠加声场; (d) 315—354阶简正波(出射角27.6°—31.7°声线)叠加声场
Figure 4. Acoustic field formed by different normal mode (ray) clusters: (a) Acoustic field formed by normal mode 1 to normal mode 120 (rays with emanating angle from 0° to 9.5°); (b) acoustic field formed by normal mode 121 to normal mode 216 (rays with ema-nating angle from 9.5° to 18.2°); (c) acoustic field formed by normal mode 217 to normal mode 314 (rays with emanating angle from 18.2° to 27.6°); (d) acoustic field formed by normal mode 315 to norm al mode 354 (rays with emanating angle from 27.6° to 31.7°).
图 5 角谱域上20°掠射角对应的两种声线示意图
Figure 5. Sketch map of two types of rays with the value of 20° in angle dimension.
图 6 声源频率变化时声场角谱域分布WKBZ仿真结果与理论预报结果比较(声源深度50 m) (a) 100 Hz; (b) 200 Hz; (c) 300 Hz
Figure 6. Comparison of WKBZ simulation and theoretical prediction about acoustic field distribution of angle dimension when source frequency varies (source depth is 50 m): (a) 100 Hz; (b) 200 Hz; (c) 300 Hz.
图 7 声源深度变化时声场角谱域分布WKBZ仿真结果与理论预报结果比较(声源频率100 Hz) (a) 30 m; (b) 50 m; (c) 80 m
Figure 7. Comparison of WKBZ simulation and theoretical prediction about acoustic field distribution of angle dimension when source depth varies (source frequency is 100 Hz): (a) 30 m; (b) 50 m; (c) 80 m.
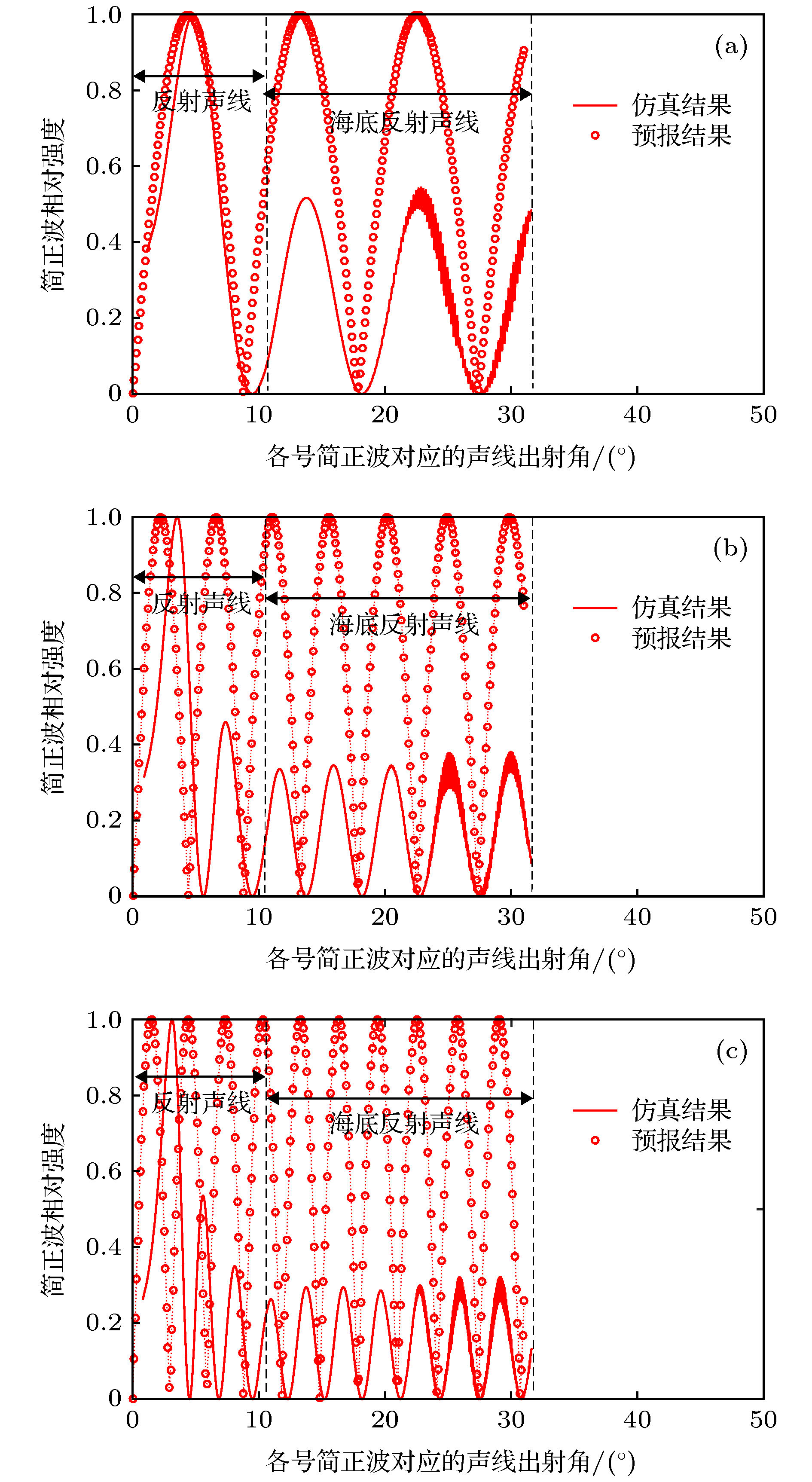
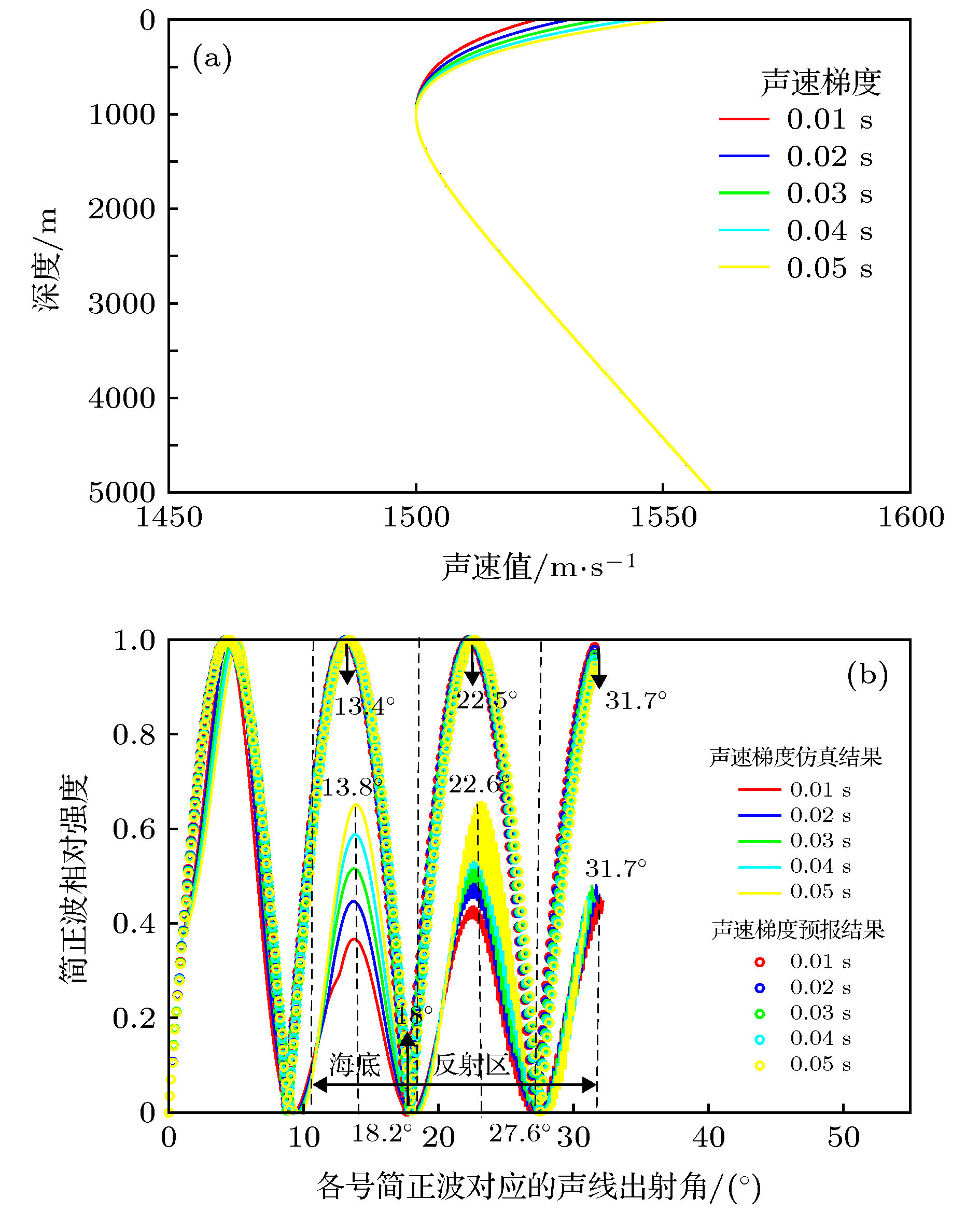
图 8 声速梯度变化时声场角谱域分布WKBZ仿真结果和理论预报结果比较 (a) 不同跃变层声速梯度下声速剖面; (b) 结果比较
Figure 8. Comparison of WKBZ simulation and theoretical prediction about acoustic field distribution of angle dimension when sound velocity gradient varies: (a) Sound velocity profiles when sound velocity gradient varies; (b) comparison of results.
图 9 声道轴深度变化时声场角谱域分布WKBZ仿真结果和理论预报结果比较 (a)不同声道轴深度下声速剖面; (b) 结果比较
Figure 9. Comparison of WKBZ simulation and theoretical prediction about acoustic field distribution of angle dimension when channel axis depth varies: (a) Sound velocity profiles when channel axis depth varies; (b) comparison of results.
图 10 海深变化时声场角谱域分布WKBZ仿真结果和理论预报结果比较 (a)不同海深下声速剖面; (b)结果比较
Figure 10. Comparison of WKBZ simulation and theoretical prediction about acoustic field distribution of angle dimension when sea depth varies: (a) Sound velocity profiles when sea depth varies; (b) comparison of results.
图 11 基于声场角谱域分布结构的主动声纳发射脉冲串信号设计
Figure 11. Pulse signal design of active sonar based on acoustic field distribution of angle dimension.
图 12 声场角谱域分布结构
Figure 12. Acoustic field distribution of angle dimension.
图 13 本文方法和随机设置方法阵增益比较 (a) 不同方法阵增益比较; (b) 声传播损失及声纳可探测区分布情况
Figure 13. Array gain comparision between method of this article and the method of random setting: (a) Array gains of different methods; (b) transmission loss and distribution of detectable areas.
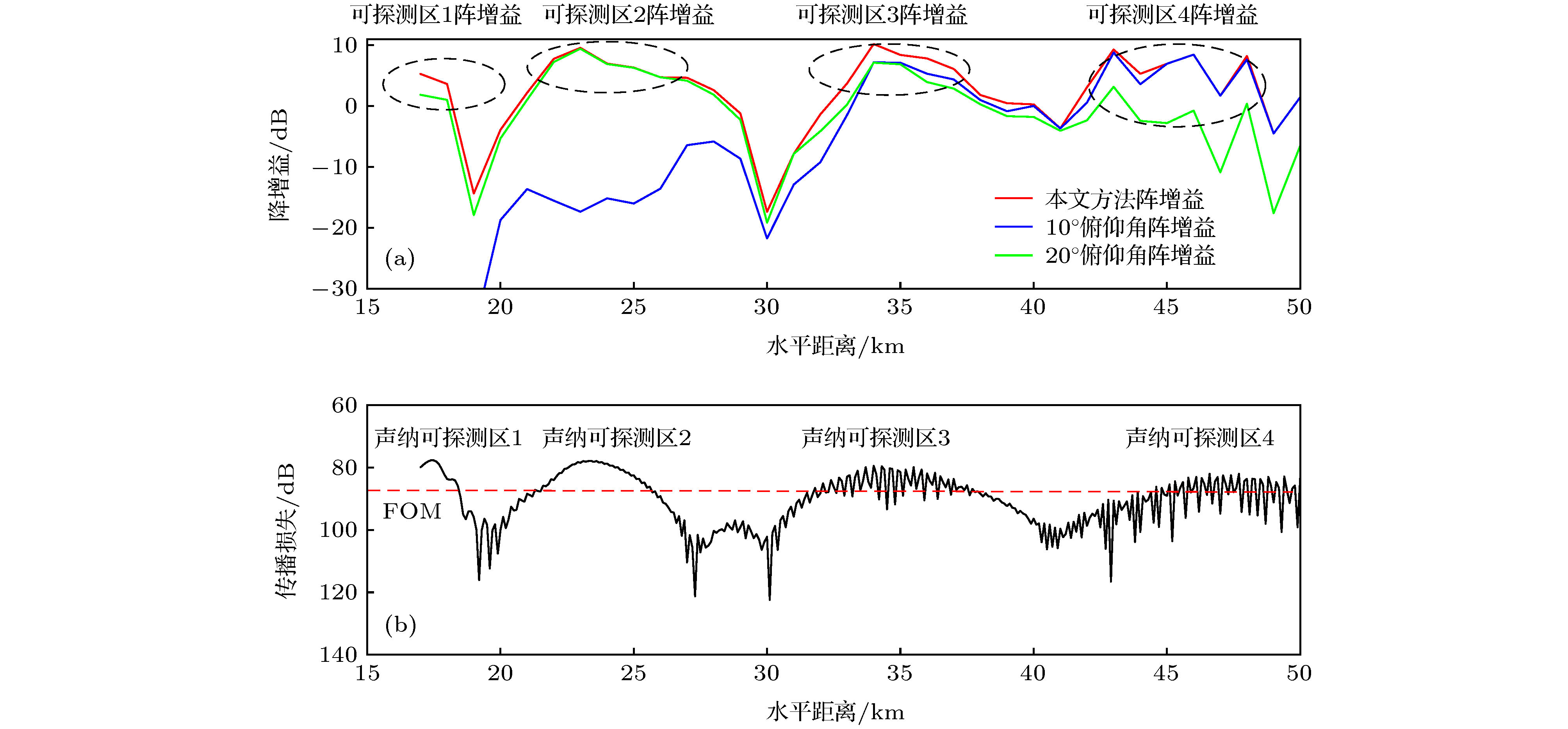
表 1 本文方法和传统随机设置波束俯仰角方法阵增益比较数据表
Table 1. Array gain comparison data form between method of this article and the method of random setting.
可探测区1 可探测区2 可探测区3 可探测区4 所有可探测区(15—50 km) 本文方法 4.5 6.0 5.7 8.0 6.4 10º俯仰角, 传统方法 –10.4 –14.0 3.7 7.0 –2.4 20º俯仰角, 传统方法 1.7 5.7 3.5 1.2 3.3 
DownLoad: CSV
-
[1] Udovydchenkov I A, Stephen R A, Duda T F, Bolmer S T, Worcester P F, Dzieciuch M A, Mercer J A, Andrew R K, Howe B M 2012 J. Acoust. Soc. Am. 132 2224
Google Scholar
[2] Chuprov S D, Maltsev N E 1981 Doklady Akademii Nauk SSSR 257 474
[3] 翁晋宝, 李风华, 郭永刚 2016 声学学报 41 330
Weng J B, Li F H, Guo Y G 2016 Acta Acustica 41 330
[4] 段睿 2016 博士学位论文 (西安: 西北工业大学)
Duan R 2016 Ph.D. Dissertation (Xi’an: Northwestern Polytechnical University) (in Chinese)
[5] 翁晋宝 2015 博士学位论文 (北京: 中国科学院大学)
Weng J B 2015 Ph.D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[6] Harrison C H 2011 J. Acoust. Soc. Am. 129 2863
Google Scholar
[7] Colosi J A, Duda T F, Morozov A K 2012 J. Acoust. Soc. Am. 131 1749
Google Scholar
[8] Finn B J, William A K, Michael B P, Henrik S 2000 Computational Ocean Acoustics (Vol. 2) (New York: AIP Press/Springer) p340
[9] 郭晓乐, 杨坤德, 马远良, 杨秋龙 2016 65 214302
Google Scholar
Guo X L, Yang K D, Ma Y L 2016 Acta Phys. Sin. 65 214302
Google Scholar
[10] 张仁和, 何怡, 刘红 1994 声学学报 9 1
Zhang R H, He Y, Liu H 1994 Acta Acustica 9 1
[11] Tindle C T, Guthrie K M 1974 J. Sound Vib. 34 291
Google Scholar
[12] Kamel A, Felsen L B 1982 J. Acoust. Soc. Am. 71 1445
Google Scholar
[13] 林巨, 赵越, 王欢, 陈鹏 2015 南京大学学报: 自然科学 51 1223
Lin J, Zhao Y, Wang H, Chen P 2015 J. Nanjing Univ. Nat. Sci. 51 1223
[14] 韩志斌, 彭朝晖, 刘扬 2019 应用声学 38 569
Google Scholar
Han Z B, Peng Z H, Liu Y 2019 Journal of Applied Acoustic 38 569
Google Scholar
[15] 吴俊楠, 周士弘, 张岩 2016 中国科学: 物理学 力学 天文学 46 094311
Google Scholar
Wu J N, Zhou S H, Zhang Y 2016 Sci. Sin. Phys. Mech. Astron. 46 094311
Google Scholar
[16] Wu J N, Zhou S H, Peng Z H, Zhang Y, Zhang R H 2016 Chin. Phys. B 25 124311
Google Scholar
[17] 刘伯胜, 雷家煜 1993 水声学原理 (哈尔滨: 哈尔滨工程大学出版社) 第106页
Liu B S, Lei J Y 1993 Principles of Underwater Sound (Haerbin: Haerbin Engineering University Press) p106 (in Chinese)
[18] 谢磊, 孙超, 刘雄厚, 蒋光禹 2016 65 144303
Google Scholar
Xie L, Sun C, Liu X H, Jiang G Y 2016 Acta Phys. Sin. 65 144303
Google Scholar
[19] 杨坤德, 孙超 2007 电声技术 31 4
Google Scholar
Yang K D, Sun C, 2007 Audio Eng. 31 4
Google Scholar
[20] 宋俊 2005 博士学位论文 (长沙: 国防科技大学)
Song J 2005 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
DownLoad:
Catalog
Metrics
- Abstract views: 9537
- PDF Downloads: 151
- Cited By: 0
