-
As a typical phase transition material, vanadium dioxide has attracted much attention in the study of metal-insulator transition behavior since its phase transition temperature is close to room temperature. The experimental results of various modulation provide important clues to studying the vanadium dioxide phase transition mechanism. These experiments not only deepen the understanding of the strong correlation between electrons with different spins in various transition metal oxides, but also make an opportunity for exploring their potential practical applications. Although the phase transition mechanism of vanadium dioxide is still controversial, one has already made tremendous efforts to understand the mechanism of metal-insulation phase transition in the past few decades, which is stimulated from various experiments on vanadium dioxide modulation. Here in this work, the single crystal and polycrystalline vanadium dioxide are investigated. Their modulation mechanisms are studied by using the continuous laser pumping-terahertz probe technique, and it is found that the absorption behaviors of terahertz pulses at the same pump fluence are obviously different. After systematically discussing the representative phase transition mechanism, it is found that the phase transition of single crystal vanadium dioxide is attributed to the Mott-type phase transition dominated by the electronic structure, and that the polycrystalline vanadium dioxide originates from the Peierls-type phase transition occurring during the lattice distortion. In the past, most of the optical modulation was implemented under the condition of femtosecond laser pumping. The new optical modulation method given in this work, is a supplement to previous all-optical modulation experiment and more likely to be conducive to a more in-depth understanding of the modulation mechanism of vanadium dioxides.
-
Keywords:
- terahertz wave /
- optical modulation /
- vanadium dioxide /
- phase transition
[1] Hahn S Y, Kim K L, Kim K M, et al. 2019 Nature 570 496
Google Scholar
[2] Chen C, Jiang K, Zhang Y, Liu C F, Wang Z Q, Wang J 2020 Nat. Phys. 16 536
Google Scholar
[3] Gogoi P K, Hu Z L, Wang Q X, et al. 2017 Phys. Rev. Lett. 119 077402
Google Scholar
[4] Li Z P, Wang T M, Lu Z G, et al. 2018 Nat. Commun. 9 1
Google Scholar
[5] Chen G, Jiang L L, Wu S, et al. 2019 Nat. Phys. 15 237
Google Scholar
[6] Shao Z W, Cao X, Luo H J, Jin P 2018 NPG Asia Mater. 10 581
Google Scholar
[7] Imada, Masatoshi, Fujimori, Atsushi, Tokura, Yoshinori 1998 Rev. Mod. Phys. 70 1039
Google Scholar
[8] Schwingenschlogl U, Eyert V 2004 Ann. Phys. Berlin. 13 475
Google Scholar
[9] Kasirga T S, Sun D, Park J, Coy J, Fei Z Y, Xu X D, Cobden D 2012 Nat. Nanotechnol. 7 723
Google Scholar
[10] Liu K, Cheng C, Cheng Z T, Wang K, Ramesh R, Wu J Q 2012 Nano Lett. 12 6302
Google Scholar
[11] Laad M S, Craco L, Muller-Hartmann E 2006 Phys. Rev. B. 73 195120
Google Scholar
[12] Vikhnin V S, Lysenko S, Rua A, Fernandez F, Liu H 2006 Solid State Commun. 137 615
Google Scholar
[13] Woodley M S 2008 Chem. Phys. Lett. 453 167
Google Scholar
[14] Lazarovits B, Kim K, Haule K, Kotliar G 2010 Phys. Rev. B 81 115117
Google Scholar
[15] Eyert V 2011 Phys. Rev. Lett. 107 016401
Google Scholar
[16] Morin F J 1959 Phys. Rev. Lett. 3 34
Google Scholar
[17] Mengkun L, Harold Y H, Hu T, et al. 2012 Nature 487 345
Google Scholar
[18] Ji C H, Wu Z M, Wu X F, et al. 2018 J. Mater. Chem. C 6 1722
Google Scholar
[19] Tiegui L, Langping W, Xiaofeng W, Yufen Z, Yonghao Y 2016 Appl. Surf. Sci. 379 179
Google Scholar
[20] Tselev S, Luk’yanchuk I A, Lvanov I N, et al. 2010 Nano Lett. 10 4409
Google Scholar
[21] Peierls R E 1991 More Surprises in Theoretical Physics (Princeton: Princeton University Press) Vol.19
[22] Mott N F 1949 Proc. Phys. Soc. 62 416
Google Scholar
[23] Tan X G, Yao T, Long R, et al. 2012 Sci. Rep. 2 1
[24] Li X Y, Gloter A, Zobelli A, Gu H, Cao X, Jin P, Colliex C 2014 Acta Mater. 80 16
Google Scholar
[25] Becker M F, Buckman A B, Walser R M, Lepine T, Georges P, Brun A 1994 Appl. Phys. Lett. 65 1507
Google Scholar
[26] He X F, Xu J, Xu X F, et al. 2015 Appl. Phys. Lett. 106 093106
Google Scholar
[27] Hyun-Tak K, Byung-Gyu C, Doo-Hyeb Y, et al. 2005 Appl. Phys. Lett. 86 242101
Google Scholar
[28] Nakano M, Shibuya K, Okuyama D, Hatano T, Ono S, Kawasaki M, Iwasa Y, Tokura Y 2012 Nature. 487 459
Google Scholar
[29] Jeon T, Grischkowsky D 1998 Appl. Phys. Lett. 72 3032
Google Scholar
[30] Hubbard J 1964 Pro. Roy. Soc (London) 276 238
[31] Cocker T L, Titova L V, Fourmaux S, et al. 2012 Phys. Rev. B 85 155120
Google Scholar
-
图 1 (a)光调制角分辨太赫兹时域光谱系统装置图; (b) 原理示意图; (c) X射线衍射光谱
Figure 1. (a) Experimental setup of optical modulation angle resolved terahertz time-domain spectroscopy; (b) schematic diagram; (c) X-ray diffraction spectrum of single crystal VO2.
图 2 太赫兹波入射角为30° (a)透射时域波形信号; (b)局部放大的透射峰值时域信号; (c)不同调制激光通量下的调制深度; (d)—(f)与透射光谱相对应的反射光谱信号
Figure 2. When the incidence angle of the terahertz pulses was fixed at 30°, the variations for (a) the transmitted terahertz temporal waveforms; (b) the zoomed in temporal transmission waveforms; (c) modulation depth under different optical modulation fluences; (d)—(f) the corresponding reflection spectra.
图 3 (a)旋转样品方位角对透射信号的影响; (b)随着调制通量的增大, 反射信号、透射信号和样品吸收的太赫兹信号的峰值变化; (c) 0.79和1.09 THz频率时, 随抽运通量线性增长的材料电导率; 不同调制通量作用下, 单晶二氧化钒在太赫兹频段的(d)消光系数; (e)折射率; 以及(f)电导率
Figure 3. (a) The effect of the rotating sample azimuth on the transmission signal; (b) with the increase of the fluence, the variation of peak value of the reflected signal, the transmitted signal, and the terahertz absorbed by the sample; (c) the linear increasing conductivity with respect to the pump fluence under two exemplified frequencies 0.79 and 1.09 THz; (d) the wide-spectrum extinction coefficient, (e) refractive index, (f) conductivity of single crystal vanadium dioxide in terahertz region under the different pump fluences.
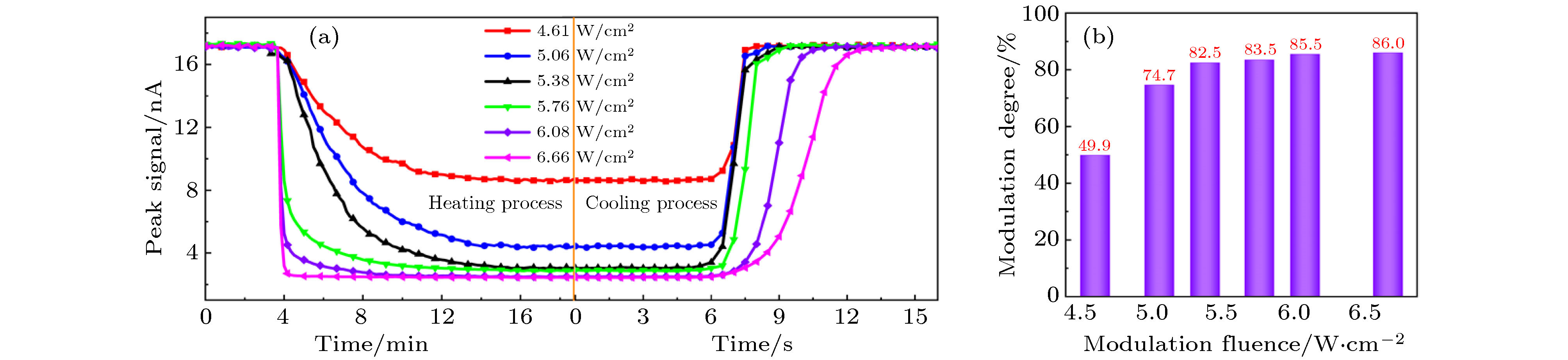
图 4 连续激光照射多晶二氧化钒对太赫兹波的调制实验结果 (a)不同调制光通量下, 太赫兹透射信号峰值随外加调制激光照射时间和撤去激光的变化过程; (b)透射调制深度随着调制光通量的变化关系
Figure 4. Experimental results for terahertz modulation in polycrystalline vanadium dioxide illuminated by various modulation fluences: (a) The transmitted THz signal peak values as a function of the illumination time and crystal cooling time under various modulation fluences, respectively; (b) modulation fluence dependent on THz modulation depth.
图 5 二氧化钒不同相的晶体结构和其对应的能带结构
Figure 5. The crystal structures of different phases of vanadium dioxide and the corresponding band structures.
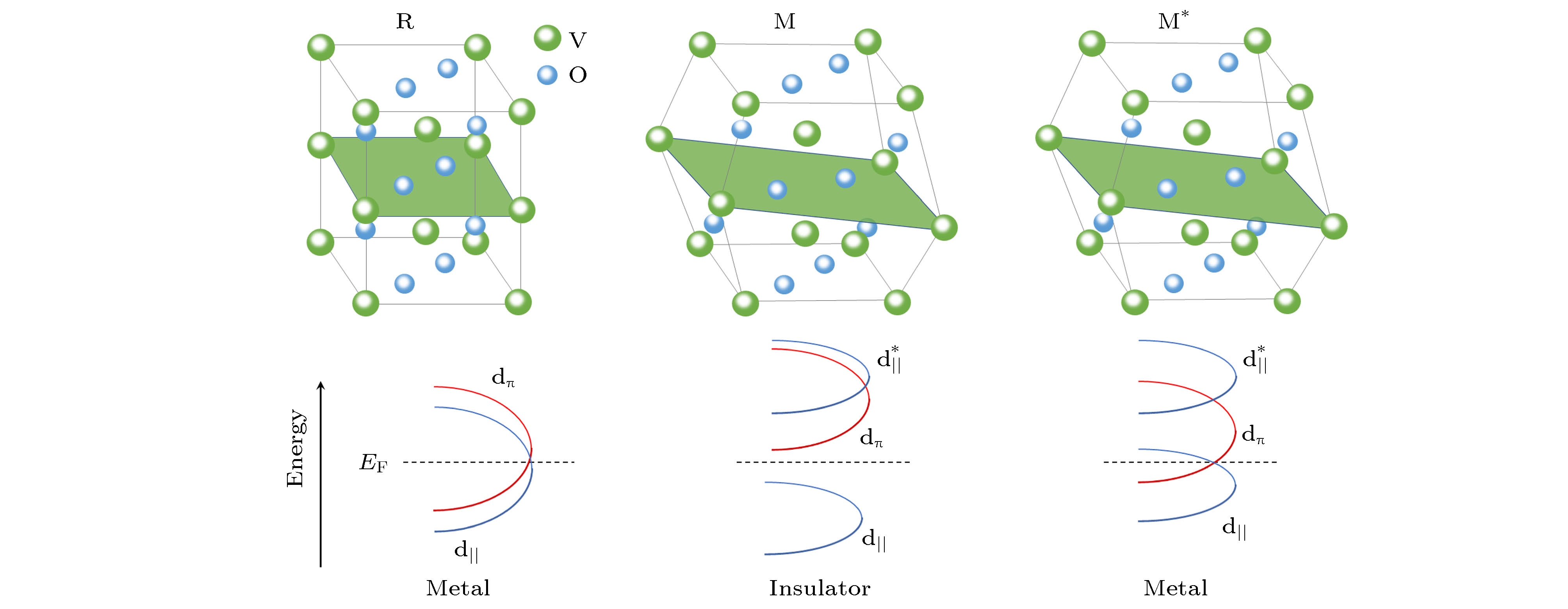
图 6 Peierls型相变原理示意图 (a)热激发直接导致声子的激发或800 nm (1.55 eV)抽运脉冲的光激发导致自由电子的激发, 并间接导致声子的激发, 这都将导致绝缘晶格到金属晶格的转变; (b)如果外界一直提供相变潜热, 则激发的声子从成核中心向四周扩散, 直到周围超过临界密度破坏单斜结构完成绝缘金属转变, 实现金属区域的扩大
Figure 6. Schematic diagram of Peierls-type phase transition. (a) Thermal excitation directly leads to the excitation of phonons or photoexcitation with 800 nm (1.55 eV) pump pulse results in the excitation of free electrons and indirectly results in excitation of phonons, which map the insulating lattice onto the metallic lattice. (b) If the external environment always provided the latent heat, the phonons would diffuse from the nucleation center to the surroundings until the phonon density exceeded the critical density and destroyed the monoclinic structure to complete the insulating metal transition and realized the expansion of the metal domain.
-
[1] Hahn S Y, Kim K L, Kim K M, et al. 2019 Nature 570 496
Google Scholar
[2] Chen C, Jiang K, Zhang Y, Liu C F, Wang Z Q, Wang J 2020 Nat. Phys. 16 536
Google Scholar
[3] Gogoi P K, Hu Z L, Wang Q X, et al. 2017 Phys. Rev. Lett. 119 077402
Google Scholar
[4] Li Z P, Wang T M, Lu Z G, et al. 2018 Nat. Commun. 9 1
Google Scholar
[5] Chen G, Jiang L L, Wu S, et al. 2019 Nat. Phys. 15 237
Google Scholar
[6] Shao Z W, Cao X, Luo H J, Jin P 2018 NPG Asia Mater. 10 581
Google Scholar
[7] Imada, Masatoshi, Fujimori, Atsushi, Tokura, Yoshinori 1998 Rev. Mod. Phys. 70 1039
Google Scholar
[8] Schwingenschlogl U, Eyert V 2004 Ann. Phys. Berlin. 13 475
Google Scholar
[9] Kasirga T S, Sun D, Park J, Coy J, Fei Z Y, Xu X D, Cobden D 2012 Nat. Nanotechnol. 7 723
Google Scholar
[10] Liu K, Cheng C, Cheng Z T, Wang K, Ramesh R, Wu J Q 2012 Nano Lett. 12 6302
Google Scholar
[11] Laad M S, Craco L, Muller-Hartmann E 2006 Phys. Rev. B. 73 195120
Google Scholar
[12] Vikhnin V S, Lysenko S, Rua A, Fernandez F, Liu H 2006 Solid State Commun. 137 615
Google Scholar
[13] Woodley M S 2008 Chem. Phys. Lett. 453 167
Google Scholar
[14] Lazarovits B, Kim K, Haule K, Kotliar G 2010 Phys. Rev. B 81 115117
Google Scholar
[15] Eyert V 2011 Phys. Rev. Lett. 107 016401
Google Scholar
[16] Morin F J 1959 Phys. Rev. Lett. 3 34
Google Scholar
[17] Mengkun L, Harold Y H, Hu T, et al. 2012 Nature 487 345
Google Scholar
[18] Ji C H, Wu Z M, Wu X F, et al. 2018 J. Mater. Chem. C 6 1722
Google Scholar
[19] Tiegui L, Langping W, Xiaofeng W, Yufen Z, Yonghao Y 2016 Appl. Surf. Sci. 379 179
Google Scholar
[20] Tselev S, Luk’yanchuk I A, Lvanov I N, et al. 2010 Nano Lett. 10 4409
Google Scholar
[21] Peierls R E 1991 More Surprises in Theoretical Physics (Princeton: Princeton University Press) Vol.19
[22] Mott N F 1949 Proc. Phys. Soc. 62 416
Google Scholar
[23] Tan X G, Yao T, Long R, et al. 2012 Sci. Rep. 2 1
[24] Li X Y, Gloter A, Zobelli A, Gu H, Cao X, Jin P, Colliex C 2014 Acta Mater. 80 16
Google Scholar
[25] Becker M F, Buckman A B, Walser R M, Lepine T, Georges P, Brun A 1994 Appl. Phys. Lett. 65 1507
Google Scholar
[26] He X F, Xu J, Xu X F, et al. 2015 Appl. Phys. Lett. 106 093106
Google Scholar
[27] Hyun-Tak K, Byung-Gyu C, Doo-Hyeb Y, et al. 2005 Appl. Phys. Lett. 86 242101
Google Scholar
[28] Nakano M, Shibuya K, Okuyama D, Hatano T, Ono S, Kawasaki M, Iwasa Y, Tokura Y 2012 Nature. 487 459
Google Scholar
[29] Jeon T, Grischkowsky D 1998 Appl. Phys. Lett. 72 3032
Google Scholar
[30] Hubbard J 1964 Pro. Roy. Soc (London) 276 238
[31] Cocker T L, Titova L V, Fourmaux S, et al. 2012 Phys. Rev. B 85 155120
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6358
- PDF Downloads: 147
- Cited By: 0
