-
Quantum phase transition of ultracold atomic gas is one of the core contents in the study of quantum correlational many-body systems. In this paper, two-dimensional (2D) optical lattices are generated by a single fold retroreflected laser beam, and this scheme is used to experimentally design and implement the 2D optical lattice of double wells suitable for isolating and manipulating an array of individual pairs of atoms and predict a topological semimetal in the high orbital bands in this 2D lattice. Two types of optical lattice structures are produced by controlling the laser polarization. One type is the usual 2D optical lattice, which is formed by two independent one-dimensional(1D) optical lattices in two directions and named in-plane lattice, and the other type is the lattice that is formed by the interference between two one-dimensional optical lattices in two directions and called out-plane lattice. When 87Rb BEC (Bose-Einstein condensation) is loaded into the 2D optical lattice, the quantum phase transition between superfluid state and Mott insulator state is observed by controlling the tunneling and in-site interaction. And the phase transition from superfluid state to Mott insulator is judged by observing whether there are interferential lattice points in momentum space. The lattice depths of two cases can be calibrated by Kapitza-Dirac scattering in the ultracold atomic experiment through the time-of-flight absorption imaging. In the in-plane optical lattice, some incorrect points appear in the 45° direction, because the linear polarization degree of beam is impure after being reflected by mirrors and two direction of beam are not completely orthogonal to each other. It is obvious that the two cases have different phase transition points, which is due mainly to the difference in structure. For the in-plane lattice, there are two independent 1D optical lattices, and for the out-plane lattice, the two direction beams mutually interfere with each other, therefore, two optical lattices are not independent of each other. The atoms come back to BEC by reducing the potentials of optical lattice to zero; the temperature of system is slightly higher, because of the jitter of the light lattice. The different behaviors of quantum phase transition are analyzed for two types of optical lattices. This work will provide a platform for the future study of large spin system and strong correlation physics in optical lattices.
-
Keywords:
- optical lattice /
- quantum transition /
- many-body physics /
- superfluid /
- Mott insulator
[1] 文小刚(胡滨译) 2003 量子多体理论(北京: 高等教育出版社) 第1页
Wen Xiaogang (translated by Hu Bin) 2003 The theory of Quantum Many-body Systems (Beijing: High Education Press) p1 (in Chinese)
[2] Sherson J F, Weitenberg C, Endres M, Cheneau M, Bloch I, Kuhr S 2010 Nature 467 68
Google Scholar
[3] Parsons M F, Huber F, Mazurenko A, Chiu C S, Setiawan W, Wooley-Brown K, Blatt S, Greiner M 2015 Phys. Rev. Lett. 114 213002
Google Scholar
[4] Bloch I, Greiner M 2005 Adv. Atom. Mol. Opt. Phys. 52 1
Google Scholar
[5] Vuletić, V, Ch an, H W, Black A T 2001 Phys. Rev. A 64 033405
Google Scholar
[6] Wang Y, Zhang X, Corcovilos T A, Kumar A, Weiss D S 2015 Phys. Rev. Lett. 115 043003
Google Scholar
[7] Kumar A, Wu T Y, Giraldo F, Weiss D S 2018 Nature 561 83
Google Scholar
[8] Kim M E, Chang T H, Fields B M, Chen C A, Hung C L 2019 Nat. commun. 10 1
Google Scholar
[9] Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39
Google Scholar
[10] Bernier J S, Sengupta K, Kim Y B 2007 Phys. Rev. B 76 014502
Google Scholar
[11] Kimura T, Tsuchiya S, Kurihara S 2005 Phys. Rev. Lett. 94 110403
Google Scholar
[12] Garcia-Ripoll J J, Martin-Delgado M A, Cirac J I 2004 Phys. Rev. Lett. 93 250405
Google Scholar
[13] Tu H-H, Zhang G-M, Yu L 2007 Phys. Rev. B 76 014438
Google Scholar
[14] Tu H-H, Zhang G-M, Yu L 2006 Phys. Rev. B 74 174404
Google Scholar
[15] Wu C, Zhang S-C 2005 Phys. Rev. B 71 155115
Google Scholar
[16] Wu C, Hu J P, Zhang S C 2003 Phys. Rev. Lett. 91 186402
Google Scholar
[17] Sebby-Strabley J, Anderlini M, Jessen P S, Porto J V 2006 Phys. Rev. A 73 033605
Google Scholar
[18] Sun K, Liu W V, Hemmerich A, Sarma S D 2012 Nat. Phys. 8 67
Google Scholar
[19] Jaksch D, Bruder C, Cirac J I, Gardiner C W, Zoller P 1998 . Phys. Rev. Lett. 81 3108
Google Scholar
[20] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885
Google Scholar
[21] Capogrosso-Sansone B, Söyler Ş G, Prokof’ev N, Svistunov B 2008 Phys. Rev. A 77 015602
Google Scholar
[22] Wen K, Meng Z M, Wang P J, Wang L W, Chen L C, Huang L H, Zhou L H, Cui X L, Zhang J 2020 Sci. Rep 10 5870
Google Scholar
[23] Xiong D Z, Wang P J, Chen H X, Zhang J 2010 Chin. Opt. Lett. 8 351
Google Scholar
[24] Chen H X, Xiong D Z, Wang P J, Zhang J 2010 Chin. Opt. Lett. 8 348
Google Scholar
[25] 陈良超, 孟增明, 王鹏军 2017 66 083701
Google Scholar
Chen L C, Meng Z M, Wang P J 2017 Acta Phys. Sin. 66 083701
Google Scholar
[26] 柴世杰, 王鹏军, 付正坤, 黄良辉, 张靖 2012 量子光学学报 18 171
Google Scholar
Chai S J, Wang P J, Fu Z K, Huang L H, Zhang J 2012 Acta Sin. Quantum Opt. 18 171
Google Scholar
[27] 王鹏军, 熊德智, 陈海霞, 张靖 2010 光学学报 30 893
Google Scholar
Wang P J, Xiong D Z, Chen H X, Zhang J 2010 Acta Opt. Sin. 30 893
Google Scholar
[28] Spielman I B, Phillips W D, Porto J V 2007 Phys. Rev. Lett. 98 080404
Google Scholar
-
图 1 超冷原子在光晶格中的隧穿
Figure 1. The tunneling of ultracold atoms in optical lattice.
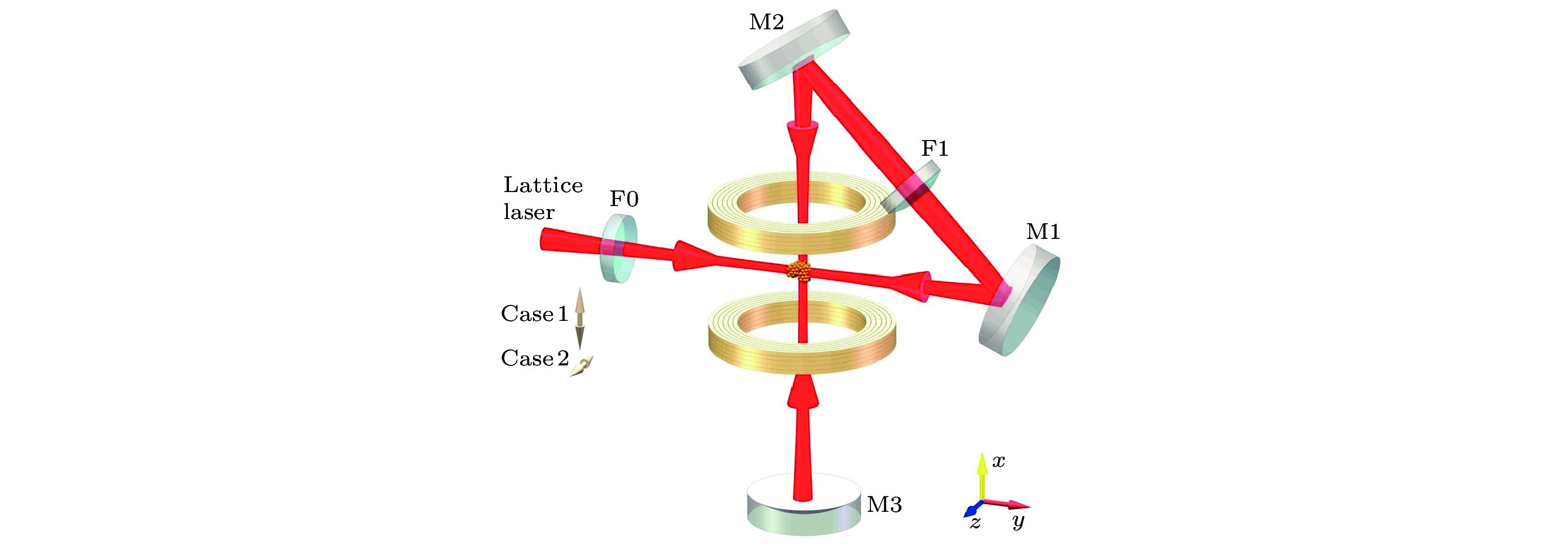
图 2 实验装置二维光晶格由一束激光往返产生, 其中方案1和方案2分别代表激光偏振平行和垂直于光束所在平面的两种情况
Figure 2. Schematic diagram of the experimental setup to realize the two-dimensional optical lattices. The two-dimensional optical lattices are made of a single fold retroreflected laser beam. The linearly polarization of the incident laser beam aligned parallel (case 1) or normal (case 2) to the drawing plane can generate two different cases of two-dimensional optical lattice potentials.
图 3 两种光晶格 (a)方案1的面内光晶格空间分布; (b)方案2的面外光晶格空间分布; (c)方案1的晶胞; (d)方案2的晶胞; (e)两种光晶格势在xz平面上的分布
Figure 3. Two types of optical lattices: (a) Spatial distribution pattern of in-plane optical lattice for case 1; (b) spatial distribution pattern of out-plane optical lattice for case 2; (c) unit cell for case 1; (d) unit cell for case 2; (e) the potentials of two types of optical lattices(V = –Er).
图 4 实验时序图 红色表示的光晶格光强的变化, 最后自由飞行12 ms吸收成像, 其中(a)表示SF到MI的时序, (b)表示BEC到MI再到BEC的时序
Figure 4. Schematic diagram of the experimental sequence: The red lines show the light intensity of optical lattice, and finally have an imaging of TOF 12 ms. The drawing (a) shows the sequence of SF to MI, drawing (b) shows the sequence of BEC to MI, and back to BEC.
图 5 方案1的量子相变 (a0)表示获得MI态的时序图, (a1)到(a4)为SF态相变到MI态的过程, (a1)中红色标注为光晶格格点, (a2)中白色标注的格点主要由于激光偏振不纯、x轴和y轴方向上的光路不完全正交所导致的, 当势阱逐渐加深, 隧穿开始加强, 这些格点也越明显; (b0)为BEC相变到MI态, 再相变回BEC的时序图, 分别对应(b1)—(b4)
Figure 5. Quantum phase transition for case 1: (a0) Reveals the sequence diagram of BEC to MI, from (a1) to (a4), show the imaging from SF to MI. In (a1), the red dashed circles show the lattice points, and in (a2), the white dashed circles show some incorrect lattice points, because the linearly polarization is impure and two beam paths along x axis and y axis are not totally orthogonal. Increasing potentials, these lattice points are more obvious; (b0) reveals the sequence diagram of MI to BEC, (b1) to (b4) show the imaging of MI to BEC after decreasing the potentials to zero.
图 6 方案2的量子相变 (a0)表示获得MI态的时序图, 其中(a1)到(a4)为体系从SF相变到MI的过程; (b0)为BEC相变到MI态, 再相变回BEC的时序图, 其中(b1)到(b4)分别对应(a)中光晶格势阱降低到零, 重新获得BEC的空间分布图像
Figure 6. Quantum transition for case 2: (a0) Reveals the sequence diagram of BEC to MI, from (a1) to (a4), show the imaging from BEC to MI; (b0) reveals the sequence diagram of MI to BEC, from (b1) to (b4), show the imaging from MI to BEC.
-
[1] 文小刚(胡滨译) 2003 量子多体理论(北京: 高等教育出版社) 第1页
Wen Xiaogang (translated by Hu Bin) 2003 The theory of Quantum Many-body Systems (Beijing: High Education Press) p1 (in Chinese)
[2] Sherson J F, Weitenberg C, Endres M, Cheneau M, Bloch I, Kuhr S 2010 Nature 467 68
Google Scholar
[3] Parsons M F, Huber F, Mazurenko A, Chiu C S, Setiawan W, Wooley-Brown K, Blatt S, Greiner M 2015 Phys. Rev. Lett. 114 213002
Google Scholar
[4] Bloch I, Greiner M 2005 Adv. Atom. Mol. Opt. Phys. 52 1
Google Scholar
[5] Vuletić, V, Ch an, H W, Black A T 2001 Phys. Rev. A 64 033405
Google Scholar
[6] Wang Y, Zhang X, Corcovilos T A, Kumar A, Weiss D S 2015 Phys. Rev. Lett. 115 043003
Google Scholar
[7] Kumar A, Wu T Y, Giraldo F, Weiss D S 2018 Nature 561 83
Google Scholar
[8] Kim M E, Chang T H, Fields B M, Chen C A, Hung C L 2019 Nat. commun. 10 1
Google Scholar
[9] Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39
Google Scholar
[10] Bernier J S, Sengupta K, Kim Y B 2007 Phys. Rev. B 76 014502
Google Scholar
[11] Kimura T, Tsuchiya S, Kurihara S 2005 Phys. Rev. Lett. 94 110403
Google Scholar
[12] Garcia-Ripoll J J, Martin-Delgado M A, Cirac J I 2004 Phys. Rev. Lett. 93 250405
Google Scholar
[13] Tu H-H, Zhang G-M, Yu L 2007 Phys. Rev. B 76 014438
Google Scholar
[14] Tu H-H, Zhang G-M, Yu L 2006 Phys. Rev. B 74 174404
Google Scholar
[15] Wu C, Zhang S-C 2005 Phys. Rev. B 71 155115
Google Scholar
[16] Wu C, Hu J P, Zhang S C 2003 Phys. Rev. Lett. 91 186402
Google Scholar
[17] Sebby-Strabley J, Anderlini M, Jessen P S, Porto J V 2006 Phys. Rev. A 73 033605
Google Scholar
[18] Sun K, Liu W V, Hemmerich A, Sarma S D 2012 Nat. Phys. 8 67
Google Scholar
[19] Jaksch D, Bruder C, Cirac J I, Gardiner C W, Zoller P 1998 . Phys. Rev. Lett. 81 3108
Google Scholar
[20] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885
Google Scholar
[21] Capogrosso-Sansone B, Söyler Ş G, Prokof’ev N, Svistunov B 2008 Phys. Rev. A 77 015602
Google Scholar
[22] Wen K, Meng Z M, Wang P J, Wang L W, Chen L C, Huang L H, Zhou L H, Cui X L, Zhang J 2020 Sci. Rep 10 5870
Google Scholar
[23] Xiong D Z, Wang P J, Chen H X, Zhang J 2010 Chin. Opt. Lett. 8 351
Google Scholar
[24] Chen H X, Xiong D Z, Wang P J, Zhang J 2010 Chin. Opt. Lett. 8 348
Google Scholar
[25] 陈良超, 孟增明, 王鹏军 2017 66 083701
Google Scholar
Chen L C, Meng Z M, Wang P J 2017 Acta Phys. Sin. 66 083701
Google Scholar
[26] 柴世杰, 王鹏军, 付正坤, 黄良辉, 张靖 2012 量子光学学报 18 171
Google Scholar
Chai S J, Wang P J, Fu Z K, Huang L H, Zhang J 2012 Acta Sin. Quantum Opt. 18 171
Google Scholar
[27] 王鹏军, 熊德智, 陈海霞, 张靖 2010 光学学报 30 893
Google Scholar
Wang P J, Xiong D Z, Chen H X, Zhang J 2010 Acta Opt. Sin. 30 893
Google Scholar
[28] Spielman I B, Phillips W D, Porto J V 2007 Phys. Rev. Lett. 98 080404
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7285
- PDF Downloads: 157
- Cited By: 0
