-
Dicke model, as an important many-body model in quantum optics, describes the interaction between multiple identical two-level atoms and a quantized electromagnetic field. This spin-boson model shows collective phenomena in light-matter interaction systems and can undergo a second-order quantum phase transition from a normal phase to a superradiant phase when the coupling strength between the two-level atoms and the optical field exceeds a critical value. Dicke model embodies unique many-body quantum theories. And it has been widely studied and obtained many significant research results in quantum information, quantum process, and other quantum systems. Meanwhile, Dicke model also has wide applications in quantum optics and condensed matter physics. The extended Dicke model, describing the interaction of a Bose-Einstein condensate in an optical cavity, provides a remarkable platform for studying extraordinary quantum phase transitions in theory and experiment. Based on the recent experiment on non-Hermitian coupling between two long-lived atomic spin waves in an optical cavity, in this work we use spin-coherent-state variational method and present the macroscopic quantum-state energy of the non-Hermitian Dicke model. The spin coherent state variational method has an advantage in the theoretical research of macroscopic quantum states, especially in the normal and the inverted pseudospin states. In the variational method, optical coherent states and atomic extremum spin coherent states are used as the trial wave functions. A Hermitian transformation operator is proposed to diagonalize the non-Hermitian Hamiltonian, which is different from the ordinary quantum mechanics where the transformation operator must be unitary. Herein, the energy function is not necessarily real in the entire coupling region. Beyond an exceptional point, the spectrum becomes complex and introducing biorthogonal sets of atomic extremum states is necessary to evaluate the average quantities. The normal phase (for the zero average photon number) possesses real energy and atomic population. The non-Hermitian interaction destroys the superradiant phase (for the stable nonzero average photon number) and leads to the absence of quantum phase transition. However, the introduced atom-photon interaction, which is induced by the pump field experimentally, can change the situation, dramatically. The pump field can balance the loss by the non-Hermitian atom-photon interaction to achieve the superradiant phase. An interesting double exceptional point are observed in the energy functional. There is the real spectrum below the first exceptional point and beyond the second exceptional point, while there is a complex spectrum between these two exceptional points. The superradiant phase appears only beyond a critical value, which is related to the nonlinear interaction and the pump laser. A new and inverted quantum phase transition from the superradiant phase to the normal phase, is observed by modulating the atom-field coupling strength. The superradiant phase of the population inversion state appears for a negative effective frequency and a large atom-photon interaction. The influence of the dissipative coupling may be observed in cold atom experiment in an optical cavity. All the parameters adopted in this work are the actual experimental parameters. -
Keywords:
- non-Hermitian Dicke model /
- nonlinear atom-photon interaction /
- quantum phase transition /
- exceptional point
-
图 1 (a) 横向泵浦激光器捕获光腔中冷原子的实验原理图; (b) 大失谐$ {\varDelta _a} $下原子能级跃迁图
Figure 1. (a) Experimental schematic for cold atoms trapped in an optical cavity with a transverse pumping laser; (b) transition diagram of atomic energy level in the large detuning $ {\varDelta _a} $.
图 2 能量本征值的虚部$\text{Im} [{\varepsilon _ \pm }]$在${n_{\text{p}}}{\text{-}}g$平面的相图
Figure 2. Phase diagram of ${n_{\text{p}}}{\text{-}}g$ plane about the imaginary part of the eigenvalues $\text{Im} [{\varepsilon _ \pm }]$.
图 3 能量本征值${\varepsilon _ \pm }$的实部(1)和虚部(2)随原子-场耦合强度$g$(a)和平均光子数${n_{\text{p}}}$(b)变化的示意图
Figure 3. The real part (1) and the imaginary part (2) of the eigenvalue ${\varepsilon _ \pm }$ as a function of the atom-field coupling strength $g$(a) and the mean photon number ${n_{\text{p}}}$(b).
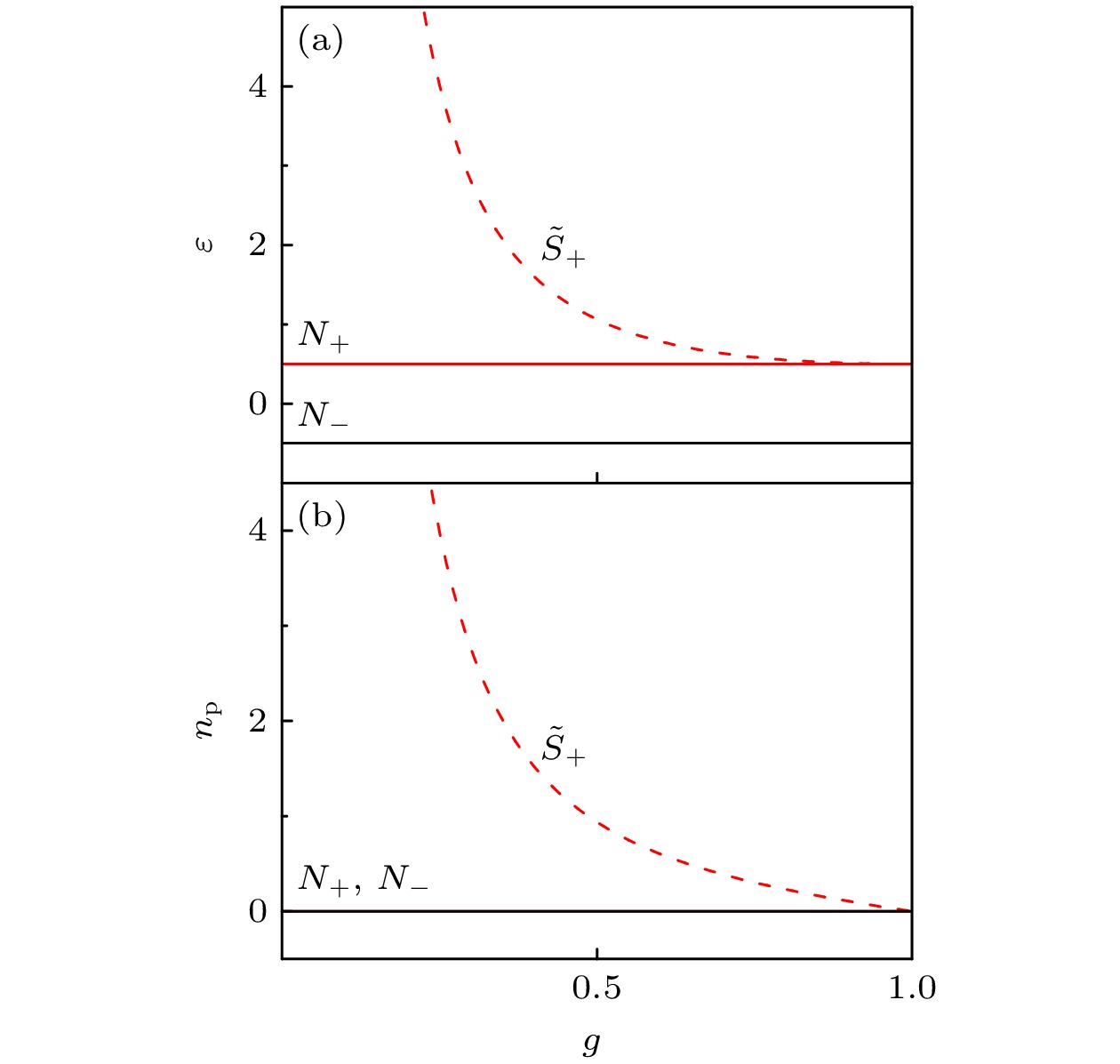
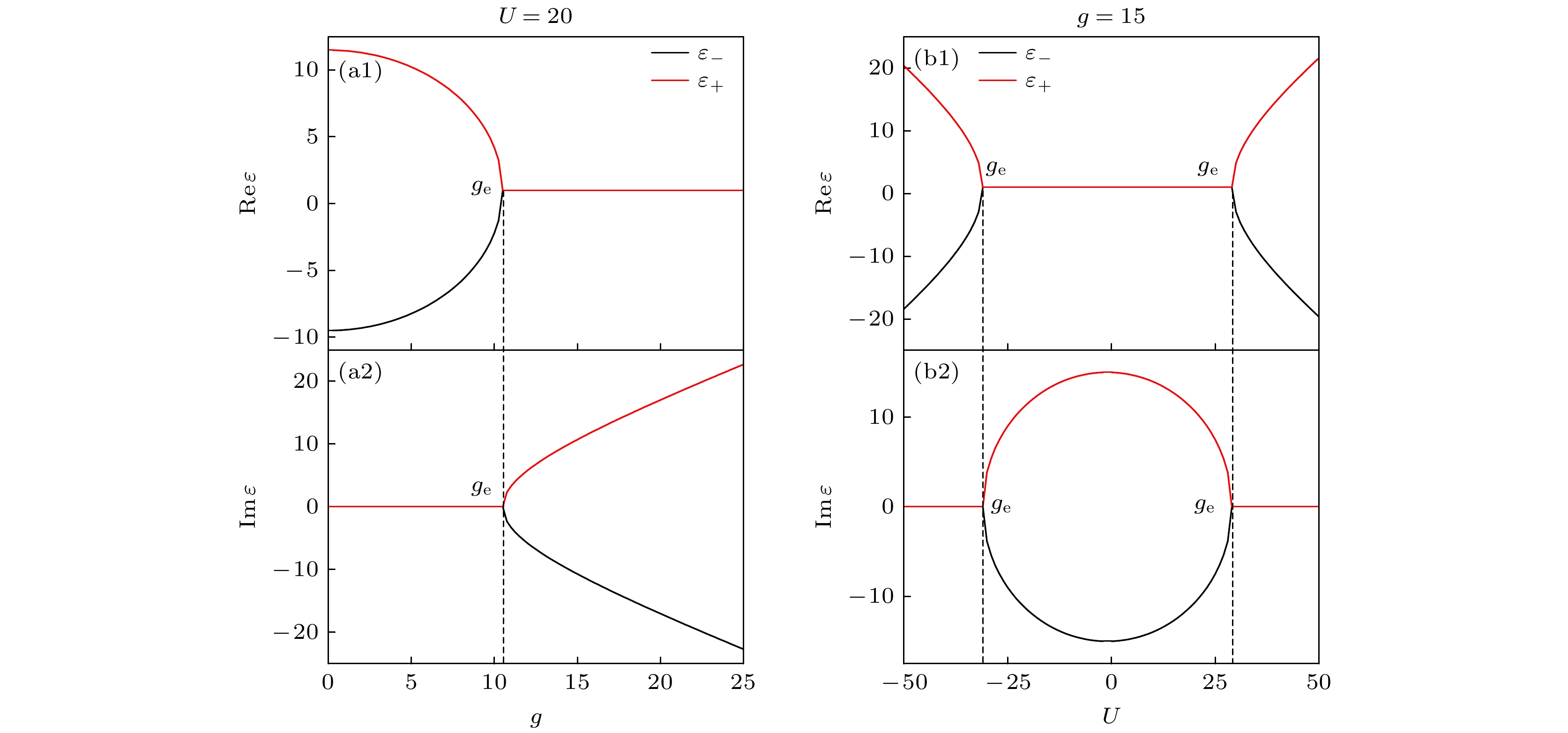
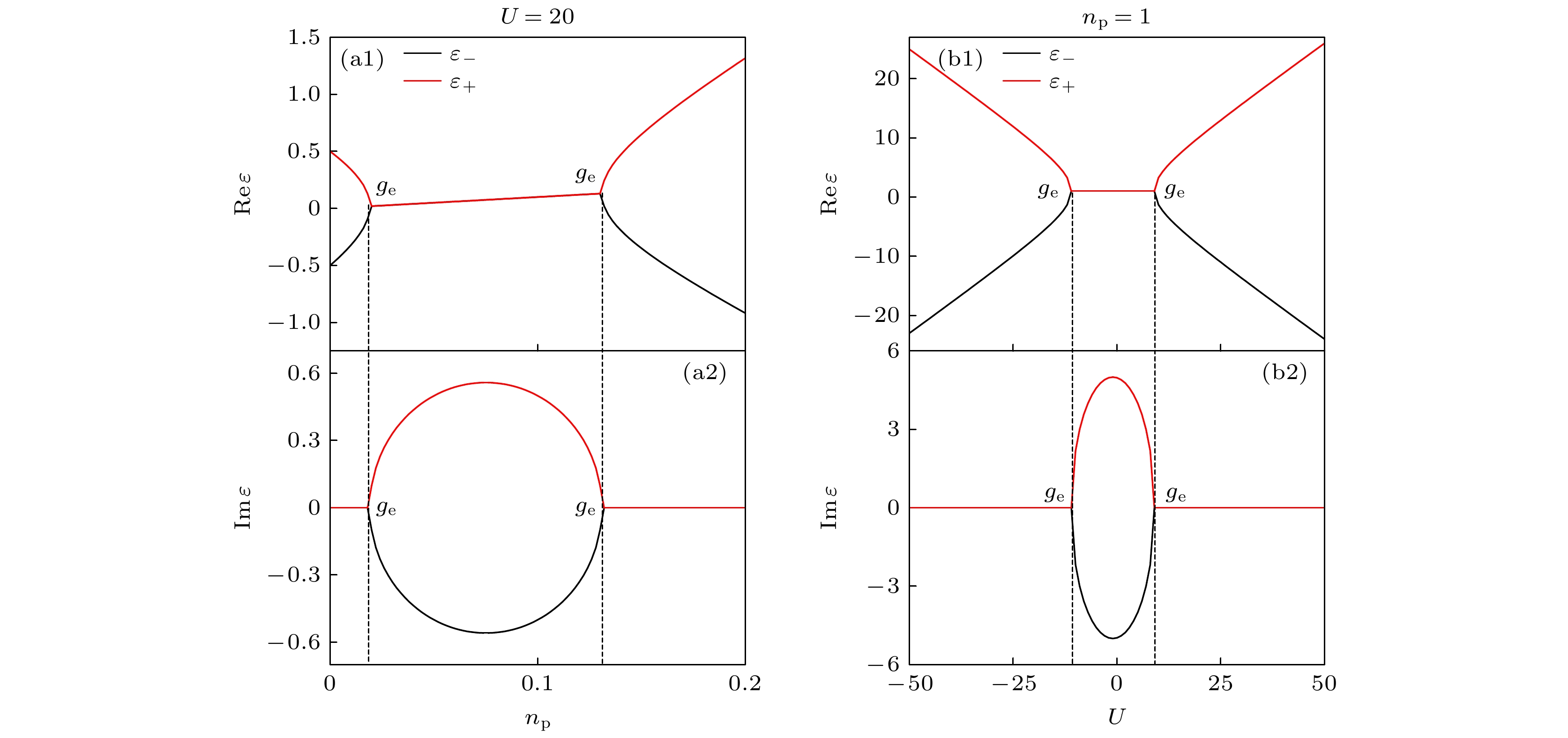
图 4 (a) 平均能量${\varepsilon _ \pm }$和(b) 平均光子数${n_{\text{p}}}$随原子-场耦合强度$g$变化的示意图, 腔频率与原子跃迁频率满足关系${\omega _{\text{f}}} = {\omega _0}$
Figure 4. (a) The average energy ${\varepsilon _ \pm }$ and (b) the average photon number ${n_{\text{p}}}$ as a function of the atom-field coupling strength $g$ with the cavity frequency and the atomic transition frequency satisfy the relation ${\omega _{\text{f}}} = {\omega _0}$.
图 5 本征值的虚部$\text{Im} [{\varepsilon _ \pm }]$在U-g平面的相图, 光子数${n_{\text{p}}} = 1$
Figure 5. Phase diagram of U-g plane about the imaginary part of the eigenvalues $\text{Im} [{\varepsilon _ \pm }]$ for mean photon number ${n_{\text{p}}} = 1$.
图 6 本征值${\varepsilon _ \pm }$的实部(1)和虚部(2)随原子-场耦合强度$g$(a)和原子-光子相互作用$U$(b)变化的示意图
Figure 6. The real part (1) and the imaginary part (2) of the eigenvalue ${\varepsilon _ \pm }$ as a function of the atom-field coupling strength $g$ (a) and the atom-photon interaction $U$(b).
图 7 本征值的虚部$\text{Im} [{\varepsilon _ \pm }]$在${n_{\text{p}}}{\text{-}}U$平面的相图, 原子-场耦合强度$g = 5$
Figure 7. Phase diagram of ${n_{\text{p}}}{\text{-}}U$ plane about the imaginary part of the eigenvalues $\text{Im} [{\varepsilon _ \pm }]$ for atom-field strength $g = 5$.
图 8 本征值${\varepsilon _ \pm }$的实部(1)和虚部(2)随光子数${n_{\text{p}}}$ (a)和原子-光子相互作用$U$(b)变化的示意图
Figure 8. The real part (1) and the imaginary part (2) of the eigenvalue ${\varepsilon _ \pm }$ as functions of the photon number ${n_{\text{p}}}$(a) and the atom-photon interaction $U$(b).
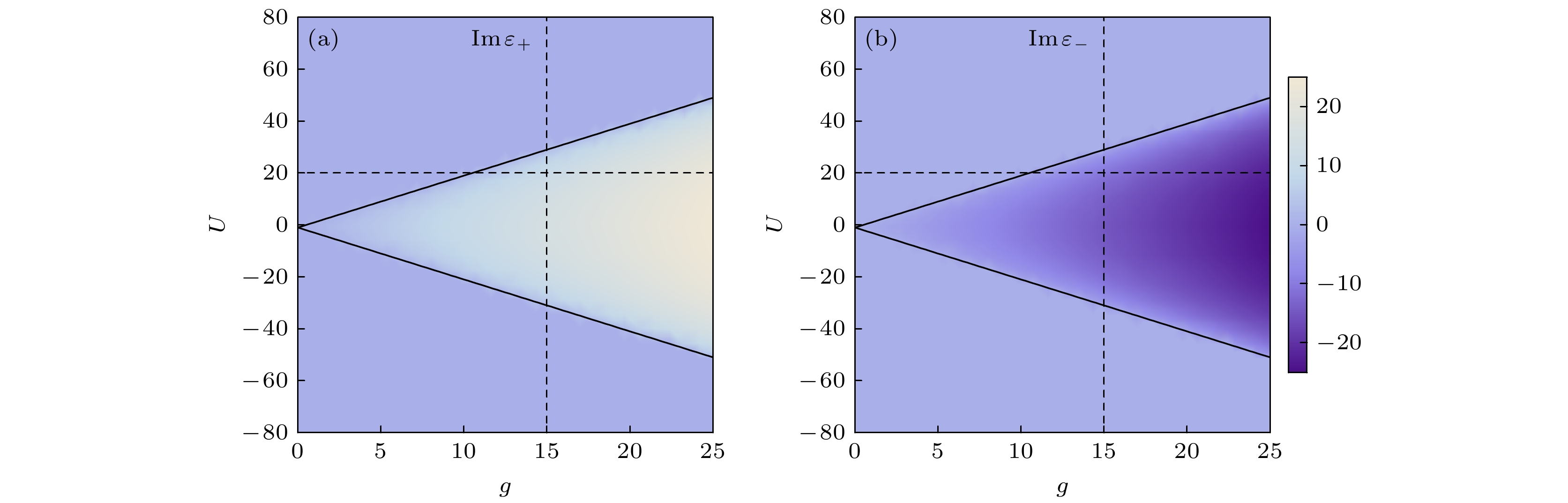
图 9 $g - U$空间红失谐(a) $\varDelta = 40$和蓝失谐(b) $\varDelta = $$ - 40$的相图, (b)中标签(1)表示${\text{NP}_{\text{co}}}\left( {{N_ - }, {S_ + }} \right)$
Figure 9. Phase diagrams in the $g - U$ space for red detuning (a) $\varDelta = 40$ and blue detuning (b) $\varDelta = - 40$. Label (1) is the NP denoted by ${\text{N}}{{\text{P}}_{{\text{co}}}}\left( {{N_ - }, {S_ + }} \right)$.
-
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201
Google Scholar
[3] Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401
Google Scholar
[4] Bender C M, Brody D C, Jones H F 2004 Phys. Rev. D. 70 025001
Google Scholar
[5] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[6] Heiss W D 2004 J. Phys. A. 37 2455
Google Scholar
[7] Brody D C, Graefe E M 2012 Phys. Rev. Lett. 109 230405
Google Scholar
[8] Roccati F, Palma G M, Bagarello F, Ciccarello F 2022 Open Syst. Inf. Dyn. 29 2250004
Google Scholar
[9] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[10] Sticlet D, Dóra B, Moca C P 2022 Phys. Rev. Lett. 128 016802
Google Scholar
[11] Peng Y, Jie J W, Yu D P, Wang Y C 2022 Phys. Rev. B. 106 L161402
Google Scholar
[12] Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[13] Hou J K, Zhu J F, Ma R X, Xue B Y, Zhu Y C, Lin J T, Jiang X S, Zheng Y L, Chen X F, Cheng Y, Ge L, Wan W J 2024 Phys. Rev. Lett. 132 256902
Google Scholar
[14] Zhang C, Liang P F, Lambert N, Cirio M 2024 Phys. Rev. Res. 6 023012
Google Scholar
[15] Masson S J, Covey J P, Will S, Asenjo- Garcia A 2024 Phys. Rev. X Quantum 5 010344
[16] 黄珊, 刘妮, 梁九卿 2018 67 183701
Google Scholar
Huang S, Liu N, Liang J Q 2018 Acta Phys. Sin. 67 183701
Google Scholar
[17] Matsumoto N, Kawabata K, Ashida Y, Furukawa S, Ueda M 2020 Phys. Rev. Lett. 125 260601
Google Scholar
[18] Turkeshi X, Schiró M 2023 Phys. Rev. B 107 L020403
Google Scholar
[19] Feng L, Wong Z J, Ma R-M, Wang Y, Zhang X 2014 Science 346 972
Google Scholar
[20] Chen W J, Özdemir Ş K, Zhao G M, Wiersig J, Yang L 2017 Nature 548 192
Google Scholar
[21] Dicke R H 1954 Phys. Rev. 93 99
Google Scholar
[22] Zhao X Q, Liu N, Liang J Q 2014 Phys. Rev. A. 90 023622
Google Scholar
[23] Bhaseen M J, Mayoh J, Simons B D, Keeling J 2012 Phys. Rev. A 85 013817
Google Scholar
[24] Keeling J, Bhaseen M J, Simons B D 2010 Phys. Rev. Lett. 105 043001
Google Scholar
[25] Buijsman W, Gritsev V, Sprik R 2017 Phys. Rev. Lett. 118 080601
Google Scholar
[26] Das P, Bhakuni D S, Sharma A 2023 Phys. Rev. A. 107 043706
Google Scholar
[27] Rodriguez J P J, Chilingaryan S A, Rodríguez-Lara B M 2018 Phys. Rev. A. 98 043805
Google Scholar
[28] Guerra C A E, Mahecha-Gómez J, Hirsch J G 2020 Eur. Phys. J. D. 74 200
Google Scholar
[29] Zhu G L, Lü X Y, Bin S W, You C, Wu Y 2019 Front. Phys. 14 52602
Google Scholar
[30] 赵秀琴, 张文慧 2024 73 240301
Google Scholar
Zhao X Q, Zhang W H 2024 Acta Phys. Sin. 73 240301
Google Scholar
[31] Colombe Y, Steinmetz T, Dubois G, Linke F, Hunger D, Reichel J 2007 Nature 450 272
Google Scholar
[32] Brennecke F, Donner T, Ritter S, Bourdel T, Köhl M, Esslinger T 2007 Nature 450 268
Google Scholar
[33] Dimer F, Estienne B, Parkins A S, Carmichael H J 2007 Phys. Rev. A. 75 013804
Google Scholar
[34] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[35] Peng P, Cao W X, Shen C, Qu W Z, Wen J M, Jiang L, Xiao Y H 2016 Nat. Phys. 2 1139
[36] Cao W X, Lu X D, Meng X, Sun J, Shen H, Xiao Y H 2020 Phys. Rev. Lett. 124 030401
Google Scholar
[37] Li A D, Wei H, Cotrufo M, Chen W J, Mann S, Ni X, Xu B C, Chen J F, Wang J, Fan S H, Qiu C W, Alù A, Chen L 2023 Nat. Nanotech. 18 706
Google Scholar
[38] Zhang Z M, Zhang F B, Xu Z X, Hu Y, Bao H, Shen H 2024 Phys. Rev. Lett. 133 133601
Google Scholar
[39] Markham D, Vedral X 2003 Phys. Rev. A. 67 042113
Google Scholar
[40] Liu N, Huang S, Liang J Q 2022 Results Phys. 40 105813
Google Scholar
[41] Mostafazadeh A 2002 Nucl. Phys. B 640 419
Google Scholar
[42] Mostafazadeh A 2002 J. Math. Phys. 43 205
Google Scholar
[43] Mostafazadeh A 2007 Phys. Lett. B. 650 208
Google Scholar
[44] Gu Y, Bai X M, Hao X L, Liang J Q 2022 Results Phys. 38 105561
Google Scholar
[45] Gu Y, Hao X L, Liang J Q 2022 Ann. Phys. (Berlin). 534 2200069
Google Scholar
[46] 梁九卿, 韦联福 2023 量子物理新进展(第3版) (北京: 科学出版社)
Liang J Q, Wei L F 2023 New Advances in Quantum Physics (3rd Ed. ) (Beijing: Science Press
[47] Lian J L, Zhang Y W, Liang J Q 2012 Chin. Phys. Lett. 29 060302
Google Scholar
[48] Chen G, Li J Q, Liang J Q 2006 Phys. Rev. A. 74 054101
Google Scholar
DownLoad:
Metrics
- Abstract views: 317
- PDF Downloads: 18
- Cited By: 0
