-
Hofstadter ladder describes a Boson ladder under a uniform magnetic field and supports nontrivial energy band and fractional quantum Hall states. Staggered hopping is illuminated from the SSH model and proved to have non-trivial effects on current phases. We introduce staggered hopping on Hofstadter ladder to study the novel current phases. Exact diagonalization (ED) and density matrix renormalization group (DMRG) methods have been employed to study the current phases of the ladder in noninteraction and strong interaction (hard core boson) cases. By observing energy singularities and the new flux patterns when increasing the staggered hopping strength, we extend Meissner and vortex phase to horizontal current phase, vertical current phase and vortex phase. The horizontal current phase has stronger chiral currents in horizontal direction, which is the long direction of the ladder. The vertical current phase has stronger chiral currents in vertical direction. The above two phases do not break translational invariance while the vortex phase does. The current patterns of horizontal current phase are proved to be continuously deformed form the Meissner phase, and the vortex phase has similar signatures. The vertical current phase is only visible when the hopping is staggered. These phases generally exist in noninteraction regimes and interacting superfluid regimes. We have defined new quantities (i.e. current inhomogeneity and nearest overlap) to characterize different quantum phases. In noninteraction case, the horizontal current phase go through the vortex phase to enter the vertical current phase by second order phase transitions, but in strong interaction case such a change can be directly made in a first order phase transition. The direct transition is made in higher fillings with almost identical flux. Surprisingly, the three phases turn into only two phases in Mott regimes, and the phase transition between the horizontal current phase and the vertical current phase has disappeared. We call the new phase as Mott-homogenous phase. The staggered hopping has exotic effects in strong interaction case. For n = 0.25 filling, the staggered hopping shrinks the region of vortex phases and produces Mott-SF transition. When the staggered hopping is weak, the system achieves Mott-SF transition just by varying the flux. This research can enrich current phases in lattice systems and illuminate further studies on chiral currents.
-
Keywords:
- quantum phase transition /
- numerical simulation /
- Hofstadter ladder /
- chiral current
[1] Thouless D J, Kohmoto M, Nightingale M P, Dennijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[2] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[3] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[4] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[5] Hügel D, Paredes B 2014 Phys. Rev. A 89 023619
Google Scholar
[6] Zupancic P, Preiss P M, Ma R C, Lukin A, Tai M E, Rispoli M, Islam R, Greiner M 2016 Opt. Express 24 13881
Google Scholar
[7] Tai M E, Lukin A, Rispoli M, Schittko R, Menke T, Borgnia D, Preiss P M, Grusdt F, Kaufman A M, Greiner M 2017 Nature 546 519
Google Scholar
[8] Atala M, Aidelsburger M, Lohse M, Barreiro J T, Paredes B, Bloch I 2014 Nat. Phys. 10 588
Google Scholar
[9] Aidelsburger M, Atala M, Lohse M, Barreiro J T, Paredes B, Bloch I 2013 Phys. Rev. Lett. 111 185301
Google Scholar
[10] Miyake H, Siviloglou G A, Kennedy C J, Burton W C, Ketterle W 2013 Phys. Rev. Lett. 111 185302
Google Scholar
[11] Aidelsburger M, Lohse M, Schweizer C, Atala M, Barreiro J T, Nascimbène S, Cooper N R, Bloch I, Goldman N 2015 Nat. Phys. 11 162
Google Scholar
[12] Jiménez-García K, LeBlanc L J, Williams R A, Beeler M C, Perry A R, Spielman I B 2012 Phys. Rev. Lett. 108 225303
Google Scholar
[13] Struck J, Ölschläger C, Weinberg M, Hauke P, Simonet J, Eckardt A, Lewenstein M, Sengstock K, Windpassinger P 2012 Phys. Rev. Lett. 108 225304
Google Scholar
[14] Celi A, Massignan P, Ruseckas J, Goldman N, Spielman I B, Juzeliūnas G, Lewenstein M 2014 Phys. Rev. Lett. 112 043001
Google Scholar
[15] Mancini M, Pagano G, Cappellini G, Livi L, Rider M, Catani J, Sias C, Zoller P, Inguscio M, Dalmonte M, Fallani L 2015 Science 349 1510
Google Scholar
[16] Cooper N R, Rey A M 2015 Phys. Rev. A 92 021401
Google Scholar
[17] Pagano G, Mancini M, Cappellini G, Lombardi P, Schäfer F, Hu H, Liu X J, Catani J, Sias C, Inguscio M, Fallani L 2014 Nat. Phys. 10 198
Google Scholar
[18] Stuhl B K, Lu H I, Aycock L M, Genkina D, Spielman I B 2015 Science 349 1514
Google Scholar
[19] Aidelsburger M 2015 Artificial Gauge Fields with Ultracold Atoms in Optical Lattices (Switzerland: Springer) pp27–44
[20] Azbel M Y 1964 Sov. Phys. JETP 19 634
[21] Harper P G 1955 Proc. Phys. Soc. London, Sect. A 68 874
Google Scholar
[22] Hofstadter D R 1976 Phys. Rev. B 14 2239
[23] Giamarchi T 2004 Quantum Physics in One Dimension (Clarendon: Oxford) p29
[24] Dolfi M, Bauer B, Keller S, Kosenkov A, Ewart T, Kantian A, Giamarchi T, Troyer M 2014 Comput. Phys. Commun. 185 3430
Google Scholar
[25] White S R 1992 Phys. Rev. Lett. 69 2863
Google Scholar
[26] Schollwöck U 2011 Ann. Phys. 326 96
Google Scholar
[27] Tsui D C, Stormer H L, Gossard A C 1982 Phys. Rev. Lett. 48 1559
Google Scholar
[28] Palmer R N, Jaksch D 2006 Phys. Rev. Lett. 96 180407
Google Scholar
[29] Hafezi M, Sørensen A S, Demler E, Lukin M D 2007 Phys. Rev. A 76 023613
Google Scholar
[30] Cooper N R, Dalibard J 2013 Phys. Rev. Lett. 110 185301
Google Scholar
[31] Strinati M C, Cornfeld E, Rossini D, Barbarino S, Dalmonte M, Fazio R, Sela E, Mazza L 2017 Phys. Rev. X 7 021033
[32] Cornfeld E, Sela E 2015 Phys. Rev. B 92 115446
Google Scholar
[33] Petrescu A, Piraud M, Roux G, McCulloch I P, Le Hur K 2017 Phys. Rev. B 96 014524
Google Scholar
[34] Petrescu A, Le Hur K 2013 Phys. Rev. Lett. 111 150601
Google Scholar
[35] Petrescu A, Le Hur K 2015 Phys. Rev. B 91 054520
Google Scholar
[36] Piraud M, Heidrich-Meisner F, McCulloch I P, Greschner S, Vekua T, Schollwöck U 2015 Phys. Rev. B 91 140406
Google Scholar
[37] Geim A K, Dubonos S V, Lok J G S, Henini M, Maan J C 1998 Nature 396 144
Google Scholar
[38] Bardeen J 1955 Phys. Rev. 97 1724
Google Scholar
[39] Abrikosov A A 1957 Sov. Phys. JETP 511 74
[40] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[41] Su W P, Schrieffer J R, Heeger A J 1983 Phys. Rev. B 28 1138
[42] Zhang J M, Dong R X 2010 Eur. J. Phys. 31 591
Google Scholar
[43] Calabrese P, Cardy J 2009 . Phys. A 42 504005
Google Scholar
[44] Holzhey C, Larsen F, Wilczek F 1994 Nucl. Phys. B 424 443
Google Scholar
[45] Vidal G, Latorre J I, Rico E, Kitaev A 2003 Phys. Rev. Lett. 90 227902
Google Scholar
[46] Roux G, Capponi S, Lecheminant P, Azaria P 2009 Eur. Phys. J. B 68 293
Google Scholar
[47] Kühner T D, White S R, Monien H 2000 Phys. Rev. B 61 12474
Google Scholar
[48] Asbóth J K, Oroszlány L, Pályi A 2016 Lect. Notes Phys. 919 87
[49] Sheikhan A, Brennecke F, Kollath C 2016 Phys. Rev. B 94 061603
[50] Feng Y L, Zhang K, Fan J T, Mei F, Chen G, Jia S T 2018 Sci. China: Phys. Mech. 61 123011
-
图 1 哈密顿量中跃迁项示意图
Figure 1. Sketch of the hopping term of the Hamiltonian.
图 2 (a) 用来识别相变的基态能导数的突变, 数据取自
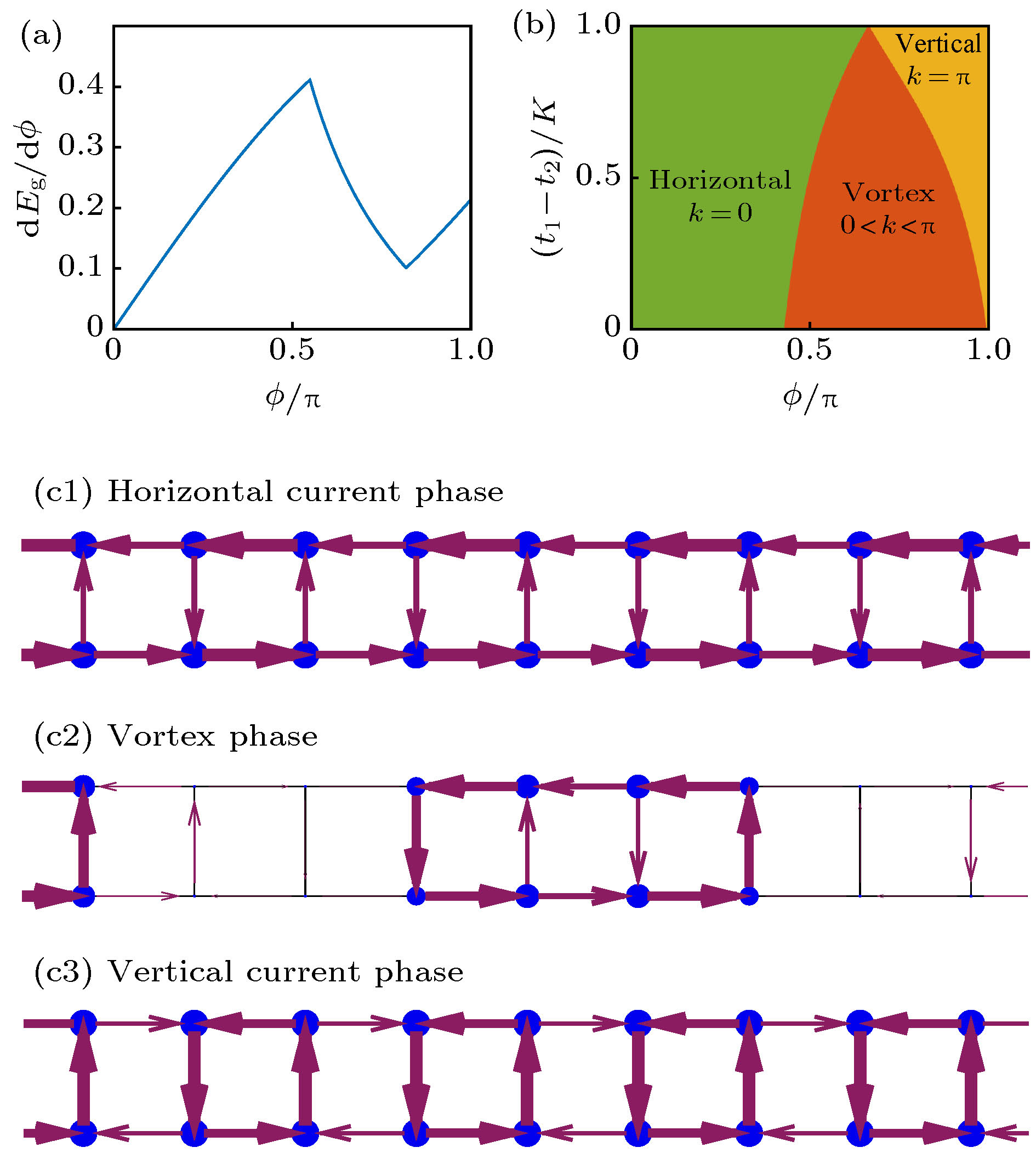
${t_1}/K = 1$ ,${t_2}/K = 0.3$ ; (b) 无相互作用相图; (c1)−(c3) 区分三种相的流图案. 图中箭头表示流, 点表示密度, 箭头的方向和粗细代表流的方向和强度, 点的大小表示密度的大小, 箭头的粗细和点的大小都已经除以当组最大的流或密度归一. 数据取自${t_1}/K = 1$ ,${t_2}/K = 0.3$ ,$\phi /{\text{π}} = $ 0.1, 0.6, 0.9, 精确对角化Figure 2. (a) Singularities in derivative of ground state energy indicate phase transitions. Data is from
${t_1}/K = 1$ ,${t_2}/K = 0.3$ ; (b) phase diagram for non-interacting case; (c1)−(c3) the current pattern used to distinguish the 3 phases. Direction and thickness of an arrow indicate the direction and strength of the current on the plotted bond. The strengths are normalized by the strongest local current. The sizes of the points indicate the density strengths and are normalized by the largest density. The current patterns are from ED calculations for$\phi /{\text{π}} = 0.1, \;0.6, \;0.9$ when${t_1}/K = 1$ ,${t_2}/K = 0.3$ .
图 3 (a) 无相互作用时扫描
$\phi $ 计算出的最近邻内积, 数据取自${t_1}/K = 1, \;{t_2}/K = 0.3$ ; (b) 保持${t_1}/K = 1$ , 逐渐改变${t_2}/K$ 时, 横流相和纵流相的态和${t_1}/K = {t_2}/K = 1$ 时态的内积; (c) 一般的, 系统在$\phi = {\text{π}}$ 处整个流图案的流会逆转方向, 交错跃迁会让流换向以一阶相变的形式进行, 数据取自${t_1}/K = 1$ Figure 3. (a) Nearest overlaps from ED calculations. Data is from
${t_1}/K = 1, {t_2}/K = 0.3$ ; (b) when${t_1}/K = 1$ , as${t_2}/K$ decays, the overlap with${t_1}/K = {t_2}/K = 1$ state decays from 1 smoothly; (c) generally all local currents in the system reverse sign in$\phi = {\text{π}}$ . The staggered hopping makes the process the first order phase transition. Data is from${t_1}/K = 1$ .
图 4 (a)
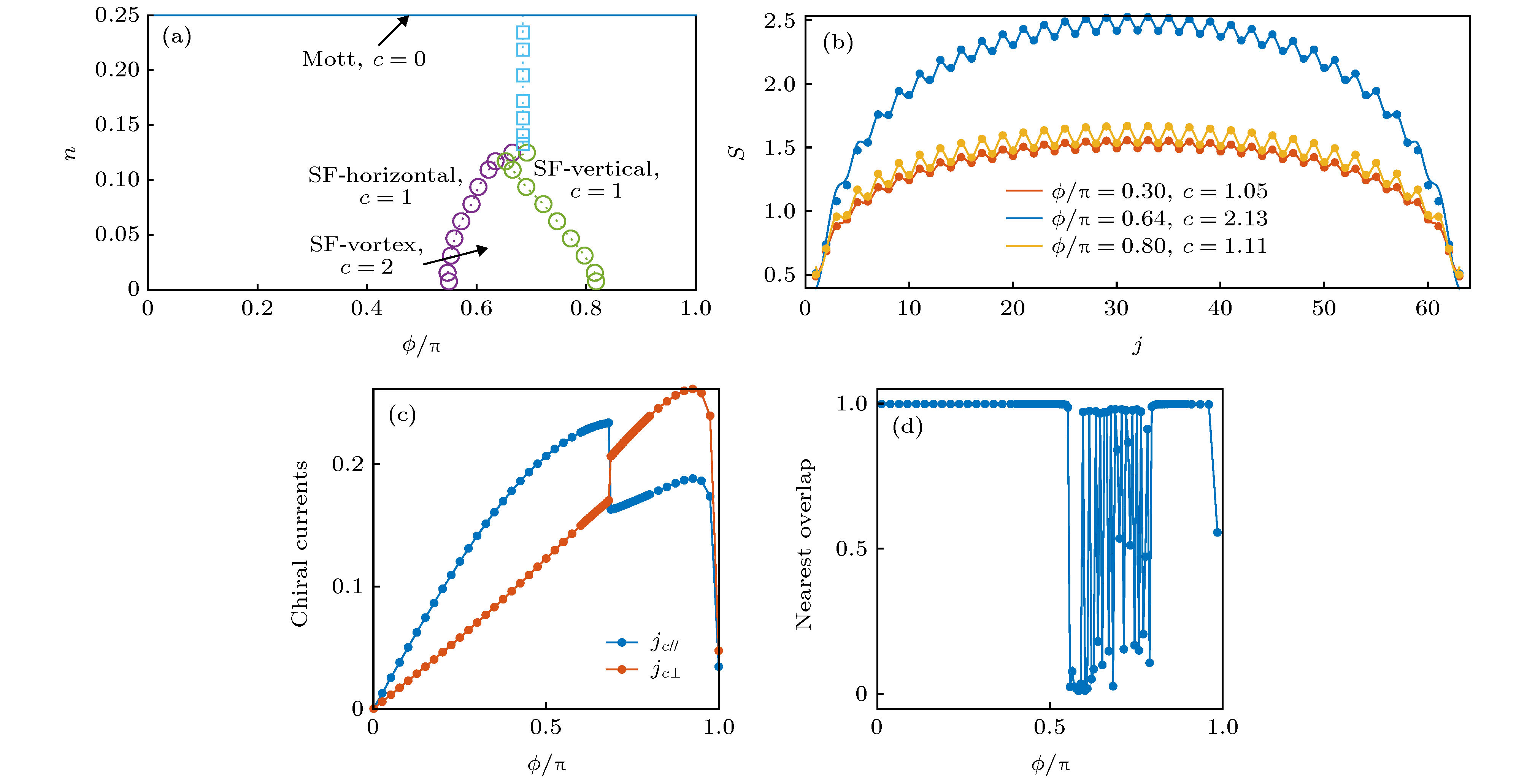
${t_1}/K = 1, \;{t_2}/K = 0.3$ 强相互作用极限(HCB)相图,$n = N/(2 L)$ 为填充; (b) 该相图中三个相对应的纠缠熵分布与拟合结果,$\phi /{\text{π}} = 0.3, 0.64, 0.8$ 分别取自横流相、涡旋相和纵流相, 散点是有限尺寸系统中计算的纠缠熵(S), 实线和中心荷(c)是将散点用公式(7)拟合的结果. 交错跃迁导致了纠缠熵空间分布的起伏, 数据取自周期边界,$L = 64$ ,$N = 12$ ; (c) 横流相-纵流相相变时横向手性流和纵向手性流的突变, 突变后二者强弱交换; 数据取自$L = 64, N = 25$ , 在手性流的计算中为了减小开边界带来的边界效应, 只截取了中间$L/2$ 部分; (d) 横流相-涡旋相-纵流相相变; 扫描$\phi $ 时, 最近邻内积进入涡旋相时会突变, 并且数值上类似于无相互作用时一样振荡; 数据取自$N = 4$ Figure 4. (a) Phase diagram for HCB when
${t_1}/K = 1$ ,${t_2}/K = 0.3$ ,$n = N/(2 L)$ ; (b) VN entropy and the corresponding fitted central charge for three phases in the phase diagram above.$\phi /{\text{π}} = 0.3, 0.64, 0.8$ are from horizontal current, vortex and vertical current phase respectively. The points are VN entropy data in PBC finite system. Solid lines and central charge are fitted from formula(7). The staggered hopping has made the VN entropy also staggered. Data is from$L = 64$ ,$N = 12$ ; (c) horizontal current phase to vertical current phase transition for$L = 64, N = 25$ . The average horizontal current and average vertical current will swap their strong and weak relations in the transition point. In order to reduce the boundary effect in average currents, we used the$L/2$ part in the middle of the ladder; (d) horizontal current to vortex and vortex to vertical current phase transition. The nearest overlap shows that in horizontal and vertical current phases the ground state changes smoothly, and numerically oscillates in the vortex phase. Data is from$N = 4$ .
图 5 (a)
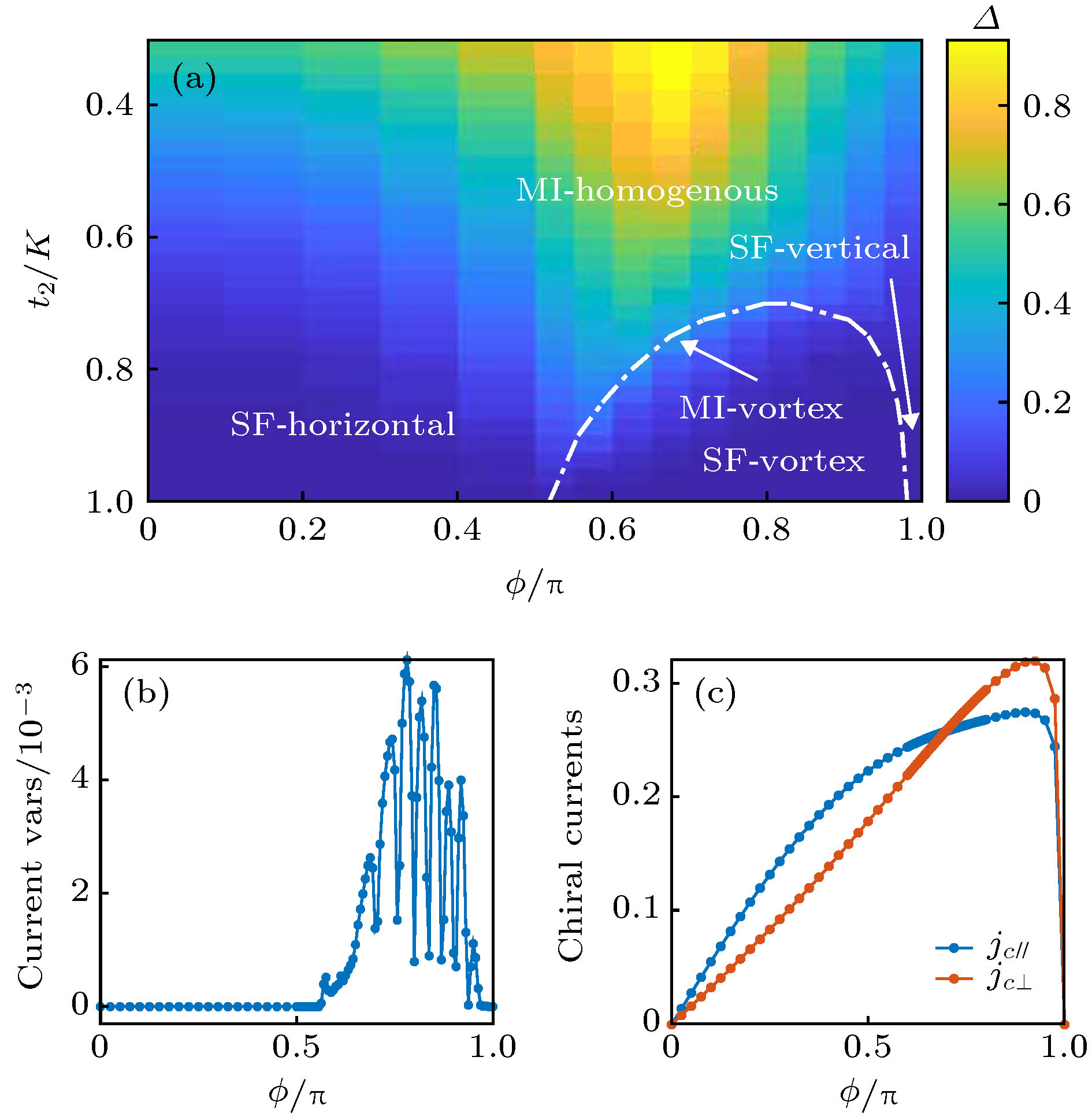
$n = 0.25$ 相图,${t_1}/K = 1$ , 虚线圈出的是vortex相; (b) 相图中均匀相与涡旋相是用量化的流的周期2不均匀性区分的, 数据取自${t_1}/K = 1$ ,${t_2}/K = 0.9$ ; (c)${t_1}/K = 1$ ,${t_2}/K = 0.3$ 的$n = 0.25$ Mott线, 系统基态平缓地从横流相变成纵流相, 这个过程中流图案的周期一直为2Figure 5. (a) Phase diagram for
$n = 0.25$ filling when${t_1}/K = 1$ ; (b) the homogenous phase and vortex phase are distinguished from the inhomogeneity of densities and currents. Data is from${t_1}/K = 1$ ,${t_2}/K = 0.9$ ; (c) the$n = 0.25$ Mott line for${t_1}/K = 1$ ,${t_2}/K = 0.3$ . The average vertical current surpasses the average horizontal current smoothly, during the process the current patterns have perfect periodicity of 2 and the density is homogenous.表 1 在有代表性的区域取点, 精确计算中心荷(c)来验证各个流相的存在, 系统取周期边界来减小纠缠熵振荡. 表格列出了散点在相图中的位置，对这些点的电荷能隙和流相性质的判断，以及对应的中心荷判据，L = 64—100, t1/K = 1
Table 1. PBC central charges (c) are accurately checked in several points in typical regions. The table has listed the points' position in the phase diagram, the judged charge gap and current phase pro-perties, and the corresponding central charge evidence, L = 64–100, t1/K = 1.
$\left( {{t_2}/K, \;\phi /{\text{π}}} \right)$ Region in phase diagram c $(0.9000, ~0.1000)$ $\varDelta = 0$, not vortex $1.00$ $(0.9000,~ 0.8000)$ $\varDelta = 0$, vortex $2.00$ $(0.8500,~0.5000)$ $\varDelta > 0$, not vortex $0.01$ $(0.8500,~0.6125)$ $\varDelta > 0$, vortex $0.98$ $(0.8000,~ 0.9750)$ $\varDelta = 0$, not vortex $1.02$ 
DownLoad: CSV
-
[1] Thouless D J, Kohmoto M, Nightingale M P, Dennijs M 1982 Phys. Rev. Lett. 49 405
Google Scholar
[2] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
Google Scholar
[3] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[4] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[5] Hügel D, Paredes B 2014 Phys. Rev. A 89 023619
Google Scholar
[6] Zupancic P, Preiss P M, Ma R C, Lukin A, Tai M E, Rispoli M, Islam R, Greiner M 2016 Opt. Express 24 13881
Google Scholar
[7] Tai M E, Lukin A, Rispoli M, Schittko R, Menke T, Borgnia D, Preiss P M, Grusdt F, Kaufman A M, Greiner M 2017 Nature 546 519
Google Scholar
[8] Atala M, Aidelsburger M, Lohse M, Barreiro J T, Paredes B, Bloch I 2014 Nat. Phys. 10 588
Google Scholar
[9] Aidelsburger M, Atala M, Lohse M, Barreiro J T, Paredes B, Bloch I 2013 Phys. Rev. Lett. 111 185301
Google Scholar
[10] Miyake H, Siviloglou G A, Kennedy C J, Burton W C, Ketterle W 2013 Phys. Rev. Lett. 111 185302
Google Scholar
[11] Aidelsburger M, Lohse M, Schweizer C, Atala M, Barreiro J T, Nascimbène S, Cooper N R, Bloch I, Goldman N 2015 Nat. Phys. 11 162
Google Scholar
[12] Jiménez-García K, LeBlanc L J, Williams R A, Beeler M C, Perry A R, Spielman I B 2012 Phys. Rev. Lett. 108 225303
Google Scholar
[13] Struck J, Ölschläger C, Weinberg M, Hauke P, Simonet J, Eckardt A, Lewenstein M, Sengstock K, Windpassinger P 2012 Phys. Rev. Lett. 108 225304
Google Scholar
[14] Celi A, Massignan P, Ruseckas J, Goldman N, Spielman I B, Juzeliūnas G, Lewenstein M 2014 Phys. Rev. Lett. 112 043001
Google Scholar
[15] Mancini M, Pagano G, Cappellini G, Livi L, Rider M, Catani J, Sias C, Zoller P, Inguscio M, Dalmonte M, Fallani L 2015 Science 349 1510
Google Scholar
[16] Cooper N R, Rey A M 2015 Phys. Rev. A 92 021401
Google Scholar
[17] Pagano G, Mancini M, Cappellini G, Lombardi P, Schäfer F, Hu H, Liu X J, Catani J, Sias C, Inguscio M, Fallani L 2014 Nat. Phys. 10 198
Google Scholar
[18] Stuhl B K, Lu H I, Aycock L M, Genkina D, Spielman I B 2015 Science 349 1514
Google Scholar
[19] Aidelsburger M 2015 Artificial Gauge Fields with Ultracold Atoms in Optical Lattices (Switzerland: Springer) pp27–44
[20] Azbel M Y 1964 Sov. Phys. JETP 19 634
[21] Harper P G 1955 Proc. Phys. Soc. London, Sect. A 68 874
Google Scholar
[22] Hofstadter D R 1976 Phys. Rev. B 14 2239
[23] Giamarchi T 2004 Quantum Physics in One Dimension (Clarendon: Oxford) p29
[24] Dolfi M, Bauer B, Keller S, Kosenkov A, Ewart T, Kantian A, Giamarchi T, Troyer M 2014 Comput. Phys. Commun. 185 3430
Google Scholar
[25] White S R 1992 Phys. Rev. Lett. 69 2863
Google Scholar
[26] Schollwöck U 2011 Ann. Phys. 326 96
Google Scholar
[27] Tsui D C, Stormer H L, Gossard A C 1982 Phys. Rev. Lett. 48 1559
Google Scholar
[28] Palmer R N, Jaksch D 2006 Phys. Rev. Lett. 96 180407
Google Scholar
[29] Hafezi M, Sørensen A S, Demler E, Lukin M D 2007 Phys. Rev. A 76 023613
Google Scholar
[30] Cooper N R, Dalibard J 2013 Phys. Rev. Lett. 110 185301
Google Scholar
[31] Strinati M C, Cornfeld E, Rossini D, Barbarino S, Dalmonte M, Fazio R, Sela E, Mazza L 2017 Phys. Rev. X 7 021033
[32] Cornfeld E, Sela E 2015 Phys. Rev. B 92 115446
Google Scholar
[33] Petrescu A, Piraud M, Roux G, McCulloch I P, Le Hur K 2017 Phys. Rev. B 96 014524
Google Scholar
[34] Petrescu A, Le Hur K 2013 Phys. Rev. Lett. 111 150601
Google Scholar
[35] Petrescu A, Le Hur K 2015 Phys. Rev. B 91 054520
Google Scholar
[36] Piraud M, Heidrich-Meisner F, McCulloch I P, Greschner S, Vekua T, Schollwöck U 2015 Phys. Rev. B 91 140406
Google Scholar
[37] Geim A K, Dubonos S V, Lok J G S, Henini M, Maan J C 1998 Nature 396 144
Google Scholar
[38] Bardeen J 1955 Phys. Rev. 97 1724
Google Scholar
[39] Abrikosov A A 1957 Sov. Phys. JETP 511 74
[40] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[41] Su W P, Schrieffer J R, Heeger A J 1983 Phys. Rev. B 28 1138
[42] Zhang J M, Dong R X 2010 Eur. J. Phys. 31 591
Google Scholar
[43] Calabrese P, Cardy J 2009 . Phys. A 42 504005
Google Scholar
[44] Holzhey C, Larsen F, Wilczek F 1994 Nucl. Phys. B 424 443
Google Scholar
[45] Vidal G, Latorre J I, Rico E, Kitaev A 2003 Phys. Rev. Lett. 90 227902
Google Scholar
[46] Roux G, Capponi S, Lecheminant P, Azaria P 2009 Eur. Phys. J. B 68 293
Google Scholar
[47] Kühner T D, White S R, Monien H 2000 Phys. Rev. B 61 12474
Google Scholar
[48] Asbóth J K, Oroszlány L, Pályi A 2016 Lect. Notes Phys. 919 87
[49] Sheikhan A, Brennecke F, Kollath C 2016 Phys. Rev. B 94 061603
[50] Feng Y L, Zhang K, Fan J T, Mei F, Chen G, Jia S T 2018 Sci. China: Phys. Mech. 61 123011
DownLoad:
Catalog
Metrics
- Abstract views: 6467
- PDF Downloads: 86
- Cited By: 0
