-
Bose-Einstein condensate (BEC) is essentially a macroscopic quantum effect with quantum volatility, macroscopic quantum coherence and artificial controllability. Owing to its unique controllability, it becomes a new ideal platform for quantum simulations and studies of interacting quantum systems. In this paper, the generation of vortices and the formation of vortex chains, as well as characteristics of vortex chains in rotating two-dimensional BEC in a potential composed of harmonic potential and optical lattice are studied numerically. Firstly, the generation of vortices, the formation and distribution of vortex chains and the effects of different physical parameters on the vortex chains in two-dimensional BEC are investigated by using the multigrid preconditioned conjugate gradient method. Secondly, the evolution of the vortex chains with time is studied by using the time-splitting spectral method. The results show that the generation of vortices in BEC trapped in the compound potential corresponds to the minimum value of the potential. When the depth of the optical lattice increases to a certain value, vortex chains are formed in the BEC. With the further increase of the depth of the optical lattice, the vortex depth in the vortex chain in the BEC decreases continuously, and finally the vortex chain disappears completely. When the interaction strength between atoms increases, the distribution range of the condensate expands, and the number of vortices and the number of vortex chains in the condensate also increase. When the interaction strength between atoms increases to a certain value, the symmetry of the vortex chains is broken. As the rotation frequency of the condensate increases, the distribution range of the condensate expands, and the number of vortices and the number of vortex chains in the condensate also increase. When the rotation frequency is close to the external trapping potential frequency, the linear alignment of the vortex chains is disrupted. It is also found that there are three stages in the evolution of the vortex chains in the BEC: in the first stage, vortex chains rotate together with the condensate, and the original chain distribution keeps unchanged; in the second stage, the phenomenon of vortex space extrusion appears, and the vortex chain is destroyed; in the third stage, the phenomenon of vortex space expansion occurs, and finally the vortex chains disappear. The results above show that the depth of the optical lattice, the interaction strength between atoms, and the rotation frequency of the condensate have important effects on the vortices and vortex chains in the condensate. By adjusting these physical quantities, the number of vortices and the shape of vortex chains in the BEC can be effectively manipulated. This may provide some theoretical reference and guidance for future experiments and applications. -
Keywords:
- Bose-Einstein condensate /
- vortex chains /
- optical lattices /
- composite potential
[1] Anderson M H, Ensher J R, Matthews M R, Wiemane C E, Cornell A 1995 Science 269 198
Google Scholar
[2] Bradley C C, Sackett C A, Tollett J J, Hulet R G 1995 Phys. Rev. Lett. 75 1687
Google Scholar
[3] Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969
Google Scholar
[4] 郭慧, 王雅君, 王林雪, 张晓斐 2020 69 010302
Google Scholar
Guo H, Wang J Y, Wang L X, Zhang X F 2020 Acta Phys. Sin. 69 010302
Google Scholar
[5] Wang L X, Dai C Q, Wen L, Liu T, Jiang HF, Saito H, Zhang S G, Zhang X F 2018 Phys. Rev. A 97 063607
Google Scholar
[6] 陈艳勃, 张素英 2020 量子光学学报 26 7
Chen Y B, Zhang S Y 2020 J. Quantum Opt 26 7
[7] 乔红霞, 张素英 2019 量子光学学报 25 319
Qiao H X, Zhang S Y 2019 Chin. J. Comput. Phys 25 319
[8] 王书松, 张素英 2021 计算物理 38 113
Wang S S, Zhang S Y 2021 Chin. J. Comput. Phys 38 113
[9] Tsubota M, Kasamatsu K, Ueda M 2002 Phys. Rev. A 65 023603
Google Scholar
[10] Li S, Prinari B, Biondini G 2018 Phys. Rev. E 97 022221
Google Scholar
[11] Yan Z, Konotop V V, Akhmediev N 2010 Phys. Rev. E 82 036610
Google Scholar
[12] 张爱霞, 姜艳芳, 薛具奎 2021 70 200302
Google Scholar
Zhang A X, Jiang Y F, Xue J K 2021 Acta Phys. Sin 70 200302
Google Scholar
[13] 李吉, 刘伍明 2018 67 110302
Google Scholar
Li J, Liu W M 2018 Acta Phys. Sin 67 110302
Google Scholar
[14] 陈光平 2015 64 030302
Google Scholar
Chen G P 2015 Acta Phys. Sin 64 030302
Google Scholar
[15] Chin C, Grimm R, Julienne P, et al. 2010 Rev. Mod. Phys. 82 1225
Google Scholar
[16] Sanz J, Frölian A, Chisholm C S, Cabrera C R, Tarruell L 2022 Phys. Rev. Lett. 128 013201
Google Scholar
[17] Nguyen J H V, Luo D, Hulet R G 2017 Science 356 422
Google Scholar
[18] Di Carli A, Henderson G, Flannigan S, Colquhoun C D, Mitchell M, Oppo G-L, Daley A J, Kuhr S, Haller E 2020 Phys. Rev. Lett. 125 183602
Google Scholar
[19] Lin Y J, Compton R L, Perry A R, Phillips W D, Porto J V, Spielman I B 2009 Phys. Rev. Lett. 102 130401
Google Scholar
[20] Chen P K, Liu L R, Tsai M J, Chiu N C, Kawaguchi Y, Yip S K, Chang M S, Lin Y J 2018 Phys. Rev. Lett. 121 250401
Google Scholar
[21] Zou P, Brand J, Liu X J, Hu H 2016 Phys. Rev. Lett. 117 225302
Google Scholar
[22] Chen K J, Wu F, Peng S G, Yi W, He L Y, 2020 Phys. Rev. Lett. 125 260407
Google Scholar
[23] Katsimiga G C, Kevrekidis P G, Prinari B, Biondini G, Schmelcher P 2018 Phys. Rev. A 97 043623
Google Scholar
[24] Gligorić G, Maluckov A, Hadžievski L, Malomed B A 2013 Phys. Rev. E 88 032905
Google Scholar
[25] Balaž A, Paun R, Nicolin A I, Balasubramanian S, Ramaswamy R 2014 Phys. Rev. A 89 023609
Google Scholar
[26] Sudharsan J B, Radha R, Fabrelli H, Gammal A, Malomed B A 2015 Phys. Rev. A 92 053601
Google Scholar
[27] Kengne E, Liu W M, Malomed B A 2021 Phys. Rep. 899 1
Google Scholar
[28] Cheng Y S, Adhikari S K 2011 Phys. Rev. A 83 023620
Google Scholar
[29] Wang C, Law K J H, Kevrekidis P G, Kevrekidis G, Porter M A 2013 Phys. Rev. A 87 023621
Google Scholar
[30] Wang D S, Song S W, Xiong B, Liu W M 2011 Phys. Rev. A 84 053607
Google Scholar
[31] Yan Z Y, Konotop V V, Yulin A V, Liu W M 2012 Phys. Rev. E 85 016601
Google Scholar
[32] Antoine X, Tang Q L, Zhang Y 2018 Commun. Comput. Phys. 24 966
[33] Williams R A, Al-Assam S, Foot C J 2010 Phys. Rev. Lett. 104 050404
Google Scholar
[34] 陈海军, 任元, 王华 2022 71 056701
Google Scholar
Chen H J, Ren Y, Wang H 2022 Acta Phys. Sin 71 056701
Google Scholar
[35] Abrikosov A A 2004 Rev. Mod. Phys. 76 975
Google Scholar
[36] Matveenko S I 2010 Phys. Rev. A 82 033628
Google Scholar
[37] Schweikhard V, Coddington I, Engels P, Mogendorff V P, Cornell E A 2004 Phys. Rev. Lett. 92 040404
Google Scholar
[38] Bao W Z, Jaksch D, Markowich P A 2003 J. Comput. Phys. 187 318
Google Scholar
[39] Bao W Z, Wang H 2006 J. Comput. Phys. 217 612
Google Scholar
[40] Fletcher R J, Shaffer A, Wilson C C, Patel P B, Yan Z J, Crépel V, Mukherjee B, Zwierlein M W 2021 Science 372 1318
Google Scholar
-
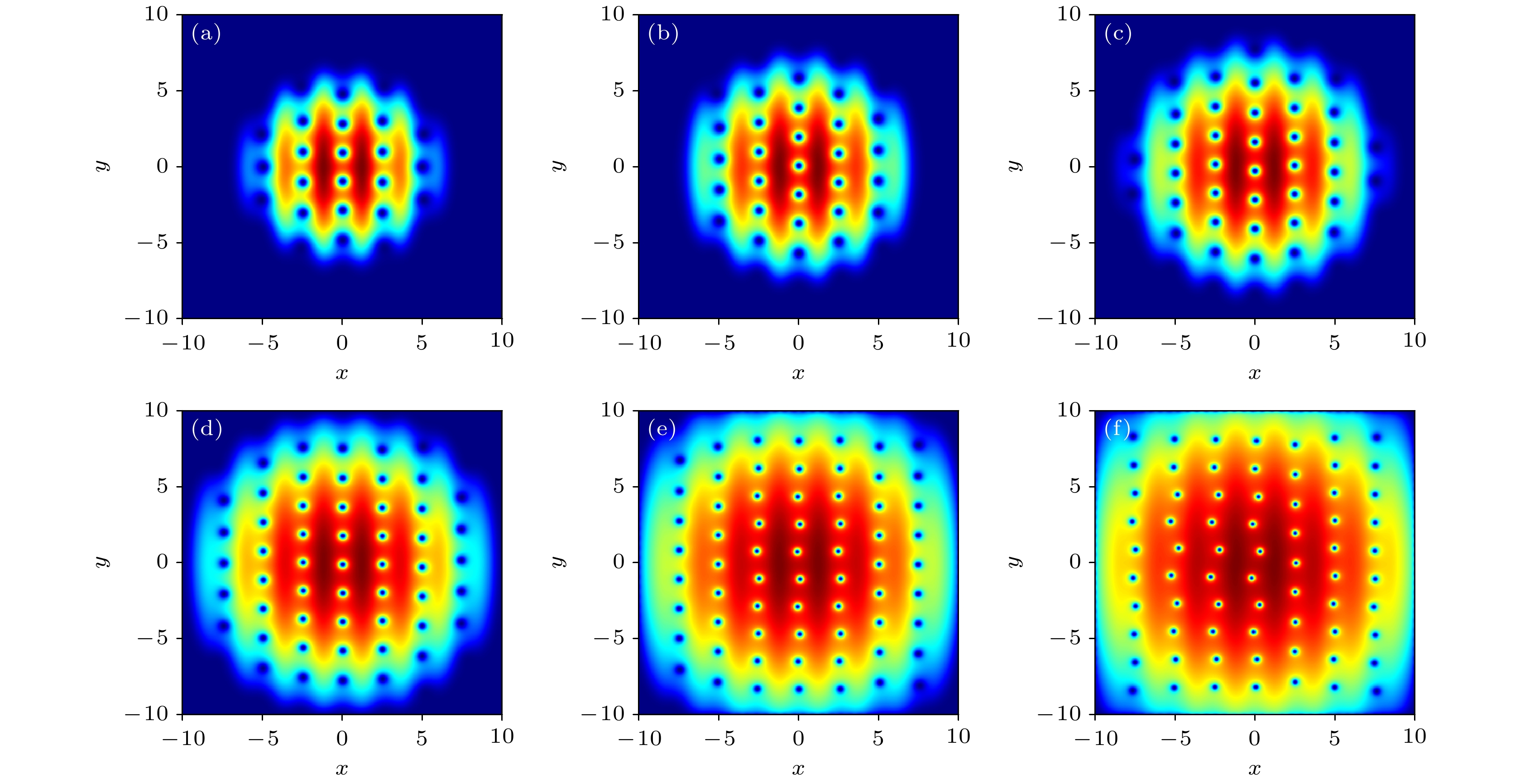
图 1 不同光晶格深度对涡旋链形成的影响 (a)
$ {V_0} = 0 $ ; (b)$ {V_0} = 0.05 $ ; (c)$ {V_0} = 0.5 $ ; (d)$ {V_0} = 1.5 $ ; (e)$ {V_0} = 3.0 $ ; (f)$ {V_0} = 4.5 $ . 其他参数设置为:$ k = 1.25 $ ,$g = 0.1$ ,$\varOmega = 0.7$ Figure 1. Effect of the depth of the optical lattice on the formation of vortex chains: (a)
$ {V_0} = 0 $ ; (b)$ {V_0} = 0.05 $ ; (c)$ {V_0} = 0.5 $ ; (d)$ {V_0} = 1.5 $ ; (e)$ {V_0} = 3.0 $ ; (f)$ {V_0} = 4.5 $ . Values of other parameters are$ k = 1.25 $ ,$g = 0.1$ , and$\varOmega = 0.7$ .
图 2 不同光晶格深度情况下, 凝聚体的密度分布
$ {\left| {\psi \left( {x, y} \right)} \right|^2} $ 的图像 (a)$ {V_0} = 3.0 $ ; (b)$ {V_0} = 6.0 $ ; (c)$ {V_0} = 9.0 $ ; (d)$ {V_0} = 15.0 $ ; (e)$ {V_0} = 21.0 $ ; (f)$ {V_0} = 30.0 $ . 其他参数与图 1 中的相同Figure 2. The density distribution of BEC at different optical lattice depths: (a)
$ {V_0} = 3.0 $ ; (b)$ {V_0} = 6.0 $ ; (c)$ {V_0} = 9.0 $ ; (d)$ {V_0} = 15.0 $ ; (e)$ {V_0} = 21.0 $ ; (f)$ {V_0} = 30.0 $ . The other parameters used are the same as those in Fig. 1.
图 3 不同原子间相互作用强度情况下, 凝聚体的密度分布
$ {\left| {\psi \left( {x, y} \right)} \right|^2} $ 的图像 (a)$ g = 0.05 $ ; (b)$ g = 0.10 $ ; (c)$ g = 0.15 $ ; (d)$ g = 0.30 $ ; (e)$ g = 0.60 $ ; (f)$ g = 0.90 $ . 其他参数设置为:$ k = 1.25 $ ,${V_0} = 3.0$ ,$\varOmega = 0.7$ Figure 3. Density distribution of BEC for different interaction strengths between atoms: (a)
$ g = 0.05 $ ; (b)$ g = 0.10 $ ; (c)$ g = 0.15 $ ; (d)$ g = 0.30 $ ; (e)$ g = 0.60 $ ; (f)$ g = 0.90 $ . Values of other parameters are$ k = 1.25 $ ,${V_0} = 3.0$ , and$\varOmega = 0.7$ .
图 4 不同旋转角速度情况下, 凝聚体的密度分布
$ {\left| {\psi \left( {x, y} \right)} \right|^2} $ 中的涡旋及涡旋链的分布情况 (a)$\varOmega = 0.1$ ; (b)$\varOmega = 0.3$ ; (c)$\varOmega = 0.5$ ; (d)$\varOmega = 0.7$ ; (e)$\varOmega = 0.9$ ; (f)$\varOmega = 0.95$ . 其他参数设置为:$ k = 1.25 $ ,$g = 0.1$ ,${V_0} = 3.0$ Figure 4. Distribution of vortices and vortex chains in the BEC under different rotation frequency: (a)
$\varOmega = 0.1$ ; (b)$\varOmega = 0.3$ ; (c)$\varOmega = 0.5$ ; (d)$\varOmega = 0.7$ ; (e)$\varOmega = 0.9$ ; (f)$\varOmega = 0.95$ . Values of other parameters are$ k = 1.25 $ ,$g = 0.1$ , and${V_0} = 3.0$ .
图 5 旋转 BEC 中涡旋和涡旋链随时间演化 (a)
$ t = 0 $ ; (b)$ t = 1.0 $ ; (c)$ t = 2.0 $ ; (d)$ t = 3.0 $ ; (e)$ t = 4.0 $ ; (f)$ t = 5.0 $ ; (g)$ t = 6.0 $ ; (h)$ t = 8.0 $ ; (i)$ t = 10.0 $ ; (j)$ t = 12.0 $ ; (k)$ t = 14.0 $ ; (l)$ t = 16.0 $ . 其他参数为$ k = 1.25 $ ,$g = 0.1$ ,${V_0} = 3.0$ ,$\varOmega = 0.7$ Figure 5. Evolution of vortices and vortex chains of the rotating BEC: (a)
$ t = 0 $ ; (b)$ t = 1.0 $ ; (c)$ t = 2.0 $ ; (d)$ t = 3.0 $ ; (e)$ t = 4.0 $ ; (f)$ t = 5.0 $ ; (g)$ t = 6.0 $ ; (h)$ t = 8.0 $ ; (i)$ t = 10.0 $ ; (j)$ t = 12.0 $ ; (k)$ t = 14.0 $ ; (l)$ t = 16.0 $ . Values of other parameters are$ k = 1.25 $ ,$g = 0.1$ ,${V_0} = 3.0$ , and$\varOmega = 0.7$ . -
[1] Anderson M H, Ensher J R, Matthews M R, Wiemane C E, Cornell A 1995 Science 269 198
Google Scholar
[2] Bradley C C, Sackett C A, Tollett J J, Hulet R G 1995 Phys. Rev. Lett. 75 1687
Google Scholar
[3] Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969
Google Scholar
[4] 郭慧, 王雅君, 王林雪, 张晓斐 2020 69 010302
Google Scholar
Guo H, Wang J Y, Wang L X, Zhang X F 2020 Acta Phys. Sin. 69 010302
Google Scholar
[5] Wang L X, Dai C Q, Wen L, Liu T, Jiang HF, Saito H, Zhang S G, Zhang X F 2018 Phys. Rev. A 97 063607
Google Scholar
[6] 陈艳勃, 张素英 2020 量子光学学报 26 7
Chen Y B, Zhang S Y 2020 J. Quantum Opt 26 7
[7] 乔红霞, 张素英 2019 量子光学学报 25 319
Qiao H X, Zhang S Y 2019 Chin. J. Comput. Phys 25 319
[8] 王书松, 张素英 2021 计算物理 38 113
Wang S S, Zhang S Y 2021 Chin. J. Comput. Phys 38 113
[9] Tsubota M, Kasamatsu K, Ueda M 2002 Phys. Rev. A 65 023603
Google Scholar
[10] Li S, Prinari B, Biondini G 2018 Phys. Rev. E 97 022221
Google Scholar
[11] Yan Z, Konotop V V, Akhmediev N 2010 Phys. Rev. E 82 036610
Google Scholar
[12] 张爱霞, 姜艳芳, 薛具奎 2021 70 200302
Google Scholar
Zhang A X, Jiang Y F, Xue J K 2021 Acta Phys. Sin 70 200302
Google Scholar
[13] 李吉, 刘伍明 2018 67 110302
Google Scholar
Li J, Liu W M 2018 Acta Phys. Sin 67 110302
Google Scholar
[14] 陈光平 2015 64 030302
Google Scholar
Chen G P 2015 Acta Phys. Sin 64 030302
Google Scholar
[15] Chin C, Grimm R, Julienne P, et al. 2010 Rev. Mod. Phys. 82 1225
Google Scholar
[16] Sanz J, Frölian A, Chisholm C S, Cabrera C R, Tarruell L 2022 Phys. Rev. Lett. 128 013201
Google Scholar
[17] Nguyen J H V, Luo D, Hulet R G 2017 Science 356 422
Google Scholar
[18] Di Carli A, Henderson G, Flannigan S, Colquhoun C D, Mitchell M, Oppo G-L, Daley A J, Kuhr S, Haller E 2020 Phys. Rev. Lett. 125 183602
Google Scholar
[19] Lin Y J, Compton R L, Perry A R, Phillips W D, Porto J V, Spielman I B 2009 Phys. Rev. Lett. 102 130401
Google Scholar
[20] Chen P K, Liu L R, Tsai M J, Chiu N C, Kawaguchi Y, Yip S K, Chang M S, Lin Y J 2018 Phys. Rev. Lett. 121 250401
Google Scholar
[21] Zou P, Brand J, Liu X J, Hu H 2016 Phys. Rev. Lett. 117 225302
Google Scholar
[22] Chen K J, Wu F, Peng S G, Yi W, He L Y, 2020 Phys. Rev. Lett. 125 260407
Google Scholar
[23] Katsimiga G C, Kevrekidis P G, Prinari B, Biondini G, Schmelcher P 2018 Phys. Rev. A 97 043623
Google Scholar
[24] Gligorić G, Maluckov A, Hadžievski L, Malomed B A 2013 Phys. Rev. E 88 032905
Google Scholar
[25] Balaž A, Paun R, Nicolin A I, Balasubramanian S, Ramaswamy R 2014 Phys. Rev. A 89 023609
Google Scholar
[26] Sudharsan J B, Radha R, Fabrelli H, Gammal A, Malomed B A 2015 Phys. Rev. A 92 053601
Google Scholar
[27] Kengne E, Liu W M, Malomed B A 2021 Phys. Rep. 899 1
Google Scholar
[28] Cheng Y S, Adhikari S K 2011 Phys. Rev. A 83 023620
Google Scholar
[29] Wang C, Law K J H, Kevrekidis P G, Kevrekidis G, Porter M A 2013 Phys. Rev. A 87 023621
Google Scholar
[30] Wang D S, Song S W, Xiong B, Liu W M 2011 Phys. Rev. A 84 053607
Google Scholar
[31] Yan Z Y, Konotop V V, Yulin A V, Liu W M 2012 Phys. Rev. E 85 016601
Google Scholar
[32] Antoine X, Tang Q L, Zhang Y 2018 Commun. Comput. Phys. 24 966
[33] Williams R A, Al-Assam S, Foot C J 2010 Phys. Rev. Lett. 104 050404
Google Scholar
[34] 陈海军, 任元, 王华 2022 71 056701
Google Scholar
Chen H J, Ren Y, Wang H 2022 Acta Phys. Sin 71 056701
Google Scholar
[35] Abrikosov A A 2004 Rev. Mod. Phys. 76 975
Google Scholar
[36] Matveenko S I 2010 Phys. Rev. A 82 033628
Google Scholar
[37] Schweikhard V, Coddington I, Engels P, Mogendorff V P, Cornell E A 2004 Phys. Rev. Lett. 92 040404
Google Scholar
[38] Bao W Z, Jaksch D, Markowich P A 2003 J. Comput. Phys. 187 318
Google Scholar
[39] Bao W Z, Wang H 2006 J. Comput. Phys. 217 612
Google Scholar
[40] Fletcher R J, Shaffer A, Wilson C C, Patel P B, Yan Z J, Crépel V, Mukherjee B, Zwierlein M W 2021 Science 372 1318
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3744
- PDF Downloads: 82
- Cited By: 0
