-
Quantum phases (QPs) and quantum phase transitions (QPTs) are very important parts of the strongly correlated quantum many-body systems in condensed matter. To study the QPs and QPTs, the systems should include rich quantum phase diagram. In this sense, the corresponding quantum spin models should have strong quantum fluctuation, strong geometric frustration, complicated spin-spin exchange or orbital degrees of freedom, which induces a variety of spontaneous symmetry breaking (SSB) or hidden spontaneous symmetry breaking. The QPs induced by the SSB can be characterized by local order parameters, a concept that originates from Landau-Ginzburg-Wilson paradigm (LGW). However, there is also a novel class of topological QPs beyond LGW, which has aroused one’s great interest since the Haldane phase was found. Such QPs can be characterized only by topological long-range nonlocal string correlation order parameters instead of local order parameters. In this paper, we investigate a spin-1/2 quantum compass chain model (QCC) with orbital degrees of freedom in x, y and z components. The prototype of QCC is the quantum compass model including novel topological QPs beyond LGW, and consequently one can also anticipate the existence of novel topological QPs in QCC. However, very little attention has been paid to the QPs and QPTs for QCC, which deserves to be further investigated. By using the infinite time evolving block decimation in the presentation of matrix product states, we study the QPs and QPTs of QCC. To characterize QPs and QPTs of QCC, the ground state energy, local order parameter, topological long-range nonlocal string correlation order parameters, critical exponent, correlation length and central charge are calculated. The results show the phase diagram of QCC including local antiferromagnetic phase, local stripe antiferromagnetic phase, oscillatory odd Haldane phase and monotonic odd Haldane phase. The QPTs from oscillatory odd Haldane phase to local stripe antiferromagnetic phase and from local antiferromagnetic phase to monotonic odd Haldane phase are continuous; on the contrary, QPTs from local stripe antiferromagnetic phase to local antiferromagnetic phase and from oscillatory odd Haldane phase to monotonic odd Haldane phase are discontinuous. The crossing point where the line of continuous QPTs meets with the line of discontinuous QPTs is the multiple critical point. The critical exponents β of local antiferromagnetic order parameter, local stripe antiferromagnetic order parameter, topological long-range nonlocal oscillatory odd string correlation order parameter, and topological long-range nonlocal monotonic odd string correlation order parameter are all equal to 1/8. Moreover,
$\beta =1/8$ and the central charges$c = 1/2$ at the critical points show that the QPTs from local phases to nonlocal phases belong to the Ising-type universality class.-
Keywords:
- quantum phase transition /
- string correlation /
- topological order /
- critical exponent
[1] Pollmann F, Fuji Y, Oshikawa M 2015 Phys. Rev. Lett. 114 177204
Google Scholar
[2] Affleck I, Kennedy T, Lieb E H, Tasaki H 1987 Phys. Rev. Lett. 59 799
Google Scholar
[3] Kennedy T 1990 J. Phys. Condens. Matter 2 5737
Google Scholar
[4] Gu Z C, Wen X G 2009 Phys. Rev. B 80 155131
Google Scholar
[5] Pollmann F, Berg E, Turner A M, Oshikawa M 2012 Phys. Rev. B 85 075125
Google Scholar
[6] Takashi T, Kiyomi O, Hiroki N, Toru S, Kiyohide N, Makoto K 2011 J. Phys. Soc. Jpn. 80 043001
Google Scholar
[7] Feng X Y, Zhang G M, Xiang T 2007 Phys. Rev. Lett. 98 087204
Google Scholar
[8] Wang Z, Li Q, Li W, Cai Z 2021 Phys. Rev. Lett. 126 237201
Google Scholar
[9] Yang Y, Ran S J, Chen X, Sun Z Z, Gong S S, Wang Z, Su G 2020 Phys. Rev. B 101 045133
Google Scholar
[10] Anderson P W 1997 Basic Notions of Condensed Matter Physics (New Jersey: Addison-Wesley) pp69−129
[11] Coleman S 1975 An Introduction to Spontaneous Symmetry Breakdown and Gauge Fields: Laws of Hadronic Matter (New York: Academic Press) pp138−215
[12] Kosterlitz J M, Thouless D J 1974 J. Phys. C 6 1181
[13] Gu S J, Lin H Q 2009 EPL 87 10003
Google Scholar
[14] He Y Y, Xu X Y, Sun K, Assaad F, Meng Z Y, Lu Z Y 2018 Phys. Rev. B 97 08110(R
[15] Wang X Q, Zhu N, Chen C 2002 Phys. Rev. B 66 172405
Google Scholar
[16] Lu L, Shao S, Lin Y C, Guo W A, Sandvik A W 2018 Phys. Rev. X 8 041040
[17] Kotov V N, Yao D X, Neto A H C, Campbell D K 2009 Phys. Rev. B 80 174403
Google Scholar
[18] Haldane F D M 1983 Phys. Rev. Lett. 50 1153
Google Scholar
[19] 陈西浩, 王秀娟 2018 67 190301
Chen X H, Wang X J 2018 Acta Phys. Sin. 67 190301
[20] Chen X H, McCulloch I, Batchelor M T, Zhou H Q 2020 Phys. Rev. B 102 085146
Google Scholar
[21] Quella T 2021 Phys. Rev. B 103 054404
Google Scholar
[22] Kugel K I, Khomskii D I 1973 Zh. Eksp. Teor. Fiz. 64 1429
[23] Chen H D, Fang C, Hu J, Yao H 2007 Phys. Rev. B 75 144401
[24] Eriksson E, Johannesson H 2009 Phys. Rev. B 79 224424
Google Scholar
[25] Wang H T, Cho S Y 2015 J. Phys. Condens. Matter 27 015603
Google Scholar
[26] Liu G H, Li W, You W L, Tian G S, Su G 2012 Phys. Rev. B 85 184422
Google Scholar
[27] Liu G H, Kong L J, Deng X Y, You W L 2015 Solid State Commun. 209 210
[28] Liu G H, Kong L J, Deng X Y, You W L 2015 Eur. Phys. J. B 88 284
Google Scholar
[29] Brzezicki W, Oles A M 2016 Phys. Rev. B 93 214402
[30] Vidal G 2007 Phys. Rev. Lett. 98 070201
Google Scholar
[31] [32] Bowley R, Sanchez M 2000 Introductory Statistical Mechanics (Oxford: Oxford University Press) pp236–239
[33] den Nijs M, Rommelse K 1989 Phys. Rev. B 40 4709
Google Scholar
[34] Tasaki H 1991 Phys. Rev. Lett. 66 798
Google Scholar
[35] Hida K 1992 Phys. Rev. B 45 2207
Google Scholar
[36] Hida K 1992 Phys. Rev. B 46 8268
Google Scholar
[37] Hida K, Takada K, Suzuki H 2013 J. Phys. Soc. Jpn. 82 064703
Google Scholar
[38] Pollmann F, Mukerjee S, Turner A M, Moore J E 2009 Phys. Rev. Lett. 102 255701
Google Scholar
[39] Tagliacozzo L, Oliveira T R, de Iblisdir S, Latorre J I 2008 Phys. Rev. B 78 024410
Google Scholar
[40] Korepin V E 2004 Phys. Rev. Lett. 92 096402
Google Scholar
[41] Calabrese P, Cardy J J 2004 Stat. Mech. 0406 P06002
[42] Bennett C H, Bernstein H J, Popescu S, Schumacher B 1996 Phys. Rev. A 53 2046
Google Scholar
-
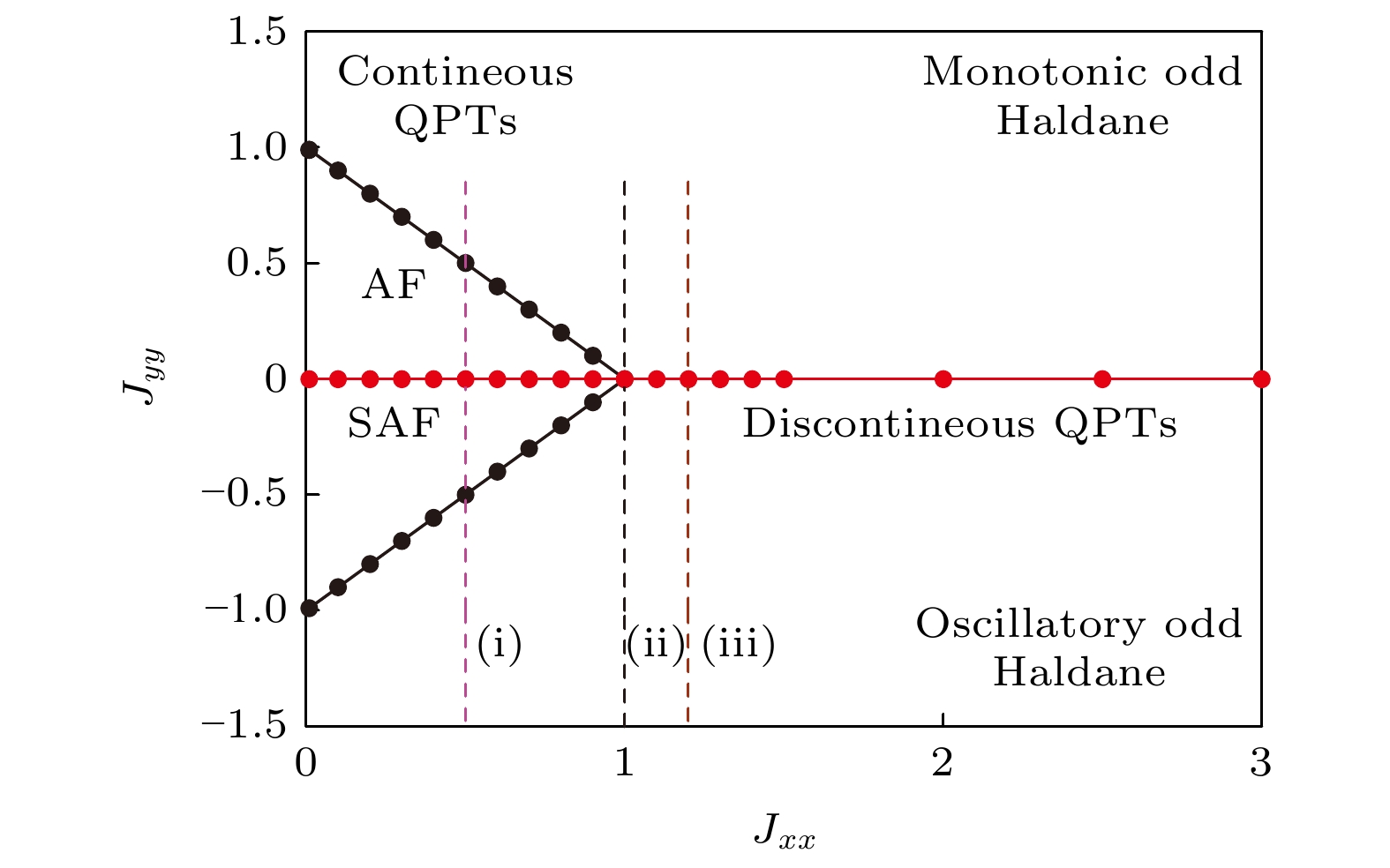
图 1 量子罗盘自旋链模型基态相图. AF, SAF, Monotonic odd Haldane和Oscillatory odd Haldane分别是反铁磁相、条纹反铁磁相、单调奇数Haldane相和振荡奇数Haldane相. 黑实线和红实线分别表示连续相变线和非连续相变线. 标记为(i)−(iii)的3条虚线是展示刻画量子相和相变策略的代表线
Figure 1. Quantum phase diagram for the QCC with orbital degrees of freedom in x, y and z components, which including antiferromagnetic phase (AF), striped antiferromagnetic phase (SAF), monotonic odd Haldane phase and oscillatory odd Haldane phase. The solid black line and solid red line represent continuous quantum phase transition line and discontinuous quantum phase transition line, respectively. The dashed paths labeled by (i)−(iii) are sample lines discussed in the text to show how to characterize quantum phases and quantum phase transitions.
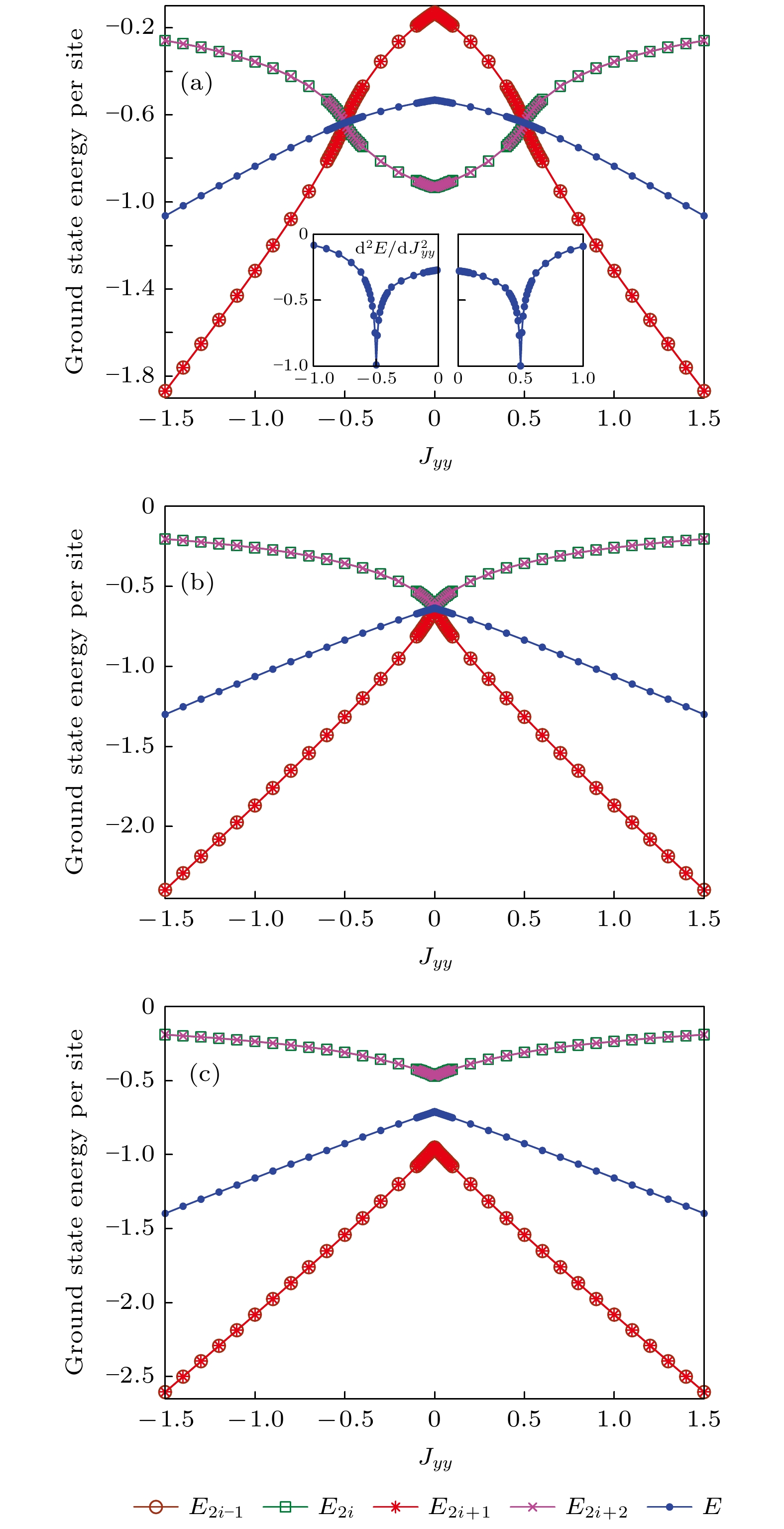
图 2 单位格点基态能量随控制参数
$J_{yy}$ 的变化行为.$E_{2 i-1}$ ,$E_{2 i+1}$ ,$E_{2 i}$ 和$E_{2 i+2}$ 分别是奇/偶数键的单位格点基态能量.$E=\dfrac{1}{4}(E_{2 i-1}+E_{2 i}+E_{2 i+1}+E_{2 i+2})$ 为平均单位格点基态能量 (a) 相变点发生在$J_{yy}^{c1}=-0.5$ ,$J_{yy}^{c2}= 0$ 和$J_{yy}^{c3}=0.5$ , 内插图为单位格点基态能量的二阶导数${\rm{d}}^{2}E/{\rm{d}}J^{2}_{yy}$ ; (b), (c) 相变点分别发生在$J_{yy}^{c4}=0$ 和$J_{yy}^{c5}=0$ Figure 2. Ground state energy per site as a function of controlling parameter
$J_{yy}$ .$E_{2 i-1}$ ,$E_{2 i+1}$ ,$E_{2 i}$ and$E_{2 i+2}$ are ground state energies per site on odd and even bonds, respectively.$E=\dfrac{1}{4}(E_{2 i-1}+E_{2 i}+E_{2 i+1}+E_{2 i+2})$ is average ground state energy per site: (a) QPTs at$J_{yy}^{c1}= $ $ -0.5$ ,$J_{yy}^{c2}=0$ and$J_{yy}^{c3}=0.5$ . The inset shows the second-order derivation of average ground state energy per site${\rm{d}}^{2}E/{\rm{d}}J^{2}_{yy}$ . (b), (c) QPTs at$J_{yy}^{c4}=0$ and$J_{yy}^{c5}=0$ , respectively.
图 3 局域磁化强度
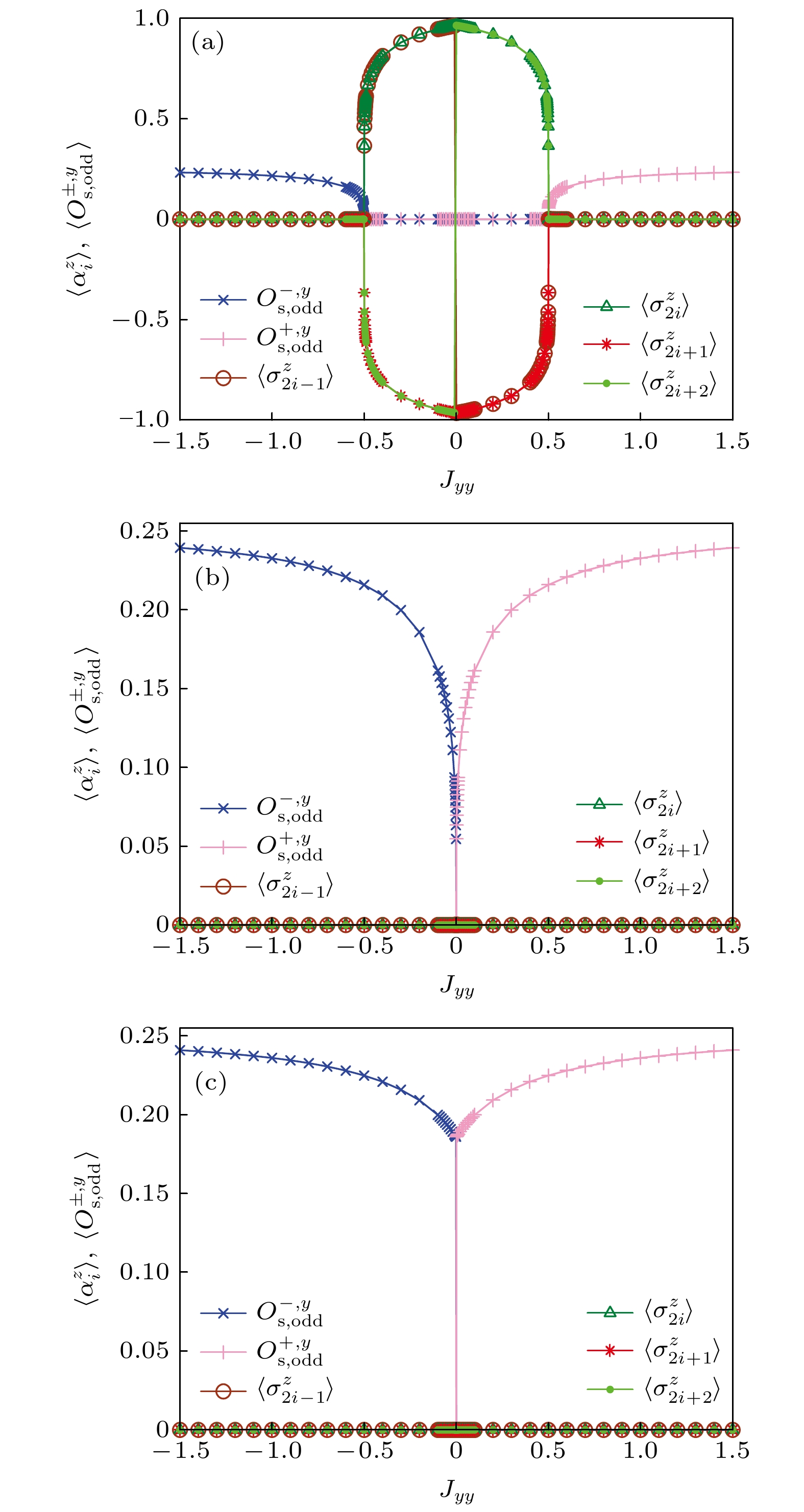
$\langle \sigma_{i}^{z}\rangle$ 奇数弦关联序参量$O_{\rm{s, odd}}^{\pm, y}$ 随控制参数$J_{yy}$ 变化 (a)$J_{yy} < -0.5$ 属于振荡奇数Haldane相,$-0.5 < J_{yy} < 0$ 属于条纹反铁磁相,$0 < J_{yy} < 0.5$ 属于反铁磁相,$J_{yy}> 0.5$ 属于单调奇数Haldane相; (b), (c)$J_{yy} < 0$ 属于振荡奇数Haldane相,$J_{yy}>0$ 属于单调奇数Haldane相Figure 3. Local magnetization
$\langle \sigma_{i}^{z}\rangle$ and odd string correlation order parameter$O_{\rm{s, odd}}^{\pm, y}$ as a function of controlling parameter$J_{yy}$ : (a) The system clearly shows the oscillatory odd Haldane phase for$J_{yy} < -0.5$ , SAF phase for$-0.5 < J_{yy} < 0$ , AF phase for$0 < J_{yy} < 0.5$ and the monotonic odd Haldane phase for$J_{yy}>0.5$ with fixed$J_{xx}=0.5$ ; (b), (c) the system clear shows the oscillatory odd Haldane phase for$J_{yy} < 0$ and the monotonic odd Haldane phase for$J_{yy}>0$ with fixed$J_{xx}=1$ and$J_{xx}=1.2$ , respectively.
图 4 局域磁化强度
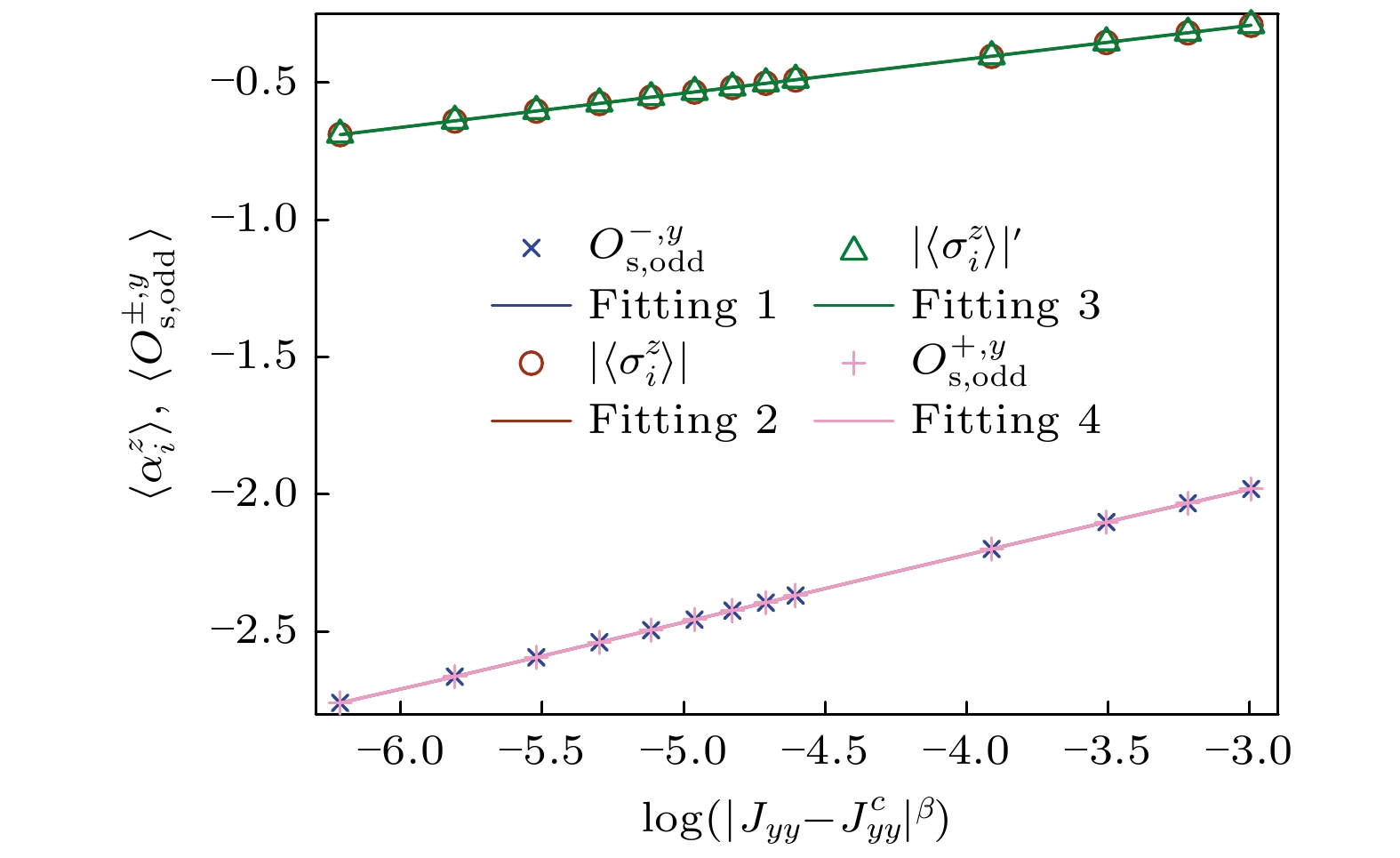
$|\langle \sigma_{i}^{z}\rangle|$ 和奇数弦关联序参量$O_{\rm{s, odd}}^{\pm, y}$ 与控制参数$|J_{yy}-J_{yy}^{c}|$ 标度关系Figure 4. Local magnetization
$|\langle \sigma_{i}^{z}\rangle|$ and odd string correlation order parameter$O_{\rm{s, odd}}^{\pm, y}$ as a function of the distance of controlling parameter$|J_{yy}-J_{yy}^{c}|$ .
图 5 (a) 冯诺依曼熵
$S_{{\rm{odd}}}$ 和$S_{{\rm{even}}}$ 随控制参数$J_{yy}$ 增加的变化行为; (b), (c) 冯诺依曼熵$S_{{\rm{odd}}}$ ,$S_{{\rm{even}}}$ 和关联长度ξ随控制参数$\chi $ 的标度关系Figure 5. (a) Behaviors of von Neumann entropy
$S_{{\rm{odd}}}$ and$S_{{\rm{even}}}$ with the increasement of controlling parameter$J_{yy}$ ; (b), (c) von Neumann entropy$S_{{\rm{odd}}}$ ,$S_{{\rm{even}}}$ and the correlation length ξ as a function of the truncation dimension -
[1] Pollmann F, Fuji Y, Oshikawa M 2015 Phys. Rev. Lett. 114 177204
Google Scholar
[2] Affleck I, Kennedy T, Lieb E H, Tasaki H 1987 Phys. Rev. Lett. 59 799
Google Scholar
[3] Kennedy T 1990 J. Phys. Condens. Matter 2 5737
Google Scholar
[4] Gu Z C, Wen X G 2009 Phys. Rev. B 80 155131
Google Scholar
[5] Pollmann F, Berg E, Turner A M, Oshikawa M 2012 Phys. Rev. B 85 075125
Google Scholar
[6] Takashi T, Kiyomi O, Hiroki N, Toru S, Kiyohide N, Makoto K 2011 J. Phys. Soc. Jpn. 80 043001
Google Scholar
[7] Feng X Y, Zhang G M, Xiang T 2007 Phys. Rev. Lett. 98 087204
Google Scholar
[8] Wang Z, Li Q, Li W, Cai Z 2021 Phys. Rev. Lett. 126 237201
Google Scholar
[9] Yang Y, Ran S J, Chen X, Sun Z Z, Gong S S, Wang Z, Su G 2020 Phys. Rev. B 101 045133
Google Scholar
[10] Anderson P W 1997 Basic Notions of Condensed Matter Physics (New Jersey: Addison-Wesley) pp69−129
[11] Coleman S 1975 An Introduction to Spontaneous Symmetry Breakdown and Gauge Fields: Laws of Hadronic Matter (New York: Academic Press) pp138−215
[12] Kosterlitz J M, Thouless D J 1974 J. Phys. C 6 1181
[13] Gu S J, Lin H Q 2009 EPL 87 10003
Google Scholar
[14] He Y Y, Xu X Y, Sun K, Assaad F, Meng Z Y, Lu Z Y 2018 Phys. Rev. B 97 08110(R
[15] Wang X Q, Zhu N, Chen C 2002 Phys. Rev. B 66 172405
Google Scholar
[16] Lu L, Shao S, Lin Y C, Guo W A, Sandvik A W 2018 Phys. Rev. X 8 041040
[17] Kotov V N, Yao D X, Neto A H C, Campbell D K 2009 Phys. Rev. B 80 174403
Google Scholar
[18] Haldane F D M 1983 Phys. Rev. Lett. 50 1153
Google Scholar
[19] 陈西浩, 王秀娟 2018 67 190301
Chen X H, Wang X J 2018 Acta Phys. Sin. 67 190301
[20] Chen X H, McCulloch I, Batchelor M T, Zhou H Q 2020 Phys. Rev. B 102 085146
Google Scholar
[21] Quella T 2021 Phys. Rev. B 103 054404
Google Scholar
[22] Kugel K I, Khomskii D I 1973 Zh. Eksp. Teor. Fiz. 64 1429
[23] Chen H D, Fang C, Hu J, Yao H 2007 Phys. Rev. B 75 144401
[24] Eriksson E, Johannesson H 2009 Phys. Rev. B 79 224424
Google Scholar
[25] Wang H T, Cho S Y 2015 J. Phys. Condens. Matter 27 015603
Google Scholar
[26] Liu G H, Li W, You W L, Tian G S, Su G 2012 Phys. Rev. B 85 184422
Google Scholar
[27] Liu G H, Kong L J, Deng X Y, You W L 2015 Solid State Commun. 209 210
[28] Liu G H, Kong L J, Deng X Y, You W L 2015 Eur. Phys. J. B 88 284
Google Scholar
[29] Brzezicki W, Oles A M 2016 Phys. Rev. B 93 214402
[30] Vidal G 2007 Phys. Rev. Lett. 98 070201
Google Scholar
[31] [32] Bowley R, Sanchez M 2000 Introductory Statistical Mechanics (Oxford: Oxford University Press) pp236–239
[33] den Nijs M, Rommelse K 1989 Phys. Rev. B 40 4709
Google Scholar
[34] Tasaki H 1991 Phys. Rev. Lett. 66 798
Google Scholar
[35] Hida K 1992 Phys. Rev. B 45 2207
Google Scholar
[36] Hida K 1992 Phys. Rev. B 46 8268
Google Scholar
[37] Hida K, Takada K, Suzuki H 2013 J. Phys. Soc. Jpn. 82 064703
Google Scholar
[38] Pollmann F, Mukerjee S, Turner A M, Moore J E 2009 Phys. Rev. Lett. 102 255701
Google Scholar
[39] Tagliacozzo L, Oliveira T R, de Iblisdir S, Latorre J I 2008 Phys. Rev. B 78 024410
Google Scholar
[40] Korepin V E 2004 Phys. Rev. Lett. 92 096402
Google Scholar
[41] Calabrese P, Cardy J J 2004 Stat. Mech. 0406 P06002
[42] Bennett C H, Bernstein H J, Popescu S, Schumacher B 1996 Phys. Rev. A 53 2046
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4782
- PDF Downloads: 102
- Cited By: 0
