-
In this work, the Hubbard model is adopted to describe fermions with on-site repulsive interaction and the nearest-neighbor hopping in anisotropic ruby lattice. The combination of cluster dynamical mean field theory and continuous-time quantum Monte Carlo algorithm is used to solve the theoretical model. It is widely accepted that the density of states and the double occupancy are two important quantities for determining the phase transition of two-dimensional strongly correlated system. Therefore, based on the self-consistent calculation, using the maximum entropy method to calculate the single particle density of states and double occupancy of fermions in anisotropic ruby lattice. Here in this work, there are 6 sites in a cluster. The influences of temperature, interaction and anisotropic parameter on metal-insulator phase transition of fermions in anisotropic ruby lattice are discussed based on the calculations of single particle density of state and double occupancy. Finally, the metal-Mott insulator phase diagram which shows the competition between temperature and on-site repulsive interaction in the phase transition of fermions in anisotropic ruby lattice is presented. The results shows that the system is in metallic state for the regime of weak interaction and low temperature, and the Mott insulator appears in the regime of strong interaction and high temperature. The metallic state and Mott insulating one are separated by the second-order transition line in the phase diagram. -
Keywords:
- anisotropic ruby lattice /
- Hubbard model /
- dynamical mean filed theory /
- quantum phase transition
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[2] Moore J E 2010 Nature 464 194
Google Scholar
[3] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[4] Qi X L, Zhang S C 2010 Phys.Today 63 33
[5] Leggett J A 2001 Rev. Mod. Phys. 73 307
Google Scholar
[6] Ho T L, Zhang S Z 2011 Phys. Rev. Lett. 107 150403
Google Scholar
[7] He M Y, Sun H M, He Q L 2019 Fron. Phys. 14 43401
Google Scholar
[8] Rasche B, Isaeva A, Ruck M, et al. 2013 Nat. Mat. 12 422
Google Scholar
[9] Lin K Y, Ma W J 1983 J. Phys. A: Math. Gen. 16 2515
Google Scholar
[10] Lin K Y, Ma W J 1983 J. Phys. A: Math. Gen. 16 3895
Google Scholar
[11] Hou J M, Wang G X 2013 Commun. Theor. Phys. 60 129
Google Scholar
[12] Hu X, Kargarian M, Fiete GA 2011 Phys. Rev. B 84 155116
Google Scholar
[13] Jahromi S S, Orús R 2020 Phys. Rev. B 101 115114
Google Scholar
[14] Cortexs LC, Ortix C, Brink Jvan den 2013 Phys. Rev. Lett. 111 146801
Google Scholar
[15] Jahromi SS, Kargarian M, Masoudi S F, Langari A 2016 Phys. Rev. B 94 125145
Google Scholar
[16] Whitsitt S, Chua V, Fiete G A 2012 New J. Phys. 14 115029
Google Scholar
[17] Gutzwiller M C 1963 Phys. Rev. Lett. 10 159
Google Scholar
[18] Wohlfarth E P 1953 Rev. Mod.Phys. 25 211
Google Scholar
[19] Hubbard J 1963 P. Roy. Soc. A-Math. Phy. 276 238
[20] Hubbard J 1964 P. Roy. Soc. A-Math. Phy. 281 401
[21] Kanamori J 1963 Prog.Theo. Phys. 30 275
Google Scholar
[22] Figueirido F, Karlhede A, Kivelson S, et al. 1990 Phys. Rev.B 41 4619
Google Scholar
[23] Lüscher A, Läuchli A M 2009 Phys. Rev. B 79 195102
Google Scholar
[24] Gull E, Millis A J, Lichtenstein A I, et al. 2011 Rev.Mod. Phys. 83 349
Google Scholar
[25] Jarrell M 1992 Phys. Rev.Lett. 69 168
Google Scholar
[26] Gagliano E R, Dagotto E, Moreo A, et al. 1986 Phys. Rev. B 34 1677
[27] Nihat Berker A, Grest G S, Soukoulis C M, et al. 1984 J. App. Phys. 55 2416
Google Scholar
[28] Vafek O, Yang K 2010 Phys. Rev. B 81 041401
[29] Chitra R, Kotliar G 1999 Phys. Rev. Lett. 83 2386
Google Scholar
[30] Lichtenstein A, Katsnelson M. 2000 Phys. Rev. B 62 R9283
Google Scholar
[31] Kotliar G, Savrasov S Y, Pálsson G, et al. 2001 Phys. Rev.Lett. 87 186401
Google Scholar
[32] Capone M, Civelli M, Kancharla S S, et al. 2004 Phys. Rev.B 69 195105
Google Scholar
[33] Wu W, Chen Y H, TaoH S, et al. 2010 Phys. Rev. B 82 245102
Google Scholar
[34] Bao A, Tao HS, Liu HD, et al. 2014 Sci. Rep. 4 6918
[35] Bao A, 2019 Chin. Phys. B 28 057101
Google Scholar
[36] Georges A, Kotliar G, Krauth W, et al. 1996 Rev. Mod. Phys. 68 13
Google Scholar
[37] Kornilovitch P 1998 Phys. Rev.Lett. 81 5382
Google Scholar
[38] Rubtsov A N, Savkin V V, Lichtenstein A I 2005 Phys. Rev.B 72 035122
Google Scholar
[39] Werner P, Comanac A, de’ Medici L, et al. 2006 Phys. Rev.Lett. 97 076405
Google Scholar
[40] Jarrell M, Gubernatis J E 1996 Phys. Rep. 269 133
Google Scholar
-
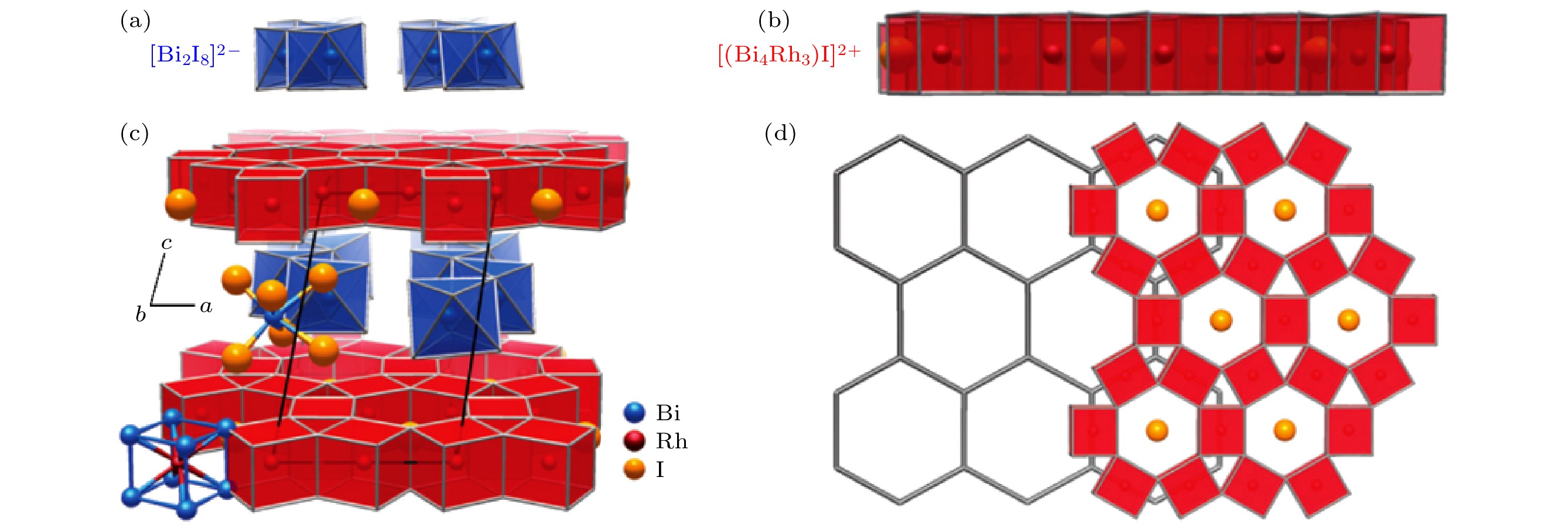
图 1 拓扑绝缘体材料Bi14Rh3I9的晶格结构示意图 (a)−(c) Bi14Rh3I9的晶体结构及其构成单元, 绝缘层[Bi2I8]2–的zigzag链分离由共棱RhBi8立方体构成的六角网格状金属间的 [(Rh4Bi)3I]2+层, 六角晶格的边由共棱RhBi8立方体覆盖; (d) 二维ruby晶格与六角晶格结构俯视图[8]
Figure 1. Sketch of crystal structure of topological insulator Bi14Rh3I9: (a)−(c) Triclinic crystal structure of Bi14Rh3I9. Insulating layers of [Bi2I8]2– zigzag chains separate the intermetallic [(RhBi4)3I]2+ layers that consist of hexagonal nets of edge-sharing RhBi8 cubes; (d) honeycomb lattice of graphene with the structure of the intermetallic layer [8].
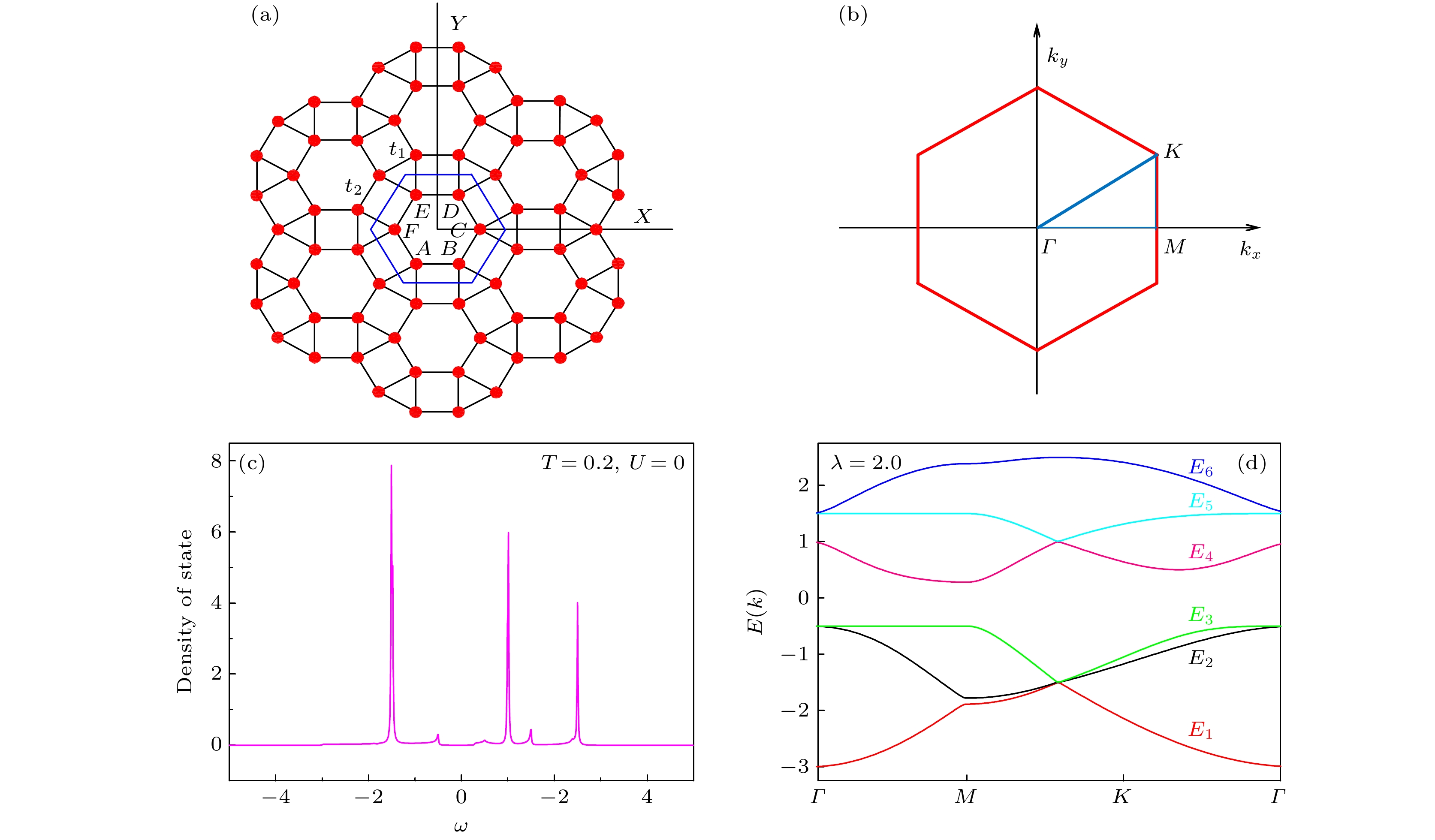
图 2 (a) Ruby晶格结构示意图; (b) ruby晶格第一布里渊区; (c) 各向异性ruby晶格(
$\lambda = 2.0$ )中费米子体系$ T = 0.2$ 和$ U = 0 $ 时的态密度; (d) 各向异性ruby晶格($\lambda = 2.0$ )中费米子体系无相互作用情况下色散关系Figure 2. (a) Sketch of ruby lattice; (b) first Brillouin zone of ruby lattice; (c) density of states of anisotropic ruby lattice (
$\lambda = 2.0$ ) for$T = 0.2$ ,$U = 0$ ; (d) energy dispersion of anisotropic ruby lattice ($\lambda = 2.0$ ) for$T = 0.2$ ,$U = 0$ .
图 3 方晶格模型映射到有效自洽场杂质模型的示意图 (a) 方晶格; (b) 具有四个格点的超级晶格; (c)有效自洽场中团簇杂质模型的示意图
Figure 3. Sketch of mapping square lattice model to impurity model in self-consistent field: (a) Square lattice; (b) sketch of supper lattice consists of 4 lattice point; (c) sketch of cluster impurity in self-consistent field.
图 4
$\kappa = 3$ 时一个随机行走示意图Figure 4. Sketch of random walk for
$\kappa = 3$ .
图 5 自洽计算的流程图
Figure 5. Flow chart of self-consistent calculation.
图 6 各向异性ruby晶格(
$\lambda =2.0 $ )中费米子体系的态密度 (a) T = 0.2时不同相互作用对应的态密度; (b) U = 8时不同温度对应的态密度Figure 6. Density of states of anisotropic ruby lattice (
$\lambda =2.0 $ ) with fermions: (a) Density of states for different interaction at$T = 0.2$ ; (b) density of states for different temperature at$U = 8.0 $ .
图 7 固定温度(
$T = 0.2$ )和固定相互作用($U = 8.0 $ )情况下, 各向异性参数对ruby晶格中费米子体系态密度的影响Figure 7. Comparison of the effect of anisotropic parameter λ on the density of states of fermions in ruby lattice on for
$T = 2 $ and$ U = 0 $ .
图 8 各向异性ruby晶格中费米子体系的双占据数 (a) 不同相互作用下体系双占据数随温度的变化; (b) 不同温度下体系双占据数随相互作用的变化
Figure 8. Double occupancy of anisotropic ruby lattice with fermions: (a) Comparison between double occupancy for different temperature with the change of interaction; (b) comparison between double occupancy for different interaction with the change of temperature.
图 9 温度和相互作用固定的情况下, ruby晶格中费米子体系的双占据数随各向异性参数的变化
Figure 9. Trend of double occupancy with the change of anisotropic parameter for fixed T and U.
图 10 各向异性ruby晶格中费米子体系的金属-绝缘相图
Figure 10. Metal-Insulator phase diagram of fermions in anisotropic ruby lattice.
-
[1] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[2] Moore J E 2010 Nature 464 194
Google Scholar
[3] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[4] Qi X L, Zhang S C 2010 Phys.Today 63 33
[5] Leggett J A 2001 Rev. Mod. Phys. 73 307
Google Scholar
[6] Ho T L, Zhang S Z 2011 Phys. Rev. Lett. 107 150403
Google Scholar
[7] He M Y, Sun H M, He Q L 2019 Fron. Phys. 14 43401
Google Scholar
[8] Rasche B, Isaeva A, Ruck M, et al. 2013 Nat. Mat. 12 422
Google Scholar
[9] Lin K Y, Ma W J 1983 J. Phys. A: Math. Gen. 16 2515
Google Scholar
[10] Lin K Y, Ma W J 1983 J. Phys. A: Math. Gen. 16 3895
Google Scholar
[11] Hou J M, Wang G X 2013 Commun. Theor. Phys. 60 129
Google Scholar
[12] Hu X, Kargarian M, Fiete GA 2011 Phys. Rev. B 84 155116
Google Scholar
[13] Jahromi S S, Orús R 2020 Phys. Rev. B 101 115114
Google Scholar
[14] Cortexs LC, Ortix C, Brink Jvan den 2013 Phys. Rev. Lett. 111 146801
Google Scholar
[15] Jahromi SS, Kargarian M, Masoudi S F, Langari A 2016 Phys. Rev. B 94 125145
Google Scholar
[16] Whitsitt S, Chua V, Fiete G A 2012 New J. Phys. 14 115029
Google Scholar
[17] Gutzwiller M C 1963 Phys. Rev. Lett. 10 159
Google Scholar
[18] Wohlfarth E P 1953 Rev. Mod.Phys. 25 211
Google Scholar
[19] Hubbard J 1963 P. Roy. Soc. A-Math. Phy. 276 238
[20] Hubbard J 1964 P. Roy. Soc. A-Math. Phy. 281 401
[21] Kanamori J 1963 Prog.Theo. Phys. 30 275
Google Scholar
[22] Figueirido F, Karlhede A, Kivelson S, et al. 1990 Phys. Rev.B 41 4619
Google Scholar
[23] Lüscher A, Läuchli A M 2009 Phys. Rev. B 79 195102
Google Scholar
[24] Gull E, Millis A J, Lichtenstein A I, et al. 2011 Rev.Mod. Phys. 83 349
Google Scholar
[25] Jarrell M 1992 Phys. Rev.Lett. 69 168
Google Scholar
[26] Gagliano E R, Dagotto E, Moreo A, et al. 1986 Phys. Rev. B 34 1677
[27] Nihat Berker A, Grest G S, Soukoulis C M, et al. 1984 J. App. Phys. 55 2416
Google Scholar
[28] Vafek O, Yang K 2010 Phys. Rev. B 81 041401
[29] Chitra R, Kotliar G 1999 Phys. Rev. Lett. 83 2386
Google Scholar
[30] Lichtenstein A, Katsnelson M. 2000 Phys. Rev. B 62 R9283
Google Scholar
[31] Kotliar G, Savrasov S Y, Pálsson G, et al. 2001 Phys. Rev.Lett. 87 186401
Google Scholar
[32] Capone M, Civelli M, Kancharla S S, et al. 2004 Phys. Rev.B 69 195105
Google Scholar
[33] Wu W, Chen Y H, TaoH S, et al. 2010 Phys. Rev. B 82 245102
Google Scholar
[34] Bao A, Tao HS, Liu HD, et al. 2014 Sci. Rep. 4 6918
[35] Bao A, 2019 Chin. Phys. B 28 057101
Google Scholar
[36] Georges A, Kotliar G, Krauth W, et al. 1996 Rev. Mod. Phys. 68 13
Google Scholar
[37] Kornilovitch P 1998 Phys. Rev.Lett. 81 5382
Google Scholar
[38] Rubtsov A N, Savkin V V, Lichtenstein A I 2005 Phys. Rev.B 72 035122
Google Scholar
[39] Werner P, Comanac A, de’ Medici L, et al. 2006 Phys. Rev.Lett. 97 076405
Google Scholar
[40] Jarrell M, Gubernatis J E 1996 Phys. Rep. 269 133
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7651
- PDF Downloads: 90
- Cited By: 0
