Effects of Si and Y co-doping on stability and oxidation resistance of <i>γ</i>-TiAl based alloys

Song Qing-Gong; Wang Li-Jie; Zhu Yan-Xia; Kang Jian-Hai; Gu Wei-Feng; Wang Ming-Chao; Liu Zhi-Feng

doi:10.7498/aps.68.20190490

Abstract

Improving the oxidation resistance of TiAl-based alloys at high temperature has great significance for expanding their application fields. Adding ternary and quaternary elements is one of the effective ways to solve the oxidation problem of this kind of alloys materials. The first-principles method based on density functional theory was used to study the Si and Y substitution co-doping effects on the oxidation resistance of γ-TiAl based alloys from the aspects of atomic average formation energy and elastic constant of system, as well as the formation energies of interstitial O atom, Ti vacancy and Al vacancy in the system. The results indicate that the atomic average formation energies of the Si and Y dual-doped systems are all negative, which imply they possess energy stability and can be prepared by experiments. In addition, the elastic constants of most Si and Y substitution co-doping γ-TiAl systems satisfy the mechanical stability criterion. For the mechanical stable systems, the analysis results about the formation energies of the interstitial O atom, Ti vacancy and Al vacancy reveal that the Ti₆SiYAl₈ series, in which both Si and Y substitute Ti, have obvious promotion effect on the improvement about oxidation resistance; system Ti₇YAl₇Si, in which Y substitutes Ti and Si substitutes Al, and system Ti₇SiAl₇Y, in which Si substitutes Ti and Y substitutes Al, have uncertain influence on improving oxidation resistance; system Ti₈Al₆SiY, in which both Si and Y substitute Al, is harmful to the improvement about oxidation resistance of the γ-TiAl based alloys. Therefore, the preparation conditions should be controlled moderately so that both Si and Y substitute Ti at the same time to form a large proportion configurations of Ti₆SiYAl₈ series in the materials. In these configurations, the outward diffusion of Ti atoms and the inward diffusion of interstitial O atoms are suppressed, meanwhile the outward diffusion of the Al atoms is facilitated. In this way, the production of α-Al₂O₃ is promoted and that of TiO₂ is weakened on the surface of co-doping γ-TiAl based alloys. Thus, a scale rich in α-Al₂O₃, i. e., a continuous, dense, and protective oxide scale can be grown on the surface of Si and Y substitution co-doping γ-TiAl alloys.

Keywords:

Authors and contacts

1.
Institute of Low Dimensional Materials and Technology, College of Science, CivilAviation University of China, Tianjin 300300, China
2.
Sino-European Institute of Aviation Engineering, Civil Aviation University of China, Tianjin 300300, China

Corresponding author: Song Qing-Gong, qgsong@cauc.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 51802343) and the Natural Science Fund of Civil Aviation University China (Grant No. 08CAUC-S02)

FullText HTML : translate this paragraph

References

[1]	Castillo R M, Nó M L, Jiménez J A, Ruano O A, San Juan J 2016 Acta Mater. 103 46 Google Scholar
[2]	Kim S W, Hong J K, Na Y S, Yeom J T, Kim S E 2014 Mater. Des. 54 814 Google Scholar
[3]	Chen G, Peng Y B, Zheng G, Qi Z X, Wang M Z, Yu H C, Dong C L, Liu C T 2016 Nature Mater. 15 876 Google Scholar
[4]	Pflumm R, Friedle S, Schütze M 2015 Intermetallics 56 1 Google Scholar
[5]	Yoshihara M, Kim Y W 2005 Intermetallics 13 952 Google Scholar
[6]	Kuranishi T, Habazaki H, Konno H 2005 Surf. Coat. Technol. 200 2438 Google Scholar
[7]	汤守巧, 曲寿江, 冯艾寒, 冯聪, 崔扣彪, 沈军 2017 稀有金属 41 81 Tang S Q, Qu S J, Feng A H, Feng C, Cui K B, Shen J 2017 Rare Metals 41 81
[8]	Hu H, Wu X, Wang R, Li W, Liu Q 2016 J. Alloys Compd. 658 689 Google Scholar
[9]	Brotzu A, Felli F, Pilone D 2013 Intermetallics 43 131 Google Scholar
[10]	平发平, 胡青苗, 杨锐 2013 金属学报 29 385 Ping F P, Hu Q M, Yang R 2013 Acta Metall. Sin. 29 385
[11]	朱绍祥, 王清江, 刘建荣, 刘羽寅, 杨锐 2010 中国有色金属学报 20 138 Zhu S X, Wang Q J, Liu J R, Liu Y Y, Yang R 2010 Chin. J. Nonferr. Met. 20 138
[12]	Izumi T, Yoshioka T, Hayashi S, Narita T 2005 Intermetallics 13 694 Google Scholar
[13]	刘杰, 薛祥义, 杨劼人 2015 稀有金属材料与工程 44 1942 Liu J, Xue X Y, Yang J R 2015 Rare Metal Mat. Eng. 44 1942
[14]	Lin J P, Zhao L L, Li G Y, Zhang L Q, Song X P, Ye F, Chen G L 2011 Intermetallics 19 136
[15]	杨忠波, 赵文金, 程竹青, 邱军, 张海, 卓洪 2017 金属学报 53 49 Yang Z B, Zhao W J, Cheng Z Q, Qiu J, Zhang H, Zhuo H 2017 Acta Metall. Sin. 53 49
[16]	Zhao L, Zhang Y, Zhu Y, Lin J, Ren Z 2016 Mater. High Temp. 33 234 Google Scholar
[17]	Zhao L L, Li G Y, Zhang L Q, Lin J P, Song X P, Ye F, Chen G L 2010 Intermetallics 18 1586 Google Scholar
[18]	周玉俊, 周雪锋, 陈光 2015 热加工工艺 44 93 Zhou Y J, Zhou X F, Chen G 2015 Hot Working Technol. 44 93
[19]	王艳晶, 宋玫锦, 王继杰, 杜兴蒿 2014 稀有金属材料与工程 43 1697 Wang Y J, Song M J, Wang J J, Du X H 2014 Rare Metal Mat. Eng. 43 1697
[20]	董利民, 崔玉友, 杨锐, 王福会 2004 金属学报 40 383 Google Scholar Dong L M, Cui Y Y, Yang R, Wang F H 2004 Acta Metall. Sin. 40 383 Google Scholar
[21]	肖伟豪, 张亮, 姜惠仁 2004 北京航空航天大学学报 32 365 Google Scholar Xiao W H, Zhang L, Jiang H R 2004 J. Beijing Univ. Aeron. Astron. 32 365 Google Scholar
[22]	张国英, 刘贵立 2011 现代电子理论在材料设计中的应用(1) (北京: 科学出版社) 第164−167页 Zhang G Y, Liu G L 2011 Application of Modern Electronic Theory in Material Design (Vol. 1) (Beijing: Science Press) pp179−182 (in Chinese)
[23]	吴红丽, 张伟, 宫声凯 2008 化学学报 66 1669 Google Scholar Wu H L, Zhang W, Gong S K 2008 Acta Chim. Sin. 66 1669 Google Scholar
[24]	陈国良, 林均品 1999有序金属间化合物结构材料物理金属学基础(1)(北京: 冶金工业出版社)第285页 Chen G L, Lin J P 1999 Physicalmetallurgy Basis of Ordered Intermetallic Compound Structure Materials (Vol. 1) (Beijing: Metallurgical Industry Press) p285(in Chinese)
[25]	李虹, 王绍青, 叶恒强 2009 58 224 Google Scholar Li H, Wang S Q, Ye H Q 2009 Acta Phys. Sin. 58 224 Google Scholar
[26]	Segall M D, Lindan P J D, Probert M J 2002 J. Phys.: Condens. Matter 14 2717 Google Scholar
[27]	Clark S J, Segall M D, Pickard C J, Hasnip P J, Payne M C 2005 Z. Kristallogr. 220 567
[28]	宋庆功, 姜恩永 2008 57 1823 Google Scholar Song Q G, Jiang E Y 2008 Acta Phys. Sin. 57 1823 Google Scholar
[29]	Born M, Huang K 1954 Dynamical Theory of Crystal Lattices (Oxford: Clarendon Press) pp113－117

Cited By

图 1 γ-TiAl晶胞结构模型　(a) L1₀型面心四方结构单元; (b)最小结构单元; (c) Sp₀(Ti₈Al₈)结构单元

Figure 1. Structure models of γ-TiAl:　(a) The L1₀ face-center tetragonal unit cell; (b) the least tetragonal unit cell; (c) the unit of Sp₀(Ti₈Al₈).

DownLoad: Full-Size Img PowerPoint

图 2 包含O原子的γ-TiAl晶胞结构模型　(a) Sp_0-Oa; (b) Sp_0-Ob; (c) Sp_0-Oc; (d) Sp_0-Od

Figure 2. Structure models of γ-TiAl including O (Ti₈Al₈O):　(a) Sp_0-Oa; (b) Sp_0-Ob; (c) Sp_0-Oc; (d) Sp_0-Od

DownLoad: Full-Size Img PowerPoint

图 3 包含Ti空位或Al空位的γ-TiAl典型结构模型　(a) Sp_0-□Ti (Ti₇□Al₈); (b) Sp_0-□Al (Ti₈Al₇□)

Figure 3. Typical structure models of γ-TiAl including Ti or Al vacancy:　(a) Sp_0-□Ti (Ti₇□Al₈); (b) Sp_0-□Al (Ti₈Al₇□)

DownLoad: Full-Size Img PowerPoint

图 4 Si和Y替位双掺杂γ-TiAl体系的典型结构模型　(a) Sd₁_x (Ti₆SiYAl₈); (b) Sd₂ (Ti₇YAl₇Si); (c) Sd₃ (Ti₇SiAl₇Y); (d) Sd₄(Ti₈Al₆SiY)

Figure 4. Typical structure models of Si and Y co-doping γ-TiAl:　(a) Sd₁_x (Ti₆SiYAl₈); (b) Sd₂ (Ti₇YAl₇Si); (c)Sd₃ (Ti₇SiAl₇Y); (d) Sd₄(Ti₈Al₆SiY)

DownLoad: Full-Size Img PowerPoint

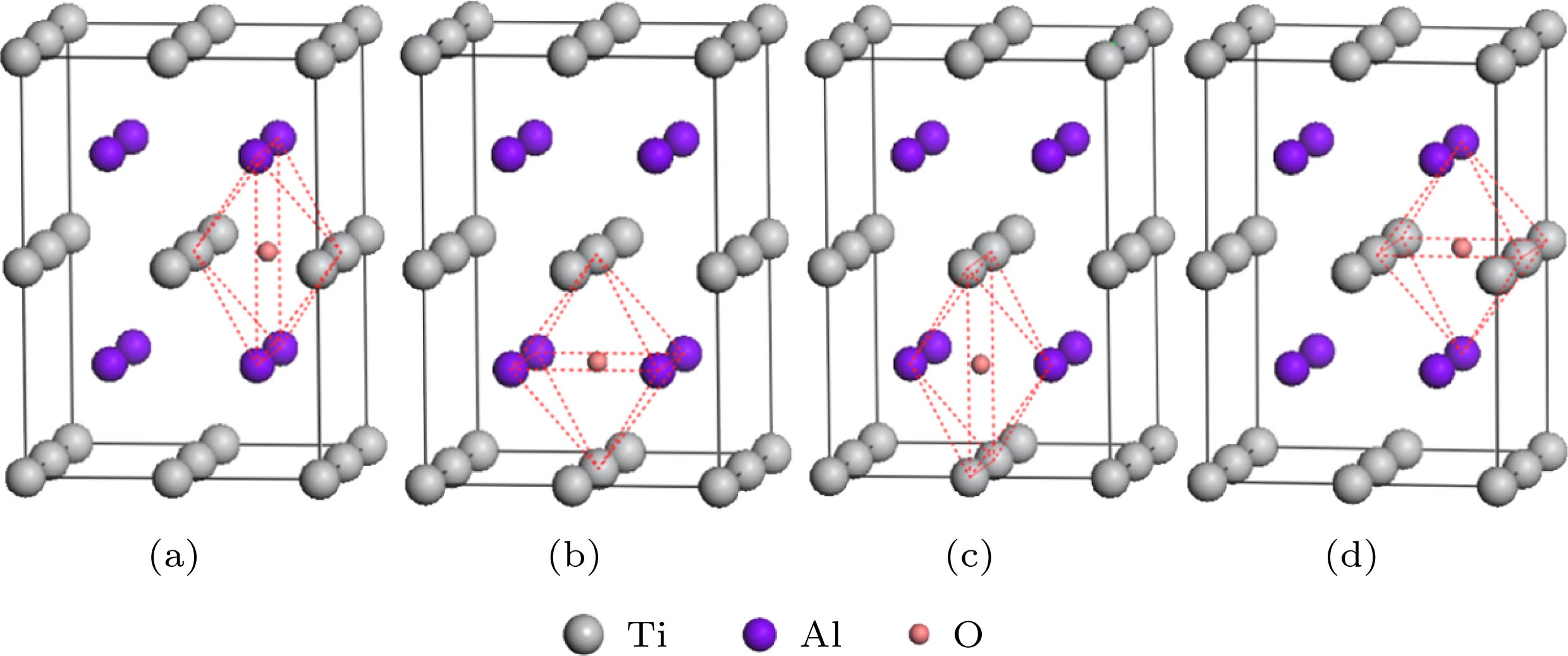
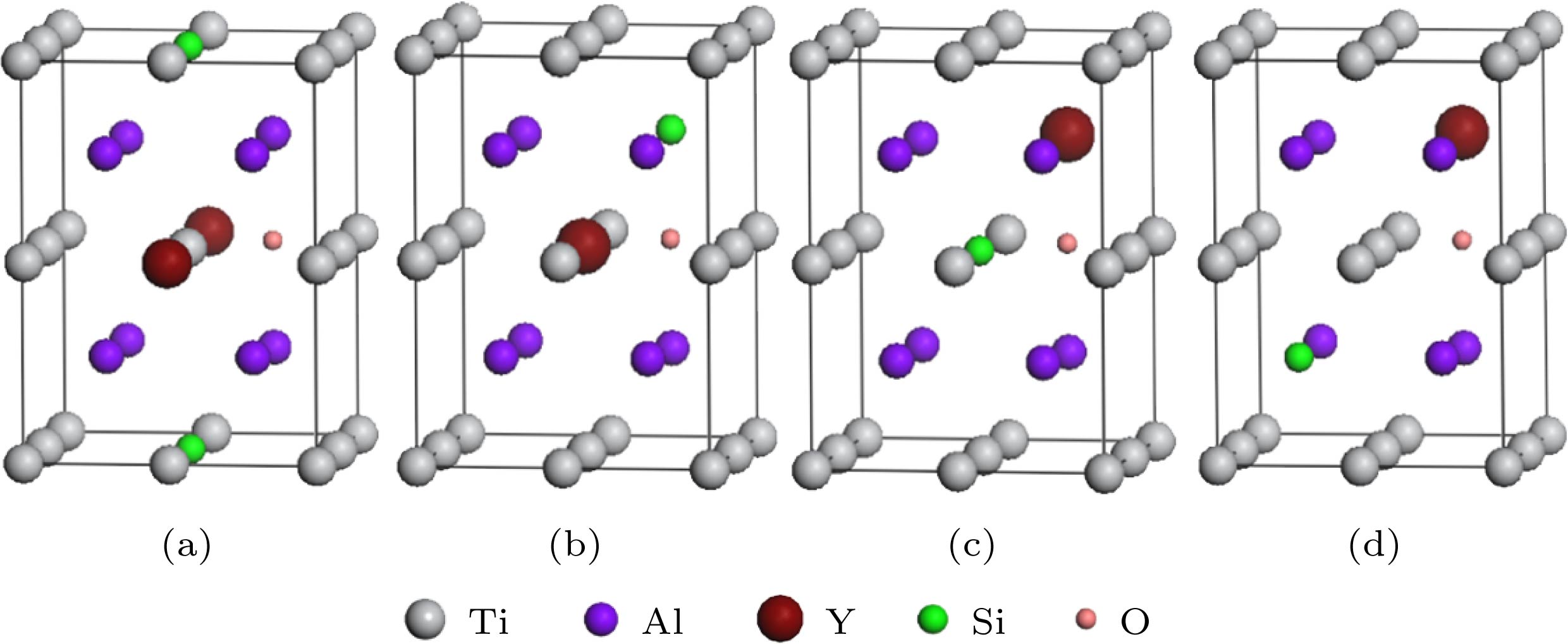
图 5 Si和Y替位双掺杂γ-TiAl含氧体系的典型结构模型　(a) Sd₁_x-_Od (Ti₆SiYAl₈O); (b) Sd_2x-Od (Ti₇YAl₇SiO); (c) Sd_3x-Od (Ti₇SiAl₇YO); (d) Sd_4x-Od(Ti₈Al₆SiYO)

Figure 5. Typical structure models of Si and Y co-doping γ-TiAl including O:　(a) Sd₁_x_-Od (Ti₆SiYAl₈O); (b) Sd₂_x_-Od (Ti₇YAl₇SiO); (c) Sd₃_x_-Od (Ti₇SiAl₇YO); (d) Sd₄_x-_Od(Ti₈Al₆SiYO)

DownLoad: Full-Size Img PowerPoint

图 6 Si和Y替位双掺杂γ-TiAl含空位体系的典型结构模型　(a) Sd₁_x-_□Ti (Ti₅SiY□Al₈); (b) Sd₂_x-_□Ti (Ti₆Y□Al₇Si); (c) Sd₃_x-_□Ti(Ti₆Si□Al₇Y); (d) Sd₄_x-_□Ti(Ti₇□Al₆SiY); (e) Sd₁_x-_□Al (Ti₆SiYAl₇□); (f) Sd₂_x-_□Al (Ti₇YAl₆Si□); (g) Sd₃_x-_□Al(Ti₇SiAl₆Y□); (h) Sd₄_x-_□Al(Ti₈Al₅SiY□)

Figure 6. Typical structure models of Si and Y co-doping γ-TiAl including vacancy:　(a)Sd₁_x-_□Ti (Ti₅SiY□Al₈); (b) Sd₂_x-_□Ti (Ti₆Y□Al₇Si); (c) Sd₃_x-_□Ti(Ti₆Si□Al₇Y); (d) Sd₄_x-_□Ti(Ti₇□Al₆SiY); (e) Sd₁_x-_□Al (Ti₆SiYAl₇□); (f) Sd₂_x-_□Al (Ti₇YAl₆Si□); (g) Sd₃_x-_□Al(Ti₇SiAl₆Y□); (h) Sd₄_x-_□Al(Ti₈Al₅SiY□)

DownLoad: Full-Size Img PowerPoint

图 7 Si和Y替位双掺杂γ-TiAl含氧体系中间隙O原子的形成能

Figure 7. Formation energies of interstitial O atoms in the Si and Y co-doping γ-TiAl systems.

DownLoad: Full-Size Img PowerPoint

图 8 Si和Y双掺杂γ-TiAl含空位体系中Ti空位和Al空位的形成能

Figure 8. Formation energies of Ti and Al vacancies in Si and Y co-doping γ-TiAl systems.

DownLoad: Full-Size Img PowerPoint

表 1 纯γ-TiAl体系与Si和Y替位双掺杂γ-TiAl体系的能量性质

Table 1. Energy properties of pure γ-TiAl and Si and Y co-doping γ-TiAl systems.

体系	能量性质
体系	E_t /eV	E ^f/eV
Sp₀	–13283.2619	–0.3579
Sd₁₇	–10375.5782	–0.2448
Sd₁₉	–10375.3125	–0.2282
Sd₂	–11923.1797	–0.3078
Sd₃	–11921.0891	–0.1771
Sd₄	–13468.5526	–0.2315

DownLoad: CSV

表 2 纯γ-TiAl体系与Si和Y替位双掺杂γ-TiAl体系中四方晶系的弹性常数

Table 2. Elastic constants of tetragonal systems in pure γ-TiAl and Si and Y co-doping γ-TiAl systems.

体系	C₁₁/GPa	C₁₂/GPa	C₁₃/GPa	C₃₃/GPa	C₄₄/GPa	C₆₆/GPa
Sp₀	232.2438	39.8470	69.3592	196.4413	112.3486	44.8147
Sd₁₁	130.8671	75.6434	87.7505	134.2535	70.0558	46.6357
Sd₁₃	136.8296	75.1812	86.9261	134.1158	64.9601	49.0225
Sd₁₄	180.5075	43.1529	81.6884	138.5193	73.0642	19.7364
Sd₁₅	136.6952	74.6364	84.6822	128.5797	67.3934	47.4253
Sd₁₆	160.1225	90.0601	87.6092	137.2518	106.8941	43.0277
Sd₁₉	130.8850	74.3862	78.7846	125.4646	68.9906	56.7747
Sd₁₁₀	132.4566	95.9060	-40.8881	351.4524	24.8135	42.5965
Sd₄	174.4526	59.4503	76.4982	151.9303	82.9168	12.5223

DownLoad: CSV

表 3 Si和Y替位双掺杂γ-TiAl体系Sd₁₇, Sd₂和Sd₃的弹性常数

Table 3. Elastic constants of Si and Y co-doping γ-TiAl systems Sd₁₇, Sd₂ and Sd₃.

体系	C₁₁/GPa	C₁₂/GPa	C₁₃/GPa	C₁₅/GPa	C₂₂/GPa	C₂₃/GPa	C₂₅/GPa
Sd₁₇	174.0489	51.0128	78.8477	–	178.6799	73.6936	–
Sd₂	177.5408	69.1504	69.7969	–3.6774	172.7134	65.2400	–1.6610
Sd₃	158.9597	58.6004	72.7099	–10.1161	160.3606	73.2300	–0.1101
体系	C₃₃/GPa	C₃₅/GPa	C₄₄/GPa	C₄₆/GPa	C₅₅/GPa	C₆₆/GPa
Sd₁₇	117.2748	–	59.8220	–	64.1452	10.4758
Sd₂	170.8100	–1.4732	77.8416	–1.2719	78.4798	38.6156
Sd₃	139.6061	–1.4377	67.2411	0.7657	67.6317	26.4129

DownLoad: CSV

表 4 纯γ-TiAl体系及其含氧体系的能量性质

Table 4. Energy properties of pure γ-TiAl and the systems including O.

体系	能量性质
体系	E_t /eV	E ^f /eV
Sp₀	–13283.2619	–0.3579
Sp_0-Oa	–13718.1429	–0.0716
Sp_0-Ob	–13720.0413	–0.1832
Sp_0-Oc	–13720.6086	–0.2166
Sp_0-Od	–13720.9863	–0.2388

DownLoad: CSV

表 5 Si和Y替位双掺杂γ-TiAl含氧体系中间隙O原子的形成能

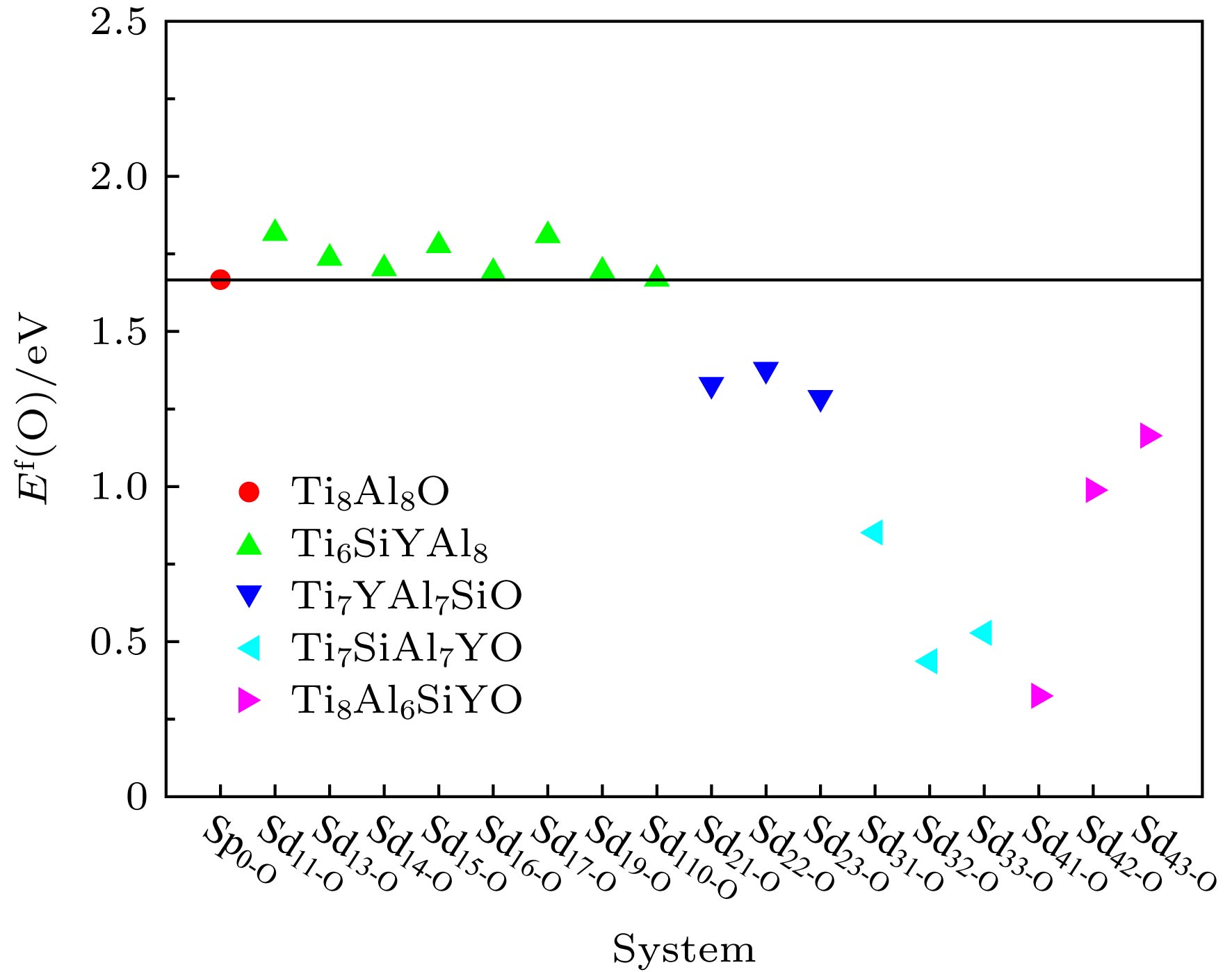
Table 5. Formation energies of interstitial O atoms in Si and Y co-doping γ-TiAl systems.

体系	能量性质
体系	E_t(Sd_O)/eV	E_t (Sd)/eV	E ^f(O)/eV
Sp_0-Od	–13720.9863	–13283.2619	1.6665
Sd_11-Od	–10812.9929	–10375.4180	1.8160
Sd_13-Od	–10813.0355	–10375.3811	1.7365
Sd_14-Od	–10813.1059	–10375.4175	1.7025
Sd_15-Od	–10813.0129	–10375.3988	1.7768
Sd_16-Od	–10813.0989	–10375.3983	1.6903
Sd_17-Od	–10813.1600	–10375.5782	1.8091
Sd_19-Od	–10813.0084	–10375.3125	1.6950
Sd_110-Od	–10813.0341	–10375.3121	1.6689
Sd_21-Od	–12361.2419	–11923.1797	1.3287
Sd_22-Od	–12361.1930	–11923.1797	1.3776
Sd_23-Od	–12361.2834	–11923.1797	1.2872
Sd_31-Od	–12359.6285	–11921.0891	0.8515
Sd_32-Od	–12360.0430	–11921.0891	0.4370
Sd_33-Od	–12359.9518	–11921.0891	0.5282
Sd_41-Od	–13907.6183	–13468.5526	0.3252
Sd_42-Od	–13906.9550	–13468.5526	0.9885
Sd_43-Od	–13906.7798	–13468.5526	1.1637

DownLoad: CSV

表 6 Si和Y双掺杂γ-TiAl含空位体系中Ti空位和Al空位的形成能

Table 6. Formation energies of Ti and Al vacancies in Si and Y co-doping γ-TiAl systems.

体系	E_t (Sd)/eV	E_t (Sd_□Al)/eV	E_t (Sd_□Ti)/eV	E ^f (□Al)/eV	E ^f (□Ti)/eV
Sp_0-□	–13283.2619	–13224.0362	–11678.3061	2.6764	1.8132
Sd_11-□	–10375.4180	–10317.9824	–8770.2288	0.8863	2.0466
Sd_13-□	–10375.3811	–10317.9645	–8770.1941	0.8673	2.0444
Sd_14-□	–10375.4175	–10317.9637	–8770.2884	0.9045	1.9865
Sd_15-□	–10375.3988	–10317.9620	–8770.2113	0.8875	2.0449
Sd_16-□	–10375.3983	–10317.9032	–8770.2649	0.9098	1.9908
Sd_17-□	–10375.5782	–10317.4973	–8770.0900	1.5316	2.3456
Sd_19-□	–10375.3125	–10318.4246	–8770.2557	0.3386	1.9143
Sd_110-□	–10375.3121	–10318.0212	–8770.2609	0.7416	1.9086
Sd_2-□	–11923.1797	–11865.3646	–10317.9810	1.2658	2.0561
Sd_3-□	–11921.0891	–11865.3095	–10317.6100	–0.7697	0.3365
Sd_4-□	–13468.5526	–13409.4369	–11865.3562	2.5664	0.0538

DownLoad: CSV

map

[1]	Castillo R M, Nó M L, Jiménez J A, Ruano O A, San Juan J 2016 Acta Mater. 103 46 Google Scholar
[2]	Kim S W, Hong J K, Na Y S, Yeom J T, Kim S E 2014 Mater. Des. 54 814 Google Scholar
[3]	Chen G, Peng Y B, Zheng G, Qi Z X, Wang M Z, Yu H C, Dong C L, Liu C T 2016 Nature Mater. 15 876 Google Scholar
[4]	Pflumm R, Friedle S, Schütze M 2015 Intermetallics 56 1 Google Scholar
[5]	Yoshihara M, Kim Y W 2005 Intermetallics 13 952 Google Scholar
[6]	Kuranishi T, Habazaki H, Konno H 2005 Surf. Coat. Technol. 200 2438 Google Scholar
[7]	汤守巧, 曲寿江, 冯艾寒, 冯聪, 崔扣彪, 沈军 2017 稀有金属 41 81 Tang S Q, Qu S J, Feng A H, Feng C, Cui K B, Shen J 2017 Rare Metals 41 81
[8]	Hu H, Wu X, Wang R, Li W, Liu Q 2016 J. Alloys Compd. 658 689 Google Scholar
[9]	Brotzu A, Felli F, Pilone D 2013 Intermetallics 43 131 Google Scholar
[10]	平发平, 胡青苗, 杨锐 2013 金属学报 29 385 Ping F P, Hu Q M, Yang R 2013 Acta Metall. Sin. 29 385
[11]	朱绍祥, 王清江, 刘建荣, 刘羽寅, 杨锐 2010 中国有色金属学报 20 138 Zhu S X, Wang Q J, Liu J R, Liu Y Y, Yang R 2010 Chin. J. Nonferr. Met. 20 138
[12]	Izumi T, Yoshioka T, Hayashi S, Narita T 2005 Intermetallics 13 694 Google Scholar
[13]	刘杰, 薛祥义, 杨劼人 2015 稀有金属材料与工程 44 1942 Liu J, Xue X Y, Yang J R 2015 Rare Metal Mat. Eng. 44 1942
[14]	Lin J P, Zhao L L, Li G Y, Zhang L Q, Song X P, Ye F, Chen G L 2011 Intermetallics 19 136
[15]	杨忠波, 赵文金, 程竹青, 邱军, 张海, 卓洪 2017 金属学报 53 49 Yang Z B, Zhao W J, Cheng Z Q, Qiu J, Zhang H, Zhuo H 2017 Acta Metall. Sin. 53 49
[16]	Zhao L, Zhang Y, Zhu Y, Lin J, Ren Z 2016 Mater. High Temp. 33 234 Google Scholar
[17]	Zhao L L, Li G Y, Zhang L Q, Lin J P, Song X P, Ye F, Chen G L 2010 Intermetallics 18 1586 Google Scholar
[18]	周玉俊, 周雪锋, 陈光 2015 热加工工艺 44 93 Zhou Y J, Zhou X F, Chen G 2015 Hot Working Technol. 44 93
[19]	王艳晶, 宋玫锦, 王继杰, 杜兴蒿 2014 稀有金属材料与工程 43 1697 Wang Y J, Song M J, Wang J J, Du X H 2014 Rare Metal Mat. Eng. 43 1697
[20]	董利民, 崔玉友, 杨锐, 王福会 2004 金属学报 40 383 Google Scholar Dong L M, Cui Y Y, Yang R, Wang F H 2004 Acta Metall. Sin. 40 383 Google Scholar
[21]	肖伟豪, 张亮, 姜惠仁 2004 北京航空航天大学学报 32 365 Google Scholar Xiao W H, Zhang L, Jiang H R 2004 J. Beijing Univ. Aeron. Astron. 32 365 Google Scholar
[22]	张国英, 刘贵立 2011 现代电子理论在材料设计中的应用(1) (北京: 科学出版社) 第164−167页 Zhang G Y, Liu G L 2011 Application of Modern Electronic Theory in Material Design (Vol. 1) (Beijing: Science Press) pp179−182 (in Chinese)
[23]	吴红丽, 张伟, 宫声凯 2008 化学学报 66 1669 Google Scholar Wu H L, Zhang W, Gong S K 2008 Acta Chim. Sin. 66 1669 Google Scholar
[24]	陈国良, 林均品 1999有序金属间化合物结构材料物理金属学基础(1)(北京: 冶金工业出版社)第285页 Chen G L, Lin J P 1999 Physicalmetallurgy Basis of Ordered Intermetallic Compound Structure Materials (Vol. 1) (Beijing: Metallurgical Industry Press) p285(in Chinese)
[25]	李虹, 王绍青, 叶恒强 2009 58 224 Google Scholar Li H, Wang S Q, Ye H Q 2009 Acta Phys. Sin. 58 224 Google Scholar
[26]	Segall M D, Lindan P J D, Probert M J 2002 J. Phys.: Condens. Matter 14 2717 Google Scholar
[27]	Clark S J, Segall M D, Pickard C J, Hasnip P J, Payne M C 2005 Z. Kristallogr. 220 567
[28]	宋庆功, 姜恩永 2008 57 1823 Google Scholar Song Q G, Jiang E Y 2008 Acta Phys. Sin. 57 1823 Google Scholar
[29]	Born M, Huang K 1954 Dynamical Theory of Crystal Lattices (Oxford: Clarendon Press) pp113－117

[1]	Lei Xue-Ling, Zhu Ju-Yong, Ke Qiang, Ouyang Chu-Ying. First-principles study of catalytic mechanism of boron-doped graphene oxide on oxygen evolution reaction of lithium peroxide. Acta Physica Sinica, 2024, 73(9): 098804. doi: 10.7498/aps.73.20240197
[2]	Chen Tun, Cui Jie-Chao, Li Min, Chen Wen, Sun Zhi-Peng, Fu Bao-Qin, Hou Qing. First-principles study on effects of alloying elements Sn and Nb on phase stability of corrosion oxide films of zirconium alloys. Acta Physica Sinica, 2024, 73(15): 157101. doi: 10.7498/aps.73.20240602
[3]	Miao Rui-Xia, Xie Miao-Chun, Cheng Kai, Li Tian-Tian, Yang Xiao-Feng, Wang Ye-Fei, Zhang De-Dong. Effect of Te doping on oxidation resistance and electronic structure of two-dimensional InSe. Acta Physica Sinica, 2023, 72(12): 123101. doi: 10.7498/aps.72.20230004
[4]	Yao Yi-Zhou, Cao Dan, Yan Jie, Liu Xue-Yin, Wang Jian-Feng, Jiang Zhou-Ting, Shu Hai-Bo. A first-principles study on environmental stability and optoelectronic properties of bismuth oxychloride/ cesium lead chloride van der Waals heterojunctions. Acta Physica Sinica, 2022, 71(19): 197901. doi: 10.7498/aps.71.20220544
[5]	Zhang Xiao-Ya, Song Jia-Xun, Wang Xin-Hao, Wang Jin-Bin, Zhong Xiang-Li. First principles calculation of optical absorption and polarization properties of In doped h-LuFeO₃. Acta Physica Sinica, 2021, 70(3): 037101. doi: 10.7498/aps.70.20201287
[6]	Lin Hong-Bin, Lin Chun, Chen Yue, Zhong Ke-Hua, Zhang Jian-Min, Xu Gui-Gui, Huang Zhi-Gao. First-principles study of effect of Mg doping on structural stability and electronic structure of LiCoO₂ cathode material. Acta Physica Sinica, 2021, 70(13): 138201. doi: 10.7498/aps.70.20210064
[7]	Hu Qian-Ku, Qin Shuang-Hong, Wu Qing-Hua, Li Dan-Dan, Zhang Bin, Yuan Wen-Feng, Wang Li-Bo, Zhou Ai-Guo. First-principles calculations of stabilities and physical properties of ternary niobium borocarbides and tantalum borocarbides. Acta Physica Sinica, 2020, 69(11): 116201. doi: 10.7498/aps.69.20200234
[8]	Wang Dan, Zou Juan, Tang Li-Ming. Stability and electronic structure of hydrogenated two-dimensional transition metal dichalcogenides: First-principles study. Acta Physica Sinica, 2019, 68(3): 037102. doi: 10.7498/aps.68.20181597
[9]	Chen Dong-Yun, Gao Ming, Li Yong-Hua, Xu Fei, Zhao Lei, Ma Zhong-Quan. First principle study of formation mechanism of molybdenum-doped amorphous silica in MoO₃/Si interface. Acta Physica Sinica, 2019, 68(10): 103101. doi: 10.7498/aps.68.20190067
[10]	Lin Qi-Min, Zhang Xia, Lu Qi-Chao, Luo Yan-Bin, Cui Jian-Gong, Yan Xin, Ren Xiao-Min, Huang Xue. First-principles study on structural stability of graphene oxide and catalytic activity of nitric acid. Acta Physica Sinica, 2019, 68(24): 247302. doi: 10.7498/aps.68.20191304
[11]	Dong Shan, Zhang Yan-Xing, Zhang Xi-Lin, Xu Xiao-Pei, Mao Jian-Jun, Li Dong-Lin, Chen Zhi-Ming, Ma Kuan, Fan Zheng-Quan, Wei Dan-Dan, Yang Zong-Xian. The first-principles study on the interaction of Ni with the yttria-stabilized zirconia and the activity of the interface. Acta Physica Sinica, 2016, 65(6): 068201. doi: 10.7498/aps.65.068201
[12]	Chen Qing-Ling, Dai Zhen-Hong, Liu Zhao-Qing, An Yu-Feng, Liu Yue-Lin. First-principles study on the structure stability and doping performance of double layer h-BN/Graphene. Acta Physica Sinica, 2016, 65(13): 136101. doi: 10.7498/aps.65.136101
[13]	Xue Li, Yi Lin. Influence of Al doping on stability of Mg1-xTix and their hydrides. Acta Physica Sinica, 2013, 62(13): 138801. doi: 10.7498/aps.62.138801
[14]	Linghu Jia-Jun, Liang Gong-Ying. First-principles study on the luminescence property of In-doped ZnTe. Acta Physica Sinica, 2013, 62(10): 103102. doi: 10.7498/aps.62.103102
[15]	Chen Hai-Jun, Li Gao-Qing, Xue Ju-Kui. Variational-method analysis of stability of Bose-Fermi mixture. Acta Physica Sinica, 2011, 60(4): 040304. doi: 10.7498/aps.60.040304.1
[16]	Liu Shuang, Liu Bin, Zhang Ye-Kuan, Wen Yan. Hopf bifurcation and stability of periodic solutions in a nonlinear relative rotation dynamical system with time delay. Acta Physica Sinica, 2010, 59(1): 38-43. doi: 10.7498/aps.59.38
[17]	Shi Pei-Ming, Liu Bin, Liu Shuang. Stability and approximate solution of a relative-rotation nonlinear dynamical system under harmonic excitation. Acta Physica Sinica, 2008, 57(8): 4675-4684. doi: 10.7498/aps.57.4675
[18]	Wang Zuo-Lei. Stability and Hopf bifurcation of the simplified Lang-Kobayashi equation. Acta Physica Sinica, 2008, 57(8): 4771-4776. doi: 10.7498/aps.57.4771
[19]	Xie Li, Lei Yin-Zhao. Uniqueness and stability of solution to the linear transient eddy current electromagnetic field problem for determining solution. Acta Physica Sinica, 2006, 55(9): 4397-4406. doi: 10.7498/aps.55.4397
[20]	Zhang Kai, Feng Jun. Symmetry and stability of a relativistic birkhoff system. Acta Physica Sinica, 2005, 54(7): 2985-2989. doi: 10.7498/aps.54.2985

Catalog

Vol. 68, Issue 19 - 2019-10-05

Metrics

Abstract views: 8944
PDF Downloads: 72
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板

Effects of Si and Y co-doping on stability and oxidation resistance of γ-TiAl based alloys

Abstract

Authors and contacts

Corresponding author: Song Qing-Gong, qgsong@cauc.edu.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Authors

Referees

About Journal

About

Search

Article

留言板

Effects of Si and Y co-doping on stability and oxidation resistance of γ-TiAl based alloys

Abstract

Authors and contacts

Corresponding author: Song Qing-Gong, qgsong@cauc.edu.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Publishing process

Authors

Referees

About Journal

About