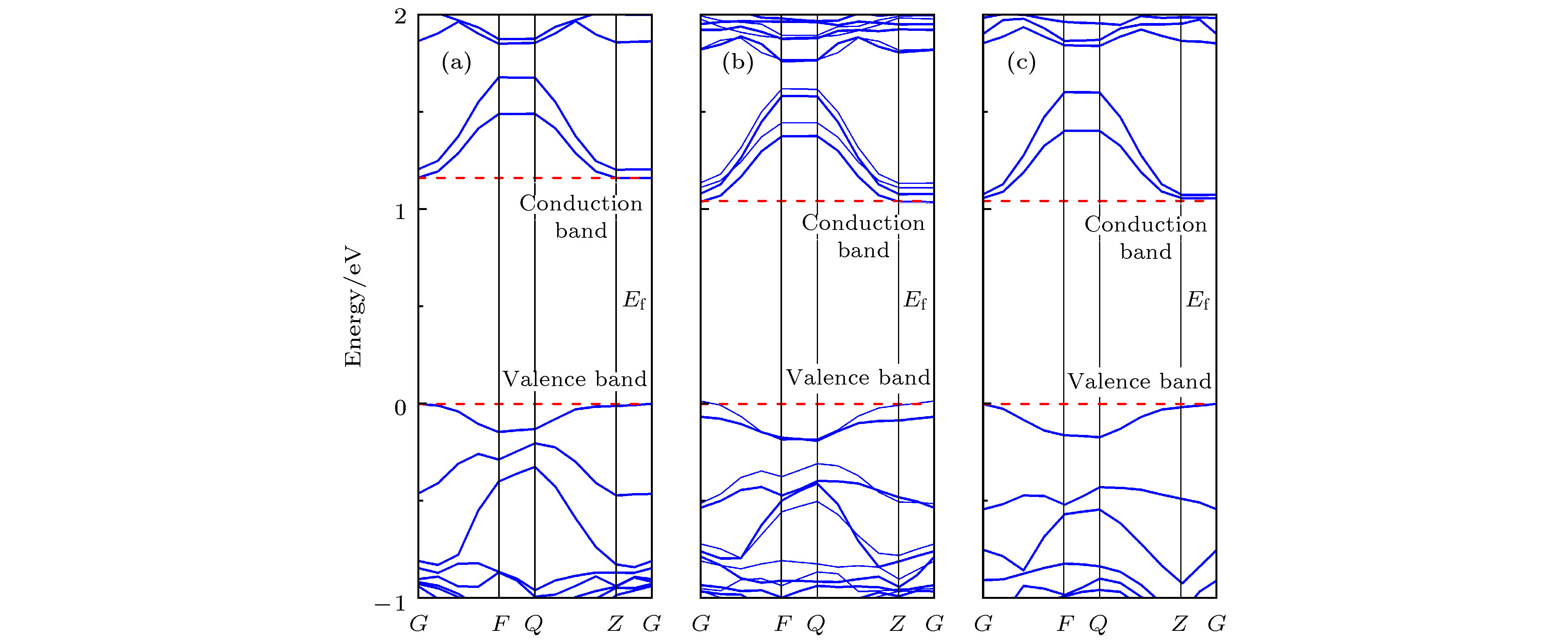
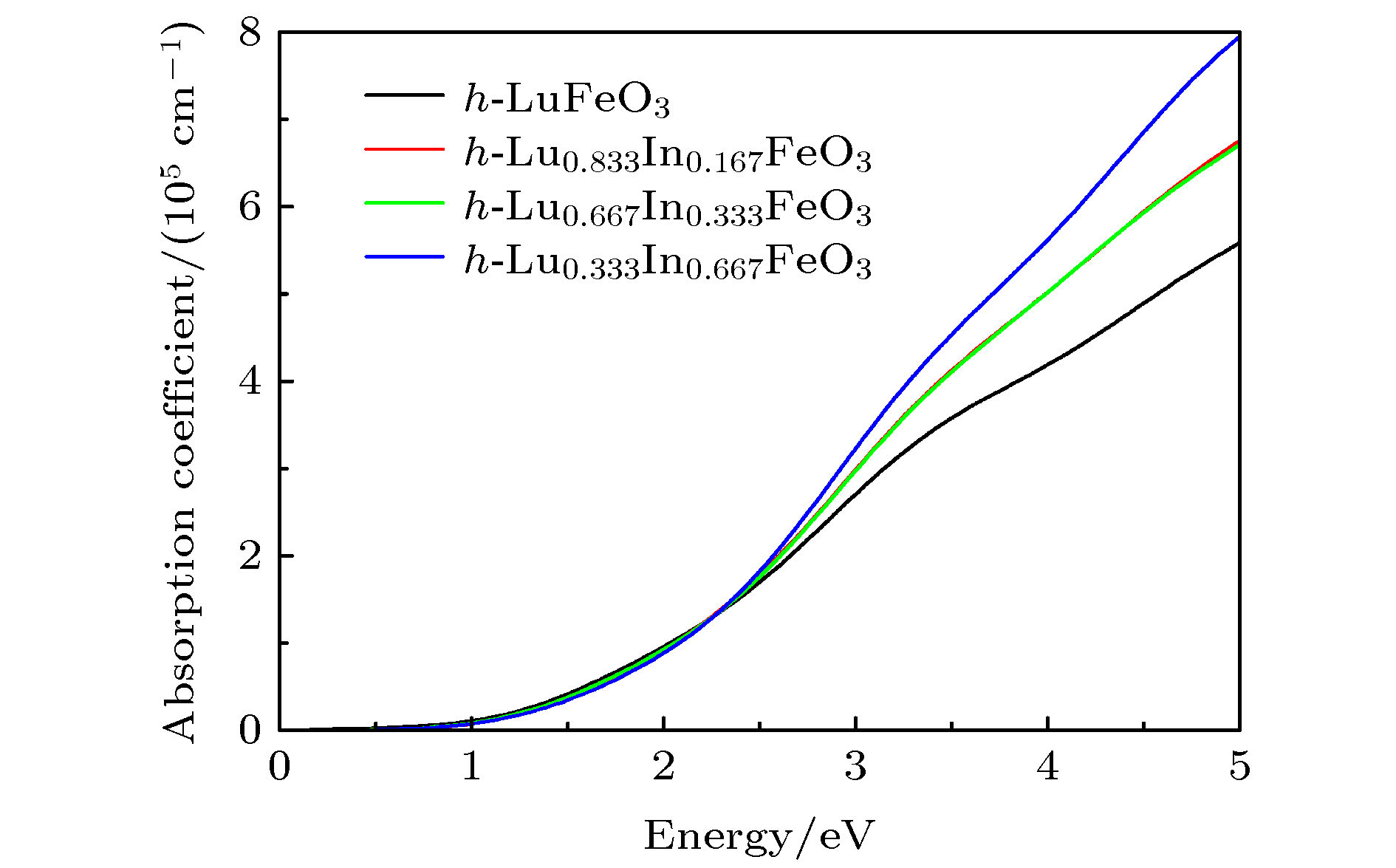
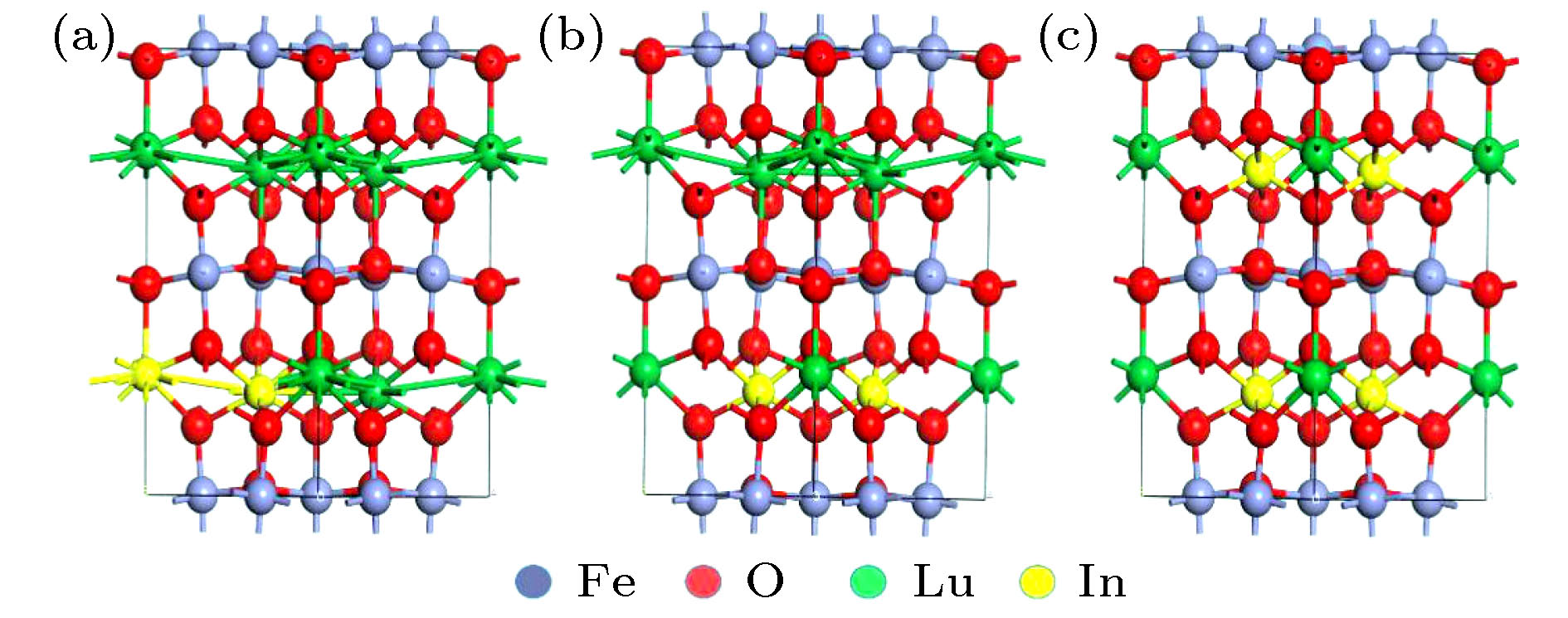
-
h-LuFeO3是一种窄带隙铁电半导体材料, 已被证明在铁电光伏领域有较好的应用前景. 然而, 较低的极化强度使光生电子-空穴对复合率大, 限制了h-LuFeO3基铁电光伏电池效率的提高. 为改善h-LuFeO3的极化强度, 提高光吸收性质, 本文利用第一性原理计算方法研究了In原子在h-LuFeO3不同位置的掺杂形成能, 得到最稳定的掺杂位置, 比较了h-Lu1–xInxFeO3 (x = 0, 0.167, 0.333, 0.667)的带隙、光吸收性能及极化强度等性质. 计算结果表明, 随着In掺杂比例的增加, h-LuFeO3的晶格常数c/a比不断增大, 铁电极化强度得到提高. 当In∶Lu = 2∶1时, 材料杂质能级出现, Fe-O轨道杂化得到增强, 提高了h-LuFeO3的光吸收性能. 此工作证明了In掺杂是改善h-LuFeO3极化强度和光吸收系数的有效方法, 对铁电光伏性能的提高提供一种新途径.The h-LuFeO3 is a kind of narrow band gap hexagonal ferrite material, with a good application prospect in the field of ferroelectric photovoltaic. However, the low polarization intensity of h-LuFeO3 makes the recombination rate of photogenerated electrons and holes large, which is not conducive to the improvement of the efficiency of h-LuFeO3-based ferroelectric photovoltaic cells. In order to improve the ferroelectricity and optical absorption properties of h-LuFeO3, the first principles method is used to calculate the doping formation energy values of In atom at different positions of h-LuFeO3, and the most stable doping position is determined. The comparisons of band gap, optical absorption performance and polarization intensity among h-Lu1-xInxFeO3 (x = 0, 0.167, 0.333, 0.667) are made. With the increase of In doping, the cells of h-Lu1–xInxFeO3 stretch along the c-axis. The ratio of the lattice constant c/a increases from 1.94 at x = 0 to 2.04 at x = 0.667 when all the positions of In replace P1 position. Using the qualitative calculation of Berne effective charge, the results show that the ferroelectric polarization intensity of h-LuFeO3, h-Lu0.833In0.167FeO3, h-Lu0.667In0.333FeO3 and h-Lu0.333In0.667FeO3 along the c-axis are 3.93, 5.91, 7.92, and 11.02 μC·cm–2, respectively. Therefore, with the increase of the number of In atoms replacing Lu atoms, the lattice constant c/a ratio of h-Lu1–xInxFeO3 increases, which can improve the ferroelectric polarization strength of the material. By analyzing the density of states of h-LuFeO3 and h-Lu0.333In0.667FeO3, we can see that In doping enhances the Fe-O orbital hybridization in h-Lu0.333In0.667FeO3, and makes the optical absorption coefficient of h-Lu0.333In0.667FeO3 in the solar light range larger. In summary, In doped h-LuFeO3 is an effective method to improve its polarization intensity and optical absorption coefficient, which is of great significance for improving the performance of ferroelectric photovoltaic.
-
Keywords:
- h-LuFeO3 /
- doping /
- optical property /
- polarization intensity /
- first principles
[1] Ji Y, Gao T, Wang Z L, Yang Y 2019 Nano Energy 64 103909
Google Scholar
[2] Teh Y S, Bhattacharya K 2019 J. Appl. Phys. 125 064103
Google Scholar
[3] Pal S, Swain A B, Biswas P P, Murali D, Pal A, Nanda B R K, Murugavel P 2018 Sci. Rep. 8 17
Google Scholar
[4] Butler K T, Frost J M, Walsh A 2015 Energy Environ. Sci. 8 838848
Google Scholar
[5] 蔡田怡, 雎胜 2018 67 157801
Google Scholar
Cai T Y, Ju S 2018 Acta Phys. Sin. 67 157801
Google Scholar
[6] 王婧, 吴霞, 邓朝勇, 朱孔军, 南策文 2014 无机材料学报 29 905911
Google Scholar
Wang J, Wu X, Deng C Y, Zhu K J, Nan C W 2014 J. Inorg. Mater. 29 905911
Google Scholar
[7] Chen Y, Chen J, Yang S, Li Y, Gao X, Zeng M, Fan Z, Gao X, Lu X, Liu J M 2018 Mater. Res. Bull. 107 456
Google Scholar
[8] Young S M, Zheng F, Rappe A M 2015 Phys. Rev. Appl. 4 054004
Google Scholar
[9] 张兴良 2010 硕士学位论文 (武汉: 武汉理工大学)
Zhang X L 2010 M. S. Thesis (Wuhan: Wuhan University Of Technology) (in Chinese)
[10] Sinha K, Zhang Y, Jiang X, Wang H, Wang X, Zhang X, Ryan P J, Kim J W, Bowlan J, Yarotski D A, Li Y, DiChiara A D, Cheng X, Wu X, Xu X 2017 Phys. Rev. B 95 094110
Google Scholar
[11] Han H, Kim D, Chae S, Park J, Nam S Y, Choi M, Yong K, Kim H J, Son J, Jang H M 2018 Nanoscale 10 13261
Google Scholar
[12] Han H, Kim D, Chu K, Park J, Nam S Y, Heo S, Yang C, Jang H M 2018 ACS Appl. Mater. Interfaces 10 18461853
Google Scholar
[13] Akbashev A R, Semisalova A S, Perov N S, Kaul A R 2011 Appl. Phys. Lett. 99 122502
Google Scholar
[14] Wang W, Zhao J, Wang W, et al. 2013 Rev. Lett. 110 237601
Google Scholar
[15] Huang X, Paudel T R, Dong S, Tsymbal E Y 2015 Phys. Rev. B 92 125201
Google Scholar
[16] Lin L, Zhang H M, Liu M F, Shen S, Zhou S, Li D, Wang X, Yan Z B, Zhang Z D, Zhao J, Dong S, Liu J M 2016 Phys. Rev. B 93 075146
Google Scholar
[17] Liu J, Sun T L, Liu X Q, Tian H, Gao T T, Chen X M 2018 Adv. Funct. Mater. 28 1706062
Google Scholar
[18] Fu Z, Nair H S, Xiao Y, Senyshyn A, Pomjakushin V, Feng E, Pomjakushin V, Su Y, Jin W T, Bruckel T 2016 Phys. Rev. B 94 125150
Google Scholar
[19] Clark S J, Segall M D, Pickard C J, Hasnip P, Probert M I, Refson K, Payne M C 2005 Z. Kristallogr. 220 567
[20] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke X 2008 Phys. Rev. Lett. 100 136406
Google Scholar
[21] Holinsworth B S, Mazumdar D, Brooks C M, Mundy J A, Das H, Cherian J G, McGill S A, Fennie C J, Schlom D G, Musfeldt J L 2015 Appl. Phys. Lett. 106 082902
Google Scholar
[22] Ridzwan M H, Yaakob M K, Taib M F M, Ali A M M, Hassan O H, Yahya M Z A 2017 Mater. Res. Express 4 044001
Google Scholar
[23] Disseler S M, Borchers J A, Brooks C M, Mundy J A, Moyer J A, Hillsberry D A, Thies E L, Tenne D A, Heron J, Holtz M, Clarkson J D, Stiehl G M, Schiffer P, Muller D A, Schlom D G, Ratcliff W D 2015 Phys. Rev. Lett. 114 217602
Google Scholar
[24] Wang W, Wang H, Xu X, Zhu L, He L, Wills E, Cheng X, Keavney D J, Shen J, Wu X, Xu X 2012 Appl. Phys. Lett. 101 241907
Google Scholar
[25] Das H, Wysocki A L, Geng Y, Wu W, Fennie C J 2014 Nat. Commun. 5 3998
Google Scholar
[26] Tu S, Zhang Y, Reshak A H, Auluck S, Ye L, Han X, Ma T, Huang H 2019 Nano Energy 56 840
Google Scholar
[27] Roy A, Mukherjee S, Gupta R, Auluck S, Prasad R, Garg A 2011 J. Phys. Condens. Matter 23 325902
Google Scholar
-
图 1 h-Lu1–xInxFeO3的球棍结构模型图 (a) P1, P2位置; (b) h-Lu0.667In0.333FeO3; (c) h-Lu0.333In0.667FeO3
Fig. 1. Model of the ball-and-stick structure of h-Lu1–xInxFeO3: (a) P1, P2 position; (b) h-Lu0.667In0.333FeO3; (c) h-Lu0.333In0.667FeO3
图 2 h-Lu1–xFexO3的能带图 (a) h-Lu0.833In0.167FeO3; (b) h-Lu0.667In0.333FeO3; (c) h-Lu0.333In0.667FeO3
Fig. 2. Energy band diagrams of h-Lu1–xFexO3: (a) h-Lu0.833In0.167FeO3; (b) h-Lu0.667In0.333FeO3; (c) h-Lu0.333In0.667FeO3
图 3 分布态密度图 (a) 未掺杂的h-LuFeO3; (b) h-Lu0.333In0.667FeO3
Fig. 3. Distribution density of states: (a) Undoped h-LuFeO3; (b) h-Lu0.333In0.667FeO3.
图 4 In掺杂前后h-LuFeO3光学吸收系数随入射光子能量的变化
Fig. 4. Change of optical absorption coefficient of h-LuFeO3 with incident photon energy before and after In doping.
图 5 不同In/Lu比的h-Lu1–xInxFeO3极化值(红色曲线)和晶格常数c/a比(蓝色曲线)
Fig. 5. Polarization values (red curve) and lattice constant c/a ratios (blue curve) of h-Lu1–xInxFeO3 with different In/Lu ratios.
表 1 不同磁序下不同位置的In掺杂相对能量变化
Table 1. Relative energy changes of In doping at different positions under different magnetic orders.
掺杂位置 G型/eV C型/eV A型/eV 铁磁型/eV 未掺 0 0.01 1.37 0.01 P1 位置 0 10.38 3.14 12.51 P2 位置 0 0.03 0.25 1.41 
下载: 导出CSV
表 2 In∶Lu为1∶2和2∶1时h-Lu1–xInxO3不同磁序的相对能量
Table 2. Relative energy of h-Lu1–xInxO3 with different magnetic sequencewhen In∶Lu is 1∶2 and 2∶1.
材料 G型/eV C型/eV A型/eV 铁磁型/eV h-Lu2/3In1/3FeO3 0 0.0126 0.8604 0.8604 h-Lu1/3In2/3FeO3 0 0.0096 0.8952 0.9487
下载: 导出CSV
表 3 h-Lu1–xInxO3的结构优化结果
Table 3. Structure optimization results of h-Lu1–xInxO3.
材料 晶格常数/Å 体积/Å3 轴角/(°) a b c α β γ (h-LuFeO3)[15] 5.965 5.965 11.702 (h-LuFeO3)[23] 5.985 5.985 11.770 h-LuFeO3 6.067 6.067 11.756 374.926 90.000 90.000 119.993 h-Lu0.833In0.167FeO3 6.042 6.042 11.880 374.770 90.047 90.004 120.214 h-Lu0.667In0.333FeO3 6.005 6.007 11.935 372.221 90.014 90.033 120.166 h-Lu0.333In0.667FeO3 5.922 5.923 12.119 367.516 89.999 90.001 120.173
下载: 导出CSV
表 4 本工作带隙计算结果与已发表结果对比
Table 4. Comparison of calculated band gap results with published results.
下载: 导出CSV
-
[1] Ji Y, Gao T, Wang Z L, Yang Y 2019 Nano Energy 64 103909
Google Scholar
[2] Teh Y S, Bhattacharya K 2019 J. Appl. Phys. 125 064103
Google Scholar
[3] Pal S, Swain A B, Biswas P P, Murali D, Pal A, Nanda B R K, Murugavel P 2018 Sci. Rep. 8 17
Google Scholar
[4] Butler K T, Frost J M, Walsh A 2015 Energy Environ. Sci. 8 838848
Google Scholar
[5] 蔡田怡, 雎胜 2018 67 157801
Google Scholar
Cai T Y, Ju S 2018 Acta Phys. Sin. 67 157801
Google Scholar
[6] 王婧, 吴霞, 邓朝勇, 朱孔军, 南策文 2014 无机材料学报 29 905911
Google Scholar
Wang J, Wu X, Deng C Y, Zhu K J, Nan C W 2014 J. Inorg. Mater. 29 905911
Google Scholar
[7] Chen Y, Chen J, Yang S, Li Y, Gao X, Zeng M, Fan Z, Gao X, Lu X, Liu J M 2018 Mater. Res. Bull. 107 456
Google Scholar
[8] Young S M, Zheng F, Rappe A M 2015 Phys. Rev. Appl. 4 054004
Google Scholar
[9] 张兴良 2010 硕士学位论文 (武汉: 武汉理工大学)
Zhang X L 2010 M. S. Thesis (Wuhan: Wuhan University Of Technology) (in Chinese)
[10] Sinha K, Zhang Y, Jiang X, Wang H, Wang X, Zhang X, Ryan P J, Kim J W, Bowlan J, Yarotski D A, Li Y, DiChiara A D, Cheng X, Wu X, Xu X 2017 Phys. Rev. B 95 094110
Google Scholar
[11] Han H, Kim D, Chae S, Park J, Nam S Y, Choi M, Yong K, Kim H J, Son J, Jang H M 2018 Nanoscale 10 13261
Google Scholar
[12] Han H, Kim D, Chu K, Park J, Nam S Y, Heo S, Yang C, Jang H M 2018 ACS Appl. Mater. Interfaces 10 18461853
Google Scholar
[13] Akbashev A R, Semisalova A S, Perov N S, Kaul A R 2011 Appl. Phys. Lett. 99 122502
Google Scholar
[14] Wang W, Zhao J, Wang W, et al. 2013 Rev. Lett. 110 237601
Google Scholar
[15] Huang X, Paudel T R, Dong S, Tsymbal E Y 2015 Phys. Rev. B 92 125201
Google Scholar
[16] Lin L, Zhang H M, Liu M F, Shen S, Zhou S, Li D, Wang X, Yan Z B, Zhang Z D, Zhao J, Dong S, Liu J M 2016 Phys. Rev. B 93 075146
Google Scholar
[17] Liu J, Sun T L, Liu X Q, Tian H, Gao T T, Chen X M 2018 Adv. Funct. Mater. 28 1706062
Google Scholar
[18] Fu Z, Nair H S, Xiao Y, Senyshyn A, Pomjakushin V, Feng E, Pomjakushin V, Su Y, Jin W T, Bruckel T 2016 Phys. Rev. B 94 125150
Google Scholar
[19] Clark S J, Segall M D, Pickard C J, Hasnip P, Probert M I, Refson K, Payne M C 2005 Z. Kristallogr. 220 567
[20] Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke X 2008 Phys. Rev. Lett. 100 136406
Google Scholar
[21] Holinsworth B S, Mazumdar D, Brooks C M, Mundy J A, Das H, Cherian J G, McGill S A, Fennie C J, Schlom D G, Musfeldt J L 2015 Appl. Phys. Lett. 106 082902
Google Scholar
[22] Ridzwan M H, Yaakob M K, Taib M F M, Ali A M M, Hassan O H, Yahya M Z A 2017 Mater. Res. Express 4 044001
Google Scholar
[23] Disseler S M, Borchers J A, Brooks C M, Mundy J A, Moyer J A, Hillsberry D A, Thies E L, Tenne D A, Heron J, Holtz M, Clarkson J D, Stiehl G M, Schiffer P, Muller D A, Schlom D G, Ratcliff W D 2015 Phys. Rev. Lett. 114 217602
Google Scholar
[24] Wang W, Wang H, Xu X, Zhu L, He L, Wills E, Cheng X, Keavney D J, Shen J, Wu X, Xu X 2012 Appl. Phys. Lett. 101 241907
Google Scholar
[25] Das H, Wysocki A L, Geng Y, Wu W, Fennie C J 2014 Nat. Commun. 5 3998
Google Scholar
[26] Tu S, Zhang Y, Reshak A H, Auluck S, Ye L, Han X, Ma T, Huang H 2019 Nano Energy 56 840
Google Scholar
[27] Roy A, Mukherjee S, Gupta R, Auluck S, Prasad R, Garg A 2011 J. Phys. Condens. Matter 23 325902
Google Scholar
下载:
计量
- 文章访问数: 6483
- PDF下载量: 129
- 被引次数: 0
