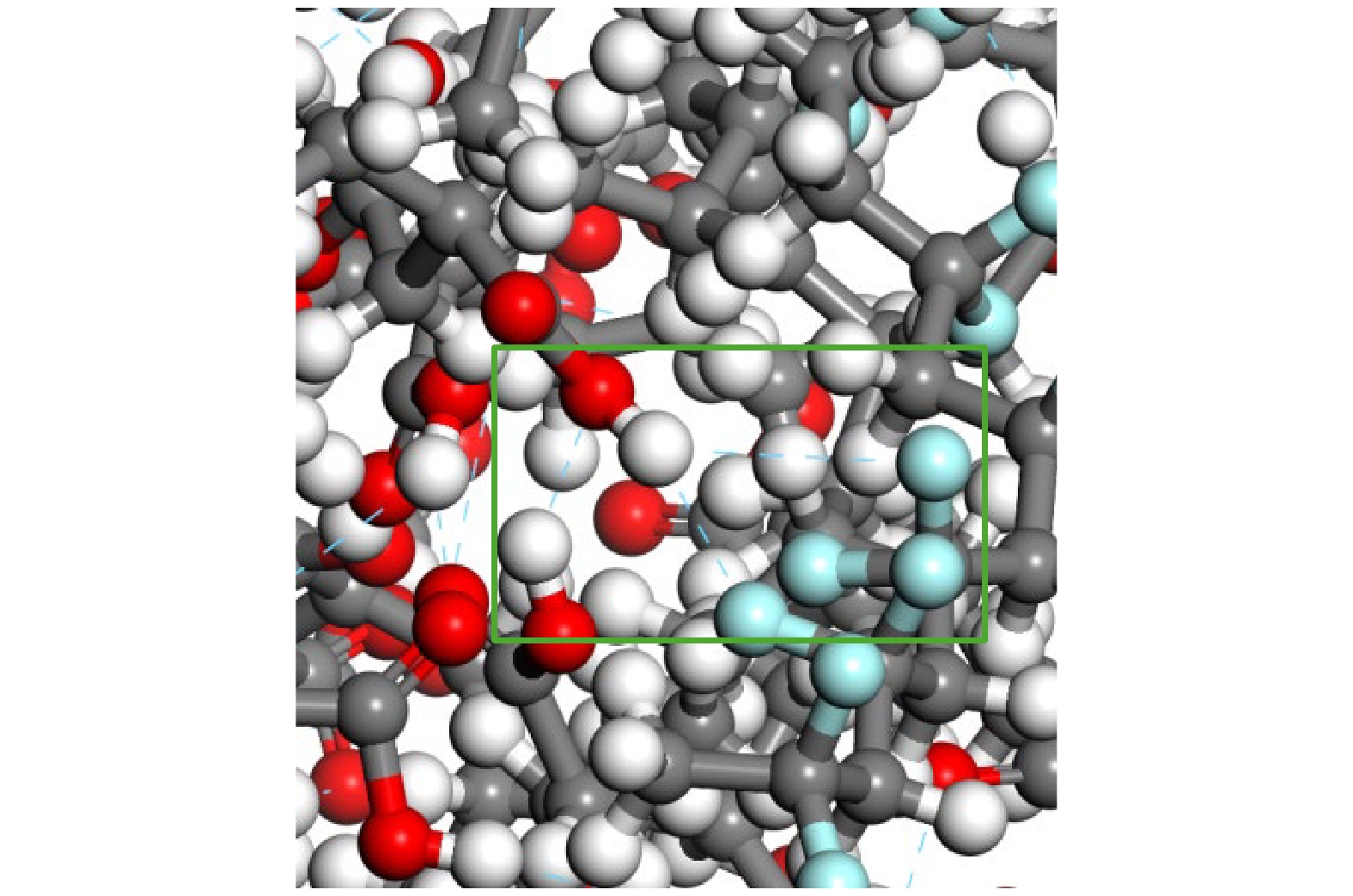
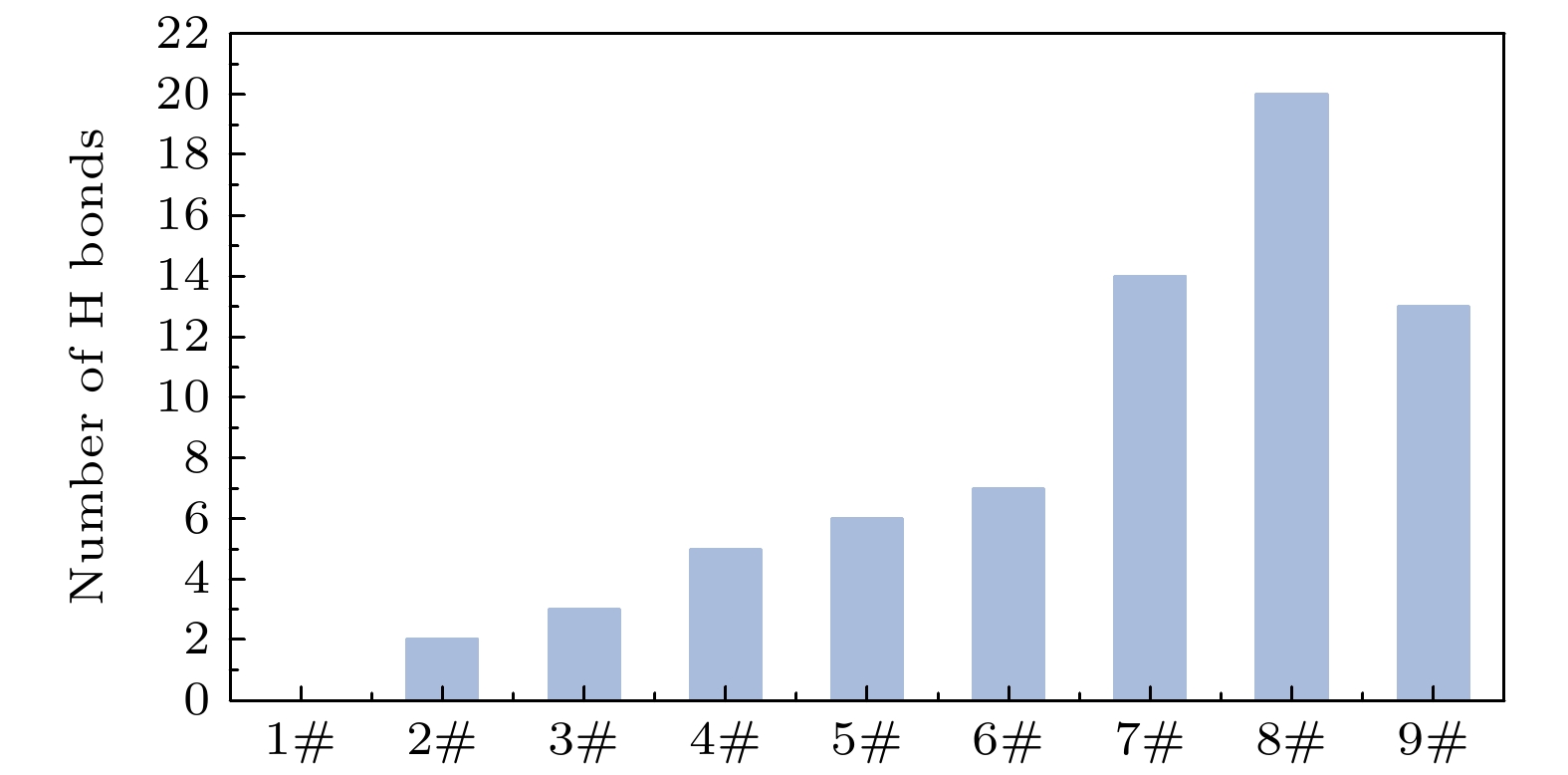
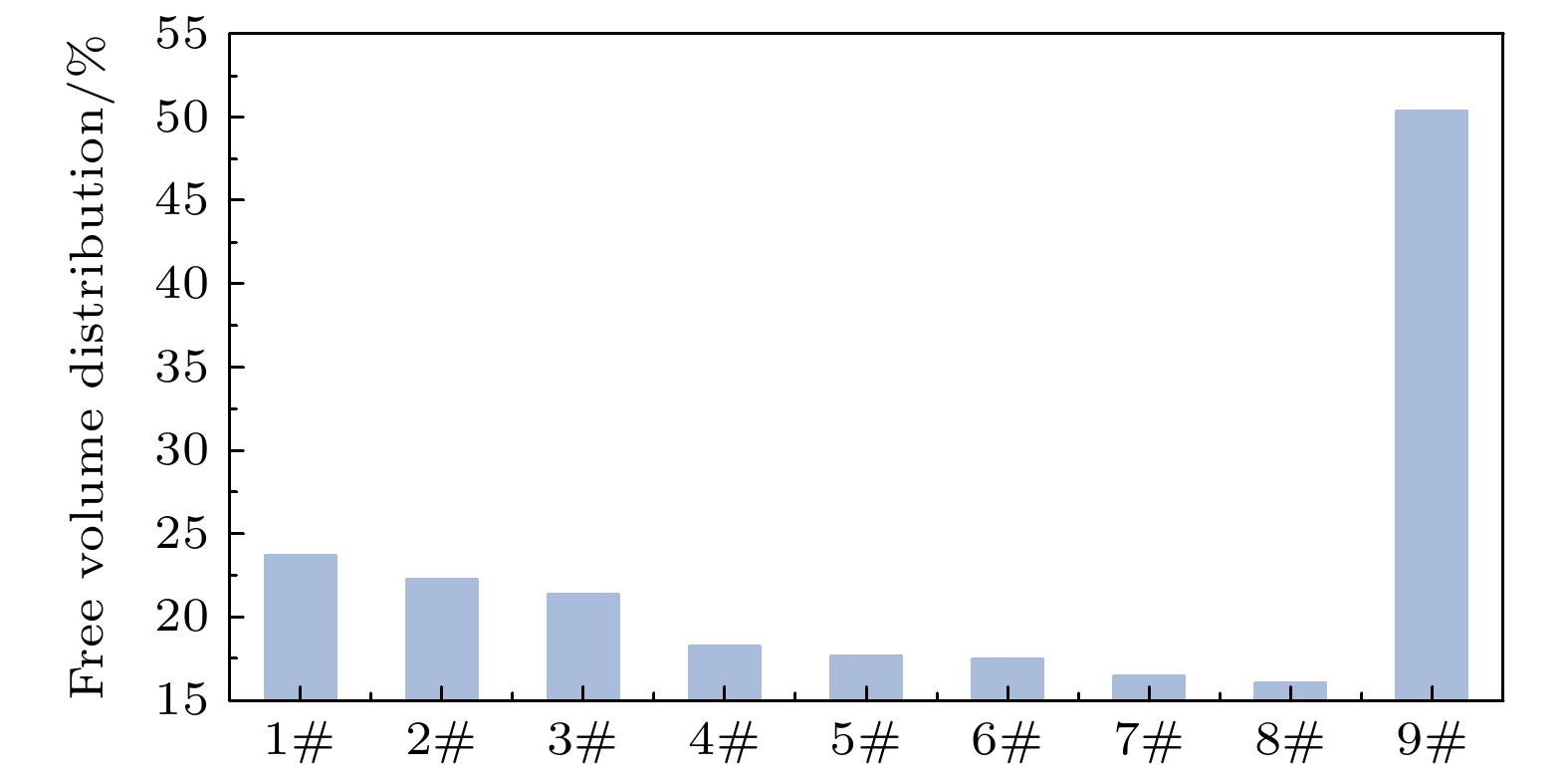
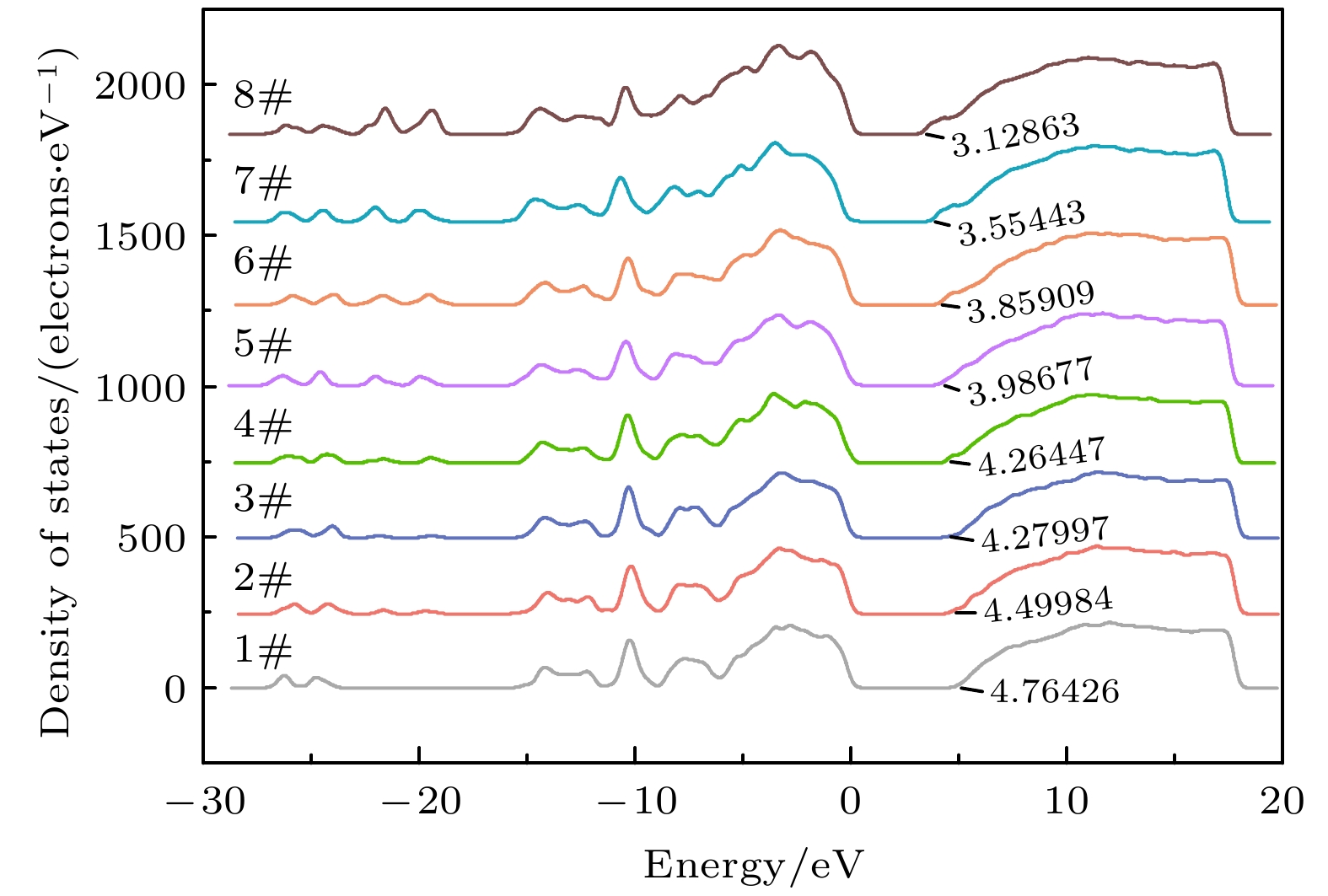
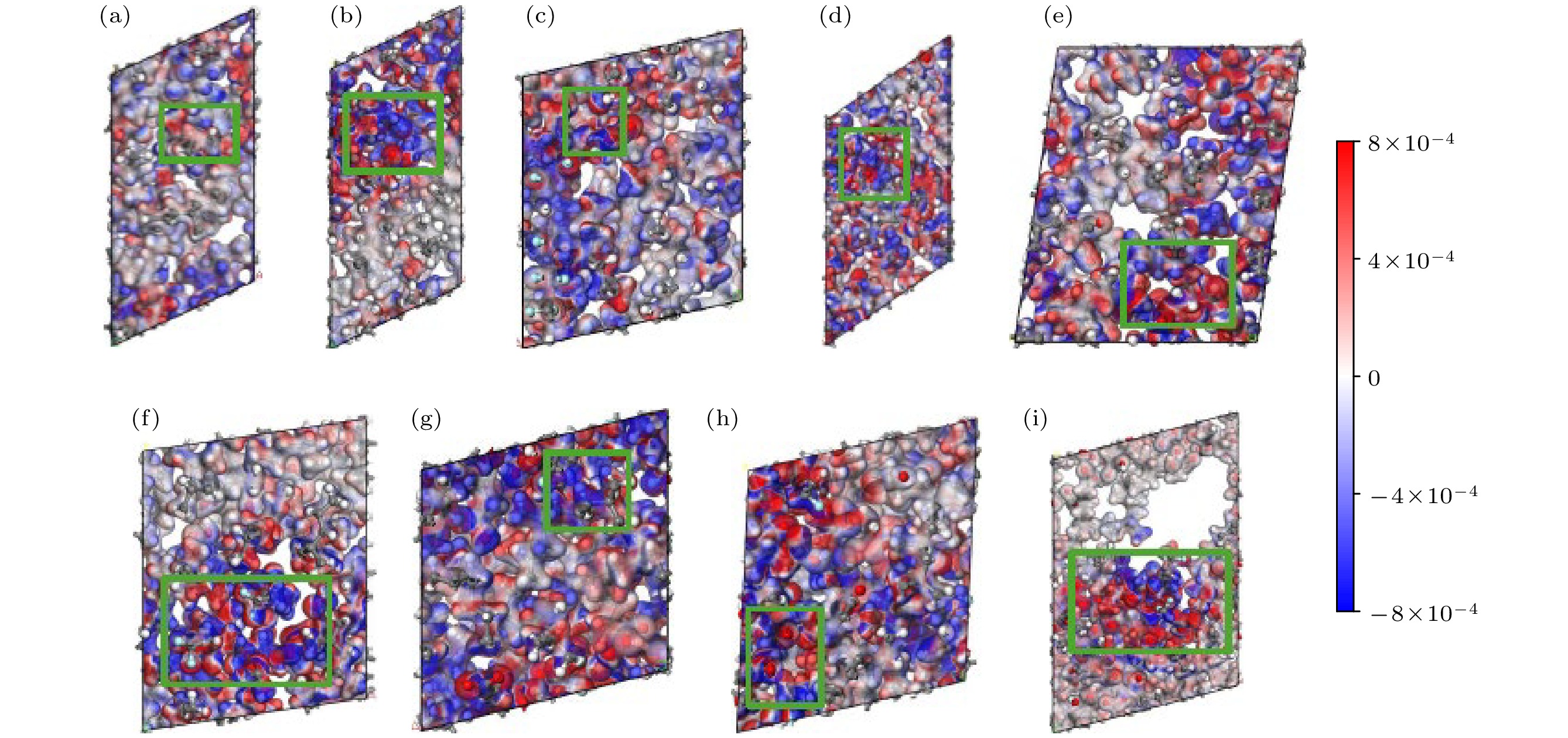
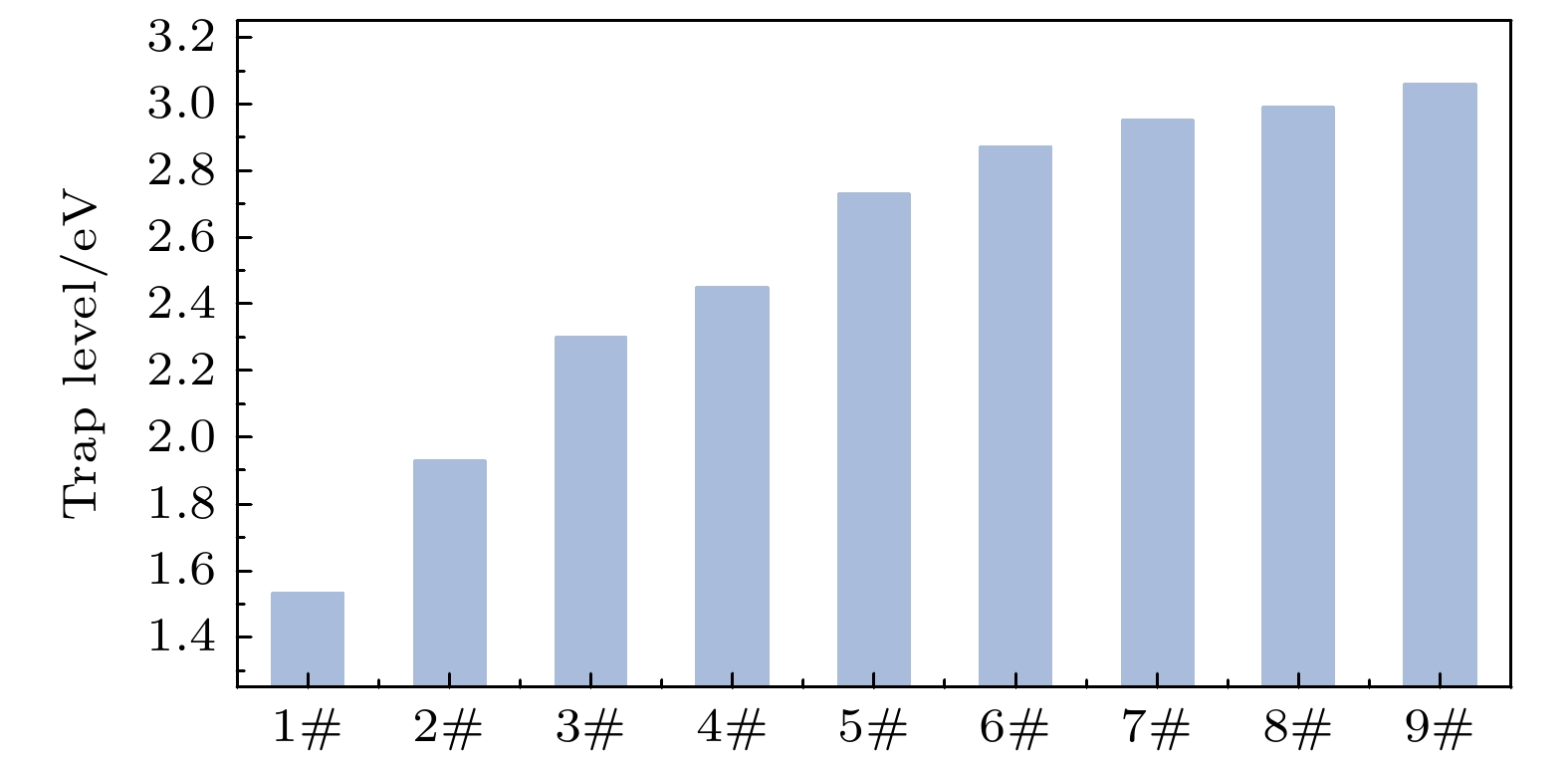
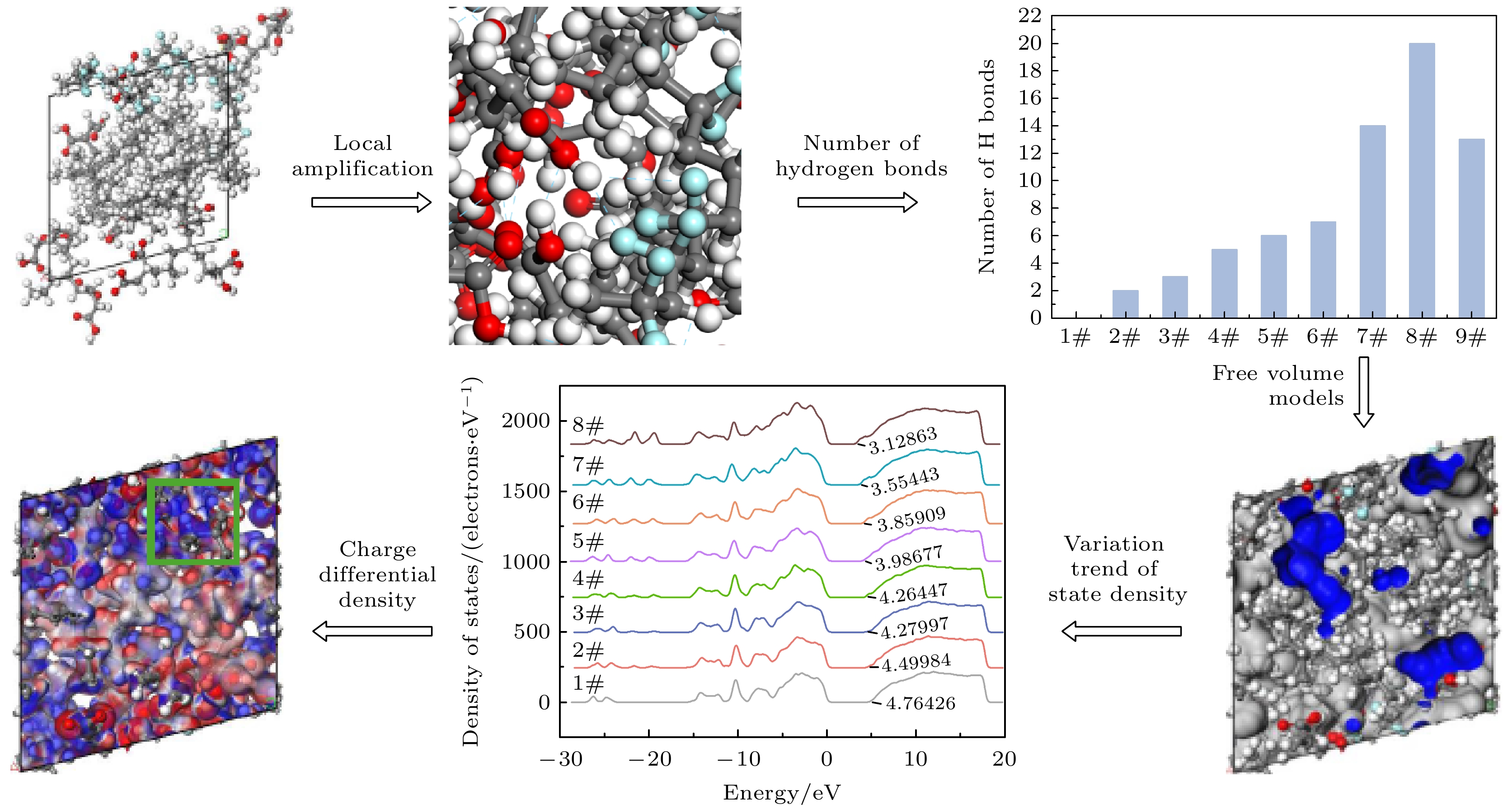
-
Simulating molecular structures and dynamic behaviors presents critical insights into the microscopic mechanisms governing variations in charge transport properties. In this work, molecular dynamics (MD) simulations integrated with the Compass II force field and molecular modeling (including geometry optimization, annealing, and dynamic equilibration) are conducted to systematically analyze intermolecular interaction energy, free volume distribution, electronic density of states (DOS), charge differential density, and trap energy levels. aiming to unravel the regulatory role of hydrogen bonds in the structural evolution and charge transport dynamics of polypropylene (PP)/polyvinylidene fluoride (PVDF) composite systems. A quantitative framework is further established to correlate hydrogen bond density with key material performance metrics, such as free volume fraction, bandgap energy, and trap energy depth, thereby elucidating the hydrogen bond-mediated modulation of molecular architecture and charge transport behavior in PP/PVDF composites. Simulation results reveal a pronounced dependence of hydrogen bond formation on maleic acid (MA) grafting content. When the mass fraction of MA is 36.22%, the number of hydrogen bonds reaches a maximum value of 20, the intermolecular interaction energy increases to 2171.63 kcal·mol–1, and the free volume fraction reaches a minimum value of 16.03%. At this point, the internal structure of the molecule is most compact. When the mass fraction of MA increases to 52.97%, the band gap of the composite material reaches a minimum value of 3.13 eV, and the depth of the trap energy levels also reaches a maximum value of 3.06 eV. Spatial charge differential density analysis demonstrates that the enhanced electron density is localized near hydrogen-bonded region, thus suppressing electron escape probability by over 40% compared with the scenario in the non-bonded domains. All of the findings highlight a dual mechanism: hydrogen bonds not only reconfigure the molecular topology but also reshape the localized charge distribution, directly suppressing the carrier mobility and changing the charge transport pathways. These findings also establish a robust structure-property relationship, showing that hydrogen bond engineering serves as a pivotal strategy to tailor dielectric performance in polymer composites. By optimizing hydrogen bond density, the trade-off between structural compactness and electronic confinement can be strategically balanced, thus enabling the designing of PP-based dielectrics with low carbon footprints and superior insulating properties. This mechanistic understanding provides actionable guidelines for advancing high-performance insulating materials in energy storage systems, aerospace components, and next-generation electrical devices, where precise control over charge transport is paramount.
-
Keywords:
- polypropylene /
- hydrogen bond /
- molecular dynamics /
- charge transport
-
图 1 PP/PVDF复合材料空间结构 (a) PP; (b) PVDF; (c) PP-g-MA; (d) PP/PVDF
Figure 1. Spacial structure of PP/PVDF composites: (a) PP; (b) PVDF; (c) PP-g-MA; (d) PP/PVDF.
图 2 不同PP/PVDF复合材料分子结构模型 (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#
Figure 2. Molecular structure models of different PP/PVDF composites: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#.
图 3 2#复合材料的能量和温度随时间的变化 (a)能量随时间的变化; (b)温度随时间的变化
Figure 3. Time-dependent energy and temperature variation curves of composite 2# in the PP/PVDF system: (a) Energy change curve with time; (b) temperature curve over time.
图 4 9#复合材料中氢键的位置
Figure 4. Spacial distribution of hydrogen bonds in composite 9#.
图 5 不同PP/PVDF复合材料的氢键数量变化趋势
Figure 5. Variation trend of hydrogen bond number of different PP/PVDF composites.
图 6 不同PP/PVDF复合材料自由体积模型 (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#
Figure 6. Free volume models of different PP/PVDF composites: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#
图 7 不同PP/PVDF复合材料的自由体积分布变化趋势
Figure 7. Variation trend of free volume distribution of different PP/PVDF composites.
图 8 不同PP/PVDF复合材料的态密度变化趋势
Figure 8. Variation trend of state density of different PP/PVDF composites.
图 9 不同PP/PVDF复合材料电荷差分密度 (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#
Figure 9. Charge differential density of different PP/PVDF composites: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#.
图 10 不同PP/PVDF复合材料的陷阱能级变化趋势
Figure 10. Variation trend of trap energy levels of different PP/PVDF composites.
表 1 Compass II力场势能和参数及单位
Table 1. Force field potential energy and parameters in COMPASS II.
Epotential Function form Parameters and units Ebond $ {E_{{\text{bond}}}} = \displaystyle\sum\limits_{{\text{bonds}}} {{k_b}{{(r - {r_0})}^2} + k_b^{(3)}{{(r - {r_0})}^3} + k_b^{(4)}{{(r - {r_0})}^4}} $ kb/(kcal·mol–1·Å–2); r, r0/Å Eangle $ {E_{{\text{angle}}}} = \displaystyle\sum\limits_{{\text{angles}}} {{k_\theta }{{(\theta - {\theta _0})}^2} + k_\theta ^{(3)}{{(\theta - {\theta _0})}^3} + k_\theta ^{(4)}{{(\theta - {\theta _0})}^4}} $ kθ/(kcal·mol–1); θ, θ0/(°) Etorsion $ {E_{{\text{torsion}}}} = \displaystyle\sum\limits_{{\text{torsions}}} {{k_\varphi }(1 + \cos (n} \varphi - {\varphi _0})) $ kφ/(kcal·mol–1); φ, φ0/(°) Eout-of-plane $ {E_{{\text{out}} - {\text{of}} - {\text{plane}}}} = \displaystyle\sum\limits_{{\text{out}} - {\text{of - plane}}} {{k_\omega }{\omega ^2}} $ kω/(kcal·mol–1); ω/(°) Evdw $ {E_{{\text{vdW}}}} = \displaystyle\sum\limits_{i, j} {4\varepsilon \left[ {{{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^{12}} - {{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^6}} \right]} $ Ε/eV; σ/Å; rij/Å Eelectrostatic $ {E_{{\text{electrostatic}}}} = \displaystyle\sum\limits_{i, j} {\frac{{{q_i}{q_j}}}{{4\pi {\varepsilon _0}{r_{ij}}}}} $ qi, qj/e; rij/Å 
DownLoad: CSV
表 2 不同PP/PVDF复合材料体系模型的编号及其质量分数
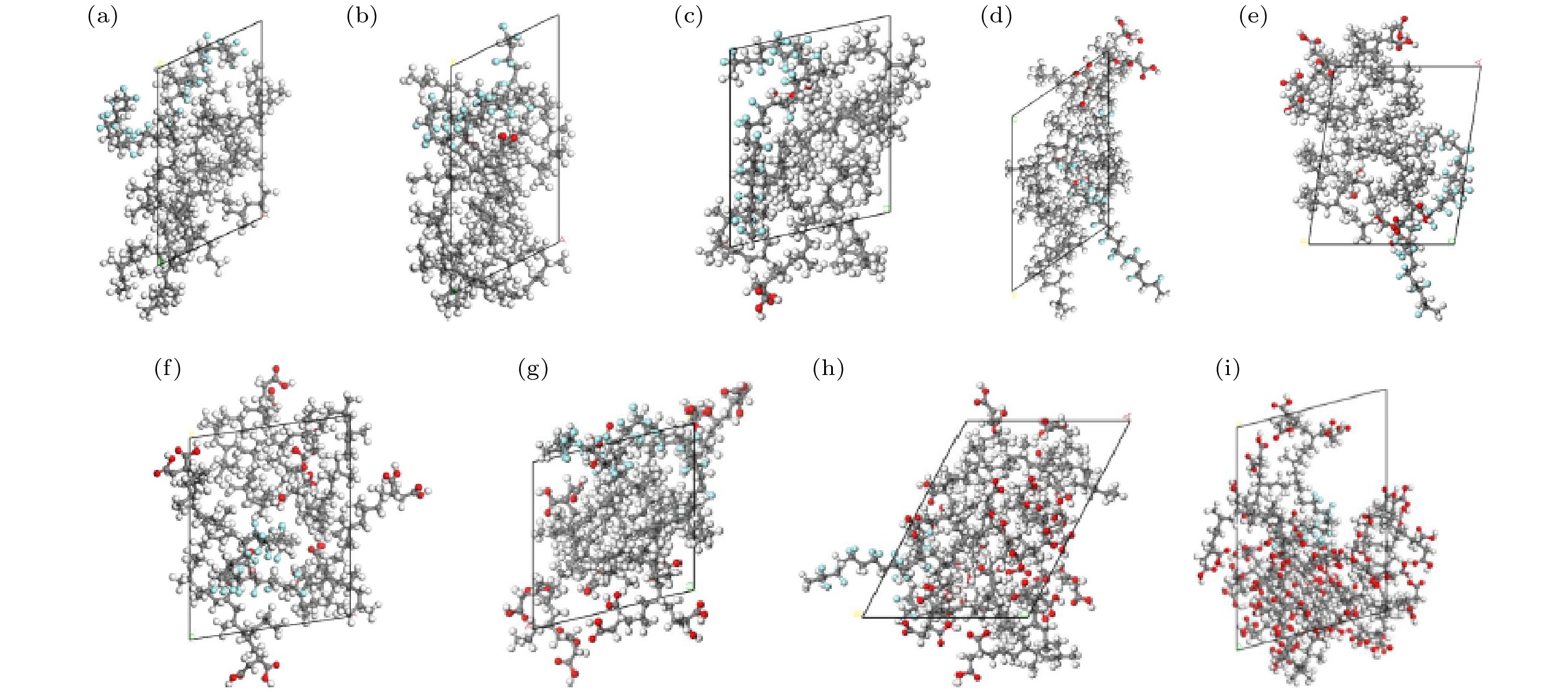
Table 2. Designation and mass fraction of different PP/PVDF composites models.
试样编号
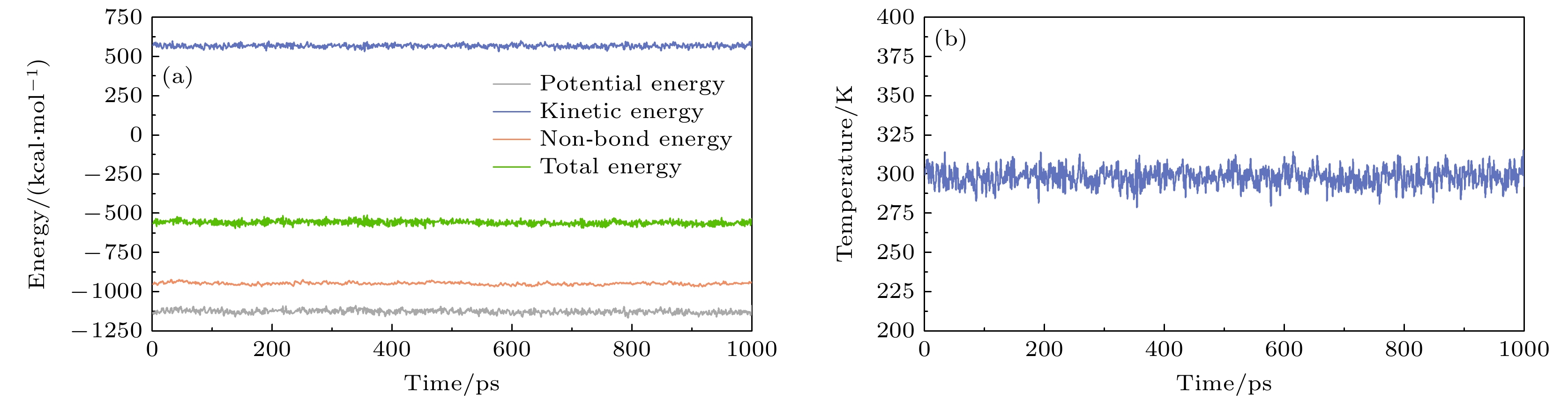
PP-g-MA/%PVDF/% MA PP 1# 0 77.94 22.26 2# 2.74 75.52 21.74 3# 5.33 73.41 21.26 4# 10.13 69.57 20.30 5# 14.50 65.94 19.56 6# 18.47 62.83 18.70 7# 22.05 59.84 18.11 8# 36.22 48.51 15.27 9# 52.97 35.34 11.69
DownLoad: CSV
表 3 NPT平衡后不同PP/PVDF复合材料能量和温度的波动范围
Table 3. Fluctuation range of energy and temperature of different PP/PVDF composites after NPT equilibrium.
试样
编号平衡
时间/ps波动/% Temperature EPotential EKinetic ENon-bond ETotal 1# 58.93 3.25 1.56 3.85 4.52 4.11 2# 74.68 2.89 2.56 4.26 1.57 2.10 3# 25.95 4.56 4.56 3.73 2.94 1.61 4# 78.59 1.12 2.76 1.52 4.51 1.52 5# 85.45 2.59 3.81 1.14 1.52 3.20 6# 36.58 3.58 4.19 2.81 2.73 2.17 7# 57.58 1.56 1.25 4.20 2.85 3.96 8# 85.42 3.20 2.48 1.52 4.22 2.57 9# 54.20 2.74 4.21 1.23 2.52 1.85
DownLoad: CSV
表 4 不同PP/PVDF复合材料的能量变化
Table 4. Energy evolution in different PP/PVDF composites.
Enon bond/(kcal·mol–1)
EDiagonal/(kcal·mol–1)EInteraction
/(kcal·mol–1)Etotal
/(kcal·mol–1)Evdw EElectrostatic Ebond Eangle Etorsion 1# 84.65 853.99 214.04 371.93 –721.02 53.49 552.18 2# 85.17 906.80 215.48 398.77 –728.18 63.88 601.15 3# 86.71 977.26 217.09 412.65 –751.63 75.86 654.46 4# 97.89 1083.01 218.45 448.12 –753.56 85.58 723.28 5# 110.28 1205.79 242.31 453.70 –770.93 88.09 828.37 6# 110.97 1332.96 264.16 536.79 –787.47 89.02 898.72 7# 122.93 1462.88 268.80 547.69 –792.07 108.50 1002.49 8# 132.42 2094.95 309.91 689.15 –858.76 127.05 1413.73 9# 55.29 3377.36 402.88 1026.23 –1028.7 74.86 2171.63
DownLoad: CSV
-
[1] Li H, Gadinski M R, Huang Y Q 2020 Energy Environ. Sci. 13 1279
Google Scholar
[2] Tan D Q 2020 Adv. Funct. Mater. 30 1808567
Google Scholar
[3] Pablo A R, Baltus C B, Sebastião V C, Sílvia H P 2024 Chem. Eng. Sci. 298 120319
Google Scholar
[4] 殷嘉鑫, 王强华 2024 73 157401
Google Scholar
Yin J X, Wang Q H 2024 Acta Phys. Sin. 73 157401
Google Scholar
[5] 罗兵, 李君洛, 王少杰, 胡世勋, 徐永生, 肖微, 徐刚毅, 何金良, 李琦 2024 中国电机工程学报 44 3371
Luo B, Li J L, Wang S J, Hu S X, Xu Y S, Xiao W, Xu G Y, He J L, Li Q 2024 Proceedings of the CSEE 44 3371
[6] 樊林禛, 李琦, 袁浩, 黄上师, 何金良 2022 中国电机工程学报 45 4227
Fan L Z, Li Q, Yuan H, Huang S S, He J L 2022 Proceedings of the CSEE 45 4227
[7] Ohuk L, Kim D, Kim H, Seong H L, Taehoon K, Kwon I, Keisuke S, Masayuki H, Jin H L, Dae H L, Kim M H, Masahiro K, Yu S G 2025 Compos. Sci. Technol. 259 110939
Google Scholar
[8] Hu S, Zhou Y, Yuan C, Wang W, Hu J 2020 High Voltage 5 249
Google Scholar
[9] 樊林禛, 郝国辉, 张雯嘉, 董新华, 屠幼萍, 胡世勋, 邵清, 郑重, 王伟, 袁浩, 李琦, 何金良 2023 中国电机工程学报 45 5251
Fan L Z, Hao G H, Zhang W J, Dong X H, Tu Y P, Hu S X, Shao Q, Zheng Z, Wang W, Yuan H, Li Q, He J L 2023 Proceedings of the CSEE 45 5251
[10] 李琳, 王暄, 孙伟峰, 雷清泉 2013 62 106201
Google Scholar
Li L, Wang X, Sun W F, Lei Q Q 2013 Acta Phys. Sin. 62 106201
Google Scholar
[11] 李丽丽, 张晓虹, 王玉龙 2017 66 087201
Li L L, Zhang X H, Wang Y L 2017 Acta Phys. Sin. 66 316
[12] Ulian G, Moro D, Valdrè G 2018 Micro Nano Lett. 13 4
Google Scholar
[13] Duan X H, Wah H S, Martin G, John L, He J L 2020 High Voltage 5 397
Google Scholar
[14] Etcheverry M, Barbosa S E 2012 Materials 5 1084
Google Scholar
[15] Kang J W, Choi K, John W H, Hu S L 1998 Polymer 39 7079
Google Scholar
[16] 庞曦, 许天蕾, 刘鹏, 魏鼎欣, 谢宗良, 彭宗仁 2024 高电压技术 50 3
Pang X, Xu T L, Liu P, Wei D X, Xie Z L, Peng Z R 2024 High Voltage Engineering 50 3
[17] 马超, 闵道敏, 李盛涛, 郑旭, 李西育, 闵超, 湛海涯 2017 66 067701
Google Scholar
Ma C, Min D M, Li S T, Zheng X, Li X Y, Min C, Zhan H Y 2017 Acta Phys. Sin. 66 067701
Google Scholar
[18] Boek E S, Coveney P V, Skipper N T 1995 Langmuir 11 46295
[19] Martínez, Mario J, Martínez L 2003 J. Comput. Chem. 24 819
Google Scholar
[20] 彭向阳, 姚驰, 余欣, 胡世勋, 范亚洲, 何金良 2023 高电压技术 49 4480
Peng X Y, Yao C, Yu X, Hu S X, Fan Y Z, He J L 2023 High Voltage Engineering 49 4480
[21] 贾海鹏, 苏勋家, 侯根良, 曹小平, 毕松, 刘朝辉 2013 化工学报 64 1862
Google Scholar
Jia H P, Su X J, Hou G L, Cao X P, Bi S, Liu Z H 2013 J. Chem. Ind. Eng. 64 1862
Google Scholar
[22] Ferraris G, Ivaldi G 1988 Acta Cryst 44 341
Google Scholar
[23] 冯阳, 渠广昊, 李盛涛 2024 高电压技术 50 2363
Feng Y, Qu G H, Li S T 2024 High Voltage Engineering 50 2363
[24] Ran Z Y, Luo Z, Li J L, Meng L, Liu Y H, Hu J 2024 IEEE 5th International Conference on Dielectrics France, August 2—6, 2024, p1241
[25] 樊金泽, 方展伯, 罗超杰, 张汇 2022 71 127103
Google Scholar
Fan J Z, Fang Z B, Luo C J, Zhang H 2022 Acta Phys. Sin. 71 127103
Google Scholar
[26] Li G C, Liu T Z, Gu Z L, Chen X L, Sun B B, Zhu Y W, Li S T, Wei Y H 2024 High Voltage 85 2397
[27] 洪迪昆, 刘亮, 郭欣 2015 中国电机工程学报 35 6099
Hong D K, Liu L, Guo X 2015 Proceedings of the CSEE 35 6099
[28] Li Q, Yao F Z, Liu Yang 2018 Annu. Rev. Mater. Res. 48 219
Google Scholar
[29] Gabriel P, Jacob P T, Mikhail I, Wu Z G, John W L 2025 J. Chem. Phys. 162 054709
Google Scholar
[30] 王进, 王军霞, 曾凡桂, 吴秀玲 2010 化学学报 68 1653
Wang J, Wang J X, Zeng F G, Wu X L 2010 Acta Chim. Sin. 68 1653
[31] 肖萌, 陈毓妍, 赵亦烁, 杜伯学 2024 高电压技术 50 2319
Xiao M, Chen Y Y, Zhao Y S, Du B X 2024 High Voltage Engineering 50 2319
[32] Le G C, Blaise G 2021 IEEE Trans. Appl. Supercond. 27 472
[33] Li H, Ai D, Ren L, L 2019 Adv. Mater. 31 1900875
Google Scholar
[34] Zhou Y, Li Q, Dang B 2018 Adv. Mater. 30 1805672
Google Scholar
[35] 李盛涛, 谢东日, 闵道敏 2019 中国电机工程学报 39 6122
Li S T, Xie D R, Min D M 2019 Proceedings of the CSEE 39 6122
[36] Wang J, David B A, Carlos A F, De L, Zhang D X, Alexander B, Aart W V, David S 2022 Composites Part A 159 16993
[37] 国家辉 2014 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Guo J H 2014 M. S. Thesis (Harbin: Harbin University of Science and Technology
DownLoad:
Metrics
- Abstract views: 287
- PDF Downloads: 8
- Cited By: 0
