-
In this paper, the quantum phase transitions caused by the interactions between light and atoms, as well as between light and mechanical oscillators, are discussed theoretically in a coupled optomechanical cavity containing two optical field modes (N atoms and mechanical oscillator). By using Holstein-Primak off transformation method, new translational boson operators and four parameters are assumed. The ground state energy functional of the system and a set of equations composed of four parameters are given. The correctness of the assumed translation boson operators is proved by two special cases. In the case of resonance, the characteristics of the obtained solutions are shown by solving the equations, graphical method and Hessian matrix judgment. The stable zero solution is called the normal phase, the unstable zero solution is named the unstable vacuum macroscopic phase, and the stable non-zero solution is referred to as the superradiation phase. The phase can transition from normal phase to superradiation phase, and the point of phase transition can be changed by adjusting the coupling intensity of the two cavity light fields. When the nonlinear photon-phonon interaction caused by radiation pressure is considered, the phase diagram of the system is expanded from the original two phase regions to three phase regions, including the coexistent normal phase and superradiation phase, the bistable superradiation phase, and the unstable vacuum macroscopic phase region, where the bistable superradiation phase is similar to the optical bistable phenomenon. At the same time, there is also a turning point curve, which overlaps with the phase transition point curve, indicating the existence of multiple quantum phase transitions in the system. These predictions can be detected by measuring the average number of photons. The coupled optomechanical cavity that we studied, when considering the coupling of the two-mode optical field and the atomic ensemble but no mechanical oscillator, reflects the interaction between the two-mode optical field and the atom, thus concluding that the transformation point is small and the quantum phase transition is easy to occur. When the coupling between the mechanical oscillator and the two-mode optical field is not considered, the interaction between the single-mode optical field and the atom is reflected, returning to the quantum phase transition of the Dicke model under rotating wave approximation.
-
Keywords:
- coupled optomechanical cavity /
- Holstein-Primak off transformation /
- coupling intensity of the light fields /
- bistable superradiation phase
[1] Dicke R H 1954 Phys. Rev. 93 99
 Google Scholar
Google Scholar
[2] Wang Y K, Hioe F T 1973 Phys. Rev. A. 7 831
 Google Scholar
Google Scholar
[3] Hioe F T 1973 Phys. Rev. A 8 1440
 Google Scholar
Google Scholar
[4] Vojta M 2003 Rep. Prog. Phys. 66 2069
 Google Scholar
Google Scholar
[5] Brennecke F, Donner T, Ritter S, Bourdel T, Köhl M, Esslinger T 2007 Nature 450 268
 Google Scholar
Google Scholar
[6] Colombe Y, Steinmetz T, Dubois G, Linke F, Hunger D, Reichel J 2007 Nature 450 272
 Google Scholar
Google Scholar
[7] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
 Google Scholar
Google Scholar
[8] Baumann K, Mottl R, Brennecke F, Esslinger T 2011 Phys. Rev. Lett. 107 140402
 Google Scholar
Google Scholar
[9] Das P, Bhakuni D S, Sharma A 2023 Phys. Rev. A 107 043706
 Google Scholar
Google Scholar
[10] Shen L T, Pei X T, Shi Z C, Yang Z B 2024 Eur. Phys. J. D 78 91
 Google Scholar
Google Scholar
[11] LuoY Q, Liu N, Liang J Q 2024 Phys. Rev. A 110 063320
 Google Scholar
Google Scholar
[12] Qin W, Zheng D C, Wu Z D, Chen Y H, Liao R Y 2024 Phys. Rev. A 109 013310
 Google Scholar
Google Scholar
[13] 赵秀琴, 张文慧, 王红梅 2024 73 160302
 Google Scholar
Google Scholar
Zhao X Q, Zhang W H, Wang H M 2024 Acta Phys. Sin. 73 160302
 Google Scholar
Google Scholar
[14] 赵秀琴, 张文慧 2024 73 240301
 Google Scholar
Google Scholar
Zhao X Q, Zhang W H 2024 Acta Phys. Sin. 73 240301
 Google Scholar
Google Scholar
[15] Wang B, Nori F, Xiang Z L 2024 Phys. Rev. Lett. 132 053601
 Google Scholar
Google Scholar
[16] Samanta A, Jana P C 2023 Journal of Optics 52 494
 Google Scholar
Google Scholar
[17] Li L C, Zhang J Q 2021 Photonics 8 588
 Google Scholar
Google Scholar
[18] Lan Z L, Chen Y W, Cheng L Y, Chen L, Ye S Y, Zhong Z R 2024 Quantum Inf. Process. 23 72
 Google Scholar
Google Scholar
[19] Zhao X Q, Liu N, Bai X M, Liang J Q 2017 Ann. Phys. 378 448
 Google Scholar
Google Scholar
[20] Bai C H, Wang D Y, Wang H F, Zhu A D, Zhang S 2016 Sci. Rep. 6 33404
 Google Scholar
Google Scholar
[21] Nejad A A, Askari H R, Baghshahi H R 2017 Appl. Opt. 56 2816
 Google Scholar
Google Scholar
[22] Huang S, Liu N, Liang J Q, Li H B 2021 Phys. Scr. 96 095801
 Google Scholar
Google Scholar
[23] Lian J L, Liu N, Liang J Q, Chen G, Jia S T 2013 Phys. Rev. A 88 043820
 Google Scholar
Google Scholar
[24] Clive E, Tobias B 2003 Phys. Rev. E 67 066203
 Google Scholar
Google Scholar
[25] Chen G, Li J Q, Liang J Q 2006 Phys. Rev. A 74 054101
 Google Scholar
Google Scholar
[26] 黄标, 于晋龙, 王文睿, 王菊, 薛纪强, 于洋, 贾石, 杨恩泽 2015 64 044204
 Google Scholar
Google Scholar
Huang B, Yu J L, Wang W R, Wang J, Xue J Q, Yu Y, Jia S, Yang E Z 2015 Acta Phys. Sin. 64 044204
 Google Scholar
Google Scholar
[27] Wang Z M, Lian J L, Liang J Q, Yu Y M, Liu W M 2016 Phys. Rev. A 93 033630
 Google Scholar
Google Scholar
[28] 刘要稳, 赵鸿, 汪映海 1999 48 198
 Google Scholar
Google Scholar
Liu Y W, Zhao H, Wang Y H 1999 Acta Phys. Sin. 48 198
 Google Scholar
Google Scholar
-
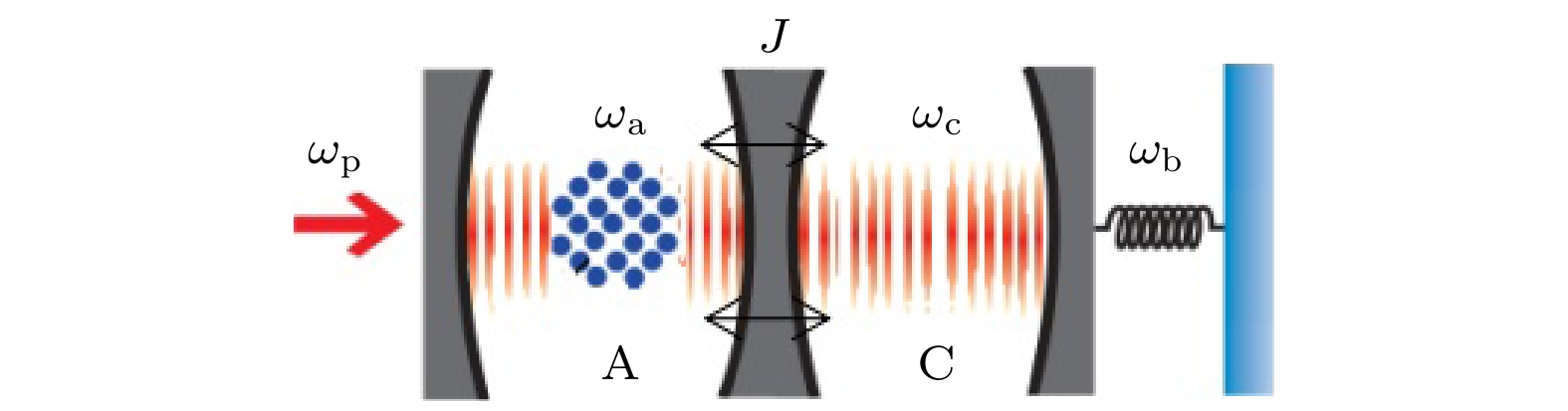
图 1 耦合光机械腔的示意图[20–22], A腔和C腔通过两模光场耦合强度J耦合, A腔中有二能级原子系综, 由具有强度$ {\varOmega _{\text{p}}} $和频率$ {\omega _{\text{p}}} $的外部单模激光场相干驱动, C腔是光机械腔
Figure 1. Schematic illustration of the coupled optomechanical cavities [20–22], cavity A and cavity C are coupled by a two-mode optical field coupling strength J. An ensemble of two-level atoms is placed into the cavity A which is coherently driven by an external monochromatic laser field with strength $ {\varOmega _{\text{p}}} $ and frequency $ {\omega _{\text{p}}} $, cavity C is a optomechanical cavity.
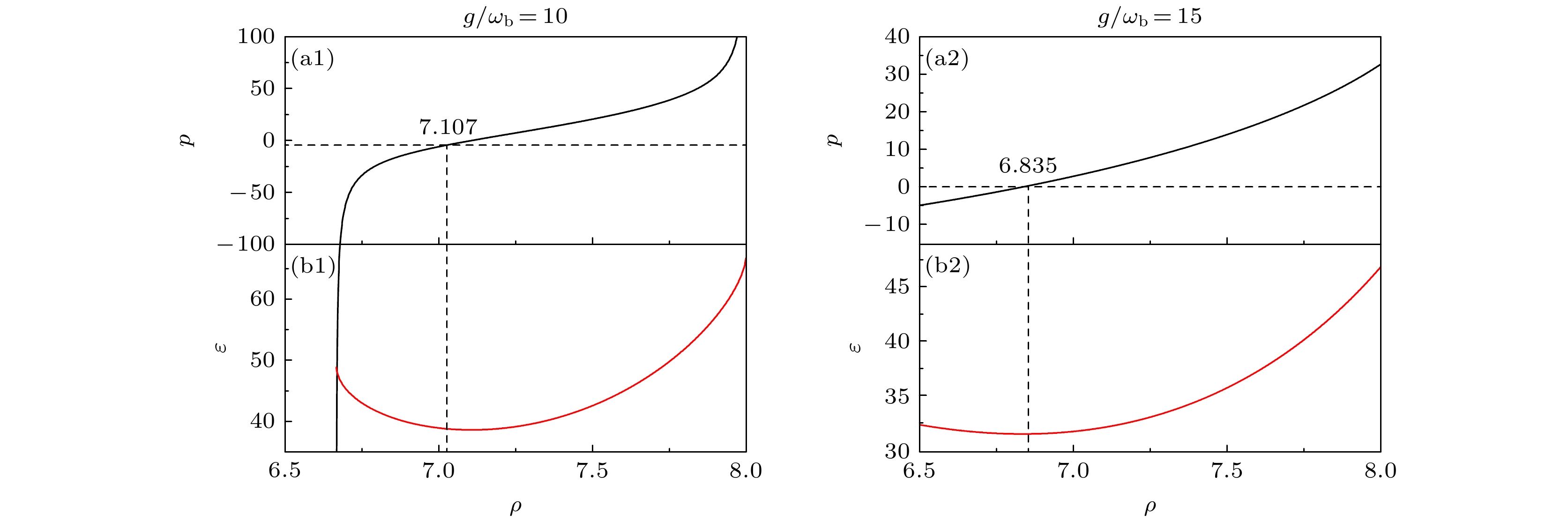
图 3 选择A, B两个点, 参量为$ J = 10{\omega _{\text{b}}} $, $ g/{\omega _{\text{b}}} = 10, 15 $, $ \zeta /{\omega _{\text{b}}} = 1.0 $ (a1), (a2)对应的一阶偏导数p; (b1), (b2)对应的平均基态能量$ \varepsilon $
Figure 3. Select points A and B, parameters $ J = 10{\omega _{\text{b}}} $, $ g/{\omega _{\text{b}}} = 10, 15 $, $ \zeta /{\omega _{\text{b}}} = 1.0 $: (a1), (a2) The corresponding first partial derivatives p; (b1), (b2) the corresponding average ground state energies $ \varepsilon $.
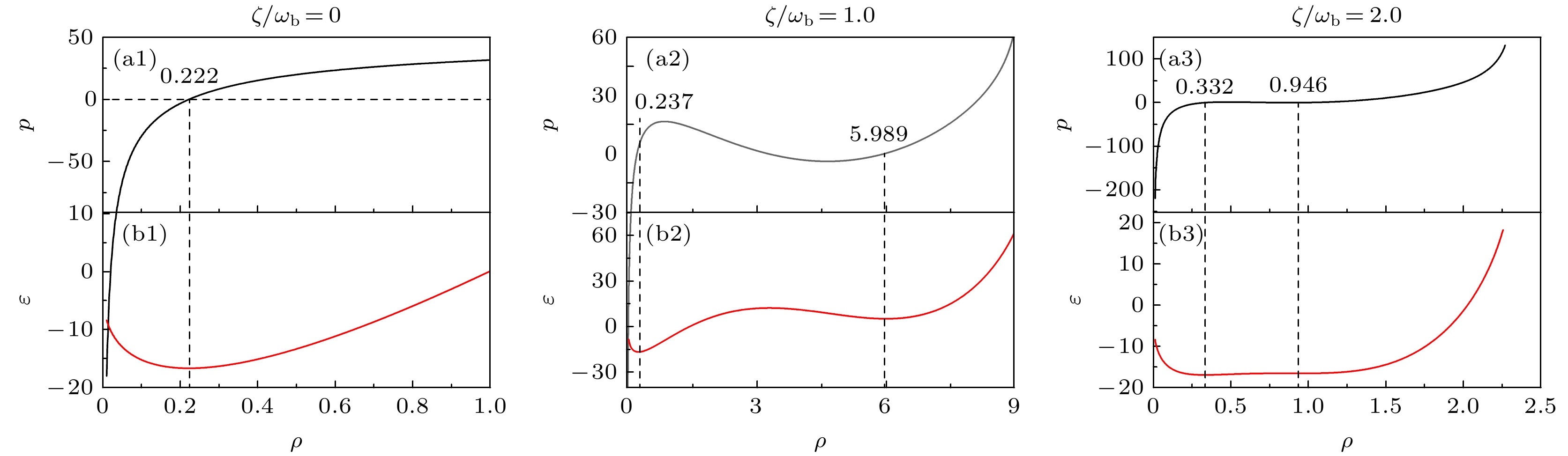
图 4 选择D点, 参量为$ J = 10{\omega _{\text{b}}} $, $ g/{\omega _{\text{b}}} = 30 $, $ \zeta /{\omega _{\text{b}}} = 0 $, $ 1.0 $, $ 2.0 $ (a1)—(a3) 对应的一阶偏导数p; (b1)—(b3) 对应的平均基态能量$ \varepsilon $
Figure 4. Select D point, parameters $ J = 10{\omega _{\text{b}}} $, $ g/{\omega _{\text{b}}} = 30 $, $ \zeta /{\omega _{\text{b}}} = 0 $, $ 1.0 $, $ 2.0 $: (a1)–(a3) Corresponding first partial derivatives p; (b1)–(b3) the corresponding average ground state energies $ \varepsilon $.
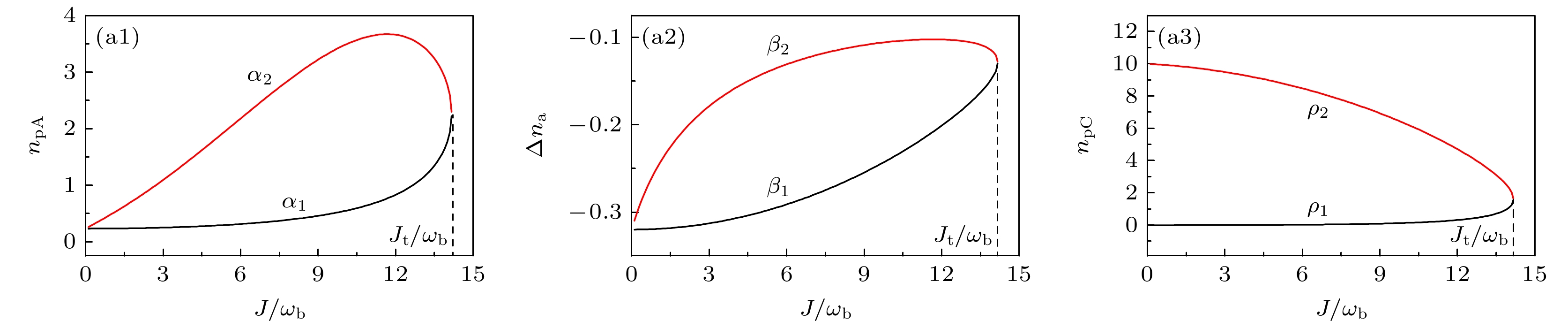
图 5 取参量$ {\text{ }}g/{\omega _{\text{b}}} = 25 $, $ \zeta /{\omega _{\text{b}}} = 1.0 $, $ {\text{ }}J/{\omega _{\text{b}}} = 0 \to 20{\text{ }} $, A腔和C腔的平均光子数分布$ {n_{{\text{pA}}}} $ (a1)和$ {n_{{\text{pC}}}} $(a3), A腔中原子布居差的分布$ \varDelta {n_{\text{a}}} $(a2)随两模光场的耦合参量J变化曲线, $ {\text{ }}{J_{\text{t}}}/{\omega _{\text{b}}} $是转折点
Figure 5. Take parameters $ {\text{ }}g/{\omega _{\text{b}}} = 25 $, $ \zeta /{\omega _{\text{b}}} = 1.0 $, $ {\text{ }}J/{\omega _{\text{b}}} = 0 \to 20{\text{ }} $: The changing curves of average photon number distribution $ {n_{{\text{pA}}}} $ (a1) and $ {n_{{\text{pC}}}} $ (a3) in cavity A and cavity C, and the distribution of atomic population difference $ \varDelta {n_{\text{a}}} $ (a2) in cavity A, with the coupling parameter J of the two-mode optical field, $ {\text{ }}{J_{\text{t}}}/{\omega _{\text{b}}} $ is a turning point.
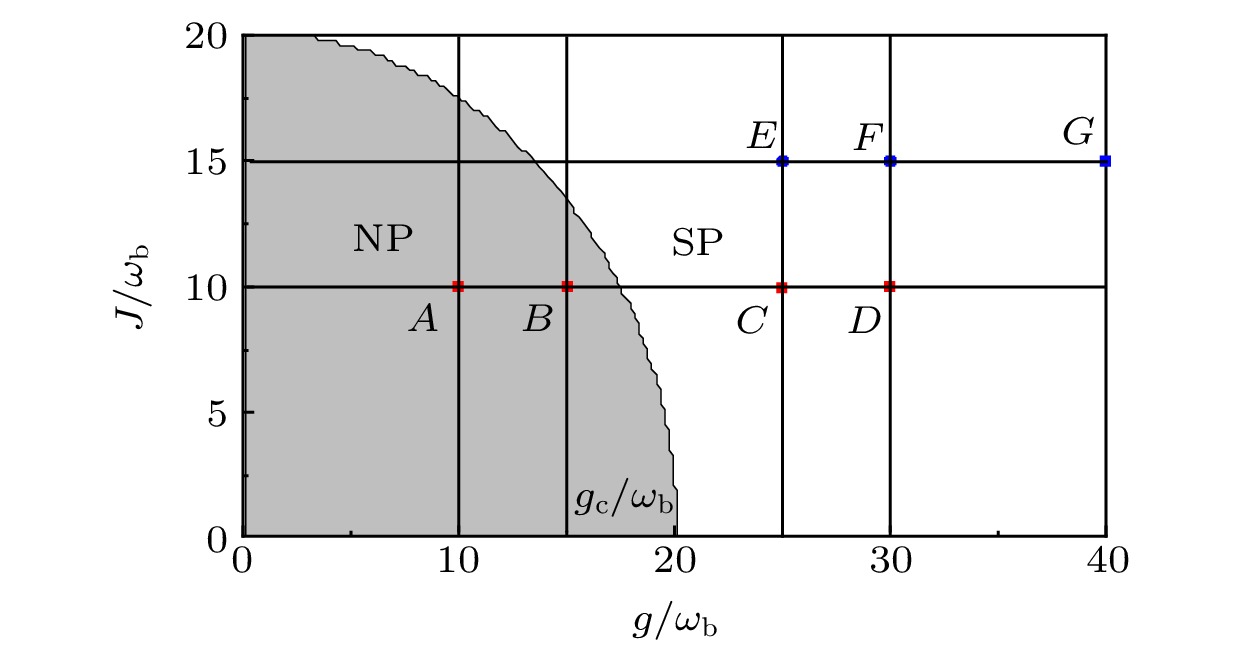
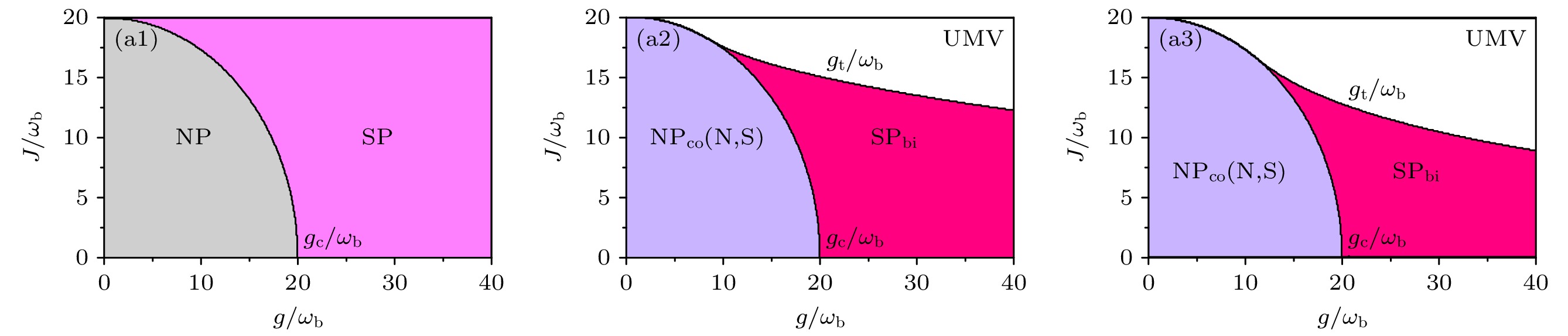
图 6 $ g/{\omega _{\text{b}}}\sim J/{\omega _{\text{b}}} $平面相图 (a1) $ \zeta /{\omega _{\text{b}}} = 0.0 $; (a2) $ \zeta /{\omega _{\text{b}}} = 1.0 $; (a3) $ \zeta /{\omega _{\text{b}}} = 2.0 $
Figure 6. Phase diagram in a plane $ g/{\omega _{\text{b}}}\sim J/{\omega _{\text{b}}} $: (a1) $ \zeta /{\omega _{\text{b}}} = 0.0 $; (a2) $ \zeta /{\omega _{\text{b}}} = 1.0 $; (a3) $ \zeta /{\omega _{\text{b}}} = 2.0 $.
表 1 旋波近似时Dicke模型基态物理量的分布情况
Table 1. Distribution of physical quantities in the ground state of Dicke model in rotating-wave approximation.
基态物理量 $g \leqslant g_{\text{c}}^{\text{R}}$ $g > g_{\text{c}}^{\text{R}}$ 平均光子数分布
${n_{{\text{pA}}}} = \alpha $0 $ \dfrac{1}{4}\dfrac{{{g^2}}}{{\varDelta _{\text{a}}^{2}}}\left( {1 - \dfrac{{g_{\text{c}}^{{\text{R4}}}}}{{{g^4}}}} \right) $ 布居数差分布
$\varDelta {n_{\text{a}}} = \beta - {1}/{2}$$ - \dfrac{1}{2}$ $ - \dfrac{{g_{\text{c}}^{{\text{R2}}}}}{{2{g^2}}} $ 平均基态能量
$ {H_0}/{\varDelta _0}$$ - \dfrac{1}{2}$ $ - \dfrac{{{g^2}}}{{4{\varDelta _{\text{a}}{\varDelta _0}}}}\left( {1 + \dfrac{{g_{\text{c}}^{{\text{R4}}}}}{{{g^4}}}} \right) $ 表 2 考虑与C腔中光场有相互作用时基态物理量的分布情况
Table 2. Distribution of physical quantities in the ground state interacting with the light field in the cavity C is considered.
基态物理量 $g \leqslant g_{\text{c}}^J$ $g > g_{\text{c}}^J$ 平均光子数分布$\left\{ \begin{aligned} {n_{{{\text{p}}_{\text{a}}}}} = \alpha \\ {n_{{{\text{p}}_{\text{c}}}}} = \rho\end{aligned} \right.$ 0 $ \left\{ \begin{aligned}& \alpha = \dfrac{{{g^2}}}{{4\varDelta _{\text{a}}^{2}}}\left(1 - \dfrac{{g_{\text{c}}^{J4}}}{{{g^4}}}\right) \\ &\rho = \dfrac{{{J^2}}}{{4\varDelta _{\text{c}}^{2}}}\dfrac{{{g^2}}}{{\varDelta _{\text{a}}^{2}}}\left(1 - \dfrac{{g_{\text{c}}^{J4}}}{{{g^4}}}\right) \end{aligned} \right. $ 布居数差分布$\Delta {n_{\text{a}}} = \beta - {1}/{2}$ $ - \dfrac{1}{2}$ $ - \dfrac{{g_{\text{c}}^{J2}}}{{2{g^2}}} $ 平均基态能量$ {H_0}/{{\varDelta _0}} $ $ - \dfrac{1}{2}$ $ - \dfrac{{{g^2}}}{{4{\varDelta _{\text{a}}{\varDelta _0}}}}\left(1 + \dfrac{{g_{\text{c}}^{J4}}}{{{g^4}}}\right) $ 表 3 4个红点A—D在$ \zeta /{\omega _{\text{b}}}{\text{ = 0, 1}}{\text{.0, 2}}{.0} $时, 3个参量$ \alpha , \beta , \rho $的解的具体数值
Table 3. When the four red dots are at $ \zeta /{\omega _{\text{b}}} = 0, 1.0, 2.0$, the specific values of the solutions of the three parameters $ \alpha, \beta, \rho $.
正常相区点A点 正常相区点B点 $ \zeta /{\omega _{\text{b}}} = 0 $ $ \zeta /{\omega _{\text{b}}} = 1.0 $ $ \zeta /{\omega _{\text{b}}} = 2.0 $ $ \zeta /{\omega _{\text{b}}} = 0 $ $ \zeta /{\omega _{\text{b}}} = 1.0 $ $ \zeta /{\omega _{\text{b}}} = 2.0 $ 0 $ \left\{ \begin{aligned} \alpha = {2}{.380} \\ \beta = {0}{.228} \\ \rho = {7}{.107}\end{aligned} \right.{\text{ }} $ $ \left\{ \begin{aligned} \alpha = {0}{.663} \\ \beta = {0}{.112} \\ \rho = {1}{.725}\end{aligned} \right.{\text{ }} $ $ 0 $ $ \left\{ \begin{aligned} \alpha = {2}{.739} \\ \beta = {0}{.313} \\ \rho = {6}{.835}\end{aligned} \right.{\text{ }} $ $ \left\{ \begin{aligned} \alpha = {0}{.868} \\ \beta = {0}{.209} \\ \rho = {1}{.571}\end{aligned} \right.{\text{ }} $ 超辐射区相点C点 超辐射区相点D点 $ \zeta /{\omega _{\text{b}}} = 0 $ $ \zeta /{\omega _{\text{b}}} = 1.0 $ $ \zeta /{\omega _{\text{b}}} = 2.0 $ $ \zeta /{\omega _{\text{b}}} = 0 $ $ \zeta /{\omega _{\text{b}}} = 1.0 $ $ \zeta /{\omega _{\text{b}}} = 2.0 $ $ \left\{ \begin{aligned} \alpha = {0}{.534} \\ \beta = {0}{.260} \\ \rho = {0}{.134}\end{aligned} \right.{\text{ }} $ $ \left\{ \begin{aligned} {\alpha _1} = {0}{.541} \\ {\beta _1} = {0}{.261} \\ {\rho _1} = {0}{.139}\end{aligned} \right.{\text{ }} $
$ \left\{ \begin{aligned} {\alpha _2} = {3}{.474} \\ {\beta _2} = {0}{.395} \\ {\rho _2} = {6}{.280}\end{aligned} \right.{\text{ }} $$ \left\{ \begin{aligned} {\alpha _1} = {0}{.568} \\ {\beta _1} = {0}{.262} \\ {\rho _1} = {0}{.162}\end{aligned} \right.{\text{ }} $
$ \left\{ \begin{aligned} {\alpha _2} = {1}{.295} \\ {\beta _2} = {0}{.334} \\ {\rho _2} = {1}{.203}\end{aligned} \right.{\text{ }} $$ \left\{ \begin{aligned} \alpha = 0.889 \\ \beta = {0}{.333} \\ \rho = {0}{.222}\end{aligned} \right. $ $ \left\{ \begin{aligned} {\alpha _1} = {0}{.905} \\ {\beta _1} = {0}{.335} \\ {\rho _1} = {0}{.237}\end{aligned} \right. $
$ \left\{ \begin{aligned} {\alpha _2} = {3}{.853} \\ {\beta _2} = {0}{.416} \\ {\rho _2} = {5}{.989}\end{aligned} \right.{\text{ }} $$ \left\{ \begin{aligned} {\alpha _1} = {1}{.000} \\ {\beta _1} = {0}{.342} \\ {\rho _1} = {0}{.332}\end{aligned} \right.{\text{ }} $
$ \left\{ \begin{aligned} {\alpha _2} = {1}{.462} \\ {\beta _2} = {0}{.367} \\ {\rho _2} = {0}{.946}\end{aligned} \right.{\text{ }} $ -
[1] Dicke R H 1954 Phys. Rev. 93 99
 Google Scholar
Google Scholar
[2] Wang Y K, Hioe F T 1973 Phys. Rev. A. 7 831
 Google Scholar
Google Scholar
[3] Hioe F T 1973 Phys. Rev. A 8 1440
 Google Scholar
Google Scholar
[4] Vojta M 2003 Rep. Prog. Phys. 66 2069
 Google Scholar
Google Scholar
[5] Brennecke F, Donner T, Ritter S, Bourdel T, Köhl M, Esslinger T 2007 Nature 450 268
 Google Scholar
Google Scholar
[6] Colombe Y, Steinmetz T, Dubois G, Linke F, Hunger D, Reichel J 2007 Nature 450 272
 Google Scholar
Google Scholar
[7] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
 Google Scholar
Google Scholar
[8] Baumann K, Mottl R, Brennecke F, Esslinger T 2011 Phys. Rev. Lett. 107 140402
 Google Scholar
Google Scholar
[9] Das P, Bhakuni D S, Sharma A 2023 Phys. Rev. A 107 043706
 Google Scholar
Google Scholar
[10] Shen L T, Pei X T, Shi Z C, Yang Z B 2024 Eur. Phys. J. D 78 91
 Google Scholar
Google Scholar
[11] LuoY Q, Liu N, Liang J Q 2024 Phys. Rev. A 110 063320
 Google Scholar
Google Scholar
[12] Qin W, Zheng D C, Wu Z D, Chen Y H, Liao R Y 2024 Phys. Rev. A 109 013310
 Google Scholar
Google Scholar
[13] 赵秀琴, 张文慧, 王红梅 2024 73 160302
 Google Scholar
Google Scholar
Zhao X Q, Zhang W H, Wang H M 2024 Acta Phys. Sin. 73 160302
 Google Scholar
Google Scholar
[14] 赵秀琴, 张文慧 2024 73 240301
 Google Scholar
Google Scholar
Zhao X Q, Zhang W H 2024 Acta Phys. Sin. 73 240301
 Google Scholar
Google Scholar
[15] Wang B, Nori F, Xiang Z L 2024 Phys. Rev. Lett. 132 053601
 Google Scholar
Google Scholar
[16] Samanta A, Jana P C 2023 Journal of Optics 52 494
 Google Scholar
Google Scholar
[17] Li L C, Zhang J Q 2021 Photonics 8 588
 Google Scholar
Google Scholar
[18] Lan Z L, Chen Y W, Cheng L Y, Chen L, Ye S Y, Zhong Z R 2024 Quantum Inf. Process. 23 72
 Google Scholar
Google Scholar
[19] Zhao X Q, Liu N, Bai X M, Liang J Q 2017 Ann. Phys. 378 448
 Google Scholar
Google Scholar
[20] Bai C H, Wang D Y, Wang H F, Zhu A D, Zhang S 2016 Sci. Rep. 6 33404
 Google Scholar
Google Scholar
[21] Nejad A A, Askari H R, Baghshahi H R 2017 Appl. Opt. 56 2816
 Google Scholar
Google Scholar
[22] Huang S, Liu N, Liang J Q, Li H B 2021 Phys. Scr. 96 095801
 Google Scholar
Google Scholar
[23] Lian J L, Liu N, Liang J Q, Chen G, Jia S T 2013 Phys. Rev. A 88 043820
 Google Scholar
Google Scholar
[24] Clive E, Tobias B 2003 Phys. Rev. E 67 066203
 Google Scholar
Google Scholar
[25] Chen G, Li J Q, Liang J Q 2006 Phys. Rev. A 74 054101
 Google Scholar
Google Scholar
[26] 黄标, 于晋龙, 王文睿, 王菊, 薛纪强, 于洋, 贾石, 杨恩泽 2015 64 044204
 Google Scholar
Google Scholar
Huang B, Yu J L, Wang W R, Wang J, Xue J Q, Yu Y, Jia S, Yang E Z 2015 Acta Phys. Sin. 64 044204
 Google Scholar
Google Scholar
[27] Wang Z M, Lian J L, Liang J Q, Yu Y M, Liu W M 2016 Phys. Rev. A 93 033630
 Google Scholar
Google Scholar
[28] 刘要稳, 赵鸿, 汪映海 1999 48 198
 Google Scholar
Google Scholar
Liu Y W, Zhao H, Wang Y H 1999 Acta Phys. Sin. 48 198
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 800
- PDF Downloads: 54
- Cited By: 0














 DownLoad:
DownLoad: