-
Magnons, as quasiparticles arising from spin wave excitations in magnetic materials, have demonstrated significant application potential in quantum information technology, spintronics, and microwave engineering in recent years. The cavity magnon optomechanical system, serving as a key platform for investigating magneto-optical interactions, has advanced the exploration of nonlinear dynamical behaviors and the innovative design of quantum devices through strong coupling between magnons, photons, and phonons. However, traditional single-cavity systems face limitations in terms of tunability, long-range interactions, and nonlinear enhancement, making them insufficient for complex quantum control requirements. In recent years, dual-cavity systems have become a research hotspot due to their multidimensional control capabilities achieved through inter-cavity coupling, such as photon mode splitting and enhanced nonlinear Kerr effects. Meanwhile, semiconductor quantum dots, provide a novel pathway for regulating magnon dynamics due to their tunable nonlinear response characteristics. In this work, we construct a novel coupled quantum system by integrating quantum dots and a dual-cavity architecture, and investigate the bistable phenomena under both forward and backward driving field inputs. By comparing the third-order nonlinear equations governing magnon populations in the two scenarios, we derive the impedance matching condition. When this condition is satisfied, the magnon responses induced by forward driving field and backward driving field are identical. Conversely, under impedance mismatch, the magnon responses exhibit different behaviors. Specifically, when the impedance matching condition is violated, the dual-cavity magnon optomechanical system incorporating three-level quantum dot molecules exhibits a lower bistability threshold than its counterpart without quantum dots. This allows for a transition from low steady state to high steady state while reducing the driving field strength, thereby achieving switching functionality at lower input power. Furthermore, we establish a multiparameter cooperative control model, revealing a three-dimensional parameter space formed by tunneling coupling, cavity-quantum dot coupling, and inter-cavity coupling. By adjusting these coupling strengths, the bistability threshold and hysteresis loop width can be effectively controlled, thereby modulating the driving field intensity required for bistability. This system is expected to experimentally observe the magnonic bistability through the vector network analyzer-based detection of abrupt changes in transmission or absorption windows in reflection spectra. Such capabilities can advance data signal transmission, switching devices, and memory technologies, and has the potential to serve as components of large-scale quantum information processing units. Additionally, this research may find important applications in the field of magnetic spintronics.
-
Keywords:
- cavity optomagnonics /
- magnonic bistability /
- quantum dot molecules
[1] Chumak A V, Serga A A, Hillebrands B 2014 Nat. Commun. 5 4700
 Google Scholar
Google Scholar
[2] Yuan H Y, Yung M H 2018 Phys. Rev. B 95 214434
 Google Scholar
Google Scholar
[3] Zhang X F, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401
 Google Scholar
Google Scholar
[4] Sharma S, Blanter Y M, Bauer G E W 2018 Phys. Rev. Lett. 121 087205
 Google Scholar
Google Scholar
[5] Wang B, Jia X, Lu X H, Xiong H 2022 Phys. Rev. A 105 053705
 Google Scholar
Google Scholar
[6] Ghasemian E, Rafeie M, Musavi S A S, Kheirabady M S, Tavassoly M K 2024 Eur. Phys. J. Plus 139 694
 Google Scholar
Google Scholar
[7] Liao Q H, Peng K, Qiu H Y 2023 Chin. Phys. B 32 054205
 Google Scholar
Google Scholar
[8] Liao Q H, Xiao X, Nie W J, Zhou N R 2020 Opt. Express 28 5288
 Google Scholar
Google Scholar
[9] 黄标, 于晋龙, 王文睿, 王菊, 薛纪强, 于洋, 贾石, 杨恩泽 2015 64 044204
 Google Scholar
Google Scholar
Huang B, Yu J L, Wang W R, Wang J, Xue J Q, Yu Y, Jia S, Yang E Z 2015 Acta Phys. Sin. 64 044204
 Google Scholar
Google Scholar
[10] Soykal O O, Flatté M E 2010 Phys. Rev. Lett. 104 077202
 Google Scholar
Google Scholar
[11] Soykal O O, Flatté M E 2010 Phys. Rev. B 82 104413
 Google Scholar
Google Scholar
[12] Li H Y 2020 Ceram. Int. 46 15408
 Google Scholar
Google Scholar
[13] Mukherjee K, Jana P C 2023 J. Korean Phys. Soc. 82 356
 Google Scholar
Google Scholar
[14] Bhatt V, Singh M K, Agrawal A, Jha P K, Bhattacherjee A B 2024 J. Opt. Soc. Am. B: Opt. Phys. 41 1187
 Google Scholar
Google Scholar
[15] Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601
 Google Scholar
Google Scholar
[16] Li J, Wang Y P, You J Q, Zhu S Y 2023 Natl. Sci. Rev. 10 nwac247
 Google Scholar
Google Scholar
[17] Yu M, Shen H, Li J 2020 Phys. Rev. Lett. 124 213604
 Google Scholar
Google Scholar
[18] Fan Z Y, Qiu L, Groblacher S, Li J 2023 Laser Photonics Rev. 17 2200866
 Google Scholar
Google Scholar
[19] Hao T L, Zhi Y F, Huai B Z, Simon G, Jie L 2024 Laser Photonics Rev. 19 2401348
 Google Scholar
Google Scholar
[20] Qian H, Fan Z Y, Li J 2022 Quantum Sci. Technol. 8 015022
 Google Scholar
Google Scholar
[21] Fabiha R, Lundquist J, Majumder S 2022 Adv. Sci. 9 2104644
 Google Scholar
Google Scholar
[22] Zhang D K, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Commun. 8 1368
 Google Scholar
Google Scholar
[23] Wang Y P, Zhang G Q, Zhang D K, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202
 Google Scholar
Google Scholar
[24] Kurizki G, Bertet P, Kubo Y, Molmerc K, Petrosyand D, Rablf P, Schmiedmayer J 2015 PNAS 112 3866
 Google Scholar
Google Scholar
[25] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391
 Google Scholar
Google Scholar
[26] Childress L, Sorensen A S, Lukin M D 2004 Phys. Rev. A 69 042302
 Google Scholar
Google Scholar
[27] Guo Y, Ma S S, Shu C C 2024 Chin. Phys. B 33 024203
 Google Scholar
Google Scholar
[28] Petroff P M, Lorke A, Imamoglu A 2001 Phys. Today 54 46
 Google Scholar
Google Scholar
[29] Liu G, Xiong W, Ying Z J 2023 Phys. Rev. A 108 033704
 Google Scholar
Google Scholar
[30] Ullah K 2019 Phys. Lett. A 383 3074
 Google Scholar
Google Scholar
[31] Chen B, Shang L, Wang X F, Chen J B, Xue H B, Liu X, Zhang J 2019 Phys. Rev. A 99 063810
 Google Scholar
Google Scholar
[32] Kong C, Xiong H, Wu Y 2019 Phys. Rev. Appl. 12 034001
 Google Scholar
Google Scholar
[33] Shen R C, Li J, Fan Z Y, Wang Y P, You J Q 2022 Phys. Rev. Lett. 129 123601
 Google Scholar
Google Scholar
[34] Yadav S, Bhattacherjee A B 2023 Phys. Scr. 98 025102
 Google Scholar
Google Scholar
[35] Xu X W, Song L N, Zheng Q, Wang Z H, Li Y 2018 Phys. Rev. A 98 063845
 Google Scholar
Google Scholar
-
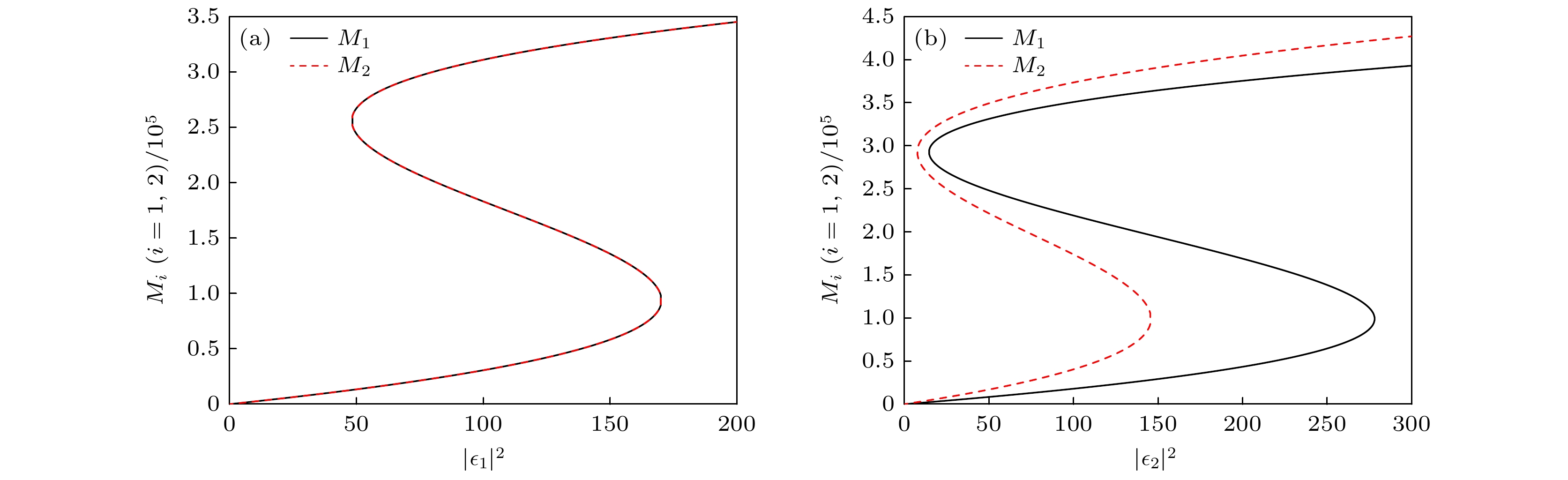
图 2 阻抗匹配条件对磁振子数随驱动场强度的变化曲线的影响 (a)阻抗匹配条件满足, $ J = \sqrt {{{\left( {\varLambda _1^2 + \varLambda _2^2} \right)} {/ } 3}} $; (b)阻抗匹配被打破, $ J = 2\pi \times 2{\text{ MHz}} $; 其他参数: $ {T_{\text{e}}} = 20{\text{ MHz}} $, $ {\varDelta _{\text{m}}} = 0{\text{ MHz}} $, $ {g_{{\text{cq}}}} = 2\pi \times 10{\text{ MHz}} $
Figure 2. Effect of impedance matching condition on the variation curves of the number of magnons with respect to the drive field intensity: (a) Impedance matching is satisfied, $ J = \sqrt {{{\left( {\varLambda _1^2 + \varLambda _2^2} \right)} {/ } 3}} $; (b) impedance matching is broken, $ J = 2 \pi \times 2{\text{ MHz}} $. Other parameters used are: $ {T_{\text{e}}} = 20{\text{ MHz}} $, $ {\varDelta _{\text{m}}} = 0{\text{ MHz}} $, $ {g_{{\text{cq}}}} = 2\pi\times 10{\text{ MHz}} $, respectively.
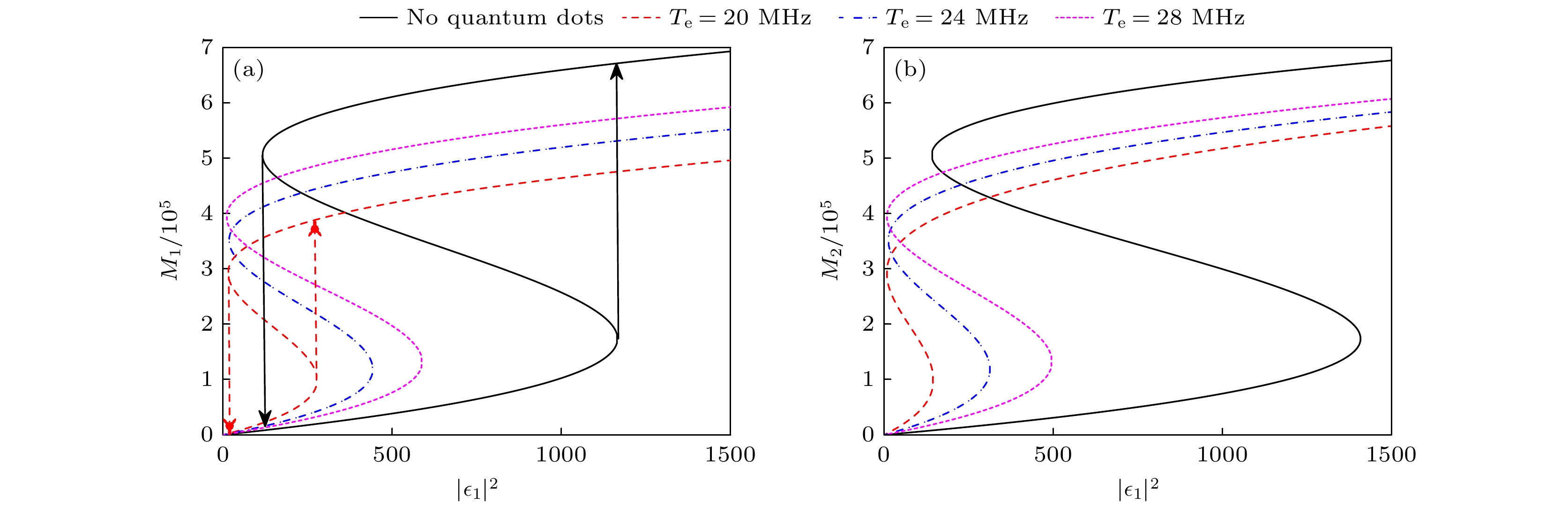
图 3 (a)在$ {\varepsilon _1} \ne 0 $和$ {\varepsilon _2} = 0 $时, 不同隧穿耦合强度下, 磁振子数随驱动场强度的变化; (b)在$ {\varepsilon _1} = 0 $和$ {\varepsilon _2} \ne 0 $时, 不同隧穿耦合强度下, 磁振子数随驱动场强度的变化; 其他参数与图2相同
Figure 3. Variation curves of the number of magnons with respect to the drive field intensity for different tunneling coupling strengths between semiconductor quantum dots under forward input (a) and reverse input (b): (a) $ {\varepsilon _1} \ne 0 $, $ {\varepsilon _2} = 0 $; (b) $ {\varepsilon _1} = 0 $, $ {\varepsilon _2} \ne 0 $. Other parameters used are the same as Fig. 2.
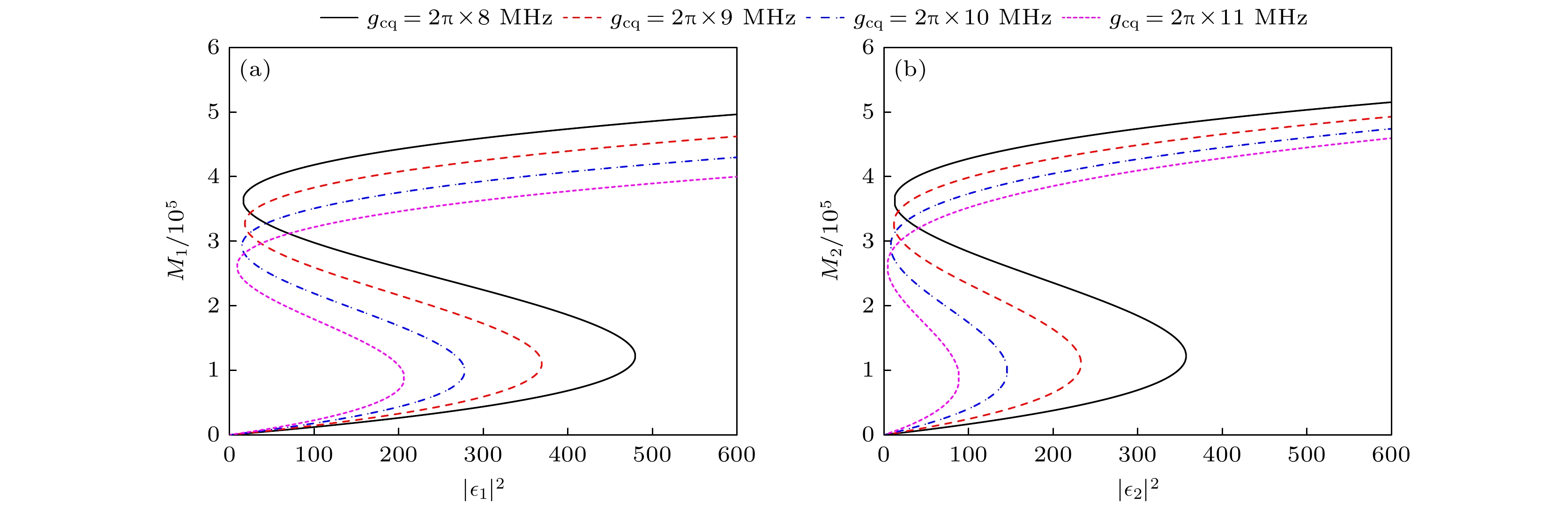
图 4 在不同腔与量子点的耦合强度下, 磁振子数随驱动场强度的变化 (a) $ {\varepsilon _1} \ne 0 $, $ {\varepsilon _2} = 0 $; (b) $ {\varepsilon _1} = 0 $, $ {\varepsilon _2} \ne 0 $. 其他参数与图2相同
Figure 4. Variation curves of the number of magnons with respect to the drive field intensity for different coupling strengths between the cavity and the quantum dots under forward input (a) and reverse input (b): (a) $ {\varepsilon _1} \ne 0 $, $ {\varepsilon _2} = 0 $; (b) $ {\varepsilon _1} = 0 $, $ {\varepsilon _2} \ne 0 $. Other parameters used are the same as Fig. 2.
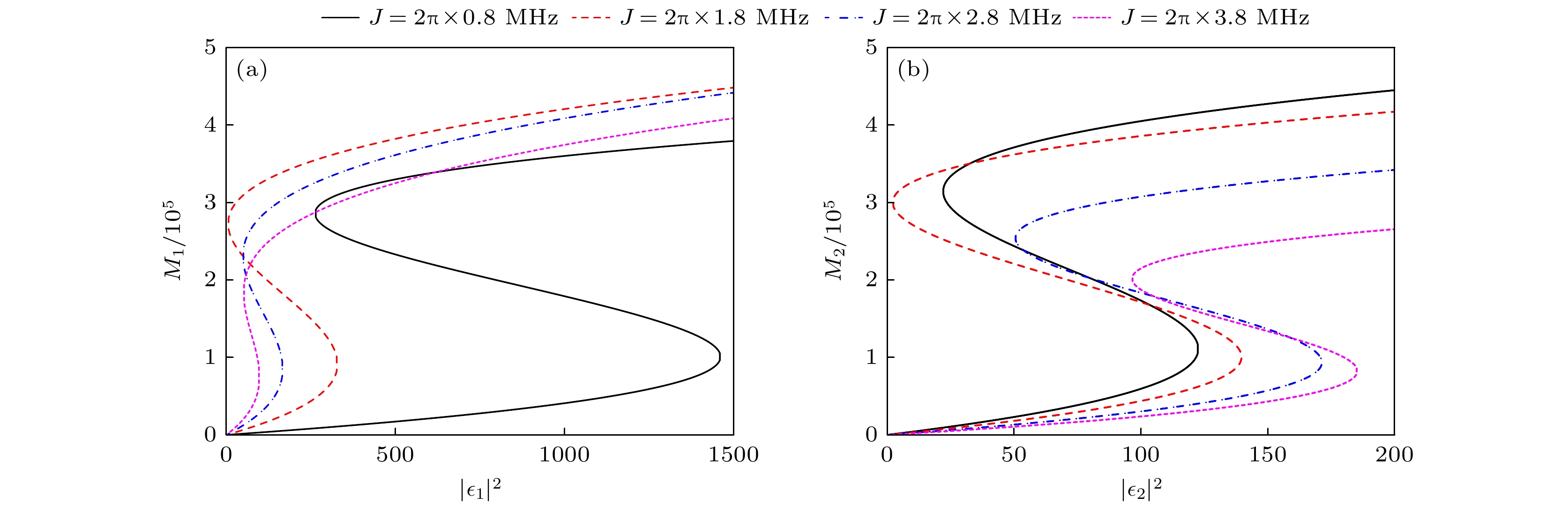
图 5 在驱动场正向输入(a)和反向输入(b)时, 不同两腔之间耦合强度下, 磁振子数随驱动场强度的变化 (a) $ {\varepsilon _1} \ne 0 $, $ {\varepsilon _2} = 0 $; (b) $ {\varepsilon _1} = 0 $, $ {\varepsilon _2} \ne 0 $. 其他参数与图2相同
Figure 5. Variation curves of the number of magnons with respect to the drive field intensity for different coupling strengths between the two cavities under forward input (a) and reverse input (b): (a) $ {\varepsilon _1} \ne 0 $, $ {\varepsilon _2} = 0 $; (b) $ {\varepsilon _1} = 0 $, $ {\varepsilon _2} \ne 0 $. Other parameters used are the same as Fig. 2.
-
[1] Chumak A V, Serga A A, Hillebrands B 2014 Nat. Commun. 5 4700
 Google Scholar
Google Scholar
[2] Yuan H Y, Yung M H 2018 Phys. Rev. B 95 214434
 Google Scholar
Google Scholar
[3] Zhang X F, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401
 Google Scholar
Google Scholar
[4] Sharma S, Blanter Y M, Bauer G E W 2018 Phys. Rev. Lett. 121 087205
 Google Scholar
Google Scholar
[5] Wang B, Jia X, Lu X H, Xiong H 2022 Phys. Rev. A 105 053705
 Google Scholar
Google Scholar
[6] Ghasemian E, Rafeie M, Musavi S A S, Kheirabady M S, Tavassoly M K 2024 Eur. Phys. J. Plus 139 694
 Google Scholar
Google Scholar
[7] Liao Q H, Peng K, Qiu H Y 2023 Chin. Phys. B 32 054205
 Google Scholar
Google Scholar
[8] Liao Q H, Xiao X, Nie W J, Zhou N R 2020 Opt. Express 28 5288
 Google Scholar
Google Scholar
[9] 黄标, 于晋龙, 王文睿, 王菊, 薛纪强, 于洋, 贾石, 杨恩泽 2015 64 044204
 Google Scholar
Google Scholar
Huang B, Yu J L, Wang W R, Wang J, Xue J Q, Yu Y, Jia S, Yang E Z 2015 Acta Phys. Sin. 64 044204
 Google Scholar
Google Scholar
[10] Soykal O O, Flatté M E 2010 Phys. Rev. Lett. 104 077202
 Google Scholar
Google Scholar
[11] Soykal O O, Flatté M E 2010 Phys. Rev. B 82 104413
 Google Scholar
Google Scholar
[12] Li H Y 2020 Ceram. Int. 46 15408
 Google Scholar
Google Scholar
[13] Mukherjee K, Jana P C 2023 J. Korean Phys. Soc. 82 356
 Google Scholar
Google Scholar
[14] Bhatt V, Singh M K, Agrawal A, Jha P K, Bhattacherjee A B 2024 J. Opt. Soc. Am. B: Opt. Phys. 41 1187
 Google Scholar
Google Scholar
[15] Li J, Zhu S Y, Agarwal G S 2018 Phys. Rev. Lett. 121 203601
 Google Scholar
Google Scholar
[16] Li J, Wang Y P, You J Q, Zhu S Y 2023 Natl. Sci. Rev. 10 nwac247
 Google Scholar
Google Scholar
[17] Yu M, Shen H, Li J 2020 Phys. Rev. Lett. 124 213604
 Google Scholar
Google Scholar
[18] Fan Z Y, Qiu L, Groblacher S, Li J 2023 Laser Photonics Rev. 17 2200866
 Google Scholar
Google Scholar
[19] Hao T L, Zhi Y F, Huai B Z, Simon G, Jie L 2024 Laser Photonics Rev. 19 2401348
 Google Scholar
Google Scholar
[20] Qian H, Fan Z Y, Li J 2022 Quantum Sci. Technol. 8 015022
 Google Scholar
Google Scholar
[21] Fabiha R, Lundquist J, Majumder S 2022 Adv. Sci. 9 2104644
 Google Scholar
Google Scholar
[22] Zhang D K, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Commun. 8 1368
 Google Scholar
Google Scholar
[23] Wang Y P, Zhang G Q, Zhang D K, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202
 Google Scholar
Google Scholar
[24] Kurizki G, Bertet P, Kubo Y, Molmerc K, Petrosyand D, Rablf P, Schmiedmayer J 2015 PNAS 112 3866
 Google Scholar
Google Scholar
[25] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391
 Google Scholar
Google Scholar
[26] Childress L, Sorensen A S, Lukin M D 2004 Phys. Rev. A 69 042302
 Google Scholar
Google Scholar
[27] Guo Y, Ma S S, Shu C C 2024 Chin. Phys. B 33 024203
 Google Scholar
Google Scholar
[28] Petroff P M, Lorke A, Imamoglu A 2001 Phys. Today 54 46
 Google Scholar
Google Scholar
[29] Liu G, Xiong W, Ying Z J 2023 Phys. Rev. A 108 033704
 Google Scholar
Google Scholar
[30] Ullah K 2019 Phys. Lett. A 383 3074
 Google Scholar
Google Scholar
[31] Chen B, Shang L, Wang X F, Chen J B, Xue H B, Liu X, Zhang J 2019 Phys. Rev. A 99 063810
 Google Scholar
Google Scholar
[32] Kong C, Xiong H, Wu Y 2019 Phys. Rev. Appl. 12 034001
 Google Scholar
Google Scholar
[33] Shen R C, Li J, Fan Z Y, Wang Y P, You J Q 2022 Phys. Rev. Lett. 129 123601
 Google Scholar
Google Scholar
[34] Yadav S, Bhattacherjee A B 2023 Phys. Scr. 98 025102
 Google Scholar
Google Scholar
[35] Xu X W, Song L N, Zheng Q, Wang Z H, Li Y 2018 Phys. Rev. A 98 063845
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 634
- PDF Downloads: 29
- Cited By: 0















 DownLoad:
DownLoad: