-
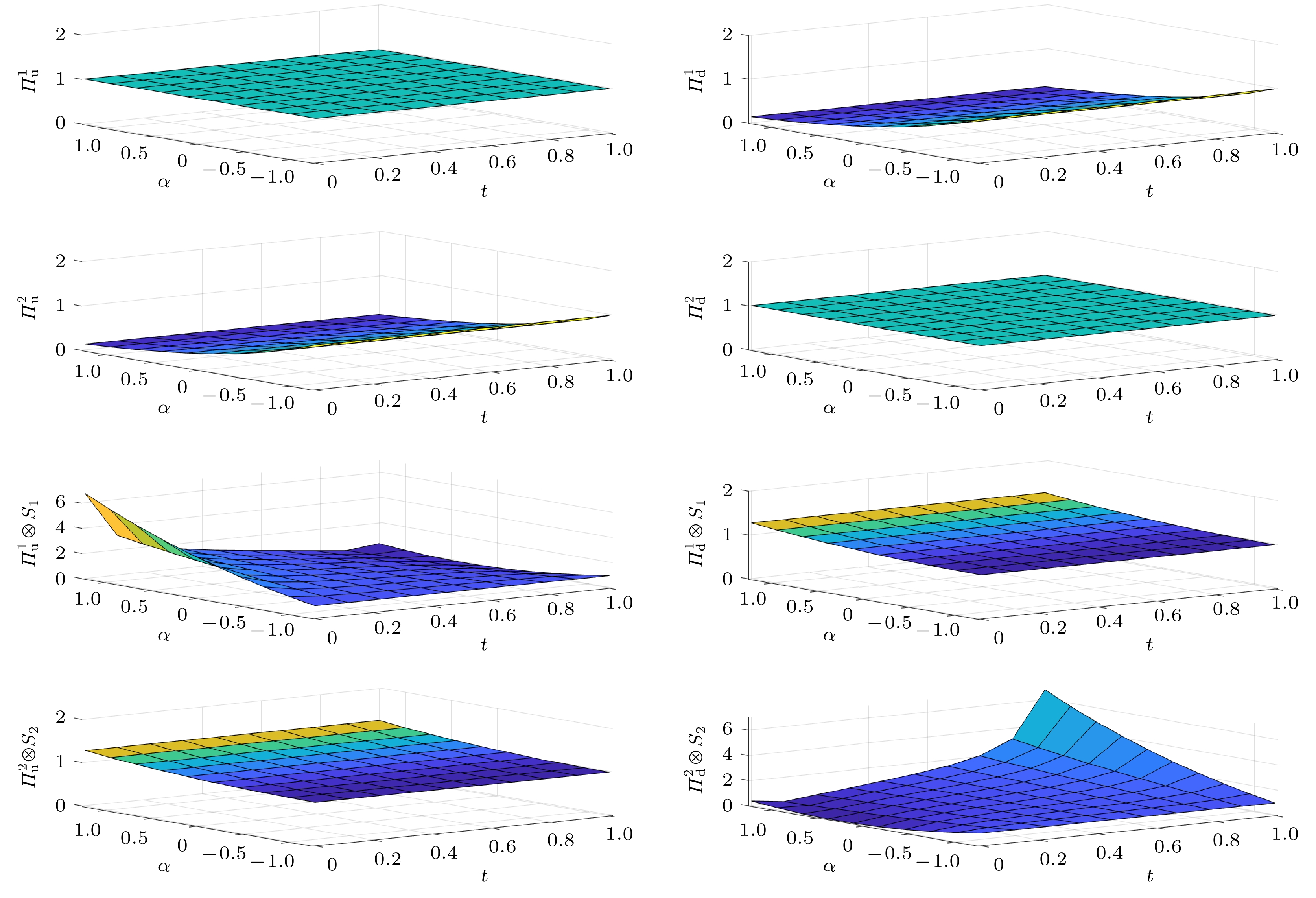
The quantum Cheshire cat effect is an important phenomenon in quantum mechanics that reveals the separability of physical properties from their carriers. This effect transcends the classical framework whose attributes must be inherently attached to objects, providing new perspectives for quantum information and precision measurement. According to the quantum Cheshire cat effect, we prepare a pre-selected state of a spin-1/2 atomic system composed of two particles through a pre-selection process. We conduct quantum weak measurements on the spins and positions of these two atoms and extract weak values by using the method of imaginary time evolution (ITE). Subsequently, we perform post-selection on these two atoms and design two distinct post-selected states. Initially, we calculate analytical solutions when both atoms encounter these two different post-selected states separately. Then, during the stage of obtaining weak values via ITE, we first discuss the scenario with only one post-selected state. In this case, our experimental goal is to achieve spin exchange between the two atoms. We use ITE to obtain normalized coincidence rate for the system. By linearly fitting these normalized coincidence rate, we derive numerical solutions for the weak values of the system. The comparison between the analytical solutions and numerical results indicates that they are in close agreement, demonstrating that our method promotes spin exchange between the two atoms. Next, we examine scenarios involving both post-selected states in the post-selection process. After completing weak measurements on particles, delayed-choice allows them to evolve along different paths ultimately leading to distinct post-selected states. One particular post-selected state that results in final measurement outcomes indicates that the spin exchange occurs between both particles with amplification. Conversely, the other post-selected state ensures that even after undergoing weak measurement and delayed-choice, the states of the two particles remain consistent with their pre-measurement conditions. We also compare the analytical and numerical solutions of the experiment involving delayed choice and find that they are very consistent with each other. This consistency indicates that delayed-choice indeed has a significant influence on whether the final exchange occurs. Our research theoretically confirms the feasibility of fermionic systems within bipartite quantum Cheshire cat effects and illustrates how delayed-choice influences quantum Cheshire cat effects in spin-1/2 atomic systems.
-
Keywords:
- quantum information /
- weak value /
- quantum Cheshire cat
[1] Aharonov Y, Popescu S, Rohrlich D, Skrzypczyk P 2013 New J. Phys. 15 113015
 Google Scholar
Google Scholar
[2] Denkmayr T, Geppert H, Sponar S, Lemmel H, Matzkin A, Tollaksen J, Hasegawa Y 2014 Nat. Commun. 5 4492
 Google Scholar
Google Scholar
[3] Danner A, Geerits N, Lemmel H, Wagner R, Sponar S, Hasegawa Y 2024 Commun. Phys. 7 14
 Google Scholar
Google Scholar
[4] Kim Y, Im D G, Kim Y S, Han S W, Moon S, Kim Y H, Cho Y W 2021 npj. Quantum. Inf. 7 13
 Google Scholar
Google Scholar
[5] Das D, Sen U 2021 Phys. Rev. A 103 012228
 Google Scholar
Google Scholar
[6] Richter M, Dziewit B, Dajka J 2018 Adv. Math. Phys. 2018 7060586
 Google Scholar
Google Scholar
[7] Li J K, Sun K, Wang Y, Hao Z Y, Liu Z H, Zhou J, Fan X Y, Chen J L, Xu J S, Li C F, Guo G C 2023 Light Sci. Appl. 12 18
 Google Scholar
Google Scholar
[8] Wagner R, Kersten W, Lemmel H, Sponar S, Hasegawa Y 2023 Sci. Rep. 13 3865
 Google Scholar
Google Scholar
[9] Ghoshal A, Sau S, Das D, Sen U 2023 Phys. Rev. A 107 052214
 Google Scholar
Google Scholar
[10] Hance J R, Ladyman J, Rarity J 2024 New J. Phys. 26 073038
 Google Scholar
Google Scholar
[11] Das D, Pati A K 2020 New J. Phys. 22 063032
 Google Scholar
Google Scholar
[12] Liu Z H, Pan W W, Xu X Y, Yang M, Zhou J, Luo Z Y, Sun K, Chen J L, Xu J S, Li C F, Guo G C 2020 Nat. Commun. 11 3006
 Google Scholar
Google Scholar
[13] Aharonov Y, Albert D Z, Vaidman L 1988 Phys. Rev. Lett. 60 1351
 Google Scholar
Google Scholar
[14] Ritchie N W M, Story J G, Hulet R G 1991 Phys. Rev. Lett. 66 1107
 Google Scholar
Google Scholar
[15] Bloch I, Zoller P 2006 New J. Phys. 8 E02
 Google Scholar
Google Scholar
[16] Puentes G 2015 J. Phys. B. 48 245301
 Google Scholar
Google Scholar
[17] Mao Y, Chaudhary M, Kondappan M, Shi J, Ilo-Okeke E O, Ivannikov V, Byrnes T 2023 Phys. Rev. Lett. 131 110602
 Google Scholar
Google Scholar
[18] Aharonov Y, Bergmann P G, Lebowitz J L 1964 Phys. Rev. 134 B1410
 Google Scholar
Google Scholar
[19] Wheeler J A 1978 Mathematical Foundations of Quantum Theory (Amsterdam: Elsevier) pp9–48
[20] Witten E 2018 Rev. Mod. Phys. 90 045003
 Google Scholar
Google Scholar
[21] Amico L, Fazio R, Osterloh A, Vedral V 2008 Rev. Mod. Phys. 80 517
 Google Scholar
Google Scholar
[22] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
 Google Scholar
Google Scholar
[23] Wick G C 1954 Phys. Rev. 96 1124
 Google Scholar
Google Scholar
[24] Landsman N, van Weert C 1987 Phys. Rep. 145 141
 Google Scholar
Google Scholar
[25] Xu J S, Sun K, Han Y J, Li C F, Pachos J K, Guo G C 2016 Nat. Commun. 7 13194
 Google Scholar
Google Scholar
[26] Dressel J, Malik M, Miatto F M, Jordan A N, Boyd R W 2014 Rev. Mod. Phys. 86 307
 Google Scholar
Google Scholar
-
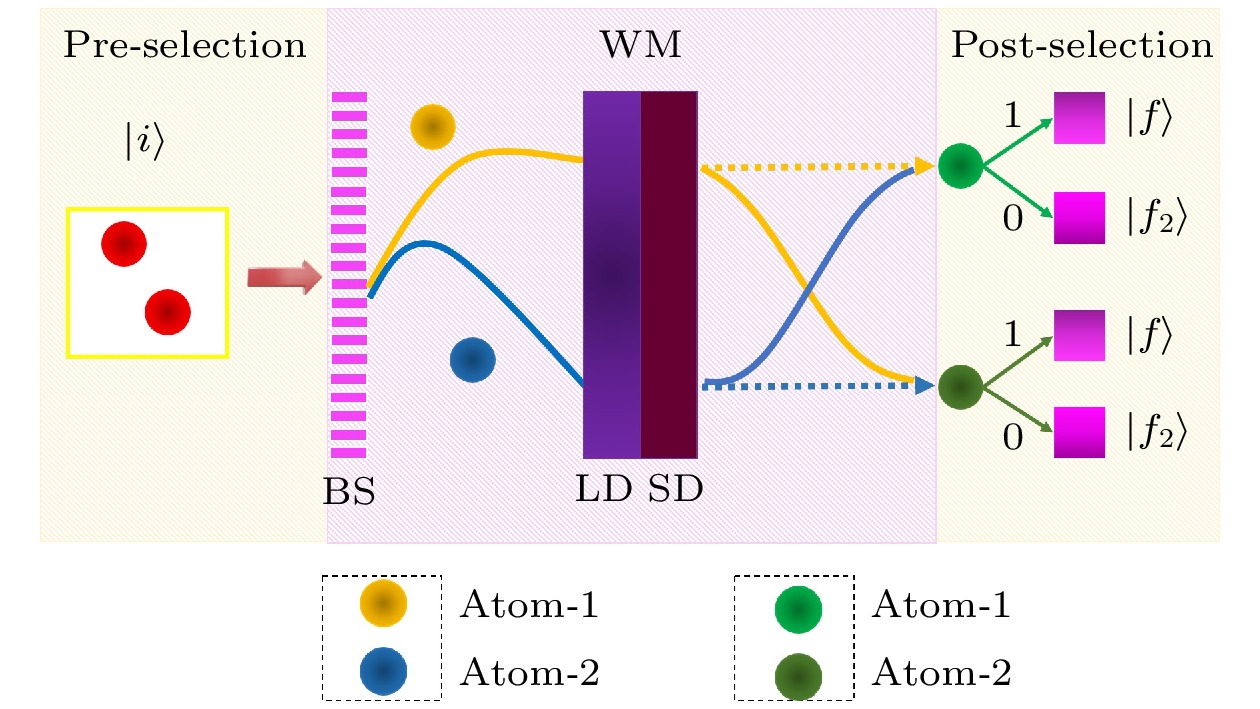
图 1 自旋-1/2原子自旋交换及自旋放大原理示意图. 在前选择部分, 制备出符合理论预期的前选态$ |i\rangle $. 在弱测量(WM)部分, 分束器(BS)将两个原子分束, 两个原子分束后进入位置密度处理器(LD)与自旋灵敏密度处理器(SD)中. 在后选择部分, 两个原子通过一个由1与0控制的随机开关同步进行选择, 确保两个原子同时随机获取其中一种后选态. 两个原子通过BS后, 将通过下路径的原子称为原子1, 以黄色表示; 将通过上路径的原子称为原子2, 以蓝色表示. 完成弱测量后, 用浅绿色表示原子1, 深绿色表示原子2
Figure 1. Schematic diagram of spin-1/2 atomic spin exchange and spin amplification principle In the pre-selection section, prepare a pre-selected state $ |i\rangle $that meets theoretical expectations. In the weak measurement (WM) section, the beam splitter (BS) splits two atoms into beams, which then enter the position density processor (LD) and spin-sensitive density processor (SD). In the post-selection section, two atoms will select synchronlusly through a random switch controlled by 1 and 0, ensuring two atoms simultaneously randomly obtain one of the post-selected states. After two atoms pass through BS, the atom passing through the downward path is called atom-1, represented in yellow; the atom passing through the upper path is called atom-2, represented in blue. After completing the weak measurement, use light green to represent atom-1 and dark green to represent atom-2.
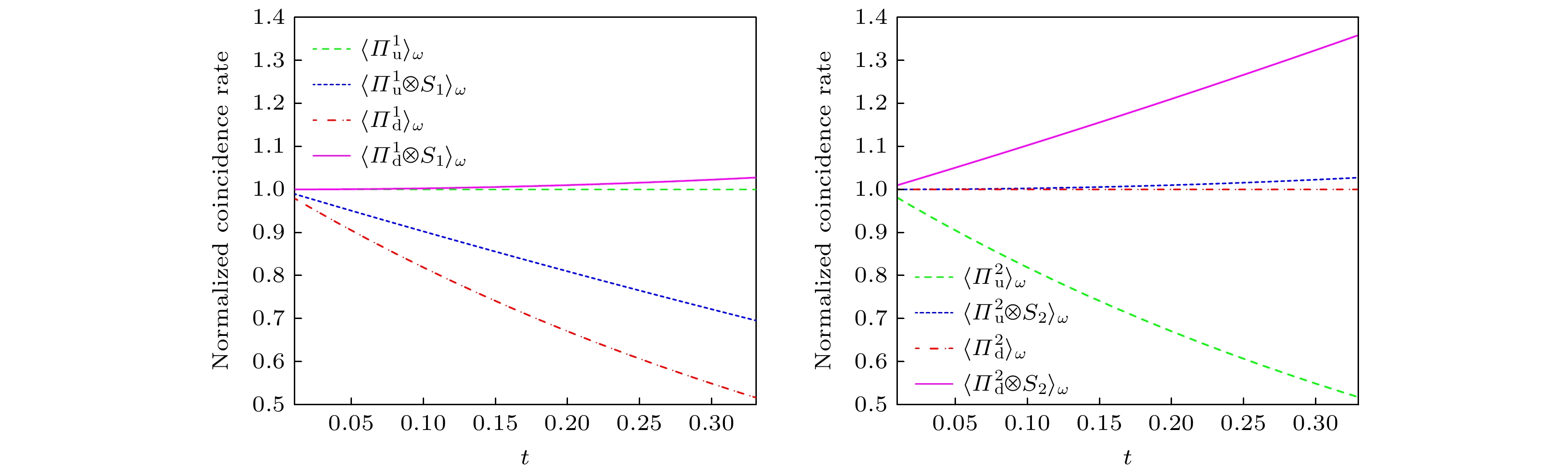
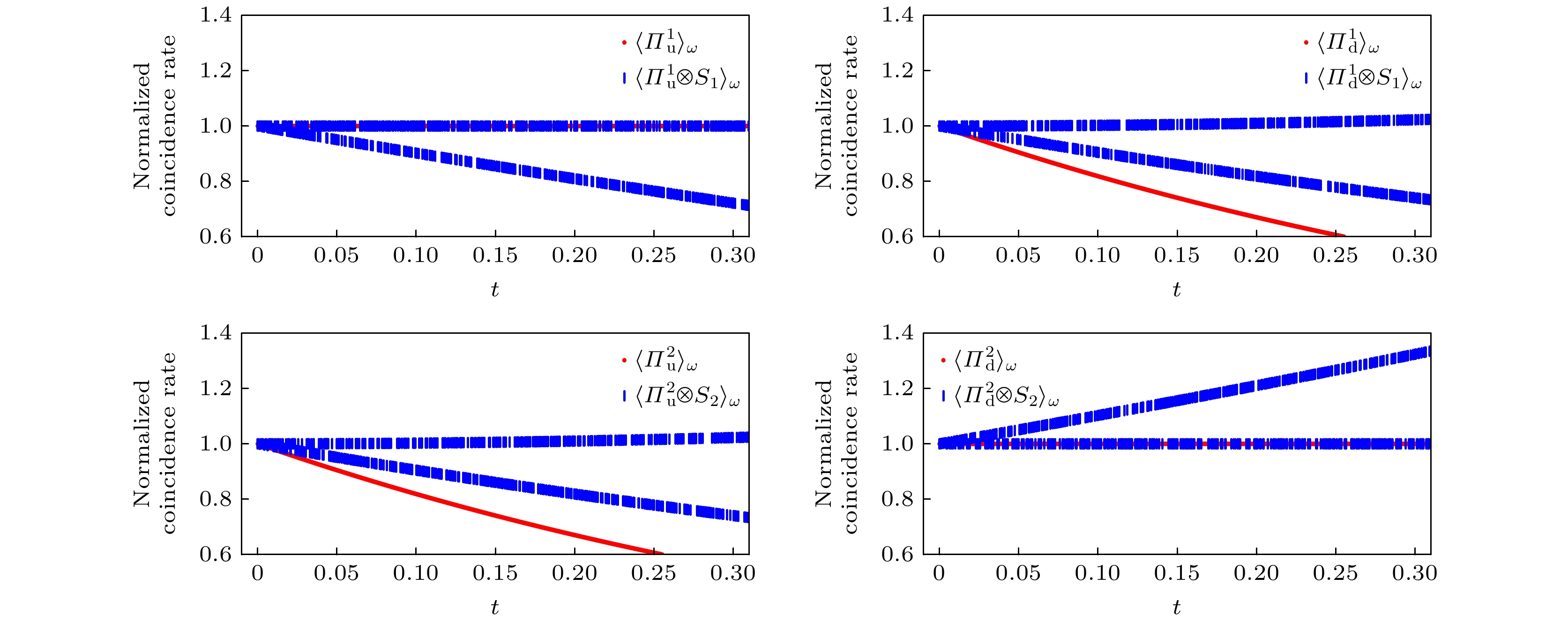
图 3 在α取$ {\pi}/{4} $时, 两个原子的归一化符合率N(t)随t的变化趋势. 左图为原子1的数据, 右图为原子2的数据. 因N(t)与t存在函数关系, 所以此处直接用弱值符号代表相关可观测量的N(t)
Figure 3. When α takes $ {\pi}/{4} $, the normalized coincidence rate N(t) of two atoms varies with t. The left image shows the data for atom-1, and the right image shows the data for atom-2. Due to the functional relationship between N(t) and t, weak values are directly used here to represent the N(t) of the relevant observables.
-
[1] Aharonov Y, Popescu S, Rohrlich D, Skrzypczyk P 2013 New J. Phys. 15 113015
 Google Scholar
Google Scholar
[2] Denkmayr T, Geppert H, Sponar S, Lemmel H, Matzkin A, Tollaksen J, Hasegawa Y 2014 Nat. Commun. 5 4492
 Google Scholar
Google Scholar
[3] Danner A, Geerits N, Lemmel H, Wagner R, Sponar S, Hasegawa Y 2024 Commun. Phys. 7 14
 Google Scholar
Google Scholar
[4] Kim Y, Im D G, Kim Y S, Han S W, Moon S, Kim Y H, Cho Y W 2021 npj. Quantum. Inf. 7 13
 Google Scholar
Google Scholar
[5] Das D, Sen U 2021 Phys. Rev. A 103 012228
 Google Scholar
Google Scholar
[6] Richter M, Dziewit B, Dajka J 2018 Adv. Math. Phys. 2018 7060586
 Google Scholar
Google Scholar
[7] Li J K, Sun K, Wang Y, Hao Z Y, Liu Z H, Zhou J, Fan X Y, Chen J L, Xu J S, Li C F, Guo G C 2023 Light Sci. Appl. 12 18
 Google Scholar
Google Scholar
[8] Wagner R, Kersten W, Lemmel H, Sponar S, Hasegawa Y 2023 Sci. Rep. 13 3865
 Google Scholar
Google Scholar
[9] Ghoshal A, Sau S, Das D, Sen U 2023 Phys. Rev. A 107 052214
 Google Scholar
Google Scholar
[10] Hance J R, Ladyman J, Rarity J 2024 New J. Phys. 26 073038
 Google Scholar
Google Scholar
[11] Das D, Pati A K 2020 New J. Phys. 22 063032
 Google Scholar
Google Scholar
[12] Liu Z H, Pan W W, Xu X Y, Yang M, Zhou J, Luo Z Y, Sun K, Chen J L, Xu J S, Li C F, Guo G C 2020 Nat. Commun. 11 3006
 Google Scholar
Google Scholar
[13] Aharonov Y, Albert D Z, Vaidman L 1988 Phys. Rev. Lett. 60 1351
 Google Scholar
Google Scholar
[14] Ritchie N W M, Story J G, Hulet R G 1991 Phys. Rev. Lett. 66 1107
 Google Scholar
Google Scholar
[15] Bloch I, Zoller P 2006 New J. Phys. 8 E02
 Google Scholar
Google Scholar
[16] Puentes G 2015 J. Phys. B. 48 245301
 Google Scholar
Google Scholar
[17] Mao Y, Chaudhary M, Kondappan M, Shi J, Ilo-Okeke E O, Ivannikov V, Byrnes T 2023 Phys. Rev. Lett. 131 110602
 Google Scholar
Google Scholar
[18] Aharonov Y, Bergmann P G, Lebowitz J L 1964 Phys. Rev. 134 B1410
 Google Scholar
Google Scholar
[19] Wheeler J A 1978 Mathematical Foundations of Quantum Theory (Amsterdam: Elsevier) pp9–48
[20] Witten E 2018 Rev. Mod. Phys. 90 045003
 Google Scholar
Google Scholar
[21] Amico L, Fazio R, Osterloh A, Vedral V 2008 Rev. Mod. Phys. 80 517
 Google Scholar
Google Scholar
[22] Horodecki R, Horodecki P, Horodecki M, Horodecki K 2009 Rev. Mod. Phys. 81 865
 Google Scholar
Google Scholar
[23] Wick G C 1954 Phys. Rev. 96 1124
 Google Scholar
Google Scholar
[24] Landsman N, van Weert C 1987 Phys. Rep. 145 141
 Google Scholar
Google Scholar
[25] Xu J S, Sun K, Han Y J, Li C F, Pachos J K, Guo G C 2016 Nat. Commun. 7 13194
 Google Scholar
Google Scholar
[26] Dressel J, Malik M, Miatto F M, Jordan A N, Boyd R W 2014 Rev. Mod. Phys. 86 307
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 796
- PDF Downloads: 37
- Cited By: 0














 DownLoad:
DownLoad: