-
In recent years, the cavity quantum photomechanics has been developed rapidly, and played a very important role in quantum information processing, quantum basic principle verification, and high-precision measurement. The kinds of quantum mechanical behaviors have also been explored and discovered in the study of cavity mechanics. By placing the Kerr medium in the system, quantum nonlinearity is introduced into the optomechanical system. Quantum phase transition is a relatively important part in the research of condensed matter physics. Since Dicke quantum phase transition was successfully observed experimentally, the problem of quantum phase transition in the optical cavity has attracted more attention. The spin-coherent-state variation method and the Holstein-Primakoff transformation are used to theoretically calculate the ground state energy functional, and the rich structure of the macroscopic multi-particle quantum state is given by adjusting the parameters. The quantum phase transition evolution equation describes the relationship between each phase and the time of generating a new phase when reaching the critical phase transition point. At the same time, the mode squeezing of multi-mode hybrid optomechanical system has also became one of the basic problems of quantum mechanical behavior in cavity quantum dynamics. In this article, we explore the quantum dynamics of optomechanical devices including single-cavity and dual-cavities. We find that the system will undergo a dynamic phase transition, which is similar to the Dicke-Hepp-Lieb superradiant type phase transition, and a new dynamic critical point appears in the coupling between the momentum quadratures of the two optical fields. By manipulating the coupling parameters, we can achieve selective energy exchange between any two modes and the critical coupling point corresponds to selective energy exchange. Mode squeezing, which is easy to measure by applying the quantum uncertainty relationship, is also revealed and consistent with selective energy exchange. The study of coordinate and momentum variances gives us the revelation that the compressed orthogonal variables are the most suitable for measurement because of the small quantum noise. In fact, phononic modes can store energy in a longer duration, while photonic modes can transfer energy in a long distance. This phenomenon makes the hybrid optomechanical cavities useful in the next-generation quantum communications and quantum information processing units. -
Keywords:
- dual-cavities optomechanical system /
- phase transition /
- selective energy exchange /
- mode squeezing
[1] Marquardt F, Girvin S M 2009 Physics 2 40
Google Scholar
[2] Brennecke F, Ritter S, Donner T, Esslingert T 2008 Science 322 235
Google Scholar
[3] Safavi-Naeini A H, Mayer Alegre T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 478 89
Google Scholar
[4] Verhagen E, Deléglise S, Weis S, Schliesser A, Kippenberg T J 2012 Nature 482 63
Google Scholar
[5] Kumar T, Bhattacherjee A, ManMohan 2010 Physical Review A 81 013835
Google Scholar
[6] Thompson J D, Zwickl B M, Jayich A M, Marquardt F, Girvin S M, Harris J G E 2008 Nature 452 900
[7] Antonio D, Czaplewski D A, Guest J R, López D 2015 Phys. Rev. Lett. 114 034103
Google Scholar
[8] Stannigel K, Komar P, Habraken S J M, Bennett S D, Lukin P, Zoller P, Rabl P 2012 Phys. Rev. Lett. 109 013603
Google Scholar
[9] Chang D E, Safavi-Naeini A H, Hafezi M, Painter O 2011 New Journal of Physics 13 023003
Google Scholar
[10] Emary C, Brandes T 2003 Phys. Rev. E 67 066203
Google Scholar
[11] 刘妮, 王建芬, 梁九卿 2020 69 064202
Google Scholar
Liu N, Wang J F, Liang J Q 2020 Acta Phys. Sin. 69 064202
Google Scholar
[12] Zhao X Q, Liu N, Bai X M, Liang J Q 2017 Ann. Phys 378 448
Google Scholar
[13] Xuereb A, Barbieri M, Paternostro M 2012 Physical Review A 86 013809
Google Scholar
[14] Xu K, Sun Z, Liu W, Zhang Y, Li H, Dong H, Ren W, Zhang P, Nori F, Zheng D, Fan H, Wang H 2020 Science Advances 6 eaba4935
Google Scholar
[15] Yan B, Chernyak V Y, Zurek W H, Sinitsyn N A 2021 Phys. Rev. Lett. 126 070602
Google Scholar
[16] Lerose A, Marino J, Zunkovic B, Gambassi A, Silva A 2018 Phys. Rev. Lett. 120 130603
Google Scholar
[17] Nicola S, Michailidis A, Serbyn M 2021 Phys. Rev. Lett 126 040602
Google Scholar
[18] Korolkova N, Perina J 1997 Optics Communications 136 135
Google Scholar
[19] Korolkova N, Perina J 1997 Journal of Modern Optics 44 1525
[20] Gröblacher S, Hammerer K, Vanner M R, Aspelmeyer M 2009 Nature 460 724
Google Scholar
-
图 1 光机械腔系统, 由频率为
${\omega _{\rm{0}}}$ 的光学模(用运算符a表示), 频率为${\omega _{\rm{m}}}$ 的机械模(用运算符b表示)和频率为${\omega _{\rm{L}}}$ (振幅为μ)的驱动场组成, 光腔与机械振子之间的耦合系数为gFig. 1. An optomechanical cavity consisting of the optical mode (the frequency
${\omega _{\rm{0}}}$ ) denoted by a, the mechanical mode b (the frequency${\omega _{\rm{m}}}$ ) and an pair of optical drivings (the frequency${\omega _{\rm{L}}}$ and the amplitude μ) with the coupling strength g.
图 2 在给定条件
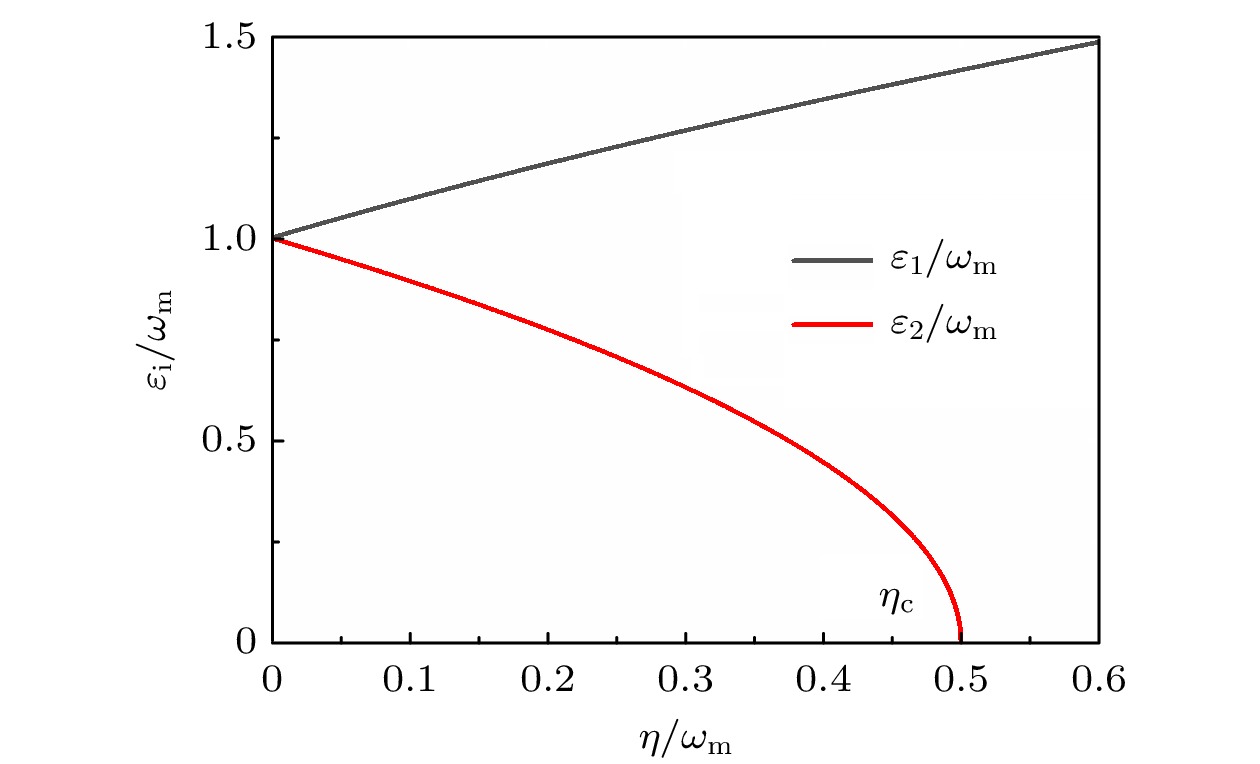
$\omega = {\omega _{\rm{m}}}$ 下, 激发能量${\varepsilon _i}/{\omega _{\rm{m}}}$ 随耦合参数$\eta /{\omega _{\rm{m}}}$ 的变化Fig. 2. Variation of the excitation energy
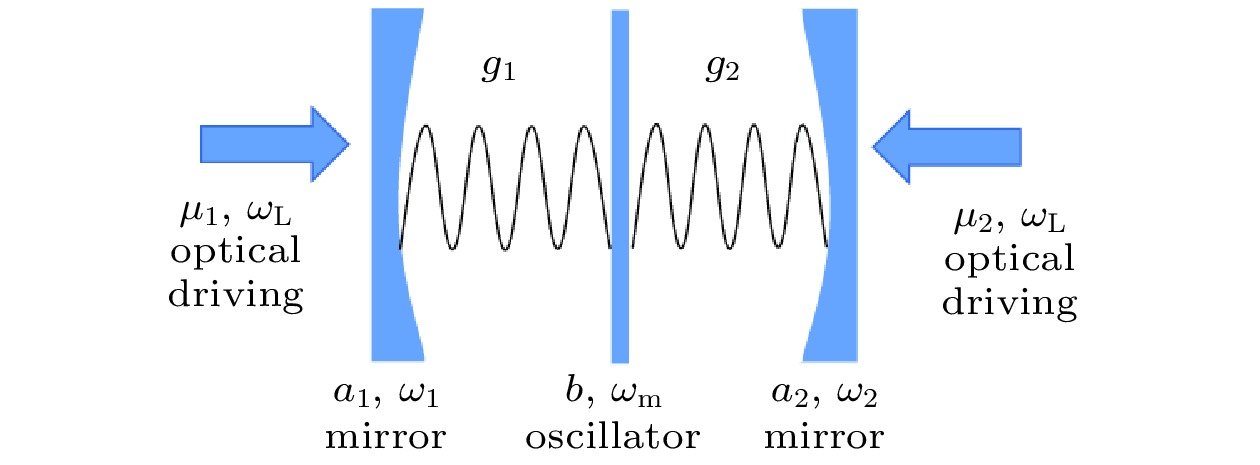
${\varepsilon _i}/{\omega _{\rm{m}}}$ with respect to the coupling parameter$\eta /{\omega _{\rm{m}}}$ in the case of$\omega = {\omega _{\rm{m}}}$ .
图 3 双光腔光机械系统, 由频率分别为
${\omega _{\rm{1}}}$ 和${\omega _{\rm{2}}}$ 的光学模(用运算符${a_1}$ 和${a_2}$ 表示), 频率为${\omega _{\rm{m}}}$ 的机械模(用运算符b表示)和频率为${\omega _{\rm{L}}}$ (振幅为${\mu _i}$ )的两束对打的驱动场组成, 两模光腔与机械振子之间的耦合系数分别为${g_1}$ 和${g_2}$ Fig. 3. A double-optical cavtiy optomechanical system consisting of two optical mode (the frequencies
${\omega _{\rm{1}}}$ and${\omega _{\rm{2}}}$ ) denoted by${a_1}$ and${a_2}$ , the mechanical mode b (the frequency${\omega _{\rm{m}}}$ ) and an pair of optical drivings (the frequency${\omega _{\rm{L}}}$ and the amplitude${\mu _i}$ ) with the coupling strength${g_1}$ and${g_2}$ .
图 4 激发能量
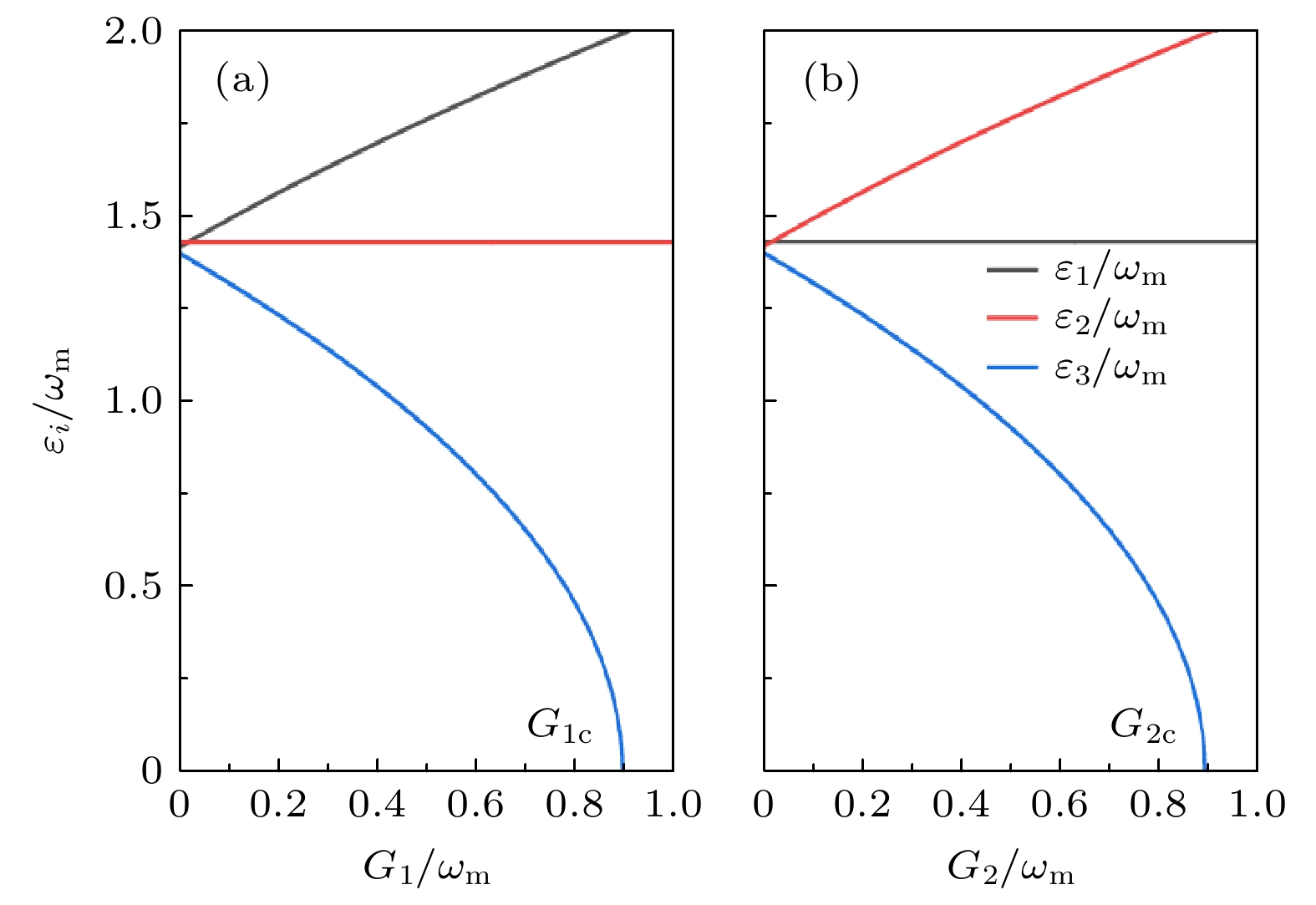
${\varepsilon _i}/{\omega _{\rm{m}}}$ 随耦合参数 (a)${G_1}/{\omega _{\rm{m}}}$ 和(b)${G_2}/{\omega _{\rm{m}}}$ 的变化, 给定的参数是${\varOmega _1} = {\varOmega _2} = {\omega _{\rm{m}}}$ Fig. 4. Variation of the excitation energy
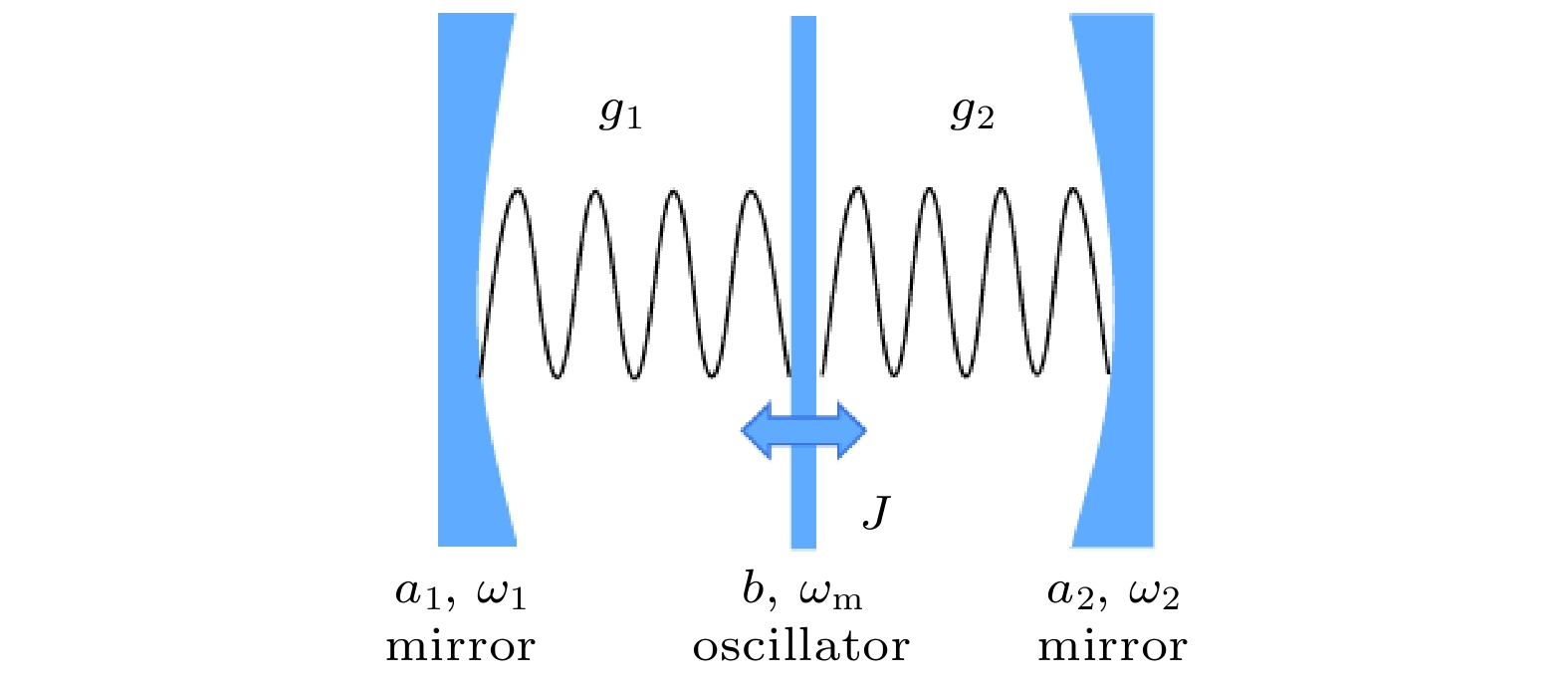
${\varepsilon _i}/{\omega _{\rm{m}}}$ with respect to the coupling parameters (a)${G_1}/{\omega _{\rm{m}}}$ and (b)${G_2}/{\omega _{\rm{m}}}$ . The given parameters are${\varOmega _1} = {\varOmega _2} = {\omega _{\rm{m}}}$ .
图 5 双光腔光机械系统, 由频率分别为
${\omega _{\rm{1}}}$ 和${\omega _{\rm{2}}}$ 的光学模(用运算符${a_1}$ 和${a_2}$ 表示)和频率为${\omega _{\rm{m}}}$ 的机械模(用运算符b表示)组成, 两模光腔与机械振子之间的耦合系数分别为${g_1}$ 和${g_2}$ , 两腔间与机械振子的耦合系数为JFig. 5. A double-optical cavtiy optomechanical system consisting of two optical mode (the frequencies
${\omega _{\rm{1}}}$ and${\omega _{\rm{2}}}$ ) denoted by${a_1}$ and${a_2}$ and the mechanical mode b with the coupling strength${g_1}$ ,${g_2}$ andJ.
图 6 激发能量
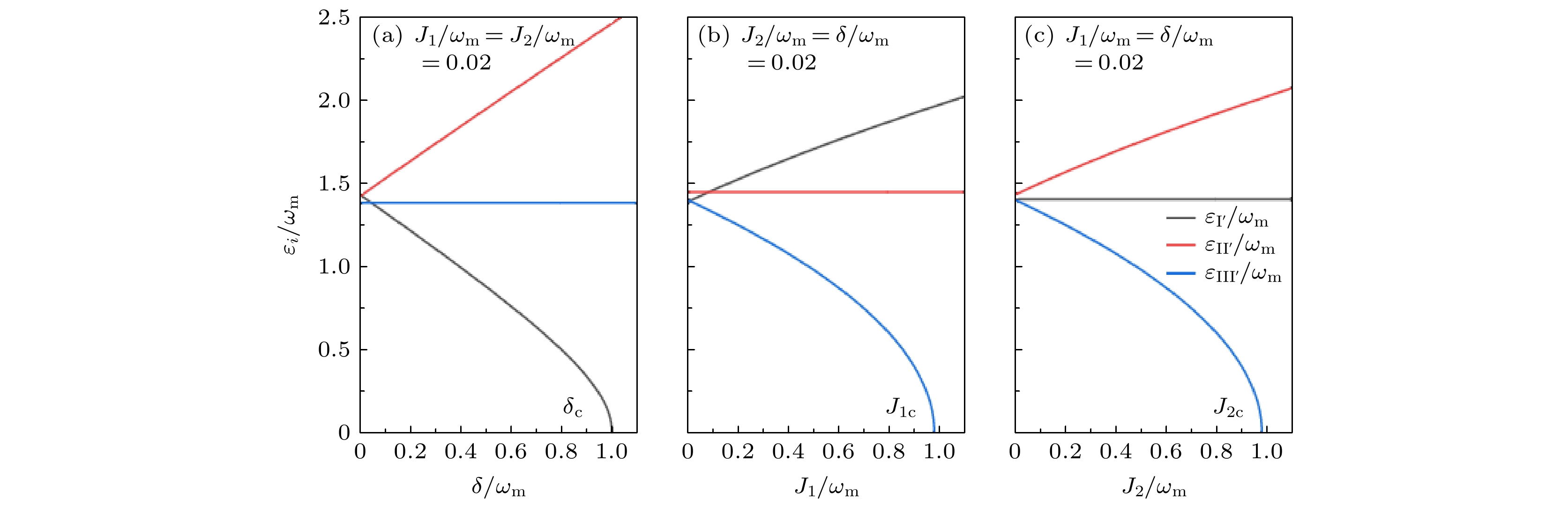
${\varepsilon _i}/{\omega _{\rm{m}}}$ 随耦合参数 (a)$\delta /{\omega _{\rm{m}}}$ , (b)${J_1}/{\omega _{\rm{m}}}$ 和(c)${J_2}/{\omega _{\rm{m}}}$ 的变化, 给定的参数是${\varOmega _1} = {\varOmega _2} = {\omega _{\rm{m}}}$ Fig. 6. Variation of the excitation energy
${\varepsilon _i}/{\omega _{\rm{m}}}$ with respect to the coupling parameters (a)$\delta /{\omega _{\rm{m}}}$ , (b)${J_1}/{\omega _{\rm{m}}}$ and (c)${J_2}/{\omega _{\rm{m}}}$ . The given parameters are${\varOmega _1} = {\varOmega _2} = {\omega _{\rm{m}}}$ .
图 7 在
$ \omega = {\omega _{\rm{m}}}$ 下, 压缩方差$ {\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ 和$ {\left( {\Delta {p_{\alpha} }} \right)^2}/{\omega _{\rm{m}}}$ 随耦合参数$ \eta /{\omega _{\rm{m}}}$ 的变化Fig. 7. Plot of the squeezing variances
${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ (solid line) and${\left( {\Delta {p_{\alpha} }} \right)^2}/{\omega _{\rm{m}}}$ (dashed line) as a function of$\eta /{\omega _{\rm{m}}}$ in the case of$\omega = {\omega _{\rm{m}}}$ .
图 8 在
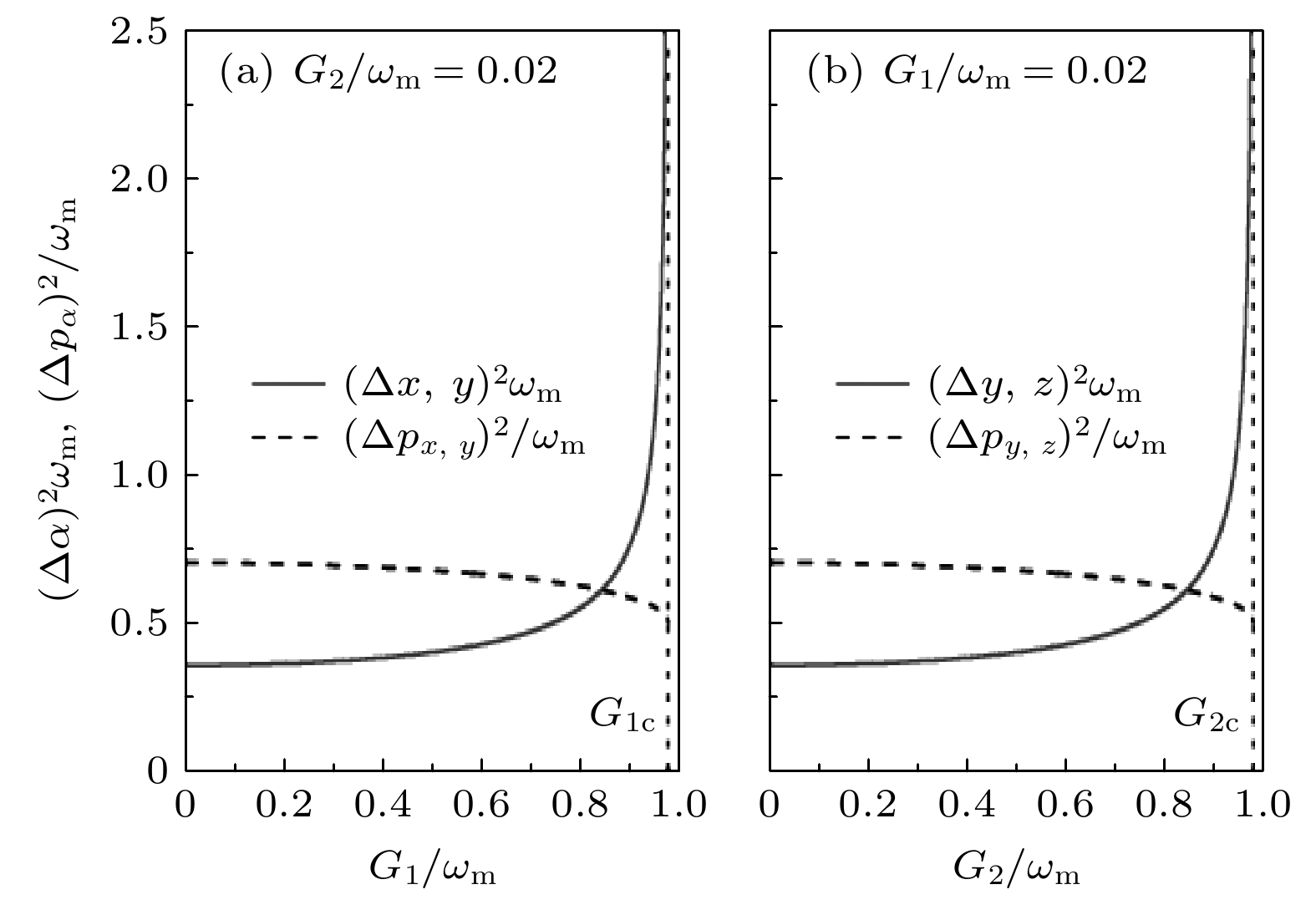
${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ 下, 压缩方差${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ 和${\left( {\Delta {p_{\alpha} }} \right)^2}/{\omega _{\rm{m}}}$ 随耦合参数(a)${G_1}/{\omega _{\rm{m}}}$ 和(b)${G_2}/{\omega _{\rm{m}}}$ 的变化Fig. 8. Plot of the squeezing variances
${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ (solid line) and${\left( {\Delta {p_{\alpha} }} \right)^2}/{\omega _{\rm{m}}}$ (dashed line) as a function of (a)${G_1}/{\omega _{\rm{m}}}$ and (b)${G_2}/{\omega _{\rm{m}}}$ .
图 9 在
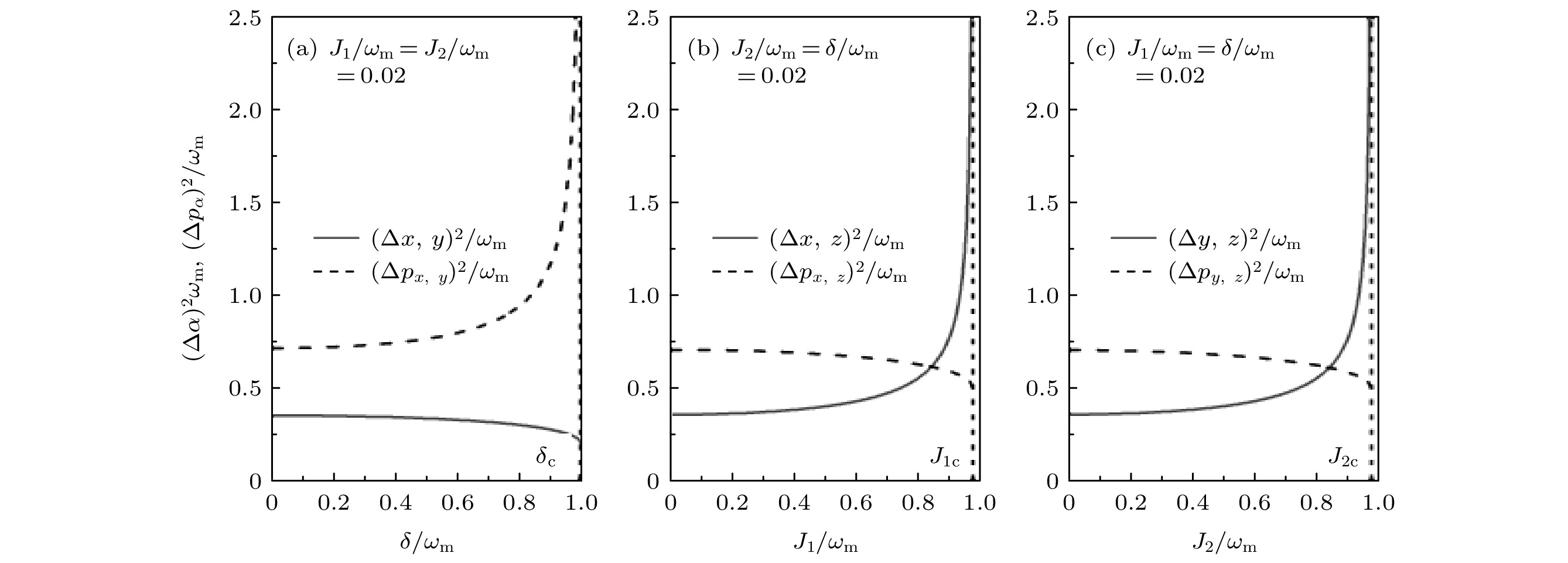
$\omega = {\omega _{\rm{m}}}$ 下, 压缩方差${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ (实线)和${\left( {\Delta {p_{\alpha} }} \right)^2}/{\omega _{\rm{m}}}$ (虚线)随耦合参数 (a)$\delta /{\omega _{\rm{m}}}$ , (b)${J_1}/{\omega _{\rm{m}}}$ 和(c)${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ 的变化Fig. 9. Plot of the squeezing variances
${\left( {\Delta \alpha } \right)^2}{\omega _{\rm{m}}}$ (solid line) and${\left( {\Delta {p_{\alpha} }} \right)^2}/{\omega _{\rm{m}}}$ (dashed line) as a function of (a)$\delta /{\omega _{\rm{m}}}$ , (b)${J_1}/{\omega _{\rm{m}}}$ , (c)${J_2}/{\omega _{\rm{m}}}$ in the case of$\omega = {\omega _{\rm{m}}}$ . -
[1] Marquardt F, Girvin S M 2009 Physics 2 40
Google Scholar
[2] Brennecke F, Ritter S, Donner T, Esslingert T 2008 Science 322 235
Google Scholar
[3] Safavi-Naeini A H, Mayer Alegre T P, Chan J, Eichenfield M, Winger M, Lin Q, Hill J T, Chang D E, Painter O 2011 Nature 478 89
Google Scholar
[4] Verhagen E, Deléglise S, Weis S, Schliesser A, Kippenberg T J 2012 Nature 482 63
Google Scholar
[5] Kumar T, Bhattacherjee A, ManMohan 2010 Physical Review A 81 013835
Google Scholar
[6] Thompson J D, Zwickl B M, Jayich A M, Marquardt F, Girvin S M, Harris J G E 2008 Nature 452 900
[7] Antonio D, Czaplewski D A, Guest J R, López D 2015 Phys. Rev. Lett. 114 034103
Google Scholar
[8] Stannigel K, Komar P, Habraken S J M, Bennett S D, Lukin P, Zoller P, Rabl P 2012 Phys. Rev. Lett. 109 013603
Google Scholar
[9] Chang D E, Safavi-Naeini A H, Hafezi M, Painter O 2011 New Journal of Physics 13 023003
Google Scholar
[10] Emary C, Brandes T 2003 Phys. Rev. E 67 066203
Google Scholar
[11] 刘妮, 王建芬, 梁九卿 2020 69 064202
Google Scholar
Liu N, Wang J F, Liang J Q 2020 Acta Phys. Sin. 69 064202
Google Scholar
[12] Zhao X Q, Liu N, Bai X M, Liang J Q 2017 Ann. Phys 378 448
Google Scholar
[13] Xuereb A, Barbieri M, Paternostro M 2012 Physical Review A 86 013809
Google Scholar
[14] Xu K, Sun Z, Liu W, Zhang Y, Li H, Dong H, Ren W, Zhang P, Nori F, Zheng D, Fan H, Wang H 2020 Science Advances 6 eaba4935
Google Scholar
[15] Yan B, Chernyak V Y, Zurek W H, Sinitsyn N A 2021 Phys. Rev. Lett. 126 070602
Google Scholar
[16] Lerose A, Marino J, Zunkovic B, Gambassi A, Silva A 2018 Phys. Rev. Lett. 120 130603
Google Scholar
[17] Nicola S, Michailidis A, Serbyn M 2021 Phys. Rev. Lett 126 040602
Google Scholar
[18] Korolkova N, Perina J 1997 Optics Communications 136 135
Google Scholar
[19] Korolkova N, Perina J 1997 Journal of Modern Optics 44 1525
[20] Gröblacher S, Hammerer K, Vanner M R, Aspelmeyer M 2009 Nature 460 724
Google Scholar
下载:
计量
- 文章访问数: 4893
- PDF下载量: 87
- 被引次数: 0
