-
Utilizing the principle of the Feynman ratchet, it is possible to rectify the random motion into directed flow of particles under a nonequilibrium environment. In this paper, an experimental setup for a dusty plasma metal straight ratchet is designed to create an asymmetric plasma environment along the ratchet channel, enabling a controllable rectification of micron-sized dust particles. Monodispersed dust particles can form a directional flow in the ratchet channel, and the transport direction could be precisely controlled by adjusting the discharge power and the gas pressure. Research on the transport of dust particles of varying sizes proves that the rectification effect is universal. To reveal the rectification mechanism of dust particles, a fluid model of plasma is employed to calculate the two-dimensional distribution of plasma parameters within the ratchet channel. Further research through Langevin simulation shows that dust particles experience ratchet potentials with distinct asymmetric orientations at different suspension heights within the ratchet channel, leading to different transport directions. The results of this paper provide a theoretical and experimental foundation for further achieving the separation of bi-disperse particles in dusty plasma metal straight ratchets.
-
Keywords:
- dusty plasma /
- ratchet /
- rectification
-
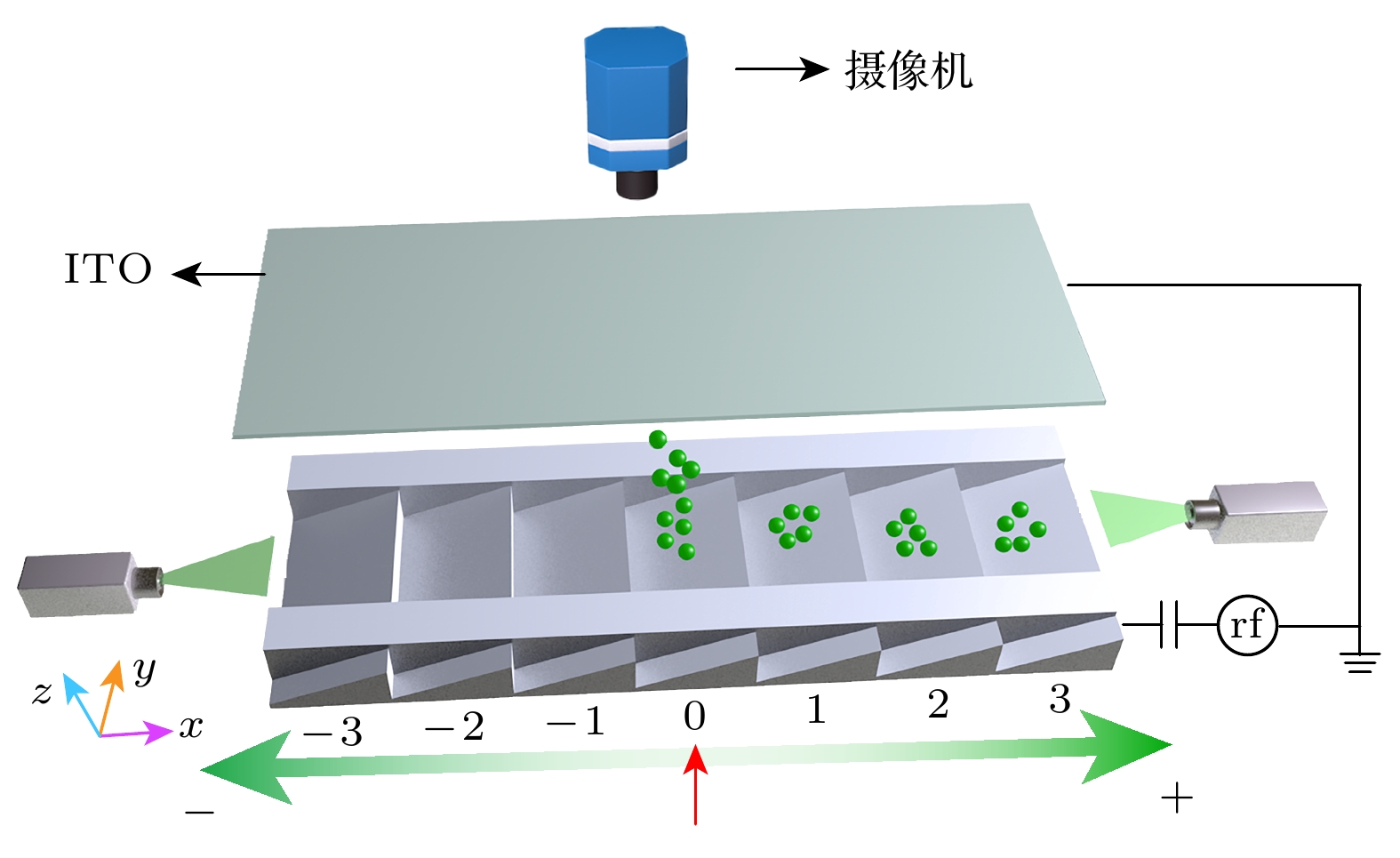
图 1 尘埃等离子体金属直棘轮实验示意图. 下极板的上表面由30个锯齿槽构成(图中只显示7个), 结合两个金属条, 形成沿x方向的棘轮通道. 单分散尘埃颗粒由棘轮通道中部的“0”号锯齿槽投入, 在特定条件沿棘轮通道会产生定向运动
Figure 1. Schematic diagram of the dusty plasma metal straight ratchet. The upper surface of the lower electrode is composed of 30 sawteeth (shown only 7 sawteeth), Combined with two metal strips, a ratchet channel along the x direction is formed. Monodispersed dust particles are introduced into the “0” sawtooth at the middle of the ratchet channel, which exhibit directional flow along the ratchet channel under specific conditions.
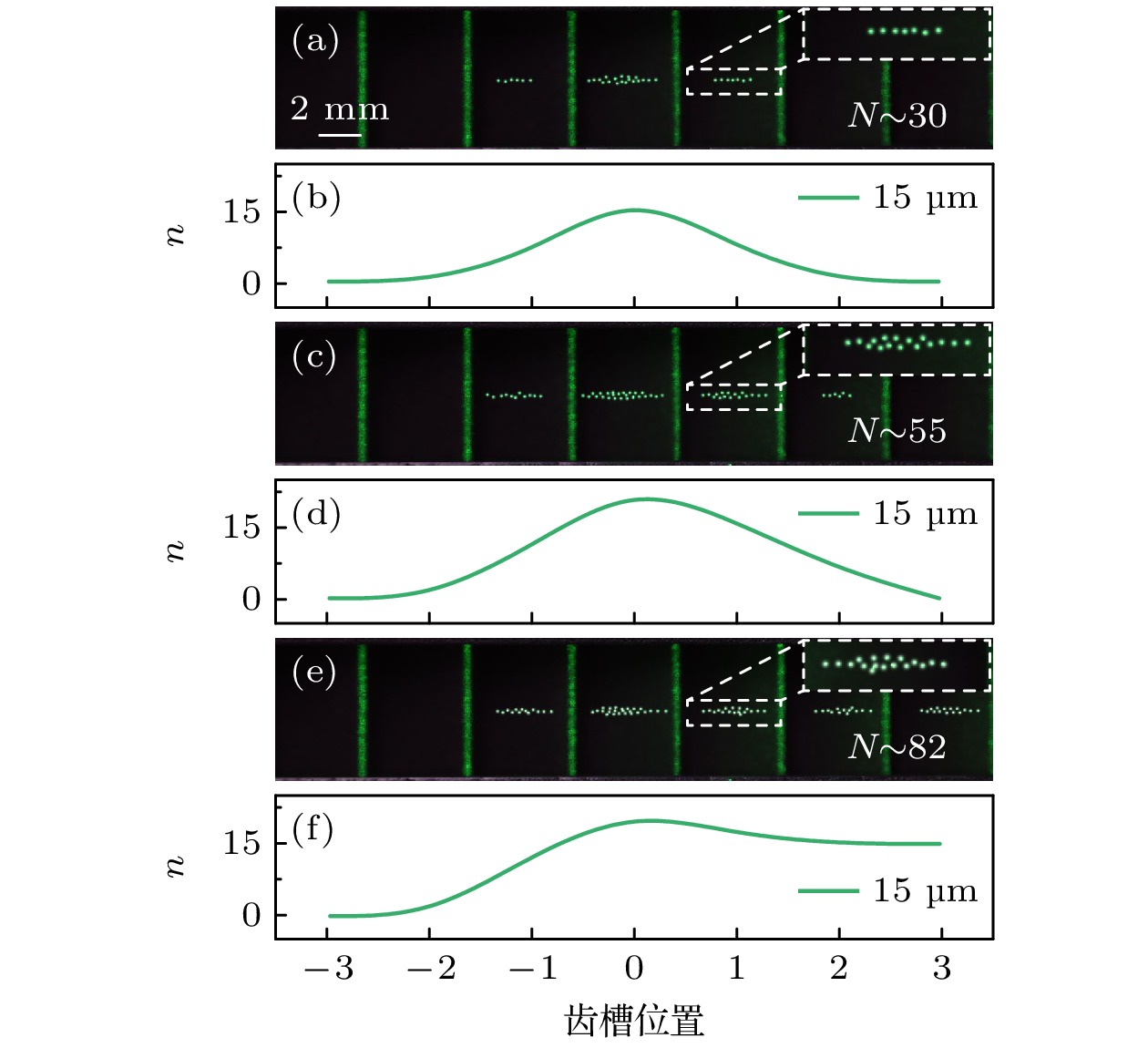
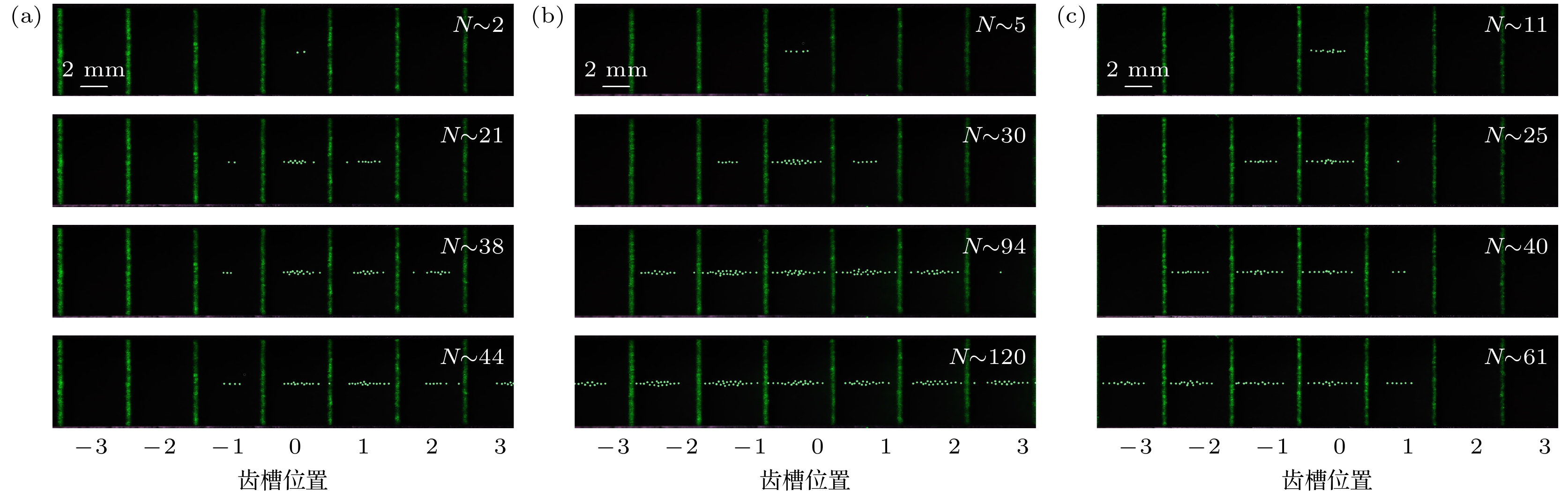
图 2 尘埃等离子体金属直棘轮中尘埃颗粒的正流. (a)、(c)和(e)表示随着投入尘埃颗粒数的增加, 尘埃颗粒在棘轮通道中的空间分布逐渐向右扩展, 形成正向整流. 图中N代表棘轮通道中尘埃颗粒总数量. (b)、(d)和(f)为对应的不同锯齿槽位置处颗粒数n的分布情况. 放电气压为$ {p=35 \ {\text{Pa}}} $, 放电功率为$ {P=40 \ {\text{W}}} $, 颗粒直径为15 µm. 图中尘埃颗粒做了亮度增强处理
Figure 2. Positive flow of dust particles in the dusty plasma metal straight ratchet. (a), (c), and (e) show that as the number of introduced dust particles increases, the spatial distribution of dust particles in the ratchet channel gradually expands to the right, forming a positive flow. N represents the total number of dust particles in the ratchet channel. (b), (d), and (f) show the corresponding distributions of particle number n along the ratchet channel. Gas pressure $ {p=35 \ {\text{Pa}}} $, discharge power $ {P=40 \ {\text{W}}} $, particle diameter is 15 µm. Brightness of dust particles in images is enhanced.
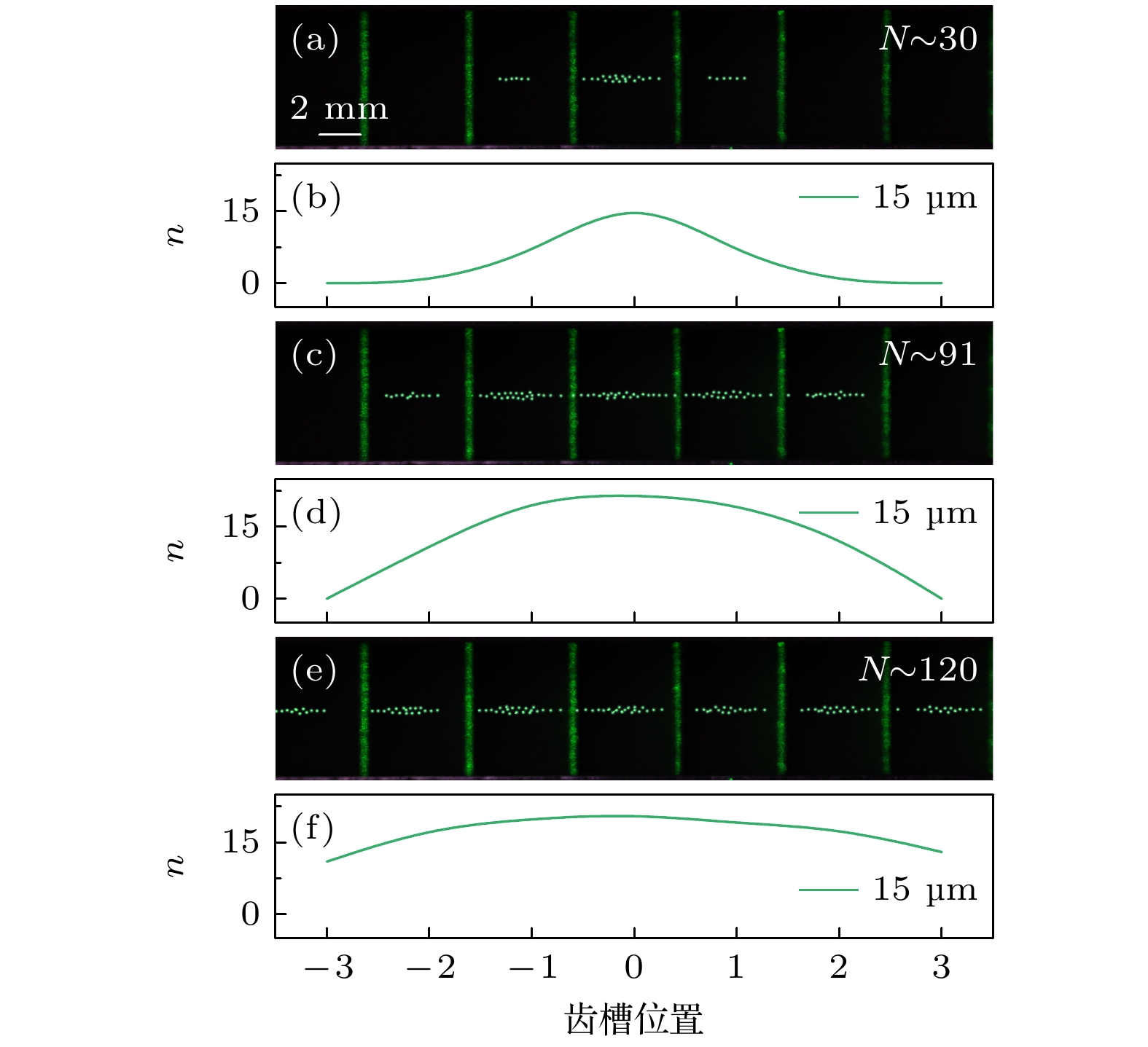
图 3 尘埃等离子体金属直棘轮中尘埃颗粒的无净位移运动. (a)、(c)和(e)表示随着投入尘埃颗粒数的增加, 尘埃颗粒在棘轮通道中的空间分布逐渐向两侧同时扩展. 图中N代表棘轮通道中尘埃颗粒总数量. (b)、(d)和(f)为对应的不同锯齿槽位置处颗粒数n的分布情况. 放电气压为$ {p=35 \ {\text{Pa}}} $, 放电功率为$ {P=25 \ {\text{W}}} $, 颗粒直径为15 µm. 图中尘埃颗粒做了亮度增强处理
Figure 3. None net flow of dust particles in the dusty plasma metal straight ratchet. (a), (c), and (e) show that as the number of introduced dust particles increases, the spatial distribution of dust particles in the ratchet channel gradually expands to both sides simultaneously. N represents the total number of dust particles in the ratchet channel. (b), (d), and (f) show the corresponding distributions of the particle number n along the ratchet channel. Gas pressure $ {p=35 \ {\text{Pa}}} $, discharge power $ {P=25 \ {\text{W}}} $, particle diameter is 15 µm. Brightness of dust particles in images is enhanced.
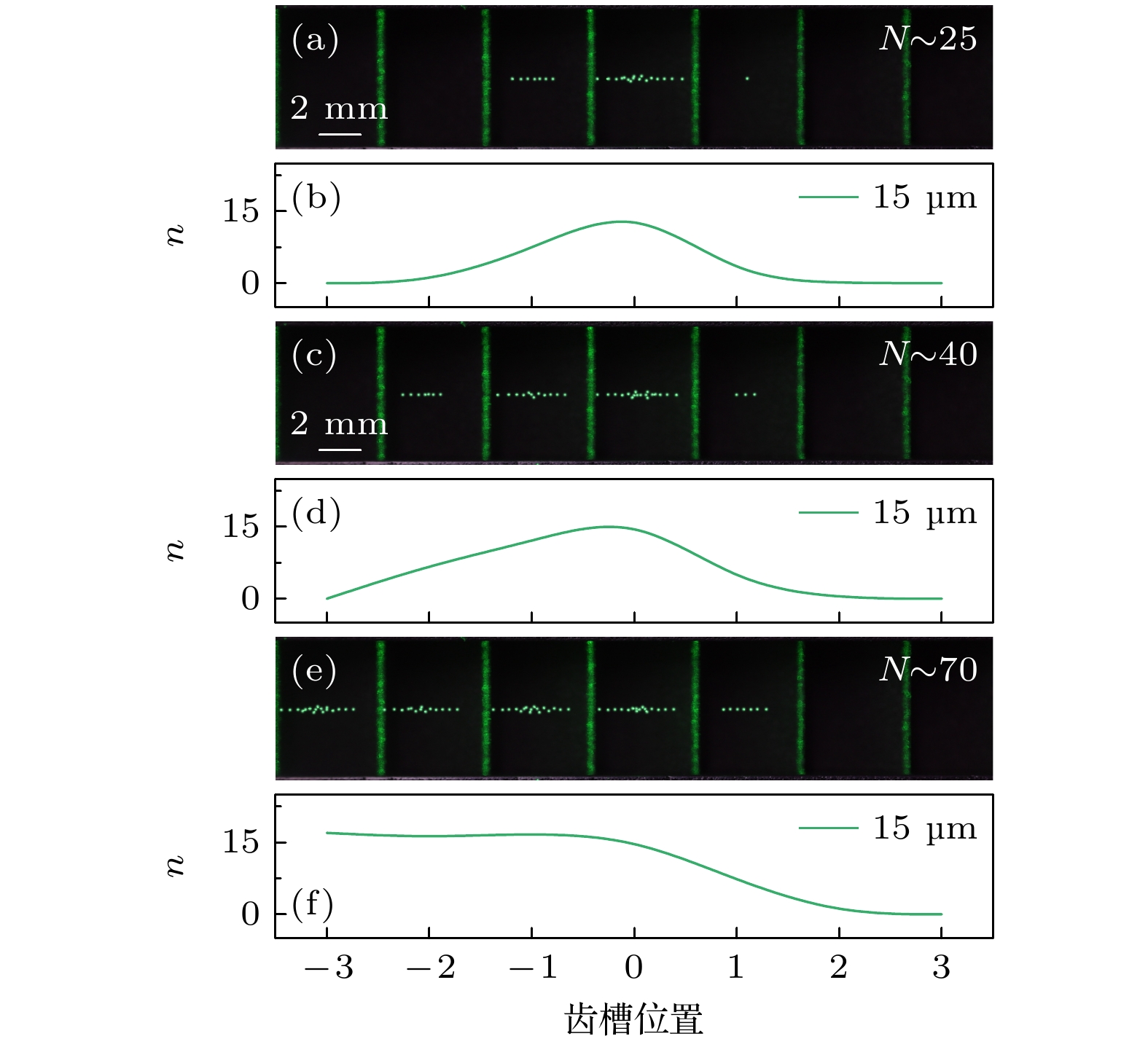
图 4 尘埃等离子体金属直棘轮中尘埃颗粒的逆向整流. (a)、(c)和(e)表示随着投入尘埃颗粒数的增加, 尘埃颗粒在棘轮通道中的空间分布逐渐向左扩展, 形成逆向整流. 图中N代表棘轮通道中尘埃颗粒总数量. (b)、(d)和(f)为对应的不同锯齿槽位置处颗粒数n的分布情况. 放电气压为$ {p=35 \ {\text{Pa}}} $, 放电功率为$ {P=15 \ {\text{W}}} $, 颗粒直径为15 µm. 图中尘埃颗粒做了亮度增强处理
Figure 4. Negative flow of dust particles in the dusty plasma metal straight ratchet. (a), (c), and (e) show that as the number of introduced dust particles increases, the spatial distribution of dust particles in the ratchet channel gradually expands to the left, forming a negative flow. N represents the total number of dust particles in the ratchet channel. (b), (d), and (f) show the corresponding distributions of the particle number n along the ratchet channel. Gas pressure $ {p=35 \ {\text{Pa}}} $, discharge power $ {P=15 \ {\text{W}}} $, particle diameter is 15 µm. Brightness of dust particles in images is enhanced.
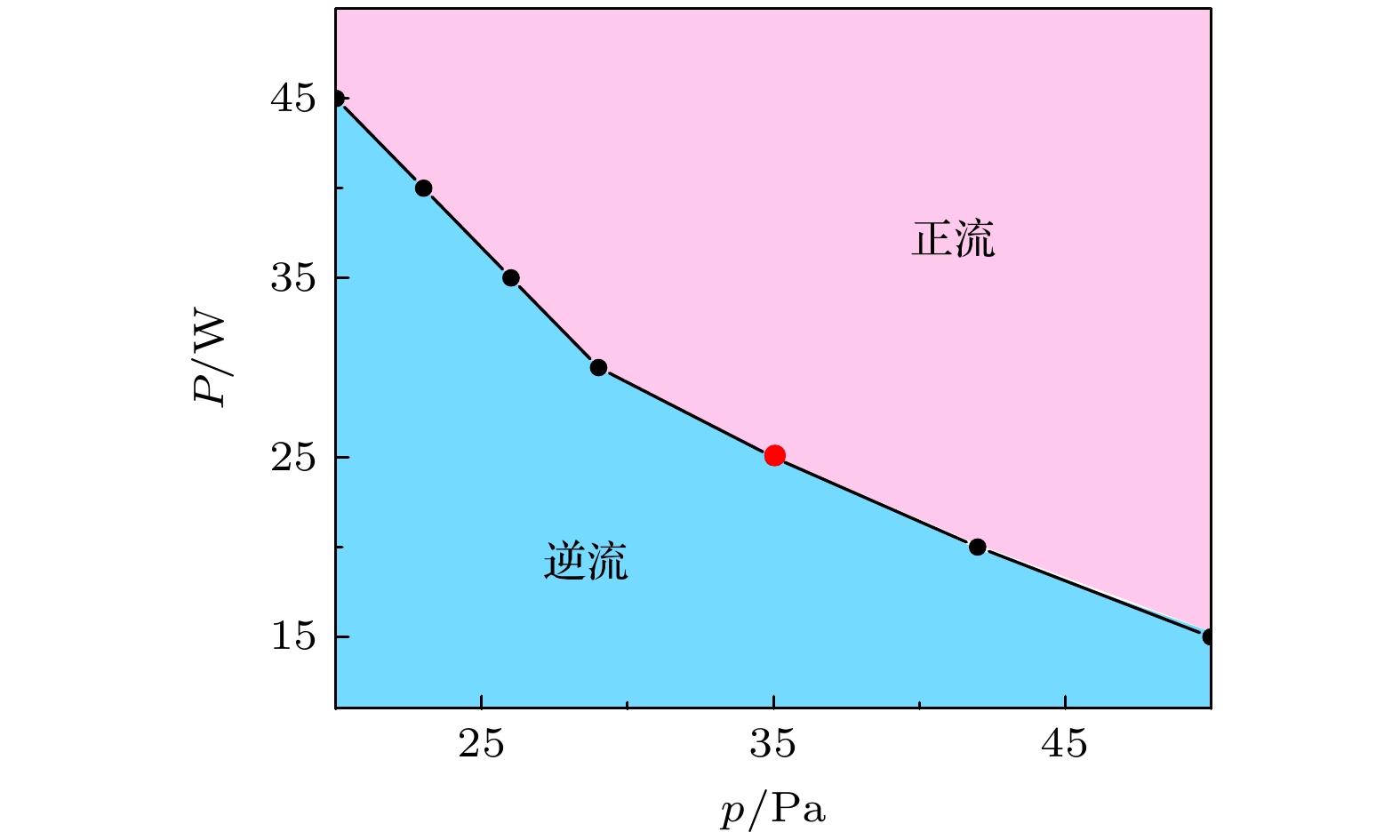
图 5 不同放电气压和功率实验条件下尘埃颗粒整流的相图. 黑色曲线表示尘埃颗粒在棘轮通道中呈现正流和逆流的临界线. 颗粒直径为15 µm
Figure 5. Phase diagram of the directional flow of dust particles under different gas pressure and power experimental conditions. The black curve represents the critical line separating the positive and negative flows of dust particles in the ratchet channel. Particle diameter is 15 µm.
图 6 同一放电条件下不同尺寸尘埃颗粒在棘轮通道内的运动情况. (a)表示直径为10 µm的尘埃颗粒随着投入颗粒数目的增加逐渐形成正流; (b)表示直径为15 µm的尘埃颗粒在棘轮通道中没有形成定向输运; (c)表示直径为24 µm的尘埃颗粒随着撒入颗粒数目的增加逐渐形成逆流. 放电气压$ {p=35 \ {\text{Pa}}} $, 功率$ {P=25 \ {\text{W}}} $. 图中尘埃颗粒做了亮度增强处理
Figure 6. The flow of dust particles with different sizes in the ratchet channel under same discharge conditions. (a)indicates that dust particles with a diameter of 10 µm gradually form a positive flow as the number of introduced dust particles increases; (b) indicates that dust particles with a diameter of 15µm do not form a directional flow in the ratchet channel; (c) indicates that dust particles with a diameter of 24µm gradually form a negative flow as the number of introduced particles increases. Gas pressure $ {p=35 \ {\text{Pa}}} $, discharge power $ {P=25 \ {\text{W}}} $. Brightness of dust particles in images is enhanced.
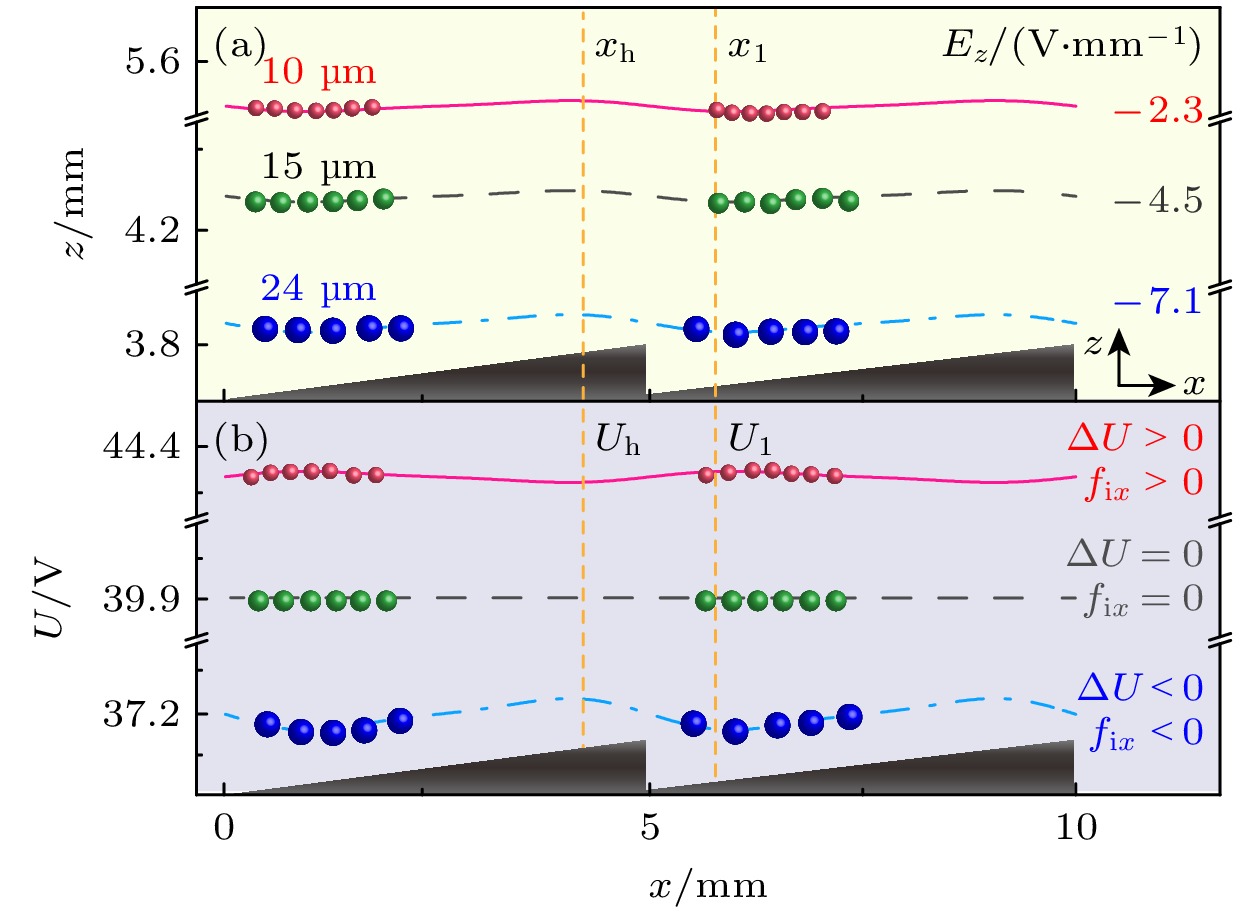
图 7 两个锯齿槽上表面的鞘层电场$ E_z $的等值线分布(a)以及在这些等值线上对应的电势变化(b). (a)中鞘层电场的竖直分量$ E_z $的等值线呈现不对称性分布. 不同尺寸的尘埃颗粒沿不同的$ E_z $的等值线悬浮于鞘层中. (b)中的电势分布具有棘轮势特征. 因此, 不同尺寸的尘埃颗粒悬浮于鞘层不同的高度, 受到的棘轮势具有不同的特征, 进而使得其形成沿棘轮通道不一样的输运结果. 图中红、绿、蓝球分别表示直径为10、15和24 µm的尘埃颗粒. 放电气压$ {p=35 \ {\text{Pa}}} $, 功率$ {P=25 \ {\text{W}}} $
Figure 7. The contour distribution of the sheath electric field $ E_z $ on the surface of two sawteeth (a) and the corresponding potential variation along these contour curves (b). (a): The contour curves of the vertical component of the sheath electric field $ E_z $ show asymmetric distributions. Dust particles of different sizes are suspended along different contour curves within the sheath. (b): The potential distribution has the characteristic of a ratchet potential. Therefore, dust particles of different sizes are suspended at different heights within the sheath, experiencing ratchet potentials with different characteristics, which leads to distinct transport outcomes along the ratchet channel. The red, green and blue balls in the curves indicate dust particles with diameter of 10, 15 and 24 µm, respectively. Gas pressure $ {p=35 \ {\text{Pa}}} $, discharge power $ {P=25 \ {\text{W}}} $.
-
[1] Merlino R L, Goree J A 2004 Phys. Today 57 32
[2] Xiao Q M, Mao A H, He X L, Zou J T, Yang X Y, Sun M M, Li F, Tang P F, Zhou T C, Wang X G 2024 Plasma Sci. Technol. 26 085301
Google Scholar
[3] Langmuir I, Jones H A 1924 Science 59 380
Google Scholar
[4] Winter J 2004 Plasma Phys. Control. Fusion 46 B583
Google Scholar
[5] Morfill G E, Ivlev A V 2009 Rev. Mod. Phys. 81 1353
Google Scholar
[6] Shukla P K, Eliasson B 2009 Rev. Mod. Phys. 81 25
Google Scholar
[7] Yuan C X, Yao J F, Bogdanov D V, Bogdanov E A, Kudryavtsev A A, Zhou Z X 2019 Plasma Sources Sci. Technol. 28 095020
Google Scholar
[8] Wang J Q, Liu Y, Wang Y, Zhu W J, Zhang W W, Huang F 2021 IEEE Trans. Plasma Sci. 49 1694
Google Scholar
[9] Zhao Y Z, Liu S F, Kong W, Yang F 2024 Chin. Phys. B 33 065201
Google Scholar
[10] Chu J H, I L 1994 Phys. Rev. Lett. 72 4009
Google Scholar
[11] Joshi E, Pustylnik M Y, Thoma M H, Thomas H M, Schwabe M 2023 Phys. Rev. Res. 5 L012030
Google Scholar
[12] Du C R, Nosenko V, Thomas H M, Lin Y F, Morfill G E, Ivlev A V 2019 Phys. Rev. Lett. 123 185002
Google Scholar
[13] Huang D, Lu S Y, Murillo M S, Feng Y 2022 Phys. Rev. Res. 4 033064
Google Scholar
[14] Guan M, Chen Z D, Li M D, Liu Z M, Wang Y M, Yu M Y 2022 Chin. Phys. B 31 025201
Google Scholar
[15] Beckers J, Berndt J, Block D, Bonitz M, Bruggeman P J, Couëdel L, Delzanno G L, Feng Y, Gopalakrishnan R, Greiner F, Hartmann P, Horányi M, Kersten H, Knapek C A, Konopka U, Kortshagen U, Kostadinova E G, Kovačevié E, Krasheninnikov S I, Mann I, Mariotti D, Matthews L S, Melzer A, Mikikian M, Nosenko V, Pustylnik M Y, Ratynskaia S, Sankaran R M, Schneider V, Thimsen E J, Thomas E, Thomas H M, Tolias P, van de Kerkhof M 2023 Phys. Plasmas 30 120601
Google Scholar
[16] 林麦麦, 王明月, 蒋蕾 2023 72 035201
Google Scholar
Lin M M, Wang M Y, Jiang L 2023 Acta Phys. Sin. 72 035201
Google Scholar
[17] Wei L, Liu B, Wang F P, Zhang H, Duan W S 2021 Chin. Phys. B 30 035201
Google Scholar
[18] Mamun A A, Shukla P K, Morfill G E 2004 Phys. Rev. Lett. 92 095005
Google Scholar
[19] 黄渝峰, 贾文柱, 张莹莹, 宋远红 2024 73 085202
Google Scholar
Huang Y F, Jia W Z, Zhang Y Y, Song Y H 2024 Acta Phys. Sin. 73 085202
Google Scholar
[20] Melzer A, Schweigert V A, Piel A 1999 Phys. Rev. Lett. 83 3194
Google Scholar
[21] Ivlev A V, Konopka U, Morfill G, Joyce G 2003 Phys. Rev. E 68 026405
Google Scholar
[22] Hänggi P, Marchesoni F 2009 Rev. Mod. Phys. 81 387
Google Scholar
[23] Feynman R P, Leighton R B, Sands M 1963 The Feynman Lectures on Physics (Vol. I) (America: Addison-Wesley Publishing Company) p46
[24] Dupont N, Gabardos L, Arrouas F, Ombredane N, Billy J, Peaudecerf B, Guéry-Odelin D 2023 Phys. Rev. Lett. 131 133401
Google Scholar
[25] Fedorova Z, Dauer C, Sidorenko A, Eggert S, Kroha J, Linden S 2021 Phys. Rev. Res. 3 013260
Google Scholar
[26] Roeling E M, Germs W C, Smalbrugge B, Geluk E J, de Vries T, Janssen R A J, Kemerink M 2011 Nat. Mater. 10 51
Google Scholar
[27] Arzola A V, Volke-Sepúlveda K, Mateos J L 2011 Phys. Rev. Lett. 106 168104
Google Scholar
[28] He Y F, Ai B Q, Dai C X, Song C, Wang R Q, Sun W T, Liu F C, Feng Y 2020 Phys. Rev. Lett. 124 075001
Google Scholar
[29] Zhang S X, Wang S, Yao T Y, Tian M, Fan W L, Liu F C, He Y F 2024 Plasma Sources Sci. Technol. 33 055008
Google Scholar
[30] Wang S, Zhang N, Zhang S X, Tian M, Cai Y W, Fan W L, Liu F C, He Y F 2022 Chin. Phys. B 31 065202
Google Scholar
[31] Melzer A 2019 Physics of Dusty Plasma: An Introduction (Switzerland: Springer Nature Switzerland AG) p8
[32] Fortov V E, Ivlev A V, Khrapak S A, Khrapak A G, Morfill G E 2005 Phys. Rep. 421 1
Google Scholar
DownLoad:
Metrics
- Abstract views: 262
- PDF Downloads: 8
- Cited By: 0
